RBSE Solutions for Class 12 Maths Chapter 11 त्रिविमीय ज्यामिति Ex 11.2

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 11 त्रिविमीय ज्यामिति Ex 11.2 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 11 त्रिविमीय ज्यामिति Ex 11.2

प्रश्न 1.
दीड किदिक-कोसाइन \(\frac{12}{13}\), \(\frac{-3}{13}\), \(\frac{-4}{13} \); \(\frac{4}{13}\), \(\frac{12}{13}\), \(\frac{3}{13}\) ; \(\frac{3}{13}\), \(\frac{-4}{13}\), \(\frac{12}{13}\) वाली तीन रेखाएँ परस्पर लम्बवत् हैं।
हल:
हम जानते हैं कि यदि दो रेखाएँ लम्बवत् हैं तो
l₁₂ + m₁m₂ + n₁n₂ = 0

अत: AB ⊥ EF
अत: AB, CD, EF तीनों रेखाएँ परस्पर लम्बवत् हैं।

प्रश्न 2.
दर्शाइए कि बिन्दुओं (1, - 1, 2), (3, 4, - 2) से होकर जाने वाली रेखा बिन्दुओं (0, 3, 2) और (3, 5, 6) से जाने वाली रेखा पर लम्ब हैं।
हल:
माना कि प्रश्नानुसार बिन्दुः A(1,- 1, 2) एवं B(3, 4, - 2) हैं। अतः बिन्दु A(1, - 1, 2) एवं B(3, 4, - 2) से होकर जाने वाली रेखा के दिक्-अनुपात 3 - 1, 4 + 1, - 2 - 2 या 2, 5, - 4 होंगे।
इसी प्रकार माना कि प्रश्नानुसार C(0, 3, 2) एवं D(3, 5, 6) हैं । अतः बिन्दु C(0, 3, 2) और D(3, 5, 6) से होकर जाने वाली रेखा के दिक्अनुपात 3 - 0, 5 - 3, 6 - 2 या 3, 2, 4 होंगे। अब यदि AB ⊥ CD तो
a₁a₂ + b₁b₂ + c₁c₂ = 0
अतः 2 × 3 + 5 × 2 + (-4) × 4 = 6 + 10 - 16 = 0
अतः प्रश्नानुसार दिए बिन्दुओं से होकर जाने वाली रेखाएँ अर्थात् AB रेखा CD पर लम्ब है।

प्रश्न 3.
दर्शाइए कि बिन्दुओं (4, 7, 8), (2, 3, 4) से होकर जाने वाली रेखा बिन्दुओं (- 1, - 2, 1), (1, 2,5) से जाने वाली रेखा के समान्तर है।
हल:
माना कि प्रश्नानुसार बिन्दु A(4, 7, 8) तथा B(2, 3, 4) हैं। अतः बिन्दु
A(4, 7, 8), B(2, 3, 4) से होकर जाने वाली रेखा AB के दिक्अनुपात 2 - 4, 3 - 7, 4 - 8 अर्थात् - 2, -4,-4 या 1, 2,2 होंगे। इसी प्रकार माना कि प्रश्नानुसार C(-1,-2, 1) तथा D(1, 2, 5) हैं।
अतः बिन्दु C(-1, -2, 1) और D(1, 2, 5) से होकर जाने वाली रेखा CD के दिक्-अनुपात 1 - (-1), 2 - (-2), 5 1 या 2, 4, 4 या 1, 2, 2 होंगे।
हम जानते हैं कि दो रेखाएँ समान्तर होंगी यदि = \(\frac{a_1}{a}=\frac{b_1}{b}=\frac{c_1}{c}\)
यहाँ पर AB और CD दोनों के दिक्-अनुपात 1, 2, 2 हैं।
अतः AB तथा CD आपस में समान्तर हैं।

प्रश्न 4.
बिन्दु (1, 2, 3) से गुजरने वाली रेखा का समीकरण ज्ञात कीजिए जो सदिश 3î + 2ĵ - 2k̂ के समान्तर है।
हल:
स्थिति बिन्दु A(\(\vec{a}\)) से गुजरने वाली रेखा P जो सदिश (\(\vec{b}\)) के समान्तर हो, उसका समीकरण
\(\vec{r}=\vec{a}+\lambda \vec{b}\)
यहाँ पर \(\vec{a}\) = î + 2ĵ + 3k̂
और \(\vec{b}\) = 3î + 2ĵ - 2k̂
अभीष्ट रेखा AP का समीकरण
\(\vec{r}\) = (î + 2ĵ + 3k̂) + λ(3î + 2ĵ - 2k̂)
जहाँ λ एक वास्तविक संख्या है।

प्रश्न 5.
बिन्दु जिसकी स्थिति सदिश 2î - ĵ + 4k̂ से गुजरने व सदिश î + 2ĵ + 4k की दिशा में जाने वाली रेखा का सदिश व कार्तीय रूपों में समीकरण ज्ञात कीजिए।
हल:
(i) बिन्दु \(\vec{a}\) से गुजरने वाली रेखा, जो सदिश 6 की दिशा में है, का समीकरण
\(\vec{r}=\vec{a}+\lambda \vec{b}\)
यहाँ \(\vec{a}\) = 2î - ĵ + 4k̂
और \(\vec{b}\) = î + 2ĵ - k̂
∴ अभीष्ट रेखा का समीकरण .
\(\vec{r}\) = (2î - ĵ + 4k̂) + λ(î + 2ĵ - k̂)
यही रेखा का सदिश रूप है।

(ii) बिन्दु (x₁, y₁, z₁) से गुजरने वाली रेखा, जिसके दिक्-अनुपात a, b, c हैं, का समीकरण
\(\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\)
यहाँ पर बिन्दु \(\vec{a}\) = 2î - ĵ + 4k̂ या (2 - 1, 4) हैं।
\(\vec{b}\) = î + 2ĵ - k̂
∴ रेखा के दिक्-अनुपात 1, 2, - 1 हैं।
∴ अभीष्ट रेखा का समीकरण
\(\frac{x-2}{1}=\frac{y+1}{2}=\frac{z-4}{-1}\)
यही रेखा का कार्तीय रूप है।

प्रश्न 6.
उस रेखा का कार्तीय समीकरण ज्ञात कीजिए जो बिन्दु (-2, 4, - 5) से जाती है और \(\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+5}{6}\) के समान्तर है।
हल:
वह रेखा जो बिन्दु (x₁, y₁, z₁) से गुजरती है और उसके दिक्-अनुपात a, b, c हों, तो उसका समीकरण
\(\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\)
यहाँ पर रेखा (-2, 4, - 5) से गुजरती है तथा \(\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+5}{6}\) के समान्तर है।
अतएव रेखा के दिक्-अनुपात = 3, 5, 6
अभीष्ट रेखा का समीकरण

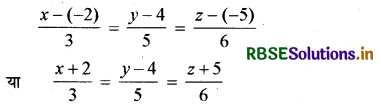
प्रश्न 7.
एक रेखा का कातीय समीकरण \(\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}\) है। इसका सदिश समीकरण ज्ञात कीजिए।
हल:
प्रश्नानुसार रेखा रखा \(\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}\) का कार्तीय समीकरण है जो बिन्दु (5, -4, 6) से होकर जाती है।
अर्थात् \(\vec{a}\) = 5î - 4ĵ + 6k̂
दी हुई रेखा के दिक्-अनुपात 3, 7, 2 हैं।
अतः \(\vec{b}\) = 3î + 7ĵ + 2k̂
∴ अभीष्ट रेखा का सदिश समीकरण
\(\vec{r}=\vec{a}+\lambda \vec{b}\)
या \(\vec{r}\) = 5î - 4ĵ + 6k̂ + λ(3î + 7ĵ + 2k̂)

प्रश्न 8.
मूल बिन्दु और (5, -2, 3) से जाने वाली रेखा का सदिश तथा कार्तीय रूपों में समीकरण ज्ञात कीजिए।
हल:
रेखा मूल बिन्दु व (5, - 2, 3) से गुजरती है .
∴ \(\vec{a}\) = 0î + 0ĵ + 0k̂ = \(\vec{0}\)
रेखा के दिक्-अनुपात = x₂ - x₁, y₂ - y₁, z₂ - z₁
या 5 - 0, - 2 - 0, 3 - 0
या 5, - 2, 3 हैं।

(i) रेखा का सदिश समीकरण
\(\vec{a}\) = \(\vec{0}\), \(\vec{b}\) = 5î - 2ĵ + 3k̂
अभीष्ट रेखा का सदिश समीकरण
\(\vec{a}=\vec{a}+\lambda \vec{b}\)
या \(\vec{r}\) = \(\vec{0}\) + λ(5î - 2ĵ + 3k̂)
या \(\vec{r}\) = λ(5î - 2ĵ + 3k̂)

(ii) रेखा बिन्दु O(0, 0, 0) से गुजरती है तथा इसके दिक्-अनुपात 5, - 2, 3 हैं।
अत: रेखा का कार्तीय समीकरण

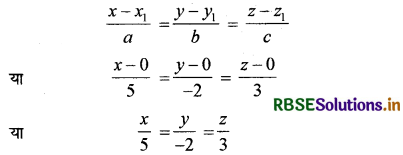
प्रश्न 9.
बिन्दुओं (3, - 2, - 5) और (3, - 2, 6) से गुजरने वाली रेखा का सदिश तथा कार्तीय रूपों में समीकरण को ज्ञात कीजिए।
हल:
(i) रेखा बिन्दु A(3, - 2, -5) और B(3, - 2, 6) से गुजरती है
∴ \(\vec{a}\) = 3î - 2ĵ - 5k̂
AB के दिक्-अनुपात = x₂ - x₁, y₂ - y₁, z₂ - z₁
या 3 - 3, - 2 + 2, 6 + 5
या 0, 0, 11 हैं।
∴ \(\vec{b}\) = 0.î + 0.ĵ + 11k̂ = 11k̂
AB का सदिश समीकरण
\(\vec{r}=\vec{a}+\lambda \vec{b}\)
= 3î - 2ĵ - 5k̂ + λ(11k̂)
या \(\vec{r}\) = 3î - 2ĵ - 5k̂ + 11λk̂

(ii) रेखा बिन्दु A(3, - 2, -5) तथा (3, - 2, 6) से गुजरती है
अतः इसके दिक्-अनुपात = 3-3, - 2 + 2, 6 +5 या 0, 0, 11
∴ रेखा AB का कार्तीय समीकरण
\(\frac{x-3}{0}=\frac{y+2}{0}=\frac{z+5}{11}\)

प्रश्न 10.
निम्नलिखित रेखा युग्मों के बीच का कोण ज्ञात कीजिए:
(i) \(\vec{r}\) = 2î - 5ĵ + k̂ + λ(3î + 2ĵ + 6k̂)
\(\vec{r}\) = 7î - 6k̂ + µ (î + 2ĵ + 2k̂)
हल:
पहली रेखा = 2î - 5ĵ + k̂ + λ(3î + 2ĵ + 6k̂)
सदिश \(\vec{b}_1\) = 3î + 2ĵ + 6k̂ दिशा में है।
दूसरी रेखा \(\vec{r}\) = 7î - 6k̂ + µ (î + 2ĵ + 2k̂)
सदिश \(\vec{b}_2\) = î + 2ĵ + 2k̂ की दिशा में हैं।
माना कि दोनों रेखाओं के बीच कोण θ है अतः

(ii) \(\vec{r}\) = 3î + ĵ - 2k̂ + λ(î - ĵ - 2k̂) और
\(\vec{r} \)= 2î - ĵ - 56k̂ + µ (3î - 5ĵ - 4k̂)
हल:
पहली रेखा \(\vec{r} \) = 3î + ĵ - 2k̂ + λ(î - ĵ - 2k̂)
\(\vec{b}_1\) = î - ĵ - 2k̂ दिशा में है।
दूसरी रेखा \(\vec{r} \) = 2î - ĵ - 56k̂ + µ (3î - 5ĵ - 4k̂)
सदिश \(\vec{b}_2\) = 3î - 5ĵ - 4k̂ की दिशा में हैं।
माना कि दोनों रेखाओं के बीच का कोण है अतः

प्रश्न 11.
निम्नलिखित रेखा युग्मों के बीच का कोण ज्ञात कीजिए:
(i) \(\frac{x-2}{2}=\frac{y-1}{5}=\frac{z+3}{-3}\) और \(\frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4}\)
हल:
(i) पहली रेखा \(\frac{x-2}{2}=\frac{y-1}{5}=\frac{z+3}{-3}\) के लिए दिक्अनुपात = 2, 5, - 3
तथा दूसरी रेखा \(\frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4}\) के दिक्अनुपात = - 1, 8, 4
हम जानते हैं कि वे दो रेखाएँ जिनके दिक्-अनुपात a₁, b₁, c₁ और a₂, b₂, c₂ हैं, के बीच का कोण θ हो, तो.

(ii) \(\frac{x}{2}=\frac{y}{2}=\frac{z}{1}\) और \(\frac{x-5}{4}=\frac{y-2}{1}=\frac{z-3}{8}\)
हल:
पहली रेखा \(\frac{x}{2}=\frac{y}{2}=\frac{z}{1}\) के दिक्-अनुपात = 2, 2, 1
तथा दूसरी रेखा \(\frac{x-5}{4}=\frac{y-2}{1}=\frac{z-3}{8}\) के दिक्-अनुपात
यहाँ a₁ = 2, b₁ = 2, c₁ = 1 तथा a₂ = 4, b₂ = 1,c₂ = 8 .
हम जानते हैं कि यदि दी हुई रेखाओं के बीच कोण θ हो तो

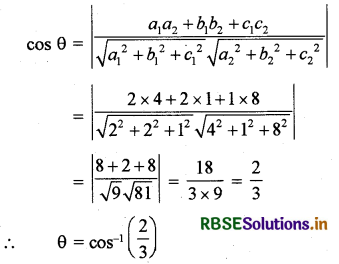
प्रश्न 12.
p का मान ज्ञात कीजिए ताकि रेखाएँ \(\frac{1-x}{3}=\frac{7 y-14}{2 p}=\frac{z-3}{2}\) आर \(\frac{7-7 x}{3 p}=\frac{y-5}{1}=\frac{6-z}{5}\) परस्पर लम्ब हों।
हल:
दी हुई रेखाओं को मानक रूप में रखने पर

प्रश्न 13.
दिखाइए कि रेखाएँ \(\frac{x-5}{7}=\frac{y+2}{-5}=\frac{z}{1}\) और \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) परस्पर लम्ब हों।
हल:
पहली रेखा \(\frac{x-5}{7}=\frac{y+2}{-5}=\frac{z}{1}\) दिक्-अनुपात = 7, -5, 1
तथा दूसरी रेखा \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) के दिक्-अनुपात = 1, 2, 3
अर्थात् माना कि
a₁ = 7, b₁ = - 5, c₁ = 1
तथा a₂ = 1, b₂ = 2, c₂ = 3
अतः दी हुई रेखाएँ परस्पर लम्ब होंगी यदि
a₁a₂ + b₁b₂ + c₁c₂ = 0
अर्थात् a₁a₂ + b₁b₂ + c₁c₂ = 7 × 1 + (-5) × 2 + 1 × 3
= 7 - 10 + 3 = 0
अतः दी हुई रेखाएँ परस्पर लम्ब हैं।

प्रश्न 14.
रेखाओं \(\vec{r}\) = (î + 2ĵ + k̂) + λ(î - ĵ + k̂) और \(\vec{r}\) =(2î - ĵ - k̂) + μ(2î + ĵ + 2k̂) के बीच की न्यूनतम दूरी ज्ञात कीजिए।
अथवा
दी गयी रेखाओं के बीच की न्यूनतम दूरी ज्ञात कीजिए।
\(\vec{r}\) = (1 + λ)î + (2 - λ)ĵ + (λ + 1)k̂
\(\vec{r}\) = (2î - ĵ - k̂) + μ(2î + ĵ + 2k̂)
हल:
हम जानते हैं कि रेखाओं
\(\vec{r}=\vec{a}_1+\lambda b_1\) और \(\vec{r}=\vec{a}_2+\lambda b_2\)
न्यूनतम दूरी

प्रश्न 15.
रेखाओं \(\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}\) और \(\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}\) के बीच की न्यूनतम दूरी ज्ञात कीजिए।
हल:
हम जानते हैं कि रेखाओं

प्रश्न 16.
रेखाएँ, जिनके सदिश समीकरण निम्नलिखित हैं, के बीच की न्यूनतम दूरी ज्ञात कीजिए।
\(\vec{r}\) = (î + 2ĵ + 3k̂) + λ(î - 3ĵ + 2k̂)
\(\vec{r}\) = (4î + 5ĵ + 6k̂) + μ(2î + 3ĵ + k̂)
अथवा
दी गयी रेखाओं के बीच की न्यूनतम दूरी ज्ञात कीजिए
\(\vec{r}\) = (î + 2ĵ + 3k̂) + λ(î - 3ĵ + 2k̂)
\(\vec{r}\) = (4 + 2μ)î + (5 + 3μ)ĵ + (6 + μ)k̂
हल:
रेखाएँ \(\vec{r}\) = \(\vec{a}_1+\lambda \vec{b}_1\) और \(\vec{r}\) = \(\vec{a}_2+\mu \vec{b}_2\)
से प्रश्नानुसार दी गई रेखाओं से तुलना करने पर

प्रश्न 17.
रेखाएँ, जिनकी सदिश समीकरण निम्नलिखित हैं, के बीच की न्यूनतम दूरी ज्ञात कीजिए :
\(\vec{r}\) = (1 - t)î + (t - 2)ĵ + (3 - 2t)k̂ और
\(\vec{r}\) = (s + 1)î + (2s - 1)ĵ - (2s + 1)k
हल:
प्रश्नानुसार पहली रेखा का समीकरण ।
\(\vec{r}\) = (1 - t)î + (t - 2)ĵ + (3 - 2t)k̂
= î - 2ĵ + 3k̂ + t(- î + ĵ - 2k̂)
\(\vec{r}=\vec{a}_1+\lambda \vec{b}_1\) से इसकी तुलना करने पर
\(\vec{a}_1\) = î - 2ĵ + 3k̂ तथा \(\vec{b}_1\) = - î + ĵ - 2k̂
प्रश्नानुसार दूसरी रेखा
\(\vec{r}\) = (s + 1)î + (2s - 1)ĵ - (2s + 1)k̂
या \(\vec{r}\) = î - ĵ - k̂ + s(î + 2ĵ - 2k̂)
\(\vec{r}=\vec{a}_2+\mu \vec{b}_2\) से इसकी तुलना करने पर