RBSE Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry Ex 11.2
Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry Ex 11.2 Textbook Exercise Questions and Answers.
Rajasthan Board RBSE Solutions for Class 12 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 12. Students can also read RBSE Class 12 Maths Important Questions for exam preparation. Students can also go through RBSE Class 12 Maths Notes to understand and remember the concepts easily.
RBSE Class 12 Maths Solutions Chapter 11 Three Dimensional Geometry Ex 11.2
Question 1.
Show that the three lines with direction cosines
\(\frac{12}{13}, \frac{-3}{13}, \frac{-4}{13} ; \frac{4}{13}, \frac{12}{13}, \frac{3}{13} ; \frac{3}{13}, \frac{-4}{13}, \frac{12}{13}\)
are mutually perpendicular.
Answer:
The direction-cosines l1, m1, n1 and l2 m2, n2 respectively of the lines are perpendicular if
l1l2 + m1m2 + n1n2 = 0.
(i) Direction cosines are
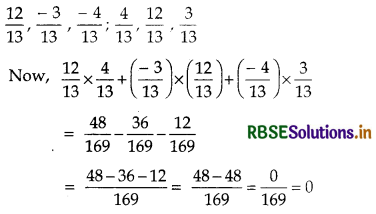
Hence, the lines are mutually perpendicular.

(ii) Direction cosines are
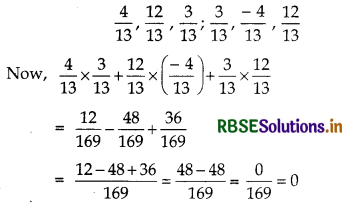
Hence, the lines are mutually perpendicular.
(ii) Direction cosines are
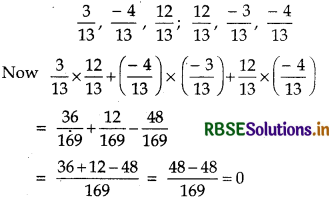
Hence, the lines are mutually perpendicular.
Hence proved.
Question 2.
Show that the line through the points (1, -1, 2), (3, 4, - 2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Answer:
Direction ratios of the line AB passing through
pointsA(1, - 1, 2) and B(3, 4, - 2) are 3 - 1, 4 + 1, - 2 - 2 or 2, 5, - 4.
Direction ratios of the line CD passing through points C(0, 3, 2) and D(3, 5, 6) are 3 - 0, 5 - 3, 6 - 2 or 3, 2, 4.
If AB ⊥ CD, then a1a2 + b1b2 + c1c2 = 0
Now, 2 × 3 + 5 × 2 + (- 4) × 4
= 6 + 10 - 16 = 16 - 16 = 0
So, AB ⊥ CD.
Hence proved.
Question 3.
Show that the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (- 1, - 2, 1), (1, 2, 5).
Answer:
Here, the direction ratios of line AB passing through points A(4, 7, 8), B(2, 3,4) are 2 - 4, 3 - 7, 4 - 8 or - 2, - 4, - 4 and the direction ratios of line CD passing through points C(- 1, - 2, 1), D(1, 2, 5) are 1 - (- 1), 2 - (- 2), 5 - 1 or 2, 4, 4.
Two lines are parallel it \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Here, direction ratios of both AB and CD are 2, 4, 4.
\(\left(\frac{-2}{2}=\frac{-4}{4}=\frac{-4}{4}=-1\right)\)
Hence, AB || CD.
Hence proved.

Question 4.
Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector 3î - 2ĵ - 2k̂.
Answer:
Equation of line AP which passes through point with position vector, A(\(\vec{a}\)) and is parallel to vector \(\vec{b}\) is
\(\vec{r} = \vec{a}+\lambda \vec{b}\)
Here, \(\vec{a}\) = î + 2ĵ + 3k̂
and \(\vec{b}\) = 3î + 2ĵ - 2k̂
Equation of the required line is
\(\vec{r}\) = (î + 2ĵ + 3k̂) + λ(3î + 2ĵ - 2k̂)
Question 5.
Find the equation of the line in vector and in cartesian form that passes through the point with position vector 2î - ĵ + 4k̂ and is in the direction î + 2ĵ - k̂.
Answer:
Equation of the line passing through the points \(\vec{a}\) and in the direction of \(\vec{b}\) is \(\vec{r}=\vec{a}+\lambda \vec{b}\)
Here \(\vec{a}\) = 2î - ĵ + 4k̂ and \(\vec{b}\) = î + 2ĵ - k̂
∴ Equation of the required line is
\(\vec{r}\) = (2î - ĵ + 4k̂) + λ(î + 2ĵ - k̂) ....... (1)
where λ is constant.
Cartesian form:

Question 6.
Find the cartesian equation of the line which passes through the point (- 2, 4, - 5) and parallel to the line given by
\(\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}\)
Answer:
Suppose, the line passes through point (x1, y1, z1) line and its direction ratios are a, b, c then equation of the line is:
\(\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\)
Here, the line passes through (- 2, 4, - 5) and is parallel to the line
\(\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}\)
Hence, the direction-ratios of the line are 3, 5, 6.
Thus, the equation of the required line is
\(\frac{x+2}{3}=\frac{y-4}{5}=\frac{z+5}{6}\)

Question 7.
The cartesian equation of a line is \(\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}\). Write its vector form.
Answer:
Line \(\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}\) passes through point (5, - 4, 6)
∴ \(\vec{a}\) = 5î - 4ĵ + 6k̂
Direction ratios of the given line are 3, 7, 2.
∴ \(\vec{b}\) = 3î + 7ĵ + 2k̂
Hence, the equation of the required line is
\(\vec{r}=\vec{a}+\lambda \vec{b}\)
or \(\vec{r}\) = (5î - 4ĵ + 6k̂) + λ(3î + 7ĵ + 2k̂)
Question 8.
Find the vector and the cartesian equations of the lines that passes through the origin and (5, -2, 3).
Answer:
Position vector of origin O(0, 0, 0) is \(\vec{a} = \vec{0}\) and position vector of point (5, -2, 3) is \(\vec{b}\) = 5î - 2ĵ + 3k̂
∴ Equation of the line passing through points \(\vec{a}\) and \(\vec{b}\) is
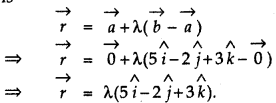
(ii) The line passes through point O(0, 0, 0) and its direction ratios are 5, -2, 3.
∴ Cartesian equation of the line is
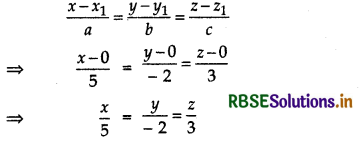
Question 9.
Find the vector and the cartesian equations of the line that passes through the points (3, -2, -5) and (3, -2, 6).
Answer:
Suppose, the line passes through the points
A(3, - 2, - 5) and B(3, - 2, 6).
Then, position vector of point A(3, -2, -5)
\(\vec{a}\) = 3î - 2ĵ - 5k̂
and the position vector of point B(3, -2,6)
\(\vec{b}\) = 3î - 2ĵ + 6k̂
(i) Vector equation of line AB.
\(\vec{r} = \vec{a}+\lambda(\vec{b}-\vec{a})\)
\(\vec{r}\) = 3î - 2ĵ - 5k̂ + λ[(3î - 2ĵ + 6k̂) - (3î - 2ĵ - 5k̂)]
\(\vec{r}\) = 3î - 2ĵ - 5k̂ + λ(3î - 3î - 2ĵ + 2ĵ + 6k̂ + 5k̂)
\(\vec{r}\) = 3î - 2ĵ - 5k̂ + (11λ)k̂
(ii) The line passes through points A(3, - 2, - 5) and B(3, - 2, 6).
So, cartesian equation of line AB is
\(\frac{x-3}{3-3}=\frac{y+2}{-2+2}=\frac{z+5}{6+5}\)
⇒ \(\frac{x-3}{0}=\frac{y+2}{0}=\frac{z+5}{11}\)

Question 10.
Find the angle between the following pairs of lines:
(i) r = 2î - 5ĵ + k̂ + λ(3î + 2ĵ + 6k̂) and
r = 7î - 6k̂ + μ(î + 2ĵ + 2k̂)
Answer:
(ii) r = 3î + ĵ - 2k̂ + λ(î - ĵ - 2k̂) and
r = 2î - ĵ - 56k̂ + μ(3î - ĵ - 4k̂)
Answer:
Here, first line is
\(\vec{r}\) = 2î - 5ĵ + k̂ + λ(3î + 2ĵ + 6k̂) is in the direction of vector \(\overrightarrow{b_1}\) = 3î + 2ĵ + 6k̂.
Second line \(\vec{r}\) = 7î - 6k̂ + μ(î + 2ĵ + 2k̂) is in the direction of vector \(\overrightarrow{b_2}\) = î + 2ĵ + 2k̂.
If θ is the angle between the lines, then
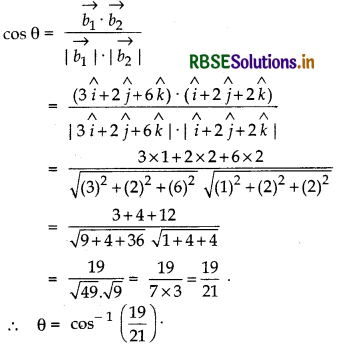
(ii) Here, first line is
\(\vec{r}\) = 3î + ĵ - 2k̂ + λ(î - ĵ + 2k̂)
vector \(\overrightarrow{b_1}\) = î - ĵ - 2k̂
Second line is \(\vec{r}\) = 2î - ĵ - 56k̂ + μ(3î - 5ĵ - 4k̂)
vector \(\overrightarrow{b_2}\) = 3î - 5ĵ - 4k̂
If θ is the angle between the lines, then
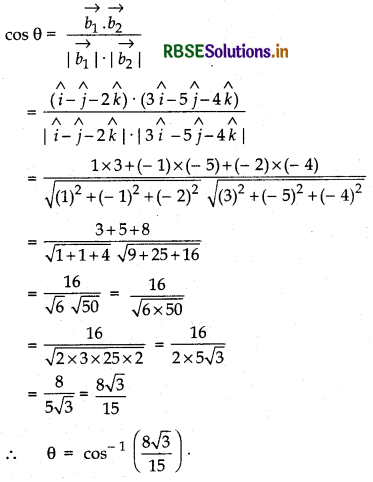

Question 11.
Find the angle between the following pair of lines:
(i) \(\frac{x-2}{2}=\frac{y-1}{5}=\frac{z+3}{-3}\) and \(\frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4}\)
Answer:
Direction ratios of line
\(\frac{x-2}{2}=\frac{y-1}{5}=\frac{z+3}{-3}\) are 2, 5, - 3
and direction ratios of line.
\(\frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4}\) are - 1, 8, 4
If θ is the angle between two lines with direction ratios a1, b1, c1 and a2, b2, c2 then

(ii) \(\frac{x}{2}=\frac{y}{2}=\frac{z}{1}\) and \(\frac{x-5}{4}=\frac{y-2}{1}=\frac{z-3}{8}\)
Answer:
Direction ratios of line
\(\frac{x}{2}=\frac{y}{2}=\frac{z}{1}\) are 2, 2, 1 and direction ratios of line \(\frac{x-5}{4}=\frac{y-2}{1}=\frac{z-3}{8}\) are 4, 1, 8
∴ a1 = 2, b1 = 2, c1 = 1
a2 = 4, b2 = 1, c2 = 8
If θ is the angle between two lines, then
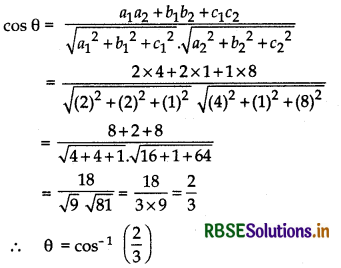
Question 12.
Find the values of p so that the lines
\(\frac{1-x}{3}=\frac{7 y-14}{2 p}=\frac{z-3}{2}\)
and \(\frac{7-7 x}{3 p}=\frac{y-5}{1}=\frac{6-z}{5}\) are at right angles.
Answer:
The standard form of the given lines are:


Question 13.
Show that the lines \(\frac{x-5}{7}=\frac{y+2}{-5}=\frac{z}{1}\) and \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) are perpendicular to each other.
Answer:
Direction ratios of line
\(\frac{x-5}{7}=\frac{y+2}{-5}=\frac{z}{1}\) are 7, - 5, 2
and direction ratios of line \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) are 1, 2, 3
Now, a1 = 7, b1 = - 5, c1 = 1
a2 = 1, b2 = 2, c2 = 3
The lines will be perpendicular to each other, if
a1a2 + b1b2 + c1c2 =0
Now, a1a2 + b1b2 + c1c2
= 7 × 1 + (- 5) × 2 + 1 × 3
= 7 - 10 + 3 = 10 - 10 = 0
Thus, the lines are perpendicular to each other. Ans.
Question 14
Find the shortest distance between the lines
\(\vec{r}\) = (î + 2ĵ + k̂) + λ (î - ĵ + k̂)
and \(\vec{r}\) = 2î - ĵ - k̂ + µ(2î + ĵ + 2k̂)
Answer:
Shortest distance between the lines \(\vec{r}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1}\) and \(\vec{r}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}\) is


Question 15.
Find the shortest distance between the lines.
\(\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}\) and \(\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}\)
Answer:
shortest distance between the lines

Question 16.
Find the shortest distance between the lines whose vector equations are
\(\vec{r}\) = (î + 2ĵ + 3k̂) + λ(î - 3ĵ + 2k̂)
and \(\vec{r}\) = 4î + 5ĵ + 6k̂+ µ(2î + 3ĵ + k̂).
Answer:


Question 17.
Find the shortest distance between the lines whose vector equations are:
\(\vec{r}\) = (1 - t) î + (t - 2)ĵ + (3 - 2t)k̂
and \(\vec{r}\) = (s + 1)î + (2s - 1)ĵ - (2s + 1)k̂
Answer:
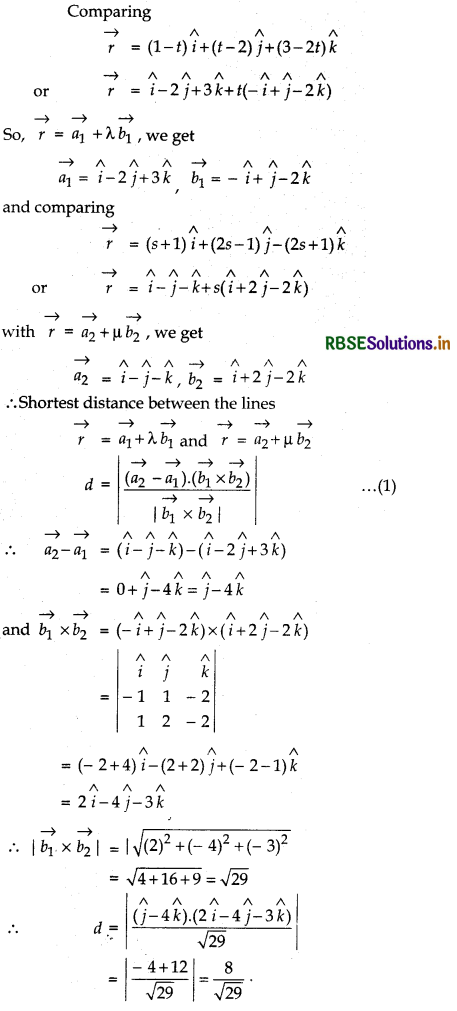

- RBSE Class 12 Maths Notes Chapter 13 Probability
- RBSE Class 12 Maths Notes Chapter 12 Linear Programming
- RBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry
- RBSE Class 12 Maths Notes Chapter 10 Vector Algebra
- RBSE Class 12 Maths Notes Chapter 9 Differential Equations
- RBSE Class 12 Maths Notes Chapter 8 Application of Integrals
- RBSE Class 12 Maths Notes Chapter 7 Integrals
- RBSE Class 12 Maths Notes Chapter 6 Application of Derivatives
- RBSE Class 12 Maths Notes Chapter 5 Continuity and Differentiability
- RBSE Class 12 Maths Notes Chapter 4 Determinants
- RBSE Class 12 Maths Notes Chapter 3 Matrices