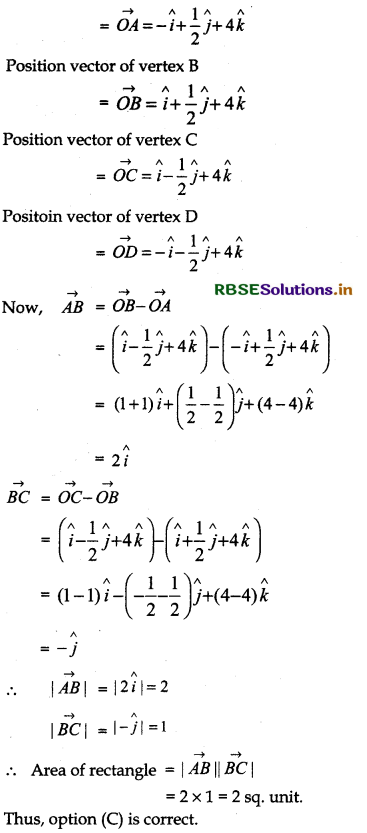RBSE Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.4

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.4 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 10 Vector Algebra Ex 10.4

Question 1.
Find |\(\vec{a} \times \vec{b}\)|, if \(\vec{a}\) = î - 7ĵ + k̂ and \(\vec{b}\) = 3î - 2ĵ + 2k̂
Answer:

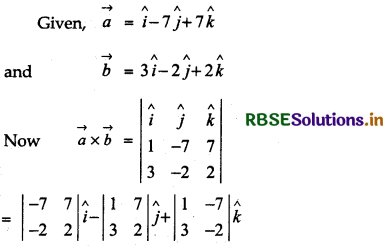
= [- 14 - (- 2) × 7]î - [1 × 2 - 3 × 7] + [1 × (- 2) - 3 (- 7)]
= [- 14 + 14)î - (2 - 21)ĵ + (- 2 + 21)k̂
= 0î + 19ĵ + 19k̂= 19ĵ + 19k̂
Now, |\(\vec{a} \times \vec{b}\)| = |19ĵ + 19k̂| = \(\sqrt{19^2+19^2}\)
= \(\sqrt{361+361}\) = \(\sqrt{722}\) = 19√2

Question 2.
Find a unit vector perpendicular to each of the vector \(\vec{a}+\vec{b}\) and \(\vec{a}-\vec{b}\), where \(\vec{a}\) = 3î + 2ĵ + 2k̂ and \(\vec{b}\) = î + 2ĵ - 2k̂.
Answer:
Given:

∴ Unit vector in the perpendicular direction of (\(\vec{a} + \vec{b}\)) and (\(\vec{a} - \vec{b}\)) is:

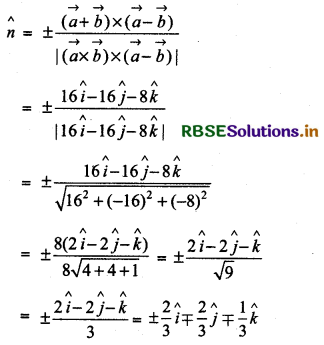
Question 3.
If a unit vector \(\vec{a}\) makes angles \(\frac{\pi}{3}\) with î, \(\frac{\pi}{4}\) with ĵ and an acute angle θ with k̂, then find θ and hence, the components of \(\vec{a}\).
Answer:

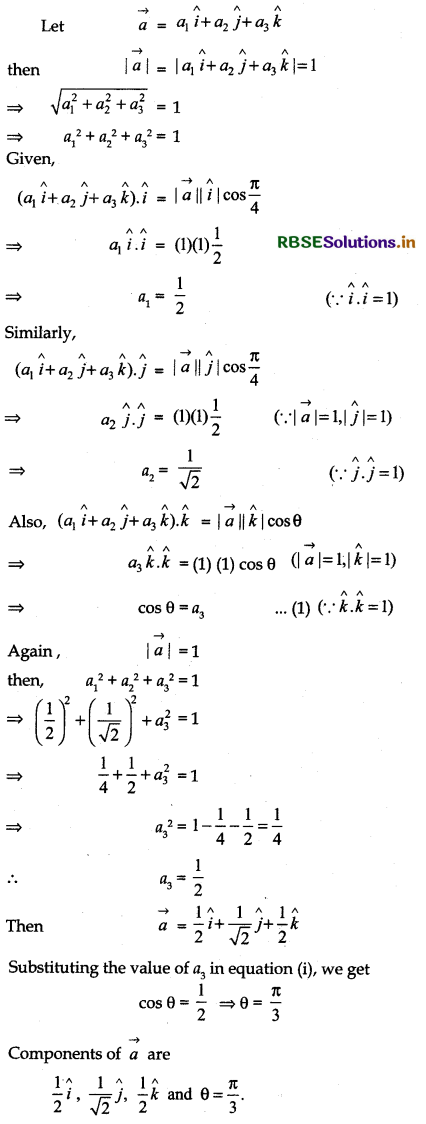
Question 4.
Show that
\((\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})=2(\vec{a} \times \vec{b})\)
Answer:

Question 5.
Find λ and μ if
(2î + 6ĵ + 27k̂) × (î + λĵ + μk̂) = 0
Answer:

Question 6.
Given that \(\vec{a} \cdot \vec{b}\) = 0 and \(\vec{a} \times \vec{b}\) = 0. What can you conclude about the vectors \(\vec{a}\) and \(\vec{b}\)?
Answer:

Question 7.
Let the vectors \(\vec{a}, \vec{b}, \vec{c}\) be given as a₁î + a₂ĵ + a₃k̂, b₁î + b₂ĵ + b₃k̂, c₁î + c₂ĵ + c₃k̂. Then show that
\(\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}\)
Answer:

Question 8.
If either \(\vec{a} =\overrightarrow{0}\) or \(\vec{b}\) = 0, then \(\vec{a} \times \vec{b}=\overrightarrow{0}\) is the converse true? Justify your answer with an example.
Answer:

Thus, the converse is not true.

Question 9.
Find the area of the triangle with vertices A (1, 1, 2), B(2, 3, 5) and C (1, 5, 5).
Answer
Let O be the origin. Then w.r.t. O
Position vector of point A
\(\overrightarrow{O A}\) = î + ĵ + 2k̂
Position vector of point B
\(\overrightarrow{O B}\) = 2î + 3ĵ + 5k̂
Position vector of point C
\(\overrightarrow{O C}\) = î + 5ĵ + 5k̂

Question 10.
Find the area of the parallelogram whose adjacent sides are determined by the vectors
\(\vec{a}\) = î - ĵ + 3k̂ and \(\vec{b}\) = 2î - 7ĵ + k̂.
Answer:
Given, adjacent sides of the parallelogram are:

Question 11.
Let the vectors \(\vec{a}\) and \(\vec{b}\) be such that |\(\vec{a}\)| = 3 and |\(\vec{b}\)| = \(\frac{\sqrt{2}}{3}\) then \(\vec{a} \times \vec{b}\) is a unit vector, if the angle between \(\vec{a}\) and \(\vec{b}\) is:
(A) π/6
(B) π/4
(C) π/3
(D) π/2
Answer:

Thus, option (B) is correct.

Question 12.
Area of a rectangle having vertices A, B, C and D with position vectors
- î + ĵ + 4k̂, î + \(\frac{1}{2}\)ĵ + 4k̂, î - \(\frac{1}{2}\)ĵ + 4k̂ and - î - \(\frac{1}{2}\)ĵ + 4k̂, respectively is:
(A) \(\frac{1}{2}\)
(B) 1
(C) 2
(D) 4
Answer:
Let O be the Origin, then w.r.t. O
Position vector of vertex A