RBSE Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.3

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.3 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 10 Vector Algebra Ex 10.3

Question 1.
Find the angle between two vectors \(\vec{a}\) and \(\vec{b}\) with magnitudes √3 and 2, respectively having \(\vec{a} \cdot \vec{b}\) = √6.
Answer:
Let angle between \(\vec{a}\) and \(\vec{a}\) is θ, then

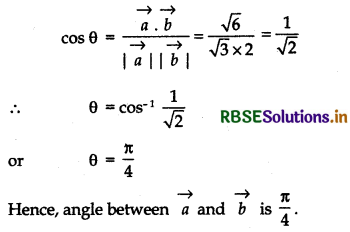
Question 2.
Find the angle between the vectors î - 2ĵ + 3k̂ and 3î - 2ĵ + k̂
Answer:

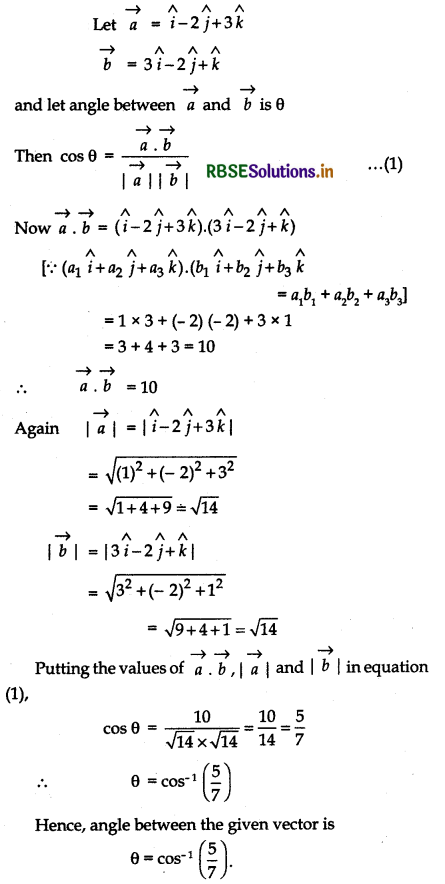
Question 3.
Find the projection of the vector î - ĵ on the vector î - ĵ.
Answer:
Let \(\vec{a}\) = î - ĵ and \(\vec{b}\) = î + ĵ
Then, projection of the vector \(\vec{b}\) = î + ĵ on the vector \(\vec{b}\) = î + ĵ is,

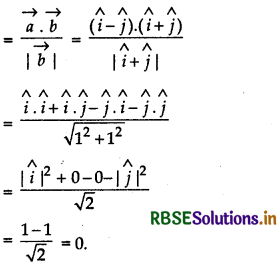
Hence, projection of the vector î - ĵ on the vector î + ĵ is 0.

Question 4.
Find the projection of the vector î + 3ĵ + 7k̂ on the vector 7î - ĵ + 8k̂.
Answer:
Let \(\vec{a}\) = î + 3ĵ + 7k̂
and \(\vec{b}\) = 7î - ĵ + 8k̂
Then, projection of the vector \(\vec{a}\) on the vector \(\vec{b}\) is

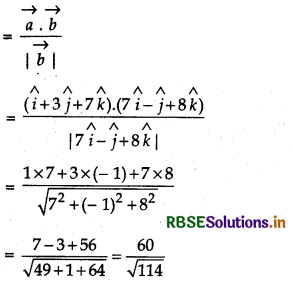
Hence, projection of the vector î + 3ĵ + 7k̂ on the vector 7î - ĵ + 8k̂ is \(\frac{60}{\sqrt{114}}\).

Question 5.
Show that each of the given three vectors is a unit vector:
\(\frac{1}{7}\)(2î + 3ĵ + 6k̂), \(\frac{1}{7}\)(3î - 6ĵ + 2k̂), \(\frac{1}{7}\)(6î + 2ĵ - 3k̂)
Also, show that they are mutually perpendicular to each other.
Answer:


Thus \(\vec{c}\) and \(\vec{a}\) are mutually perpendicular.
Hence, vectors \(\vec{a}, \vec{b}\) and \(\vec{c}\) are mutually perpendicular to each other.

Question 6.
Find |\(\vec{a}|\) and |\(\vec{b}\)| if \((\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})\) = 8 and |\(\vec{a}\)| = 8|\(\vec{b}\)|.
Answer:

Question 7.
Evaluate the product
\((3 \vec{a}-5 \vec{b}) \cdot(2 \vec{a}+7 \vec{b})\).
Answer:

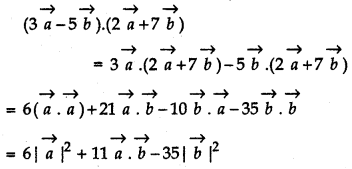
Question 8.
Find the magnitude of two vectors \(\vec{a}\) and \(\vec{b}\), having the same magnitude and such that the angle between them is 60° and their scalar product is \(\frac{1}{2}\).
Answer:

Question 9.
Find |\(\vec{x}\)|, if for a unit vector |\(\vec{a}\)|
\((\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})\) = 12.
Answer:

Question 10.
If \(\vec{a}\) = 2î + 2ĵ + 3k̂, \(\vec{b}\) = - î + 2ĵ + k̂ and \(\vec{c}\) = 3î + ĵ are such that \(\vec{a} + λ\vec{b}\) is perpendicular to \(\vec{c}\), then find the value of λ.
Answer:

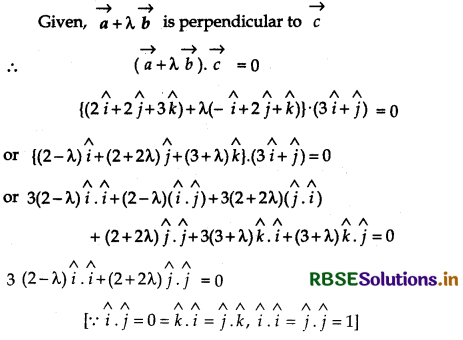
or 3(2 - λ) + (2 + 2λ) = 0
or 6 - 3λ + 2 + 2λ = 0
or 8 - λ =0
∴ λ = 8

Question 11.
Show that \(|\vec{a}| \vec{b}+|\vec{b}| \vec{a}\) is perpendicular to \(|\vec{a}| \vec{b}-|\vec{b}| \vec{a}\), for any two non zero vectors \(\vec{a}\) and \(\vec{b}\).
Answer:

Question 12.
If \(\vec{a} \cdot \vec{a}\) = 0 and \(\vec{a} \cdot \vec{b}\) = 0, then what can be concluded about the vector b ?
Answer:
Given,

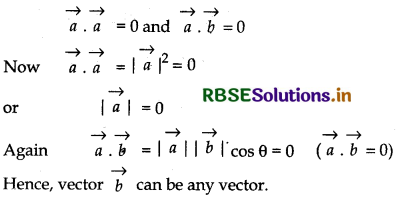
Question 13.
If \(\vec{a}, \vec{b}, \vec{c}\) are unit vectors such that \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\), find the value of \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}\).
Answer:
Given,

Question 14.
If either vector \(\vec{a}=\overrightarrow{0}\) or \(\vec{b}=\overrightarrow{0}\), then \(\vec{a} \cdot \vec{b}\) = 0. But the converse need not be true. Justify your answer with an example.
Answer:

Question 15.
II the vertices A, B, C of a triangle ABC are (1, 2, 3), (- 1, 0, 0), (0, 1, 2) respectively, then find ∠ABC.
[∠ABC is the angle between the vectors \(\overrightarrow{B A}\) and \(\overrightarrow{B C}\)].
Answer:
Let O be the origin. Then Position vector of point A.
\(\overrightarrow{O A}\) = î + 2ĵ + 3k̂
Position vector of point B
\(\overrightarrow{O B}\) = - î

Position vector of point C

Question 16.
Show that the points A(1, 2, 7), B(2, 6, 3) and C (3, 10, -1) are collinear.
Answer:
Let O be the origin. Then w.r.t. O
Position vector of point A

i.e., \(\overrightarrow{A B}\) and \(\overrightarrow{B C}\) represent the same vector. So, A, B and C are the points of this vector. Thus, A, B and C are collinear.
Hence Proved.

Question 17.
Show that the vectors 2î - ĵ + k̂, î - 3ĵ - 5k̂ and 3î - 4ĵ - 4k̂ form the vertices of a right angled triangle.
Answer:
Let A, B and C be the vertices of the triangle and O be the origin. Then w.r.t. O
Position vector of point A

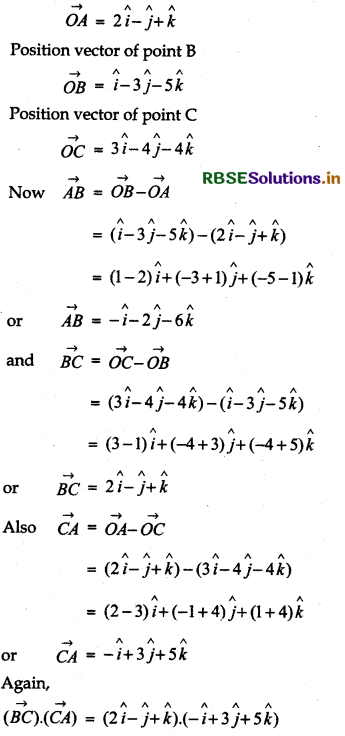
= 2 × (- 1) + (- 1) × 3 + 1 × 5
= - 2 - 3 + 5 = 0
[From \(\vec{a} \cdot \vec{b}\) = (a₁b₁ + a₂b₂ + a₃b₃]
So, BC ⊥ CA
∴ ∆ ABC is a right angled triangle.
Thus, the given points form a right-angled triangle.

Question 18.
If \(\vec{a}\) is a non-zero vector of magnitude ‘a’ and λ a non-zero scalar, then λ \(\vec{a}\) is unit vector if:
(A) λ = 1
(B) λ = - 1
(C) a = |λ|
(D) a = 1/|λ|
Answer:
λ\(\vec{a}\) ia an unit vector. Then

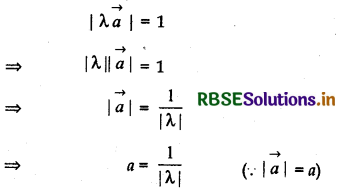
Thus, option (D) is correct.