RBSE Solutions for Class 12 Maths Chapter 1 Relations and Functions Ex 1.4

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 1 Relations and Functions Ex 1.4 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 1 Relations and Functions Ex 1.4

Question 1.
Determine whether or not each of the definition of * given below gives a binary operation. In the event that * is not a binary operation, give justification for this.
(i) On Z⁺, define * by a * b = a-b
Answer:
a*b = a - b, where a, b ∈ Z⁺, * is not binary operation.
Since, 3 - 2 = 1 ∈ Z⁺, but 2 - 3 = -1 ∉ Z⁺

(ii) On Z⁺, define * by a * b = ab
Answer:
Operation * is binary operation in Z⁺,
since 3*2 = 6 ∈ Z⁺, 2 × 3 = 6 ∈ Z⁺

(iii) On R, define * by a* b = ab²
Answer:
Operation * is binary operation in R,
since 3*4 = 3 × 4² = 48 ∈ R
and 4*3 = 4 × 32 = 3² = 36 ∈ R

(iv) On Z⁺, define * by a* b = |a - b|
Answer:
Operation * is a binary operation in Z+,
since a*b = |a - b|
2*3 = | 2 - 3 |
= | - 1 | = 1 ∈ Z⁺
and 3*2 = | 3 - 2 |
= | 1 | = 1 ∈ Z⁺.

(v) On Z⁺, define * by a* b = a
Answer:
Operation * is binary operation in Z⁺,
since 3*4 = 3 ∈ Z⁺
and 4*3 = 4 ∈ Z⁺

Question 2.
For each binary operation * defined below, determine whether * is binary, commutative or associative.
(i) On Z, define a * b = a - b
(ii) On Q, define a * b = ab + 1
(iii) On Q, define a * b = \(\frac{a b}{2}\)
(iv) On Z⁺, define a * b = 2^ab
(v) On Z⁺, define a * b = a^b
(vi) On R - {- 1}, define a * b = \(\frac{a}{b+1}\)
Answer:
Operation * is neither commutative nor associative,
since 3 - 2 = 1, 2 - 3 = - 1 ⇒ 3*2 ≠ 2*3
and (3*4)*5 = (3 -4)*5 = - 1 - 5 = - 6
(∵ According to definition )
and 3*(4*5) = 3*(4 - 5) = 3 * (- 1)
= 3 - (- 1) = 4
∴ (3*4)*5 ≠ 3*(4*5)

(ii) Operation * is commutative but not associative.
2*3 = 2.3 + 1 = 6 + 1 = 7,
3*2 = 3.2 + 1 = 6 + 1 = 7
⇒ 2*3 = 3*2
and (2*3)*4 = (2.3 + 1)*4
= 7*4 = 7 × 4 + 1 = 29
2*(3*4) = 2*(3.4 + 1)
= 2*(13) = 2.13 + 1 = 27
⇒ (2*3)*4 ≠ 2*(3*4)

(iii) In Q, binary operation * is defined by
a * b = \(\frac{a b}{2}\)

(a) a * b = \(\frac{a b}{2}\), b * a = \(\frac{b a}{2}\) = \(\frac{a b}{2}\)
∴ a * b = b * c
Thus, operation * is commutative.

(b)

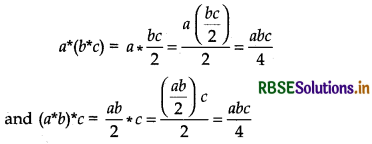
∴ a * (b * c) = (a * b) * a
∴ Operation * is associative.
Thus, operation * is commutative and associative.

(iv) Operation * on Z⁺ is defined by a*b = 2^ab
(a) ∴ a*b = 2ab, b*a = 2^ba = 2^ab
⇒ a*b = b*a
Thus, operation * is commutative.

(b) a*(b*c) = a*(2^bc) = 2^a.2bc
(a*b)*c = 2ab*c = 2^2ab . c
∴ a*(b*c) ≠ (a*b)*c
∴ Operation * is not associative.
Thus, operation * is commutative but not associative.

(v) Operation * on Z⁺ is defined by a*b = a^b
(a) a*b = a^b, b*a = b^a
∴ a*b ≠ b*a
So, operation * is not commutative.

(b) a*(b*c) = a*b^c = a^(bc)
(a*b)*c = a^b*c = (a^b)^c = a^bc
∴ (a*b)*c ≠ a*(b*c)
So, operation * is not associative.
Thus, operation * is neither commutative nor associative.

(vi) On R - {- 1} operation * is defined by
a*b = \(\frac{a}{b+1}\)

(a) a * b = \(\frac{a}{b+1}\), b * a = \(\frac{b}{a+1}\)
a * b ≠ b * a
So, operation * is not commutative.

(b)

So, operation is not associative.
Thus, operation * is neither commutative nor associative.

Question 3.
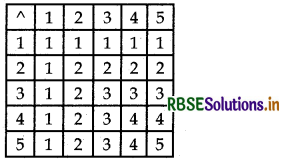
Consider the binary operation A on the set {1, 2, 3, 4, 5} defined by a ∧ b = min [a, b}. Write the operation table of the operation ∧.
Answer:
Table for ∧

Question 4.
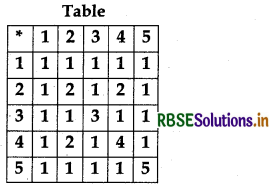
Consider a binary operation * on the set {1, 2, 3, 4, 5} given by the following multiplication table.
(i) Compute (2 * 3) * 4 and 2 * (3 * 4)
(ii) Is * commutative ?
(iii) Compute (2 * 3) * (4 * 5).
(Hint: Use the following table)

Answer:
(i) (2 * 3) * 4 = 1 * 4 = 1
(∵ 2 * 3 = 1)
2 * (3 * 4) = 2 * 1 = 1
(∵ 3 * 4 = 1)

(ii) 2 * 4 = 2, 4 * 2 = 2 ⇒ 2 * 4 = 4 * 2
Yes, * is commutative.

(iii) (2 * 3) * (4 * 5) = (1 * 1) = 1

Question 5.
Let *' be the binary operation on the set {1, 2, 3, 4, 5} defined by a*' b = H.C.F. of a and b. Is the operation *' same as the operation * defined in question 4 above ? Justify your answer.
Answer:
Given set is {1, 2, 3, 4, 5}
a*' b = H.C.F. of a and b. Table for *' is as follows :

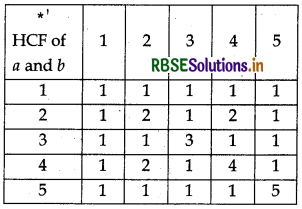
This table is same as given is question 4.
Thus, operation *' is same as operation * as given in Q. 4 above.

Question 6.
Let * be the binary operation on N given by a * b = L.C.M. of a and b. Find
(i) 5 * 7,20 * 16
(ii) Is * commutative ?
(iii) Is * associative ?
(iv) Find the identity of * in N.
(v) Which elements of N are invertible for the operation * ?
Answer:
(i) 5*7 = LCM of 5 and 7 = 35
20*16 = LCM of 20 and 16 = 80

(ii) Yes, operation * is commutative,
since a*b = LCM of a and b
or b*a = LCM of b and a
We know that LCM of a and b in set M of natural numbers = LCM of b and a
⇒ a*b = b*a
As 2*6 = LCM of 2 and 6
6*2 = LCM of 6 and 2 = 6
Thus, 2*6 = 6*2

(iii) Yes, * is associative,
since (a*b)*c = (LCM of a and b)*c
= LCM of a and c
And a*(b*c) = a*(LCM of b and c)
= LCM of a and b and c
∴ (a*b)*c = a*(b*c)
As (2*3)*4 = (LCM of 2 and 3 LCM)*4 = 6*4
= LCM of 6 and 4 = 12
2*(3*4) = 2*(LCM of 3 and 4)
= 2*12
= LCM of 2 and 12 = 12.
Thus, (2*3)*4 = 2*(3*4)

(iv) * Identity element of * operation is 1.
∵ 1*a = a* 1 = a, [Since, LCM of 1 and a = a]

(v) N*N → N, binary operation * is defined as a*b = LCM of a, b
If a = 1, b = 1, a*b = 1
⇒ 1*1 = 1
⇒ 1 is invertible for * operation.

Question 7.
Is * defined on the set {1, 2, 3, 4, 5} by a*b = L.C.M. of a and b a binary operation? Justify your answer.
Answer:
* is not a binary operation,
since 3*4 = LCM of 3 and 4
= 12 ∉ {1, 2, 3, 4, 5}

Question 8.
Let * be the binary operation on N defined by a * b = H.C.F. of a and Is * commutative ? Is * associative ? Does there exists identity for this binary operation on N ?
Answer:
(i) Yes, * is commutative.
a*b = HCF of a and b
and b*a = HCF of b and a
∵ HCF of a and b = HCF of b and a

Example:
2*3 = HCF of 2 and 3 = 1
3*2 = HCF of 3 and 2 = 1
∴ 2*3 = 3*2

(ii) Yes * is associative, since
(a*b)*c = (HCF of a and b)*c
= HCF of a and b and c
= HCF of a, b, c
And a*(b*c) = a*(HCF of b and c)
= HCF of a and b and c
= HCF of a, b and c
∴ (a*b)*c = a*(b*c)

Example: (2*3)*4 = (HCF of 2 and 3)*4
= HCF of 1 and 4
= 1
2*(3*4) = 2*(HCF of 3 and 4)
= HCF of 2 and 1
= 1
∴ (2*3)*4 = 2*(3*4)

(iii) There is no identity element in N for binary operation *.
Thus, identity element does not exist for * operation in N.

Question 9.
Let * be a binary operation on the set Q of rational numbers as follows:
(i) a * b = a - b
(ii) a * b = a² + b²
(iii) a * b = a + ab
(iv) a * b = (a - b)²
Find which of the binary operations are commutative and which are associative.
Answer:
(i) Operation * is not commutative,
since a*b = a - b and b * a = b - a
∵ a - b ≠ b - a ⇒ a*b ≠ b*a

Example:
2 - 3 = - 1 and 3 - 2 = 1 ⇒ 2 - 3 ≠ 3 - 2
and operation * is not associative,
since (a*b)*c = (a - b)*c = a - b - c
and a*(b*c) = a*(b - c) = a - (b - c)
= a - b + c
∵ a - b - c ≠ a - b + c
⇒ (a*b)*c ≠ a*(b*c)

Example:
(3*4)*5 = (3 - 4)*5
= - 1*5 = - 1 - 5 = - 6
and 3*(4*5) = 3*(4 - 5)
= 3*(- 1)
= 3 - (- 1) = 3 + 1 = 4
∴ (3*4)*5 ≠ 3*(4*5)

(ii) Operation * is commutative, since
a*b = a² + b² and b*a = b² + a²
∴ a² + b² = b² + a² ⇒ a*b = b*a
Example:
2*3 = 2² + 3² = 4 + 9 = 13
3*2 = 3² + 2² = 9 + 4 = 13
∴ 2*3 =3*2
a*b = a² + b² is not associative,
since (a*b)*c = (a² + b²)*c
= (a² + b²)² + c²
= a⁴ + b⁴ + 2a²b² + c²
and a*(b*c) = a*(b² + c²) = a² + (b² + c²)²
= a² + b⁴ + c⁴ + 2b²c²
∵ a⁴ + b⁴ + 2a²b² + c⁴ ≠ a² + b⁴ + c⁴ + 2b²c²
⇒ (a*b)*c ≠ a* (b*c)
So * is not associative.

Example:
(2*3) * 4 = (2² + 3²)*4 = 13*4
= 13² + 4²
= 169 + 16 = 185
and 2*(3*4) = 2*(3² + 4²)
= 2*(9 + 16)
= 2*25
= 2² + 25²
= 4 + 625 = 629
∴ 185 ≠ 629 ⇒ (2*3)*4 ≠ 2*(3*4)

(iii) Operation * is neither commutative nor associative,
since a*b = a + ab
and b*a = b + ba = b + ab
∵ a + ab ≠ b + ab ⇒ a*b ≠ b*a

Example:
2*3 = 2 + 2.3 = 2 + 6 = 8
and 3*2 = 3 + 3.2 = 3 + 6 = 9
8 ≠ 9 ⇒ 2*3 ≠ 3*2
For associativity
(a*b)*c = (a + ab)*c
= a + ab + (a + ab)c
= a + ab + ac + abc
and a*(b*c) = a*(b + bc)
= a + a(b + bc)
= a + ab + abc
∵ a + ab + ac + abc ≠ a + ab + abc
⇒ (a*b)*c ≠ a*(b*c)
Thus, * is not associative.

Example:
(2*3) *4 = (2 + 2 3)*4
= 8*4 = 8 + 8.4 = 40
and 2*(3*4) = 2*(3 + 3.4) = 2*15
= 2 + 215 = 32
40 ≠ 32
⇒ (2*3)*4 ≠ 2*(3*4)

(iv) a*b = (a - b)², operation * is commutative.
Since (a*b) = (a - b)² = (b - a)² = b*a
⇒ (a*b) = b*a

Example:
(2*3) = (2 - 3)² = (- 1)² = 1
(3*2) = (3 - 2)² = 1² = 1
⇒ 2*3 = 3*2
Operation * is not associative.
(a*b)*c = (a - b)²*c
= (a² + b² - 2ab)*c
= (a² + b² - 2ab - c)²
and a*(b*c) = a*(b - c)²
= a*(b² + c² - 2 bc)
= (a - b² - c² + 2bc)²
∵ (a² + b² - 2ab - c)² ≠ (a - b² - c² + 2bc)²
⇒ (a*b)*c ≠ a*(b*c)

Example:
(2*3)*4 = (2 - 3)²*4
= 1*4 = (1 - 4)² = 9
and 2*(3*4) = 2*(3 - 4)² = 2*1
= (2 - 1)² = 1
⇒ (2*3)*4 ≠ 2*(3*4)
∴ Operation * is not associative.

(v) a*b = \(\frac{a^{b}}{4}\)
Operation * is not commutative and associative.
Since a*b = \(\frac{a^{b}}{4}\) and b*a = \(\frac{b^{a}}{4}\)
∵ \(\frac{a^{b}}{4}\) ≠ \(\frac{b^{a}}{4}\)
⇒ a*b ≠ b*a
Thus, operation * is not commutative.

Example:

Thus, operation * is not associative.

Example:

(vi) * is neither commutative nor associative.
Since a*b = ab² and b*a = ba²
⇒ a*b ≠ b*a

Example: 2*3 = 2.3² = 18
3*2 = 3.2² = 12
⇒ 2*3 * 3*2
For associativity
(a*b)*c = (ab²)*c
= (ab²)c² = ab²c²
And a*(b*c) = a*(bc²) = a (bc²)² = ab²c⁴
∵ ab²c² ≠ ab²c⁴
⇒ (a*b)*c ≠ a*(b*c)
Thus, * is not associative.

Example:
(2*3)*4 = (2.3²)*4 = 18*4
= (18.4²) = 18 × 16 = 288
And 2*(3*4) = 2*(3.4²) = 2*48 = 2.48²
= 2 × 2304 = 4608
∵ 288 ≠ 4608
⇒ (2*3)*4 ≠ 2*(3*4)

Question 10.
Find which of the operations given above in Q. 9, has identity.
Answer:
(i) a*b = a - b
If, e is identity element for *, then
a*e = a - e ≠ a and e*a = e - a ≠ a
∴ a - e ≠ e - a ⇒ a*e ≠ e*a ≠ a
Thus, identity element e does not exist, i.e., it is not an identity element of any element.

(ii) a*b = a² + b²
Let e be identity element, then
∴ a*e = a² + e² ≠ a and e*a = e² + a² ≠ a
∴ a*e = e*a ≠ a
Thus, e does not exist, i.e., no element has identity element.

(iii) a*b = a + ab
Let e is an identity element, then
a*e = a + ae ≠ a, e*a = e + ea ≠ a
∴ a*e ≠ e*a ≠ a
Thus, identity element does not exist.

(iv) a*b = (a - b)²
Let e be an identity element, then
a*e = (a - e)² ≠ a and e*a = (e - a)² ≠ a
∴ a*e = e*a = a
Thus, identity element e does not exists.

(v)

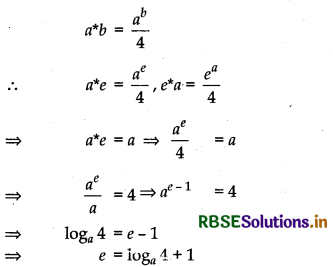
Thus, identity element e does not exists.

(vi) a*b = ab²
Let e be an identity element, then
a*e = ae² ≠ a, e*a = ea² ≠ a
∴ a*e ≠ e*a ≠ a.
Thus identity element e does not exist.

Question 11.
Let A = N × N and * be the binary operation on A defined by
(a, b)* (c,d) = (a + c,b + d)
Show that * is commutative and associative. Find the identity element for * on A, if any.
Answer:
(i) If (a, b) ∈ A and (c, d) ∈ A then a, b, c, d ∈ N
(a, b)*(c, d) = (a + c, b + d) ∈ A
[∵ (a + c) ∈ N, (b × d) ∈ N
(a, b)*(c, d) = (a + c, b + d)
= (c + a, d + b)
[∵ a + c = c + a and b + d = d + b]
= (c, d)*(a, b), (Commutative)
Again [(a, b)*(c, d)]*(e, f)
= (a + c, b + d)*(e,f)
= [(a + c) + e, (b + d) + f]
= [a + (c + d), b + (d + f)]
= (a, b)*(c + e, d +f)
= (a, b)*[(c, d)*(e,f)] (Associative)

(ii) (a, b)*(0, 0) = (a + 0, b + 0) = (a, b)
But (0, 0) ∉ A, since 0 ∉ N
Thus, in set A, for binary operation * no identity element exists.

Question 12.
State whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation * on a set N, a * a = d ∀ a ∈ N.
(ii) If * is a commutative binary operation on N, then a* (b* c) = (c*b)* a
Answer:
Here, binary operation * is defined on set
a*a = a, ∀ a ∈ N

(i) Here, for operation * only one element a is used, so this statement is false.

(ii) Operation * is commutative on set of real numbers i.e.,
b*c = c*b
⇒ (c*b)*a = (b*c)*a = a*(b*c)
∴ a*(b*c) = (c*b)*a
Thus, statement is true.

Question 13.
Consider a binary operation * on N defined as a * b = a³ + b³. Choose the correct answer.
(A) Is * both associative and commutative ?
(B) Is * commutative but not associative ?
(C) Is * associative but not commutative ?
(D) Is * neither commutative nor associative ?
Answer:
Here, binary operation * is defined on set N such that
a*b = a³ + b³ ∀ a, b ∈ N
= b³ + a³ = b*a
∴ a*b = b*a
Thus, operation * is commutative.
Again a*(b*c) = a*(b³ + c³)
= a³ + (b³ + c³)³
and (a*b)*c = (a³ + b³)*c
= (a³ + b³)³ + c³
Clearly, (a*b)*c ≠ a*(b*c)
Thus operation * is not associative.
∴ * is commutative but not associative.
Thus, option (B) is correct.