RBSE Solutions for Class 12 Maths Chapter 1 संबंध एवं फलन Ex 1.3

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 1 संबंध एवं फलन Ex 1.3 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 1 संबंध एवं फलन Ex 1.3

प्रश्न 1.
मान लीजिए कि f: {1, 3, 4} → {1, 2, 5} तथा g : {1, 2, 5} → {1, 3},f= {(1, 2), (3, 5), (4, 1)} तथा g = {(1, 3), (2, 3), (5, 1)} द्वारा प्रदत्त हैं। gof ज्ञात कीजिए।
हल:
{1, 3, 4} → {1, 2, 5}, g : {1, 2, 5} → {1, 3}
f = {(1, 2), (3, 5), (4, 1)},
g = {(1, 3), (2, 3), (5, 1)}
⇒ f(1) = 2, f(3) = 5, f(4) = 1
और g(1) = 3, g(2) = 3, g(5) = 1
gof(1) = g [(1)] = g(2) = 3
gof(3) = g [f(3)] = g(5) = 1
gof(4) = g [f(4)] = g(1) = 3
gof = {(1, 3), (3, 1), (4, 3)}

प्रश्न 2.
मान लीजिए कि f, g तथा h, R से R तक दिए फलन हैं। सिद्ध कीजिए कि
(f + g) oh = foh + goh
(f. g) oh = (foh) . (goh)
हल:
प्रश्नानुसार, f, g, h, R → R में फलन हैं।
(i) ∴ {f + g) oh} (x) = (f + g) [h(x)]
= f [h(x)] + g [h(x)]
= (foh) (x) + (goh) (x)
= (foh + goh) (x)
= ( + g) oh = foh + goh

(ii) {f . g) oh} (x) = (f . g) [h(x)]
= f [h(x)] . g[h(x)]
= (foh) (x) . (goh) (x)
= {{foh) (goh)} (x)
∴ (f. g) oh = (foh) . (goh)

प्रश्न 3.
gof तथा fog ज्ञात कीजिए, यदि ।
(i) (x) = x तथा g(x) = |5x - 2|
(ii) (x) = 8x³ तथा g(x) = x^1/3
हल:
(i) f(x) = |x| तथा g(x) = |5x - 2|
gof (x) = g[f(x)] = g (x) = |5|x|- 2 = {|5x - 2|, यदि x ≥ 0 |- 5x - 2|, यदि x < 0
fog (x) = f [g(x)] = f (|5x - 2|) = ||5x - 2|| = |5x - 2| [∵ ||Z|| = Z]]

(ii) f(x) = 8x³ तथा g(x) = x^1/3
gof (x) = g [f(x)] = g (8x³) = (8x³)^1/3 = 2x
fog (x) = f [g(x)]
= f(x^1/3) = 8.(x^1/3)³ = 8x

प्रश्न 4.
यदि f(x) = \(\frac{(4 x+3)}{(6 x-4)}\). x ≠ \(\frac{2}{3}\), तो सिद्ध कीजिए कि सभी x ≠ \(\frac{2}{3}\) के लिए fof(x) = x है। f का प्रतिलोम फलन क्या हैं
हल:

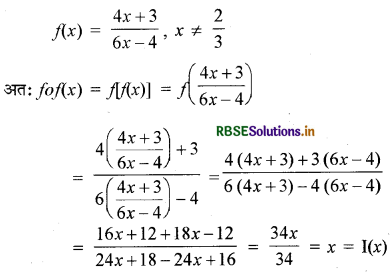
तत्समक फलन
fof = I = f = f-1
अर्थात् f(x) = y = f^-1(y) = x
पुनः y = f (x) = \(\frac{4 x+3}{6 x-4}\)
y(6x - 4) = 4x + 3
या 6xy - 4y= 4x + 3
या x (6y - 4)= 4y + 3
∴ x = \(\frac{4 y+3}{6 y-4}\)
अतः f^-1(y) = x = 1
f^-1(x) = \(\frac{4 x+3}{6 x-4}\) = f(x) ⇒ f^-1 = f

प्रश्न 5.
कारण सहित बतलाइए कि क्या निम्नलिखित फ्लनों के प्रतिलोम हैं :
(i) f: {1, 2, 3, 4} → {10} जहाँ
f = {(1, 10), (2, 10), (3, 10), (4, 10)}
(ii) g : {5, 6, 7, 8} → {1, 2, 3, 4} जहाँ
g = {(5, 4), (6, 3), (7, 4), (8, 2)}
(iii) h : {2, 3, 4, 5} → {7, 9, 11, 13} जहाँ
h = {(2, 7), (3, 9), (4, 11), (5, 13)}
हल:
(i) f: {1, 2, 3, 4} → {10} तथा
f = {(1, 10), (2, 10), (3, 10), (4, 10)} , 1, 2, 3, 4 सभी अवयवों का प्रतिबिम्ब 10 है।
∴ f एकैकी नहीं है।
⇒ f^-1 का अस्तित्व नहीं है।

(ii) g : {5, 6, 7, 8} → {1, 2, 3, 4} तथा
g = {(5, 4), (6, 7), (7, 4), (8, 2)} g में 5 व 7 का प्रतिबिम्ब 4 है।
g एकैकी नहीं है ⇒ g^-1 का अस्तित्व नहीं है।

(iii) h : {2, 3, 4, 5} → {7, 9, 11, 13} तथा ।
h = {(2, 7), (3, 9), (4, 11), (5, 13)} में 2, 3, 4 व 5 के प्रतिबिम्ब क्रमशः 7, 9, 11, 13 हैं तथा प्रत्येक अवयव का पूर्वप्रतिबिम्ब विद्यमान है।
⇒ h एकैकी तथा आच्छादक है।
⇒ h^-1 का अस्तित्व है।
अतः h^-1 = {(v, x) : (x, y) ∈ h}
h^-1 = {(7, 2), (9, 3), (11, 4), (13, 5)}

प्रश्न 6.
सिद्ध कीजिए कि f : [- 1, 1] → R, f(x) = 1 , द्वारा प्रदत्त फलन एकैकी है। फलन f : [- 1, 1] → (f का परिसर), का प्रतिलोम फलन ज्ञात कीजिए।
हल:
f: [- 1, 1] → R (दिया है)
f(x) = 2+ - 2
माना x₁, x₂ ∈ [- 1, 1] इस प्रकार है कि f (x₁) = f (x₂)
f(x₁) = f(x₂) ⇒ \(\frac{x_1}{x_1+2}=\frac{x_2}{x_2+2}\)
x₁ (x₂ + 2) = x₂ (x₁ + 2)
x₁x₂ + 2x₁ = x₁x₂ + 2x₂
2x₁ = 2x₂
x₁ = x₂
= f एकैकी है।

माना कि y = \(\frac{x}{x+2}\) ⇒ y (x + 2) = x
या x (y - 1) + 2y = 0
∴ x = \(\frac{2 y}{1-y}\)
दिया गया है x वास्तविक है।
अतः 1 - y ≠ 0 ⇒ y ≠ 1
अतः फलन का परिसर R = R - {1}
चूँकि फलन f : [-1, 1] ⇒ R - {1} में एकैकी आच्छादक है।
अतः फलन का प्रतिलोम विद्यमान होगा और f^-1(y) = x ⇔ f (x) = y
अब : f (x) = y

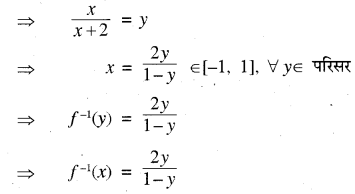
प्रश्न 7.
f(x) = 4x + 3 द्वारा प्रदत्त फलन f : R → R पर विचार कीजिए। सिद्ध कीजिए कि fव्युत्क्रमणीय है। f का प्रतिलोम फलन ज्ञात कीजिए।
हल:
f : R = R और f(x) = 4x + 3 माना x₁, x₂, ∈ R
इस प्रकार है कि f (x₁) = f (x₂)
∵ f(x₁) = (x₂) ⇒ 4x₁ + 3 = 4x₂ + 3
या 4x₁ = 4x₂ ⇒ x₁ = x₂
⇒ f एकैकी है
साथ ही माना कि y = 4x + 3 ∴ x = \(\frac{y-3}{4}\)
अब f(\(\frac{y-3}{4}\)) = 4. \(\frac{y-3}{4}\) + 3 = y - 3 + 3 = y
⇒ f (x) = y
अतः फलन आच्छादक है।
चूँकि फलन एकैकी आच्छादक है, अतः f^-1 विद्यमान होगा एवं
f^-1(y) = x = \(\frac{y-3}{4}\)
⇒ f^-1(x) = \(\frac{x-3}{4}\)

प्रश्न 8.
f(x) = x² + 4 द्वारा प्रदत्त फलन f: R₊ → [4, ∞) पर विचार कीजिए। सिद्ध कीजिए कि fव्युत्क्रमणीय है तथा का प्रतिलोम f^-1,f^-1(y) = \(\sqrt{y-4}\), द्वारा प्राप्त होता है, जहाँ R, सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है।
हल:
प्रश्नानुसार f R₊ → [4, ∞) जबकि f(x) = x² + 4
माना x₁, x₂, ∈ R. इस प्रकार है कि
f(x₁) = f (x₂)
∴ f (x₁) = f(x₂) = x₁² + 4 = x₂² + 4
⇒ x₁² = x₂² या x₁ = x₂ [:: x₁, x₂ ≥ 0]
⇒ f एकैकी है।
माना y ∈ f का परिसर, तब y = f (x)
⇒ y = x² + 4
⇒ x = y - 4 (∵ x ≥ 0)
x. तभी परिभाषित होगा जब y - 4 ≥ 0 या y ≥ 4
अतः f का परिसर = (4, 3) के प्रत्येक अवयव का पूर्व प्रतिबिम्ब R, (सहप्रान्त) में विद्यमान है। इसलिए / आच्छादक
∵ f एकैकी आच्छादक है इसलिए f व्युत्क्रमणीय है। तब
f (x) = y ⇔ f^-1(v) = x तथा f^-1 : [4, ∞] → R₊
f^-1(y) = \(\sqrt{y-4}\)
= f^-1(x) = \(\sqrt{x-4}\) ∀ x ∈ [4, ∞]

प्रश्न 9.
f(x) = 9x² + 6x - 5 द्वारा प्रदत्त फलन f: R₊ → [-5, ∞) पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा
f^-1(y) = \(\left(\frac{(\sqrt{y+6})-1}{3}\right)\) है।
हल:
प्रश्नानुसार f : R₊ → [-5, ∞) जबकि दिया है f(x) = 9x² + 6x - 5
माना कि y = 9x² + 6x - 5 = (3x + 1)² - 6
या y + 6 = (3x + 1)² या 3x + 1 = \(\sqrt{y-6}\) [∵ x ≥ 0]
∴ x = \(\frac{\sqrt{y+6}-1}{3}\) = g(y)

पुनः माना कि g : f का परिसर → R₊ इस प्रकार है कि

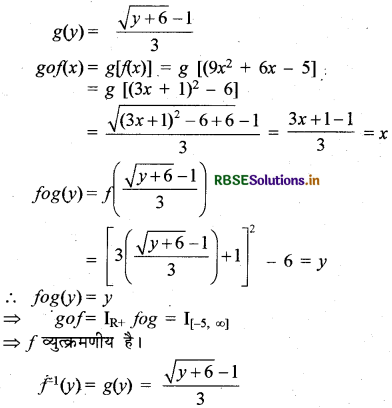
प्रश्न 10.
मान लीजिए कि f: x → Y एक व्युत्क्रमणीय फलन है। सिद्ध कीजिए कि f का प्रतिलोम फलन अद्वितीय (unique) है।
हल:
f: X → Y तथा f व्युत्क्रमणीय है।
∴ f एकैकी व आच्छादक है।
⇒ gof(x) = I_x fogy) = I_y

मान लीजिए कि f के दो प्रतिलोम g₁ और g₂ हैं।
fog₁(y) = I_y fog₂(y) = I_y
(fog₁) (y) = (fog₂) (y) = y
⇒ f[g₁ (y)] = f [(g₂ (v)]
⇒ g₁ (y) = g₂ (y) [∵ f एकैकी है।]
⇒ g₁ = g₂
∴ f का प्रतिलोम भी अद्वितीय है।

प्रश्न 11.
f: {1, 2, 3} → {a, b, c}, f(1) = a, f(2) = b तथा f(3) = c, द्वारा प्रदत्त फलन f पर विचार कीजिए। ज्ञात कीजिए और सिद्ध कीजिए कि (f^-1)^-1 = f है।
हल:
f : {1, 2, 3} → {a, b, c} इस प्रकार है कि
f(1) = a, f(2) = b, f(3) = c ⇒ f = {(1, a), (2, b), (3, c)} ⇒ f एकैकी आच्छादक है।
माना कि X = {1, 2, 3}, Y = {a, b, c}
∴ f: X → Y या f^-1 : Y → X,
f^-1(a) = 1, f^-1(b) = 2, f^-1(c) = 3.
f^-1 = {(a, 1), (b, 2), (c, 3)}
⇒ (f^-1)^-1 : X →Y
(f^-1)^-1(1) = a, (f^-1)^-1(2) = b, (f^-1)^-1(3) = c
⇒ (f^-1)^-1 = {(1, a), (2, b), (3, c)} = f
⇒ (f^-1)^-1 = f

प्रश्न 12.
मान लीजिए कि f: X → Y एक व्युत्क्रमणीय फलन है। सिद्ध कीजिए कि f^-1 का प्रतिलोम f है अर्थात् (f^-1)^-1 = f है।
हल:
f: x → Y व्युत्क्रमणीय है।
∴ f एकैकी तथा आच्छादक है। माना f का प्रतिलोम g : Y → x है।
⇒ g : Y → X भी एकैकी व आच्छादक है
gof(x) = I_x और fog(y) = I_y = g = f^-1
अतः f^-1o (f^-1)^-1 = I
अब fo [f^-1o (f^-1)^-1] = foI
या (fo f^-1) o (f^-1)^-1 = f [साहचर्यता]
Io (f^-1)^-1 = f
⇒ (f^-1)^-1 = f

प्रश्न 13.
यदि f : R → R, f(x) = (3 - x³)^1/3, द्वारा प्रदत्त है, तो fof(x) बराबर है
(A) x^1/3
(B) x³
(C) x
(D) (3 - x³)
हल:

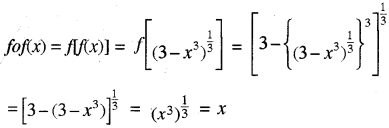
अतः सही विकल्प (C) है।

प्रश्न 14.
मान लीजिए कि f(x) = \(\frac{4 x}{3 x+4}\) द्वारा परिभाषित एक फलन f:R - {-\(\frac{4}{3}\)} → R है। 'का प्रतिलोम, अर्थात् प्रतिचित्र (map) g : परिसर f-> R - {-\(\frac{4}{3}\)}, निम्नलिखित में से किसके द्वारा प्राप्त होगा :
(A) g(y) = \(\frac{3 y}{3-4 y}\)
(B) g(y) = \(\frac{4 y}{4-3 y}\)
(C) g(y) = \(\frac{4 y}{3-4 y}\)
(D) g(y) = \(\frac{3 y}{4-3 y}\)
हल:
दिया गया है-y = f(x) = \(\frac{4 x}{3 x+4}\) ⇔ f^-1(y) = x
⇒ 3xy + 4y = 4x
⇒ 4y = 4x - 3xy
⇒ 4y = x (4 - 3y)
.या x = \(\frac{4 y}{4-3 y}\) ∴ f^-1(y) = \(\frac{4 y}{4-3 y}\)
अतः सही विकल्प (B) है।