RBSE Solutions for Class 12 Maths Chapter 1 Relations and Functions Ex 1.3

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 1 Relations and Functions Ex 1.3 Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 1 Relations and Functions Ex 1.3

Question 1.
Let f: {1, 3, 4} {1, 2, 5} and g : {1, 2, 5} → {1, 3} be given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof.
Answer:
According to question.
f = {(1, 2), (3, 5), (4, 1)}
and g = {1, 3), (2, 3), (5, 1)}
then f(1) = 2, f(3) = 5, f(4) = 1
and g(1) = 3, g(2) = 3, g(5) = 1
Now, (gof)(1) = g(f(1)) = g(2) = 3
(gof) (3) = g(f(3)) = g(5) = 1
(gof)(4) = g(f(4)) = g(1) = 3
Thus, gof = {(1, 3), (3, 1), (4, 3)}

Question 2.
Let f, g and h be functions from R to R. Show that:
(i) (f + g) oh = foh + goh
(ii) (f . g) oh = (foh).(goh)
Answer:
Given functions are f, g, h, R → R.
(i) ∴ (f + g)oh (x) = (f + g) (h(x))
= f(h(x)) + g(h(x))
= (foh)(x) + (goh)(x)
Thus (f + g)oh = foh + goh

(ii) (f.g)oh(x) = (f.g)(h(x))
= f(h(x)).g(h(x))
= {(foh)(x)}.{goh(x)}
= {(goh) > (goh)} (x)
Thus (f.g)oh = (foh).(goh)
Hence Proved.

Question 3.
Find gof and fog, if
(i) f(x) = |x| and g(x) = |5x - 2|
(ii) f(x) = 8x³ and g(x) = x^1/3
Answer:
(i) Given, f(x) = |x| and g(x) = | 5x - 2 |
Then gof(x) = g(f(x)) = g(|x|)
= |5| x |- 2
Now fog(x) = f(g(x)) = f(|5x - 2|)
= | | 5x - 2 | |

(ii) Given, f(x) = 8x³ and g(x) = x^1/3
then gof(x) = g(f(x)) = g( 8x³)
= (8x³)^1/3
= [(2x)³]^1/3
= 2x
Now fog(x) = f(g(x)) = f(x^1/3)
= 8(x^1/3)³ = 8x

Question 4.
If f(x) = \(\frac{(4 x+3)}{(6 x-4)}\), x ≠ \(\frac{2}{3}\), show that fof(x) = x, for all x ≠ \(\frac{2}{3}\). What is the inverse of f? 
Answer:

Note: We can find inverse of /in the following way, also.
Let y = \(\frac{4 x+3}{6 x-4}\)
⇒ 6xy - 4y = 4x + 3
⇒ x(6y - 4) = 4y + 3
⇒ x = \(\frac{4 y+3}{6 y-4}\)
= f(y) (By definition of function)
∴ x = f(y)
⇒ f^-1 (x) = y = \(\frac{4 x+3}{6 x-3}\)
∴ f^-1 (x) = \(\frac{4 x+3}{6 x-4}\)
Thus, f is inverse of itself.

Question 5.
State with reason whether following functions have inverse
(i) f: {1, 2, 3, 4} → {10} with
f = {(1, 10), (2, 10), (3, 10), (4, 10)}
Answer:
f = {1, 2, 3, 4} → {10}
where f = {(1, 10), (2, 10), (3, 10), (4, 10)}
Inverse, of function f does not exist since it is not one-one onto it is many-one onto.
f(1) = 10, f(2) = 10, f(3) = 10, f(4) = 10

(ii) g: {5, 6, 7, 8} → {1, 2, 3, 4} with
g = {(5, 4), (6, 3), (7, 4), (8, 2)}
Answer:
g = {5, 6, 7, 8} → {1, 2, 3, 4}
where g = {(5, 4), (6, 3), (7,4), (8, 2)}
Here, g(5) = 4, g(6) = 3, g(7) = 4, g(8) = 2
Function is not one-one onto.
It is many one into.
Element 1 of set {1, 2, 3, 4} is not image of any element of set {5, 6, 7, 8}.
Thus, function g is not one-one onto.
Thus, g will not have inverse function.

(iii) h : {2, 3, 4, 5} → {7, 9, 11, 13} with
h = {(2, 7), (3, 9), (4, 11), (5, 13)}
Answer:
h = {2,3, 4, 5} → {7, 9,11,13}
where h = {(2, 7), (3, 9), (4, 11), (5, 13)}
Here, h(2) = 7, h(3) = 9, h(4) = 11, h(5) = 13
Thus, each element of set {2, 3, 4, 5} has unique image in set {7, 9, 11, 13} and there is no element in set {7, 9,11,13}
which has no image of element of set {2,3,4,5}.
Thus, function h is one-one onto.
∴ Inverse of function h is
h^-1 = {(7, 2), (9, 3), (11, 4), (13, 5)}
where h^-1: {7, 9, 11, 13} → {2, 3, 4, 5}

Question 6.
Show that f: [- 1, 1] → R, given by f(x) = \(\frac{x}{(x+2)}\) is one-one. Find the inverse of the function f: [- 1, 1] → Range f.
(Hint: For y ∈ Range f, y = f(x) = \(\frac{x}{(x+2)}\), or some x in [- 1, 1], i.e., x = \(\frac{2 y}{1-y}\))
Answer:
Let x₁, x₂ ∈ [- 1, 1] then
f(x₁) = f(x₂) ⇒ \(\frac{x_{1}}{x_{1}+2}\) = \(\frac{x_{2}}{x_{2}+2}\)
⇒ x₁(x₂ + 2) = x₂(x₁ + 2)
⇒ x₁x₂ + 2x₁ = x₂x₁ + 2x₂
⇒ 2x₁ = 2x₂ ⇒ x₁ = x₂
Thus, function f: [- 1,1] → R is one-one.
Let y ∈ (range f) is any arbitrary element and y = f(x), where x ∈ [- 1, 1],
Then f(x) = y ⇒ \(\frac{x}{x+2}\) = y
⇒ y(x + 2) = x
⇒ yx + 2y = x
⇒ yx - x = - 2y
⇒ x(y - 1) = - 2y
⇒ x = \(\frac{-2 y}{y-1}\) ⇒ = \(\frac{2 y}{1-y}\), y ≠ 1 ...... (i)
Thus, range of f = R - {1}
Again x = \(\frac{2 y}{1-y}\), y ≠ 1

So, f is onto.
Since, f is one-one onto.
f:[- 1, 1] → R - {1}
Thus, f will be invertible.
Then fof^-1(x) = f(f^-1(x)) = x
⇒ \(\frac{f^{-1}(x)}{f^{-1}(x)+2}\) = x (by definition of f)
⇒ f^-1(x) = xf^-1 (x) + 2x
⇒ f^-1(x) - xf^-1(x) = 2x
⇒ (1 - x)f^-1(x) = 2x
⇒ f^-1(x) = \(\frac{2 x}{1-x}\)
Thus, inverse of f^-1: R - {1} → [-1, 1] is
⇒ f^-1(x) = \(\frac{2 x}{1-x}\) (∵ x ≠ 1)

Question 7.
Consider f: R → R given by f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.
Answer:
f(x) = 4x + 3 and f: R → R
Let x₁, x₂ ∈ R (domain), then
f(x₁) = f(x₂) ⇒ 4x₁ + 3 = 4x₂ + 3
⇒ 4x₁ = 4x₂ ⇒ x₁ = x₂
Thus, f is one-one.
Again, let y ∈ R (co-domain) is an arbitrary element then in set R (domain) x will be such element for which
f(x) = y
Now y = f(x) ⇒ y = 4x + 3
⇒ y - 3 = 4x ⇒ x = 6 R (domain)
⇒ f(x) = f\(\left(\frac{y-3}{4}\right)\) = 4\(\left(\frac{y-3}{4}\right)\) + 3
= y - 3 + 3 = y
f\(\left(\frac{y-3}{4}\right)\) = y ∈ R (co-domain)
∴ Function is onto.
∵ Function is one-one onto;
so, f is invertible.
Now, for inverse f^-1 of f
fof^-1 (x) = x
⇒ f(f^-1(x)) = x
⇒ 4(f^-1(x)) + 3 = x
⇒ 4 (f^-1(x)) = x - 3
⇒ f^-1(x) = \(\frac{x-3}{4}\)
Thus, inverse of f, f^-1(x): R → R is such that
f^-1(x) = \(\frac{x-3}{4}\)

Question 8.
Consider f: R₊ → [4, ∞) given by f(x) = x² + 4. Show that f is invertible with the inverse f^-1 of given by f^-1 (y) = \(\sqrt{y-4}\), where R₊ is the set of all non-negative real numbers. 
Answer:
Let x₁, x₂ ∈ R, then
f(x₁) = f(x₂) ⇒ x₁² + 4 = x₂² + 4
x₁² = x₂² ⇒ x₁ = x₂
Thus, f is one-one.
Again, let y ∈ [4, ∞) is an arbitrary element then x ∈ R₊ will be such element for which y = f(x)
Now y = f(x)
⇒ y = x² + 4
⇒ x² = y - 4
⇒ x = \(\sqrt{y-4}\), y ≥ 4
For each y ≥ 4, \(\sqrt{y-4}\) ∈ R₊
Now f(x) = f(\(\sqrt{y-4}\))
= (\(\sqrt{y-4}\))² + 4
= y - 4 + 4
= y (By definition of f)
∴ f(\(\sqrt{y-4}\)) = y
Thus, f is onto.
Now, f is one-one onto then it will be invertible.
Thus, f is invertible.
Now, for f^-1, inverse of f
fof^-1(x) = x
⇒ f(f^-1(x)) = x
⇒ [f^-1(x)]² + 4 = x (By definition of f)
⇒ (f^-1(x))² = x - 4
⇒ f^-1(x) = \(\sqrt{x-4}\)
⇒ f^-1(y) = \(\sqrt{y-4}\)
Note: f(\(\sqrt{y-4}\)) = y
∴ f^-1 = \(\sqrt{y-4}\)
Which is inverse function of f.

Question 9.
Consider f: R₊ → [- 5, ∞) given by f(x) = 9x² + 6x - 5.
Show that f is invertible with f^-1 (y) = \(\left(\frac{\sqrt{(y+6)}-1}{3}\right)\)
Answer:
Let x₁, x₂ ∈ R₊ then
f(x₁) = f(x₂)
9x₁² + 6x₁ - 5 = 9x₂² + 6x₂ - 5
⇒ 9x₁² + 6x + 1 - 6 = 9x₂² + 6x₂ + 1 - 6
⇒ (3x₁ + 1)² - 6 = (3x₂ + 1)² - 6
⇒ 3x₁ + 1 = 3x₂ + 1 [∵ x₁, x₂ ∈ R₊]
⇒ 3x₁ = 3x₂
⇒ x₁ = x₂
Thus, f is one-one.
Again, let y ∈ [- 5, ∞) is any arbitrary element then x e R+ will be such element for which y = f(x), then
y = f(x)
⇒ y = 9x² + 6x - 5
⇒ y = 9x² + 6x + 1 - 1 - 5
⇒ y = (3x + 1)² - 6
⇒ (3x + 1)² = y + 6

Thus, f is onto.
Since, f is one-one onto so f is invertible.
From (i), f^-1(y) = \(\left(\frac{\sqrt{y+6}-1}{3}\right)\)
or
fof^-1(x) = x (∵ f^-1, inverse of function f)
⇒ f(f^-1(x)) = x
⇒ 9(f^-1(x))² + 6f^-1(x) - 5 = x
⇒ 9(f^-1(x))² + 6f^-1(x) + 1 - 1 - 5 = x
⇒ (3f^-1(x) + 1)² = x + 6
⇒ 3f^-1(x) + 1 = \(\sqrt{x+6}\)
⇒ 3f^-1(x) = \(\sqrt{x+6}\) - 1
⇒ f^-1 (x) = \(\left(\frac{\sqrt{x+6}-1}{3}\right)\)
Thus f^-1 (y) = \(\left(\frac{\sqrt{(y+6)}-1}{3}\right)\)
where f^-1 (y), is inverse of f(y).
Hence Proved.

Question 10.
Let f: X → Y be an invertible function. Show that/has unique inverse. (Hint: Suppose^ andg2 are two inverses off. Then for all y ∈ Y, fog₁(y) = I_Y(y) = fog₂(y). Use one-one ness of f).
Answer:
Given that f: X → Y, is invertible so it will be one- one onto.
Let g₁, g₂ are two inverse of f.
then fog₁(y) = I_y(y) ......... (i)
and fog₂(y) = I_y(y) ......... (ii)
From (i) and (ii), we get
fog₁(y) = fog₂(y)
(Since, I_y(y) will be one not two )
⇒ f(g₁(y)) = f(g₂(y))
⇒ g₁(y) = g₂(y)
⇒ g₁ = g₂ [Since f is one-one]
Thus f(x₁) = f(x₂)
⇒ x₁ = x₂
i.e., inverse of f is unique.
Hence Proved.

Question 11.
Consider f: {1, 2, 3} → {a, b, c} given by f(1) = a, f(2) = b and f(3) = c. Find f^-1 and show that (f'^-1)^-1 = f.
Answer:
f: {1, 2, 3} → {a, b, c}, f(1) = a, f(2) = b, f(3) = c.
Writing function f in ordered pair form:
f = {(1, a), (2, b), (3, c)}
Clearly, each element of set {1, 2, 3} has distinct image in set {a, b, c} and there is no element in set {a, b, c) which is not the image of any element of set {1, 2, 3}. Thus, function f is one-one onto. Hence, function f is invertible.
Let inverse of f is f^-1.
Then in f = {(1, a), (2, b), (3, c)} by interchanging the elements f^-1 will be obtained.
Thus, f^-1 = {(a, 1), (b, 2), (c, 3)}
i.e., f^-1: {a, b, c} → {1, 2, 3} will be defined as:
f^-1(a) = 1, f^-1(b) = 2, f^-1(c) = 3
Since, function f is one-one onto so its inverse f^-1 be one-one onto then inverse of f^-1 will be (f^-1)^-1.
Thus, by interchanging the elements of ordered pair in
f^-1 = {(a, 1), (b, 2), (c, 3)} we will get (f^-1)^-1.
Thus, (f^-1)^-1 = {(1, a), (2, b), (3, c)} = f (By definition of f)
Here (f ^-1)^-1(1) = a, (f^-1)^-1 (2) = b and (f^-1)^-1(3) = c, which is definition of f.
Hence Proved.

Question 12.
Let f: X → Y be an invertible function. Show that the inverse of f^-1 is f, i.e., (f^-1)^-1 = f.
Answer:
It is given that f: X → Y is invertible. We have to prove that inverse of f^-1 is f i.e.
(f^-1)^-1 = f
Here, to show f^-1of = I_X and fof^-1 = I_y will be sufficient for(f^-1)^-1 = f.
Clearly f: X → Y is one-one onto.
∴ f^-1: Y → X is one-one onto.
Let x ∈ X and f(x) = y then f^-1(y) = x
∴ (f^-1of) = f^-1(f(x))
= f^-1(y) [∵ f(x) = y]
= x = I_x(x)

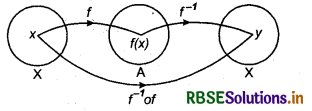
where I_x(x) is identity function.
∴ f^-1of = I_x
Again, function f is onto, then x ∈ X will be such that f(x) = y, then f^-1(y) = x
∴ (fof^-1) (y) = f(f^-1(y)) = f(x)
= y (∵ f^-1(y) = x)
= I_Y(y)
Thus, f^-1of = I_X and fof^-1 = I_Y
∴ (f^-1)^-1 = f
Hence Proved.

II^nd Method: Since, we know that inverse of any bijective function is bijective.
∴ f^-1: Y → X will also be bijective
Now, f^-1 : Y → X is bijective, then (f^-1)^-1: X → Y will also be bijective
Let x ∈ X is an arbitrary element.
∴ (f^-1)^-1 (x) = f(x), ∀ x ∈ A
Thus, (f^-1)^-1 = f
Hence Proved.

Question 13.
If f: R → R be given by f(x) = \(\left(3-x^{3}\right)^{\frac{1}{3}}\) , then fof(x) is:
(A) \(x^{\frac{1}{3}}\)
(B) x³
(C) x
(D) (3 - x³)
Answer:
Given f(x) = (3 - x³)^1/3,f: R → R
Now, fof(x) = f(f(x))
= f[(3 - x³)^1/3]
= [{3 - {3 - x³)^1/3}³]^1/3
= [3 - (3 - x³)]^1/3
= (3 - 3 + x³)^1/3
= (x³)^1/3
= x
Thus, option (C) is correct.

Question 14.
Let f: R - \(\left\{-\frac{4}{3}\right\}\) → R be a function defined as f(x) = \(\frac{4 x}{3 x+4}\). The inverse of f is the map g: Range f → R - \(\left\{-\frac{4}{3}\right\}\) given by.
(A) g(y) = \(\frac{3 y}{3-4 y}\)
(B) g(y) = \(\frac{4 y}{1-3 y}\)
(C) g(y) = \(\frac{4 y}{34-4}\)
(D) g(y) = \(\frac{4 y}{3-4 y}\)
Answer:

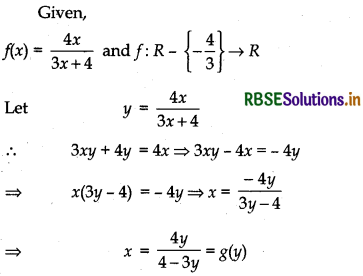
Thus, option (B) is correct.