RBSE Solutions for Class 12 Chemistry Chapter 4 रासायनिक बलगतिकी

Rajasthan Board RBSE Solutions for Class 12 Chemistry Chapter 4 रासायनिक बलगतिकी Textbook Exercise Questions and Answers.

RBSE Class 12 Chemistry Solutions Chapter 4 रासायनिक बलगतिकी

RBSE Class 12 Chemistry रासायनिक बलगतिकी InText Questions and Answers

प्रश्न 1. 
R → P, अभिक्रिया के लिए अभिकारक की सान्द्रता 0.03 M से 25 मिनट में परिवर्तित होकर 0.02 M हो जाती है। औसत वेग की गणना सेकण्ड तथा मिनट दोनों इकाइयों में कीजिए। 
उत्तर:
औसत वेग

औसत वेग = 4 x 10 + mol L^-1 min^-l
= \(\frac{4 \times 10^{-4}}{60}\) mol L^-1 S^-1
= 6.66 x 10^-6 mol L^-1 S^-1 
अतः औसत वेग = 4 x 104 mol L^-1 min^-1
औसत वेग = 6.66 x 10^-6 mol L^-1 S^-1 

 

प्रश्न 2.
2.2 A → उत्पाद, अभिक्रिया में A की सान्द्रता 10 मिनट में 0.5mol L^-1 से घटकर 0.4 mol L^-1 रह जाती है। इस समय अन्तराल के लिए अभिक्रिया बेग की गणना कीजिए। 
उत्तर:
2A → उत्पाद के लिए
अभिक्रिया की दर 
= 1/2 [अभिकारक की गस होने की दर]

अभिक्रिया की दर = 0.05 mol L^-I min^-4

प्रश्न 3. 
एक अभिक्रिया A+ B → उत्पाद के लिए वेग नियम \(r=k[\mathrm{~A}]^{1 / 2}[\mathrm{~B}]^2\) से दिया गया है। अभिक्रिया की कोटि क्या है? 
उत्तर:
\(r=k[\mathrm{~A}]^{1 / 2}[\mathrm{~B}]^2\)
अभिक्रिया को कोटि = 1/2 + 2
= 5/2  = 2.5
यहाँ अभिक्रिया की कोटि 2.5 है।

प्रश्न 4.
अणु x का Y में रूपान्तरण द्वितीय कोटि की बलगतिकी के अनुरूप होता है। यदि x की सान्द्रता तीन गुनी कर दी जाये तो। के निर्माण होने के वेग पर क्या प्रभाव पड़ेगा?
उत्तर:
प्रश्नानुसार, \(r_1=k[\mathrm{X}]^2\)  .......... (1)
यदि सान्द्रता तीन गुनी कर दें तो
\(r_2=k[3 \mathrm{X}]^2\)
या \(r_2=k 9[\mathrm{X}]^2\)
या \(r_2=9 \times k \times[\mathrm{X}]^2\) ............. (2)
समी. (2) को समी. (1) से भाग देने पर,
\(\frac{r_2}{r_1}=\frac{9 k[\mathrm{X}]^2}{k[\mathrm{X}]^2}\)
या   \(\frac{r_2}{r_1}=9\)
r₂ = 9 x r₁
अर्थात् सान्दता तीन गुनी करने पर अभिक्रिया का वेग नौ गुना हो जायेगा।

प्रश्न 5. 
एक प्रथम कोटि की अभिक्रिया का वेग स्थिरांक 1.15 x 10^-3 s^-1 है। इस अभिक्रिया में अभिकारक की 5g मात्रा को घटकर 3g होने में कितना समय लगेगा? 
उत्तर:
प्रथम कोटि की अभिक्रिया के लिए
,\(\begin{aligned} &k=\frac{2 \cdot 303}{t} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]} \\ &k=\frac{2 \cdot 303}{t} \log \frac{5}{3} \end{aligned}\) 
या
\(1.15 \times 10^{-3}=\frac{2.303}{t} \log \frac{5}{3}\)
\(t=\frac{2.303 \times 0.222}{1.15 \times 10^{-3}}\)
या  \(t=\frac{2.303 \times 0.222}{1.15} \times 10^3\)
या t = 0.444 × 10^{3
∴ t = 444S}

प्रश्न 6. 
SO₂Cl₂ को अपनी प्रारम्भिक मात्रा से आधी मात्रा में वियोजित होने में 60 मिनट का समय लगता है। यदि अभिक्रिया प्रथम कोटि की हो तो वेग स्थिरांक की गणना कीजिए।
उत्तर: 
t_1/2  = 60 मिनट 
प्रथम कोटि के लिए,
\(\begin{aligned} k &=\frac{0 \cdot 693}{t_{1 / 2}} \\ &=\frac{0 \cdot 693}{60} \end{aligned}\)
या  k = 0.01155 min^-1 
या     ^{\(k=\frac{1.155}{60} \times 10^{-2} \mathrm{~s}^{-1}\)}
∴ K = 1.925 x 10^-4 s^-1
अतः वेग स्थिरांक = 1.925 x 10^-4 s^-1

प्रश्न 7. 
ताप का वेग स्थिरांक पर क्या प्रभाव होगा?'
उत्तर: 
किसी अभिक्रिया का ताप 10°C बढ़ाने पर वेग स्थिरांक में लगभग दोगुनी वृद्धि होती है। वेग स्थिरांक की ताप पर निर्भरता आरेनियस समीकरण की सहायता से दे सकते हैं:
\(k=A e^{-\mathrm{E}_a / \mathrm{RT}}\)
यहाँ A = आवृति गुणक या पूर्व चरघातांकी गुणक है।
Ea =  सक्रियण ऊर्जा 
R = गैस नियतांक
T = ताप 

प्रश्न 8. 
परम ताप 298K में 10K की वृद्धि होने पर रासायनिक अभिक्रिया का वेग दोगुना हो जाता है। इस अभिक्रिया के लिए Ea की गणना कीजिए। 
उत्तर: 
ताप T₁ = 298K
ताप T₂ = 308K 
वेग स्थिरांक K₂ = 2 x K₁
\(\log \frac{k_2}{k_1}=\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{R}}\left[\frac{\mathrm{T}_2-\mathrm{T}_1}{\mathrm{~T}_1 \mathrm{~T}_2}\right]\)
या 
\(\log \frac{2 \times k_1}{k_1}=\frac{\mathrm{E}_a}{2 \cdot 303 \times 8 \cdot 314}\left[\frac{308-298}{308 \times 298}\right]\)
या \(\log 2=\frac{E_a}{2 \cdot 303 \times 8.314}\left[\frac{10}{298 \times 308}\right]\)
या \(0.3010=\frac{\mathrm{E}_a}{2.303 \times 8.314}\left[\frac{10}{91784}\right]\)
या \(\mathrm{E}_a=\frac{0.3010 \times 2.303 \times 8.314 \times 91784}{10}\)
या Ea = 52897.78 J/mol
\(\therefore\) Ea = 52.9 kJ/mol

प्रश्न 9.
58IK ताप पर अभिक्रिया 2HI(g) → H₂(g) + I के लिये सक्रियण ऊर्जा का मान 209.5 RJ mol^-1 है। अणुओं के उस अंश की गणना कीजिए जिसकी ऊर्जा सक्रियण ऊर्जा के बराबर अथवा इससे अधिक है।
उत्तर:
सक्रियण ऊर्जा से अधिक या बराबर ऊर्जा वाले अणुओं का
अंश
\(\begin{aligned} x &=\frac{n}{\mathrm{~N}}=e^{-\mathrm{E}_a / \mathrm{RT}} \\ \ln x &=-\frac{\mathrm{E}_a}{\mathrm{RT}} \end{aligned}\)
या  \(\log x=-\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{RT}}\)
या \(\log x=-\frac{209 \cdot 5 \times 10^3}{2 \cdot 303 \times 8.314 \times 581}\)
या log χ = - 18.8323
या χ = Antilog (-18.8323)
= \(\text { Antilog } \overline{19} \cdot 1677\)
∴ x = 1.471 × 10^-19
अतः अणुओं का अंश जिनकी कर्जा सक्रियण कर्जा के बराबर या अधिक है = 1.471 x 10^-19

RBSE Class 12 Chemistry रासायनिक बलगतिकी Textbook Questions and Answers

प्रश्न 1. 
निम्नलिखित अभिक्रियाओं के वेग व्यंजकों से इनकी अभिक्रिया की कोटि तथा वेग स्थिरांकों की इकाइयाँ ज्ञात कीजिए:
(I) 3NO(g)+N₂O(g) + NO₂(g) वेग = K [NO]²
(ii) H₂O2(aq) + 3I^- (aq) + 2H^- 2H₂O + I₃
वेग = k[H₂O.]
(iii) CH₃CHO(g) → CH₄(R) + CO(g)
वेग = k[CH₃CHO]^3/2 
(iv) C₂H₅Cl(g) → C₂H₄(g) + HCI(g) वेग= [C₂H₅Cl] 
उत्तर:
(i) 3NO_(g) →  N₂O_(g)  + NO₂(g) वेग =K[NO]²
अभिक्रिया की कोटि = 2
वेग स्थिरांक की इकाई = \(\left(\frac{\mathrm{mol}}{\mathrm{L}}\right)^{1-n} \mathrm{~s}^{-1}\)
यहाँ
n = अभिक्रिया की कोटि 
= \(\left(\frac{\mathrm{mol}}{\mathrm{L}}\right)^{1-2} \mathrm{~s}^{-1}\)
= mol^-1 L^-1 s^-1
उपर्युक्त अभिक्रिया की कोटि 2 तथा वेग स्थिरांक की इकाई mol^-1 L^-1 s^-1 है।

(ii) H₂O₂ + 3I^-_(aq) + 2H⁺ + 2H₂O_(I) + I^-₃
वेग = K[H₂O₂] [I^-] 
अभिक्रिया की कोटि = 1 + 1 = 2 
वेग स्थिरांक की इकाई = \(\left(\frac{\mathrm{mol}}{\mathrm{L}}\right)^{1-n} \mathrm{~s}^{-1}\)
= \(\left(\frac{\mathrm{mol}}{\mathrm{L}}\right)^{1-2} \mathrm{~s}^{-1}\)
= \(=\left(\frac{\mathrm{mol}}{\mathrm{L}}\right)^{-1} \mathrm{~s}^{-1}\)
= mol^-1 L^-1 s^-1
उपर्युक्त अभिक्रिया की कोटि 2 तथा वेग स्थिरांक की इकाई mol^-1 L^-1 s^-1 है।

(iii) CH₃CHO_(g)  → CH_4(g) + CO_2(g)
वेग = k[CH₃ CHO]^3/2
अभिक्रिया की कोटि = 3/2
वेग स्थिरांक की इकाई = \(\left(\frac{\mathrm{mol}}{\mathrm{L}}\right)^{1-\frac{3}{2}} \mathrm{~s}^{-1}\)
\(\begin{aligned} &=\left(\frac{\mathrm{mol}}{\mathrm{L}}\right)^{-\frac{1}{2}} \mathrm{~s}^{-1} \\ &=(\mathrm{mol})^{-1 / 2}(\mathrm{~L})^{1 / 2} \mathrm{~s}^{-1} \end{aligned}\)
उपर्युक्त अभिक्रिया की कोटि 3/2 तथा वेग स्थिरांक की इकाई mol^-1 L^-1 s^-1 है।

(iv) CH₂CI(g) → C₂H₄(g) + HCI(g),
वेग = k[C₂H₅CI] 
अभिक्रिया की कोटि = 1 
वेग स्थिरांक की इकाई = imm\(\left(\frac{\mathrm{mol}}{\mathrm{L}}\right)^{1-n} \mathrm{~s}^{-1}\)
\(=\left(\frac{\mathrm{mol}}{\mathrm{L}}\right)^{1-1} \mathrm{~s}^{-1}\)
= s^-1
उपरोक्त अभिक्रिया की कोटि 1 तथा इकाई sec^-I है। 

प्रश्न 2.
अभिक्रिया 2A+B → A₂B के लिए वेग = [A][B₂ यहाँ का मान 2.0 x 10^-6 mol^-2 L² s^-1 है। प्रारम्भिक वेग की गणना कीजिए, जब [A] = 0.1 mol L^-1 एवं [B] = 0.2 mol L^-1 हो तथा अभिक्रिया वेग की गणना कीजिए, जब [A] घटकर 0.06mol L^-I रह जाये। 
उत्तर:
प्रारम्भिक वेग = k[A] [B]2
= (2.0 x 10^-6 mol^{- 2} L² s^-1) x (0.1 molL^-1)(0.2 mol L^-1)2 
= 8.0 x 10^-9 mol L^-1 s^-1
जब [A]0.10 mol L^-1 से घटकर 0.06 mol L^-1 रह जाता है अर्थात् 0.04 mol L^-1 A अभिकृत हो जाता है, तब अभिकृत B की सान्द्रता
= 1/2 x 0.04 mol L^-1
= 0.02 mol
अतः [B] = 0.2 - 0.02
= 0.18 molL^-I 
वेग = (2.0 x 10^-6 mol^-2 L^-2 s^-1 )
(0.06 mol L^-1) (0.18moIL^-1)² 
= 3.89 x 10^-9 mol L^-1 s^-1

प्रश्न 3. 
प्लैटिनम सतह पर NH₃ का अपघटन शून्य कोटि की अभिक्रिया है। N₂ एवं H₂ के उत्पादन की दर क्या होगी जब का मान 2.5 x 10^-4 mol L^-1 s^-1 हो?
उत्तर:
2NH₃ → N₂ + 3H₂ 
अभिक्रिया का वेग = 1/2 (NH₃ के छस की दर)
= (N₂  के उत्पादन की दर)
= 1/3 (H₂ के उत्पादन की दर) 
= \(\frac{1}{2}\left[-\frac{d\left[\mathrm{NH}_3\right]}{d t}\right]=\left[\frac{d\left[\mathrm{~N}_2\right]}{d t}\right]=\frac{1}{3}\left[\frac{d\left[\mathrm{H}_2\right]}{d t}\right]\)
चूँकि अभिक्रिया शून्य कोटि की है तो 
अभिक्रिया वेग = K[NH₃]⁰      
अभिक्रिया वेग = 2.5 x 10^-4 mol L^-1 s^-1 
N₂ के उत्पादन की दर
अभिक्रिया का वेग = [N₂ के उत्पादन की दर] 
N₂ के उत्पादन की दर = 2.5 x 10^-4 mol L^-1 s^-1
H₂  के उत्पादन की दर
अभिक्रिया का वेग = 1/3 (H₂ के उत्पादन की दर) 
H₂ के उत्पादन की दर = 3 x अभिक्रिया का वेग
= 3 x 2.5 x 10^-4 
= 7.5 x 10^-4 mol L^-1 s^-1

प्रश्न 4. 
डाइमेथिल ईयर के अपघटन से CH₄ H₂ तथा CO  बनते हैं। इस अभिक्रिया का वेग निम्नलिखित समीकरण द्वारा दिया जाता है: वेग = k[CH₃OCH₃]_3/2  अभिक्रिया के वेग का अनुगमन बन्द पात्र में बढ़ते दाब द्वारा किया जाता है, अतः वेग समीकरण को डाइमेथिल ईथर के आंशिक दाब के पद में भी दिया जा सकता है। अतः वेग = k(PCH₃OCH)_3/2  यदि दाब को bar में तथा समय को मिनट में मापा जाये तो अभिक्रिया के वेग एवं वेग स्थिरांक की इकाइयाँ क्या होंगी?
उत्तर: 
अभिक्रिया की कोटि = 3/2 
अत: दाब के पदों में वेग स्थिरांक का नियतांक
= (bar)^1-n min^-1 
= (bar)^1-3/2 min^-1
= bar^1/2 min^-1 
वेग स्थिरांक की इकाई = (bar)^1/2 min^-1 
अभिक्रिया के वेग की इकाई = bar min^-1

प्रश्न 5. 
रासायनिक अभिक्रिया के वेग पर प्रभाव डालने वाले कारकों का उल्लेख कीजिए।
उत्तर:
अभिक्रिया के वेग को प्रभावित करने वाले कारक निम्न है।

1. सान्दण (Concentration): अभिकारक की सान्द्रता बढ़ाने पर, अणुओं के आपस में टकराने की सम्भावना बढ़ जाती है फलस्वरूप अभिक्रिया का वेग बढ़ जाता है।
2. ताप (Temperature): ताप बढ़ाने पर अणुओं की गतिज ऊर्जा बढ़ जाती है जिसके कारण उनकी आपस में टक्कर भी बढ़ जाती है और अभिक्रिया का वेग भी बढ़ जाता है।
3. दाब (Pressure): दाब बढ़ाने पर गैसों के अणु पास - पास आ जाते है जिसके फलस्वरूप उनकी परस्पर टक्कर बढ़ जाती है फलतः अभिक्रिया का वेग भी बढ़ जाता है।
4. अभिकारकों का पृष्ठ क्षेत्रफल (Surface area of reactants): अभिकारकों का पृष्ठ क्षेत्रफल बढ़ाने पर भी अभिक्रिया का वेग बढ़ जाता है। उदाहरणार्थ, चूर्णित धातुओं में अभिक्रिया तीव्र गति से होती है।
5. अभिकारकों की प्रकृति (Nature of renctants): यदि अभिकारक आयनिक है तो उस अभिक्रिया का वेग अनायनिक अभिक्रियाओं की तुलना में अधिक होता है।
    

प्रश्न 6. 
किसी अभिकारक के लिए एक अभिक्रिया द्वितीय कोटि की है। अभिक्रिया का वेग कैसे प्रभावित होगा; यदि अभिकारक की सान्द्रता (i) दोगनी कर दी जाये (ii) आधी कर दी जाये।
उत्तर:
वेग = K[A]₂ यदि सान्द्रता - a तो
वेग = ka₂
(i) यदि सान्द्रता दोगुनी कर दी जाये,
[A] = 2a 
(वेग)₁ = K(a)₂ 
(वेग)₂ = K(2a)₂
अतः

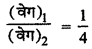
(वेग),₂ = 4 x (वेग)₁ 
अर्थात् वेग चार गुना हो जायेगा। 

(ii) यदि सान्दता आधी कर दी जाये,

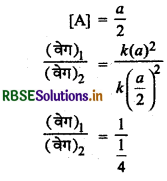
∴ (वेग),₂ = 1/4 x (वेग)₁ 
अर्थात वेग एक चौथाई रह जायेगा।

प्रश्न 7. 
वेग स्थिरांक पर ताप का क्या प्रभाव पड़ता है? ताप के इस प्रभाव को मात्रात्मक रूप में कैसे प्रदर्शित कर सकते हैं?
उत्तर:
किसी ससायनिक अभिक्रिया का ताप 100 (दस डिग्री) बढ़ाने पर वेग स्थिरांक के मान में दोगुनी वृद्धि होती है।
आरेनियस ने ताप एवं वेग स्थिरांक के मध्य में निम्न सम्बन्ध स्थापित किया
\(k=\mathrm{A} e^{-\mathrm{E}_a / \mathrm{RT}}\)
यहाँ A = आवृत्ति गुणक या आरैनियस गुणक या पूर्व चरघातांकी गुणक।
R = गैस नियतांक 
E = सक्रियण ऊर्जा 
T = ताप 
k = वेग नियतांक 

प्रश्न 8. 
प्रश्चम कोटि अभिक्रिया के निम्नलिखित आँकड़े प्राप्त:

t/s	0	30	60	90
[ एस्र ] mol\L-1	0.55	0.31	0.17	0.85

30 से 60 सेकण्ड समय-अन्तराल में औसत वेग की गणना कीजिए। 
उत्तर:
30 से 60 सेकण्ड समय-अन्तराल में औसत वेग
\(\begin{aligned} &=\frac{C_2-C_1}{t_2-t_1} \\ &=\frac{0.31-0 \cdot 17}{60-30}=\frac{0.14}{30} \end{aligned}\)
= 4.67 × 10^-3 mol L^{- 1} s^-1

प्रश्न 9. 
एक अभिक्रिया A के प्रति प्रथम तथा B के प्रति द्वितीय कोटि की है।
(i) अवकलन वेग समीकरण लिखिए। 
(ii) B की सान्दता तीन गुनी करने से वेग पर क्या प्रभाव पड़ेगा?
(iii) A तथा B दोनों की सान्दता दोगुनी करने से वेग पर क्या प्रभाव पड़ेगा?
उत्तर:
(i) अभिक्रिया की दर या वेग
= \(\frac{d x}{d t}=k[\mathrm{~A}][\mathrm{B}]^2\)
यहाँ अवकलन वेग समीकरण,
दर = k[A] [B]₂ 

(ii) माना कि [A] = a [B] = b 
चूँकि [B] की सान्द्रता तीन गुनी कर दी गई है, अत:
वेग - k[A] [B]₂
(वेग)₁ = ka x b₂ ........(1)
[B]  = 3b, तब
(वेग)₂ = ka x (3b)₂ 
समी. (1) व (2) से,

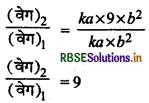
∴ (वेग)₂ = 9x (वेग)
अर्थात् अभिक्रिया का वेग नौ गुना बढ़ जायेगा। 

(iii) [A] तथा [B] दोनों की सान्द्रता दोगुनी करने पर, 
[A] = 2a, [B] = 2b, तब
(वेग)₁ = ka x b₂
(वेग)₂ = k x 2a x (2b)₂
समी. (1) व (2) से,

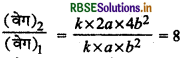
∴ (वेग)₂ = 8x (वेग), 
अर्थात् अभिक्रिया का वेग आठ गुना हो जायेगा। 

प्रश्न 10.
A और B के मध्य अभिक्रिया में A और B की विभिन्न प्रारम्भिक सान्द्रताओं के लिए प्रारम्भिक वेग (r₀) नीचे दिये गये हैं:
A और B के प्रति अभिक्रिया की कोटि क्या हैं? 
उत्तर:
माना कि A की कोटि तथा B की कोटिहै, तब
प्रारम्भिक वेग r⁰ = K[A]x [B]y
दी गई सारणी की सहायता से, 
(r₀)₁ = 5.07 x 10^-5
= k(0.20)^χ x (0.30)^y .......(1) 
(r_o)₂  = 5.07 x 10^-5 
= k(0.20)^χ x (0.10)^y ........(2) 
(r_o)₃ = 1.43 x 10^-4 
=    (0.40)^χ x (0.05)^y .......(3) 
समी. (1) में (2) का भाग देने पर,
\(\frac{\left(r_0\right)_1}{\left(r_0\right)_2}=\left(\frac{5.07 \times 10^{-5}}{5.07 \times 10^{-5}}\right)\)
\(=\frac{k}{k}\left(\frac{0.20}{0.20}\right)^x \times\left(\frac{0.30}{0.10}\right)^y\)

या \(1=\left(\frac{0.30}{0.10}\right)^y\)

या 1 = 3y
या (3)⁰ = (3)^y
अतः y = 0
समी. (3) में समी. (2) का भाग देने पर,
\(\frac{\left(r_0\right)_3}{\left(r_0\right)_2}=\frac{14.3 \times 10^{-5}}{5.07 \times 10^{-5}}\)
= \(\frac{k}{k}\left(\frac{0-40}{0-20}\right)^x\left(\frac{0.05}{0.10}\right)^y\)
या \(\frac{14 \cdot 3}{5.07}=(2)^x\left(\frac{1}{2}\right)^y\)

चूँकि y = 0 अत:
\(\frac{14 \cdot 3}{5 \cdot 07}=(2)^x\)
या  2.820 = (2)χ
दोनों तरफ log लेने पर,
log 28,20 = χ log 2
या 0.543 = χ x 0.3010
∴ \(x=\frac{0.4503}{0.3010}=1.5\)
अत: वेग =  \(k[\mathrm{~A}]^{1 \cdot 5}[\mathrm{~B}]^0\)
अभिक्रिया की कोटि = 1.5 + 0 = 1.5

प्रश्न 11.
2A + B + C + D अभिक्रिया की बल- गतिकी का अध्ययन करने पर निम्नलिखित परिणाम प्राप्त हुए। अभिक्रिया के लिए वेग नियम तथा वेग स्थिरांक ज्ञात कीजिए।
उत्तर:
माना कि समीकरण, वेग = k[A]χ [B]y है तो दिये गये प्रयोगों
के अनुसार,
(वेग)I = 6.0 x 10-3 = k(0.1)χ(0.1)y  .......... (1)
(वेग)II = 7.2 x 10-2 = k(0.3)χ (0.2)y ............ (2)
(वेग)III = 2.88 x 10-1 = k(0.3)χ (0.4)y .............. (3)
(वेग)Iv = 2.40 x 10-2 = k(0.4)χ (0.1)y .............. (4)
समीकरण (2) तथा (3) से,

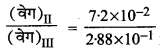
= \(\frac{k}{k}\left(\frac{0.3}{0.3}\right)^x\left(\frac{0.2}{0.4}\right)^y\)

था  \(\frac{7.2 \times 10^{-2}}{2.88 \times 10^{-1}}=\left(\frac{0.2}{0.4}\right)^y\)

था \(\frac{0.72 \times 10^{-1}}{0.288}=\left(\frac{1}{2}\right)^y\)

था \(\frac{0.072}{0.288}=\left(\frac{1}{2}\right)^y\)

था \(\frac{1}{4}=\left(\frac{1}{2}\right)^y\)
था \(\left(\frac{1}{2}\right)^2=\left(\frac{1}{2}\right)^y\)

यहाँ  y = 2
समीकरण (1) व (4) से,

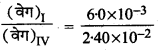
= \(\frac{k}{k}\left(\frac{0-1}{0-4}\right)^x \cdot\left(\frac{0-1}{0-1}\right)^y\)
\(\frac{0 \cdot 6}{2 \cdot 4}=\left(\frac{1}{4}\right)^x\)
\(\left(\frac{1}{4}\right)^1=\left(\frac{1}{4}\right)^x\)
 यहाँ χ = 1
अतः  वेग = k[A]χ [B]y
चूंकि x = 1 y = 1
वेग नियम का व्यंजक.
वेग = k[A]χ [B]y
6.0 × 10^-3 = k(0.1)(0.1)²

∴ \(k=\frac{6.0 \times 10^{-3}}{10^{-3}}\)
= 6.0 mol^-2 L² min^-1

प्रश्न 12.
A तथा  B के मध्य अभिक्रिया A के प्रति प्रथम तथा $B$ के प्रति शन्य कोटि की है। अग्रांकित तालिका में रित्त स्थान भरिए:

प्रयोग	[A]/mol L-1	[B]/mol L-1	प्रारासिक वेग /mol L-1 min-1
I	0.1	0.1	2.0 × 10-2
II	-	0.2	4.0 × 10-2
III	0.4	0.4	-
IV	-	0.2	2.0 × 10-2

उत्तर:
प्रश्नानुसार, वेग व्यंजक निम्न प्रकार होगा, वेग = \(k[\mathrm{~A}]^1[\mathrm{~B}]^0\)

 वेग = \(k[\mathrm{~A}]^1[\mathrm{~B}]^0\)

प्रयोग I के लिए, 
2 × 10^-2   = k(0.1)(0.1)⁰
2 × 10^-2   = k(0.1)
∴ \(k=\frac{2 \times 10^{-2}}{0 \cdot 1}\)
= 2 × 10^-1
= 0.2 min^-1

प्रयोग II के लिए,

  वेग = \(k[\mathrm{~A}]^1[\mathrm{~B}]^0\)

4.0 × 10^-2 = 0.2 × [A]¹

∴ \([A]=\frac{4 \cdot 0 \times 10^{-2}}{0.2}\)

= 0.2 mol L^-1

प्रयोग III के लिए,
वेग  = \(k[\mathrm{~A}]^1[\mathrm{~B}]^0\)
वेग = 0.2 × (0.4)¹ × (0.4)
वेग = 0.2 × 0.4 
वेग = 0.08 mol L^-1 min^-1
= 8.0 × 10^-2 mol L^-1 min^-1

प्रयोग IV के लिये,
 वेग  = \(k[\mathrm{~A}]^1[\mathrm{~B}]^0\)

2.0 × 10^-2 = 0.2 × [A] [0.2]⁰

⇒ \(\frac{2.0 \times 10^{-2}}{0.2}=[\mathrm{A}]\)

∴ [A] = 0.1 mol L^-1

प्रश्न 13.
नीचे दी गई प्रथम कोटि की अभिक्रियाओं के वेग स्थिरांक से अर्द्ध-आयु की गणना कीजिए:
(i) 200 s-1 (ii) 2 min-1 (iii) 4 year-1
उत्तर:
प्रथम कोटि की अभिक्रिया के लिए अर्द्ध-आयु,
\(t_{1 / 2}=\frac{0 \cdot 693}{k}\)
(i) \(t_{1 / 2}=\frac{0 \cdot 693}{200}=3.46 \times 10^{-3} \mathrm{~s}\)

(ii) \(t_{1 / 2}=\frac{0-693}{2}\) = 0.3465 min
(iii)  \(t_{1 / 2}=\frac{0 \cdot 693}{4}\) = 0.713 year

प्रश्न 14.
14c के रेडियोऐक्टिव क्षय की अर्द्ध-आयु 5730 वर्ष है। एक पुरातत्व कलाकृति की लकड़ी में,जीवित वृक्ष की लकड़ी की तुलना में 80% 14c की मात्रा है। नमूने की आयु का परिकलन कीजिए।
उत्तर:
रेडियोऐक्टिव क्षय एक प्रथम कोटि की अभिक्रिया है। प्रश्नानुसार, जीवित वृक्ष में 80% ¹⁴c है।

\(k=\frac{2 \cdot 303}{t} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)

\(t=\frac{2 \cdot 303}{k} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
क्योंकि \(k=\frac{0 \cdot 693}{t_{1 / 2}}\) 
\(t=\frac{2.303 \times t_{1 / 2}}{0.693} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)

\(\begin{aligned} t &=\frac{2.303 \times 5730}{0.693} \log \frac{100}{80} \\ t &=\frac{2.303 \times 5730 \times 0.0969}{0.693} \\ t &=1845 \text { years } \end{aligned}\)

= 1845 

प्रश्न 15, 
गैस प्रावस्था में 318K पर N₂O₅ के अपघटन की [2N₂O₅ → 4NO₂ +O₂] अभिक्रिया के आंकड़े नीचे दिए गए हैं:

t/s	0	400	800	1200	1600	2000	2400	2800	3200
10-2 × [N2O5]/mol L-1	1.64	1.36	1.14	0.93	0.78	0.64	0.53	0.43	0.35

(i) [N₂O₅] एवं t के मध्य आलेख खींचिए। 
(ii) अभिक्रिया के लिए अर्द्ध-आयु की गणना कीजिए। 
(iii) log [N₂O₅] एवं t के मध्य ग्राफ खींचिए। 
(iv) अभिक्रिया के लिए वेग नियम क्या है? 
(v) वेग स्थिरांक की गणना कीजिए। 
(vi) k की सहायता से अर्द्ध-आयु की गणना कीजिए तथा इसकी तुलना (ii) से कीजिए।
उत्तर:

t/s	0	400	800	1200	1600	2000	2400	2800	3200
10-2 × [N2O5]/mol L-1	1.64	1.36	1.14	0.93	0.78	0.64	0.53	0.43	0.35
log [N2O5]	-1.79	-1.87	-1.94	-2.3	-2.11	-2.19	-2.28	-2.37	-2.46

(i) [N₂O₅] तथा समय (t) के मध्य आलेख:

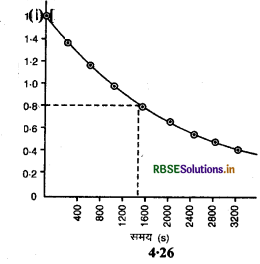
(ii) [N₂O₅] का प्रारम्भिक सान्द्रण =1.63 × 10^-2
इस सान्द्रण का आधा = 0.815 × 10^-2
इस सान्द्रण से सम्बन्धित समय =1440S

(ii) log [N₂O₅] तथा t के मध्य ग्राफ:


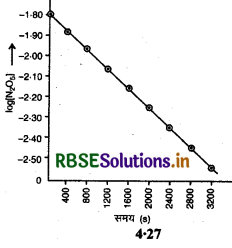
जबकि ग्राफ द्वारा अर्द्ध-आयु 14405 प्राप्त हुई थी।

(iv) log [N₂O₅] तथा समय (t) के मध्य ग्राफ एक सरल रेखा है, अतः यह एक प्रथम कोटि की अभिक्रिया है। चूँकि यह अभिक्रिया प्रथम कोटि की है 
अत: 
वेग = K[N₂O₅] 
(v) रेखा की दाल = \(-\frac{k}{2 \cdot 303}\)
\(\begin{aligned} &=-\left(\frac{-2.46-(-1.79)}{3200-0}\right) \\ &=\left(\frac{0.67}{3200}\right) \end{aligned}\)
अर्थात्
\(\begin{aligned} \frac{k}{2.303} &=\frac{0.67}{3200} \\ k &=\frac{0.67 \times 2.303}{3200} \end{aligned}\)
= 4.82 × 10^-4 mol L^-1 s^-1
जबकि ग्राफ द्वारा अर्द्ध-आयु 14405 प्राप्त हुई थी। 

प्रश्न 16. 
प्रथम कोटि की अभिक्रिया के लिए वेग स्थिरांक 60s^-1 है। अभिकारक को अपनी प्रारम्भिक सान्द्रता से 1/16 वाँ भाग रह नाने में कितना समय लगेगा? 
उत्तर:
प्रथम कोटि की अभिक्रिया के लिए,
\(t=\frac{2 \cdot 303}{k} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)

चूँकि प्रश्नानुसार, अभिकारक प्रारम्भिक सान्द्रता का 1/16 भाग रह जाता है। 
अतः [A] = [A]_o/16
\(t=\frac{2 \cdot 303}{k} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
या \(t=\frac{2 \cdot 303}{60} \log \frac{[\mathrm{A}]_0}{\frac{[\mathrm{A}]_0}{16}}\)
या \(t=\frac{2 \cdot 303}{60} \log 16\)
या \(t=\frac{2 \cdot 303}{60} \log (2)^4\)
या \(t=\frac{2 \cdot 303}{60} \times 4 \times \log 2\)
या  \(t=\frac{2.303}{60} \times 4 \times 0.3010\)
 ∴ t = 4.62 x 10^-2s

प्रश्न 17. 
नाभिकीय विस्फोट का 28.1 वर्ष अर्द्ध-आयु वाला एक उत्पाद 90Sr होता है। यदि कैल्सियम के स्थान पर 1 ug, 90Sr नवजात शिशु की अस्थियों में अवशोषित हो जाये और उपापचयन से ह्रास न हो तो इसकी 10 वर्ष एवं 60 वर्ष पश्चात् कितनी मात्रा रह जायेगी?
उत्तर:
क्षय नियतांक (k) = \(\frac{0-693}{t_{1 / 2}}\)
\(=\frac{0 \cdot 693}{28 \cdot 1}\)
= 0.25
= 2.5 x 10^-2 year^-1 
10 वर्ष के पश्चात् शेष मात्रा की गणना
[A]o = 1 ug 
[A] = ? 
t = 10 years
K = 2.5 x 10^-2 year^-1
अतः \(k=\frac{2 \cdot 303}{t} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
या \(2.5 \times 10^{-2}=\frac{2.303}{10} \log \frac{1}{[\mathrm{~A}]}\)
या \(2 \cdot 5 \times 10^{-2}=\frac{2 \cdot 303}{10}[\log 1-\log [A]]\)
या \(2 \cdot 5 \times 10^{-2}=\frac{2.303}{10}(-\log [A])\)
log [A] = - 0.1086 
[A] = Antilog(- 0.1086)
∴ [A] = 0.78 ug
10 वर्ष पश्चात् 0.78 ug शेष रह जायेगा।
60 वर्ष पश्चात शेष मात्रा की गणना
t = 60 years
[A]o = 1ug
K = 2.5 × 10^-2 year^-1

[A] = ?
\(k=\frac{2 \cdot 303}{t} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
या \(\log [\mathrm{A}]_0-\log [\mathrm{A}]=\frac{k \times t}{2 \cdot 303}\)
या    \(\log 1-\log [A]=\frac{2.5 \times 10^{-2} \times 60}{2.303}\)
या  \(-\log [A]=\frac{2.5 \times 10^{-2} \times 60}{2.303}\)
या  - log [A] = 65.13 × 10^-2
या - log [A] = 0.6513
या [A] = Antilog (-0.6513)
∴  [A] = 0.2232 ug

60 वर्ष पश्चात् 0.2232 u g पदार्थ शेष रह जायेगा।

प्रश्न 18. 
दर्शाइए कि प्रथम कोटि की अभिक्रिया में 99% अभिक्रिया पूर्ण होने में लगा समय 90% अभिक्रिया पूर्ण होने में लगने वाले समय से दोगुना होता है।
उत्तर:
99% अभिक्रिया पूर्ण होने में लगा समय,
\(t_{99 \%}=\frac{2 \cdot 303}{k} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)

या \(t_{99 \%}=\frac{2 \cdot 303}{k} \log \frac{100}{100-99}\)

या \(t_{99 \%}=\frac{2 \cdot 303}{k} \log 100\)

या \(t_{99 \%}=\frac{2 \cdot 303}{k} \times 2\)  ......... (i)
या \(t_{90 \%}=\frac{2 \cdot 303}{k} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)

या   \(t_{90 \%}=\frac{2 \cdot 303}{k} \log \frac{100}{100-90}\)

या \(t_{90 \%}=\frac{2.303}{k} \log \frac{100}{10}\)

या \(t_{90 \%}=\frac{2.303}{k} \log 10\)

या \(t_{90 \%}=\frac{2 \cdot 3.03}{k}\) ......... (ii)
समी. (1) में  (2) का भाग लगाने पर,
\(\frac{t_{99 \%}}{t_{90 \%}}=\frac{\left(\frac{2 \cdot 303}{k}\right) \times 2}{\frac{2 \cdot 303}{k}}\)
\(\frac{t_{99 \%}}{t_{90 \%}}=2\)
∴ \(t_{99 \%}=2 \times t_{90 \%}\)
अतः सिद्ध हुआ कि प्रथम कोटि की अभिक्रिया में 99% अभिक्रिया पूर्ण होने में लगा समय 90% अभिक्रिया पूर्ण होने में लगने वाले समय से दोगुना होता है।

प्रश्न 19.
एक प्रथम कोटि की अभिक्रिया में 30% वियोज़न होने में 40 मिनट लगते हैं। t1/2 की गणना कीजिए।
उत्तर:
\(k=\frac{2 \cdot 303}{t} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
या  \(k=\frac{2 \cdot 303}{t} \log \frac{100}{100-30}\)

या  \(k=\frac{2 \cdot 303}{t} \log \frac{100}{70}\)

या \(k=\frac{2.303}{t} \times 0.1548\)

या \(k=\frac{2.303}{40} \times 0.1548\)

∴ k = 8.913 × 10-3 min-1
अतः \(t_{1 / 2}=\frac{0.693}{k}\)
\(=\frac{0.693}{8.913 \times 10^{-3}}\)
∴ t_1/2 = 77.7 min
अर्द्व-आयु काल = 77.7 min

प्रश्न 20.
543 K ताप पर ऐजोआइसोप्रोपेन के हेक्सेन तथा नाइट्रोजन में विघटन के निम्नांकित आँकड़े प्राप्त हुए। वेग स्थिरांक की गणना कीजिए।

t (sec)	P (mm Hg )
0	35.0
360	54.0
720	63.0

उत्तर:
\(\left(\mathrm{CH}_3\right)_2 \mathrm{CHN}=\mathrm{NCH}\left(\mathrm{CH}_3\right)_2(\mathrm{~g}) \rightarrow \mathrm{N}_{2(\mathrm{~g})}\) \(+\mathrm{C}_6 \mathrm{H}_{14(\mathrm{~g})}\)

t समय बाद कुल दाब 
\(\left(\mathrm{P}_t\right)=\left(\mathrm{P}_0-p\right)+p+p=\mathrm{P}_0+p\)
या 
\(\begin{aligned} &\dot{p}=\mathrm{P}_t-\mathrm{P}_0 \\ &a \propto \mathrm{P}_0 \end{aligned}\)
तथा
\((a-x) \propto \mathrm{P}_0-p\)
p का मान रखने पर,
\((a-x) \propto \mathrm{P}_0-\left(\mathrm{P}_t-\mathrm{P}_0\right)\)
\((a-x) \propto 2 \mathrm{P}_0-\mathrm{P}_t\)

चूँकि ऐजोआइसोप्रोपेन का विघटन एक प्रथम कोटि अभिक्रिया है, अतः
\(k=\frac{2.303}{t} \log \frac{a}{a-x}\)
\(=\frac{2.303}{t} \log \frac{\mathrm{P}_0}{2 \mathrm{P}_0-\mathrm{P}_t}\)
जब t = 360 sec
\(\begin{aligned} k &=\frac{2.303}{360 \mathrm{~s}} \log \frac{35 \cdot 0}{2 \times 35 \cdot 0-54 \cdot 0} \\ &=\frac{2.303}{360 \mathrm{~s}} \log \frac{35}{16} \\ &=\frac{2.303}{360 \mathrm{~s}}(0.3401) \end{aligned}\)
= 2.175 x 10^-3 s^-1

जब t = 360 sec
\(\begin{aligned} k &=\frac{2 \cdot 303}{720 \mathrm{~s}} \log \frac{35 \cdot 0}{2 \times 35 \cdot 0-63 \cdot 0} \\ &=\frac{2 \cdot 303}{720 \mathrm{~s}} \log 5 \\ &=\frac{2 \cdot 303}{720}(0 \cdot 6990) \end{aligned}\)
= 2.35  x 10^-3 s^-1

जब t =  720 sec
\(\begin{aligned} k &=\frac{2.303}{720 \mathrm{~s}} \log \frac{35 \cdot 0}{2 \times 35 \cdot 0-63 \cdot 0} \\ &=\frac{2.303}{720 \mathrm{~s}} \log 5 \\ &=\frac{2.303}{720}(0.6990) \end{aligned}\)

= 2.175 x 10^-3 s^-1
 ∴ K का औसत मान = \(\frac{2 \cdot 175+2 \cdot 235}{2} \times 10^{-3} \mathrm{~s}^{-1}\)
= 2.20 x 10^-3 s^-1

प्रश्न 21. 
स्थिर आयतन पर, SO₂Cl₂ के प्रथम कोटि के ताप अपघटन पर निम्नांकित आँकड़े प्राप्त हुए:
\(\mathrm{SO}_2 \mathrm{Cl}_2(g) \longrightarrow \mathrm{SO}_2(g)+\mathrm{Cl}_2(g)\)
अभिक्रिया वेग् की गणना कीजिए जब कुल दाब 0.65 atm हो।

प्रयोग	समय/s	कुल दाब/atm
1	0	0.5
2	100	0/6

उत्तर:
\(\mathrm{SO}_2 \mathrm{Cl}_2(\mathrm{~g}) \longrightarrow \mathrm{SO}_{2(\mathrm{~g})}+\mathrm{Cl}_{2(\mathrm{~g})}\)

t समय बाद कुल दाब,
\(\mathrm{P}_t=\left(\mathrm{P}_0-x\right)+x+x\)
या  pt = p⁰ + x
या x = (p_t - p₀)
प्रारम्भिक दाब = p₀
अन्तिम दाब = p₀ - x
= p₀ - (p_o - x) + x + x
या p_t = p₀ + x

\(k=\frac{2 \cdot 303}{t} \log \frac{\mathrm{P}_0}{2 \mathrm{P}_0-\mathrm{P}_t}\)
या \(k=\frac{2.303}{100} \log \frac{0.5}{(2 \times 0.5)-0.6}\)
या  \(k=\frac{2 \cdot 303}{100} \log \frac{0 \cdot 5}{1 \cdot 0-0 \cdot 6}\)

या     \(k=\frac{2 \cdot 303}{100} \log \frac{5}{4}\)
या  \(k=\frac{2.303}{100} \log (1.25)\)

या \(k=\frac{2.303}{100} \times 0.0969\)
∴ K = 2.316 x 10^-3 s^-1
जब, P_t = 0.65  atm, अत:
\(\begin{aligned} \left(\mathrm{P}_0+p\right) &=0.65 \mathrm{~atm} \\ p &=0.65-\mathrm{P}_0 \\ &=0.65-0.50 \\ &=0.15 \mathrm{~atm} \end{aligned}\)

SO₂Cl₂  का समय t पर दाब \(\mathrm{P}_{\mathrm{SO}_2 \mathrm{Cl}_2}=\mathrm{P}_0-p\)

यहाँ  p = x अतः
\(\mathrm{P}_{\mathrm{SO}_2 \mathrm{Cl}_2}=\mathrm{P}_0-x\)
= 0.50 - 0.15
= 0.35 atm
उस ' t ' समय पर, 
वेग = k × POSO₂Cl
= 2.2316 × 10^-3 × 0.35 
= 7.8 × 10^-4 atm s^-1

प्रश्न 22. 
विभिन्न तापों पर N₂O₅ के अपघटन के लिए वेग स्थिरांक नीचे दिये गये हैं:

T/C	0	20	40	60	80
10-5 × k s-1	0.787	1.70	25.7	178	2140
T/C	0	20	40	60	80
10-5 × k s-1	0.787	1.70	25.7	178	2140

In k एवं 1/T के मध्य ग्राफ खींचिए तथा A एवं Ea की गणना कीजिए। 30°C तथा 50°C पर वेग स्थिरांक को प्रागुक्त कीजिए। gy % log k तथा 1 के मध्य ग्राफ खींचने के लिए हम निम्न सारणी बनाते हैं:

T(K)	273	293	313	333	353
1/T	0.00363	0.003413	0.003195	0.003003	0.00283
K (s-1)	0.0787 × 10-5	1.70 × 10-5	25.7 × 10-5	178 × 10-5	2140 × 10-5
Log k	-6.140	-4.786	-3.591	-2.4796	-1.6996

उपर्युक्त मानों पर आधारित ग्राफ निम्नलिखित चित्र में प्रदर्शित है:
उत्तर:

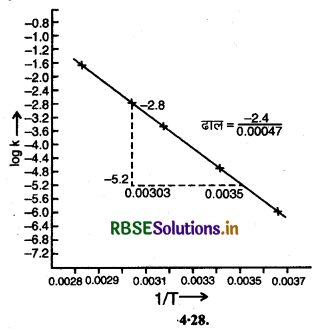
स्पष्ट हैं कि:
ढाल = \(\frac{-2.4}{0.00047}=\frac{-E_a}{2.303 R}\)

∴ सक्रियण ऊर्जा Ea = \(\frac{2.4 \times 2.303 \times R}{0.00047}\)

 \(=\frac{2.4 \times 2.303 \times 8.314 \mathrm{~J} \mathrm{~mol}^{-1}}{0.00047}\)
= 9772.64 J mol-1
= 97.772 KJ mol-1
हम जानते हैं कि = \(\log k=\log \mathrm{A}-\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{RT}}\)
= \(\log k=\left(-\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{R}}\right) \frac{1}{\mathrm{~T}}+\log \mathrm{A}\)

इस समीकरण की तुलना y = mx + c से करते हैं जो अन्त:खण्ड रूप में रेखा का समीकरण है। 
log A - y अक्ष पर अर्थात् अक्ष पर अन्त:खण्ड का मान 
= (-1 + 7 - 2) 
= 6.2
[Y₂ - Y₁ = 1 - (- 7.2)] 
आवृत्ति गुणक A = antilog 6.2
= 1585000
= 1.585  x 10^-6 collisions s^-1. 
वेग स्थिरांक k के मान हम ग्राफ से ज्ञात कर सकते हैं:

T	1/T	Log K का मान ग्राफ से	K का मान
303 K	0.003300	- 4.2	6.31 × 10-5 s-1
323 K	0.003096	- 2.8	1.585 × 10-3 s-1

प्रश्न 23.
546 K ताप पर हाइड्रोकार्बन के अपघटन में वेग स्थिरांक 2.418 x 10^-5 s^-1 है। यदि सक्रियण ऊर्जा 179.9 kJ/mol हो तो पूर्व-घातांकी गुणन का मान क्या होगा?
उत्तर:
समीकरण (1) व (2) की तुलना करने पर,
\(\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{RT}}=\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\)

∴ Ea = 2.303 × R × 1.25 × 10⁴ k
= 2.303 × 125 × 10⁴ × 8.314 JK^-1 mol^-1 K
= 2393407 J
= 23.34KJ mol^-1

\(\begin{aligned} k &=\frac{0 \cdot 693}{t_{1 / 2}} \\ &=\frac{0 \cdot 693}{256 \times 60} \\ &=4 \cdot 51 \times 10^{-5} \mathrm{~s}^{-1} \end{aligned}\)

k का मान समीकरण (2) में रखने पर, 
\(\begin{aligned} \log \left(4.51 \times 10^{-5}\right) &=14.34-\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}} \\ \left(\log 4.51+\log 10^{-5}\right) &=14.34-\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}} \\ (0.6542-5) &=14.34-\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}} \end{aligned}\)

या 
\(\begin{aligned} &0.6542-5-14.34=-\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}} \\ &-18.6858=-\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}} \end{aligned}\)
∴  \(T=-\frac{1.25 \times 10^4}{18.6858} K\)

= 699K

प्रश्न 24. 
किसी अभिक्रिया A → उत्पाद के लिए k = 2.0 x 10^-2 S^-1 है। यदि A की प्रारम्भिक सान्द्रता 1.0 mol^-1 हो तो 100 sec के पश्चात् इसकी सान्द्रता क्या रह जायेगी? 
उत्तर:
k = 20 x 10^-2 s^-1
[A]o = 10 mol L^-1
t = 100s 
[A] = ?
अतः
\(k=\frac{2 \cdot 303}{t} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
या
\(2 \cdot 0 \times 10^{-2}=\frac{2 \cdot 303}{100}[\log 1 \cdot 0-\log [\mathrm{A}]]\)
या \(-\log [\mathrm{A}]=\frac{2 \cdot 0 \times 10^{-2} \times 100}{2 \cdot 303}\)
- log [A] =0-8684 
या log [A] = - 0.8684
[A] =Antilog(-0.8684) 
[A] = Antilog (1.1316)
[A] = 0.1354 mol L^-1 
अत: 100 के पश्चात् सान्द्रता 0.354 mol L^-1 रह जायेगी।

प्रश्न 25. 
अम्लीय माध्यम में सुक्रोस का ग्लूकोस एवं फ्रक्टोस में विघटन प्रथम कोटि की अभिक्रिया है। इस अभिक्रिया की अर्द्ध-आयु 3.0 घण्टे है। 8 घण्टे के बाद नमूने में सुक्रोस का कितना अंश बचेगा? 
उत्तर:
अभिक्रिया प्रथम कोटि की है, अतः,
\(k=\frac{2 \cdot 303}{t} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
∴ \(\begin{aligned} k &=\frac{0 \cdot 693}{t_{1 / 2}} \\ &=\frac{0 \cdot 693}{3} \end{aligned}\)
∴ k = 0.231 घण्टे-1
अत:   \(k=\frac{2 \cdot 303}{t} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
या  \(\log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}=\frac{k \times t}{2 \cdot 303}\)
या  \(\log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}=\frac{0.231 \times 8}{2 \cdot 303}\)
या  \(\log \frac{[A]_0}{[A]}=0 \cdot 8024\)
या \(\frac{[\mathrm{A}]_0}{[\mathrm{~A}]}=\text { Antilog }(0 \cdot 8024)\)
या  \(\frac{[\mathrm{A}]_0}{[\mathrm{~A}]}=6.344\)
कि प्रारम्भिक मात्रा 1 mol/L थी, तो
\(\begin{aligned} {[\mathrm{A}]_0 } &=1 \\ \frac{[\mathrm{A}]_0}{[\mathrm{~A}]} &=6.344 \end{aligned}\)

या  \(\frac{1}{[\mathrm{~A}]}=6.344\)
या \([\mathrm{A}]=\frac{1}{6.344}\)
∴  \([\mathrm{A}]=0.157 \mathrm{~mol} / \mathrm{L}\)
अत: 8 घण्टे के पश्चात् सुक्रोस का 0.57 M अंश बचेगा।

प्रश्न 26. 
हाइड्रोकार्बन का विघटन निम्नांकित समीकरण के अनुसार होता है। सक्रियण ऊर्जा (Ea) की गणना कीजिए।
k = (4.5 x 1011 s^-1) e^-2800K/T
उत्तर:
आरैनियस समीकरण के अनुसार,
\(k=\mathrm{A} e^{-\mathrm{E}_\alpha / \mathrm{RT}}\)  ........ (1)
प्रश्नानुसार, = \(k=\left(4 \cdot 5 \times 10^{11} \mathrm{~s}^{-1}\right) e^{-28000 \mathrm{~K} / \mathrm{T}}\) .......... (2)
समीकरण (1) व (2) की तुलना करने पर, 
\(-\frac{\mathrm{E}_a}{\mathrm{RT}}=\frac{-28000 \mathrm{~K}}{\mathrm{~T}}\)
या Ea = 28000K x R
Ea = 28000K x 8.314JK^-1 mol^-1 
या Ea = 232792J/mol
Ea = 232.79kJ/mol 
अतः सक्रियण ऊर्जा का मान 232.79 KJ/mol है। 

प्रश्न 27. 
H₃O₂ के प्रथम कोटि के विघटन को निम्नांकित समीकरण द्वारा लिख सकते हैं logk = 14.34 - 1.25 x 10⁴ KT इस अभिक्रिया के लिएE,की गणना कीजिए। कितने ताप पर इस अभिक्रिया की अर्द्ध-आयु 256 मिनट होगी?
उत्तर:
आरॅनियस समीकरण से,
\(\log k=\log \mathrm{A}-\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{RT}}\)
प्रश्नानुसार,
log k = 14.34 - 1.25 x 10 K/T

समीकरण (1) व (2) की तुलना करने पर,
\(\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{RT}}=\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\)

∴ Ea = 2.303 × R × 1.25 × 10⁴ k
= 2.303 × 125 × 10⁴ × 8.314 JK^-1 mol^-1 K
= 2393407 J
= 23.34KJ mol^-1

\(\begin{aligned} k &=\frac{0 \cdot 693}{t_{1 / 2}} \\ &=\frac{0 \cdot 693}{256 \times 60} \\ &=4 \cdot 51 \times 10^{-5} \mathrm{~s}^{-1} \end{aligned}\)

k का मान समीकरण (2) में रखने पर, 
\(\begin{aligned} \log \left(4.51 \times 10^{-5}\right) &=14.34-\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}} \\ \left(\log 4.51+\log 10^{-5}\right) &=14.34-\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}} \\ (0.6542-5) &=14.34-\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}} \end{aligned}\)

या 
\(\begin{aligned} &0.6542-5-14.34=-\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}} \\ &-18.6858=-\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}} \end{aligned}\)
∴  \(T=-\frac{1.25 \times 10^4}{18.6858} K\)

= 699K

प्रश्न 28. 
10°C ताप पर A के उत्पाद में विघटन के लिए का मान 4.5 x 10³ तथा सक्रियण ऊर्जा 60kJ morहै। किस ताप परk का मान 1.5 x 10⁴ होगा?
उत्तर:
k1 = 4.5 x 10³ s^-1
T1 = 10 + 273 
= 283
K2 = 1.5 x 10⁴ s^-1 
T2 = ?
Ea = 60 kJ/mol = 60 x 10³ J/mol 
आईनियस समीकरण के अनुसार,

\(\begin{aligned} \log \frac{k_2}{k_1} &=\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{R}}\left(\frac{\mathrm{T}_2-\mathrm{T}_1}{\mathrm{~T}_1 \mathrm{~T}_2}\right) \\ \text { } \log \frac{1.5 \times 10^4}{4 \cdot 5 \times 10^3} &=\frac{60000}{2 \cdot 303 \times 8.314}\left(\frac{\mathrm{T}_2-283}{283 \mathrm{~T}_2}\right) \\ \text { } \log \frac{15}{4 \cdot 5} &=\frac{60,000}{2 \cdot 303 \times 8.314}\left(\frac{\mathrm{T}_2-283}{283 \mathrm{~T}_2}\right) \end{aligned}\)

= 297 K
= 297 - 273
∴  T₂ =  24⁰c
अतः ताप T₂ =  24⁰c 

प्रश्न 29.
298 K ताप पर प्रथम कोटि की अभिक्रिया के 10% पूर्ण होने का समय 308 K ताप पर 25% अभिक्रिया पूर्ण होने में लगे समय के बराबर है। यदि A का मान 4 x 10¹⁰ s^-1 हो तो 318 K ताप पर तथा E, की गणना कीजिए।
उत्तर:
ताप 298 K पर, अभिक्रिया 10% पूर्ण होती है।

ताप 308 K पर अभिक्रिया 25% पूर्ण होती है।

परन्तु t₁ = t₂
या \(\frac{0.1052}{k_{298 \mathrm{~K}}}=\frac{0.2876}{k_{308 \mathrm{~K}}}\)
या \(\frac{k_{308 \mathrm{~K}}}{k_{298 \mathrm{~K}}}=\frac{0.2876}{0.1052}=2.7338\)

आर्रेनियस समी. के अनुसार,
\(\log \frac{k_{308 \mathrm{~K}}}{k_{298 \mathrm{~K}}}=\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{R}}\left[\frac{\mathrm{T}_2-\mathrm{T}_1}{\mathrm{~T}_1 \mathrm{~T}_2}\right]\)

या  \(\log (2.7338)=\frac{E_a}{2 \cdot 303 R}\left[\frac{308-298}{.308 \times 298}\right]\)

या  \(0.4367=\frac{E_a \times 10}{2.303 \times 8.314 \times 298 \times 308}\)
\(\mathrm{E}_a=\frac{0.4367 \times 2.303 \times 8.314 \times 298 \times 308}{10}\)
= 76457 KJ /mol
= 76.745 KJ/mol
318 K पर k की गणना,
\(\log k=\log \mathrm{A}-\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{RT}}\)

\(=\log \left(4 \times 10^{10}\right)-\frac{76745}{2.303 \times 8.314 \times 318}\)
= 10 .6021 - 12.6403
=-2.0022
∴ k = Antilog (-2.0022)
= Antilog (3.9978)
= 9.49 x 10³ s^-1
k का मान 318 K ताप पर 9.949 × 10^-3 s^-1 है।

प्रश्न 30. 
ताप में 293 K से 313 K तक वृद्धि करने पर किसी अभिक्रिया का वेग चार गुना हो जाता है। इस अभिक्रिया के लिए सक्रियण ऊर्जा की गणना यह मानते हुए कीजिए कि इसका मान ताप के साथ परिवर्तित नहीं होता।
उत्तर:
प्रश्नानुसार, \(\frac{k_2}{k_1}=4\)
∴  \(\log \frac{k_2}{k_1}=\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{R}}\left[\frac{\mathrm{T}_2-\mathrm{T}_1}{\mathrm{~T}_1 \mathrm{~T}_2}\right]\)
या \(\log 4=\frac{E_a}{2 \cdot 303 \times 8 \cdot 314}\left[\frac{T_2-T_1}{T_1 T_2}\right]\)
या \(2 \times 0.3010=\frac{E_a}{2.303 \times 8.314}\left[\frac{313-293}{313 \times 293}\right]\)
या \(0.6020=\frac{\mathrm{E}_a}{2 \cdot 303 \times 8.314}\left[\frac{20}{91709}\right]\)
∴ \(\mathrm{E}_a=\frac{0.6020 \times 2.303 \times 8.314 \times 91709}{20}\)
= 52853 KJ/mol
= 52.854 KJ/mol