RBSE Solutions for Class 12 Chemistry Chapter 4 Chemical Kinetics

Rajasthan Board RBSE Solutions for Class 12 Chemistry Chapter 4 Chemical Kinetics Textbook Exercise Questions and Answers.

RBSE Class 12 Chemistry Solutions Chapter 4 Chemical Kinetics

RBSE Class 12 Chemistry Chemical Kinetics InText Questions and Answers

Question 4.1. 
For the reaction R P, the concentration of a reactant changes from 0.03 M to 0.02 M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds. 
Answer:
Average rate 

= \(-\left[\frac{0.02-0.03}{25}\right]\)

= \(-\left[\frac{-0.01}{25}\right]\)
= 0.01/25
= 4 x 10^-4 mol L^-1 min^-1 
= \(\frac{4 \times 10^{-4}}{60}\) mol L^-1 s^-1 
= 6.66 x 10^-6 mol L^-1 s^-1 
Hence, Average rate = 4 x 10^-4 mol L^-1 min^-1 
= 666 x 10^-6 mol L^-1 sec^-1.

Question 4.2. 
In a reaction, 2A → Products, the concentration of A decreases from 0.5 mol L^-1 to 0.4 mol L^-1 in 10 minutes. Calculate the rate during this interval? 
Answer:
For the reaction 2A → Products 
= 1/2 [rate of disappearance of A] 

Rate of reaction = 0.005 mol L^-1 min^-1. 

Question 4.3. 
For a reaction, A + B Product, the rate is given by 
r = k[A]^1/2 [B]² What is the order of reaction? 
Answer:
Order of reaction= 1/2 + 2 
Here order of reaction is 2.5. 

 

Question 4.4. 
The conversion of molecules X to y follows second order kinetics. If concentration of X is increased three times, how will it affect rate of formation of Y? 
Answer:
According to the question, r₁ = k[X]²  ........ (1)
If concentration of X is increased three times then 
r₂ = k[3x]² 
or
r₂ = k x 9[X]² 
r₂ = 9k[X]² 
Dividing equation (2) by equation (1), 
\(\frac{r_2}{r_1}=\frac{9 k[\mathrm{X}]^2}{k[\mathrm{X}]^2}\)
or
\(\frac{r_2}{r_1}=9\)
r₂ = 9 x r₁ 
i.e., if the concentration of X is increased three times, rate of reaction will become nine times.

Question 4.5. 
A first order reaction has a rate constant 1.15 x 10^-3 s^-1. How long will 5 g of this reactant take to reduce to 3g? 
Answer:
For the first order reaction, 

t = 0.444 x 10³ 
t = 444 sec. 

Question 4.6. 
Time required to decompose SO₂Cl₂ to half of its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction. 
Answer:
t_1/2 = 60 minutes = 60 x 60 sec 
For thefirst order reaction, 
\(k=\frac{0.693}{t_{1 / 2}}=\frac{0.693}{60 \times 60}\)
= 1925 x 10⁴ sec^-1 
So therate constant = 1.925 x 10^-4 sec^-1. 

Question 4.7. 
What will be the effect of temperature on rate constant? 
Answer:
It has been observed that rate constant almost becomes double for every 10 K rise in temperature. The ratio of rate constants at the two temperatures differ by 10 K is called temperature coefficient and is generally lies between 2 and 3. 

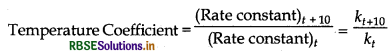
The temperature dependence of the rate of a chemical reaction is explained by Arrhenius equation. 
According to Arrhenius equation, 
k = Ae^-Ea/RT 
where A = Arrhenius factor or frequency factor or pre-exponential factor 
R = Gas constant 
T =Temperature 
Eq = Activation energy 

Question 4.8. 
The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate Ea. 
Answer:
T₁ = 298 K,
T₂ = 308 K 
k₂ = 2k₁ 

E_a = 5,2897.78J/mol 
E_a = 52.9 kJ/mol. 

Question 4.9. 
The activation energy for the reaction 
2HI(g) → H₂(g) + I₂(g) 
is 209.5 kJ mol^-1 at 581 K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy. 
Answer:
The fraction of molecules having energy equal to or greater than activation energy is 
X = n/N= e^-Ea/RT 

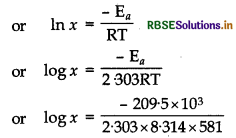
log x = -18.8323
x = Antilog (-18.8323)
= Antilog (19.1677)
x = 1.47 x 10^-19
Hence, the fraction of molecules of reactants having energy equal to or greater than activation energy is 1.471 x 10^-19.

RBSE Class 12 Chemistry Chemical Kinetics Textbook Questions and Answers

Question 4.1. 
From the rate expression for the following reactions, determine their order of reaction and dimensions of the rate constants. 
(i) 3NO(g) → N₂O(g) + N₂O(g)  
Rate = k[NO]₂
(ii) H₂O2(aq) + 3I^-(aq) + 2H⁺ + 2H₂O(l) + I^-₃, 
Rate = k[H₂O₂] [I^-] 
(iii) CH₃CHO(g) → CH₄(g) + CO(g)
Rate = k[CH₃CHO]^3/2 
(iv) C₂H₅Cl(g) → C₂H₄(g) + HCl(g), 
Rate = k[C₂H₅Cl] 
Answer:
(i) 3NO(g) → N₂O(g) + N₂O(g)  
Rate = k[NO]₂
Order of reaction = 2 
Unit of rate constant = (mol L^-1)^1-n sec^-1 
(where, n = order of reaction) 
= (mol L^-1)^1-2 sec^-1 
= mol^-1 L sec^-1 
Order of above reaction is 2 and unit of rate constant is mol^-1 L sec^-1. 

(ii) H₂O₂(aq) + 3I^-(aq) + 2H⁺ + 2H₂O(l) + I^-₃, 
Rate = k[H₂O₂] [I^-] 
Order of reaction = 1 + 1 = 2 
Unit of rate constant = (mol L^-1)^1-n sec^-1 
= (mol L^-1)^1-2 sec^-1 
= (mol L^-1)^-1 sec^-1 
= mol^-1 L^-1 sec^-1 
Order of above reaction is 2 and unit of rate constant is mol^-1 L sec^-1 

(iii) CH₃CHO(g) → CH₄(g) + CO(g)
Rate = k[CH₃CHO]^3/2 
Order of reaction = 3/2
Unit of, rate constant = (mol L^-1)^1-n sec^-1 
= (mol L^-1)^1-3/2 sec^-1 
= (mol L^-2)^-1/2 sec^-1 
= mol^-1/2 L^1/2 sec^-1 
Order of above reaction is 3/2 and unit of rate constant is mol^-1/2 L^1/2 sec^-1. 

(iv) C₂H₅Cl(g) → C₂H₄(g) + HCl(g), 
Rate = k[C₂H₅Cl] 
Order of reaction = 1 

Unit of rate constant = (mol L^-1)^1-n sec^-1 
= (mol L^-1)^1-1 sec^-1 
= (mol L^-1)⁰ sec^-1 
= sec^-1 
The order of above reaction is 1 and unit of rate constant is sec^-1. 

Question 4.2. 
For the reaction 2A + B → A2B, the rate = k[A] [B]? with k = 2.0 x 10^-6 mol^-2 L² sec^-1. Calculate the initial rate of the reaction when [A] = 0.1 mol L^-1, [B] = 0.2 mol^-1 Calculate the rate of reaction after (A] is reduced to 0.06 mol L^-1. 
Answer: 
Initial rate = k[A] [B]² 
= 20 x 10^-6 x [0.1] x [0.2]² 
= 20 x 10^-6 x 0.1 x 0.04 
= 8.0 x 10^-9 mol L^-1 sec^-1 
When the concentration of [A] is reduced to 0.06 mol L^-1 from 0.1 mol L^-1 i.e.0.04 mol L^-1 of A is reacted then, 
Concentration of Breacted = 1/2 x 0.04 
= 0.02 mol L^-1 
Thus [B] = 0.2 - 0.02 
= 0.18 mol L^-1 
rate = k[A] [B]² 
Rate = 2.0 x 10^-6 x 0.06 x 0.18 x 0.18 
= 3.89 x 10^-9 mol L^-1 sec^-1. 

Question 4.3. 
The decomposition of NH₃ on platinum surface is zero order reaction. What are the rates of production of N₂ and H₂ k = 2.5 x 10^-4 mol^-1 L sec^-1. 
Answer:
 2NH₃ → N₂ + 3H₂ 
 Rate of reaction = 1/2 (Rate of disappearance of NH₃) 
= (Rate of appearance of N₂) 
= 1/3 (Rate of appearance of H₂) 
Rate of reaction 
= \(\frac{1}{2}\left[\frac{-\Delta\left[\mathrm{NH}_3\right]}{\Delta t}\right]=\left[\frac{\Delta\left[\mathrm{N}_2\right]}{\Delta t}\right]=\frac{1}{3}\left[\frac{\Delta\left[\mathrm{H}_2\right]}{\Delta t}\right]\)
Since the reaction is of zero order, 
Rate = k[NH₃] or 
Rate = 2.5 x 10^-4 mol L^-1 sec^-1.
Rate of production of N₂: 
Rate of reaction = Rate of production of N₂
Rate of production of N2 = 2.5 x 10^-4 mol L^-1 sec^-1. 

Rate of production H₂: 
Rate of reaction = 1/3(Rate of production of H2) 
Rate of production of H₂ = 3 x Rate of reaction 
= 3 x 2.5 x10^-4 
= 7.5 x 10^-4 mol L^-1 sec^-1. 

Question 4.4. 
The decomposition of dimethyl ether leads to the formation of CH₄, H₂ and CO and the reaction rate is given by 
Rate = k[CH₃OCH₃]^3/2 The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e., 
Rate = (PCH₃OCH₃)^3/2 
 If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants? 
Answer:
Order of reaction = 3/2
Unit of rate constant = (bar)^1-n min^-1 
= (bar)^1-3/2 min^-1 
= bar^-1/2 min^-1 
Unit of rate of reaction is bar min^-1 

Question 4.5. 
Mention the factors that affect the rate of a chemical reaction. 
Answer:
The factors which affect the rate of reaction are as follows: 

1. Concentration of reactants: Rate of a chemical reaction is directly proportional to the concentration of reactants. Higher the concentration of the reactant, faster is the reaction, Hence higher will be rate of reaction. 
2. Nature of the reactant: In a chemical reaction, old bonds present in the reactants are broken and new bonds are formed in products. Thus, the rate of reaction depends on the energies of the bonds broken during the reaction and also the number of such bonds involved. 
3. Surface area: Larger the surface area of the reactants, higher is the rate of reaction. Therefore, finely divided solids react faster than solid substances. 
4. Effect of pressure: On increasing pressure, the gaseous reacting molecules come closer to each other hence, the collision between these gaseous molecules increases so the rate of reaction also increases. 
5. Effect of temperature: When the temperature of the reaction is increased, the kinetic energy of reacting molecules increases. Hence rate of reaction also increases. 
6. Effect of Catalyst: The substance which alters the rate of a chemical reaction without itself being consumed in the reaction is called catalyst. It has been observed that use of catalyst increase the speed of many reactions. 

Question 4.6. 
A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concen tration of the reactant is: 
(i) doubled (ii) reduced to half. 
Answer: 
Rate = k[A]₂,
if concentration = a 
then (Rate)₁ = k a? 
(i) If concentration is doubled [A] =2a 
(Rate)₂ = k(2a)² = 4 ka
Thus,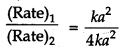
(Rate)₂ = 4 x (Rate),1
i.e., the rate will become 4 times. 

(ii) If concentration is reduced to half 
[A] = a/2
(Rate)₂ = k (a/2)²
(Rate)₂ = 1/4 ka? 
Thus, 

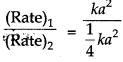
(Rate)₂ = 1/4 x (Rate)₁
 i.e., the rate will become 1/4 times. 

Question 4.7. 
What is the effect of temperature on the rate constant of a reaction? How can this temperature effect on rate constant be represented quantitatively? 
Answer:
The value of rate constant almost becomes double for every 10°C rise in the temperature of reaction. 
Arrhenius gave the following relationship between rate constant and temperature: 
k = Ae^-Ea/RT 
where, A = frequency factor or Arrhenius constant 
or pre-exponential factor 
R = Gas constant 
Ea = Activation energy 
T= Temperature 
k = Rate constant 

Question 4.8. 
In a pseudo first order hydrolysis of ester in water, the following results were obtained: 

t/s	0	30	60	90
Ester/moL-1	0.55	0.31	0.17	0.085

(i) Calculate the average rate of reaction between the time interval 30 to 60 seconds. 
(ii) Calculate the pseudo first order rate constant for  the hydrolysis of ester. 
Answer:
(i) Average rate during the time interval 30 - 60 seconds 
Average rate = \(\frac{C_2-C_1}{t_2-t_1}=\frac{0 \cdot 17-0.31}{60-30}=\frac{-0 \cdot 14}{30}\)
= -4.67 x 10^-3 mol L^-1 s^-1 

(ii) Pseudo first order rate constant 
\(k^{\prime}=\frac{2 \cdot 303}{t} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
Here [A]_o = 0.55 M 
for t = 30 s, 
\(k^{\prime}=\frac{2.303}{30} \log \frac{0.55}{0.31}\)
= 1.91 x 10^-2 s^-1
for t = 60s,
\(k^{\prime}=\frac{2 \cdot 303}{60} \log \frac{0.55}{0 \cdot 17}\)
= 1.96 x 10^-2 s^-1
for t = 90s
\(k^{\prime}=\frac{2.303}{90} \log \frac{0.55}{0.085}\)
= 2.07 x 10^-2 s^-1
Average 
\(k^{\prime}=\left(\frac{1.91+1.96+2.07}{3}\right) \times 10^{-2}\)
= 1.98 x 10^-2 sec^-1 
Here the value of rate constant is 1.98 x 10^-2 sec^-7. 

Question 4.9. 
A reaction is first order in A and second order in B. 
(i) Write the differential rate equation. 
(ii) How is the rate affected on increasing the concentration of B three times. 
(iii) How is the rate affected when the concentration of both A and B are doubled? 
Answer:
(i) Rate = \(\frac{-d x}{d t}\) = k[A] [B]? 
(ii) Let [A] = a, [B] = b. 
(Rate)₁ = k[A] [B]? 
=k x a x b₂ = kab₂ 
When concentration of B is increased to three times 
[B] = 3b 
(Rate)₂ =k x a x (3b)₂ 

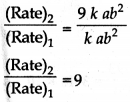
i.e., Rate will become nine times. 

(ii) When concentration of A and B both are doubled 
[A] = 2a, 
[B] = 2b 
(Rate)₂ = k x 2a x (2b)₂ = 8 kab? 

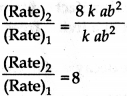
i.e., The rate will become eight times. 

Question 4.10. 
In a reaction between A and B, the initial rate of reaction (ro) was measured for different initial concentration of A and B as given below: 

A/mol L-1	0.20	0.20	0.40
B/mol L-1	0.30	0.10	0.05
C/mol L-1	5.07 x 10-5	5.07 x 10-5	1.43 x 10-4

What is the order of reaction with respect A and B? 
Answer:
Let the order of reaction with respect to A and B are x and y respectively. 
Initial rate, ro =k [A]_x [B]_Y 
with the help of given table 
(ro)₁ = 5.07 x10^-5 = k (0.20)_x x (0.30)y ......... (1)
(ro)₂ = 5.07 x 10^-5 = k (0.20)_x  x (0.10)_y  ........... (2)
(ro)₃ = 1.43 x 10^-4 = k (0.40)_x  x (0.05)_y ....(3) 
on dividing equation (1) by (2) 

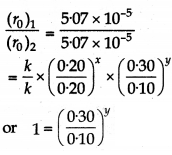
or
1 = (3)^y
or
(3)^o = (3)^y
Thus, y = 0 
on dividing equation (3) by (2) 
\(\frac{\left(r_0\right)_3}{\left(r_0\right)_2}=\frac{14.3 \times 10^{-5}}{5.07 \times 10^{-5}}\)
\(=\frac{k}{k} \times\left(\frac{0.40}{0.20}\right)^x \times\left(\frac{0.05}{0.10}\right)^y\)
or
\(\frac{14.3}{5.07}=(2)^x \times\left(\frac{1}{2}\right)^y\)
Since y = 0
Thus,
\(\frac{14.3}{5.07}\) = (2)_x
2.820 = (2)_x
taking log on both sides 
log 2.820 = log (2)_x 
log 2.820 = x log 2 
0.4503 = x x 0.3010 
\(x=\frac{0 \cdot 4503}{0 \cdot 3010}\)
= 1.5 
Rate 
= k [A]1.5 [B]° 
Overall order of reaction = 1.5 + 0 = 15 

Question 4.11. 
The following results have been obtained during the kinetic studies of the reaction: 
2A + B → C + D 
Experiment [A]/mol L^-2 [B] mol L^-1 Initial rate of formation of 0/mol L^-1 min^-1 

Experiment	[A]/mol L-1	[B] mol L-1	Intial rate of formation of 0/mol L-1 min-1
I	0.1	0.1	6.0 x 10-3
II	0.3	0.2	7.2 x 10-2
III	0.3	0.4	2.88 x 10-1
IV	0.4	0.1	2.40 x 10-2

Determine the rate law and the rate constant for the reaction. 
Answer:
Let, Rate =k[A]_x [B]_y 
on the basis of given experiments 
(Rate)₁ = 60 x 10^-3 = k (0.1)_x (0.1)_y ... (1) 
(Rate)₂ = 7.2 x 10^-2 = k (0.3)_x (0.2)_y ... (2) 
(Rate)₃ = 2.88 10^-1 = k (0.3)_x (0.4)_y ... (3) 
(Rate)₄ = 2.40 10^-2 = k (0.4)_x (0.1)_y ...(4) 
from equation (2) and (3) 

or y = 2 
from equation (1) and (4) 

or x = 1 
Thus, Rate = k[A] [B]² 
Calculation of rate constant from equation (1) 
Rate = k[A] [B]² 
6.0 x 10^-3 = k (0.1) (0.1)² 
k = \(\frac{6.0 \times 10^{-3}}{10^{-3}}\)
= 6.0 mol^-2L² min^-1 

Question  4.12. 
The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table. Experiment [A]/mol L^-1 [B] mol L^-1 Initial rate 

Experiment	[A]/mol L-1	[B] mol L-1	Intial rate of formation of 0/mol L-1 min-1
I	0.1	0.1	2.0 x 10-2
II	-	0.2	4.0 x 10-2
III	0.4	0.4	-
IV	-	0.2	2.0 x 10-2

Answer:
According to the question, 
Rate = k[A] [B]° 
for experiment I, 
2 x 10^-2 = k (0.1)1 (0.1)° 
2 x 10^-2 = k (0.1) 
k = \(\frac{2 \times 10^{-2}}{0.1}\)
= 0.2 min^-1 

for experiment II, 
Rate = k[al]¹ [B]° 
4.0 x 10^-2 = 0.2 x [A]¹ 
[A] = \(\frac{4.0 \times 10^{-2}}{0.2}\)
= 0.2 mol L^-1 

for experiment III, 
Rate = k[A]¹ [B]° 
Rate = 0.2 x (0.4) x (0.4)^o 
Rate = 0.2 x 0.4 
= 0.08 mol L^-1 min^-1 
= 8.0 x 10^-2 mol L^-2 min^-1 

for experiment IV, 
Rate = k[A]¹ [B]² 
2 x 10^-2 = 0.2 x [A]¹ [0.2]° 
\(\frac{2.0 \times 10^{-2}}{0.2}\) = [A] 
[A] = 0.1 mol L^-1 

Question 4.13. 
Calculate the half life of a first order reaction from their rate constants given below: 
(i) 200 s^-1 (ii) 2 min^-1 (iii) 4 years^-1 
Answer:
Half life for the first order reaction is given by 

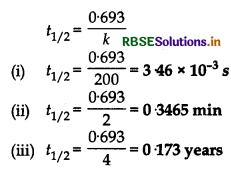
Question 4.14. 
The half life for radioactive decay of 14C is 5730 years. An archeological artifact contained wood had only 80% of the 14C found in a living trees. Estimate the age of the sample. 
Answer: 
Radioactive decay is of first order reaction 

= 1845 years
hence the age of sample = 1845 years 

Question  4.15. 
The experimental data for decomposition of N₂O₅, [2N₂O₅ → 4NO₂ + O₂] in gas phase at 318 k are given below:

t/s	0	400	800	1200	1600	2000	2400	2800	3200
102 x [N2O5]/mol L-1	1.63	1.36	1.14	0.93	0.78	0.64	0.53	0.43	0.35

(i) Plot a graph [N₂O₅] against t. 
(ii) Find the half life period for the reaction.
(üi) Plot a graph between log [N2O5] and t. 
(iv) What is the rate law?
(v) Calculate the rate constant. 
(vi) Calculate the half life period from k and compare it with (ii). 
Answer:
(i) [N₂O₅] Vst plot 

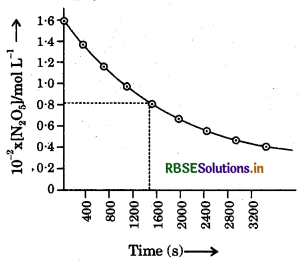
(ii) Initial concentration of 
N₂O₅ = 1.63 x 10^-2 M 
Half of initial concentration 
\(\frac{1.63 \times 10^{-2}}{2}\)
= 0.815 x 10^-2 M 
Time corresponding to half of initial concentration from the [N₂O₅] Vst plot = 1440 s 
i.e.,  t_1/2 = 1440 sec. 

(ii) A graph between log [N₂O₅] and t 

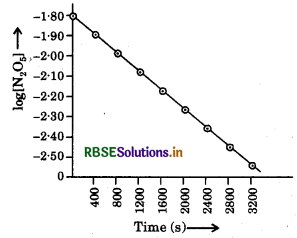
(iv) A graph between log [N₂O₅] and t is a straight line. Hence, it is a first order reaction. 
Thus, 
Rate = k[N₂O₃] 

(v) Slope of the line 

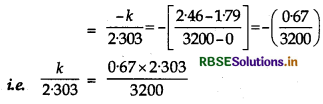
= 4.82 x 10^-4 mol L^-1 s^-1

(vi) 
\(\mathrm{t}_{1 / 2}=\frac{0.693}{k}=\frac{0.693}{4.82 \times 10^{-4}}\)
but t_1/2 calculated from [N₂O₅] vs t plot is 1440 s. 

Question 4.16. 
The rate constant for a first order reaction is 60 s^-4. How much time will it take to reduce the initial concentration of the reactant to its th value? 
Answer:
For first order reaction, 
\(t=\frac{2 \cdot 303}{k} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
According to the question, the final concentration of reaction is a part of the initial concentration 

t = 4.62 x 10^-2 sec 

Question 4.17. 
During nuclear explosion, one of the products 90Sr with half life of 28.1 years. If I ug of 90Sr was. absorbed in the bones of a newly born baby instead of calcium. How much of it will remain after 10 years and 60 years if it is not lost metabolically? 
Answer:
Decay constant (k) = \(\frac{0.693}{t_1}=\frac{0.693}{28.1}\)
= 2.5 x 10^-2 years^-1 
Calculation of amount left ofter 10 years 
[A]_o = 1 ug 
[A] = ? 
t = 10 years 
k = 2.5 x 10^-2 years^-1 
\(k=\frac{2 \cdot 303}{t} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
or
2.5 x 10^-2 = \(\frac{2 \cdot 303}{10} \log \frac{1}{[\mathrm{~A}]}\)
or
2.5 x 10^-2 = \(\frac{2 \cdot 303}{10}\) (-log[A])
or
\(-\log [\mathrm{A}]=\frac{2.5 \times 10^{-2} \times 10}{2.303}\)
or
log[A] = -0.1086
or
[A] = Antilog (-0.1086)
[A] = 0.78 ug
0.2232 ug substance is left after 10 years. Calculation of amount left after 60 years 

Question 4.18. 
For a first order reaction show that time required for 99% completion is twice the time required for the completion of 90% reaction. 
Answer:
Time required for 99% completion, 

dividing equation (1) by (2) 
or
\(\frac{t_{99 \%}}{t_{90 \%}}=\frac{\left(\frac{2.303}{k}\right) \times 2}{\frac{2.303}{k}}=2\)
t99% = 2 x t90%
Hence, proved that time required for 99% completion is twice the time required for the completion of 90% reaction. 

Question 4.19. 
A first order reaction takes 40 minutes for 30% decomposition. Calculate t_1/2 
Answer: 

k = 8.913 x 10^-3 min^-1 
\(t_{1 / 2}=\frac{0.693}{k}=\frac{0.693}{8.913 \times 10^{-3}}\) = 77.7 min 
half life Period = 77.7 min 

Question 4.20. 
For the decomposition of ozoisopropane to hexane and nitrogen at 543 K, the following data is obtained:

T (sec)	P(mm of Hg)
0	35.0
360	54.0
720	63.0

Calculate the rate constant. 
Answer: 
(CH₃)₂CHN = NCH (CH₃)₂(g) → N₂(g) + C₆H₁₄(g)
P Total pressure after time t 
p_t = (P_o - P) + P + P
= P_o + P 
or 
P = P_t -P_o 
since the decomposition of azoisopropane is a first order reaction, therefore 
\(k=\frac{2 \cdot 303}{t} \log \frac{\text { initial pressure }}{\text { final pressure }}\)
or
\(k=\frac{2 \cdot 303}{t} \log \frac{\mathrm{P}_0}{\mathrm{P}_0-\mathrm{P}}\)
substituting the value of P 

= 2.235 x 10^-3 sec^-1
average value of k = \(\left(\frac{2 \cdot 175+2 \cdot 235}{2}\right)\) x 10^-3 
= 2.20 × 10^-3 sec^-1 

Question 4.21. 
The following data were obtained during the first order thermal decomposition of SO₂Cl₂ at a constant volume. 
SO₂Cl₂(g) → SO₂(g) + Cl₂(g) 
Calculate the rate of reaction when total pressure is 0.65 atm 

Experiment	Time/S-1	Total pressure /atm
1	0	0.5
2	100	0.6

Answer:
SO₂Cl₂(g) → SO₂(g) + Cl₂(g) 

Intial pressure	po	O	O
After time t	Po - P	P	P

Total pressure after timet 
P_t = (P_o - x) + x + x 
P_t = P_o + x 
x = P_t - P_o 
initial pressure = P_o 
final pressure = P_o - x = P_o - (P_t - P_o) = 2P_o - P_t 

k = 2.2316 x 10^-3 sec^-1. 
when P = 0.65 atm 
(P_o + P) = 0 65 atm 
P = 0 65 - P_o
= 0 65 - 0.50 
= 0.15 atm 
PSO₂Cl₂ = P_o - P 
= 0.50 - 0.15 = 0 35 atm 
at time'ť 
Rate = k x PSO₂Cl₂ 
= 2.2316 x 10^-3 x 0.35 atm
= 78 x 10^-4 atm sec^-1 
hence when total pressure is 0.65 atm them rate will be 7.8 x 10^-4 atm sec^-1 

Question 4.22. 
The rate constant for the decomposition of N₂O₅ at various temperatures is given below: 

T/C	0	20	40	60	80
105 x k/s-1	0.0787	1.70	25.7	178	2140

Draw a graph between In k and and calculate the values of A and E, Predict the rate constant to 30°C and 50° C. 
Answer:
For drawing a curve between log k and 1/T following table is needed:

T(K)	273	293	313	333	353
1/T	0.003663	0.00343	0.003195	0.003003	0.002833
K(s)-1	0.0181 x 10-5	1.70 x 10-5	25.7 x 10-5	178 x 10-5	2140 x 10-5
Log k	-6.1040	-4.7696	-3.5901	-2.7496	-1.6996

A graph between logk and 
 
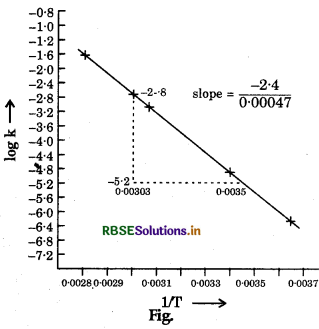
Slope = \(\frac{-2 \cdot 4}{0 \cdot 00047}=\frac{-E_a}{2 \cdot 303 R}\)
Activation energy (Ea) 
= \(\frac{2.4 \times 2.303 \times R}{0.00047}=\frac{2.4 \times 2.303 \times 8.314}{0.00047}\)
= 97772 67 J mol^-1 
we know that 
log k = log A - \(\frac{E_a}{2303 R T}\)
logk = \(\left(\frac{E_a}{2 \cdot 303 R}\right) \frac{1}{T}+\log A\)
Comparing with y = mx + C
Log A = intercept on Y axis 
i.e. value of intercept on k axis 
= (-1 + 72) = 6.2 [y₂ - Y_ı]
= -1- (-72)] 
froquency factor A = antilog 6.2 = 1585000 
= 1.585 x 106 collisions sec^-1 
value of k can be calculated with the help of curve 

T	1/T	Value of log k from curve	Value of k
303 k	0.003300	-4.2	6.31 x 10-5 sec-1
323 k	0.003096	-2.8	1.585 x 10-3 sec-1

Question 4.23. 
The rate constant for the decomposition of hydrocarbons is 2.418 x 10^-2 S^-1 at 546 k. If the energy of activation is 179.9 kJ/mol, what will be the value of pre exponential factor? 
Answer:
K = 2.418 x 10^-5 sec^-1 
Ea = 179.9 kJ/mol = 179.9 103 J/mol 
T = 546 K 
According to Arrhenius equation, 
log k = log A - \(\frac{\mathrm{E}_a}{2.303 \mathrm{RT}}\)
log A = log k + \(\frac{\mathrm{E}_a}{2.303 \mathrm{RT}}\)
= log 2.418 x 10⁵ + \(\frac{179.9 \times 10^3}{2.303 \times 8.314 \times 546}\)
= (-5 + 0.3834) + 17.2081 = 12.5915 
A = Anti log (12.5915) 
or A = 3.904 x 10¹² s^-1.
Hence, the value of pre exponential factor is 3.904 x 10¹² s^-1 

Question 4.24. 
Consider a certain reaction A → products with k = 2.0 x 10^-2 s^-1. Calculate the concentration of A remaining after 100 s, if the initial concentration of A is 10 mol L^-1
Answer:
k = 20 x 10^-2 sec^-1 
[A]_o = 1.0 mol L^-1 
t = 100 sec 
[A] = ? 
\(k=\frac{2 \cdot 303}{t} \log \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)
2.0 x 10^-2 = \(\frac{2 \cdot 303}{100} \log \frac{1 \cdot 0}{[\mathrm{~A}]}\)
or
\(\frac{2.0 \times 10^2 \times 100}{2 \cdot 303}\) = - log [A]
or
- log [A] = 0.8684
or
log[A] = -0.8684 
[A] = Anti log(-0.8684) 
[A] = 0.1354 mol L^-1 
Hence, after 10 sec the remaining concentration will be 0.1354 mol L^-1. 

Question 4.25. 
Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t₁₂ = 3. 00 hours. What fraction of sample of sucrose remains after 8 hours? 
Answer:
For first order reaction, 

Let, initial concentration is 1 mol/L, then 
[A]o = 1 
∴ 
\(\frac{[\mathrm{A}]_0}{[\mathrm{~A}]}=6.344\)
or
1/[A] = 6.344
or 
[A] = 1/6344
∴[A] = 0.157 mol/L 
Hence, after 8 hours the remaining concentration of surcose will be 0.157 mol L^-1. 

Question 4.26. 
The decomposition of hydrocarbon follows the equation 
k = (4.5 x 10¹¹ s^-1) e^{- 28000K/T}. Calculate Ea. 
Answer:
According to Arrhenius equation, 
k= Ae^-Ea/RT ...... (1)
According to question, 
k = (4.5 x 10¹¹ s^-1) e^{- 28000 K/T} ...(2) 
Comparing equations (1) and (2), 
\(\frac{-\cdot \mathrm{E}_a}{\mathrm{RT}}=\frac{-28000 \mathrm{~K}}{\mathrm{~T}}\)
or
E_a = 28000K xR 
E_a = 28000K x 8.314 JK^-1 mol^-1 
or
E_a = 232.792J mol 
∴ E_a = 232.792 kJ mol^-1 
Hence, the value of activation energy will be 232.792 kJ/mol. 

Question 4.27. 
The rate constant for the first order decom position of H₂O₂ is given by the following equation: 
log k = 14.34 - 1.25 x 10⁴ K/T 
Calculate E, for this reaction and at what temperature will the half period be 256 minutes. 
Answer:
From Arrhenius equation, 
log k = log A - \(\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{RT}}\) ...(1) 
According to question, 
log k = 14.34 - 1.25 x 10⁴ K/T 
Comparing equations (1) and (2), 
\(\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{RT}}=\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\)
∴Ea = 2 303 x R x 125 x 10⁴ K 
= 2.303 x 1.25 x 10⁴ x 8.314 
= 239340 J mol^-1 
= 239.34 kJ mol^-1 
Now 
t_1/2 = 256 minutes = 256 x 60 sec. 
\(k=\frac{0 \cdot 693}{t_{1 / 2}}\)

= \(\frac{0.693}{256 \times 60}\)
= 4.51 x 10^-5 sec^-1 
Substituting the value of k in equation (2), 
log (4.51 x 10^-5) = 14.34 - \(\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\)
or (log 4.51 + log 10^-5) = 14.34 - \(\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\)
or (0.6542 - 5) = 14 34 - \(\frac{1.25 \times 10^4 \mathrm{~K}}{\mathrm{~T}}\)
∴  \(T=\frac{1 \cdot 25 \times 10^4}{186858}\)
K = 669K 
Hence, temperature = 669 K. 

Question 4.28. 
The decomposition of A into product has value of k as 4.5 x 10's^-1 at 10°C and energy of activation 60 kJ mol^-1. At what temperature would kbe 1.5 x 10⁴ s^-1? 
Answer:
k₁ = 4.5 x 10³ s^-1 
T₁ = 10 + 273 
= 283 K 
k₂ = 1.5 x 10⁴ s^-1 
T₂ = ? 
Ea = 60 kJ/mol = 60 x 10°J/mol 
According to Arrhenius equation 
 
0.0472T₂ = T₂ - 283 
T₂ - 0.0472T₂ = 283 
0.9528T₂ = 283 
∴ T₂ = \(\frac{283}{0.9528}\)
= 297 K 
= (297 - 273)°C 
Hence, 
Temperature = 24°C.

Question 4.29. 
The time required for 10% completion of a first order reaction at 298 K is equal to that required for its 25% completion at 308 K. If the value of A is 4 x 1010 8-1, Calculate k at 318 K and Ea. 
Answer:
At 298 K, reaction is 10% completed, 

At 308 K, the reaction is 25% completed. 

= 2.7338 
According to Arrhenius equation, 

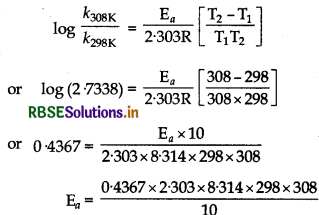
= 76745J/mol 
= 76745 kJ/mol 
Calculation of k at 318 K, 
log k = log A - \(\frac{\mathrm{E}_a}{2 \cdot 303 \mathrm{RT}}\)

\(=\log \left(4 \times 10^{10}\right) \times \frac{76745}{2 \cdot 303 \times 8 \cdot 314 \times 318}\)
= 10.6021 - 12.6043
= -2.022
 k = Anti log (-2.0022)
 = Anti log (3.9978)
 = 9.949 x 10^-3 s^-1
Hence, at 318 K temperature the value of k is 9.949 x 10^{- 3} sec^-1. 

Question 4.30. 
The rate of reaction quadruples when the temperature changes from 298 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature. 
Answer:
According to the question, 

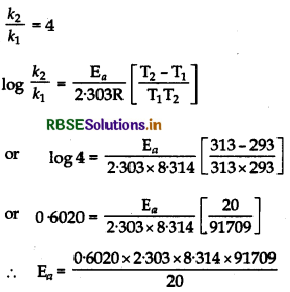
= 52854J/mol 
= 52.854 kJ/mol.