RBSE Solutions for Class 12 Chemistry Chapter 3 Electrochemistry

Rajasthan Board RBSE Solutions for Class 12 Chemistry Chapter 3 Electrochemistry Textbook Exercise Questions and Answers.

RBSE Class 12 Chemistry Solutions Chapter 3 Electrochemistry

RBSE Class 12 Chemistry Electrochemistry InText Questions and Answers

Question 3.1. 
How would you determine the standard electrode potential of the system Mg²⁺Mg?
Answer:
To determine the standard electrode potential of Mg/Mg²⁺ electrode, a magnesium electrode is placed in 1.0 M Mg SO₄ solution and is combined with S.H.E. as shown in Fig.

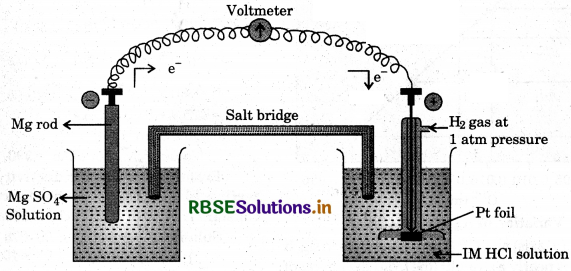
The E.M.F. of the cell is measured with the help of voltameter. In this case, the reading by the voltameter is 2.37 volt and the direction of current is from SHE to Mg / Mg²⁺ electrode. Thus, in this cell, Mg /Mg²⁺ electrode acts as anode and SHE acts as cathode. 
The cell may be represented as:
Mg | Mg²⁺ (1M) | | H⁺ (1M)/H₂ (1 atm), Pt
E°cell = E°_H+/1/2H2 - E°Mg²⁺/Mg
= 0.0 - E°Mg²⁺|Mg
Thus, 
E°Mg²⁺|Mg = -E°Cell
In this way, we can determine the electrode potential of Mg²⁺/Mg electrode.

Question 3.2. 
Can you store copper sulphate solution in a zinc pot?
Answer:    
E°zn²⁺| zn = -0.76 V
E°cu²⁺| CU = 0.34 V
This indicates that zinc is stronger reducing agent than copper. It displaces the copper from CuSO₄ solution as 
Zn(s) + CuSO₄(aq) → ZnSO₄(aq) + Cu(s)
Hence, we cannot store copper sulphate solution in a zinc pot.

 

Question 3.3. 
Consult the table of standard electrode potentials and suggest three substances which can oxidise ferrous ions under suitable conditions.
Answer: 
The oxidation of Fe²⁺ ions takes place as follows:
Fe²⁺ → Fe³⁺ + E°red = 0.77V
Only those substances can oxidise Fe²⁺ ions which have their reduction potential values higher than that of Fe²⁺ ions. For example: acidified KMnO₄, acidified Cr₂O₇^2- , acidified H₂O₂.

Question 3.4. 
Calculate the potential of hydrogen electrode in contact with a solution whose pH is 10.
Answer:    
pH = 10
PH = -log[H⁺]
[H⁺] = 10-PH 
[H⁺] = 10^-10 mol L^-1 
For hydrogen electrode
H⁺ + e^- → 1/2 H₂
Thus,

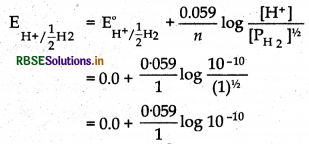
= 0.059 (-10 log 10)
= 0.059 x -10
= - 0.59 V
E°_H+/1/2H2 = - 0.59 V

Question 3.5. 
Calculate EMF of the cell in which the following reaction takes place:
Ni(s) + 2Ag⁺ (0.002M) → Ni²⁺ (0.160M) + 2Ag(s)
Given that E°ce11 = 1.05 V
Answer:
Nemst equation for the above cell,
\(\mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^{\mathrm{o}}+\frac{0.059}{n} \log \frac{[\mathrm{Ni}]\left[\mathrm{Ag}^{+}\right]^2}{\left[\mathrm{Ni} i^{2+}\right][\mathrm{Ag}]^2}\)
Since [Ni] = [Ag] = 1
Thus

= 1.05 - 0.14
= 0.19 V
E°ce11 = 0.19 v

Question 3.6. 
The cell in which the following reaction occurs:
2Fe³⁺(aq) + 2I^-(aq)  → 2Fe²⁺(aq)  + I₂(s)
has E°cell = 0.236V at 298 K. Calculate the standard Gibbs energy and the equilibrium constant of the cell reaction.
Answer:
2Fe³⁺ + 2e^- → 2Fe²⁺
2I^- → I₂ + 2e^-
Thus, for the given cell reaction n = 2
∆G° = -nFE°cell    
= -2 x 96500 x 0.236J 
= -45.55 kJ/mol 
∆G° = -2.303 RT log Kc 

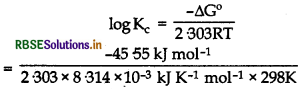
logKc = 7.983
Kc = Antilog (7.983) 
= 9.616 x 10⁷

Question 3.7. 
Why does the conductivity of a solution decrea¬ses with dilution ?
Answer: 
Conductivity of the solutionis the conductance of ions present per unit volume of electrolytic solution. On dilution, number of ions per unit volume decreases, hence, conductivity also decreases.

Question 3.8. 
Suggest a way to determine value of water.
Answer: 
Water is a weak electrolyte for water
can be obtained from the knowledge of molar conductance at infinite dilution of sodium hydroxide, hydrochloric acid and sodium chloride. (All are strong electrolyte)
\(\Lambda_{m\left(\mathrm{H}_2 \mathrm{O}\right)}^0=\Lambda_{m(\mathrm{NaOH})}^0+\Lambda_{m(\mathrm{HCl})}^0-\Lambda_{m(\mathrm{NaCl})}^0\)

Question 3.9. 
The molar conductance of 0.05 mol L-¹ of methanoic acid is 46.15 cm² mol^-1. Calculate its degree of dissociation and dissociation constant Given  λ°(H⁺) = 349.6
S cm² mol^-1 and  λ°(Hcoo^-) = 54.6 S cm² mol^-1
 Answer:
\(\Lambda_m^o(\mathrm{HCOOH})=\lambda_{\left(\mathrm{H}^{+}\right)}^o+\lambda_{\left(\mathrm{HCOO}^{-}\right)}^{\circ}\)
 = 349.6 + 54.6
 = 404.2 SCm² mol^-1
 Given λm(HCOOH) = 461. S cm² mol^-1

= 0.114
\(\mathrm{K}=\frac{\mathrm{C} \alpha^2}{1-\alpha}=\frac{0.025 \times(0.114)^2}{1-0.114}\)
 = 3.67 x 10^-4
 value of dissociation constant is 3.67 x 10^-4
 
Question 3.10. 
If a current of 0.5 ampere flows through a metallic wire for 2 hours, then how many electrons flow through the wire?
Answer: 
Q = It
I = 0.5 A
t = 2 x 60 x 60s
Q = 0.5 x 2 x 60 x 60 = 3600 C
96500 C is equivalent to flow of → 1 mol electrons
3600 C is equivalent to flow of → \(\frac{3600}{96500}\) mol electrons
= \(\frac{3600 \times 6.023 \times 10^{23}}{96500}\)
= 2.246 x 10²² electrons
Thus, 2.246 x 10²² electrons flow through the wire.

Question 3.11. 
Suggest a list of metals which can be extracted electrolytically.
Answer: 
Na, Ca, Mg and Al.

Question 3.12. 
Consider the reaction:
Cr₂O₇^2- + 14H⁺ + 6e^- → 2Cr³⁺ + 7H₂O
What is the quantity of electricity in coulombs needed to reduce 1 mole of Cr₂O₇^2- ions?
Answer:
I mol of Cr₂O₇^2- need 6 mol of electrons for reduction to Cr³⁺
Thus, quantity of electricity = 6F
= 6 x 96500C = 579000C. 

Question 3.13. 
Write the chemistry of recharging the lead storage battery highlighting all the material that are involved during rechargin
Answer: 
During charging. electrical energy is supplied to cell using an external source of electrical energy. It means cell behaves like an electrolytic cell. Reactions occuring
during the charging is opposite to the reaction occuring during the discharging of cell. Following reactions take place during charging:
PbSO₄(5) + 2e^- → Pb(s) + SO₂^-4(aq)
PbSO₄(s) + 2H₂O → PbO₂(s) + SO₂^-4(aq) + 4H⁺(aq) + 2e^-
2PbSO₄(s) + 2H₂O → Pb(s) + PbO₂(s) + 4H⁺ + 2SO₂^-4(aq)

Question 3.14. 
Suggest two materials other than hydrogen that can be used as fuels in the fuel cells.
Answer: 

1. Methanol (CH₃OH)
2. Methane (CH4)

Question 3.15. 
Explain how rusting of iron can be envisaged as setting up of an electrochemical cell.
Answer:
Rusting of iron is an electrochemical process since it considers the formation of small electrochemical cell on the surface of iron in which pure iron acts as anode, impure iron acts as cathode and water drops containing dissolved CO₂ and O₂ acts as electrolyte. Reaction at anode: Iron is oxidised and Fe²⁺, ions go into the solution.
Fe → Fe²⁺ + 2e (oxidation)
Reaction at cathode: The electron released at anode are accepted by W ions which are formed by the ionisation of H₂O and H₂CO₃ (formed by the reaction between CO₂ and H₂O)
\(\mathrm{H}_2 \mathrm{CO}_3 \rightleftharpoons 2 \mathrm{H}^{+}+\mathrm{CO}_3^{2-}\)
\(\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}^{+}+\mathrm{OH}^{-}\)
These hydrogen atoms reduce dissolved oxygen in water,
2H + 1/2 O₂ → H₂O
The over reaction at cathode  can be written as
2H⁺ + 1/2O2 + 2e^- → H₂O
Thus, the overall reaction occuring in electrochemical cell is: 
Fe(s) + 1/2O₂ + 2H⁺ → Fe²⁺ + H₂O
These Fe²⁺ ions are oxidesd by atom pherse or diisolved oxygen and form ferric oxide on the surface of iron.
4Fe²⁺ + O₂ + 4H₂O → 2Fe₂O₃ + 8H⁺
Fe₂O₃ + xH₂O → Fe₂O₃. xH₂O Rust

RBSE Class 12 Chemistry Electrochemistry Textbook Questions and Answers

Question 3.1.
Arrange the following metals in the order in which they displace each other from the solution of their salt. Al, Cu, Fe, Mg and Zn.
Answer:
Mg, Al, Zn, Fe, Cu

Question 3.2. 
Given the standard electrode potentials
K⁺/K = 2.93 V, 
Ag⁺/Ag = 0.80V
Hg²²⁺/Hg = 0.79V, 
Mg²⁺/Mg = -2.37V
Cr²⁺/Cr = -0.74V
Arrange these metals in increasing order of their reducing power
Answer:
Higher the value of oxidation potential, greater is the tendency of element to get oxidised and hence, greater is the reducing power. Thus, increasing order of reducing
power of metals is as follows:
Ag < Hg < Cr < Mg < K

Question 3.3. 
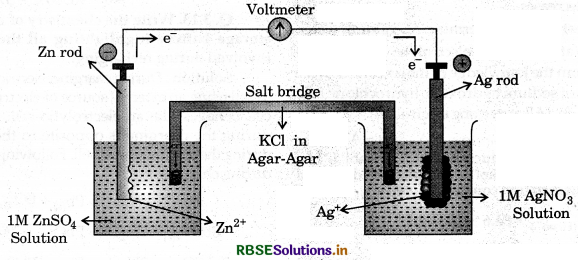
Depict the galvanic cell in which the reaction
Zn(S) + 2Ag) → Zn²⁺(aq) + 2Ag(s)
takes place. Further show:
(j) Which of the electrode is negatively charged?
(ii) The carriers of the current in the cell.
(iii) Individual reaction at each electrode.
Answer:
(i) The electrode at which oxidation occurs i.e. anode is negatively charged. Hence, Zn electrode is negatively charged.
(ii) Electrons are the carrier of the current in the cell,
(iii) Reaction taking place at the electrodes are as
follows:
At anode Zn(s) → Zn²⁺(aq) + 2e^-
At cathode Ag⁺(aq) + e^- → Ag(s)
The cell can be represented by the following diagram.

Question 3.4. 
Calculate the standard cell potentials of galvanic cells In which the following reactions take place:
(i) 2Cr(s)  + 3Cd²⁺(aq) → 2Cr³⁺(aq)  + 3Cd(s)
Given that E°Cr³⁺/Cr  = - 0.74V
E°Cd²⁺/Cd = -0.40 V
(ii) Fe²⁺(aq)  +  Ag⁺(aq) → Fe³⁺(aq) + Ag(s)
Given E°Ag⁺/Ag = 0.80V, E°Fe³⁺/Fe²⁺ = -0.77 V
Also calculate ∆rG° and equilibrium constants of the reactions.
Answer:
(i) 2Cr(s) + 3Cd²⁺(aq)  → 2Cr³⁺(aq) + 3Cd(s)
E°Cell = E°(Cathode) - E°(Anode)
= E°_(Cd²⁺/Cd) - E°_(Cr³⁺/Cr)
= - 0.40V - (- 0.74V)
= - 0.40V + 0.74V 
= + 0.34V
∆G° = -nFE°Cell
= -6 x 96500 x 0.34
= - 196860 J mol^-1
= - 196.860 kJ mol^-1
∆G° = - 2.303 RT log K_c
-196.860 kJ  = -2.303 x  8.314 x 298 x log K_c
or 196860J = 2.303 x 8.314 x 298 x 1ogK_c
\(\frac{196860 \mathrm{~J}}{2.303 \times 8.314 \times 298}\) = logK_c
logKc = 34.5014
Kc = Antilog 34.5014
= 3.173 x 10³⁴
Gibbs energy of the cell (∆G°) = -19686 kJ/mol
Equilibrium cortant of the cell (Kc) = 3.173 x 10³⁴

(ii) Fe²⁺(aq) + Ag⁺(aq) → 
E°Cell = E°(cathode) - E°(Anode)
= 0.80V - 0.77V
= + 0.03 V
∆G° = -nFE°Cell
= -1 x 96500 x 0.03
= -2.895 kJ/mol
∆G° = -2.303RT logK_c
-2895 =  - 2.303 x 8.314 x 298 x log K_c
\(\frac{2895}{2.303 \times 8.314 \times 298}\) = log Kc
log K_c = 0.5074
K_c = Antilog 0.5074
K_c = 3.22
Gibbs free energy of the cell
= - 2.895kJ/mol
Equilibrium constant of the cell
= 3.22

Question 3.5. 
Write the Nemst equation and the e.m.f. of the following cells at 298 K:
(i) Mg(s) | Mg²⁺ (0.001 M) || Cu²⁺ (0.0001M) | Cu(S)
(ii) Fe(s) | Fe²⁺(0.001M) || H⁺(1M) | H₂(g) (lbar)/Pt(s)
(iii) Sn(s) | Sn²⁺(o.o50M) || H⁺(0.020M) | H₂(g)(1bar) | Pt(s)
(iv) Pt(s) | Br₂(I) | Br^- (0.10M) || H⁺ (0.030M) | H₂(g) (1bar) | Pt(s)
Answer:
(i) Mg(s) | Mg²⁺ (0.001 M) || Cu²⁺ (0.0001M) | Cu(S)
EMg²⁺/Mg = -2.37V, E(Cu²⁺/Cu) = + 0.34V
Cell reaction for the above cell is
Mg + Cu²⁺ → Mg²⁺ + Cu 
Nemst equation is
\(\mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^{\circ}+\frac{0 \cdot 059}{n} \log \frac{[\mathrm{Mg}]\left[\mathrm{Cu}^{2+}\right]}{\left[\mathrm{Mg}^{2+}\right][\mathrm{Cu}]}\)

Since [Mg] = [Cu] = 1 then

= 2.71 - 0.0295 
= 2.6805 
= 2.68 v

(ii) Fe(s) | Fe²⁺(0.001M) || H⁺(1M) | H₂(g) (lbar)/Pt(s)
Cell reaction for the above cell is
Fe + 2H⁺ → Fe²⁺ + H₂ (n = 2)
E(Fe²⁺/Fe) = - 0.44 V, 
E°_H+/1/2H2 = 0.0V
Nemst equation is
\(\mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^{\circ}+\frac{0.059}{n} \log \frac{[\mathrm{Fe}]\left[\mathrm{H}^{+}\right]^2}{\left[\mathrm{Fe}^{2+}\right]\left[\mathrm{P}_{\mathrm{H}_2}\right]}\)
Here [Fe] = (pH₂) = 1

= 0.44 + 0.0887
= 0.528V    

(iii) Sn(s) | Sn²⁺(0.050M) || H⁺(0.020M) | H₂(g)(1bar) | Pt(s)
Cell reaction for the above cell is
Sn + 2H⁺ → Sn²⁺ + H₂, E(Sn²⁺/Sn) = 0.14v
\(\mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^o+\frac{0.059}{n} \log \frac{[\mathrm{Sn}]\left[\mathrm{H}^{+}\right]^2}{\left[\mathrm{Sn}^{2+}\right]\left(\mathrm{P}_{\mathrm{H}_2}\right)}\)
Since [Sn] = 1, (PH₂) = 1

= 0.14 - 0.062 = 0.078 V

(iv) Pt(s) | Br₂(I) | Br^- (0.10M) || H^₊ (0.030M) | H₂(g) (1bar) | Pt(s)
Cell reaction for the above cell is
2Br^- + 2H⁺ → Br₂ + H₂ (n = 2)
E°_H+/1/2H2 = 0.0v,
E°_{(1/2Br2/Br^-)} = +1.08 v
\(\mathrm{E}_{\text {cell }}=\mathrm{E}_{\text {cell }}^{\circ}+\frac{0.059}{n} \log \frac{\left[\mathrm{Br}^{-}\right]\left[\mathrm{H}^{+}\right]^2}{\left[\mathrm{Br}_2\right]\left[\mathrm{P}_{\mathrm{H}_2}\right]}\)
Here, [Br₂] = 1,
[PH₂] = 1

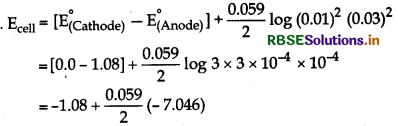
= -1.08V - 0.2078 
= 1.2878 V
= 1.288 V

Question 3.6. 
In the button cell widely used in watches and other devices, the following reaction takes place:
Zn(s) + Ag₂O(s) + H₂O(I) → Zn²⁺(aq) + 2Ag(s) + OH^-(aq)
Determine E° and ∆rG° for the reaction
Given Zn → Zn²⁺ + 2e^-
E° = 0.76 V
Ag₂O + H₂O + 2e^- → 2Ag + 2OH^-, E° = 0.344 v
Answer:
Here Zn is oxidised hence, it acts as anode and AgO is reduced i.e., Ag⁺ ions are reduced into Ag. There¬fore, it acts as cathode.
E°(Zn²⁺/Zn) = -0.76 V' E°(Ag⁺/Ag) = 0.80 V
E°cell = [E°(Cathode) - E°(Anode)]
= E°(Ag⁺/Ag) - E°(Zn²⁺/Zn)
= 0.80 - (-0.76)
= 0.80 + 0.76 
= 1.56 V
∆G° = -nFE°Cell
= - 2 x 96500 x 1.56 
= 301080 J/mol 
= -3.01 x 10⁵ J/mol 
= - 3.01 x 10² kJ/mol
∆G°  = - 3.01 x 10² KJ/mol

Question 3.7. 
Define conductivity and molar conductivity for solution of an electrolyte. Discuss their variaton with concentration. Discuss their variation with concentration.
Answer:
Let us explain some basic terms before we study the conductance of electricity through electrolytic solutions:
(1) Specific conductance or conductivity: The reciprocal of resistivity of a conductõr is called conductivity.
It is represented by the symbol ic(Greek : kappa).

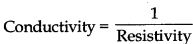
K = 1/p
or
K = 1/R x (l/A)
or
K = G x l/A
Its units are \(\Omega\)^-1 cm^-1 or Sm^-1
if = 1 cm, A =1cm² then K
Thus, conductivity is the conductance of solution of an electrolyte placed between two electrodes of 1cm² area of cross-section separated by one cm i.e., conductance of one centimeter cube of the solution of an electrolyte is called conductivity.

(6) Molar conductivity: Molar conductivity is defined as conductance of the solution containing one mole of the electrolyte placed between the two electrodes lying 1 cm apart and having area of cross-section large enough to accommodate whole of the solution. It is represented by 
Molar conductivity \(\left(\Lambda_m\right)\) = \(\frac{\kappa \times 1000}{C}\)

where, k is specific conductance or conductivity, C is concentration of solution in mol L^-1 which is also called molar concentration and is denoted by M.
\(\Lambda_m=\frac{\kappa \times 1000}{\mathrm{M}}\)
Units of molar conductivity are ohm^-1 cm² mol^-1 or SCm² mol^-1
Debye Huckel and Onsagar gave the following equation to show the variation of molar conductivity with concentration:
\(\lambda_m^c=\lambda_m^{\infty}-\mathrm{A} \sqrt{\mathrm{C}}\)
Here, \(\lambda_m^c\) = molar conductivity at concentration C
\(\lambda_m^{\infty}\) =  molar conductivity at infinite dilution
C = molar concentration of solution
A = Constant which depends upon nature of solvent and temperature.

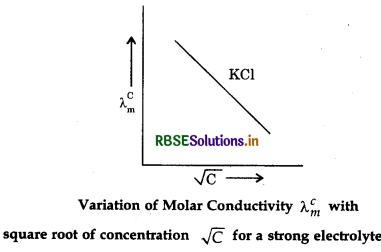
The value of constant A foragivenlvent and temperature depends upon the type of electrolyte i.e., charges on the cation and anion produced on the dissociation of electrolyte. Thus, KCl is konwn as 1-1 electrolyte, CaCl₂ as 2-1 electrolyte, Na₂SO₄ as 1-2 electrolyte. The variation of molar conductivity with concentration can also be shown by plotting a graph between \(\Lambda_m\) and \(\sqrt{C}\) A graph between \(\Lambda_m\) and \(\sqrt{C}\) for KCI (a strong electrolyte) is shown in Fig. 3.4 in molar conductivity with dilution. When the graph is extrapolated to zero concentration, the intercept gives the molar conductivity atinfinite dilution \(\Lambda_m^{\circ}\)

Question 3.8. 
The conductivity of 0.20 M solution of KCl at 298 K is 0.0248 S cm^-1. Calculate its molar conductivity.
Answer:
Molarity (Q) = 0.02 M
Conductivity (K) = 0.0248 S cm^-1
Molar Condcutivity imm    
= 124 S cm² mol^-1
Molar conductivity of solution = 124 S cm² mol^-1

Question 3.9. 
The resistance of a conductivity cell contain-ing 0.001 M KCl solution at 298 K is 1500 ft. What is the cell constant if conductivity of 0.001 M KCl solution at 296 K is 0.146 x 10^-3 S cm^-1 ?
Answer:
Molarity (M)= 0.001 M 
Resistance (R) = 1500 Ω
Conductivity ( K ) = 0.146 x 10^-3 S cm^-1 
Cell constant (G) = ?
Conductivity (K)= 1/R x G*
Cell Constant (G*) = K x R
= 0.146 x 10^-3 x 1500 
= 0.219 cm^-1    

Question 3.10. 
The conductivity of NaCl at 298 K has been determined at different concentrations and the results are given below Calculate ∧m for all concentrations and draw a plot between ∧m and C1/2. Find the value of ∧m from the graph.
Answer:


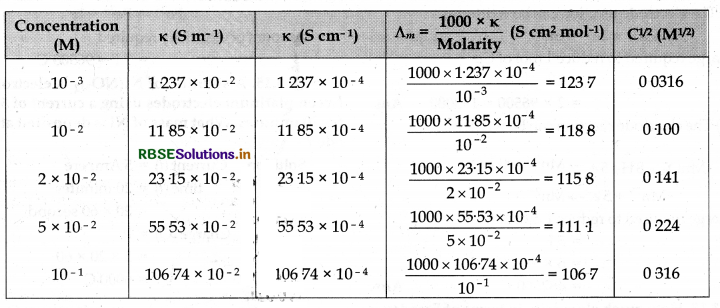
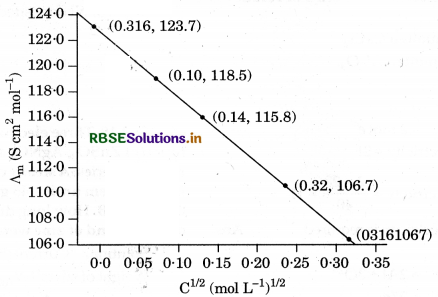
∧°m = intercept on ∧m axis = 124.0 S cm² mol^-1 

Question 3.11. 
Conductivity of 0.00241 M acetic acid is 7.896 x 10^-5 S cm^-1. Calculate its molar conductivity. If ∧m for acetic acid is 390.5 S cm² mol^-1, what is its dissociation constant ?
Answer:
Concentration (C) = 0.00241 M

Conductivity ( K ) = 32.76 
Molar Conductivity (∧m) = ?
Molar conductivity at infinite dilution (∧m) = 390.5 S Cm² mol^-1
= 0.084
\(\begin{aligned} \alpha &=\frac{\Lambda_m^c}{\Lambda_m^{\circ}} \\ &=\frac{32.76}{390.5} \end{aligned}\)
= 1.86 x 10^-5
Dissociation constant = 1.86 x 10^-5

Question 3.12. 
How much charge is required for the following reduction of:
(i) 1 mol of Al³⁺ to Al
(ii) 1 mol of Cu²⁺ to Cu
(iii) 1 mol of MnO^-4 to Mn²⁺
Answer:
(i) The electrode reaction can be written as 
Al³⁺ + 3e^-  → Al
Charge required to reduce 1 mol of Al³⁺
= 3F
= 3 x 96500 C 
= 289500 C

(ii)  The electrode reaction can be written as
Cu²⁺ + 2e^- → Cu
Charge required to reduce 1 mol of Cu²⁺
= 2F
= 2 x 96500 
= 193000 

(iii)  The electrode reaction can be written as
MnO^-4 + 8H⁺ + 5e^- → Mn²⁺ + 4H₂O 
Mn⁷⁺ + 5e^- → Mn²⁺
Charge required to reduce 1 mol of Mn²⁺
= 5F
= 5 x 96500 C
= 482500 C    

Question 3.13. 
How much electricity in terms of Faraday is required to produce:
(i) 20.0 g of Ca from molten CaCl₂
(ii) 40.0 g of Al from molten Al₂O3.
Answer:
(i) In CaCl₂
Ca²⁺ + 2e^- → Ca 
40 g of Ca require electricity = 2F
20 g of Ca require electricity = \(\frac{2 \times 20}{40}\) = IF
i.e., one Faraday of electricity is required.    

(ii) In Al₂O₃
Al₂O₃ + 6e^- →    2Al + 3O^2-
3 mol 27g electrons
2 x 27 g Al require electricity = 6F
40 g Al require electricity = \(\frac{6 \times 40}{54}\)F
i.e., 4.44 Faraday of electricity is required. 

Question 3.14. 
How much electricity is required in Coulomb for the oxidation of:
(i) 1 mol of H₂O to O₂?
(ii) 1 mol of FeO to Fe₂O₃?
Answer:
(i) The electrode reaction can be written as
H₂O → 2H⁺ + 1/2 O₂ + 2e^-
i.e, Amount of electricity required
= 2F
= 2 x 96500C
= 193000 C

(ii) The electrode reaction can be written as
2FeO + 1/2 O₂ → Fe₂O₃
Fe²⁺ → Fe³⁺ + 1e^-
Amount of electricity required
= 1F = 96500 C

Question 3.15. 
A solution of Ni(NO₃)₂ is electrolysed be¬tween platinum electrodes using a current of 5 amperes for 20 minutes. What mass of Ni is deposited at the cathode?    
Answer:
Current (i) = 5 Ampere 
time (t) = 20 minutes
= 20 x 60 seconds
Charge (Q) = If
= 5 x 20 x 60 
= 6000 C
Mass of Ni deposited =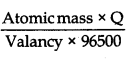
= \(\frac{58.7 \times 6000}{2 \times 96500}\)
= 1.825 g    

Question 3.16. 
Three electrolytic cells A, B, C containing so-lution of ZnSO₄, AgNO₃ and CuSO₄ respectively are con-nected in series. A steady current of 1.5 ampere was passed through them until 1.45 g of silver deposited at the cathode of cell B. How long did the current flow? What mass of copper and of zinc were deposited ?
Answer:
Current (I) = 1.5 Ampere 
Weight of silver (W_Ag) = 1.45 g 
Ag⁺ + e^- → Ag 
108 g of Ag is deposited by = IF
= 96500 C electricity 
1.45 g of Ag is deposited by
= \(\frac{96500 \times 1.45}{108}\)
Q = i x t
\(t=\frac{\mathrm{Q}}{\mathrm{I}}=\frac{1295.6}{1.5}\)
= 14 min 24 s 
Cu²⁺ + 2e^- → Cu 63.5 g
2 x 96500 C electricity deposit
= 63.5 g of Cu
1295.6 C electricity deposit
= \(\frac{63.5 \times 1295.6}{2 \times 96500}\)
= 0.426 g of Cu
Similarly, 
Zn²⁺ + 2e^- → Zn
2 x 96500 C electricity deposit = 65.4g of Zn
1295.6 C electricity deposit
\(=\frac{65.4 \times 1295.6}{2 \times 96500}\)
= 0.44g of Zn

Question 3.17. 
Using the given standard electrode potential, predict if the reaction between the following is feasible:
(i) Fe³⁺(aq) and I^-(aq)
(ii) Ag⁺(aq) and Cu (s)
(iii) Fe³⁺(aq) and Br^-(aq)
(iv)  Ag(s) and Fe³⁺(aq)
(v) Br₂(aq) and Fe²⁺(aq)
Given standard electrode potentials:
\(\begin{aligned} &\mathrm{E}_{1 / 2 \mathrm{I}_2, \mathrm{I}^{-}}^{\Theta}=0.541 \mathrm{~V} \\ &\mathrm{E}_{\mathrm{Cu}^{2+}, \mathrm{Cu}}^{\Theta}=+0.34 \mathrm{~V} \end{aligned}\)
\(\begin{aligned} \mathrm{E}_{1 / 2 \mathrm{Br}_2, \mathrm{Br}^{-}}^{\Theta} &=+1.09 \mathrm{~V} \\ \mathrm{E}_{\mathrm{Ag}^{+}, \mathrm{Ag}}^{\Theta} &=0.80 \mathrm{~V} \end{aligned}\)
\(\mathrm{E}_{\mathrm{Fe}^{3+}, \mathrm{Fe}^{2+}}^{\Theta}=+0.77 \mathrm{~V}\)
Answer:
A reaction is feasible if EMF of the cell reaction is positive
(i) Reaction taking place between Fe³⁺(aq) and I^-(aq) is 
Fe³⁺(aq) + I^-(aq) → Fe²⁺ + 1/2I₂
Fe³⁺ is reduced and I" is oxidised
E°cell = E°(Cathode) -  E°(Anode)
= E°(Fe³⁺/Fe²⁺) - E°(l/2I₂/I^-)
= 0.770 - 0.541 
= 0.229 V
(Reaction is feasible)    

(ii)  2Ag⁺(aq) + Cu → 2Ag(s) + Cu²⁺(aq)
Here, Ag⁺ is reduced and Cu is oxidised
E°cell = E°(Cathode) - E°(Anode)
E°cell = E°(Ag⁺/Ag) - E°(Cu²⁺/Cu)
 = 0.80 - 0.34 
 = 0.46        
(Reaction is feasible) 

(iii)  Fe³⁺(aq) + Br^-(aq) → Fe²⁺(aq) + 1/2Br₂ 
Here, Fe³⁺ is reduced and Br^- is oxidised
E°cell = E°(Cathode) - E°(Anode)
= E°(Fe³⁺/Fe²⁺) - E°(l/2Br₂/Br^-)
= 0.77 -1.09 
= - 0.32 V
(Reaction is not feasible) 

(iv)  Ag(s) + Fe³⁺(aq) → Ag⁺(aq) + Fe²⁺(aq)
Here, Ag is oxidised and Fe³⁺ is reduced
E°cell = E°(cathode) - E°(Anode)
= E°(Fe³⁺/Fe²⁺) - E°(Ag⁺/Ag)
= 0.77 - 0.80 
= - 0.03 V
(Reaction is not f easible) 

(V) 1/2Br₂(aq) + Fe²⁺(aq) → Br^- + Fe³⁺(aq)
Here, Br₂ is reduced and Fe²⁺ is oxidised
E°cell = E°(Cathode) - E°(Anode)
= 1.09 - 0.77    v
= 0.32V
(Reaction is feasible) 

Question 3.18. 
Predict the products of electrolysis in each of the following:
(i) An aqueous solution of AgNO₃ with silver electrodes.
(ii) An aqueous solution of AgNO₃ with platinum electrodes.
(iii)  A dilute solution of of H₂SO₄ with platinum electrodes.
(iv) An aqueous solution of CuCl₂ with platinum electrodes.
Answer:
(i) Electrolysis of aqueous solution of AgNO₃ with silver electrodes:

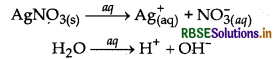
At cathode: Discharge potential of Ag⁺ ion is lower than that of H⁺ ions. Hence, Ag⁺ ions will be deposited in preference to H⁺ ions.
Ag⁺ + e^- → Ag
At anode: As silver electrode is attacked by NO₃ ions, Ag from anode dissolves to form Ag⁺ ions which go into the solution 
Ag⁺ + e^- → Ag
Thus, Ag is deposited at cathode and an equivalent amount of silver is oxidised to Age ions from anode.

(ii) Electrolysis of an aqueous solution of AgNO₃ with platinum electrodes.

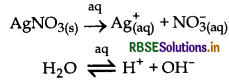
At cathode: Ag ions have lower discharge potential than H’ ions. Hence, Ag ions will be deposited at cathode in preference to H⁺ ions.
Ag⁺ + e^- → Ag
At anode: Here, OH^- ions have lower discharge potential than NO ions. Hence, OH^- ions will decompose to give O₂
OH^- → OH + e^-
4OH → 2H₂O + O₂
Thus, Ag is deposited at cathode and O₂ is liberted at anode. 

(iii) Electrolysis of dilute solution of H₂SO₄ with platinum electrodes
H₂SO₄(aq) → 2H⁺(aq) + SO₂^-4(aq)

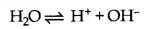
At Cathode: H⁺ + e^- → 1/2H₂

At anode: Since OH^- has lower discharge pontential.
it decomposes to give O₂
OH^- → OH + e^-
4OH → 2H₂O + O₂
Thus, H₂ gas is liberated at cathode and O₂ gas is liberated at anode. 

(iv) Electrolysis of an aqueous solution of CuCl₂ with platinum electrodes

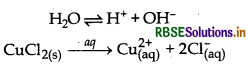
At Cathode: Cu²⁺ have lower discharge potential than H⁺ ions, hence Cu²⁺ ions are deposited at cathode.
Cu²⁺ + 2e^- → Cu
At anode: Cl- ions has lower discharge potenetial than OH^- ions. Hence CI ions are oxidised in preference to OH^- ions 
2Cl^- → Cl₂ + 2e^-
Thus, Cu is deposited at cathode and Cl₂ is liberated at anode.