RBSE Solutions for Class 12 Chemistry Chapter 2 विलयन

Rajasthan Board RBSE Solutions for Class 12 Chemistry Chapter 2 विलयन Textbook Exercise Questions and Answers.

RBSE Class 12 Chemistry Solutions Chapter 2 विलयन

RBSE Class 12 Chemistry विलयन InText Questions and Answers

प्रश्न 1. 
यदि 22g बेन्जीन में 122 g कार्बन टेट्राक्लोराइड घुली हो तो बेन्जीन एवं कार्बन टेट्राक्लोराइड के द्रव्यमान प्रतिशत की गणना कीजिए।
उत्तर:
विलयन का द्रव्यमान = बेन्जीन का द्रव्यमान + कार्बन टेट्राक्लोराइड का द्रव्यमान।
- 22 g+ 122 g - 144g 
बेन्जीन का द्रव्यमान प्रतिशत

\(=\frac{22 \mathrm{~g}}{144 \mathrm{~g}} \times 100\)
= 15.28%
कार्बन टेट्राक्लोराइड का द्रव्यमान प्रतिशत

\(=\frac{122 \mathrm{~g}}{144 \mathrm{~g}} \times 100\)
= 84.72%
वैकल्पिक रूप में,
कार्बन टेट्राक्लोराइड का द्रव्यमान प्रतिशत 
= 100 - बेन्जीन का द्रव्यमान प्रतिशत 
= 100 - 15.28 = 84.72%

प्रश्न 2. 
एक विलयन में बेन्जीन का 30% द्रव्यमान कार्बन टूटाक्लोराइड में घुला हुआ हो तो बेन्जीन के मोल-अंश की गणना कीजिए। 
उत्तर:
माना विलयन का द्रव्यमान = 100g 
अत: बेन्जीन का द्रव्यमान = 30g 
कार्बन टेट्राक्लोराइड का द्रव्यमान = 100 - 30.70g 
बेन्जीन के मोलों की संख्या

\(=\frac{30 \mathrm{~g}}{78 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 0.385g mol-
इसी प्रकार CCl₄ के मोलों की संख्या
\(=\frac{70 \mathrm{~g}}{154 \mathrm{~g} \mathrm{~mol}^{-1}}=0.455 \mathrm{~mol}\)
बेन्जीन के मोल-अंश

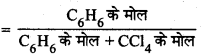
कार्बन टेट्राक्लोराइड के मोल-अंश 
= 1 - 0.458 = 0.542
\(=\frac{0.385}{0.205+0.455}=0.458\)

 

प्रश्न 3. 
निम्नलिखित प्रत्येक विलयन की मोलरता की गणना कीजिए:
(क) 30g, CO(NO)₂.6H₂O 43 लीटर विलयन में घुला हुआ
(ख) 30 mL 0.5M H₂SO₄ को 500 mL तनु करने पर। 
उत्तर:
(क) CO(NO)₂.6H₂O का मोलर द्रव्यमान
=58.7 + 2(14 + 48) + 6 x 18g mol-
= 58.7 + 124 + 108 gmol-
= 290.7g mol-
CO(NO)₂.6H₂O के मोल की संख्या

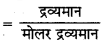
\(=\frac{30 \mathrm{~g}}{290.7 \mathrm{~g} \mathrm{~mol}^{-1}}=0 \cdot 103\)
विलयन का आयतन = 4.3 L

\(\frac{0 \cdot 103}{4 \cdot 3 \mathrm{~L}}\)
= 0.02M

(ख) दिया गया है,
V₁ = 30m 
M₁ = 0.5M
V₂ = 500 ml 
M₂ = ?
M₁V₁ = M₂V₂ 
= 0.5 x 30 = M₂ x 500
\(\frac{0.5 \times 30}{500}=\mathrm{M}_2\)
∴ M₂ = 0.03 M 
विलयन की मोलरता = 0.03 M

प्रश्न 4. 
यूरिया (NH₂CONH₂) के 0.25 मोलर, 2.5 kg जलीय विलयन को बनने के लिए आवश्यक यूरिया के द्रव्यमान की गणना कीजिए।
उत्तर:
n_b = 0.25 mol 
विलेय का अणु भार
= NH₂CONH₂ 
= 14 x 2 + 1 x 4 + 12 + 16
= 28 + 4 + 12 + 16 = 60g/mol 
विलेय का भार = मोलों की संख्या - मोलर द्रव्यमान
= 0.25 x 60 
विलेय का भार = 15g 
विलयन का कुल भार = (1000 + 15) = 1015g
अतः
∵ 1015g विलयन में यूरिया = 15g 
∴ 2500 g विलयन में यूरिया = \(\frac{15}{1015} \times 2500\)
= 37g

प्रश्न 5. 
20% (w/W) जलीय KI का घनत्व 1-202 g/mL हो तो KI विलयन की (क) मोलरता, (ख) मोललता (ग) मोल अंश की गणना कीजिए।
उत्तर:
विलेय का भार = 20g 
विलायक का भार = 100 - 20
= 80g 
KI का अणुभार = 39 + 127
= 166g/mol 

(क) मोलरता : विलयन का आयतन V(_mL)
=  
= \(\frac{100}{1 \cdot 202} \mathrm{~mL}\)
w_B = 20g 
M_B = 166 g/mol

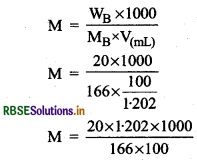
M = 1.44 mol/L

(ख) मोललता: 
\(\begin{aligned} m &=\frac{\mathrm{W}_{\mathrm{B}} \times 1000}{\mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}} \\ &=\frac{20 \times 1000}{166 \times 80} \end{aligned}\)
 ∴ m = 1.5 mol/kg 
 
(ग) KI के मोल अंश

KI के मोल अंश = 0.0263

प्रश्न 6. 
सड़े हुए अण्डे जैसी गन्ध वाली विषैली H₂S गुणात्मक विश्लेषण में उपयोग की जाती है। यदि H₂S गैस की जल में STP पर विलेयता 0.195m हो तो हेनरी स्थिरांक की गणना कीजिए।
उत्तर:
H₂S की विलेयता = 0.195m 
अर्थात् 
विलेय के मोल n_B = 1000g 
विलायक का भार W_B = 2 x 1 + 32
= 34g 
विलायक का मोलर द्रव्यमान M_A = 18g
विलायक के मोल = \(\frac{1000}{18}\)
= 55.5 mol-
\(x_{\mathrm{H}_2 \mathrm{~S}}=\frac{n_{\mathrm{H}_2 \mathrm{~S}}}{n_{\mathrm{H}_2 \mathrm{~s}}+n_{\mathrm{H}_2 \mathrm{O}}}=\frac{0 \cdot 195}{0 \cdot 195+55 \cdot 5}\)
\(=\frac{0 \cdot 195}{55 \cdot 695}\) = 0.0035
SIP पर दाब (PH₂S) = 0.987 bar 
अत: हेनरी के नियमानुसार,
PH₂s = K_H x H₂S
या \(\mathrm{K}_{\mathrm{H}}=\frac{p_{\mathrm{H}_2 \mathrm{~s}}}{x_{\mathrm{H}_2 \mathrm{~s}}}\)
या \(\mathrm{K}_{\mathrm{H}}=\frac{0.987}{0.0035}\)
∴  KH = 282 bar 
हेनरी का नियतांक = 282 bar

प्रश्न 7.
298 K पर CO₂ गैस की जल में विलेयता के लिए हेनरी स्थिरांक का मान 1.67x 10⁸ Pa है। 500 mL सोडा जल 2.5 atm दाब पर बन्द किया गया है। 298 K ताप पर घुली हुई CO₂ की मात्रा की गणना कीजिए। 
उत्तर:
KH = 1.67 x 108 Pa
PCO₂  = 2.5 atm
= 2.5 x 101325 Pa 
= 2.533 x 105 Pa 
\(\begin{aligned} &x_{\mathrm{CO}_2}=\frac{p_{\mathrm{CO}_2}}{\mathrm{~K}_{\mathrm{H}}}=\frac{2.533 \times 10^5}{1.670 \times 10^8} \\ &x_{\mathrm{CO}_2}=1.517 \times 10^{-3} \end{aligned}\)

\(x_{\mathrm{CO}_2}=\frac{{ }^n \mathrm{CO}_2}{{ }^n \mathrm{CO}_2+{ }^n \mathrm{H}_2 \mathrm{O}}\)
चूंकि
\(n_{\mathrm{CO}_2} \ll n_{\mathrm{H}_2 \mathrm{O}}\)
अतः
\(x_{\mathrm{CO}_2}=\frac{{ }^n \mathrm{CO}_2}{{ }^n \mathrm{H}_2 \mathrm{O}}\)
जल का आयतन = 500ml. 
अत: जल का भार = 500g (क्योंकि d = 1.00 gmL) 
nH₂O = \(\frac{500}{18}\)
अत: 1.517 x 10^-3 =  \(\frac{{ }^n \mathrm{CO}_2}{27 \cdot 78}\)
1.517 x 10^-3 x 27.78 = nCO₂
या 42.14 x 10^-3 mol = nco2 
CO₂ की मात्रा = 42.14 x 10^-3 x 44
= 1.854g 
अत: CO₂ की मात्रा 1.854g है।

प्रश्न 8. 
350 K पर शुद्ध द्रवों A एवं B के वाष्प दाब क्रमशः 450 एवं 750 mm Hg है। यदि कुल वाध्य दाब 600 mmHg हो तो दव मिश्रण का संघटन ज्ञात कीजिए। साथ ही वाष्य प्रावस्था का संघटन भी ज्ञात कीजिए। 
उत्तर:
A का वाष्प दाब P⁰_A = 450 mmHg
B का वाष्प दाब P⁰_B = 750 mm Hg 
कुल वाध्य दाब PT = PA + Ps.
= P⁰_A χ_A + P⁰_B  χ_B
600 = 450(χ_A) + 750 (1 - χ_A)​​
600 =  450(χ​​​​​​​_A) + 750 - 750 χ​​​​​​​_A
300(χ​​​​​​​_A) = 150

 

A का मोल अंश χ​​​​​​​_A = ​​​​\(\frac{150}{300}\) = 0.5
B का मोल अंश χ​​​​​​​_B = 1 - 0.5 = 0.5
वाष्प प्रावस्था में, 
p_A = 0.5 × 450 = 225 mm Hg
P_B = 0.5 × 750 = 375 mm Hg

A का मोल अंश \(y_{\mathrm{A}}=\frac{p_{\mathrm{A}}}{p_{\mathrm{A}}+p_{\mathrm{B}}}\)

(वाष्प प्रावस्था में) 

A का मोल अंश  \(y_{\mathrm{A}}=\frac{225}{225+375}\)

(वाष्प प्रावस्था में) 
= \(\frac{225}{600}\) = 0.375
B का मोल अंश \(y_{\mathrm{B}}=\frac{375}{225+375}\)
= \(\frac{375}{600}\) = 0.625
मिश्रण में, A का मोल अंश = 0.5
B का मोल अंश = 0.5
वाष्प प्रावस्था में, A का मोल अंश =  0.375
B का मोल अंश = 0.625

प्रश्न 9.
298K पर शुद्ध जल का वाष्प दाब 23.8mm Hg है। 850g जल में 50g यूरिया NH₂CONH₂ घोला जाता है। इस विलयन के लिए जल के वाष्प दाब एवं इसके आपेक्षिक अवनमन का परिकलन कीजिए।

उत्तर:
दिया है:
P0 = 23.8 mm
W_B = 50 g  M_B (यूरिया) = 60g mol-

W_A = 950 g M_A (जल) = 18g mol-
हमें विलयन के वाष्प दाब, p_s तथा आपेक्षिक अवनमन \(\left(p^0-p_{\mathrm{S}}\right) / p^0\) की गणना करनी है। रॉउल्ट का नियम लागू करने पर,

= 0.017
अतः वाष्प दाब का आपेक्षिक अवनमन = 0.017
\(\frac{p^0-p_{\mathrm{s}}}{p^0}\) = 0.017
\(\frac{23 \cdot 8-p_5}{23 \cdot 8}\) = 0.017
या  23.8 - P_s = 0.017 × 23.8
23.8 - P_s = 0.4046
 या  p_s = 23.8 - 0.406
या p_s = 23.3954mm
\(p_{\mathrm{s}} \approx 23.40 \mathrm{~mm}\)
अतः विलयन में जल का वाष्प दाब 23.40mm है।

प्रश्न 10.
750 mm Hg दाब पर जल का क्वथनांक \(99.63^{\circ} \mathrm{C} \) है। 500g जल में कितना सुक्रोस मिलाया जाए कि इसका \(100^{\circ} \mathrm{C}\) पर. क्वथन हो जाए ?
उत्तर:
सुक्रोस ( C₁₂ H₂₂ O₁₁) का आण्विक द्रव्यमान
= 12 × 12 + 22 × 1 + 11 × 16 = 342g mol-
जल के लिए  kb = 0.52 g mol- 
∆ Tb = 100 - 99.63 = 0.37 K
W_A = 500g
सूत्र \(\Delta \mathrm{T}_b=\mathrm{K}_b \cdot \frac{1000 \mathrm{~W}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{B}} \mathrm{W}_{\mathrm{A}}}\)
\(\mathrm{W}_{\mathrm{B}}=\frac{\Delta \mathrm{T}_b \times \mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}}{1000 \times \mathrm{K}_b}\)
\(=\frac{0.37 \mathrm{~K} \times 0.342 \mathrm{~kg} \mathrm{~mol}^{-1} \times 500 \mathrm{~g}}{1000 \times 0.52 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}}\)

= 0.122 Kg = 122g
जल में सुक्रोस का भार = 122g

प्रश्न 11.
ऐस्कॉर्बिक अम्ल (विटामिन C,C₆H₈O₆ ) के उस द्रव्यमान का परिकलन कीजिए जिसे 75 g ऐसीटिक अम्ल में घोलने पर उसके हिमांक में \(1.5^{\circ} \mathrm{C}\) की कमी हो जाए। K_f = 3.9 K kg mol^-1
उत्तर:
ऐस्कॉर्बिक अम्ल का आण्विक द्रव्यमान
= 6  × 12 + 8  × 1 + 6  × 16
= 176g mol-

\(\Delta \mathrm{T}_f=\mathrm{K}_f \frac{1000 \mathrm{~W}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{B}} \mathrm{W}_{\mathrm{A}}}\)
\(\mathrm{W}_{\mathrm{B}}=\frac{\Delta \mathrm{T}_f \times \mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}}{\mathrm{K}_f \times 1000}\)
\(=\frac{1.5 \times 176 \times 75}{3.9 \times 1000}\)
= 5.08g
विटामिन C का भार = 5.08g

प्रश्न 12.
185000 मोलर द्रव्यमान वाले एक बहुलक के 1.0g को \(37^{\circ} \mathrm{C}\) पर 450mL जल में घोलने से उत्पन्न विलयन के परासरण दाब का पास्कल में परिकलन कीजिए।
उत्तर:
मोलर द्रव्यमान M_B = 185000g mol
विलेय का भार W_B =1.0g
ताप T = 37 + 273 = 310 K
आयतन V = 450 mL = 0.450L
गैस नियतांक R = 8.314 kPa LK^-1 mol^-1 = 8.314 \(\times\) 10³ Pa L K^-1 mol^-1
परासरण दाब  \(\pi\)  = ?
\(\pi=\frac{\mathrm{W}_{\mathrm{B}} \times \mathrm{R} \times \mathrm{T}}{\mathrm{M}_{\mathrm{B}} \times \mathrm{V}}\)
\(=\frac{1 \times 8.314 \times 10^3 \times 310}{185000 \times 0.45}\)
= 30.96 a
विलयन का परासरण दाब = 30.96 a

RBSE Class 12 Chemistry विलयन Textbook Questions and Answers

प्रश्न 1. 
विलयन का परिभाषित कीजिए। कितन विभिन्न प्रकार के विलयन सम्भव हैं? प्रत्येक प्रकार के विलयन के सम्बन्ध में एक उदाहरण देकर संक्षेप में लिखिए।
उत्तर:
विलयन-यह दो या दो से अधिक अवयवों का समांगी मिश्रण है। इसमें दो अवयव होते हैं
(i) विलेय-जो अवयव कम मात्रा में उपस्थित होता है, उसे विलेय कहते हैं।
(ii) विलायक-जो अवयव अधिक मात्रा में उपस्थित होता है, उसे विलायक कहते हैं। 
'विलयन के प्रकार (Type of Solution):

विलयनों के प्रकार	विलेय	विलेय	सामान्य उदाहरण
1. गैसीय विलयन	गैस द्रव ठोस	गैस गैस गैस	ऑक्सीजन व नाइट्रोजन गैस का मिश्रण क्लोरोफॉर्म व नाइट्रोजन गैस का मिश्रण
2. द्रव विलयन	गैस द्रव ठोस	द्रव द्रव द्रव	कपूर का नाइट्रोजन गैस में मिश्रण जल में घुली हुई ऑक्सीजन जल में घुला हुआ एथेनॉल जल में घुला हुआ ग्लूकोस
3. ठोस विलयन	गैस द्रव ठोस	ठोस ठोस ठोस	हाइड्रोजन का पैलेडियम में विलयन पारे का सोडियम के साथ अमलगम ताँबे का सोने में विलयन

प्रश्न 2. 
एक ठोस विलयन का उदाहरण दीजिए जिसमें विलेय कोई गैस हो।
उत्तर:
हाइड्रोजन गैस का पैलेडियम में विलयन जिसमें विलेय हाइड्रोजन गैस है।

प्रश्न 3. 
निम्नलिखित पदों को परिभाषित कीजिए:
(i) मोल अंश, 
(ii) मोललता, 
(iii) मोलरता, 
(iv) द्रव्यमान प्रतिशत
उत्तर:
(i) द्रव्यमान प्रतिशत (Mass Percentage; w/W): विलेय पदार्थ के द्रव्यमान भागों की वह संख्या जो विलयन के 100 ग्राम द्रव्यमान भागों में उपस्थित हो, विलयन की द्रव्यमान प्रतिशतता कहलाती है।
द्रव्यमान % या % w/W
= 
या

द्रव्यमान प्रतिशतता = \(\frac{\mathrm{W}_{\mathrm{A}}}{\mathrm{W}_{\mathrm{A}}+\mathrm{W}_{\mathrm{B}}} \times 100\)

W_A = विलेय का द्रव्यमान g में
W_B = विलायक का द्रव्यमान g में
W_A  + W_B = विलायक का द्रव्यमान g में
उदाहरणार्थ:  10%(w/W) का अर्थ है कि 10 g विलेय 100g विलयन में उपस्थित है, यहाँ विलायक की मात्रा (100 - 10) = 90 g है।

(ii) आयतन प्रतिशत (Volume Percentage; v/V): विलेय पदार्थ के आयतन भागों की वह संख्या जो विलयन के 100 mL आयतन भागों में घुली हो, विलयन की आयतन/आयतन प्रतिशतता कहलाती है। अवयव का प्रतिशत आयतन ( % v /V)

या

\(=\frac{\frac{72}{18}}{\frac{72}{18}+\frac{92}{46}}\)
= 4/6 = 0.067
एथिल ऐल्कोहॉल का मोल अंश = 1 - 0.067
= 0.33

(vi) मोलरता (Molarity): एक लीटर (1 dm³ ) विलयन में घुले हुए विलेय के मोलों की संख्या को उस विलयन की मोलरता M कहते हैं।

माना B विलेय तथा A विलायक है, तो

\(\mathrm{M}=\frac{n_{\mathrm{B}}}{\mathrm{V}_{(\mathrm{L})}}\)
यहाँ nB =  विलेय के मोल की संख्या
V(L) = विलयन का आयतन  L में
\(\begin{aligned} &\mathbf{M}=\frac{\mathrm{W}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{B}} \times \mathrm{V}_{(\mathrm{L})}} \\ &\mathbf{M}=\frac{\mathbf{W}_{\mathbf{B}} \times \mathbf{1 0 0 0}}{\mathbf{M}_{\mathbf{B}} \times \mathbf{V}_{(\mathrm{mL})}} \end{aligned}\)
यहाँ 
W_B = विलेय की मात्रा ग्राम में
M_B = विलेय का मोलर द्रव्यमान 
(V_mL) = विलयन का आयतन mL में
अतः 
1000 mL जल का द्रव्यमान = 1000g
1000 mL जल में जल के मोल = 1000/18 = 55.5

(vii) मोललता (Molality): किसी विलयन की मोललता (m) 1kg विलायक में उपस्थित विलेय के मोलों की संख्या होती है।

माना कि B विलेय तथा A विलायक है, तो 
मोललता = \(\frac{n_{\mathrm{B}}}{\mathrm{W}_{\mathrm{A}}(\mathrm{kg})}\)

मोललता = \(\frac{\mathrm{W}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}(\mathrm{kg})}\)

मोललता = \(\frac{\mathrm{W}_{\mathrm{B}} \times 1000 \times m}{\mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}(\mathrm{g})}\)
W_A (g) = विलायक का द्रव्यमान g में
n_B = विलेय के मोलों की संख्या
W_B = विलेय का द्रव्यमान g में 
M_B = विलेय का मोलर द्वव्यमान

प्रश्न 4. 
प्रयोगशाला कार्य के लिए प्रयोग में लाया जाने वाला सान्द्र नाइट्रिक अम्ल द्रव्यमान की दृष्टि से नाइट्रिक अम्ल का 68% जलीय विलयन है। यदि इस विलयन का घनत्व 1.504 g/mL हो तो अम्ल के नमूने की मोलरता क्या होगी?
उत्तर:
विलेय का द्रव्यमान W_B = 68g
विलेय का अण भार W_B = 63 g / mol
(घनत्व) d = 1.504 g /mL
विलयन का भार = 100 g
विलयन का आयतन = 
=\(\frac{100}{1 \cdot 504} \mathrm{~mL}\)

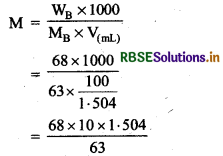
= 16.23M
दिये नमूने की मोलरता 16.23M text है। 

प्रश्न 5.
ग्लूकोस का एक जलीय विलयन 10 % (w / W) है। विलयन की मोललता तथा विलयन में प्रत्येक घटक का मोल-अंश क्या है ? यदि विलयन का घनत्व 1.2 g mL^-1 हो तो विलयन की मोलरता क्या होगी ?
उत्तर:
 10 % (w/W) ग्लूकोस के जलीय विलयन का अर्थ है कि 10 g  ग्लूकोस 100g  विलयन में उपस्थित है। अर्थात् इसमें 90 g = 0.09kg जल उपस्थित है।
(i) मोललता 
10 g ग्लूकोस  = \(\frac{10}{180} \mathrm{~mol}\) = 0.0555mol
90 g H2O = \(\frac{90}{18}\) = 5mol
मोललता = \(\frac{0.0555 \mathrm{~mol}}{0.090 \mathrm{~kg}}\) = 0.617m

(ii) मोल अंश
x(ग्लूकोस)   \(=\frac{0.0555}{5+0.0555}\) = 0.01
\(x_{\left(\mathrm{H}_2 \mathrm{O}\right)}\) = 1 - 0.01 = 0.99

(iii) मोलरता

100 g विलयन = \(\frac{100}{1.2} \mathrm{~mL}\)
= 83.33mL = 0.08333L
मोलरता = \(\frac{0.0555}{0.08333}\) = 0.67 M

प्रश्न 6.
यदि 1g मिश्रण में Na₂CO₃ एवं NaHCO₃ के मोलों की संख्या समान हो तो इस मिश्रण से पूर्णत: क्रिया करने के लिए 0.1 M HCI के कितने mL की आवश्यकता होगी?
उत्तर:
मिश्रण में अवयवों के मोलों की संख्या ज्ञात करना-माना मिश्रण में Na₂CO₃ के x g उपस्थित हैं।
∴ मिश्रण में उपस्थित NaHCO3 = (1 - x) g 
Na₂CO₃ का मोलर द्रव्यमान
= 2 x 23 + 12 + 3 x 16 = 106 g mol^-1
NaHCO₃ का मोलर द्रव्यमान
= 23 + 1 + 12 + 3 × 16
=84 g mol-1
x g में Na₂CO₃ के मोल = \(\frac{x}{106}\)
तथा (1 - x) g में NaHCO₃ के मोल = \(\frac{1-x}{84}\)
चूँकि मिश्रण में दोनों के मोलों की संख्या समान है, अत
\(\frac{x}{106}=\frac{1-x}{84}\)
या 106 - 106 x = 84 x
या x = \(\frac{106}{190} \mathrm{~g}\) = 0.558 g
अत: Na₂CO₃ के मोलों की संख्या
= \(\frac{0.558}{106}\) = 0.00526
NaHCO₃ के मोलों की संख्या
= \(\frac{1-0.558}{84}\)
= \(\frac{0 \cdot 442}{84}\) = 0.00526
आवश्यक HCI के माल ज्ञात करना:

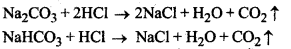
उपर्युक्त अभिक्रिया-समीकरणों से स्पष्ट है कि 1 मोल Na₂CO₃ के लिए आवश्यक
HCl = 2mol
∴ 0.00526 मोल Na₂CO₃ के लिये आवश्यक
HCI = 0.00526 × 2mol
= 0.010502 mol
1 मोल NaHCO₃ के लिए आवश्यक

HCl = 1 mol
∴ 0.00526 मोल NaHCO₃ के लिए आवश्यक
HCI = 0.00526 × 1mol
= 0.010526 mol
 कुल आवश्यक  HCl = 0.01052 + 0.00526 
= 0.01578 mol

0.1 M HCI का आयतन ज्ञात करना:
0.1 M HCI के 0.1 mol उपस्थित हैं
= 1000 mL HCl में
0.01578 mol 0.1 M HCl उपस्थित होंगे
= \(\frac{1000}{0.1}\) ×  0.01578 mL HCI  में 
= 157.8 mL 

प्रश्न 7.
द्रव्यमान की दृष्टि से 25 % विलयन के 300 g एव 40% के 400g को आपस में मिलाने पर प्राप्त मिश्रण का द्रव्यमान प्रतिशत सान्द्रण निकालिए।
उत्तर:
 25% विलयन के 300 g में उपस्थित विलेय
= \(\frac{25}{100} \times 300\) = 75 g
40 % विलयन के 400 g में उपस्थित विलेय
= \(\frac{40}{100} \times 400\) = 160 g
विलेय की कुल मात्रा
= 75 + 160 = 235 g
विलयन का कुल द्रव्यमान
= 300 + 400 = 700 g
परिणामी विलयन में विलेय की प्रतिशत
= \(\frac{235}{700} \times 100\) = 33.57%
परिणामी विलयन में विलायक का प्रतिशत
= 100 - 33.57 =  66.43 %

प्रश्न 8. 
222.6 g ऐथिलीन ग्लाइकॉल, C₂ H₄(OH) ₂ तथा 200 g जल को मिलाकर प्रतिहिम मिश्रण बनाया गया। विलयन की मोललता की गणना कीजिए। यदि विलयन का घनत्व 1.072g mL-1 हो तो विलयन की मोलरता निकालिए।
उत्तर:
विलेय का द्रव्यमान W_B = 222.6 g
विलेय C₂ H₄(OH)₂ का अणुभार
M_B = 62 g mol
विलायक का द्रव्यमान W_A = 200 g
विलायक का अणुभार M_A = 18 g mol^-1
मोललता M = \(\frac{\mathrm{W}_{\mathrm{B}} \times 1000}{\mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}}\)

\(=\frac{222 \cdot 6 \times 1000}{62 \times 200}\)

= 179.5 mol/Kg
विलयन का घनत्व = 1.072 g ml
विलयन का द्रव्यमान = (222.6 + 200)
= 422.6 g
विलयन का आयतन =  =  \(\frac{422 \cdot 6}{1 \cdot 072}\) = 394.2 Ml
मोलरता M = \(\frac{\mathrm{W}_{\mathrm{B}} \times 1000}{\mathrm{M}_{\mathrm{B}} \times \mathrm{V}_{(\mathrm{mL})}}\)

\(=\frac{222 \cdot 6 \times 1000}{62 \times 394 \cdot 2}\)
= 9.1 mol/L

प्रश्न 9. 
एक पेय जल का नमूना क्लोरोफॉर्म CHCl₃ से कैंसरजन्य समझे जाने की सीमा तक बहुत अधिक संदूषित है। इसमें संदूषण की सीमा 15ppm (द्रव्यमान मे) है:
(i) इसे द्रव्यमान प्रतिशत में व्यक्त कीजिए।
(ii) जल के नमूने में क्लोरोफॉर्म की मोललता ज्ञात कीजिए।
उत्तर:
(i) 15 ppm का अर्थ है कि विलयन के 106 भाग में क्लोरोफॉर्म के 15 भाग हैं।
अत: 106 भाग विलयन में क्लोरोफॉर्म = 15 भाग
100 भाग विलयन में क्लोरोफॉर् = \(\frac{15 \times 100}{10^6}\)

\(=1.5 \times 10^{-3} \%(\mathrm{w} / \mathrm{W})\)

(ii) 1.5 x 10^-3  (w/W) क्लोरोफॉर्म में 
विलेय का द्रव्यमान w_B = 15 x 10g 
विलेय का अणु भार M_B = 12 + 1 + 3 x 35.5
= 119.5gmol 
विलायक का भार w_A = 100 - 00015
= 99.9985g
मोललता = \(\frac{\mathrm{W}_{\mathrm{B}} \times 1000}{\mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}}\)
\(=\frac{1.5 \times 10^{-3} \times 1000}{119.5 \times 99.9985}\)
= 0.000125
= 1.25 10^-4
विलयन की प्रतिशत मात्रा
= 1.5 x 10^-3 % (w/W) 
विलयन की मोललता = 1.25 x 10^-4 m

प्रश्न 10. 
ऐल्काहॉल एवं जल के एक विलयन में आण्विक अन्योन्यक्रिया की क्या भूमिका है?
उत्तर:
जल के अणुओं की तरह ही ऐल्कोहॉल अणुओं में प्रबल हाइड्रोजन बन्ध उपस्थित होता है। जब जल व ऐल्कोहॉल को मिश्रित किया जाता है तो आण्विक अन्योन्य क्रिया (molecular interaction) दुर्बल हो जाती है एवं वे आदर्श व्यवहार से धनात्मक विचलन प्रदर्शित करते हैं। इसी कारण इनका वाष्प दाब उच्च परन्तु क्वथनांक निम्न होताहै।

प्रश्न 11. 
ताप बढ़ाने पर गैसों की द्रवों में विलेयता में हमेशा कमी आने की प्रवृत्ति क्यों होती है?
उत्तर:
गैसें द्रव में ऊष्माक्षेपी प्रक्रिया के साथ घुलती है। अत: ताप बढ़ाने पर साम्यावस्था पश्च दिशा में स्थानान्तरित हो जाती है तथा दाब में कमी आ जाती है जिसके फलस्वरूप विलेयता में सदैव कमी आती अन्योन्यकि, ऐल्काहाल

प्रश्न 12.
हेनरी का नियम तथा इसके कुछ महत्वपूर्ण अनुप्रयोग लिखिए।
उत्तर:
हेनरी का नियम: किसी गैस का वाष्य अवस्था में आंशिक दाब (p), उस विलयन में गैस के मोल अंश (\(\boldsymbol{x}\)) के समानुपाती होता है।
\(p \propto x\).
\(p=\mathrm{K}_{\mathrm{H}} x\)
जहाँ K_H = हेनरी स्थिरांक
हेनरी नियम के अनुप्रयोग:

1. सोडा जल एवं शीतल पेयों में CO₂, की विलेयता बढ़ाने के लिए बोतल को अधिक दाब पर बन्द किया जाता है।
2. अधिक ऊँचाई वाली जगहों पर ऑक्सीजन का आंशिक दाब सतही स्थानों से कम होता है अतः इन जगहों पर रहने वाले लोगों एवं आरोहों के रुधिर और ऊतकों में ऑक्सीजन की सान्द्रवा निम्न हो जाती है। इसके कारण आरोहक कमजोर हो जाते हैं और स्पष्टतया सोच नहीं पाते। इसे 'ऐनॉक्सिया' (Anoxia) कहते हैं।

प्रश्न 13.
6.56 x 10^-3 एथेन युक्त एक संतप्त विलयन में एथेन का आशिक दाब 1 bar है। यदि विलयन में 5.00 x 10^-2 g एथेन हो तो गैस का आंशिक दाब क्या होगा? 
उत्तर:
सम्बन्ध m = K_H x p से, 
प्रथम स्थिति में
सम्बन्ध m = K_H x p से, 
प्रथम स्थिति में
6.56 x 10^-3 
g = K_H x 1bar

K_H = 6.56 × 10^-3 g bar-1

द्वितीय स्थिति में,
5.00  × 10^-2 g = (6.56 × 10^-2 g bar-1) p
या \(p=\frac{5 \cdot 00 \times 10^{-2} \mathrm{~g}}{6.56 \times 10^{-2} \mathrm{~g} \mathrm{bar}^{-1}}\)
= 0.762 bar



प्रश्न 14. 
रॉउल्ट के नियम से धनात्मक एवं ऋणात्मक विचलन का क्या अर्थ है तथा \(\Delta_{\operatorname{mix}} \mathrm{H}\) का चिह्न इन विचलनों से कैसे सम्बन्धित है ?
उत्तर:
जब कोई विलयन सभी सान्द्रताओं पर रॉउल्ट के नियम का पालन नहीं करता तो वह अनादर्श विलयन (non-ideal solution) कहलाता है। इस प्रकार के विलयनों का वाष्प दाब रॉउल्ट के नियम द्वारा निर्धारित किए गए वाष्प दाब से या तो अधिक होता है या कम। यदि यह अधिक होता है तो यह विलयन रॉउल्ट नियम से धनात्मक विचलन (positive deviation) प्रदर्शित करता है और यदि यह कम होता है तो यह ऋणात्मक विचलन (negative deviation) प्रदर्शित करता है।

धनात्मक विचलन दिखाने वाले अनादर्श विलयन (Nonideal solutions showing (+ ve) deviation):
(i) PA > P⁰_A χ​​​​​​​_A > P⁰_B  χ​​​​​​​_B
(ii) ∆v = + ve
(iii) ∆H(max) = + ve    

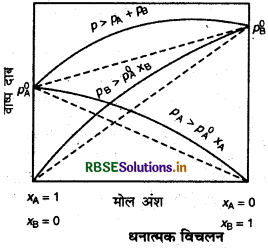
यहाँ विलयन का वाष्प दाब रॉउल्ट के नियम से निर्धारित किये गये वाष्प दाब की अपेक्षा अधिक होता है। यहाँ पर विलायक-विलायक और विलेय-विलेय अन्तरा-आण्विक आकर्षण बल विलायक-विलेय अन्तरा-आण्विक आकर्षण बल की अपेक्षा प्रबल होता है अर्थात् A - A और B - B आकर्षण बल A - B आकर्षण बल की अपेक्षा प्रबल होता है। यही कारण है कि विलयन का आयतन बढ़ जाता है।
धनात्मक विचलन प्रदर्शित करने वाले कुछ अनादर्श विलयनों के उदाहरण अग्रलिखित हैं:

1. ऐथेनॉल + जल
2. ईथर + ऐसीटोन
3. कार्बन डाइसल्फाइड + ऐसीटोन
4. कार्बन टेट्राक्लोराइड + मेथेनॉल
5. ऐथेनॉल + साइक्लोहेक्सेन
6. कार्बन टेट्राक्लोराइड + टॉलुईन
7. कार्बन टेट्राक्लोराइड + क्लोरोफॉर्म
8.  मेथेनॉल + जल
9. ऐसीटोन + ऐथेनॉल

ऋणात्मक विचलन दिखाने वाले अनादर्श विलयन (nonideal solutions showing (-ve) deviation) कृपया अनुच्छेद का अध्ययन करें।
(i) PA < P⁰_A χ​​​​​​​_A < P⁰_B  χ​​​​​​​_B
(ii) ∆v = - ve
(iii) ∆H(max) = - ve    

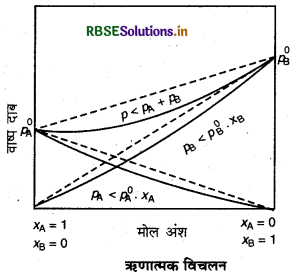
राउल्ट के नियम से ऋणात्मक विचलन की स्थिति में A - A व B - B के बीच अंतराआण्विक आर्कषण बल $A-B$ की तुलना में कमज़ोर होता है। इसके फलस्वरूप वाष्पदाब कम हो जाता है अतः ॠणात्मक विचलन प्रदर्शित होता है।
उदाहरण के लिए:

1. फ़ीनॉल व ऐनिलीन का मिश्रण में फ़ीनॉलिक प्रोटॉन व ऐनिलीन के नाइट्रोजन अणु के एकाकी इलेक्ट्रॉन युगल के मध्य अंतराआण्विक हाइड्रोजन बंध एक से अणुओं के मध्य हाइड्रोजन बंध की तुलना में मज़बूत होता है।
2. क्लोराफॉर्म व ऐसीटोन का मिश्रण भी ऐसा विलयन बनता है जो राउल्ट के नियम से ऋणात्मक विचलन दर्शाता है। इसका कारण यह है। कि क्लोरोफॉर्म का अणु ऐसीटोन के अणु के साथ हाइड्रोजन बंध बना सकता है।

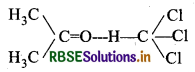
इसके कारण प्रत्येक घटक के अणुओं की पलायन की प्रवृत्ति कम हो जाती है, जिससे वाष्प दाब में कमी आ जाती है तथा राउल्ट नियम से ऋणात्मक विचलन होता है।

प्रश्न 15. 
विलायक के सामान्य क्वथनांक पर एक अवाष्पशील विलेय का 2 % जलीय विलयन का 1.004 bar वाष्प दाब है। विलेय का मोलर द्रव्यमान क्या है?
उत्तर:
क्वथनांक पर शुद्ध जल का वाष्प दाब  (p⁰) = 1 atm = 1.013 bar
विलयन का वाष्प दाब (p_s) = 1.004 bar
विलेय का द्रव्यमान (W₂) = 2g
विलयन का द्रव्यमान = 100g
विलायक का द्रव्यमान (W₁) = 100 - 2 = 98g 
तनु विलयन (2 %) के लिए रॉउल्ट का नियम लागू करने पर,

= 41.35 g mol-1

प्रश्न 16. 
हेप्टेन एवं ऑक्टेन एक आदर्श विलयन बनाते हैं। 373K  पर दोनों द्रव घटकों के वाष्य दाब क्रमश: 105.2k Pa तथा 46.8
kPa हैं। 26.0 g  हेप्टेन एवं 35 - 0 g ऑक्टेन के मिश्रण का वाष्प दाब क्या होगा?
उत्तर:
हेप्टेन C₇ H₁₆ का मोलर द्रव्यमान = 100g mol^-1
ऑक्टेन C8 H18 का मोलर द्रव्यमान = 114 g mol^-1
26.0 g  हेप्टेन  = \(\frac{26 \cdot 0 \mathrm{~g}}{100 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 0.26 mol
35.0 g ऑक्टेन = \(=\frac{35 \cdot 0 \mathrm{~g}}{114 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 0.31 mol
x_{हेप्टेन} =  \(\frac{0.26}{0.26+0.31}\)

= \(\frac{0.26}{0.57}\) = 0.456
= 1 - 0.456 = 0.544

x_{ऑक्टेन} = 0.456 × 10.52 pa
p_{हेप्टेन} = 479.97 Kpa
= 0.544 × 46.8 Kpa 
= 25.46 Kpa

p_{ऑक्टेन} = 47.97 + 25.46
p_कुल  = 73.43 Kpa

प्रश्न 17.
300K पर जल का वाष्प दाब 12.3kPa है। इसमें बने अवाष्पशील विलेय के एक मोलल विलयन का वाष्प दाब ज्ञात कीजिए।
उत्तर:
एक मोलल विलयन का अर्थ है, विलायक के 1kg में उपस्थित विलेय के 1 mol,
अतः विलायक के मोलों की संख्या
\(=\frac{1000 \mathrm{~g}}{18 \mathrm{~g}}=55 \cdot 5\)

विलेय के मोल अंश  \(\left(x_2\right)=\frac{1}{1+.55 \cdot 5}\)
\(=\frac{1}{56 \cdot 5}\) = 0.0177

\(\frac{p^0-p_{\mathrm{s}}}{p^0}=x_2\)
\(\frac{12 \cdot 3-p_{\mathrm{s}}}{12 \cdot 3}\) = 0.0177
12.3 - P_s = 12.3 × 0.0177
12.3 - P_s = 0.2177
p_s = 12.08 Kpa
दिये गये विलयन का वाष्प दाब
= 12.08 kpa

प्रश्न 18. 
114 g ऑक्टेन में किसी अवाष्पशील विलेय (मोलर द्रव्यमान 40 g mol^-1) की कितनी मात्रा घोली जाए कि ऑक्टेन का वाष्प दाब घट कर मूल का 80% रह. जाए?
उत्तर:
विलायक का द्रव्यमान W_A = 114 g
विलायक का अणुभार M_A = 114 g
विलेय का अणुभार M_B = 40 g mol
ऑक्टेन का वाष्प दाब p⁰ = 100mm
विलयन का वाष्प दाब p_s = 80 mm
विलेय का भार W_B = ?

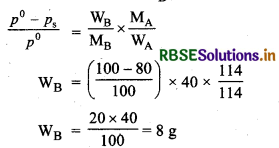
विलेय का भार = 8 g

प्रश्न 19. 
एक विलयन जिसे एक अवाष्पशील ठोस के 30g  को 90g जल में विलीन करके बनाया गया है। उसका 298K पर वाष्प दाब 2.8 kPa है। विलयन में 18 g जल और मिलाया जाता है जिससे नया वाष्प दाब 298 K पर 2.9 kPa हो जाता है। निम्नलिखित की गणना कीजिए:
(i) 298 K पर जल का वाष्प दाब
(ii) विलेय का मोलर द्रव्यमान।
उत्तर:
पहला केस,
विलेय का द्रव्यमान W_B = 30g
विलायक का मोलर द्रव्यमान M_A = 18 g
विलायक का द्रव्यमान W_A = 90 g
विलयन का वाष्पदाब p_s = 2 .8 kPa
द्वितीय केस (जल मिलाने के बाद),
विलेय का द्रव्यमान W_B = 30 g
विलायक का मोलर द्रव्यमान M_A = 18 g
विलायक का द्रव्यमान W_A = 90 + 18 = 108 g
विलयन का वाष्प दाब p_s = 2 .9 kPa
चूँकि दोनों केसों में विलेय एक ही है अतः दोनों में मोलर द्रव्यमान समान होगा।
\(\begin{aligned} &\text { (i) } \mathrm{M}_{\mathrm{B}} \\ &\frac{\mathrm{W}_{\mathrm{B}} \times \mathrm{M}_{\mathrm{A}}}{\mathrm{W}_{\mathrm{A}}}\left(\frac{p^0}{p^0-p_{\mathrm{s}}}\right)=\frac{\mathrm{W}_{\mathrm{B}} \times \mathrm{M}_{\mathrm{A}}}{\mathrm{W}_{\mathrm{A}}}\left(\frac{p^0}{p^0-p_{\mathrm{s}}}\right) \\ &\text { } \frac{30 \times 18}{90}\left(\frac{p^0}{p^0-2 \cdot 8}\right)=\frac{30 \times 18}{108}\left(\frac{p^0}{p^0-2 \cdot 9}\right) \end{aligned}\)
या 90 (p⁰ - 2.8) = 108 (p⁰ - 2.9)
या 90 p⁰ - 90 × 2.8 = 108 p⁰ - 108 2.9
90 p⁰ - 252 = 108 p⁰ - 313.2
 108 p⁰ - 90 p^o = 313.2 - 252
18 p⁰ = 61.2
या  \(p^0=\frac{61 \cdot 2}{18}\)
∴ p⁰ = 3.4 kpa

शुद्ध विलायक का वाष्प दाब = 3.4 kPa
(ii) विलेय का मोलर द्रव्यमान M_B = ?

\(\mathrm{M}_{\mathrm{B}}=\frac{\mathrm{W}_{\mathrm{B}} \times \mathrm{M}_{\mathrm{A}}}{\mathrm{W}_{\mathrm{A}}}\left(\frac{p^0}{p^0-p_{\mathrm{s}}}\right)\)
\(\mathrm{M}_{\mathrm{B}}=\frac{30 \times 18}{90}\left(\frac{3.4}{3.4-2 \cdot 8}\right)\)
\(=\frac{18}{3}\left(\frac{3.4}{0.6}\right)\) = 34 g/mol

(i) विलायक का वाष्प दाब = 3.4k P a
(ii) विलेय का मोलर द्रव्यमान = 34 g mol

प्रश्न 20. 
शक्कर 5 % (द्रव्यमान) जलीय विलयन का हिमांक 271K है। यदि शुद्ध जल का हिमांक 273.15 K है तो ग्लूकोस के 5% जलीय विलयन के हिमांक की गण़ना कीजिए।
उत्तर:
शक्कर के लिए,
विलेय का द्रव्यमान W_B = 5 g
विलायक का द्रव्यमान W_A = 100 - 5
= 95 g
विलेय का अणुभार M_B = 342 g mol
विलयन का हिमांक = 271 K
शुद्ध जल का हिमांक =273.15K
\(\Delta \mathrm{T}_f\) = जल का हिमांक - विलयन का हिमांक
= 273.15 - 271 
= 2 .15 K

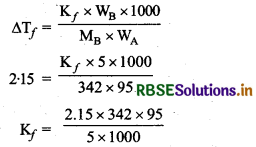
K_f = 13.9 K kg mol-1
K_f का मान ग्लूकोज के विलयन में रखने पर,
W_B = 8 g
M_B = 180 g
W_A = 95 g
\(\begin{aligned} \Delta \mathrm{T}_f &=\frac{\mathrm{K}_f \times \mathrm{W}_{\mathrm{B}} \times 1000}{\mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}} \\ &=\frac{13.97 \times 5 \times 1000}{180 \times 95} \end{aligned}\)
= 4.085 K
जल में 5 % ग्लूकोस के विलयन का हिमांक
= 273.15  - 4.085 = 269.065k
विलयन का हिमांक = 269.065k
= 269.065k

प्रश्न 21. 
दो तत्व A एवं B मिलकर A B₂ एवं AB₄ सूत्र वाले दो यौगिक बनाते हैं। 20g बेन्जीन में घोलने पर 1g AB₂ हिमांक को 2.3K  अवनमित करता है, जबकि 1.0g  AB₄ से 1.3 K का अवनमन होता है। बेन्जीन के लिए मोलर अवनमन स्थिरांक 5.1K kg mol^-1  है। A एवं B के परमाण्वीय द्रव्यमान की गणना कीजिए।
उत्तर:
AB₂ के लिए,
W_A = 20 g (विलायक का द्रव्यमान)
W_B = 1 g (विलेय का द्रव्यमान)
\(\Delta \mathrm{T}_f\) = 2.3 K 
M_B = ?
K_f = 5.1 K Kg mol^{-
\(\mathrm{M}_{\mathrm{B}}=\frac{\mathrm{K}_f \times \mathrm{W}_{\mathrm{B}} \times 1000}{\Delta \mathrm{T}_f \times \mathrm{W}_{\mathrm{A}}}\)
\(=\frac{5 \cdot 1 \times 1 \times 1000}{2 \cdot 3 \times 20}\)}
= 110. 87 g/mol
AB₄  के लिए
W_A = 20 g (विलायक का द्रव्यमान)
W_B = 1g (विलेय का द्रव्यमान)
\(\Delta \mathrm{T}_f\)  = 1.3K (हिमांक में अवनमन)
M_B = ?
K_f = 5.1 KKg mol^-1 (मोलर अवनमन स्थिरांक)
\(\mathrm{M}_{\mathrm{B}}=\frac{\mathrm{K}_f \times \mathrm{W}_{\mathrm{B}} \times 1000}{\Delta \mathrm{T}_f \times \mathrm{W}_{\mathrm{A}}}\)

\(\mathrm{M}_{\mathrm{B}}=\frac{5 \cdot 1 \times 1 \times 1000}{1 \cdot 3 \times 20}\)
= 196.15 g /mol
AB₂ का मोलर द्रव्यमान = 110.87 g/mol
AB₄ का मोलर द्रव्यमान = 196.15 g/mol
माना. कि A का परमाणु द्रव्यमान ' a ' है तथा B का परमाणु द्रव्यमान:
a + 2b = 110.87 समीकरण ......(1)
a + 4b = 196.15 समीकरण .....(2)
समी (1) व समी (2) को हल करने पर
- 2b = - 85.28
2b = 85.28
∴ \(b=\frac{85 \cdot 28}{2}\)
= 42.64 g/mol
b का मान समीकरण (1) में रखने पर,
a + 2b = 110.87
या a + 2 × 42.64 = 110.87
या a + 85.28 = 110.87
या a = 110.87 - 85.28
∴  a = 25.59 g/mol
A का परमाणु द्रंव्यमान  = 25.59 g /mol
B का परमाणु द्रव्यमान = 42.64 g /mol

प्रश्न 22.
300 K पर 36g प्रति लीटर सान्द्रता वाले ग्लूकोस के विलयन का परासरण दाब 4.98 bar है। यदि इसी ताप पर विलयन का परासरण दाब 1.52 bar हो तो उसकी सान्द्रता क्या होगी?
उत्तर:
\(\pi\) = 4.8 bar , T = 300k
V = 1L
ग्लूकोस का द्रव्यमान W_B = 6g
ग्लूकोस (C₆ H1₂ O₆)   का मोलर द्रव्यमान
= 6 × 12 + 12 × 1 + 6 × 16
M_B =  72 + 12 + 96
= 180 g/mol-1
प्रथम विलयन के लिए.
\(\begin{aligned} \pi \mathrm{V} &=n_{\mathrm{B}} \mathrm{RT} \\ \pi \mathrm{V} &=\frac{\mathrm{W}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{B}}} \times \mathrm{R} \times \mathrm{T} \end{aligned}\)
\(4.98 \times 1=\frac{36}{180} \times \mathrm{R} \times 300\)
∴ \(\mathrm{R}=\frac{4.98 \times 180}{36 \times 300}\)
= 0.083 L bar K^-1 mol^-1

दुसरे विलयन के लिए,
(परासरण दाब) = 1.52 bar
C (सान्द्रता) = ?
(गैस नियतांक) = 0.083 L bar K^-I mol
T (ताप) = 300K
v (आयतन) = 1L
\(\pi=CRT\)
∴ \(\mathrm{C}=\frac{\pi}{\mathrm{RT}}\)
\(=\frac{1.52}{0.083 \times 300}\)

= 0.06 moL^-1
विलयन की सान्द्रता = 0-061 mol L^-I

प्रश्न 23. 
निम्नलिखित युग्मों में उपस्थित सबसे महत्वपूर्ण अन्तराआण्विक आकर्षण बलों का सुझाव दीजिए
1. n - हेक्सेन व - ऑक्टेन 
2. I₂ तथा CCl₄
3. NaCIO₄  H₂O 
4. मेथेनॉल तथा ऐसीटोन ( ऐसीटोनाइदाइल (CH₃ CN) तथा ऐसीटोन C₃H₆O)।
उत्तर:

1. दोनों अधुवी हैं। अत: इनमें अन्तराआण्विक अन्योन्यक्रियाएँ लण्डन प्रकीर्णन बल हैं।।
2. इनके मध्य लण्डन प्रकीर्णन बल विद्यमान है।
3. NaCIO₄, विलयन में Na⁺ तथा CIO_-4 आयन देता है, जबकि जल धुवी अणु है। अतः इनमें अन्तराआण्विक अन्योन्यक्रियाएँ आयन-द्विध्रुव अन्योन्यक्रियाएँ हैं।
4. दोनों ध्रुवी अणु हैं। अत: इनमें अन्तराआण्विक अन्योन्यक्रियाएँ द्विधुव-द्विधुव अन्योन्यक्रियाएँ हैं।
5. इनके मध्य द्विध्रुव-द्विध्रुव अन्योन्यक्रियाएँ हैं।

प्रश्न 25. 
पहचानिए कि निम्नलिखित यौगिकों में से कौन-से जल में अत्यधिक विलेय, आंशिक रूप से विलेय तथा अविलेय हैं0 फीनॉल
1. टॉलुईन 
2. फॉर्मिक अम्ल 
3. एथिलीन ग्लाइकॉल 
4. क्लोरोफॉर्म 
5. पेन्टेनॉल।
उत्तर:
फीनॉल जल में आंशिक रूप से विलेय होता है, क्योंकि फीनॉल में धूवी: OH समूह होता है, परन्तु अधूवी ऐरोमैटिक फेनिल (C₆H₅) समूह के कारण यह जल में अत्यधिक विलेय नहीं होता।

1. टॉलईन जल में अविलेय है, क्योंकि यह अधूवी है, जबकि जल धुवी है।
2. फॉर्मिक अम्ल जल में अत्यधिक विलेय है, क्योंकि फॉर्मिक अम्ल जल के साथ हाइड्रोजन बन्ध बना सकता है।
3. ऐथिलीन ग्लाइकॉल जल में अत्यधिक विलेय है, क्योंकि यह जल के साथ हाइड्रोजन बन्ध बना सकता है।
4. क्लोरोफॉर्म जल में अविलेय है, क्योंकि यह एक कार्बनिक द्रव है।
5. पेन्टेनॉल जल में आंशिक रूप से विलेय होता है, क्योंकि - OH समूह धुवी है, परन्तु दीर्घ हाइड्रोकार्बन भाग (C₅H₁₁) अध्रुवी होता है।

प्रश्न 26. 
यदि किसी झील के जल का घनत्व 1.25g/mL है तथा उसमें 92 g Na⁺ आयन प्रति किलो जल में उपस्थित हैतो झील में Na⁺ आयन की मोललता ज्ञात कीजिए।
उत्तर:
घनत्व
d=1.25gmL 
विलेय का द्रव्यमान W_B = 92g(1kg- 1000g) 
विलायक का द्रव्यमान W_A = 1 kg 
विलेय का मोलर द्रव्यमान M_B = 23 g molL^-I 
मोललता m = ?
\(\begin{aligned} m &=\frac{\mathrm{W}_{\mathrm{B}} \times 1000}{\mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}} \\ &=\frac{92 \times 1000}{23 \times 1000}=\frac{92}{23} \end{aligned}\)

= 4 mol / Kg
विलेय की मोललता 4 mol / Kg है।

प्रश्न 27. 
अगर Cus का विलेयता गुणनफल 6 x 10^-16 है तो जलीय विलयन में उसकी अधिकतम मोलरता ज्ञात कीजिए। 
उत्तर:

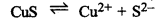
K_SP = [CU²⁺] [S^2-]
K_SP = S \(\times\) S
K_SP = S²
S = \(\sqrt{\mathrm{K}_{s p}}\)

= \(\sqrt{6 \times 10^{-16}}\)
=  2.45 \(\times\) 10^-8 mol L^-1

CuS की मोलरता  2.45 \(\times\) 10^-8 mol L^-1 है। 

प्रश्न 28. 
जब 6.5g ऐस्पिरीन (C9H8O4) को 450g ऐसीटोनाइदाइल (CH₃CN) में घोला जाए तो ऐस्पिरीन का ऐसीटोनाइट्राइल में भार प्रतिशत ज्ञात कीजिए।
उत्तर:

= \(\frac{6 \cdot 5}{6 \cdot 5+450} \times 100\)
= \(\frac{650}{456 \cdot 5}\) = 1.422%

ऐस्पिरीन का द्रव्यमान प्रतिशत 1.424 % है।

प्रश्न 29. 
बैलोफीन (C₉H₂₁NO₃) जो कि मॉर्फीन जैसी होती है, का उपयोग स्वापक उपभोक्ताओं द्वारा स्वापक छोड़ने से उत्पन्न लक्षणों को दूर करने में किया जाता है। सामान्यतः नैलॉर्फीन की 1.5 mg खुराक दी जाती है। उपर्युक्त खुराक के लिए 1.5 x 10^-3 m जलीय विलयन का कितना दव्यमान आवश्यक होगा?
उत्तर:
विलेय का द्रव्यमान w_B = 1.5mg
= 1.5 x 10^-3 g 
मोललता m = 1.5 x 10^-3 mol kg^-l 
विलेय का मोलर द्रव्यमान
M_B = 19 x  12 + 21 x 1 + 14 + 3 x 16
= 228 + 21 + 14 + 48
= 311 g/mol 
विलायक का द्रव्यमान W_A = ?

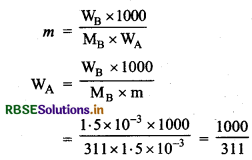
∴ W_A = 3.21 g

विलयन का द्रव्यमान = विलेय का द्रव्यमान + विलायक का द्रव्यमान
= 0.0015 + 3.21 = 3.2115 g
विलयन का भार = 3.2115 g

प्रश्न 30. 
बेन्जोइक अम्ल का मेथेनॉल में 0.15 m विलयन बनाने के लिए आवश्यक मात्रा की गणना कीजिए।
उत्तर:
0.15m का मतलब है कि विलेय के 0.15 मोल 1kg विलायक में उपस्थित हैं।
बेन्जोइक अम्ल का मोलर द्रव्यमान (C₆H₅COOH) 
= 6  x 12 + 5 x 1 + 12 + 2 x 16 + 1
= 122g/mol 
विलेय का भार = विलेय के मोल x मोलर द्रव्यमान
= 0.15  x  1223 = 18.3g 
विलेय का भार = 18.38 g

प्रश्न 31.
ऐसीटिक अम्ल, ट्राइक्लोरोऐसीटिक अम्ल एवं ट्राइफ्लुओरो-ऐसीटिक अम्ल की समान मात्रा से जल के हिमांक में अवनमन इनके उपर्युक्त दिए गए क्रम में बढ़ता है। संक्षेप में समझाइए।
उत्तर:
हिमांक का क्रम:
ऐसीटिक अम्ल < ट्राइक्लोरोऐसीटिक अम्ल < ट्राइफ्लुओरोऐसीटिक अम्ल

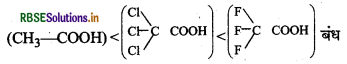
फ्लुओरीन में अत्यधिक ऋण विद्युती गुण होने के कारण उच्च इलेक्ट्रॉन प्र तिकर्षी प्रेरकीय प्रभाव होता है। परिणामस्वरूप ट्राइफ्लुओरोऐसीटिक अम्ल प्रबलतम अम्ल है तथा ऐसीटिक अम्ल दुर्बलतम अम्ल है। अतः ट्राइफ्लुओरोऐसीटिक अम्ल जल के अपने विलयन में अत्यधिक आयनीकृत होता है, जबकि ऐसीटिक अम्ल अल्प मात्रा में आयनीकृत होता है। अधिक आयन उत्पन्न होने पर हिमांक में अवनमन भी अधिक होगा, अतः ट्राइफ्लुओरोऐसीटिक अम्ल के लिए हिमांक में अवनमन अधिकतम तथा ऐसीटिक अम्ल के लिए न्यूनतम होगा।

प्रश्न 32. 
CH₃ - CH₂ - CHCl - COOH के 10 g को 250 g जल में मिलाने से होने वाले हिमांक का अवनमन परिकलित कीजिए। 
(Ka = 1.4 × 10^-3  K_f = 1.86 K kg mol ^-1)
उत्तर:
CH₃ CH₂ - CHCl - COOH का मोलर द्रव्यमान 
MB = 12 + 3 + 12 + 2 + 12 + 1 + 35.5 + 12 + 32 + 1 
= 122.5 g mol^-1
विलेय का द्रव्यमान W_B = 10 g
विलायक का द्रव्यमान W_A = 250 g
\(m=\frac{\mathrm{W}_{\mathrm{B}} \times 1000}{\mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}} \begin{aligned} &=\frac{10 \times 1000}{122.5 \times 250} \\ &=0.3264 \mathrm{~mol} / \mathrm{kg} \end{aligned} \)
माना कि विलेय की वियोजन मात्रा x है तो,

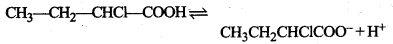
वाण्ट्हॉफ गुणांक (i) की गणना:

\(\alpha \doteq \frac{i-1}{m-1}\)
यदि m = 2 तो
a + 1 = i
या  1 + 0.065 = i
∴ i = 1.065

\(\Delta \mathrm{T}_f=i \mathrm{~K}_f m\)
= 1.065 ×​​​​​​​ 1.86 × 0.324
= 0.65 K

प्रश्न 33. 
CH₂ FCOOH के 19.5g  को 500g H₂O में घोलने पर जल के हिमांक में \(1^{\circ} C\) का अवनमन देखा गया। फ्लुओरोऐसीटिक अम्ल का वान्ट हॉफ गुणांक तथा वियोजन स्थिरांक परिकलित कीजिए। जल के लिए K_f = 1.86 K kg mol^-1 है।
उत्तर:
W_B = 19: 5 g (विलेय का द्रव्यमान)
W_A = 500 g (विलायक का द्रव्यमान)
\(\Delta \mathrm{T}_f=1 \cdot 0^{\circ} \mathrm{C}\)(हिमांक में अवनमन)
M_B = 78 g / mol
(विलेय का मोलर द्रव्यमान)

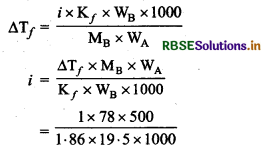
= 1.0573
हम जानते हैं कि वियोजन के लिए,
ka = Cα^{2
\(\begin{aligned} &\alpha=\frac{i-1}{m-1} \\ &\alpha=\frac{1 \cdot 0753-1}{2-1} \end{aligned}\)}
α = 0.0753
ka = Cα^{2
\(\begin{aligned} &\mathrm{K}_a=\left(\frac{\mathrm{W}_{\mathrm{B}} \times 1000}{\mathrm{M}_{\mathrm{B}} \times \mathrm{W}_{\mathrm{A}}}\right) \times \alpha^2 \\ &\mathrm{~K}_a=\frac{19 \cdot 5 \times 1000 \times(0 \cdot 0753)^2}{78 \times 500} \end{aligned}\)}
Ka = 2.835 × 10^-3
वियोजन स्थिरांक = 2.835 \(\times 10^{-3}\)

प्रश्न 34. 
293 K पर जल का वाष्प दाब 17.535 mm of Hg है। यदि 25 g ग्लूकोज को 450 g जल में घोलें तो 293 K पर जल का वाष्प दाब परिकलित कीजिए।
उत्तर:
p⁰ = 17.535 mm Hg (जल का वाष्प दाब)
W_B = 25 g (विलेय का द्रव्यमान)
W_A = 450 g (विलायक का द्रव्यमान)
M_B = 180 g/mol (विलेय का अणुभार)
M_A = 18 g/mol (विलायक का अणुभार)
p_s = ?
\(\begin{array}{r} \frac{p^0-p_{\mathrm{s}}}{p^0}=\frac{\mathrm{W}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{B}}} \times \frac{\mathrm{M}_{\mathrm{A}}}{\mathrm{W}_{\mathrm{A}}} \\ \frac{17 \cdot 535-p_{\mathrm{s}}}{17 \cdot 535}=\frac{25}{180} \times \frac{18}{450} \end{array}\)
या  17.535  - p_s = \(\frac{25}{180} \times \frac{18}{450} \times 17 \cdot 535\)

या  17.535  - p_s  =  0.0974
या p_s  =  0.0974 - 17.535
∴  = 17.436
= 17.44 mm Hg
विलयन का वाष्प दाब p_s = 17.44 mm Hg

प्रश्न 35. 
298 K पर मथेन की बेन्जीन पर मोललता का हनरी स्थिरांक 4.27 × 10⁵ Hg है। 298 K तथा 760 mm Hg दाब पर मेशेन की बेन्जीन में विलेयता परिकलित कीजिए।
उत्तर:
यहाँ K_H = 4.27  × 10⁵ Hg
p = 760 mmHg
हेनरी का नियम लागू करने पर,
p = K_{H x} गैस 

\(x_{\text { }}=\frac{p}{\mathrm{~K}_{\mathrm{H}}}=\frac{760 \mathrm{~mm}}{4.27 \times 10^5 \mathrm{~mm}}\)

= 1.78 × 10^-3  =  178 × 10^-5
\(\begin{aligned} x_{\text { }} &=\frac{n_{\mathrm{CH}_4}}{n_{\mathrm{CH}_4}+n_{\mathrm{C}_6 \mathrm{H}_6}} \\ &=\frac{n_{\mathrm{CH}_4}}{n_{\mathrm{C}_6 \mathrm{H}_6}} \end{aligned}\)
\(\left[\because n _ { \mathrm { CH } _ { 4 } } \left\langle\left\langle\left\langle n_{\mathrm{C}_6 \mathrm{H}_6}\right]\right.\right.\right.\)
\(\begin{aligned} 1.78 \times 10^{-3} &=\frac{n \mathrm{CH}_4}{1000 / 78} \\ n_{\mathrm{CH}_4} &=\frac{1.78 \times 1000 \times 10^{-3}}{78} \end{aligned}\)
\(=\frac{1.78}{78}\) = 0.0228 = 0.023 mol
मेथेन की बेन्जीन में विलेयता मोल अंश में = 178 \(\times 10^{-5}$\)
मोल में = 0.023 mol L-1

प्रश्न 36.
100 g  द्रव A मोलर द्रव्यमान 140 g mo -1 को 1000 g द्रव B (मोलर द्रव्यमान 180 g mo -1) में घोला गया। शुद्ध द्रव B का वाष्प दाब 500 torr पाया गया। शुद्ध द्रव A का वाष्प दाब तथा विलयन में उसका वाष्प दाब परिकलित कीजिए यदि विलयन का कुल वाष्प दाब 475 torr हो।
उत्तर:
द्रव A (विलेय) के मोलों की संख्या
\(=\frac{100 \mathrm{~g}}{140 \mathrm{~g} \mathrm{~mol}^{-1}}=\frac{5}{7} \mathrm{~mol}\)

द्रव B (विलायक) के मोलों की संख्या:
\(=\frac{1000 \mathrm{~g}}{180 \mathrm{~g} \mathrm{~mol}^{-1}}=\frac{50}{9} \mathrm{~mol}\)

 विलयन में द्रव A के मोल-अंश x_A
\(\begin{aligned} &=\frac{5 / 7}{5 / 7+50 / 9} \\ &=\frac{5 / 7}{395 / 63} \end{aligned}\)
= \(\frac{5}{7} \times \frac{63}{395}=\frac{45}{395}\) = 0.414

∴   विलयन में द्रव B के मोल-अंश (x_B)

= 1 - 0.114 = 0.886

दिया है: \(p_{\mathrm{B}}^0=500 \text { torr }\)

p_कुल = 475torr 

p_कुल = P_A + P_B
p_कुल = \(p_{\mathrm{A}}^0 x_{\mathrm{A}}+p_{\mathrm{B}}^0 x_{\mathrm{B}}\)

या 475 = P⁰_A  × 0.114 + 500 × 0.886
या  475 = 0.114  P⁰_A
या  475 - 443 = 0.114  P⁰_A
या     _{\(\frac{32}{0 \cdot 114}=p_{\mathrm{A}}^0\)
\(\begin{aligned} &p_{\mathrm{A}}^0=280 \cdot 7 \text { torr } \\ &p_{\mathrm{A}}=p_{\mathrm{A}}^0 x_{\mathrm{A}} \end{aligned}\)}
= 28.097 × 0.114 = 32.0 torr
शुद्ध द्रव A का वाष्प दाब = 280.7 torr
द्रव A का विलयन में वाष्प दाब = 32.0 torr

प्रश्न 37.
328 K पर शुद्ध ऐसीटोन एवं क्लोरोफॉर्म के वाष्प दाब क्रमशः 741.8 mm Hg  तथा 632. mm Hg हैं। यह मानते हुए कि संघटन के सम्पूर्ण परास में ये आदर्श विलयन बनाते हैं, p कूल, p क्लोरोफॉर्म तथा p ऐसीटोन को x ऐसीटोन के फलन के रूप में आलेखित कीजिए। मिश्रण के विभिन्न संघटनों के प्रेक्षित प्रायोगिक आँकड़े निम्नलिखित हैं:
उत्तर:

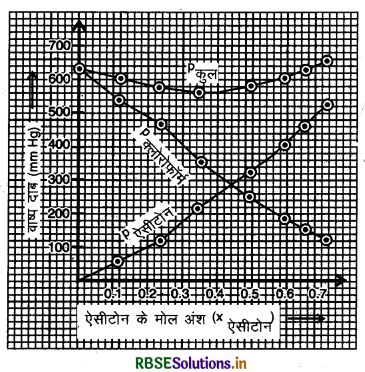
चूँकि p_कुल  के लिए वक्र नीचे की ओर गिरता है, अतः विलयन आदर्श व्यवहार से ऋणात्मक विचलन प्रदर्शित करता है।

प्रश्न 38. 
संघटनों के सम्पूर्ण परास में बेन्जीन तथा टालुईन आदर्श विलयन बनाते हैं। 300 K शुद्ध बेन्जीन तथा टॉलुईन का वाष्प दाब क्रमशः 50.71 mm Hg तथा 32.06mm Hg है। यदि 80 g बेन्जीन को 100g टॉलुईन में मिलाया जाए तो वाष्प अवस्था में उपस्थित बेन्जीन के मोल-अंश परिकलित कीजिए।
उत्तर:
बेन्जीन (C₆H₆) का मोलर द्रव्यमान 
= 78 g mol-1
टॉलुईन (C₆H₅CH₃) का मोलर द्रव्यमान
= 92 g mol-1
∴ बेन्जीन के 80 g में मोलों की संख्या
\(=\frac{80 \mathrm{~g}}{78 \mathrm{~g} \mathrm{~mol}^{-1}}=1.026 \mathrm{~mol}\)

∴ टॉलुईन के 100 g  में मोलों की संख्य
\(=\frac{100 \mathrm{~g}}{92 \mathrm{~g} \mathrm{~mol}^{-1}}=1.087 \mathrm{~mol}\)

∴ विलयन में बेन्जीन के मोल-अंश

\(=\frac{1 \cdot 026}{1 \cdot 026+1 \cdot 087}\)
= \(\frac{1 \cdot 026}{2 \cdot 113}\) = 0.486
टॉलईन के मोल-अंश 
p⁰ बेन्जीन = 50.71 mm Hg
p⁰ टॉलुईन = 32.06 mm Hg
रॉउल्ट का नियम लागू करने पर,
p_कुल =p_{बेन्जीन} +p_{टॉलुईन} 
p_कुल =p⁰ _{बेन्जीन}  x बेन्जीन + p⁰ _{टॉलॉईन} x टॉलुईन 
= 50.71 × 0.486 + 32.06 × 0.514
= 24 .645 + 16.479
= 41.124 mm Hg
p_{बेन्जीन} = y_{बेन्जीन}   p_कुल 
p⁰ बेन्जीन =  y_{बेन्जीन} × p_कुल
50.71 × 0.486 = y_{बेन्जीन} × 41.124
y_{बेन्जीन} = \(\frac{24 \cdot 645}{41 \cdot 124}\)

= 0.599
y _{टॉलुईन} = 1 - 0.599
= 0.401
वाष्प अवस्था में बेन्जीन के मोल = 0.599

प्रश्न 39. 
वायु अनेक गैसों की मिश्रण है। 298 K पर आयतन में मुख्य घटक ऑक्सीजन और नाइट्रोजन लगभग 20 % एवं 79 % के अनुपात में हैं। 10 वायुमण्डल दाब पर जल वायु के साथ साम्य में है। 298 K पर यदि ऑक्सीजन तथा नाइट्रोजन के हेनरी स्थिरांक क्रमशः 3.30 × 10^-7 mm तथा 6.5 1× 10⁷ mm हैं तो जल में इन गैसों का संघटन ज्ञात कीजिए।
उत्तर:
साम्यावस्था में जल के साथ वायु का कुल दाब = 10 atm.
चूँकि आयतन की दृष्टि से वायु में 20% ऑक्सीजन तथा 79% नाइट्रोजन है,
∴ ऑक्सीजन का आंशिक दाब pO_{2
\(=\frac{20}{100} \times 10 \mathrm{~atm}\)} = 2 atm
= 2  × 760 mm = 1520 mm
नाइट्रोजन का आंशिक दाब pN_{2
\(=\frac{79}{100} \times 10 \mathrm{~atm}=7.9 \mathrm{~atm}\)}
= 7.9 × 760 mm = 6004 mm
KH (O₂) = 3.30 ×107 mm
KH (N₂) = 6.51 × 107 mm
हेनरी का नियम लागू करने पर,
\(\begin{aligned} &p_{\mathrm{o}_2}=\mathrm{K}_{\mathrm{H}} \times x_{\mathrm{O}_2} \\ &x_{\mathrm{O}_2}=\frac{p_{o_2}}{\mathrm{~K}_{\mathrm{H}}} \end{aligned}\)
\(=\frac{1520 \mathrm{~mm}}{3 \cdot 30 \times 10^7 \mathrm{~mm}}\)
= 461 × 10^{-5
P_N = K_H × χ_N2}

^{\(x_{\mathrm{N}_2}=\frac{p_{\mathrm{N}_2}}{\dot{\mathrm{K}}_{\mathrm{H}}}=\frac{6004 \mathrm{~mm}}{6 \cdot 51 \times 10^7 \mathrm{~mm}}\)}
= 9.22 × 10^-5

ऑक्सीजन के मोल अंश = 4.61 \(\times 10^{-5}\)
नाइट्रोजन के मोल अंश = 9.22 \(\times 10^{-5}\)

प्रश्न 40.
यदि जल का परासरण दाब 27\(^{\circ} \)C पर 0.75 वायुमण्डल हो तो 2.5 लीटर जल में घुले CaCl₂ (i = 2.47) की मात्रा परिकलित कीजिए।
उत्तर:
\(\pi\) = CRT
\(=i \frac{n}{\mathrm{~V}} \mathrm{RT}\)
\(n=\frac{\pi \times \mathrm{V}}{i \times \mathrm{R} \times \mathrm{T}}\)
\(=\frac{0.75 \mathrm{~atm} \times 2 \cdot 5 \mathrm{~L}}{2.47 \times 0.0821 \mathrm{~L} \mathrm{~atm} \mathrm{\textrm {K } ^ { - 1 } \mathrm { mol } ^ { - 1 } \times 3 0 0 \mathrm { K }}}\)
\(=\frac{1 \cdot 875}{60 \cdot 836}\) = 0.0308 mol
CaCl₂  का मोलर द्रव्यमान  = 40 + 2 × 35.5
= 111 g mol-1
∴ घुली मात्रा = 0.38 × 111g = 3.42g
CaCl₂ की जल में घुली हुई मात्रा = 3.42g

प्रश्न 41.
2 लीटर जल में 25\(^{\circ}\) C पर K₂SO₄ के 25mg को घोलने पर बनने वाले विलयन का परासरण दाब, यह मानते हुए ज्ञात कीजिए कि K₂SO₄ पूर्णतः वियोजित हो गया है।
उत्तर:
 घुला हुआ K₂SO₄   = 25 mg  = 0.25g
विलयन का आयतन = 2L
T = 2 \(^{\circ}\) C = 25 + 273 = 298K
K₂SO₄  का मोलर द्रव्यमान = 2 × 39 + 32 + 4 × 16
= 174 g mol-1
चूँकि K₂SO₄   निम्नलिखित प्रकार पूर्णतः वियोजित हो जाता है
\(\mathrm{K}_2 \mathrm{SO}_4 \rightarrow 2 \mathrm{~K}^{+}+\mathrm{SO}_4^{2-}\)
अत: उत्पन्न आयन = 3
∴ i = 3

 
= 0.0308 mol
​​​​​​​K₂SO₄ का परासरण दाब  = 5.27 × 10³