RBSE Class 12 Physics Notes Chapter 3 विद्युत धारा

These comprehensive RBSE Class 12 Physics Notes Chapter 3 विद्युत धारा will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 3 Notes विद्युत धारा

भूमिका (Introduction):
स्थिर वैद्युतिकी (अध्याय 1) में आवेशों को विरामावस्था में माना गया था। चाहे वे स्वतंत्र हों अथवा परिबद्ध। परन्तु जब आवेश गति करते हैं विद्युत धारा का निर्माण करते हैं। तड़ित विद्युत धारा निर्माण की प्रकृति में घटित परिघटना है जिसमें आवेश बादलों से पृथ्वी तक वायुमंडल से होकर पहुँचता है, जिनका परिणाम कभी-कभी भयंकर होता है। तड़ित में आवेश का प्रवाह स्थायी नहीं होता, परन्तु टॉर्च तथा सेल से चलने वाली घड़ी इस प्रकार की युक्तियों के उदाहरण हैं जिनमें अपरिवर्ती अथवा स्थायी विद्युत धारा प्रवाहित होती है। इस अध्याय में हम इसी स्थायी धारा का अध्ययन करेंगे। इसके अलाव सरल परिपथों के लिए किरखोफ के नियमों का अध्ययन करेंगे।

विद्युत धारा (Electric Current):
हम जानते है प्रत्येक द्रव्य का प्रवाह उच्च गुरुत्वीय तल (gravity plane) से निम्न गुरुत्वीय तल की ओर होता है, ऊष्मा का प्रवाह उच्च ऊष्मीय तल (Thermal plane) (अर्थात् उच्च ताप) से निम्न ऊष्मीय तल (निम्न ताप) की ओर होता है, ठीक इसी प्रकार आवेश का प्रवाह भी उच्च विद्युत तल (उच्च विभव) से निम्न विभव तल (निम्न विभव) की ओर होता है। जिस प्रकार द्रवों के प्रवाह की दर को द्रव धारा (liquid Current) कहते हैं; ऊष्मा के प्रवाह की दर को ऊष्मीय धारा (Heat Current) कहते हैं; ठीक इसी प्रकार विद्युत आवेश के प्रवाह की दर को विद्युत धारा कहते हैं। धन आवेश का प्रवाह उच्च विभव से निम्न विभव की ओर होता है, अतः धनावेश के प्रवाह की दिशा ही विद्युत धारा की दिशा होती है। ऋण आवेश का प्रवाह निम्न विभव से उच्च विभव की ओर होता है, इसलिए धारा की दिशा ऋणावेश की गति के विपरीत दिशा में होती हैं, इस प्रकार "आवेश के प्रवाह की दर को विद्युत धारा कहते है

यदि किसी चालक के परिच्छेद से 4 आवेश प्रवाहित होने में । सेकण्ड का समय लगता है तो चालक में प्रवाहित विद्युत धारा
i = \(\frac{q}{t}\) .......(i)
पद्धति में विद्युत धारा एक मूल राशि (Fundamental quantity) है, अतः इसका मात्रक ऐम्पियर मूल मात्रक होता है।
i का मात्रक = कूलॉम/सेकण्ड या ऐम्पियर

एक ऐम्पियर की परिभाषायदि q= 1 C, t = 1 sec तो i = 1A
"अर्थात् यदि किसी बन्द परिपथ (closed ciruit) में किसी स्थान से 1 सेकण्ड में 1 कूलॉम आवेश प्रवाहित होता है तो परिपथ में बहने वाली धारा 1 ऐम्पियर (1 A) होगी।" . एक कूलॉम आवेश में इलेक्ट्रॉन की संख्या
q = ne से
n = \(\frac{q}{e} = \frac{1}{1.6 \times 10^{-19}}\)
= 6.25 × 10¹⁸
चूँकि 1 कूलॉम 6.25 × 10¹⁰ इलेक्ट्रॉनों के आवेश के तुल्य है, अतः 1 ऐम्पियर धारा का तात्पर्य है चालक के परिच्छेद से 1 सेकण्ड में 6.25 × 10¹⁸ इलेक्ट्रॉनों का प्रवाहित होना।
1A = Cs^-1
= 6.25 × 10¹⁸ इलेक्ट्रॉन/सेकण्ड

 

महत्वपूर्ण बिन्दु
(i) धारा, जो उच्च विभव (धनात्मक विभव) से निम्न विभव (ऋणात्मक विभव) की ओर बहती है, परम्परागत धारा (conventional current) कहलाती है।

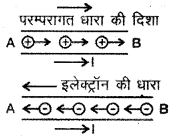
(ii) किसी चालक के अनुप्रस्थ परिच्छेद (cross-section) से 1 सेकण्ड में यदि धनावेश q₁ बिन्दु A से B की ओर तथा ऋणात्मक आवेश q₂ बिन्दु B से A की ओर बहता है तो चालक से प्रवाहित कुल धारा
i = \(\frac{q_1}{t}+\frac{q_2}{t}\)
होगी जिसकी दिशा A से B की ओर होगी।

(iii) धारा की दिशा-धनात्मक आवेश के प्रवाह की दिशा में। धारा की दिशा-ऋणात्मक आवेश के प्रवाह के विपरीत दिशा में अर्थात् इलेक्ट्रॉन की गति के विपरीत दिशा में।

धारा की अन्य छोटी इकाइयाँ
मिली ऐम्पियर 1mA = 10^-3A
माइक्रो ऐम्पियर 1µA = 10^-6A
यदि किसी चालक में प्रवाहित आवेश की दर समय के साथ नहीं बदलती है तो धारा को स्थायी धारा (steady current) कहते हैं।
यदि किसी परिपथ में से किसी स्थान से 1 सेकण्ड में n इलेक्ट्रॉन गुजरते हैं तो धारा
t = \(\frac{q}{t}=\frac{n e}{t}\) ऐम्पियर
इसी प्रकार यदि t सेकण्ड में ऐसे n आयन प्रवाहित हो रहे हों जिनमें प्रत्येक पर आवेश 2e हो तो धारा
i = \(\frac{n \times 2 e}{t}\) ऐम्पियर
विद्यत धारा हमेशा अपरिवर्ती (non-varying) नहीं होती है, अतः हम धारा को निम्न प्रकार परिभाषित करते हैं
"माना समय अन्तराल Δt में किसी चालक की अनुप्रस्थ काट से प्रवाहित होने वाला नेट आवेश Δq है। तब समय t पर चालक के इस अनुप्रस्थ काट से प्रवाहित विद्युत धारा को Δq या Δt की सीमा (limit) शून्य की ओर प्रवृत्त (tending) है
I(t) = \(\lim _{\Delta t \rightarrow 0} \frac{\Delta q}{\Delta t}=\frac{d q}{d t}\)

महत्वपूर्ण बिन्दु

• एक घरेलू उपकरण (home appliances) में बहने वाली धारा का परिमाण = 1A.
• तड़ित विद्युत् (lighting) में बहने वाली धारा का परिमाण ≈ 10⁴ A.
• हमारी धमनियों में बहने वाली धारा का परिमाण ≈ 10^-6A

वैद्यत धारा एक अदिश राशि है (Electric Current is a Scalar Quantity):
दिष्ट धारा परिपथों में धारा की दिशा प्रदर्शित की जाती है, लेकिन इसका अर्थ यह नहीं है कि वैद्युत धारा सदिश राशि है। वास्तव में वैद्युत धारा एक अदिश राशि है। इसका कारण यह है कि विद्युत धारा की दिशा होते हुए भी यह सदिश नियम का पालन नहीं करती है। धाराओं का योग उनके मध्य कोण पर निर्भर नहीं करता है जबकि सदिशों का योग उनके मध्य कोण पर निर्भर करता है।

आवेश वाहक (Charge Carriers):
आवेश को एक दिशा में ले जाने का काम करने वाले कण आवेश वाहक कहलाते हैं।

• ठोस चालकों में आवेश वाहक-संयोजी मुक्त इलेक्ट्रॉन
• द्रवों में आवेश वाहक (विद्युत अपघट्य)-धनात्मक व ऋणात्मक आयन
• गैसों में आवेश वाहक-धनात्मक आयन व इलेक्ट्रॉन

धारा घनत्व (Current Density):
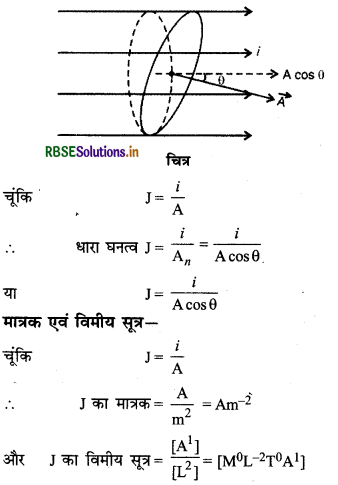
"एकांक अनुप्रस्थ परिच्छेद क्षेत्रफल से होकर बहने वाली धारा को धारा घनत्व कहते हैं।" इसे J से व्यक्त करते हैं। यह सदिश राशि है जिसकी दिशा धारा की दिशा में

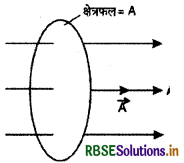
होती है। यदि A अनुप्रस्थ क्षेत्रफल वाले चालक में i धारा बहती है तो धारा घनत्व
J = \(\frac{i}{A}\) ..........(1)
परन्तु यदि चालक का परिच्छेद क्षेत्रफल धारा के लम्बवत् नहीं है, बल्कि अभिलम्ब से θ कोण बनाता है तो धारा घनत्व के लिए परिच्छेद क्षेत्रफल A का धारा के अभिलम्बवत् घटक A, लेना होगा।
A_n = A cos θ

आंकिक उदाहरण
विद्युत् धारा व धारा घनत्व पर आधारित आंकिक उदाहरण के लिए
प्रयुक्त सूत्र

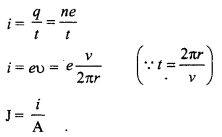
प्रयुक्त इकाईयाँ
विद्युतधारा - ऐम्पियर
आवेश - कूलॉम
धारा घनत्व - Am^-2
क्षेत्रफल - m²
प्रयुक्त नियतांक
e = 1.6 × 10^-19 कूलॉम

चालक में विद्युत् धारा का प्रवाह (Flow of Electric Current in Conductors)
सभी धातुएँ विद्युत् की सुचालक (good conductors) होती हैं। इनमें विद्युत् चालन मुक्त इलेक्ट्रॉनों द्वारा होता है। मुक्त इलेक्ट्रॉन मॉडल (free electron model) के आधार पर चालन की व्याख्या निम्न प्रकार से की जाती है

प्रत्येक पदार्थ परमाणुओं से मिलकर बना होता है और परमाणु में एक धनावेशित नाभिक के परितः कुछ निश्चित कक्षाओं में इलेक्ट्रॉन गतिशील रहते हैं। ये इलेक्ट्रॉन दो प्रकार के होते हैं

• सम्बद्ध इलेक्ट्रॉन (bound electrons) और
• मुक्त इलेक्ट्रॉन (free electrons)।

नाभिक के पास वाली कक्षाओं (orbits near to nucleus) के इलेक्ट्रॉनों पर नाभिक का नियन्त्रण (control) अधिक होता है, ये सामान्यतः (normally) अपनी कक्षा नहीं छोड़ सकते हैं। इन्हीं को सम्बद्ध इलेक्ट्रॉन कहते हैं। इलेक्ट्रॉनों की नाभिक से दूरी जैसे-जैसे बढ़ती जाती है, इन पर नाभिक का नियन्त्रण कम होता जाता है। आखिरी कक्षा के इलेक्ट्रॉनों पर नियन्त्रण इतना कम हो जाता है कि इन्हें थोड़ी भी ऊर्जा देकर संगत (corresponding) परमाणु से अलग किया जा सकता है। ये इलेक्ट्रॉन ही मुक्त इलेक्ट्रॉन (free electrons) कहलाते हैं। सामान्य ताप पर भी अनेक इलेक्ट्रॉन मुक्त होकर चालक की परिसीमाओं (boundaries) के अन्दर उसी प्रकार अनियमित (random) गति करते रहते हैं जिस प्रकार आदर्श गैस के अणु बर्तन के अन्दर गति करते हैं।

नोट-एक ग्राम जल में लगभग 10²² अणु होते हैं।

धातुओं में मुक्त इलेक्ट्रॉन ही आवेश वाहक का कार्य करते हैं। इसीलिए धातुओं की विद्युत् चालकता उनमें उपस्थित मुक्त इलेक्ट्रॉनों की संख्या पर निर्भर करती है। जिस धातु में मुक्त इलेक्ट्रॉनों की संख्या जितनी अधिक होती है, उसकी चालकता उतनी ही अधिक होती है। ऐसी धातुएँ ही विद्युत् की सुचालक होती हैं। चाँदी की चालकता सबसे अधिक होती है। इसके बाद ताँबा, सोना, ऐलुमिनियम आदि का क्रम आता है।

जिन पदार्थों में मुक्त इलेक्ट्रॉनों की संख्या बहुत कम होती हैं, उन्हें विद्युतीधी अथवा कुचालक (bad conductor) कहते हैं; जैसे-काँच, क्वार्ट्ज, ऐबोनाइट, अभ्रक, मोम आदि ।

ओम का नियम (Ohm's Law):
सन् 1828 में जर्मन वैज्ञानिक डॉ. जॉर्ज साइमन ओम (George Simon Ohm) ने वैद्युत धारा के सम्बन्ध में एक मूल नियम प्रस्तुत किया जिसे ओम का नियम कहते हैं। इस नियम के अनुसार, “यदि किसी चालक की भौतिक अवस्था (physical conditions) (जैसे-ताप, लम्बाई, क्षेत्रफल आदि) न बदलें तो उसके सिरों पर लगाये गये विभवान्तर एवं उसमें बहने वाली धारा का अनुपात नियत रहता है।" माना यदि चालक के सिरों पर V विभवान्तर लगाने पर उसमें । धारा बहे तो ओम के नियम से,
\(\frac{V}{i}\) = नियतांक

इस नियतांक को चालक का वैद्युत प्रतिरोध (Electric Resistance) कहते हैं और इसे R से व्यक्त करते हैं।
अतः \(\frac{V}{i}\) = R
इस सूत्र से, V = Ri ...(1)
या V ∝ i या i ∝ V
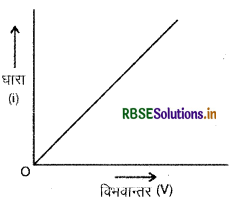
अर्थात् किसी चालक में बहने वाली धारा चालक पर लगाये गये विभवान्तर के समानुपाती (propotional) होती है, यदि चालक की भौतिक अवस्थाएँ न बदली जायें।

चूँकि V ∝ i या i ∝ V अत: V एवं । के मध्य खींचा गया ग्राफ एक सरल रेखा होगी (चित्र)।

(किसी चालक का प्रतिरोध (Resistance of a Conductor):
"किसी चालक द्वारा धारा के मार्ग में जो रुकावट (hinderance) डाली जाती है, उसे उस चालक का वैद्युत प्रतिरोध कहते हैं।" इसे R से व्यक्त करते हैं। यदि चालक के सिरों का विभवान्तर V हो और उसमें बहने वाली धारा i हो तो ओम के नियम से चालक का प्रतिरोध
R = \(\frac{V}{i}\)
मात्रक - R का मात्रक

अतः 1Ω = 1 VA^-1

एक ओम की परिभाषायदि
V = 1 वोल्ट, i = 1 ऐम्पियर
R = 1 ओम (Ω)

"यदि किसी चालक के सिरों पर 1 वोल्ट का विभवान्तर लगाने पर उसमें 1 ऐम्पियर की धारा प्रवाहित हो तो चालक का प्रतिरोध 1 2 होगा।"
विमीय सूत्र-चूँकि
R = \(\frac{\mathrm{V}}{i}=\frac{\mathrm{W}}{q i}=\frac{\mathrm{W}}{i^2 t}\)
∴ R का विमीय सूत्र = \(\frac{\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2}\right]}{\left[\mathrm{A}^2 \cdot \mathrm{T}^1\right]}\)
= [M¹L²T^-3A^-2]

चालक के प्रतिरोध का कारण-चालक में उपस्थित मुक्त इलेक्ट्रॉनों के संघट्ट के कारण उनके मार्ग में अवरोध होता है, इसे ही प्रतिरोध कहते हैं।

किसी चालक के प्रतिरोध की ज्यामितीय संरचना पर निर्भरता (dependence on geometrical structure):
किसी चालक का प्रतिरोध (R), उसकी लम्बाई (l), अनुप्रस्थ परिच्छेद (A) व चालक के पदार्थ के विशिष्ट प्रतिरोध (p) में निम्नलिखित सम्बन्ध होता हैR=P
R = ρ.\(\frac{l}{A}\)...(1)
अतः स्पष्ट है कि
(i) R ∝ l
अर्थात् चालक का वैद्युत प्रतिरोध उसकी लम्बाई के अनुक्रमानुपाती होता है।
(ii) R ∝ \(\frac{l}{A}\)
अर्थात् चालक का वैद्युत प्रतिरोध उसके अनुप्रस्थ परिच्छेद क्षेत्रफल के व्युत्क्रमानुपाती होता है।
(iii) R ∝ ρ
अर्थात् चालक का प्रतिरोध उसके पदार्थ के विशिष्ट प्रतिरोध या पदार्थ की प्रकृति (nature of substance) के अनुक्रमानुपाती होता है।

महत्वपूर्ण बिन्दु:
जिन पदार्थों की प्रतिरोधकता (resistivity) बहुत कम (चाँदी, ताँबा, ऐल्युमिनियम) होती है, उनसे संयोजक-तार (connection wires) बनाये जाते हैं क्योंकि इनके प्रतिरोध को नगण्य (negligible) माना जाता है। इसके विपरीत जिन पदार्थों की प्रतिरोधकता बहुत अधिक (नाइक्रोम, मैंगनिन, कॉन्स्टेन्टन आदि) होती है, उनसे प्रतिरोधक- तार (resistance wires) बनाये जाते हैं।

विशिष्ट प्रतिरोध अथवा प्रतिरोधकता (Specific Resistance or Resistivity):
चालक का विशिष्ट प्रतिरोध ρ एक आनुपातिकता स्थिरांक है जो चालक के पदार्थ की प्रकृति एवं ताप पर निर्भर करता है, इसेक विस्तार (अर्थात् लम्बाई व अनुप्रस्थ काट क्षेत्रफल) पर नहीं।
ρ = R.\(\frac{A}{l}\)

विमीय सूत्र : ρ = R\(\frac{A}{l}\) से
= \(\frac{\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-3} \mathrm{~A}^{-2}\right]\left[\mathrm{L}^2\right]}{\mathrm{L}}\)
= [M¹L³T^-3A^-2]
मात्रक - ओम-मी. (Ω - m)

महत्वपूर्ण बिन्दु
1. यदि किसी तार को

• खींच कर उसकी लम्बाई बढ़ायी गयी,
• पिघलाकर और दुबारा खींचने पर यदि लम्बाई पहले की लम्बाई से कम है, तो दोनों ही स्थितियों में तार का आयतन नियत रहता है।

2. माना किसी चालक तार को खींचने से पहले उसकी लम्बाई l₁, अनुप्रस्थ काट का क्षेत्रफल A₁, त्रिज्या l₁, व्यास d₁ एवं प्रतिरोध R₁ = ρ एक आनुपातिकता स्थिरांक है जो चालक के पदार्थ की प्रकृति एवं ताप पर निर्भर करता है, इसेक विस्तार (अर्थात् लम्बाई व अनुप्रस्थ काट क्षेत्रफल) पर नहीं।
ρ = R.\(\frac{A}{l}.\frac{l_1}{\mathrm{~A}_1}\) है।
खींचने के बाद माना उसकी लम्बाई l₂, अनुप्रस्थ काट का क्षेत्रफलं A₂, त्रिज्या r₂, व्यास (d₂) व प्रतिरोध R₂ = R.\(\frac{A}{l}.\frac{l_2}{\mathrm{~A}_2}\), है।
चूँकि खींचने के पश्चात् आयतन नियत रहता है अतः A₁l₁ = A₂l₂ खींचने के पश्चात् प्रतिरोधों का अनुपात

3. यदि संख्यात्मक प्रश्नों में लम्बाई दी गई है, तब
R ∝ l²
\(\frac{\mathrm{R}_1}{\mathrm{R}_2}=\left(\frac{l_1}{l_2}\right)^2\)
यदि संख्यात्मक प्रश्नों में त्रिज्या दी गई है, तब
R ∝ \(\frac{1}{r^4}\)
⇒ \(\frac{\mathrm{R}_1}{\mathrm{R}_2}=\left(\frac{r_2}{r_1}\right)^4\)

4. किसी चालक का प्रतिरोध उसकी लम्बाई, अनुप्रस्थ परिच्छेद क्षेत्रफल एवं चालक के पदार्थ की प्रकृति पर निर्भर करता है जबकि विशिष्ट प्रतिरोध केवल पदार्थ की प्रकृति पर निर्भर करता है, चालक की विमाओं पर नहीं। प्रतिरोध चालक की विशेषता है जबकि विशिष्ट प्रतिरोध उसके पदार्थ की विशेषता है।
ओम × मीटर प्रतिरोधकता का मात्रक है, जबकि ओम-मीटर प्रतिरोध मापन के लिए एक उपकरण है।

आंकिक उदाहरण
प्रतिरोध तथा प्रतिरोधकता पर आधारित आंकिक उदाहरण के लिए
प्रयुक्त सूत्र (i) R = \(\frac{V}{I}\)
(ii) ρ = R\(\frac{A}{l}\)
प्रयुक्त इकाई-
प्रतिरोध - ओम
प्रतिरोधकता - ओम-मी

ओम के नियम का सदिश रूप (Vector Form of Ohm's Law):
प्रतिरोध R तथा प्रतिरोधता ρ में संबंध से,
R = ρ\(\frac{l}{A}\) ............(i)

ओम के नियम के अनुसार
V ∝ I
V = RI

इस समीकरण को ओम के नियम का सदिश रूप कहते हैं। जहाँ σ\(\frac{1}{ρ}\) चालक के पदार्थ की विशिष्ट चालकता (Specific conductivity) कहलाती है।

इलेक्ट्रॉन का अपवाह (Driff Motion of Electron):
किसी विलगित (isolated) धात्वीय चालक में मुक्त इलेक्ट्रॉनों की गति वैसी ही होती है जैसी कि किसी बर्तन में भरे गैस-अणुओं की होती है। इसीलिए धातु में मुक्त इलेक्ट्रॉनों के समूह को 'इलेक्ट्रॉन गैस' (electron gas) भी कहते हैं। गैस अणुओं की भाँति मुक्त इलेक्ट्रॉनों की गति भी अनियमित होती है। ये धातु के स्थिर आयनों के खाली स्थान में अनियमित गति करते हुए उनसे टकराते (collide) रहते हैं जिससे उनका वेग निरन्तर बदलता रहता है। यह गति केवल ऊष्मीय ऊर्जा (thermal energy) के कारण होती है। कमरे के ताप पर इनका वेग लगभग 10⁵ ms^-1 की कोटि (order) का होता है, परन्तु यह वेग सभी दिशाओं में अनियमित रूप से वितरित रहता है; किसी विशेष दिशा (specific direction) में कोई नेट गति नहीं होती है। इस गति को चित्र में दिखाया गया है। यदि धातु में n इलेक्ट्रॉन हों तथा उनके अलग-अलग वेग क्रमशः \(\overrightarrow{u_1}, \overrightarrow{u_2}, \overrightarrow{u_3}, \ldots, \overrightarrow{u_n}\) हों तो इलेक्ट्रॉनों का औसत वेग

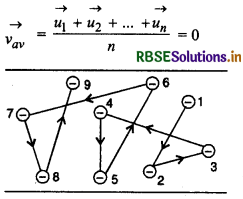
अतः आवेश का किसी भी दिशा में नैट प्रवाह नहीं होता है।

महत्त्वपूर्ण स्मरणीय तथ्य
"धातु के मुक्त इलेक्ट्रॉनों की अनियमित गति का औसत वेग शून्य रहता है। इसीलिए बिना विभवान्तर लगाये चालक में कोई धारा नहीं बहती है।"

अनुगमन वेग (Drift Velocity):
जब किसी चालक के सिरों के मध्य विभवान्तर लगाया जाता है तो चालक के अन्दर एक विद्युत् क्षेत्र (धन सिरे से ऋण सिरे की ओर) \(\vec{E}\) उत्पन्न हो जाता है और प्रत्येक मुक्त इलेक्ट्रॉन पर एक वैद्युत बल (F = – E.e) लगने लगता है। इस बल के प्रभाव में इलेक्ट्रॉन त्वरित (a = \(\frac{F}{m}\)) होता है और वह चालक के धनात्मक सिरे की ओर गति करने लगता है। गति के दौरान वह अन्य इलेक्ट्रॉनों एवं चालक के धन आयनों से टकराता हुआ वेग में परिवर्तन करता हुआ चलता है। इलेक्ट्रॉन की इस गति को अनुगमन गति (Drift motion) कहते हैं और दो उत्तरोत्तर टक्करों (Successive collisions) के मध्य इलेक्ट्रॉन के औसत वेग को अनुगमन वेग (Drift velocity) कहते हैं। इसे v_d से व्यक्त करते हैं। अर्थात् आरोपित विद्युत् क्षेत्र (imposed electric field) के कारण इलेक्ट्रॉनों द्वारा प्राप्त अधिकतम वेग (drift velocity) जिससे इलेक्ट्रॉन अन्य आयनों से टकराते हैं उसे अनुगमन वेग कहते हैं। टकराने में लगे समय को श्रांतिकाल कहते हैं। अधिकतर चालकों के लिए श्रांतिकाल 10^-14 s कोटि का होता है।

किसी आयन से टकराने के ठीक पहले इलेक्ट्रॉनों का वेग अधिकतम (maximum) तथा टकराने के ठीक बाद क्षण भर के लिए वेग शून्य हो जाता है। पुनः इलेक्ट्रॉन विद्युत् क्षेत्र में त्वरित होता है और आयनों से टकराने वाली पूर्व स्थिति (previous position) को दोहराता है। "इस प्रकार बैटरी का विभवान्तर इलेक्ट्रॉनों को त्वरित (accelerated) गति प्रदान नहीं कर पाता है बल्कि यह उन्हें चालक की लम्बाई के अनुदिश (along) एक छोटा नियत वेग ही दे पाता है जो कि इलेक्ट्रॉनों की अनियमित गति के ऊपर आरोपित रहता है। इलेक्ट्रॉनों के इस नियत वेग को ही अनुगमन वेग कहते हैं।" अनुगमन वेग का कोटि मान 10^-4 ms^-1 होता है।

अनुगमन वेग के कम होने का कारण-चित्र में विद्युत् क्षेत्र आरोपित करने पर मुक्त इलेक्ट्रॉनों की अनियमित गति (मोटी रेखा) के साथ उसका अनुगमन (बिन्दुवत्) भी दिखाया गया है। चित्र से स्पष्ट है कि विद्युत् क्षेत्र की अनुपस्थिति में इलेक्ट्रॉन 8 टक्करों के पश्चात् स्थिति 1 से X तक अनियमित गति करता हुआ पहुँचता है, जबकि वैद्युत क्षेत्र आरोपित करने पर इलेक्ट्रॉन की अन्तिम स्थिति X के बजाय X' हो जाती है। इस प्रकार विद्युत् क्षेत्र द्वारा नैट विस्थापन XX' हो जाता है जिसका मान काफी कम होता है। इसीलिए अनुगमन वेग भी कम होता है।

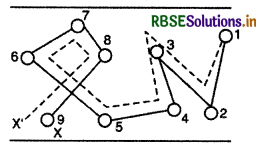
श्रांतिकाल (Relaxation Time):
"मुक्त इलेक्ट्रॉन की धातु के परमाणुओं से हुई दो क्रमागत टक्करों के बीच लगे औसत समय को श्रान्तिकाल कहते हैं।" इसे 1 से व्यक्त करते हैं। यदि दो उत्तरोत्तर टक्करों के बीच औसत दूरी अर्थात् माध्य मुक्त पथ (mean free path) λ हो तथा उसकी औसत चाल या वर्ग माध्य मूल चाल (root mean square speed) v_r हो तो

λ का मान 10^-9 m तथा τ का मान 10^-14 सेकण्ड की कोटि का होता है।

अनुगमन वेग तथा विभवान्तर में सम्बन्ध (Relation between Drift Velocity and Potential Difference):
माना PQ एक l लम्बाई का चालक है जिसके सिरों पर चित्र की भाँति V विभवान्तर लगाया जाता है। चालक

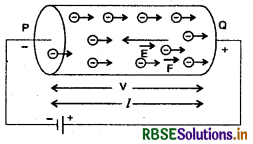
के अन्दर धनात्मक सिरे Q से ऋणात्मक सिरे P की ओर एक विद्युत् क्षेत्र \(\vec{E}\) पैदा हो जाता है। इस क्षेत्र की तीव्रता
\(\vec{E} = \frac{V}{l}\) .....(1)

चालक का प्रत्येक मुक्त इलेक्ट्रॉन इसी क्षेत्र में स्थित है अतः प्रत्येक मुक्त इलेक्ट्रॉन पर लगने वाला वैद्युत बल
\(\overrightarrow{\mathrm{F}}=-\overrightarrow{\mathrm{E}}\)e ...(2)

यदि इलेक्ट्रॉन का द्रव्यमान m हो तो वैद्युत बल के कारण इलेक्ट्रॉन में उत्पन्न त्वरण
\(\vec{a}=\frac{\overrightarrow{\mathrm{F}}}{m}=-\frac{\overrightarrow{\mathrm{E}} . e}{m}\) ..(3)

चूंकि मुक्त इलेक्ट्रॉन का औसत वेग शून्य होता है।
∴ प्रारम्भिक वेग u = 0 [अनुच्छेद (b) में स्पष्ट है]
अन्तिम वेग v = \(\overrightarrow{v_d}\) = अनुगमन वेग

इलेक्ट्रॉन द्वारा प्राप्त अधिकतम त्वरण (maximum acceleration)
\(\vec{a}=-\frac{e \overrightarrow{\mathrm{E}}}{m}\) [समी. (3) से]

टकराने में लगा समय (श्रान्तिकाल) = t
∴ गति के प्रथम समीकरण से,
v = u + at

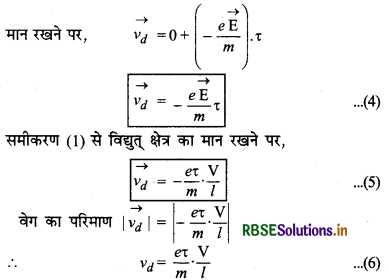
यह समीकरण अनुगमन वेग तथा विभवान्तर में सम्बन्ध प्रदर्शित करता है।

अनुगमन वेग एवं विद्युत् धारा में सम्बन्ध (Relation between Drift Velocity and Electric Current)
माना A अनुप्रस्थ परिच्छेद एवं l लम्बाई का PQ चालक है। इसके सिरों के मध्य चित्र की भाँति विभवान्तर लगाते हैं। जैसे ही विभवान्तर लगाया जाता है, चालक का प्रत्येक मुक्त इलेक्ट्रॉन अनुगमन वेग v_d से धनात्मक सिरे Q की ओर गति करने लगता है। सबसे पहले Q सिरे पर स्थित इलेक्ट्रॉन चालक को छोड़ेगा (release) और उसके बाद क्रमशः उसके पीछे वाले इलेक्ट्रॉन Q सिरे को छोड़ते रहेंगे।

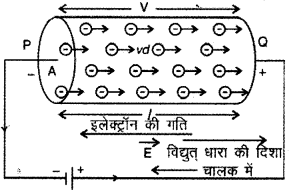
जिस समय P सिरे का इलेक्ट्रॉन Q सिरे को पार कर रहा होगा, तब तक चालक के समस्त मुक्त इलेक्ट्रॉन Q सिरे को पार कर चुके होंगे। इस क्रिया में लगा समय
t = \(\frac{l}{v_d}\)
यदि चालक के एकांक आयतन में मुक्त इलेक्ट्रॉनों की संख्या अर्थात् इलेक्ट्रॉन धनत्व (electron density) n हो तो चालक का प्रवाहित होने वाला आवेश
q = इलेक्ट्रॉनों की संख्या - इलेक्ट्रॉन का आवेश
= आयतन × इलेक्ट्रॉन घनत्व × इलेक्ट्रॉन आवेश
या q = Al.ne
∴ चालक में प्रवाहित धारा
i = \(\frac{q}{t}=\frac{\mathrm{A} \ln e}{l / v_d}\) = Anev_d
या v_d = \(\frac{i}{\mathrm{~A} n e}\) .......(i)
यही अनुगमन वेग एवं विद्युत् धारा में सम्बन्ध है।

महत्वपूर्ण निष्कर्ष
(i) समी. (1) से,

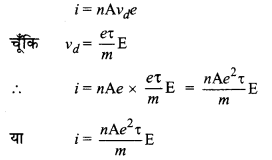
(ii) यदि चालक का व्यास (d) दुगुना कर दिया जाये तब इलेक्ट्रॉनों का अनुगमन वेग अप्रभावित रहता है।

आंकिक उदाहरण
अनुगमन वेग पर आधारित आंकिक उदाहरण के लिए
प्रयुक्त सूत्र- v_d = \(\frac{i}{\text { Ane }}\)

प्रयुक्त इकाई
अनुगमन वेग -मीटर/सेकण्ड
विद्युतधारा - ऐम्पियर
क्षेत्रफल - मीटर²

प्रयुक्त नियतांक
e = 1.6 × 10^-19 कूलॉम

गतिशीलता (Mobility)
हम जानते हैं कि चालकता गतिमान आवेश वाहकों से उत्पन्न होती है। धातुओं में ये गतिमान आवेश वाहक इलेक्ट्रॉन होते हैं, आयनित गैस में ये इलेक्ट्रॉन तथा धनावेशित आयन होते हैं, विद्युत् अपघट्य में ये धनायन तथा ऋणायन दोनों हो सकते हैं।

एक महत्वपूर्ण राशि गतिशीलता (mobility) है जिसे प्रति एकांक विद्युत् क्षेत्र के अनुगमन वेग के परिमाण के रूप में परिभाषित करते हैं।

किसी अर्द्धचालक के लिए विद्युत् धारा एवं गतिशीलता में सम्बन्ध
अर्द्धचालक में इलेक्ट्रॉन व होल दोनों के कारण चालकता होती है, अतः
I = I_e + I_h
= en_eAv_e + e.n_hAv_h
= en_eAµ_eE + e.n_hAµ_hE
= eAE (n_eµ_e + n_hµ_h)

महत्वपूर्ण बिन्दु
धात्विक चालक (metallic conductors) में इलेक्ट्रॉन आवेश वाहक होते हैं, जबकि अर्द्धचालक में इलेक्ट्रॉन एवं होल दोनों आवेश वाहक की भूमिका निर्वाह (work as) करते हैं। अर्द्धचालक में इलेक्ट्रॉन की कमी (deficiency) ही होल होती है और ये धनावेश की तरह व्यवहार (behave) करते हैं। यदि होल का द्रव्यमान m द्वारा व्यक्त करें और औसत श्रान्तिकाल से व्यक्त करें तो होलों की गतिशीलता निम्न सूत्र से प्राप्त होगी
µ_h = \(\frac{e \tau_h}{m_h}\)
यह ध्यान देने की बात है कि इलेक्ट्रॉनों एवं होलों दोनों की गतिशीलता धनात्मक है, परन्तु दोनों के अनुगमन वेग विपरीत दिशा में होंगे।

आंकिक उदाहरण
गतिशीलता (mobility) पर आधारित आंकिक उदाहरण के लिए
प्रयुक्त सूत्र
µ = \(\frac{v_d}{\mathrm{E}}=\frac{e \tau}{m}\)

प्रयुक्त इकाइयाँ
µ - ms^-1v^-1
v_d - मीटर/सेकण्ड
E – न्यूटन/कूलॉम

प्रयुक्त नियतांक
e = 1.6 × 10^-19 कूलॉम

ओम के नियम की अनुगमन वेग के सिद्धांत से व्युत्पत्ति । (Deduction of Ohm's Law by theory of drift velocity)
इस अध्याय में हम विद्युत धारा तथा अपवाह वेग के मध्य संबंध का विस्तृत अध्ययन कर चुके हैं जिसके अनुसार

जहाँ ρ चालक पदार्थ की प्रतिरोधकता है जो कि आनुपातिक नियतांक है। यदि चालक की भौतिक अवस्थाएँ न बदलें तो l तथा A भी नियत रहेंगे, अतः
ρ\(\frac{l}{\mathrm{~A}}\) = नियतांक = R (चालक का प्रतिरोध)
\(\frac{V}{I}\) = नियतांक
V ∝ l
यही ओम का नियम है अर्थात् “किसी चालक में बहने वाली धारा उस के सिरों के मध्य आरोपित विभवान्तर के अमुक्रमानुपाती होती है। बशर्ते कि चालक की भौतिक अवस्थाएँ न बदलें।" ।

ओम के नियम का सदिश रूप (Vector form of Ohm's Law)

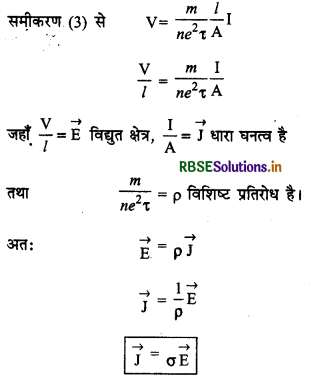
इस समीकरण को ओम के नियम का सूक्ष्म रूप (macroscopic form) कहते हैं।

ओम के नियम की सीमाएँ (Limitations of Ohm's Law):
ओम के नियम की असफलता (Failure of Ohm's Law):
ओम का नियम प्रकृति का मूल नियम (fundamental law of nature) नहीं है। अनेक स्थितियों में सम्बन्ध
V = iR
का पालन पूर्णतः नहीं होता है और ये स्थितियाँ ही ओम के नियम की असफलता की जनक हैं। इनमें से कुछ स्थितियाँ निम्नलिखित हैं

1. विभवान्तर धारा के साथ अरैखिक रूप से बदल सकता है (Potential difference mayvarynon-linearly with current):
धात्विक चालक के सिरों पर उत्पन्न विभवान्तर धारा के साथ चित्र में प्रदर्शित बिन्दुवत् रेखा (dotted line) के अनुसार रैखिक रूप (linearly) से बदलना चाहिए, लेकिन विभवान्तर को लगातार बढ़ाते रहने पर धारा का वास्तविक परिवर्तन (actual variation) मोटी रेखा के अनुसार होता है। इस परिवर्तन का कारण धारा का ऊष्मीय प्रभाव (thermal effect) है। लगातार धारा बढ़ने से चालक का प्रतिरोध बढ़ जाता है।

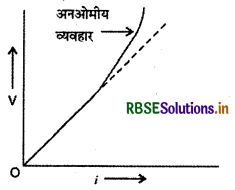
2. विभवान्तर के साथ धारा का परिवर्तन लगाये गये विभवान्तर के चिह्न पर निर्भर कर सकता है। (The variation of current with potential difference may depend upon sign of the potential difference applied):
जब p-n संधि अथवा अर्द्धचालक पर लगाये

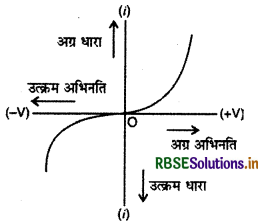
गये विभवान्तर (अभिनति) का चिह्न बदल देते हैं तो विभवान्तर के साथ धारा का परिवर्तन बदल जाता है (चित्र)। जब p-संधि के p सिरे को बैटरी के धन ध्रुव से एवं n सिरे को ऋण ध्रुव से जोड़ते हैं अर्थात् अग्र अभिनति लगाते हैं तो धारा तेजी से बदलती है और इसकी विपरीत वोल्टता अर्थात् उत्क्रम अभिनति (reverse biasing).लगाने पर धारा परिवर्तन की दर बहुत कम हो जाती है।

3. विभवान्तर के बढ़ाने पर धारा घट सकती है (The current may decrease on increasing the potential difference):
एक थाइरिस्टर (thyristor) में p व n प्रकार के अर्द्धचालकों की क्रमागत (alternative) चार पर्ते होती हैं। .

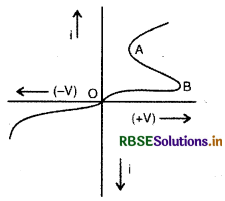
थाइरिस्टर के लिए V-i ग्राफ (अग्र एवं उत्क्रम दोनों अभिनतियों के लिए) चित्र में दिखाया गया है। ग्राफ का AB भाग यह व्यक्त करता है कि विभवान्तर घटाने पर धारा का मान बढ़ता है। यह थाइरिस्टर के ऋणात्मक प्रतिरोध (negative resistance) क्षेत्र के संगत है। यहाँ यह ध्यान देने की बात यह है कि थाइरिस्टर में विभवान्तर बदलने पर धारा का परिवर्तन अरैखिक (non-linear) तो है ही, साथ ही साथ धारा परिवर्तन का परिमाण विभवान्तर के चिह्न पर भी निर्भर करता है।

नोट-अनओमीय चालक-वे चालक जो ओम के नियम का पालन नहीं करते हैं, उन्हें अनओमीय चालक कहते हैं; जैसे-डायोड, ट्रायोड, ट्रांजिस्टर आदि।,

विभिन्न पदार्थों की वैद्युत प्रतिरोधकता (Specific Resistivity of Various materials):
विभिन्न पदार्थों का वैद्युत प्रतिरोधकता में परिवर्तन काफी वृहद् परास में होता है। धातुओं की प्रतिरोधकता 10^-2Ω m से 10^-6Ω m के परिसर में होती है। इसके विपरीत सिरेमिक (मृत्तिका), रबर तथा प्लास्टिक जैसे विद्युतरोधी पदार्थों की प्रतिरोधकता धातुओं की तुलना में 10¹⁸ गुनी या अधिक है। इन दोनों के मध्य अर्द्धचालक हैं। इनकी प्रतिरोध कता ताप बढ़ाने पर अभिलाक्षणिक रूप से घटती है।

पदार्थ का नाम	प्रतिरोधकता (ρ)	प्रतिरोध ताप गणांक ∝ 0°C पर
चालक: चाँदी (सिल्वर)	1.6 × 10-8	0.0041
ताँबा (कॉपर)	1.7 × 10-8	0.0068
ऐल्युमिनियम	2.7 × 10-8	0.0043
टंगस्टन	5.6 × 10-8	0.0045
लोहा (आयरन)	10 × 10-8	0.0065
प्लैटिनम	11 × 10-8	0.0039
पारा (मर्करी)	98 × 10-8	0.0009
नाइक्रोम	-100 × 10-8	0.0004
मैंगनिन	48 × 10-8	0.002 × 10-3
अर्द्धचालक : कार्बन (ग्रेफाइट)	3.5 × 10-5	-0.0005
जर्मेनियम	0.46	-0.05
सिलिकॉन	2300	- 0.07
विद्युतरोधी : शुद्ध जल	2.5 × 105
काँच (ग्लास)	1010-1014
कठोर रबर	1013-1016
सोडियम क्लोराइड (NaCl)	~ 1014
संयुक्त स्फटिक (फ्यूज्ड क्वार्ट्स)	~ 1016

घरेलू या प्रयोगशालाओं में प्रयोग हेतु व्यापारिक दृष्टिकोण से बनाए जाने वाले प्रतिरोधक मुख्यतः दो प्रकार के होते हैं-तार आबद्ध प्रतिरोधक तथा कार्बन प्रतिरोधक।
(i) तार आबद्ध प्रतिरोधक: किसी मिश्र धातु जैसे मैंगनिन, कान्सटेन्टन, नाइक्रोम या उनके जैसे तारों को लपेट कर बनाए जाते हैं। बहुधा इन पदार्थों का चयन इस तथ्य पर निर्भर करता है कि उनकी प्रतिरोधकता पर ताप का प्रभाव अपेक्षाकृत नगण्य है। इन प्रतिरोधों का परिसर एक ओम के किसी अंश से लेकर कुछ सौ ओम तक होता है।

(ii) कार्बन प्रतिरोध एवं वर्ण कोड(Carbon Resistance and Colour Codes for Carbon): विद्युत एवं इलेक्ट्रॉनिक परिपथों में प्रयुक्त वृहत् (Vast) होता है। उच्चतर परिसर (higher range) के प्रतिरोधक मुख्यतः कार्बन से बनाये जाते हैं।
कार्बन के प्रतिरोधक सुसंहत (compact) और सस्ते होते हैं, इसलिए इलेक्ट्रॉनिक परिपथों में व्यापक रूप से उपयोग किये जाते हैं। कार्बन प्रतिरोध आमाप (size) में छोटे होते हैं, अतः उनके मान वर्ण कोड (colour code) के द्वारा व्यक्त किये जाते हैं। वर्ण कोड निम्न तालिका में दिया गया है

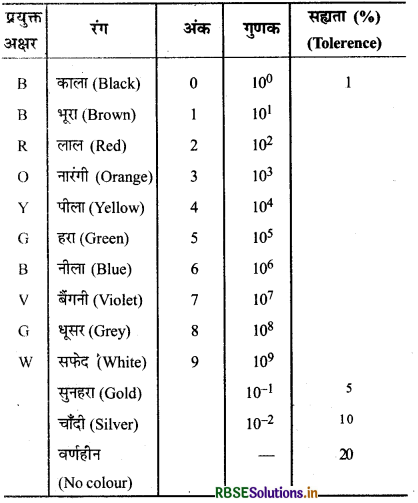
तालिका को याद रखने के लिए तथ्य

दूसरा वाक्य याद रखने के लिये-
Black Brown Rods Of Your Gate Became
Very Good When Given Silver Colour

प्रतिरोधक पर समाक्ष (coaxial) रंगीन वलयों (rings) का समूह होता है जिनकी सार्थकता (significance) उक्त सारणी में दी गई है। सिरे से पहली दो धारियाँ ओम में प्रतिरोध के पहले दो सार्थक अंकों को निर्देशित करती हैं। तीसरी धारी दशमलव गुणक (multiplier) को निर्देशित करती है तथा अन्तिम धारी सह्यता (tolerance) अथवा निर्देशित मान के प्रतिशत में सम्भावित विचरण (probable variation) को व्यक्त करती है। कभी-कभी यह अन्तिम धारी नहीं होती है जिसका आशय यह है कि सह्यता 20% है (चित्र)। उदाहरण के लिए, यदि चार रंग नारंगी, नीला, पीला और सुनहरा (golden) हैं, तो प्रतिरोध का मान 5% सह्यता मान के साथ 36 × 10⁴Ω होगा।।

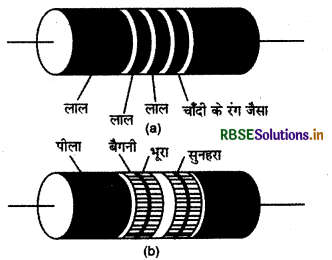
प्रतिरोधों के प्रतीक

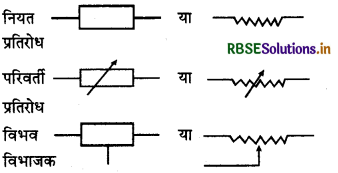
आकिक उदाहरण
कार्बन प्रतिरोध के वर्णकोड पर आधारित वर्णकोड याद करने की युक्ति

प्रतिरोधकता पर ताप का प्रभाव (Effect of Temperature on Specific Resistance)
ताप के साथ धात्विक चालक, मिश्र धातु एवं अर्द्धचालक की प्रतिरोधकता में परिवर्तन समान नहीं होता है, बल्कि भिन्न-भिन्न होता
(A) धात्विक चालक की प्रतिरोधकता पर ताप का प्रभाव (Effect of temperature or resistivity of Mettalic Conductor):
विशिष्ट प्रतिरोध निम्न सूत्र से दिया जाता है
ρ = \(\frac{m}{n e^2 \tau}\) ....(1)
जहाँ m = इलेक्ट्रॉन का द्रव्यमान
n = एकांक आयतन में मुक्त इलेक्ट्रॉनों की संख्या
e = इलेक्ट्रॉन का आवेश
τ = श्रांतिकाल
सूत्र (1) में m व e पर तापवृद्धि का कोई प्रभाव नहीं पड़ता है और यदि ताप वृद्धि बहुत अधिक नहीं है तो n भी अप्रभावित (uneffective) रहेगा। अब हमें श्रांतिकाल पर ताप के प्रभाव का अध्ययन करना है।
∴ श्रांतिकाल τ = \(\frac{\lambda}{v_r}\)
जहाँ λ माध्य मुक्त पथ एवं , अनियमित (random) गति में इलेक्ट्रॉन की वर्ग माध्य मूल चाल है।

ताप बढ़ाने पर चालक के अणुओं की दोलन ऊर्जा (oscillating energy) बढ़ती है, अतः उनके दोलन का आयाम (amplitude) बढ़ जाता है; फलस्वरूप माध्य मुक्त पथ (mean free path) 2 का मान कम हो जाता है। दूसरे ताप बढ़ाने पर इलेक्ट्रॉनों की वर्ग माध्य मूल चाल का मान भी बढ़ जाता है। इस प्रकार का मान कम होने और v, का मान बढ़ने से श्रांतिकाल 1 का मान कम हो जाता है, अतः समी. (1) से स्पष्ट है कि का मान कम होने से p का मा बढ़ जायेगा। इस प्रकार ताप बढ़ाने से विशिष्ट प्रतिरोध अर्थात् प्रतिरोधकता बढ़ जाती है। धात्विक चालक की प्रतिरोधकता का परिवर्तन आगे दिये गये चित्र में प्रदर्शित है। ताप के साथ प्रतिरोधकता का परिवर्तन निम्न सूत्र से मिलता है
ρ_t = ρ₀ (1+ αt) ...(2)

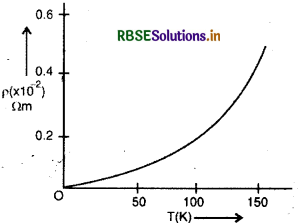
जहाँ ρ_t = t°C पर विशिष्ट प्रतिरोध;
ρ₀ = 0°C पर विशिष्ट प्रतिरोध
α = प्रतिरोध ताप गुणांक (temperature coeffi-cient of resistance)

महत्वपूर्ण बिन्दु
"वह घटना, जिसमें किसी पदार्थ को क्रान्तिक ताप (critical temperature) तक ठण्डा करने पर वह प्रतिरोध के सभी चिह्नों को खो देता है अर्थात् उसका प्रतिरोध शून्य हो जाता है, अतिचालकता (Super conductivity) कहलाती है।"

वे पदार्थ जो अतिचालकता प्रदर्शित करते हैं, अतिचालक (Super conductors) कहलाते हैं। जब किसी चालक का ताप कम किया जाता है तो उसका प्रतिरोध घटता है अर्थात् यह अच्छा चालक बन जाता है।

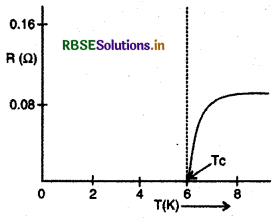
(पारा 4.2K पर अपना पूर्ण प्रतिरोध खो देता है।)

अतिचालकता अनेक धातुओं एवं मिश्र धातुओं द्वारा प्रदर्शित की जाती है। अतिचालकता का कारण यह है कि अतिचालक में इलेक्ट्रॉन आपस में कला सम्बद्ध (mutually coherent) होते हैं। धन आयनों के दोलन, जो धातुओं में मुक्त इलेक्ट्रॉनों को विक्षेपित (deffect) कर सकते हैं, अतिचालक में कला सम्बद्ध मुक्त इलेक्ट्रॉनों को विक्षेपित करने में असमर्थ होते हैं।

उपयोग

• अतिचालकों का प्रयोग सुपर कम्प्यूटर बनाने में किया जाता है।
• अतिचालक केबिल के उपयोग से बिना ऊर्जा क्षय (decay) के विद्युत् ऊर्जा का स्थानान्तरण (transfer) किया जा सकता है।
• बिना विद्युत् शक्ति के व्यय (loss) के अतिचालक उच्च चुम्बकीय क्षेत्र उत्पन्न कराने में सहायक हो सकते हैं।

(B) मिश्रधातु की प्रतिरोधकता पर ताप का प्रभाव (Effect of temperature on resistivity of an alloy):
मिश्रधातु जैसे नाइक्रोम के लिए प्रतिरोधकता काफी अधिक होती है और ताप पर इसकी निर्भरता बहुत क्षीण (weak) होती है। उदाहरण के लिए, मैगनिन जो ताँबे, निकल, लोहे एवं मैंगनीज की मिश्रधातु होती है; का प्रतिरोध शुद्ध ताँबे के प्रतिरोध का 30 से 40 गुना होता है। लेकिन इसका प्रतिरोध ताप गुणांक बहुत कम (0.00001°C^-1) होता है। इसी कारण यह प्रामाणिक प्रतिरोध कुण्डली बनाने के लिए आदर्श पदार्थ है। चित्र में मिश्रधातु के लिए ताप के साथ प्रतिरोधकता का परिवर्तन प्रदर्शित है।

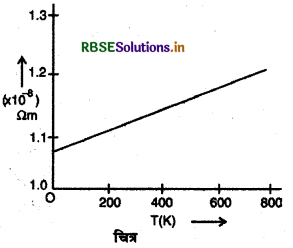
(C) अर्द्धचालक एवं अचालक की प्रतिरोधकता की ताप पर farefcall (Temperature dependence of the resistivity of a semiconductor and insulator):
अर्द्धचालक एवं अचालक की प्रतिरोधकता का ताप के साथ परिवर्तन, धात्विक चालकों की प्रतिरोधकता के ताप के साथ परिवर्तन (variation) से भिन्न होता है। चालक के लिए ताप के साथ प्रतिरोधकता का परिवर्तन रैखिक (linear) होता है। अर्द्धचालक या अचालक की प्रतिरोधकता का ताप के साथ परिवर्तन चरघातांकी (exponential) वक्र द्वारा प्रदर्शित होता है (चित्र)। अर्द्धचालक या अचालक की प्रतिरोधकता का ताप के साथ अग्र सम्बन्ध होता है

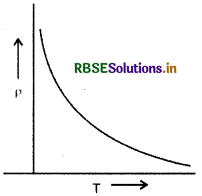
ρ_t = ρ₀e^E_g/kT ...(1)
जहाँ ρ_t = t°C पर प्रतिरोधकता
ρ₀ = 0°C पर प्रतिरोधकता
E_g = ऊर्जा अन्तराल ;
k = बोल्ट्जमैन नियतांक .
T = (273 + t)K, ताप केल्विन स्केल में।

महत्वपूर्ण बिन्दु-थर्मिस्टर:
“थर्मिस्टर एक ऐसा ऊष्मा सुग्राही (heat sensitive) प्रतिरोधक होता है जो सामान्यतः अर्द्ध-चालक पदार्थ से बनाया जाता है और ताप परिवर्तन से इसके प्रतिरोध में अच्छा परिवर्तन हो जाता है।" थर्मिस्टर अर्द्धचालकों के ऑक्साइडों से बनाये जाते हैं। थर्मिस्टर की संरचना (structure) के आधार पर इनका प्रतिरोध परिवर्तन 0.1 2 से 1072 तक हो सकता है। थर्मिस्टर साधारण प्रतिरोधक (resistor) से निम्न प्रकार भिन्न होता है

• थर्मिस्टर का प्रतिरोध ताप परिवर्तन के साथ तेजी से बदलता है।
• थर्मिस्टर का प्रतिरोध ताप गुणांक बहुत उच्च होता है।
• थर्मिस्टर का प्रतिरोध ताप गुणांक धनात्मक एवं ऋणात्मक दोनों हो सकता है।

उपयोग

• ताप के साथ तीव्र प्रतिरोध परिवर्तन के कारण इनका उपयोग छोटे ताप परिवर्तन के संकुचन (contraction) एवं निम्न ताप' (≈ 10 K) के मापन के लिए किया जाता है।
• इनका उपयोग ताप नियन्त्रण इकाइयों (temperature controlled units) एवं मोटर बाइण्डिंग जेनरेटर एवं ट्रान्सफॉर्मर के संरक्षण के लिए किया जाता है।
• इनका उपयोग धारा परिवर्तन के कारण TV सेट के हीटर की सुरक्षा के लिए किया जाता है।
• इनका उपयोग वोल्टता नियन्त्रण, ताप नियन्त्रण एवं दूर संवेदन (remote sensing) में किया जाता है।

(D) प्रतिरोध पर ताप का प्रभाव (Effect of temperature on resistance) हम जानते हैं कि किसी चालक का वैद्युत प्रतिरोध
R = ρ\(\frac{l}{A}\)
यदि ताप वृद्धि बहुत अधिक नहीं है तो ! व A पर विशेष प्रभाव नहीं पड़ेगा, अतः
R ∝ ρ
∵ ताप बढ़ाने पर विशिष्ट प्रतिरोध (specific resistance) बढ़ता है, अतः ताप बढ़ाने पर प्रतिरोध भी बढ़ेगा।
\(\frac{\mathrm{R}_t}{\mathrm{R}_0}=\frac{\rho_t}{\rho_0}\)
जहाँ R_t = t°C पर प्रतिरोध एवं R = 0°C पर प्रतिरोध
\(\frac{\mathrm{R}_t}{\mathrm{R}_0}=\frac{\rho_t}{\rho_0}\)

जहाँ α, प्रतिरोध ताप गुणांक है और उक्त समीकरण से इसका मान
α = \(\frac{\mathrm{R}_t-\mathrm{R}_0}{\mathrm{R}_0 \cdot t}\)
यदि t₁°C पर प्रतिरोध R₁, और t₂°C का प्रतिरोध R₂, हो तो
R₁ = R₀(1 + at₁)
R₂ = R₀(1 + at₂)
\(\frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{1+\alpha t_1}{1+\alpha t_2}\)
या R₁ + R₁at₂ = R₂ + R₂at₁
R₁t₂ - R₂t₁ = R₂ - R₁
या (R₁t₂ -R₂t₁) = R₂ - R₁

α की इकाई °C^-1 है। अधिकांश धातुओं के लिए a का मान लगभग 1/273 प्रति °C होता है। धातुओं के लिए a का मान धनात्मक होता है। अधिकांश धात्विक तत्वों के लिए a का मान 4 × 10^-3 °C^-1 होता है।

आकिक उदाहरण
प्रतिरोध पर ताप के प्रभाव पर आधारित आंकिक उदाहरण के लिए(i) प्रयुक्त सूत्र
R_t = R₀(1 + αt)
α = \(\frac{\mathrm{R}_2-\mathrm{R}_1}{\left(\mathrm{R}_1 t_2-\mathrm{R}_2 t_1\right)}\)

(ii) प्रयुक्त इकाईयाँ
R_t, R₀ = ओम
α = 0°C^-1, t-0°C या K

विद्युत् ऊर्जा एवं विद्युत् शक्ति (Electric Energy and Electric Power):
हम सब जानते हैं कि विद्युत् धारा बहने पर कोई चालक तार गर्म हो जाता है। इसका कारण यह है कि जब किसी चालक के सिरों पर विभवान्तर लगाया जाता है तो उसके मुक्त इलेक्ट्रॉन अनुगमन वेग से चालक के धनात्मक सिरे की ओर चलने लगते हैं और तार में विद्युत् धारा बहने लगती है। अपनी गति के दौरान मुक्त इलेक्ट्रॉन चालक के धन आयनों से बार-बार टेकराते हैं और अपनी ऊर्जा उन्हें देते रहते हैं। मुक्त इलेक्ट्रॉन लगातार बैटरी से ऊर्जा लेते रहते हैं और चालक के धन आयनों को देते रहते हैं। इस प्रकार धन आयनों की ऊर्जा बढ़ने से उनकी ऊष्मीय गति (thermal motion) बढ़ जाती है और चालक तार का ताप बढ़ जाता है अर्थात् वह गर्म हो जाता है। इस प्रकार बैटरी से ली गई ऊर्जा ऊष्मा में बदलती रहती है।

माना किसी चालक तार का प्रतिरोध R है और उसके सिरों पर V विभवान्तर लगाने पर उसमें धारा i बहने लगती है। यदि धारा t सेकण्ड तक प्रवाहित हो तो प्रवाहित आवेश
q = it कूलॉम

इस आवेश के प्रवाहित होने में कृत कार्य
W = Vq = Vit
या W = Vit ...(1)

परन्तु ओम के नियम से,
V = iR
W = iRit ⇒ W = i²Rt

पुनः I = \(\frac{V}{R}\)
∴ W = \(\frac{\mathrm{V}^2}{\mathrm{R}^2}\).Rt
⇒ W = \(\frac{\mathrm{V}^2}{\mathrm{R}}\).t ......(3)
∵ "किसी वैद्युत परिपथ में ऊर्जा क्षय होने की दर (rate of energy loss) अर्थात् कार्य करने की दर को वैद्युत शक्ति कहते हैं।" अतः
P=
समी. (1), (2) व (3) से,
P = VI ...(4)
P = I²R .......(5)
एवं P = \(\frac{\mathrm{V}^2}{\mathrm{R}}\) ....(6)
विद्युत शक्ति की SI इकाई वॉट है।
1 वॉट = 1 वोल्ट × 1 ऐम्पियर

किलोवाट घण्टा (Kilowatt hour):
घरों, कारखानों तथा अन्य सभी कार्यों में व्यय होने वाली बिजली का मूल्य वैद्युत ऊर्जा (electrical energy) के आधार पर ज्ञात किया जाता है न कि वैद्युत शक्ति (electrical power) के आधार पर। विद्युत् ऊर्जा का ऑफ ट्रेड यूनिट (B.T.U.) प्रयोग किया जाता है। साधारण बोलचाल की भाषा में इसे केवल यूनिट कहते हैं। “एक किलोवाट घण्टा अथवा एक यूनिट वैद्युत ऊर्जा की वह मात्रा है जो एक किलोवाट की वैधुत शक्ति वाले परिपथ में एक घण्टे में व्यय (consumed) होती है।"
∴ 1 किलोवाट घण्टा = 1 किलोवाट × 1 घण्टा
= 1000 वाट × 3600 सेकण्ड
= 3.6 × 106 जूल
विद्युत् ऊर्जा की गणना निम्न सूत्र से की जा सकती हैकिसी विद्युत् उपकरण में व्यय ऊर्जा

जूल का नियम (Joule's law of heating):
किसी चालक में t समय में ऊष्मा के रूप में व्यय (dissipate) ऊर्जा निम्न सूत्र द्वारा दी जाती है
H = VIt जूल = I²Pt जूल = \(\frac{\mathrm{V}^2 t}{\mathrm{R}}\) जूल
या H = \(\frac{\mathrm{VI} t}{4 \cdot 18}\) कैलोरी = \(\frac{I^2 \mathrm{R} t}{4 \cdot 18}\) कैलोरी
= \(\frac{\mathrm{V}^2 t}{4 \cdot 18 \mathrm{R}}\) कैलोरी

विद्युत् ऊर्जा व विद्युत् शक्ति पर आधारित आंकिक उदाहरण के लिएप्रयुक्त सूत्र
H = I²Rt जूल = \(\frac{\mathrm{I}^2 \mathrm{R} t}{4.18}\) कैलोरी
या H = VIt जूल = \(\frac{\mathrm{VI} t}{4.18}\)  कैलोरी
P = \(\frac{\mathrm{VI} t}{4.18}\) = VI= I²R = y
W = Pt = VIt = I²Rt

प्रयुक्त इकाईयाँ
'I - ऐम्पियर
R - ओम, t - सेकण्ड
P - वॉट, E - जूल या kWh

प्रतिरोधों का संयोजन
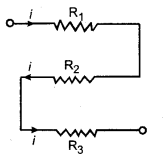
(Combination of Resistors) (A) श्रेणी-संयोजन (Series Combination) इस प्रकार के संयोजन में चित्र 3.15 की तरह पहले प्रतिरोध का दूसरा सिरा दूसरे प्रतिरोध के पहले सिरे से और दूसरे का दूसरा सिरा तीसरे के पहले सिरे से तथा इसी प्रकार क्रमशः जोड़ते जाते हैं। इस संयोजन को E वि. वा. बल एवं नगण्य आन्तरिक प्रतिरोध वाली बैटरी से जोड़ देते हैं। प्रतिरोधों के सिरों के विभवान्तर क्रमशः V₁, V₂, V₃, हैं।

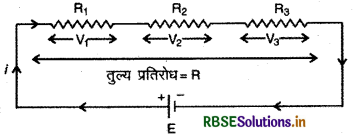
चित्र अतः चित्र में प्रदर्शित परिपथ में कुल विभवान्तर
E = V₁ + V₂ + V₃
या E = iR₁ + iR₂ + iR₃
या E = i (R₁ + R₂ + R₃)

यदि संयोजन का तुल्य प्रतिरोध R मान लें तो तुल्य परिपथ चित्र के अनुसार होगा। अतः इस परिपथ से,
E = iR

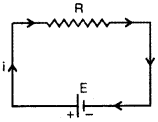
समी. (1) व (2) की तुलना करने पर,
iR = i (R₁ + R₂ + R₃)
या R = R₁ + R₂ + R₃

इसी प्रकार n प्रतिरोधों के श्रेणीक्रम संयोजन का तुल्य प्रतिरोध
R = R₁ + R₂ + R₃ + ......+ R_n ...(3)
अतः श्रेणीक्रम में सभी प्रतिरोधों का योग हो जाता है।

निष्कर्ष:
अतः तुल्य (equivalent) प्रतिरोध सबसे बड़े प्रतिरोध से भी बड़ा होता है।

उपयोग:
श्रेणीक्रम संयोजन में तुल्य प्रतिरोध का उपयोग अधिकतम प्रतिरोध प्राप्त करने के लिए किया जाता है।

स्मरणीय तथ्य:
(i) प्रत्येक प्रतिरोध में बहने वाली धारा का मान समान होता है। यदि एक प्रतिरोध कहीं से टूट (break) जाये तो सभी प्रतिरोधों में धारा बहना बन्द हो जायेगी।
(ii) ∵ V = iR और i का मान सबके लिए समान है
V ∝ R
अतः V₁ : V₂ : V₃ = R₁ : R₂ : R₃
(iii) ∵ P = I²R और I नियत है
P ∝ R
अतः P₁ : P₂ : P₃ = R₁ : R₂ : R₃
(iv) इस संयोजन में सभी प्रतिरोध जुड़ जाते हैं, अतः छोटे प्रतिरोधों से बड़ा प्रतिरोध प्राप्त करने के लिए इस संयोजन का उपयोग किया जाता है।
(v) यदि R1 प्रतिरोध के n प्रतिरोधक (resistors) श्रेणीबद्ध किये जायें तो R = nRI

(B) समान्तर क्रम संयोजन (Parallel Combination):
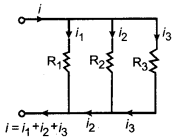
इस संयोजन में सभी प्रतिरोधों का एक सिरा एक संधि पर और दूसरे सिरे दूसरी संधि पर जोड़ दिये जाते हैं। चित्र में तीन प्रतिरोधों का समान्तर क्रम संयोजन दिखाया गया है। संधि A पर परिणामी धारा
i = i₁ + i₂ + i₃ ...(4)

सभी प्रतिरोध A व B के मध्य जुड़े हैं, अतः सभी प्रतिरोधों के सिरों के मध्य विभवान्तर (V) समान होगा।

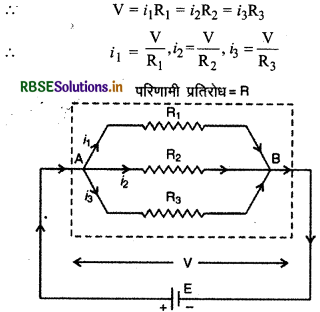
यदि संयोजन का तुल्य प्रतिरोध R मान लें तो तुल्य परिपथ निम्न चित्र 3.18 के अनुसार होगा। इस परिपथ से,

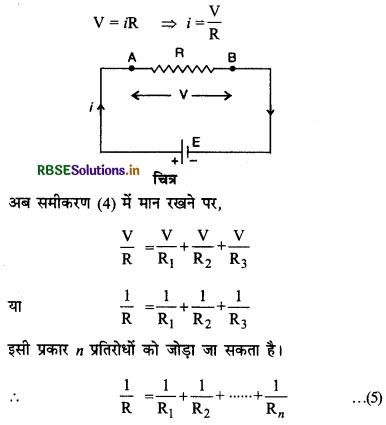
निष्कर्ष-तुल्य या परिणामी प्रतिरोध सबसे छोटे प्रतिरोध से भी छोटा होता है।

उपयोग:
समान्तर क्रम संयोजन में तुल्य प्रतिरोध का उपयोग प्रतिरोध को कम करने के लिए किया जाता है।

स्मरणीय तथ्य
(i) समान्तर क्रम संयोजन में परिणामी प्रतिरोध का मान जोड़े गये प्रतिरोधों में न्यूनतम प्रतिरोध से भी कम प्राप्त है, अतः बड़े प्रतिरोधों से छोटा प्रतिरोध प्राप्त करने के लिए इस संयोजन का उपयोग किया जाता है।
(ii) ∵ V = iR ⇒ i = \(\frac{V}{R}\) और V का मान नियत है।
i ∝ \(\frac{1}{R}\)
अतः i₁ : i₂ : i₃ = \(\frac{1}{\mathrm{R}_1}: \frac{1}{\mathrm{R}_2}: \frac{1}{\mathrm{R}_3}\)

(i) ∵ P = \(\frac{\mathrm{V}^2}{\mathrm{R}}\) और V नियत है।
अत: P₁ : P₂ : P₃ = \(\frac{1}{\mathrm{R}_1}: \frac{1}{\mathrm{R}_2}: \frac{1}{\mathrm{R}_3}\)
(iv) यदि R, प्रतिरोध के n प्रतिरोधक समान्तरबद्ध किये जायें तो
R = \(\frac{\mathrm{R}_1}{n}\)

स्मरणीय बिन्दु
किसी समान्तर परिपथ के लिए

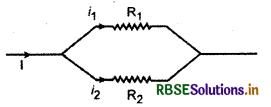
प्रतिरोध R₁, में धारा i₁ = \(\frac{\mathrm{R}_2 i}{\mathrm{R}_1+\mathrm{R}_2}\)

प्रतिरोध R₂ में धारा i₂ = \(\frac{\mathrm{R}_1 i}{\mathrm{R}_1+\mathrm{R}_2}\)

श्रेणीक्रम व समान्तर क्रम में तुलना

श्रेणीक्रम	समान्तर क्रम
धारा के लिए केवल एक पथ होता है।	धारा के लिए अनेक पथ हो सकते हैं।
प्रत्येक बिन्दु पर धारा का मान समान होता है।	प्रत्येक शाखा में धारा का मान अलग हो सकता है।
'प्रत्येक प्रतिरोध पर विभव का पतन (potential drop) होता है।	प्रत्येक प्रतिरोध पर विभव का पतन समान होता है।
बीच में परिपथ को तोड़ने पर पूरे परिपथ में धारा का प्रवाह रुक जाता है।	बीच में परिपथ को तोड़ने पर केवल एक ही शाखा (branch) में धारा नहीं बहती है, बाकी में बहती रहती है।
श्रेणीक्रम में जोड़ने पर परिणामी धारा घटती है।	समान्तर क्रम में जोड़ने पर परिणामी धारा बढ़ती है।

आकिक उदाहरण
प्रतिरोधों के श्रेणी क्रम व समान्तर क्रम संयोजन पर आधारित
आंकिक उदाहरण के लिए प्रयुक्त सूत्र
श्रेणीक्रम, R = R₁ + R₂ + R₃

समान्तर क्रम,
\(\frac{1}{\mathrm{R}}=\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\frac{1}{\mathrm{R}_3}\)

प्रयुक्त इकाईयाँ-
R - ओम

विद्युत् सेल (Electric Cell):
"विद्युत् सेल वह युक्ति (device) है जो किसी परिपथ के किन्हीं दो बिन्दुओं के मध्य विभवान्तर बनाये रखती है अर्थात् परिपथ में धारा के प्रवाह को बनाये रखती है।" सभी सेलें धारा देते समय रासायनिक ऊर्जा (chemical energy) को विद्युत् ऊर्जा में बदलती हैं। इस प्रकार सेल की परिभाषा निम्न प्रकार भी कर सकते हैं

"वैद्यत सेल वह युक्ति है जो रासायनिक ऊर्जा को वैद्यत ऊर्जा में बदलती है।" यह ध्यान रखने योग्य तथ्य है कि सेल आवेश अथवा इलेक्ट्रॉनों का स्रोत नहीं है, बल्कि ऊर्जा का स्रोत है। सेल केवल ऊर्जा देता है, बहने वाला आवेश तो परिपथ में मौजूद रहता है। समझने के लिए सेल की तुलना एक पानी निकालने वाले पम्प से की जा सकती है। पम्प भी सेल की तरह केवल ऊर्जा का स्रोत है, पानी का नहीं।

सेल में विभिन्न धातुओं की दो छड़ें होती हैं जिन्हें 'इलेक्ट्रोड' अथवा 'प्लेटें' कहते हैं। ये एक द्रव में डूबी रहती हैं, जिसे 'विद्युत्-अपघट्य' (electrolytes) कहते हैं। विद्युत्-अपघट्य में प्लेटों को डुबोने (dip) पर एक प्लेट धनावेशित हो जाती है तथा दूसरी ऋणावेशित हो जाती है। जब दोनों प्लेटों को किसी तार से जोड़ देते हैं तो तार में आवेश प्रवाहित होने लगता है। सेल के भीतर विद्युत्-अपघट्य में ऐसी रासायनिक क्रिया (chemical reaction) होती है जिससे प्लेटों पर आवेशों की पूर्ति होती रहती है तथा तार में आवेश-प्रवाह (वैद्युत धारा) बना रहता है। इस प्रकार सेल रासायनिक ऊर्जा को वैद्युत ऊर्जा में बदलता रहता है।

क्या आप जानते हैं कि
(1) जब किसी सेल के टर्मिनलों को किसी बाह्य विद्युत् परिपथ से नहीं जोड़ा जाता है तो सेल से कोई धारा प्रवाहित नहीं होती है। यह परिपथ खुला परिपथ (open circuit) कहलाता है।

(2) जब किसी सेल के टर्मिनलों को किसी बाह्य विद्युत् परिपथ से जोड़ा जाता है, तो सेल से धारा प्रवाहित होती है। यह परिपथ बन्द परिपथ (close Circuit) कहलाता है। सेलों के प्रकार-सेल मुख्यतः दो प्रकार के होते हैं

• प्राथमिक सेल (Primary Cell),
• द्वितीयक सेल (Secondary Cell)।

(i) प्राथमिक सेल-वे सेल जो सीधे-सीधे रासायनिक ऊर्जा को वैद्युत ऊर्जा में बदलते हैं और जिन्हें दोबारा चार्ज नहीं किया जा सकता है (not rechargeable), प्राथमिक सेल (primary cells) कहलाते हैं; जैसे-लेक्लांशी सेल, डेनियल सेल, शुष्क सेल आदि।
(ii) द्वितीयक सेल-वे सेल जिनमें वैद्युत ऊर्जा को पहले रासायनिक ऊर्जा के रूप में एकत्र (stored) किया जाता है और फिर आवश्यकता पड़ने पर इसी रासायनिक ऊर्जा से वैद्युत ऊर्जा प्राप्त करते हैं। इन्हें बार-बार चार्ज किया जा सकता है; जैसे-सीसा संचायक सेल (lead storage cells)।

सेल का आन्तरिक प्रतिरोध (Internal Resistance of Cell):
“सेल के अन्दर धारा के मार्ग में आने वाली रुकावट (hinderance) को सेल का आन्तरिक प्रतिरोध कहते हैं।" इसे ' से व्यक्त करते हैं। इसका मात्रक ओम (2) होता है। सेल का आन्तरिक प्रतिरोध निम्न बातों पर निर्भर (follow) करता है

• विद्युत्-अपघट्य की प्रकृति (nature of the electrolyte), ताप व सान्द्रता पर।
• प्लेटों के मध्य दूरी पर।
• प्लेटों के (विद्युत अपघट्य में) डूबे (immersed) हुए भाग पर।

एक निश्चित ताप पर सेल का आन्तरिक प्रतिरोध प्लेटों के बीच की दूरी
(1) के अनुक्रमानुपाती एवं प्लेटों के डूबे हुए भाग के क्षेत्रफल A के व्युत्क्रमानुपाती होता है अर्थात्
r ∝ l
एवं r ∝ \(\frac{l}{A}\)
या r ∝ \(\frac{l}{A}\) या r = K\(\frac{l}{A}\)
जहाँ K एक नियतांक है जो सेल के विद्युत्-अपघट्य की प्रकृति एवं सान्द्रता पर निर्भर करता है। प्राथमिक सेलों का आन्तरिक प्रतिरोध अधिक होता है, जबकि द्वितीयक सेलों का आन्तरिक प्रतिरोध कम होता है। इसीलिए समान विद्युत् वाहक बल (electromotive force) वाली द्वितीयक सेल प्राथमिक सेल की अपेक्षा अधिक धारा देती है।

क्या आप जानते हैं कि
1. किसी नए बने हुए सेल का आन्तरिक प्रतिरोध ज्यादातर कम होता है पर जैसे-जैसे हम ज्यादा धारा लेते हैं तो इसका मान बढ़ जाता है।
2. किसी सेल का आन्तरिक प्रतिरोध विद्युत् अपघट्य के ताप | के कम होने पर बढ़ता है। . 3. विद्युत् वाहक बल को हम निम्न प्रकार भी परिभाषित कर सकते हैं... "जब किसी सेल को बाह्य बन्द परिपथ से नहीं जोड़ा जाता है अर्थात् सेल से कोई धारा नहीं ली जाती है तब इसके टर्मिनलों के मध्य विभवान्तर को सेल का विद्युत् वाहक बल कहते हैं।" :

सेल का विद्युत् वाहक बल (Electromotive Force or e.m.f.):
"इकाई धनावेश को परिपथ में प्रवाहित करने में सेल द्वारा जितना कार्य किया जाता है अर्थात् एकांक आवेश को परिपथ में बहने के लिए सेल द्वारा जितनी ऊर्जा दी जाती है, उसे ही सेल का विद्युत् वाहक बल कहते हैं। इसे E से व्यक्त करते हैं; अतः सेल का वि. वा. बल
E = \(\frac{W}{q}\) ...(1)
जहाँ W सेल द्वारा q आवेश को प्रवाहित करने में किया गया कार्य है।
∴ E का मात्रक = \(\frac{J}{C}\) = वोल्ट
यदि W = 1 J, q = 1 C तो E = 1 JC^-1 या वोल्ट
अर्थात् यदि 1C आवेश को परिपथ में प्रवाहित करने में सेल द्वारा 1J कार्य किया जाता है तो सेल का वि. वा. बल 1JC^-1 या 1 वोल्ट होगा।

वि. वा. बल का मान एक सेल के लिए नियत होता है और विभिन्न सेलों के लिए भिन्न-भिन्न होता है। उदाहरण के लिए, वोल्टीय सेल का वि. वा. बल 1.08 वोल्ट; डेनियल सेल का वि. वा. बल 1.08 वोल्ट; लेक्लांशी एवं शुष्क सेल के लिए वि. वा. बल 1.5 वोल्ट होता है।

महत्वपूर्ण बिन्दु
1. यद्यपि विद्युत् वाहक बल को बल कहकर पुकारते हैं, लेकिन यह बल नहीं है बल्कि यह ऊर्जा है जो एकांक आवेश को परिपथ में बहने के लिए सेल द्वारा मिलती है।
2. यदि परिपथ में बाह्य प्रतिरोध लगा हो तो नापा गया विभव टर्मिनल विभवान्तर होता है।

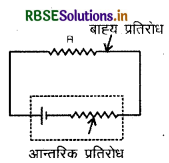
3. यदि परिपथ में बाह्य प्रतिरोध न लगा हो तो नापा गया विभव सेल का विद्युत् वाहक बल होता है।

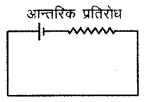
टर्मिनल विभवान्तर (Terminal Potential Difference):
"इकाई धनावेश को एक टर्मिनल से दूसरे टर्मिनल तक बाहरी परिपथ में प्रवाहित करने में सेल द्वारा जितना कार्य किया जाता है अर्थात् सेल जितनी ऊर्जा देता है; वह टर्मिनल विभवान्तर के तुल्य होता है।" यदि बाह्य प्रतिरोध (R) में q आवेश प्रवाहित करने में सेल W_ext कार्य करता है तो टर्मिनल विभवान्तर
V = \(\frac{\mathrm{W}_{\mathrm{ext}}}{q}\) वोल्ट ...(2)

यदि बाह्य प्रतिरोध में बहने वाली धारा । हो तो
V = \(\frac{\mathrm{W}_{\mathrm{ext}}}{q}\) = IR (ओम के नियम से)

इसी प्रकार आन्तरिक प्रतिरोध (r) के कारण व्यय ऊर्जा अर्थात् विभव-पतन (potential drop)
V = Ir

∴ विद्युत् वाहक बल की परिभाषानुसार, विद्युत् वाहक बल
E = (बाह्य कार्य + आन्तरिक कार्य)
एकांक आवेश को प्रवाहित करने में
या E = V + v
या E = IR + Ir = I(R + r)

E = V + Ir
∴ टर्मिनल विभवान्तर V = E - Ir ...(4)
इस समीकरण से यह भी स्पष्ट है कि यदि
I = 0 तो V = E
"खुले परिपथ में किसी सेल का टर्मिनल विभवान्तर ही उसके विद्युत् वाहक बल के तुल्य होता है।" समी. (4) से स्पष्ट है :
Ir = E - V
r = \(\frac{E-V}{I}\) ....(5)
∵ V = IR ∴ IP
∴ r = \(\frac{\mathrm{E}-\mathrm{V}}{\mathrm{V} / \mathrm{R}}\) या r = \(\frac{(E-V) R}{V}\) ...(6)
v समीकरण (5) व (6) की सहायता से सेल का आन्तरिक प्रतिरोध ज्ञात किया जा सकता है।

महत्वपूर्ण बिन्दु

• सेल के आन्तरिक प्रतिरोध के सिरों पर । उत्पन्न विभवान्तर (Ir) को ही विभव पतन कहते हैं।
• सेल से धारा लेते समय उसकी टर्मिनल वोल्टता V= E - Ir अर्थात् आन्तरिक प्रतिरोध के सिरों पर विभवान्तर विद्युत् वाहक बल का विरोध करता है।
• जब सेल को चार्ज किया जाता है तो उसकी टर्मिनल वोल्टता V = E + Ir अर्थात् आन्तरिक प्रतिरोध के सिरों के मध्य उत्पन्न विभवान्तर (Ir) विद्युत् वाहक बल में जुड़ जाता है।

आंकिक उदाहरण
विद्युत सेल पर आधारित आंकिक उदाहरण के लिए
प्रयुक्त सूत्र- V = E - Ir
I = \(\frac{\mathrm{E}}{\mathrm{R}+r} r = \frac{(E-V) R}{V}\)
प्रयुक्त इकाईयाँ
VE - वोल्ट
R,r-ओम
I-ऐम्पियर

सेलों का संयोजन (Combination of Cells):
एक सेल से एक सीमित (limited) धारा ही प्राप्त की जा सकती है। अनेक प्रयोगों में एक सेल से प्राप्त धारा से अधिक धारा की आवश्यकता होती है, अतः ऐसी स्थिति में वांछित (desired) धारा प्राप्त करने के लिए हमें सेलों को श्रेणी क्रम में या समान्तर क्रम में अथवा मिश्रित क्रम में जोड़ना पड़ता है।

(i) सेलों का श्रेणी क्रम संयोजन (Series Combination of Cells)
(a) जब सेलों के विद्युत् वाहक बल एवं आन्तरिक प्रतिरोध समान होते हैं
चित्र में समान विद्युत् वाहक बल E एवं समान आन्तरिक प्रतिरोध r वाले n सेलों का श्रेणी क्रम संयोजन दिखाया गया है।
यह संयोजन एक बाह्य प्रतिरोध R में धारा भेजता है। इस संयोजन का परिणामी विद्युत् वाहक बल = nE
संयोजन का कुल आन्तरिक प्रतिरोध = nr

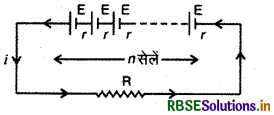
अतः परिपथ का कुल प्रतिरोध = R + nr
∴ परिपथ में प्रवाहित धारा

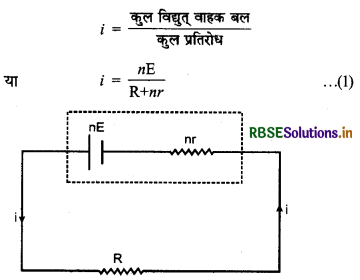
(i) यदि R >> nr तो nr को नगण्य (negligible) मानने पर,
i = \(\frac{n \mathrm{E}}{\mathrm{R}}\) = n × \(\frac{\mathrm{E}}{\mathrm{R}}\)
= n × एक सेल से प्राप्त धारा
अतः संयोजन सार्थक (significant) है।

(ii) यदि R < nr तो Rको छोड़ने पर,
i = \(\frac{n \mathrm{E}}{n r}=\frac{\mathrm{E}}{r}\) = एक सेल से प्राप्त धारा
अतः संयोजन निरर्थक (non-significant) है।

(b) जब सेल भिन्न विद्युत् वाहक बल एवं भिन्न आन्तरिक प्रतिरोध के हों-चित्र में E₁, व E₂, विद्युत् वाहक बलों एवं आन्तरिक प्रतिरोधों व 2 के दो सेलों का श्रेणीक्रम संयोजन दिखाया गया है और यह संयोजन R प्रतिरोध में धारा भेजता है। यदि परिपथ में प्रवाहित धारा । हो तो पहली सेल की टर्मिनल वोल्टता
V₁ = सेल का वि. वा. बल - आन्तरिक प्रतिरोध के सिरों पर विभव-पतन

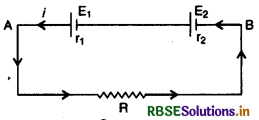
V₁ = E₁ - ir₁
इसी प्रकार दूसरे सेल की टर्मिनल वोल्टता

V₂ = E₂ - ir₂
यदि परिपथ के बिन्दुओं A व B के मध्य विभवान्तर V हो तो
V = V₁ + V₂
= (E₁ - ir₁) + (E₂ - ir₂)
V = (E₁ + E₂) - i (r₁ + r₂) ...(2)

यदि प्रभावी विद्युत् वाहक बल E हो एवं प्रभावी आन्तरिक प्रतिरोध r हो तो
V = E - ir ...(3)

समी. (2) व (3) की तुलना करने पर,
E = E₁ + E₂ ...(4)
r = r₁ + r₂ ...(5)

∴ सेलों का श्रेणीक्रम संयोजन प्रतिरोध R में धारा भेज रहा है, अतः
i = \(\frac{\mathrm{E}}{\mathrm{R}+r}\)
i = \(\frac{\mathrm{E}_1+\mathrm{E}_2}{\mathrm{R}+\left(r_1+r_2\right)}\) ...(6)

यदि सेलों का संयोजन इस प्रकार है कि वे एक-दूसरे का विरोध कर रहे हों तो
E = E₁ ~ E₂
अतः I = \(\frac{\mathrm{E}_1 \sim \mathrm{E}_2}{\mathrm{R}+\left(r_1+r_2\right)}\) ...(8)

(ii) सेलों का समान्तर क्रम संयोजन (Parallel Combination of Cells)
(a) जब सेल समान विद्युत् वाहक बल एवं समान आन्तरिक प्रतिरोध के हों-समान विद्युत् वाहक बल E एवं समान आन्तरिक प्रतिरोध r के n सेल समान्तर क्रम में जुड़े हैं और यह संयोजन (combination) R प्रतिरोध में धारा भेजता है। सभी सेलों के धन ध्रुव संधि A से एव ऋण
I = R+(r+ra)

ध्रुव संधि B से जुड़े हैं। इस संयोजन में परिपथ में प्रवाहित आवेश किसी एक सेल से होकर गुजरता है, अतः
संयोजन का विद्युत् वाहक बल = एक सेल का विद्युत् वाहक बल
= F

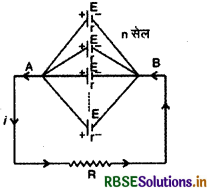
संयोजन का आन्तरिक प्रतिरोध यदि r' हो तो
\(\frac{1}{r^{\prime}}=\frac{1}{r}+\frac{1}{r}+\ldots \cdot+\frac{1}{r}=\frac{n}{r}\)
∵ r' = \(\frac{r}{n}\)
अत: परिपथ का कुल प्रतिरोध = R + r' = (R + \(\frac{r}{n}\))

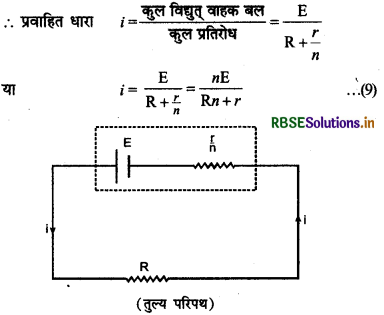
(i) जब R > > \(\frac{r}{n}\) तो \(\frac{r}{n}\) को छोड़ने पर,
i = \(\frac{E}{R}\) = एक सेल से प्राप्त धारा अतः संयोजन निरर्थक है।

(ii) जब R < < \(\frac{r}{n}\) तो R को छोड़ने पर,
i = \(\frac{\mathrm{E}}{\frac{r}{n}}=\frac{n \mathrm{E}}{r}\)
= n × एक सेल से प्राप्त धारा अतः संयोजन सार्थक है।

(b) जब सेलों के विद्युत् वाहक बल एवं आन्तरिक प्रतिरोध भिन्न होते हैं-चित्र में E₁ व E₂, विद्युत् वाहक बलों एवं r₁ व r₂ आन्तरिक प्रतिरोधों वाले दो सेलों का समान्तर क्रम संयोजन दिखाया गया है। यह संयोजन प्रतिरोध R में धारा भेजता है। यदि प्रथम सेल द्वारा भेजी गई धारा i₁, एवं दूसरे सेल से भेजी गई धारा से i₂, हो तो मुख्य धारा
i = i₁ + i₂ ...(10)

माना A व B संधियों के मध्य विभवान्तर V हो तो प्रथम सेल की टर्मिनल वोल्टता
V = E₁ - i₁r₁

यदि संयोजन का परिणामी विद्युत् वाहक बल E हो एवं परिणामी आन्तरिक प्रतिरोध r हो, तो
V = E - Ir ...(14)

समीरण (13) व (14) से स्पष्ट है कि
E = \(\frac{\mathrm{E}_1 r_2+\mathrm{E}_2 r_1}{\left(r_1+r_2\right)}\) ....(15)
और r = \(\frac{r_1 r_2}{\left(r_1+r_2\right)}\) ..........(16)

तथा बाह्य प्रतिरोध में प्रवाहित धारा
i = \(\frac{E}{(R+r)}\) ....(17)
इस समीकरण में E का मान समीकरण (15) से व का मान समीकरण (16) से प्राप्त होगा।

(iii) सेलों का मिश्रित संयोजन (Mixed Combination of Cells)
चित्र में समान विद्युत् वाहक के बल E एवं समान आन्तरिक प्रतिरोध r की सेलों का मिश्रित संयोजन दिखाया गया है। प्रत्येक लाइन में n सेलें श्रेणीबद्ध हैं और m लाइनें समान्तर क्रम में जोड़ी गई हैं। पूरे संयोजन का परिणामी विद्युत् वाहक बल = nE

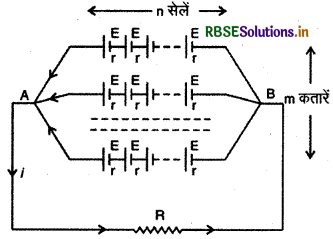
प्रत्येक लाइन का आन्तरिक प्रतिरोध = n.r
अतः पूरे संयोजन का कुल आन्तरिक प्रतिरोध यदि r' हो, तो

इस समीकरण (18) से स्पष्ट है कि धारा का मान तब अधिकतम होगा जब (mR + nr) का मान न्यूनतम होगा।

∵ \(\frac{nr}{m}\) = पूरी बैटरी का आन्तरिक प्रतिरोध

मिश्रित क्रम में धारा तब अधिकतम होगी जब बाह्य प्रतिरोध का मान संयोजन के आन्तरिक प्रतिरोध के बराबर होगा, अतः समी. (18) से,
I_max = \(\frac{n \mathrm{E}}{\mathrm{R}+\mathrm{R}}\)
I_max = \(\frac{n \mathrm{E}}{2 \mathrm{R}}\) .........(20)
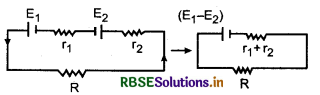
महत्वपूर्ण निष्कर्ष:
जब E₁, तथा E₂, विद्युत् वाहक बलों के दो सेलों को इस प्रकार जोड़ा जाता है कि इनके ऋणात्मक सिरे (negative terminals) एक-दूसरे से जोड़े जाएँ (यहाँ E₁ > E₂) तो संयोजन का तुल्य विभवान्तर बल = |E₁ - E₂|

आंकिक उदाहरण
सेलों के संयोजन पर आधारित आंकिक उदाहरण के लिए
प्रयुक्त सूत्र
(1) श्रेणीक्रम में,
(a) i = \(\frac{n \mathrm{E}}{\mathrm{R}}\)
(b) i = \(\frac{\mathrm{E}_1 \sim \mathrm{E}_2}{\mathrm{R}+\left(r_1+r_2\right)}\)

(2) समान्तर क्रम में,
(a) i = \(\frac{nE}{r}\)
(b) i = \(\frac{\mathrm{E}_1 r_2+\mathrm{E}_2 r_1}{r_1 r_2} - V \frac{\left(r_2+r_1\right)}{r_1 r_2}\)
(c) मिश्रित संयोजन (mixed combination) में,
i = \(\frac{m n \mathrm{E}}{m \mathrm{R}+n r}\)
i_max = \(\frac{nE}{2R}\)
प्रयुक्त इकाईयाँ
E - वोल्ट, R - ओम, i – ऐम्पियर

विद्युत तड़ित (Lighting):
विद्युत तड़ित (Lighting): बादल बर्फ के टुकड़ों से बने होते हैं। ये टुकड़े आपस में टकराते हैं, टूटते हैं तथा टुकड़े-टुकड़े होकर अलग हो जाते हैं। इनमें छोटे कणों पर धनात्मक आवेश तथा बड़े कणों पर ऋणात्मक आवेश आ जाता है। बादलों के ऊपरी दिशा में प्रवाह के कारण एवं गुरुत्व के कारण ये आवेशित कण आपस में टूट जाते हैं, जिसके कारण बादलों का ऊपरी भाग धनात्मक तथा मध्य भाग ऋणात्मक आवेशित हो जाता है और ये एक द्विध्रुव की रचना करते हैं। कभी-कभी बादलों के तल पर एक अत्यन्त दुर्बल धनावेश मिलता है।

तफान के कारण धरती धनावेशित हो जाती है एवं अंतरिक्ष तथा रेडियोधर्मी विकिरण वायु को धन तथा ऋण आयनों में आयनित कर देते हैं और हवा में विद्युत चालन होता हैं। धरती तथा बादल के मध्य के अतिरिक्त आवेशों का पृथक्करण बादल के अन्दर विशाल मात्रा में विद्युत विभव उत्पन्न करता है (≈ 1,00,000 वोल्ट)। यह वायु में क्षण मात्र के लिए विद्युत प्रतिरोध को नगण्य कर देता है जिससे तड़ित स्फुर क्षणदीप्ति होती है एवं हजारों ऐम्पियर की धारा प्रवाहित होती है। विद्युत क्षेत्र 10⁵ V/m की कोटि | का होता है और यह वज्रपात करती है।

किरखोफ के नियम (Kirchhoff's Laws):

• ओम का नियम केवल सरल विद्युत परिपथों के लिए ही उपयोगी है। ऐसे परिपथ जिनमें एक से अधिक विद्युत वाहक स्रोत जुड़े हैं, उनमें
• ओम के नियम के प्रयोग में कठिनाई होती है। सन् 1842 में जटिल वैद्युत परिपथों के लिए दो नियमों का प्रतिपादन गुस्ताव रॉबर्ट किरखोफ ने किया। किरखोफ के नियमों को समझने से पूर्व हम कुछ शब्दावली को परिभाषित करेंगे।
• संधि (Juction)-किसी विद्युत परिपथ में जिस बिन्दु पर तीन या तीन से अधिक धारावाही शाखाएँ (Branchs) मिलती हैं, उसे संधि कहते है।
• शाखा (Branch)-किसी विद्युत परिपथ के जाल (network) का वह भाग जिसमें विद्युत धारा नियत रहती है, शाखा कहलाती है।
• लूप या पाश (Loop)-विभिन्न चालकों, प्रतिरोधों एवं अन्य अवयवों से मिलकर बना विद्युत परिपथ, लूप या पाश कहलाता है।

किरखॉफ का प्रथम नियम या संधि नियम । | (Kirchhoff's First Law or Junction Law):
प्रथम नियम-"किसी वैद्युत परिपथ में किसी संधि पर मिलने वाली समस्त धाराओं का बीजगणितीय योग (algebraic sum) शून्य होता है।" अर्थात्
Σi = 0 ...(1)
किसी संधि की ओर आने वाली (incoming) धाराओं को धनात्मक एवं संधि से दूर जाने वाली (outgoing) धाराओं को ऋणात्मक मान लिया जाता है (चित्र)। संधि O पर मिलने वाली धाराओं के लिए,

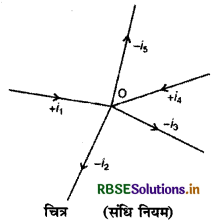
i₁ - i₂ - i₃ + i₄ - i₅ = 0
या i₁ + i₄ = i₂ + i₃ + i₅
या संधि की ओर आने वाली धाराओं का योग = संधि से दूर जाने वाली धाराओं का योग

इस प्रकार किरखॉफ के प्रथम नियम को इस प्रकार भी कह सकते, हैं, "किसी परिपथ में किसी संधि की ओर आने वाली धाराओं का योग संधि से दर जाने वाली धाराओं के योग के बराबर होता है।" किरखॉफ का प्रथम नियम आवेश संरक्षण (law of Conservation of Charge) के सिद्धान्त पर आधारित है।

महत्वपूर्ण नियम
प्रथम नियम लगाने के लिए चिह्न परिपाटी जंक्शन पर आने वाली धारा = धनात्मक (+) जंक्शन पर निकलने या दूर जाने वाली धारा = ऋणात्मक (-)

किरखॉफ का द्वितीय नियम या लूप नियम (Kirchhoff's Second Law or Loop Law):
द्वितीय नियम-"किसी बन्द परिपथ में परिपथ का परिणामी विद्युत वाहक बल परिपथ के विभिन्न अवयवों (elements) के सिरों पर उत्पन्न विभवान्तरों के योग के बराबर होता है।" किरखॉफ का यह नियम ऊर्जा संरक्षण (Law of Conservation of Energy) के सिद्धांत पर आधारित होता है अर्थात्
ΣE = ΣV = ΣiR .....(2)

महत्वपूर्ण नियम:
इस नियम के लिए चिह्न परिपाटी (sign convention)
1. जब हमें दिये गये परिपथ में धारा प्रवाहित करने के लिए सेल दिया जाता है तो यदि हम सेल के ऋणात्मक (-) इलेक्ट्रोड से धनात्मक (+) इलेक्ट्रोड की दिशा में जाते हैं तो सेल का विद्युत वाहक बल धनात्मक होता है।
उदाहरण

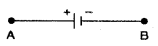
जब B से A की तरफ जाते हैं तो

2. जब हम परिपथ में धनात्मक (+) इलेक्ट्रोड से ऋणात्मक (-) इलेक्ट्रोड की तरफ जाते हैं तो सेल का विद्युत वाहक बल ऋणात्मक होता है।
उदाहरण

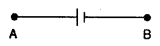
जब A से B की तरफ जाते हैं तो
E = -

3. जब हम परिपथ में लगे प्रतिरोध के सिरों के बीच विभवान्तर लेते हैं तो यदि हम धारा की दिशा में जाते हैं तो विभव पतन (potential drop) धनात्मक लिया जाता है।
उदाहरण

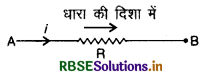
यदि हम AB की दिशा में चलते हैं तो AB की दिशा में विभव पतन
V_AB = + iR

4. जब हम परिपथ में लगे प्रतिरोध के सिरों के बीच विभवान्तर लेते हैं तो यदि हम धारा की दिशा के विपरीत जाते हैं तो विभव पतन ऋणात्मक होता है।
उदाहरण

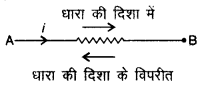
यदि हम B से A की दिशा में जाते हैं तो BA के मध्य विभव पतन
V_BA = - iR

उदाहरण के लिए, चित्र में किरखॉफ के नियम लगाते हैं

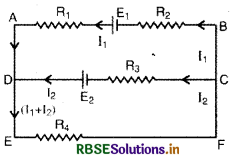
उपर्युक्त नियमों के आधार पर,
A से B'की दिशा में E₁ = -
B से A की दिशा में E₂ = +
D से C की दिशा में E₁ = -
C से D की दिशा में E₂ = +

बन्द पाश ABCDA में,
ΣE = ΣiR

बन्द पाश का रास्ता A → B → C → D → A
-E₁ + E₂ = -i₁R₁ - R₂ + i₂R₃
E₂ - E₁ = i₂R₃- i₁(R₁ + R₂) ...(3)

बन्द पाश DCFED में,
बन्द पाश का रास्ता D → C → F → E → D
ΣE = Σi.R
-E₂ = -i₂.R₃ - (i₁ + i₂) R₄
-E₂ = i₂R₃ + (i₁+ i₂)RA ...(4)

आकिक उदाहरण
किरखॉफ के नियम पर आधारित आंकिक उदाहरणों के लिए
(i) प्रयुक्त सूत्र
(a) Σi = 0 (जंक्शन नियम)
(b) ΣE = ΣV = ΣiR (लूप नियम)

(ii) प्रयुक्त इकाइयाँ
V -वोल्ट
R - ओम
i - ऐम्पियर

हीटस्टोन सेतु (Wheatstone's Bridge):
इंग्लैण्ड के वैज्ञानिक प्रोफेसर सी. एफ. ह्वीटस्टोन (C.F. Wheatstone) ने चार प्रतिरोधों, एक धारामापी एवं एक सेल को जोड़कर एक विशेष प्रकार का परिपथ तैयार किया जो ह्वीटस्टोन सेतु के नाम से जाना गया। इसकी सहायता से हम अज्ञात (unknown ) प्रतिरोध ज्ञात कर सकते हैं।
रचना-ह्वीटस्टोन सेतु की सैद्धान्तिक रचना चित्र 3.28 में दिखाई गई है। चार प्रतिरोधों P, Q, R, S को जोड़कर एक चतुर्भुज ABCD बनाते हैं। बिन्दुओं A व C के मध्य एक सेल जोड़ देते हैं। बिन्दुओं B व D के मध्य एक धारामापी जोड़ दिया जाता है। K, बैटरी कुंजी है और K, धारामापी कुंजी है। यदि कुंजी K, को हम पहले बन्द (close) करें और फिर K, को, तब यदि धारामापी में कोई विक्षेप (deflection) न दें तब इस अवस्था में,

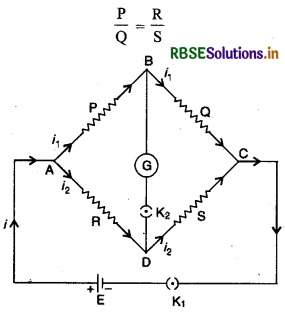
सिद्धान्त-जब बैटरी कुंजी (battery key) K₁, को दबाते हैं तो परिपथ में मुख्य धारा i बहती है। इस धारा को A बिन्दु पर दो मार्ग मिलने से यह दो भागों i₁ व i₂ में बँट जाती है। i₁ को B बिन्दु पर और i₂, को D बिन्दु पर पुनः दो मार्ग मिलते हैं। B व D पर i₁ व i₂ के विभाजन की निम्न तीन स्थितियाँ सम्भव हैं

• जब V_B > B_D तो B बिन्दु पर i का एक भाग धारामापी से गुजर कर उसमें एक दिशा में विक्षेप उत्पन्न करता है और शेष भाग (remaining part) प्रतिरोध Q से होकर गुजरता है। बिन्दु D पर धारा का कोई बँटवारा (distribution) नहीं होता है।
• जब V_B < V_D होता है तो B पर धारा का विभाजन नहीं होता है, बल्कि D पर धारा i₂, का एक भाग धारामापी से गुजरकर पहले की विपरीत दिशा में विक्षेप उत्पन्न करेगा और शेष भाग प्रतिरोध से गुजरता है।
• V_B = B_D तो धारामापी वाली भुजा में कोई धारा न बहने से उसमें शून्य विक्षेप (zero deflection) की स्थिति रहती है। यही सेतु के सन्तुलन की स्थिति कहलाती है। स्पष्ट है कि परिपथ में तो धारा बहती है, लेकिन धारामापी वाली भुजा पर इस धारा का कोई प्रभाव नहीं पड़ता है। यह घटना ठीक उसी प्रकार की है कि नदी की धारा का सेतु पर कोई प्रभाव नहीं पड़ता है। इसीलिए इसे सेतु परिपथ कहते हैं।

इस प्रकार सेतु के सन्तुलन की स्थिति में,
V_B = V_D
अतः V_A - V_B = V_A - V_D
या i₁P = i₂R ...(1)
V_A - V_C =V_D - V_C
i₁Q = i₂SI

समीकरण. (1) व (2) से,
या \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\) .......(3)

अतः स्पष्ट है कि "जब सेतु सन्तुलित होता है तो चतुर्भुज ABCD की किन्हीं भी दो संलग्न (corresponding) भुजाओं के प्रतिरोधों का अनुपात शेष दो संलग्न भुजाओं के प्रतिरोधों के अनुपात (ratio) के बराबर होता है।"
समी. (3) से, S = \(\frac{Q}{P}\) × R
अतः सेतु के सन्तुलन की स्थिति ज्ञात करके हम S का मान उक्त सूत्र से ज्ञात कर सकते हैं।

P और Q वाली भुजाओं को हम अनुपातिक भुजाएँ (ratio arms), R वाली भुजा को प्रामाणिक भुजा (standard arms) और S भुजा को अज्ञात भुजा कहते हैं।

महत्वपूर्ण तथ्य

• ह्वीटस्टोन सेतु की सुग्राहिता (sensitivity) सेतु की भुजाओं के प्रतिरोधों के मानों पर निर्भर करती है। जब चारों प्रतिरोध P, Q, R व S एक ही कोटि (order) के होते हैं तो सेतु सबसे अधिक सुग्राही होता है।
• सन्तुलन की अवस्था में यदि धारामापी तथा बैटरी की स्थितियों (positions) को आपस में बदल दें तो सेतु की सन्तुलन की अवस्था पर कोई प्रभाव नहीं पड़ता है, जबकि उसकी सुग्राहिता बदल जाती है, इसीलिए सेतु की भुजाओं AC व BD को संयुग्मी भुजाएँ (conjugate arms) कहते हैं।
• सन्तुलन की अवस्था में बिन्दुओं A व C के बीच तुल्य प्रतिरोध ज्ञात करने के लिए B व D के बीच लगा कोई प्रतिरोध छोड़ा जा सकता है क्योंकि इस अवस्था में इस भुजा से होकर कोई धारा नहीं बहती है।

वैकल्पिक विधि (Alternative Method): किरखॉफ के नियमसे,
कुंजी K₁, को दबाने पर परिपथ में मुख्य धारा i बिन्दु A पर दो भागों में बँट जाती है। धारा i₁, प्रतिरोध P से होकर और (i - i₁) प्रतिरोध R से होकर गुजरती है। चित्र में धाराओं की स्थिति यह मानकर दिखाई गई है कि V_B > V_D धारा i_g, धारामापी वाली भुजा से गुजरती है और बिन्दु D पर R से होकर आने वाली धारा (i - i₁) के साथ जुड़ जाती है और प्रतिरोध S में होकर निकलती है। बिन्दु C पर पुनः सभी धाराएँ मिल जाती हैं।

जब सेतु सन्तुलित होता है तो धारामापी वाली भुजा से कोई धारा नहीं बहती है अर्थात्
i_g = 0

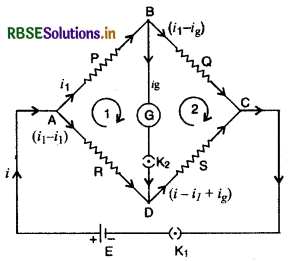
धारामापी का प्रतिरोध G मान लेते हैं।
बन्द पाश ABDA में किरखॉफ के द्वितीय नियम से,
i₁P + i_g.G - (i - i₁) R = 0
:: सन्तुलनावस्था में, i_g = 0
i₁P + 0 - (i - i₁) R = 0
i₁P = (i - i₁)R
\(\frac{i_1}{\left(i-i_1\right)}=\frac{\mathrm{R}}{\mathrm{P}}\) .......(4)

इसी प्रकार बन्द पाश BCDB में किरखॉफ के द्वितीय नियम से,
(i₁ - i_g)Q - i_g.G - (i - i₁ + i_g)S = 0

पुनः सन्तुलनावस्था में,
i_g = 0
.:.(i₁ - 0)Q - 0 - (i - i₁ + 0)S = 0
i₁Q - (i - i₁) S = 0
या i_Q = (i - i₁)S
\(\frac{i_1}{\left(i-i_1\right)}=\frac{\mathrm{S}}{\mathrm{Q}}\) ......(5)

समी. (4) व (5) से,
\(\frac{R}{P}=\frac{S}{Q}\)
या \(\frac{P}{Q}=\frac{R}{S}\)

नोट
1. प्रेरण प्रभाव (induction effect) से बचने के लिए हमेशा बैटरी कुंजी (K) पहले दबायी जाती है फिर धारामापी कुंजी (K2) दबायी जाती है।
2. सन्तुलित व्हीटस्टोन सेतु में भुजा BD का प्रतिरोध अप्रभावी होता है। अतः A व C के मध्य परिणामी प्रतिरोध
R_eq = \(\frac{(\mathrm{P}+\mathrm{Q}) \times(\mathrm{R}+\mathrm{S})}{\mathrm{P}+\mathrm{Q}+\mathrm{R}+\mathrm{S}}\)
3. व्हीटस्टोन सेतु का प्रयोग बहुत ही निम्न (very low) एवं बहुत ही उच्च (very high) प्रतिरोधों को ज्ञात करने के लिए नहीं करते
4. व्हीटस्टोन सेतु विधि को सन्तुलन विधि भी कहते हैं। यह विधि स्रोत (source) के आन्तरिक प्रतिरोध तथा धारामापी के प्रतिरोध से अप्रभावित होती है।

आंकिक उदाहरण
व्हीटस्टोन सेतु पर आधारित आंकिक उदाहरण के लिए
प्रयुक्त सूत्र
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)

प्रयुक्त इकाईयाँ
P, Q, R, S → ओम

मीटर सेतु (Meter Bridge):
व्हीटस्टोन सेतु के सिद्धान्त पर आधारित यह एक ऐसा उपकरण है जिसकी सहायता से अज्ञात प्रतिरोध (unknown resistance) ज्ञात किया जा सकता है। सिद्धान्त-मीटर सेतु ऐसा उपकरण है जो व्हीटस्टोन सेतु के सिद्धान्त पर कार्य करता है।

रचना-मीटर सेतु की रचना चित्र में दिखायी गई है। इसमें समान परिच्छेद (uniform cross-section) का 1 मीटर कॉन्स्टेन्टन या मैंगनिन का तार होता है जो एक लकड़ी के बोर्ड पर एक मीटर पैमाने के सहारे कसा रहता है। तार के सिरों A व C पर ताँबे की दो L के आकार की पत्तियाँ (L-shaped thick copper strips) जुड़ी रहती हैं जिनके ऊपर संयोजक पेंच लगे रहते हैं। इन पत्तियों के बीच एक और ताँबे की पत्ती चित्र के अनुसार लगी होती है जिस पर तीन संयोजक पेंच लगे होते हैं। चित्र में अंकित बिन्दु A, B, C व D क्रमशः व्हीटस्टोन सेतु से संगत (corres-ponding) चारों बिन्दुओं को व्यक्त (represent) करते हैं। इस पत्ती के मध्य में लगे पेंच D से एक सुग्राही (sensitive) धारामापी जुड़ा होता है जिसका दूसरा सिरा सी कुंजी (jockey) से जुड़ा होता है। सी कुंजी तार AC के सहारे खिसक सकती है। सी कुंजी की स्थिति (position) ही तार AC पर बिन्दु B को व्यक्त करती है।

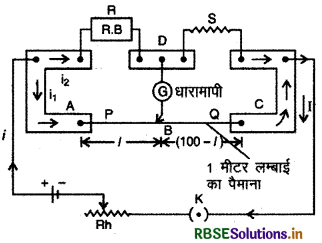
प्रयोग विधि
परिपथ व्यवस्था चित्र के अनुसार करते हैं। संयोजक पेंचों A व D के मध्य प्रतिरोध बॉक्स (resistance box) एवं D व C के मध्य अज्ञात प्रतिरोध S को जोड़ देते हैं। A व C के मध्य एक सेल व एक धारा नियन्त्रक (rheostat) को कुंजी K के द्वारा जोड़ देते हैं। अनुपात भुजाएँ (ratio arms) P व Q तार AC के दो भागों से प्राप्त होती हैं जो जॉकी द्वारा निर्धारित बिन्दु से विभक्त (divide) होते हैं।

प्रतिरोध बॉक्स में कोई समुचित (suitable) प्रतिरोध (R) लगाकर कुंजी K को बन्द करते हैं और सी कुंजी को तार AC पर दायें या बायें खिसकाकर (moved) बिन्दु B की वह स्थिति ज्ञात कर लेते हैं जब धारामापी में शून्य विक्षेप होता है। यह सेतु के सन्तुलन की स्थिति है (जब V_B = B_D)। इस स्थिति में मीटर पैमाने पर बिन्दु B की स्थिति पढ़कर तार के दोनों भागों AB व BC की लम्बाइयाँ सेमी में ज्ञात कर लेते हैं। यदि AB की लम्बाई । सेमी है तो BC की लम्बाई (100 - l) सेमी होगी।
प्रतिरोध ∝ लम्बाई
अतः P ∝ l
तथा Q ∝ (100 - l)
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l}{(100-l)}\)

सेतु सन्तुलन की स्थिति में,
\(\frac{P}{Q}=\frac{R}{S}\)
∴ \(\frac{l}{(100-l)}=\frac{\mathrm{R}}{\mathrm{S}}\)

∴ S = \(\frac{\mathrm{R}(100-l)}{l}\) .....(1)
यहाँ R प्रतिरोध बॉक्स में लगाया गया प्रतिरोध है। इसी सूत्र की सहायता से अज्ञात प्रतिरोध s का मान ज्ञात किया जा सकता है।

आंकिक उदाहरण
मीटर सेतु पर आधारित आंकिक उदाहरण के लिए
प्रयुक्त सूत्र
अज्ञात प्रतिरोध s = \(\frac{\mathrm{R}(100-l)}{l}\)

प्रयुक्त इकाई- S,R-ओम
l-मीटर

विभवमापी (Potentiometer):
विभवमापी एक ऐसा उपकरण (instrument) है जिसकी सहायता से हम किसी विभवान्तर या विद्युत् वाहक बल की शुद्धता (accurately) से माप कर सकते हैं।
यह यन्त्र परिपथ से कोई धारा न लेकर विभवान्तर को मापता है। परिपथ में बहने वाली धारा वास्तविक मान से कुछ कम होती है जिसके कारण वोल्टमीटर की तुलना में विभवमापी विभवान्तर को अधिक शुद्धता से मापती है। अतएव हम कह सकते हैं कि विभवमापी विभव मापन का वोल्टमीटर की तुलना में आदर्श उपकरण हैं।

सिद्धान्त-माना L लम्बाई का कोई AB प्रतिरोध तार है जिसके सिरों पर E विद्युत् वाहक बल एवं नगण्य (neglegible) आन्तरिक प्रतिरोध वाला सेल जोड़ा जाता है, अतः तार AB के सिरों पर E विभवान्तर उत्पन्न हो जायेगा क्योंकि आन्तरिक प्रतिरोध नगण्य है। तार की प्रति इकाई लम्बाई में विभव पतन (potential drop) को विभव प्रवणता (potential gradient) कहते हैं। अतः तार में उत्पन्न विभव प्रवणता
k = \(\frac{E}{L}\) ...(1)

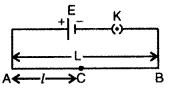
अब यदि तार AB पर कोई बिन्दु C ले लें तो A व C के मध्य विभवान्तर V_AC, दूरी AC अर्थात् L पर निर्भर करेगा। बिन्दु C को बिन्दु B की ओर खिसकाने पर V_AC का मान बढ़ेगा और A की ओर खिसकाने (sliding) पर घटेगा। यदि A से C की दूरी । है तो विभवान्तर
V_AC = k.l ...(2)

अब यदि चित्र की भाँति A व C के मध्य एक अज्ञात विद्युत् वाहक बल E' की एक सेल एक धारामापी

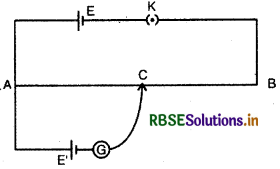
द्वारा जोड़ दें तो धारामापी में उत्पन्न विक्षेप इस बात पर निर्भर करेगा कि V_AC व E' में कौन बड़ा है। सुविधा के लिए (for convenient) A व C के मध्य तुल्य परिपथ चित्र के अनुसार दिखा सकते हैं। चित्र में V_ac को परिवर्तनशील (variable) दिखाया गया है क्योंकि इसका मान बिन्दु C की स्थिति पर निर्भर करता है। चित्र के अनुसार E' व V_ACइस प्रकार जुड़े (combined) हैं कि वे एक-दूसरे को प्रतिरोध करते हैं। इस परिपथ का परिणामी विद्युत् वाहक बल (E' ~ V_AC) होगा, अतः स्पष्ट है कि जब V_AC = E' होगा तो परिणामी विद्युत् वाहक बल (resultant electro-motive force) शून्य होगा और परिपथ में कोई धारा नहीं बहेगी, फलस्वरूप धारामापी में अविक्षेप (no deflection) की स्थिति होगी।

उक्त विवेचना से स्पष्ट है कि यदि किसी अज्ञात विद्युत् वाहक बल E' को धारामापी द्वारा चित्र की भाँति जोड़कर C की स्थिति तार AB पर इस प्रकार ज्ञात कर लें कि धारामापी शून्य विक्षेप (zero deflection) की स्थिति प्रदर्शित करे तो अज्ञात विद्युत् वाहक बल E' का मान VAC के बराबर होगा, अतः
E' = V_ac = kl ....(3)

इस प्रकार सूत्र (3) की सहायता से l का मान ज्ञात करके अज्ञात विद्युत् वाहक बल E' की माप की जा सकती है। यही विभवमापी का सिद्धान्त है।

विभव प्रवणता पैदा करने वाले सेल E एवं AB से बना परिपथ प्राथमिक परिपथ (primary circuit) और अज्ञात विद्युत् वाहक बल E' वाले सेल तथा धारामापी से AC के मध्य तैयार परिपथ को द्वितीयक परिपथ (secondary circuit) कहते हैं।

विभवमापी की रचना-विभवमापी में मुख्यतः उच्च विशिष्ट प्रतिरोध (high specific resistance) व निम्न प्रतिरोध ताप गुणांक (low temperature coefficient) की मिश्र धातु (alloys) (जैसे-कॉन्स्टेन्टन या मैगनिन आदि) का 4 से 12 मीटर लम्बा एक समान व्यास (diameter) का एक तार होता है जो चित्र की भाँति एक-एक मीटर के फेरों (turns) के रूप में धातु की घिरनियों (pulleys) से होकर गुजरता है अथवा एक-एक मीटर लम्बे टुकड़े ताँबे की पत्तियों द्वारा सिरों पर जुड़े होते हैं। प्रारंभिक एवं अंतिम सिरे A व B संयोजक पेंचों से जोड़ दिये जाते हैं। तारों की लम्बाई के समान्तर एक मीटर पैमाना लगा रहता है जिसके द्वारा जॉकी की सहायता से पाठ्यांक (reading) लिया जाता है।

विभवमापी की सग्राहिता (Sensitivity of Potentiometer)
(1) विभवमापी के प्रयोग में तार जॉकी को शून्य विक्षेप स्थिति में थोड़ा-सा ही खिसकाने पर यदि धारामापी में पर्याप्त विक्षेप (sufficient deflection) हो जाये तो विभवमापी सुग्राही (sensitive) होता है।

(2) विभवमापी की सुग्राहिता विभव प्रवणता पर निर्भर करती है। विभव प्रवणता जितनी कम होगी, विभवमापी (rheostat) उतना ही अधिक सुग्राही होता है।

(3) विभव प्रवणता (k)

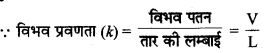
अतः तार की लम्बाई (L) जितनी अधिक होगी, विभव प्रवणता उतनी ही कम होगी और विभवमापी अधिक सुग्राही होता है।
V व L के मध्य ग्राफ-चूँकि रेखा का ढाल (slope) = tan θ

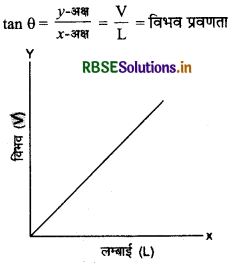
विशेष तथ्य

• लम्बाई अक्ष के साथ जो कोण कम होगा, वह विभवमापी की अधिक सुग्राहिता को प्रदर्शित करता है।
• (एक दिये हुए निश्चित लम्बाई (fixed length) के विभवमापी के लिए विभव प्रवणता को विभवमापी के तार में विभव विभाजक (rheostat) के द्वारा धारा को घटाकर, विभव प्रवणता को कम (decrease) किया जा सकता है।

विभवमापी के उपयोग (Uses of Potentiometer)
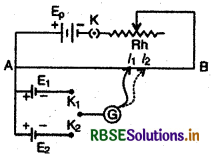
1. दो सेलों के विद्युत् वाहक बलों की तुलना करना-जिन सेलों के विद्युत् वाहक बलों E₁ व E₂ की तुलना करनी है, उन्हें चित्र के अनुसार द्विमार्गी कुंजी (two waykey) एवं धारामापी के द्वारा विभवमापी से जोड़ देते हैं। प्राथमिक परिपथ में एक बैटरी E_p, एक कुंजी K एवं परिवर्ती प्रतिरोध (variable resistance) Rh भी चित्र की भाँति जोड़ देते

एक प्रतिरोधक बॉक्स से (R.B) एक उच्च प्रतिरोध R को लगाया जाता है ताकि धारामापी से होकर उच्च धाराएँ ना जाएँ।

प्रयोग विधि
(i) पहले कंजी K को दबाकर विभवमापी तार AB के सिरों के मध्य विभवान्तर स्थापित कर लेते हैं। अब कुंजी K₁, व K₂ को बारी-बारी से लगाकर धारा नियन्त्रक (Theostat) को इस प्रकार व्यवस्थित (adjust) करते हैं कि जॉकी को तार के सिरों A व B के मध्य स्पर्श (touch) कराने पर धारामापी में विक्षेप दोनों ओर प्राप्त हो जाये। माना इस स्थिति में तार की विभव प्रवणता k है।

(ii) अब द्विमार्गी कुंजी की कुंजी K₂ को खुला रखकर K₁, को लगाकर सेल E₁, को द्वितीयक परिपथ में जोड़ते हैं और धारामापी में अविक्षेप स्थिति (no deflection position) ज्ञात करके तार की लम्बाई l₁ ज्ञात कर लेते हैं, अतः
E₂ = kl₁ ...(1)

(iii) अब K₁ को खुला रखकर K₂ को लगाकर E₂ को द्वितीयक परिपथ में जोड़ते हैं और शून्य विक्षेप (zero deflection) की स्थिति में l₂ ज्ञात कर लेते हैं, अतः
E = kl₂ ....(2)

समी. (i) व (ii) से, .
\(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{l_1}{l_2}\) ....(3)

यदि दोनों सेलों में कोई एक प्रमाणिक सेल (standard cell) है तो दूसरे सेल का विद्युत् वाहक बल भी ज्ञात कर सकते हैं।

नोट-विभवमापी में शून्य विक्षेप की स्थिति में, सेल (E₁) अथवा (E₂) में कोई धारा नहीं बहती है अर्थात् सेल खुले परिपथ (open circuit) में होता है, अतः विभवमापी से सेल का यथार्थ (exact) विद्युत् वाहक बल (electromotive force) प्राप्त होता है।

विशेष सावधानियाँ

• सभी सेलों के धनात्मक ध्रुव एक ही बिन्दु (A) से जुड़े रहने चाहिए।
• बैटरी B' का विद्युत् वाहक बल सेल E₁, तथा E₂, में से प्रत्येक के विद्युत् वाहक बल से अधिक होना चाहिए, नहीं तो शून्य विक्षेप स्थिति प्राप्त नहीं होगी।
• तार में अधिक समय तक धारा प्रवाहित नहीं होनी चाहिए, अन्यथा तार गर्म हो जायेगा और तार का प्रतिरोध बदल जायेगा जिससे विभव प्रवणता बदल जायेगी।

विभवमापी व वोल्टमीटर में अन्तर

• वोल्टमीटर द्वारा विद्युत् वाहक बल नापने के लिए वोल्टमीटर में विक्षेप पढ़ना पड़ता है। विक्षेप के पढ़ने में त्रुटि (error) रह जाती है, जबकि विभवमापी द्वारा विद्युत् वाहक बल अविक्षेप (null) विधि से नापा जाता है, इसे तार पर शून्य विक्षेप स्थिति पढ़ना कहते हैं। अतः विभवमापी को आदर्श वोल्टमीटर (ideal voltmeter) भी कहते हैं।
• विभवमापी द्वारा सेल का विद्युत् वाहक बल नापते (measurement) समय शून्य विक्षेप स्थिति में सेल के परिपथ में कोई धारा प्रवाहित नहीं होती है अर्थात् सेल खुले परिपथ (open circuit) पर होता है। अतः सेल के विद्युत् वाहक बल का वास्तविक मान प्राप्त होता है। इस प्रकार विभवमापी अनन्त प्रतिरोध (infinite resistance) के आदर्श (ideal) वोल्टमीटर के समान कार्य करता है।

2. सेल का आन्तरिक प्रतिरोध ज्ञात करना:
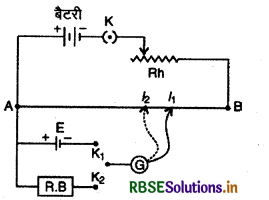
बैटरी, कुंजी K एवं धारा नियन्त्रक को संयोजक पेंचों A व B से जोड़कर प्राथमिक परिपथ तैयार कर लेते हैं। अब जिस सेल का आन्तरिक प्रतिरोध ज्ञात करना है उसे और एक प्रतिरोध बॉक्स को चित्र की तरह पेंच A व द्विमार्गी कुंजी (two way key) से जोड़ते हैं तथा द्विमार्गी कुंजी को धारामापी एवं जॉकी से जोड़कर द्वितीयक परिपथ (secondary circuit) तैयार करते

प्रयोग विधि:
(i) कुंजी K को बन्द करके तार AB में विभवान्तर (potential difference) स्थापित कर लेते हैं। अब धारा नियन्त्रक को इस प्रकार व्यवस्थित करते हैं कि जॉकी को तार के सिरों A व B के बीच स्पर्श कराने पर धारामापी में विक्षेप दोनों ओर प्राप्त हो जाये। माना इस स्थिति में तार की विभव प्रवणता k है।

(ii) कुंजी K₂, को खुला (open) रखकर K₁, को बन्द करके सेल को द्वितीयक परिपथ में डालते हैं और जॉकी से शून्य विक्षेप की स्थिति में तार की लम्बाई l₁, ज्ञात कर लेते हैं, अतः
E = kl₁

(iii) अब K₁, को बन्द (close) रखते हुए K₂, को बन्द करते हैं और प्रतिरोध बॉक्स में कोई समुचित प्रतिरोध (Proper resistance) R लगाकर पुनः अविक्षेप स्थिति में तार की लम्बाई l₂, ज्ञात कर लेते हैं। यह सेल के टर्मिनल विभवान्तर के सन्तुलन के संगत है, अतः
V = kl₂ ....(5)
माना सेल का आन्तरिक प्रतिरोध । है यदि सेल को R ओम के प्रतिरोध से शंट करने पर सेल में i धारा बहती है, तो ओम के नियम से

अतः आन्तरिक प्रतिरोध r = R\(\left[\frac{l_1-l_2}{l_2}\right]\)

विभवमापी पर आधारित आंकिक उदाहरण के लिए
प्रयुक्त सूत्र
(a) विभव प्रवणता k = \(\frac{V}{L}\)
(b) \(\frac{\mathrm{E}_2}{\mathrm{E}_1}=\frac{l_2}{l_1}\)
(c) r = \(\left(\frac{l_1-l_2}{l_2}\right)\)R
(d) अज्ञात (unknown) वि. वा. बल, E = kL
प्रयुक्त इकाईयाँ
E₁, E₂,V-वोल्ट
l₁, l₂-मीटर

→ वैद्युत धारा-आवेश के प्रवाह की दर ही वैद्युत धारा कहलाती है। इसका मात्रक ऐम्पियर होता है। यह एक अदिश राशि है। यदि किसी चालक में q आवेश t सेकण्ड में प्रवाहित होता है तो चालक
में प्रवाहित धारा i = \(\frac{q}{t}\), कूलॉम/सेकण्ड या ऐम्पियर होगी।

→ धारा घनत्व:

• किसी चालक के एकांक अनुप्रस्थ परिच्छेद (unit cross-sectional) से होकर बहने वाली धारा को ही धारा घनत्व कहते हैं। यदि चालक का अनुप्रस्थ परिच्छेद क्षेत्रफल A हो और उसमें बहने वाली धारा । हो तो धारा घनत्व J = \(\frac{i}{A}\) ऐम्पियर/मीटर ।
• धारा घनत्व एक सदिश राशि है जिसकी दिशा चालक में प्रवाहित धारा की दिशा में होती है।

→ धातुओं का मुक्त इलेक्ट्रॉन मॉडल

• वे इलेक्ट्रॉन जिन पर नाभिक का नियन्त्रण बहुत कम होता है और जिन्हें थोड़ी सी ऊर्जा देकर संगत परमाणु से अलग किया जा सकता है, मुक्त इलेक्ट्रॉन कहलाते हैं। ये चालक की सीमाओं के अन्तर्गत (within the boundaries of the conductor) उसी प्रकार गति करते हैं जिस प्रकार गैस के अणु बन्द बर्तन में गति करते हैं।
• धातुओं में मुक्त इलेक्ट्रॉन ही आवेश वाहक (charge carriers) का कार्य करते हैं।
• यदि चालक पर कोई विभवान्तर न लगाया जाये तो मुक्त इलेक्ट्रॉनों की अनियमित गति (random motion) का औसत वेग शून्य होता है।

→ अनुगमन वेग
(i) धन आयनों से मुक्त इलेक्ट्रॉन की दो उत्तरोत्तर टक्करों (successive collisions) के मध्य इलेक्ट्रॉन का औसत वेग अनुगमन वेग कहलाता है।
(ii) अनुगमन वेग एवं विभवान्तर में निम्नलिखित सम्बन्ध होता है
v_d = \(\frac{e \tau}{m} \cdot \frac{\mathrm{V}}{l}\)
जहाँ τ श्रांतिकाल (relaxation time) है।
(iii) अनुगमन वेग एवं धारा में निम्नलिखित सम्बन्ध होता है
V_d = \(\frac{i}{\text { Ane }}\)

→ ओम का नियम:
यदि किसी चालक की भौतिक अवस्थाएँ न बदलें तो उसके सिरों पर उत्पन्न विभवान्तर उसमें बहने वाली धारा के अनुक्रमानुपाती होता है अर्थात्
V ∝ i या \(\frac{V}{i}\) = नियतांक = R चालक का प्रतिरोध
यदि चालक का प्रतिरोध R, विशिष्ट प्रतिरोध p, लम्बाई । एवं अनुप्रस्थ परिच्छेद का क्षेत्रफल A हो तो ।
R = ρ\(\frac{l}{A}\)

→ विशिष्ट प्रतिरोध या प्रतिरोधकता:
(i) एकांक लम्बाई एवं एकांक
अनुप्रस्थ परिच्छेद क्षेत्रफल वाले चालक का प्रतिरोध ही चालक के पदार्थ का विशिष्ट प्रतिरोध या प्रतिरोधकता (resistivity) कहलाती है। इसका मान
ρ = R\(\frac{A}{l}\)

(ii) विशिष्ट प्रतिरोध का मान निम्न सूत्र द्वारा भी ज्ञात कर सकते
ρ = \(\frac{m}{n e^2 \tau}\)
जहाँ m = इलेक्ट्रॉन का द्रव्यमान,
e = इलेक्ट्रॉन का आवेश,
n = एकांक आयतन में मुक्त इलेक्ट्रॉनों की संख्या और
l = श्रांतिकाल।

(iii) विशिष्ट प्रतिरोध पदार्थ की विशेषता है, चालक की नहीं।

(iv) इसका मात्रक ओम मीटर होता है।

(v) इसका विमीय सूत्र [M¹L³T^-3A^-2 है।

→ ओम के नियम की असफलता-ओम के नियम (V = iR) का पालन अनेक स्थितियों में पूर्णतः नहीं होता है। ऐसी कुछ स्थितियाँ निम्न हैं

• विभवान्तर धारा के साथ अरैखिक रूप (non-linear) से बदल सकता है। इस परिवर्तन का कारण धारा का ऊष्मीय प्रभाव (thermal effect of current) है।
• विभवान्तर के साथ धारा का परिवर्तन लगाये गये विभवान्तर के चिह्न पर निर्भर कर सकता है।
• विभवान्तर के बढ़ाने पर धारा घट सकती है।

→ चालकता एवं विशिष्ट चालकता
(i) प्रतिरोध के व्युत्क्रम को ही चालकता (conductivity) कहते हैं। इसे G से व्यक्त करते हैं।
G = \(\frac{1}{R}\) प्रति ओम या म्हो
(ii) विशिष्ट प्रतिरोध के व्युत्क्रम को विशिष्ट चालकता कहते हैं। इसे σ से व्यक्त करते हैं।
σ = \(\frac{1}{ρ}\) Ωm^-1 या mho m
(iii) विशिष्ट चालकता एवं गतिशीलता (mobility) में निम्न सम्बन्ध होता है
σ = neµ
जहाँ µ गतिशीलता है।
(iv) विशिष्ट चालकता व धारा घनत्व में सम्बन्ध
J = σE

→ विशिष्ट प्रतिरोध एवं प्रतिरोध पर ताप का प्रभाव-ताप बढ़ाने पर विशिष्ट प्रतिरोध अर्थात् प्रतिरोधकता बढ़ जाती है। ताप के साथ विशिष्ट प्रतिरोध निम्न समीकरण के अनुसार बदलता
है
ρ_t = ρ₀ (1 + αt)
जहाँ ρ_t = t°C पर विशिष्ट प्रतिरोध, ρ₀ = 0°C पर विशिष्ट प्रतिरोध एवं α = प्रतिरोध ताप गुणांक (temperature coefficient of resistance) है।

→ ऊर्जा व्यय एवं शक्ति
(i) यदि किसी चालक के सिरों के मध्य विभवान्तर V, उसमें बहने वाली धारा i, समय एवं चालक का प्रतिरोध R हो तो व्यय ऊर्जा
W = Vit = i²Rt = \(\frac{\mathrm{V}^2}{\mathrm{R}}\)t = जूल
(ii) व्यय शक्ति P= Vi = i²R = \(\frac{\mathrm{V}^2}{\mathrm{R}}\)वाट
(iii) व्यय विद्युत् ऊर्जा का मात्रक
1 यूनिट = 1 किलोवाट घण्टा

→ प्रतिरोधों का संयोजन
(i) श्रेणीक्रम संयोजन में तुल्य प्रतिरोध
R = R₁ + R₂ + R₃ + ...... + R_n
(ii) समान्तरक्रम संयोजन में तुल्य प्रतिरोध ।
\(\frac{1}{\mathrm{R}}=\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\ldots \ldots+\frac{1}{\mathrm{R}_n}\)

→ सेल एवं सेल का विद्युत् वाहक बल
(i) सेल वह युक्ति है जो परिपथ में धारा के प्रवाह को बनाये रखती है।
(ii) सेल दो प्रकार के होते हैं
(a) प्राथमिक सेल,
(b) द्वितीयक सेल।
(iii) एकांक आवेश को परिपथ में प्रवाहित करने में सेल द्वारा किया गया कार्य ही सेल का विद्युत् वाहक बल कहलाता है।
E = \(\frac{\mathrm{W}}{q}\) वोल्ट
(iv) खुले परिपथ में सेल के सिरों के बीच विभवान्तर सेल का विद्युत् वाहक बल कहलाता है।

→ सेल का टर्मिनल विभवान्तर
(i) बन्द परिपथ में सेल के सिरों के मध्य विभवान्तर को टर्मिनल विभवान्तर कहते हैं।
V = E - ir
जहाँ ir = सेल के ध्रुवों के मध्य विभव-पतन (potential drop)।
(ii) सेल द्वारा एकांक आवेश को बाहरी परिपथ में बहने के लिए जितनी ऊर्जा दी जाती है वही टर्मिनल विभवान्तर के बराबर होती है अर्थात्
V = \(\frac{\mathrm{W}_{\mathrm{ext}}}{q}\)

→ सेल का आन्तरिक प्रतिरोध

• सेल के अन्दर धारा के मार्ग में आने वाली रुकावट (hinderance) को सेल का आन्तरिक प्रतिरोध कहते हैं।
• सेल का आन्तरिक प्रतिरोध r = \(\frac{\mathrm{E}-\mathrm{V}}{i}\)

→ सेलों का संयोजन
(i) जब समान विद्युत्वाहक बल E एवं समान आन्तरिक प्रतिरोध की n सेलें श्रेणीक्रम में जोड़ी जाती हैं तो प्राप्त धारा
i = \(\frac{n \mathrm{E}}{\mathrm{R}+n r}\)

(ii) जब असमान विद्युत् वाहक बल E₁, व E₂, एवं आन्तरिक प्रतिरोध क्रमशः ।। व 12 की दो सेलें श्रेणीबद्ध की जाती हैं तो
i = \(\frac{\left(\mathrm{E}_1 \sim \mathrm{E}_2\right)}{\mathrm{R}+\left(r_1+r_2\right)}\)

(iii) जब समान विद्युत् वाहक बल E व आन्तरिक प्रतिरोध की n सेलें समान्तरबद्ध की जाती हैं तो प्राप्त धारा
i = \(\frac{\mathrm{E}}{\mathrm{R}+\frac{r}{n}}=\frac{n \mathrm{E}}{n \mathrm{R}+r}\)

(iv) जब असमान विद्युत् वाहक बल E₁, व E₂ तथा आन्तरिक प्रतिरोध r₁ व r₂ की दो सेलें समान्तरबद्ध की जाती हैं तो
i = \(\frac{E}{R+r}\)
जहाँ E = \(\frac{\left(\mathrm{E}_1 r_2+\mathrm{E}_2 r_1\right)}{\left(r_1+r_2\right)}, r = \frac{r_1 r_2}{\left(\eta+r_2\right)}\) R = बाह्य प्रतिरोध।

→ किरखॉफ के नियम
(i) विद्युत् परिपथ में किसी सन्धि (junction) पर मिलने वाली समस्त धाराओं का बीजीय योग (algebric sum) शून्य होता है अर्थात्
Σi = 0
(ii) बन्द पाश (closed mesh) में परिणामी विद्युत् वाहक बल परिपथ के समस्त विभवान्तरों के योग के बराबर होता है अर्थात्
ΣE = ΣV या ΣE = ΣUR

→ व्हीटस्टोन सेतु-सेतु के सन्तुलन की स्थिति में,
\(\frac{P}{Q}=\frac{R}{S}\)
जहाँ P, Q, R ज्ञात प्रतिरोध हैं और S अज्ञात प्रतिरोध है।

→ मीटर सेतु-अज्ञात प्रतिरोध
S = \(\frac{(100-l)}{l}\) × R
जहाँ R ज्ञात प्रतिरोध है और सन्तुलन की स्थिति में जॉकी की A सिरे से लम्बाई l है।

→ विभवमापी
(i) यदि विभवमापी के तार का विभवान्तर V_AB है और उसकी लम्बाई L है तो तार AB की विभव प्रवणता k = \(\frac{\mathrm{V}_{\mathrm{AB}}}{\mathrm{L}}\)

(ii) यदि द्वितीयक परिपथ में सेल का सन्तुलन बिन्दु । दूरी पर मिलता है तो उस सेल का विद्युत् वाहक बल
E' = kl

(iii) दो सेलों के लिए द्वितीयक परिपथ में सन्तुलन बिन्दु क्रमशः 11 व 2 दूरियों पर मिलते हैं तो सेलों के विद्युत् वाहक बलों (E₁ व E₂) का अनुपात
\(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{l_1}{l_2}\)

(iv) द्वितीयक परिपथ में जोड़े गये किसी सेल के लिए सन्तुलन बिन्दु l₁ पर मिलता है और उसके सिरों को R ओम प्रतिरोध से जोड़ने पर सन्तुलन बिन्दु l₂, पर मिलता है तो सेल का आन्तरिक प्रतिरोध
r = \(\left(\frac{l_1-l_2}{l_2}\right)\)R

→ विद्युत् धारा, i = \(\frac{q}{t}=\frac{n e}{t}\)

→ धारा घनत्व, j = \(\frac{i}{\mathrm{~A}}=\frac{i}{\mathrm{~A} \cos \theta}\)

→ अनुगमन वेग, v_d = \(\frac{-e \mathrm{E}_c}{m}=\frac{e \tau \mathrm{V}}{m l}=\frac{i}{\text { Ane }}\)

→ गतिशीलता, µ = \(\frac{v_d}{E}=\frac{e \tau}{m}\)

→ ओम का नियम, V = ρ.\(\frac{l}{A}\) ⇒ V = Ri

→ ओम के नियम का सदिश रूप \(\overrightarrow{\mathrm{J}}=\overrightarrow{\sigma \mathrm{E}}\)

→ किसी चालक का प्रतिरोध R = ρ.\(\frac{l}{A}\)

→ विशिष्ट प्रतिरोध, ρ = \(\frac{\mathrm{RA}}{l}=\frac{\mathrm{E}}{\mathrm{J}}=\frac{m}{n e^2 \tau}\)

→ विशिष्ट चालकता, σ = neµ = \(\frac{1}{ρ}\)

→ श्रांतिकाल, τ = \(\frac{\lambda}{v_r}\)

→ चालक के विशिष्ट प्रतिरोध का ताप परिवर्तन पर प्रभाव
ρ_t = ρ₀ (1 + αt)

→ चालक के प्रतिरोध पर ताप का प्रभाव
R_t = R₀ (1 + αt)

→ विद्युत् शक्ति, P = \(\frac{\mathrm{V}^2}{\mathrm{R}}\)

→ उपकरण द्वारा व्यय विद्युत् ऊर्जा = \(\frac{\mathrm{P} \times \mathrm{H} \times \mathrm{D}}{1000}\)

→ प्रतिरोधों का संयोजन

• श्रेणीक्रम R = R₁ + R₂ + R₃ + ...
• समान्तर क्रम \(\frac{1}{\mathrm{R}}=\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\frac{1}{\mathrm{R}_3}\) + ........

→ सेल का विद्युत वाहक बल E = \(\frac{W}{q}\)

→ सेल का टर्मिनल विभवान्तर V = E - ir

→ सेल को चार्ज करने पर टर्मिनल विभवान्तर
V = E + ir

→ सेलों का श्रेणीक्रम संयोजन
(i) जब सेलों के विद्युत् वाहक बल एवं आन्तरिक प्रतिरोध समान होते हैं
i = \(\frac{n \mathrm{E}}{\mathrm{R}+n r}\)
यदि R > > nr, तब i = \(\frac{nE}{R}\)
यदि R< < nr, तब i = \(\frac{E}{r}\)
 

(ii) जब सेल भिन्न विद्युत् वाहक बल एवं भिन्न आन्तरिक प्रतिरोध के हों, i = \(\frac{\mathrm{E}_1+\mathrm{E}_2}{\mathrm{R}+\left(r_1+r_2\right)}\)

→ सेलों का समान्तर क्रम संयोजन
(i) जब सेल समान विद्युत् वाहक बल एवं समान आन्तरिक प्रतिरोध के हों i = \(\frac{n \mathrm{E}}{\mathrm{R} n+r}\) यदि R > > \(\frac{r}{n}\), तब i = \(\frac{E}{R}\)
यदि R < < \(\frac{r}{n}\), तब i = \(\frac{nE}{r}\)

(ii) जब सेलों के विद्युत् वाहक बल एवं आन्तरिक प्रतिरोध भिन्न होते हैं
V = \(\left[\frac{\mathrm{E}_1 r_2+\mathrm{E}_2 r_1}{\left(r_1+r_2\right)}\right]-i\left[\frac{r_1 r_2}{\left(r_1+r_2\right)}\right]\)

→ सेलों का मिश्रित संयोजन
i = \(\frac{m n \mathrm{E}}{m \mathrm{R}+n r}\), m-कतारें, n-सेलें
i_max = \(\frac{nE}{2R}\)

→ किरखॉफ का नियम

• प्रथम नियम Σi = 0
• द्वितीय नियम ΣE = ΣV = ΣiR

→ व्हीटस्टोन सेतु सन्तुलन = \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)

→ मीटर सेतु
S = \(\frac{\mathrm{R}(100-l)}{l}\)

→ विभवमापी
k = \(\frac{V}{L}\)
\(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{l_1}{l_2}\)
r = \(\left(\frac{l_1-l_2}{l_2}\right)\)R

→ धारावाहक (Charge carriors):
वे आवेशित कण जिनका एक निश्चित दिशा में प्रवाह विद्युत् धारा का निर्माण करता है।

→ विभव प्रवणता (Potential gradient):
तार की प्रति इकाई लम्बाई के विभवान्तर या विभव पतन को कहते हैं।

→ सुग्राहिता (Sensitivity):
अत्यन्त सूक्ष्म अवयव को अधिक शुद्धता से मापना।

→ तड़ित (Lightning):
आकाशीय बिजली। कोटर या होल (hole)-अर्द्धचालक में इलेक्ट्रॉन की कमी।

→ संयोजक तार (Connecting wires):
परिपथों में जोड़े जाने वाले तार।

→ विद्युत् अपघट्य (Electrolytes):
सेल की प्लेटों को जिस द्रव में डुबोया जाता है।

→ सन्तुलन की स्थिति (Balance condition):
जिस पाठ्यांक पर धारामापी शून्य विक्षेप देता है।

→ बाह्य परिपथ (Auxiliary circuit):
यह एक विद्युत् परिपथ होता है जिसमें एक बैटरी, एक कुंजी, एक विभव विभाजक होता है जो श्रेणीक्रम में होते हैं, यह विभवमापी के तार में धारा भेजता है।

→ बैटरी (Battery):
कई सेलों का संयोग।

→ जौकी (Jockey):
इसको खिसकाकर तार पर शून्य विक्षेप की स्थिति लाई जाती है।

→ विभव विभाजक (Rheostat):
इससे परिपथ में परिवर्ती प्रतिरोध डाला जाता है।