RBSE Class 12 Physics Notes Chapter 2 स्थिर वैद्युत विभव तथा धारिता

These comprehensive RBSE Class 12 Physics Notes Chapter 2 स्थिर वैद्युत विभव तथा धारिता will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 2 Notes स्थिर वैद्युत विभव तथा धारिता

भूमिक (Introduction)
कक्षा 11 में हम स्थितिज ऊर्जा की धारणा का भली प्रकार अध्ययन कर चुके हैं। जब कोई बाह्य बल किसी वस्तु को एक बिन्दु से दूसरे बिन्दु तक, स्प्रिंग बल, गुरुत्वीय बल जैसे किसी अन्य बल के विरुद्ध, ले जाता है, तो उस बाह्य बल द्वारा कृत कार्य उस वस्तु या निकाय में विद्युत स्थितिज ऊर्जा के रूप में संचित हो जाता है। बाह्य बल हटाने पर वस्तु गति करने लगती है। अर्थात् वस्तु में कुछ गतिज ऊर्जा अर्जित कर लेती है। इस प्रकार वस्तु की स्थितिज ऊर्जा तथा गतिज ऊर्जा का योग संरक्षित रहता है। इन बलों को संरक्षी बल कहते हैं।

इस अध्याय में हम कूलॉम बल के बारे में उस तथ्य का अध्ययन करेंगे जिसके अंतर्गत दो स्थिर बिन्दु आवेशों के बीच लगने वाला कूलॉम बल संरक्षी बल ही है। गुरुत्वाकर्षण नियम में प्रयुक्त संहतियाँ (द्रव्यमान) कूलॉम नियम में आवेशों से प्रतिस्थापित की जाती है।

 

(स्थिर वैद्युत स्थितिज ऊर्जा (Electrostatic Potential Energy)):
जिस प्रकार गुरुत्वीय क्षेत्र में किसी द्रव्यमान की स्थितिज ऊर्जा (potential energy) को परिभाषित किया जाता है, उसी प्रकार किसी विद्युत क्षेत्र में किसी आवेश की स्थितिज ऊर्जा की परिभाषा कर सकते हैं।

माना एक स्रोत आवेश +Q के कारण किसी बिन्दु पर उत्पन्न विद्युत् क्षेत्र की तीव्रता $\vec{E}$ है। एक सूक्ष्म धन परीक्षण आवेश (small positive test charge) + q₀ को स्रोत आवेश + Q के प्रतिकर्षण के विरुद्ध बिन्दु A से B तक लाया जाता है (चित्र)।

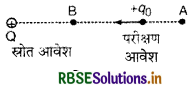
परीक्षण स्रोत आवेश आवेश
चित्र हम यह मान लेते हैं कि परीक्षण आवेश + go इतना छोटा है कि यह + Q के विन्यास (configuration) में कोई परिवर्तन नहीं करता है। हम यह भी मान लेते हैं कि परीक्षण आवेश पर एक बाहरी बल $\overrightarrow{\mathrm{F}}_{\mathrm{ext}}$ इस प्रकार लगाया जाता है कि यह परीक्षण आवेश पर लगने वाले विद्युत् बल $\overrightarrow{\mathrm{F}}_{\mathrm{e}}$ को ठीक प्रकार से सन्तुलित करता है अर्थात् १० पर परिणामी (resultant) बल शून्य हो जाता है। अतः परीक्षण आवेश की गति में त्वरण (acceleration) नहीं होता है।

इस स्थिति में बाह्य बल द्वारा किया गया कार्य विद्युत् बल द्वारा किये गये कार्य के बराबर एवं ऋणात्मक होगा और पूर्णतः परीक्षण आवेश q₀ में इसकी स्थितिज ऊर्जा के रूप में एकत्र हो जाता है।

बिन्दु B पर पहुँचते ही यदि बाहरी बल (external force) को हटा दिया जाये तो वैद्युत बल परीक्षण आवेश + q₀ को स्रोत आवेश + Q से दूर ले जायेगा। बिन्दु B पर परीक्षण आवेश में एकत्र स्थितिज ऊर्जा परीक्षण आवेश को गतिज ऊर्जा देने में इस प्रकार प्रयुक्त (used) होगी कि प्रत्येक बिन्दु पर गतिज एवं स्थितिज ऊर्जाओं का योग संरक्षित (conserved) रहता है।
धन परीक्षण आवेश + q₀ को A से B तक ले जाने में बाह्य बल द्वारा कृत कार्य
W_AB = $\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{F}}_{\mathrm{ext}} \cdot d \vec{r}=-\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{F}_e} \cdot \overrightarrow{d r}$ ............ (1)

वैद्युत बल के विरुद्ध किया गया यह कार्य स्थितिज ऊर्जा के रूप में निहित (stored) हो जाता है। यह ध्यान देने की बात है कि विद्युत् क्षेत्र में प्रत्येक बिन्दु पर + q₀ आवेश की कुछ-न-कुछ स्थितिज ऊर्जा निश्चित रूप से होगी। अत: + q₀ आवेश को A से B तक ले जाने में कृत कार्य (work done) बिन्दुओं B व A पर उसकी स्थितिज ऊर्जाओं के अन्तर के बराबर होगा।
∴ ΔU =U_B - U_A = W_AB ...(2)
इस प्रकार वैद्युत स्थितिज ऊर्जा में परिवर्तन (change in electric potential energy) की परिभाषा निम्न प्रकार से दी जा सकती हैं

"बिन्दुओं B व A के मध्य वैद्युत स्थितिज ऊर्जा में परिवर्तन उस न्यूनतम कार्य (minimum work) के तुल्य (equivalent) है जो बाह्य बल द्वारा धन परीक्षण आवेश को बिना त्वरण के A से B तक ले जाने में किया जाता है।" यह ध्यान रखने योग्य है कि स्थिर-वैद्युत क्षेत्र द्वारा किसी आवेश को एक बिन्दु से दूसरे बिन्दु तक ले जाने में किया गया कार्य केवल प्रारम्भिक एवं अन्तिम बिन्दु की स्थितियों पर ही निर्भर करता है, उस पथ पर निर्भर नहीं करता जिससे होकर वह आवेश एक बिंदु से दूसरे बिंदु तक जाता है।

समीकरण (2) द्वारा स्थितिज ऊर्जा में परिवर्तन की परिभाषा कार्य के पदों में की गई है। इस प्रकार ऊर्जा में परिवर्तन ही महत्वपूर्ण है, उसका किसी बिन्दु पर वास्तविक मान नहीं। अतः शून्य ऊर्जा वाले बिन्दु को चुनने की स्वतन्त्रता होती है। एक निश्चित संख्या में आवेश वितरण के लिए स्थितिज ऊर्जा को अनन्त पर शून्य मान लेते हैं। अतः जब बिन्दु A अनन्त पर है तो समी. (2) से,
W_∞B = U_B - U_A =U_B - 0 = U_B
या U_B = W_∞B ...(3)
अत: किसी आवेश विन्यास (charge configuration) के कारण उत्पन्न विद्युत् क्षेत्र में किसी बिन्दु पर किसी आवेश की स्थितिज ऊर्जा उस कार्य के बराबर होती है जो किसी बाह्य बल द्वारा उस आवेश को अनन्त से उस बिन्दु तक लाने में किया जाता है।

स्थिर वैद्युत विभव (Electrostatic Potential)
"विद्युत विभव वह कारण है जो आवेश के प्रवाह की दिशा निर्धारित करता है अर्थात् विद्युत् विभव किसी आवेशित वस्तु के वैद्युत तल (plane) को व्यक्त करता है।" जिस प्रकार द्रवों का प्रवाह सदैव उच्च गुरुत्वीय तल (gravity plane) से निम्न तल की ओर होता है, ऊष्मा का प्रवाह उच्च ताप की वस्तु से निम्न ताप की वस्तु की ओर होता है, ठीक उसी प्रकार आवेश (धनात्मक) का प्रवाह भी उच्च विभव से निम्न विभव की ओर होता है। विद्युत् विभव एक अदिश राशि है। इसे V से व्यक्त करते हैं।

चित्र में दिखाया गया है कि आवेशों के एक विन्यास के कारण उत्पन्न विद्युत् क्षेत्र में किसी परीक्षण आवेश (+ q₀) को बिन्दु A से B

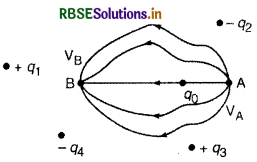
तक ले जाने में कृत कार्य केवल प्रारम्भिक एवं अन्तिम बिन्दुओं की स्थिति पर निर्भर करता है, इस बात पर नहीं कि परीक्षण आवेश को किस मार्ग से ले जाया गया है अर्थात् कृत कार्य मार्ग पर निर्भर नहीं करता है।
यदि बिन्दुओं A व B पर विद्युत् विभव क्रमश: V_A व V_B हों, तो उनके मध्य विभवान्तर की परिभाषा निम्न प्रकार से की जायेगी
V_B - V_A = $\frac{\mathrm{W}_{\mathrm{AB}}}{q_0}$ ...(1)

जहाँ W_AB = + q₀ आवेश को A से B तक ले जाने में किया गया कार्य अनु के समीकरण (2) के आधार पर,
W_AB = U_B - U_A = ΔU
V_B - V_A = $\frac{\mathrm{U}_{\mathrm{B}}-\mathrm{U}_{\mathrm{A}}}{q_0}=\frac{\mathrm{W}_{\mathrm{AB}}}{q_0}$ ........(2)

समी. (1) में यदि q₀ = + 1 C, तो
V_B - V_A = W_AB "अर्थात् किन्हीं दो बिन्दुओं के मध्य विभवान्तर (potential difference) उस कार्य के तुल्य है जो एकांक धनावेश को निम्न विभव (lower potential) के बिन्दु से उच्च विभव (higher potential) के बिन्दु तक ले जाने में करना पड़ता है।"

महत्वपूर्ण बिन्दु

• यदि 'धन' परीक्षण आवेश को बिन्दु A से B तक ले जाने में किसी बाह्य कर्ता (external source) को वैद्युत बल के विरुद्ध कार्य करना पड़े तो बिन्दु B का विभव बिन्दु A के विभव से उच्च होता है। इसका यह तात्पर्य है कि वैद्युत क्षेत्र में एक स्वतन्त्र (free) धन आवेश वैद्युत बल के कारण उच्च विभव से निम्न विभव की ओर चलता है। इसके विपरीत स्वतन्त्र ऋण आवेश निम्न विभव से उच्च विभव की ओर चलता है।
• विद्युत विभव यान्त्रिकी में ऊँचाई के एवं ऊष्मा में ताप के तुल्य है।

समी. (1) से विभवान्तर (V_B - V_A) का मात्रक

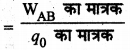
=$\frac{\mathrm{J}}{\mathrm{C}}$ = JC^-1 = वोल्ट
1V = 1 JC^-1
q₀ = +1C,
यदि W_AB = 1J, तो
V_B - V_A = 1 volt
"अर्थात् एकांक धनावेश (unit positive charge) को यदि एक बिन्दु से दूसरे बिन्दु तक ले जाने में कृत कार्य 1J, हो, तो उन बिन्दुओं के मध्य विभवान्तर 1V होगा।"
यदि बिन्दु A को बिन्दु B से दूर करते जायें तो V का मान घटता जायेगा और अनन्त पर शून्य हो जायेगा। अतः यदि बिन्दु A अनन्त पर है, तो

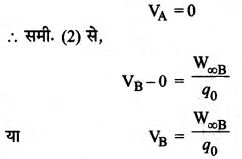
या किसी भी बिन्दु के लिए व्यापक रूप से,
V = $\frac{\mathrm{W}}{q_0}$
यदि q₀ = + 1 C, तो V = W
"अर्थात् किसी बिन्दु पर विद्युत् विभव उस कार्य के तुल्य है जो +1C आवेश को अनन्त से उस बिन्दु तक लाने में करना पड़ता है।" मात्रक एवं विमीय सूत्र-किसी बिन्दु पर विद्युत् विभव
V = $\frac{\mathrm{W}}{q_0}$

यदि q₀ = + 1 C, W = 1J, तो V = 1 वोल्ट

"अर्थात् यदि +1C आवेश को अनन्त से किसी बिन्दु तक लाने में 1J कार्य करना पड़ता है, तो उस बिन्दु पर विद्युत् विभव 1 वोल्ट होगा।"

क्या आप जानते हैं
C.GS. पद्धति में विभव की दो इकाइयाँ हैं
(i) विभव का e.s.u. या स्टेट वोल्ट (stat volt)

(ii) विभव का e.m.u. या एबवोल्ट (abvolt)

1 वोल्ट = $\frac{1}{300}$ स्टेट वोल्ट
1 वोल्ट = 10⁸ abvolt
1 stat volt = 3 × 10¹⁰ abvolt

महत्वपूर्ण बिन्दु
विभव की सबसे छोटी इकाई एबवोल्ट (abvolt) है जबकि स्टेट वोल्ट (stat volt) सबसे बड़ी इकाई है।

संरक्षी स्थिरवैद्युत बल (Conservative Electrostatic Forces):
यह सिद्ध करने के लिए कि स्थिर वैद्युत बलों की प्रकृति (nature) संरक्षी होती है, हमें यह दर्शाना होगा कि किसी विद्युत् क्षेत्र में एकांक धनावेश (परीक्षण आवेश) को किसी बन्द लूप (closed loop) पर चलाने में कृत कार्य शून्य होगा। . चित्र 2-3 में किसी विद्युत् क्षेत्र में दो बिन्दु A व B प्रदर्शित हैं जिन पर विद्युत् विभव क्रमश: VA व VB हैं। यदि बिन्दु A से B तक किसी मार्ग x से होते हुए एकांक आवेश को ले जाया जाये, तो

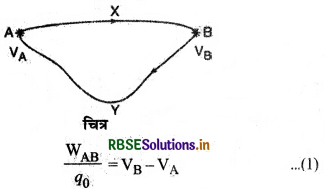
इसी प्रकार यदि बिन्दु B से A तक किसी अन्य मार्ग Y से होते हुए एकाक धनावेश को लाया जाये, तो

स्पष्ट है कि वैद्युत क्षेत्र में एकांक धनावेश को किसी बन्द पथ पर चलाने में कोई कार्य नहीं किया जाता है। अतः स्थिर-वैद्युत क्षेत्र (electrostatic field) की प्रकृति संरक्षी होती है और स्थिर-वैद्युत बलों (electrostatic forces) की प्रकृति भी संरक्षी होती है।
इस परिणाम को गणित की भाषा में निम्न प्रकार व्यक्त कर सकते
$\oint \overrightarrow{\mathrm{E}} \cdot d \vec{l}$ = 0 ............(3)
अर्थात् किसी विद्युत् क्षेत्र में बन्द लूप के लिए विद्युत् क्षेत्र का रेखीय समाकलन सदैव शून्य होता है।

किसी बिन्दु पर बिन्दु आवेश के कारण विद्युत् विभव (Electric Potential at a Point due to Point Charge)
विद्युत् विभव की परिभाषा के अनुसार किसी बिन्दु पर विद्युत् विभव ज्ञात करने के लिए एकांक धनावेश को अनन्त से उस बिन्दु तक लाने में कृत कार्य ज्ञात करना होगा।
माना एक बिन्दु आवेश + q बिन्दु O पर रखा है और इससे दूरी पर स्थित बिन्दु P पर विद्युत् विभव ज्ञात करना है। इसके लिए एकांक धनावेश को अनन्त (infinite) से P बिन्दु तक लाने में किया गया कार्य ज्ञात करना होगा और यह कार्य ज्ञात करने के लिए बिन्दु P के आगे OP दिशा

में ही एक अन्य बिन्दु A चुन लेते हैं जिसकी O बिन्दु से दूरी x है। इस बिन्दु A पर धन परीक्षण आवेश (+ q₀) पर लगने वाला वैद्युत बल
F = $\frac{1}{4 \pi \varepsilon_0} \frac{q \cdot q_0}{x^2}$

इस बल के विरुद्ध परीक्षण आवेश को dx विस्थापन देने में कृत कार्य

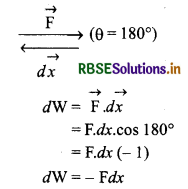
अतः + q₀ आवेश को अनन्त से P बिन्दु तक लाने में कृत कार्य

यदि आवेश q धनात्मक है, तो उसके कारण धनात्मक विभव उत्पन्न होगा और ऋणात्मक आवेश के कारण ऋणात्मक विभव उत्पन्न होगा।
समी. (1) से,

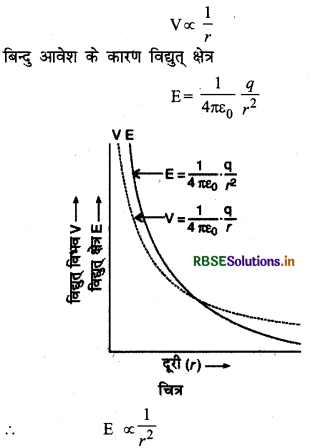
अतः यदि विद्युत् विभव V एवं विद्युत् क्षेत्र E को एक ही ग्राफ पर प्रदर्शित करें, तो ग्राफ चित्र की भाँति मिलेगा।
ऋणात्मक आवेश के लिए V तथा r के मध्य ग्राफ निम्न प्रकार होगा :

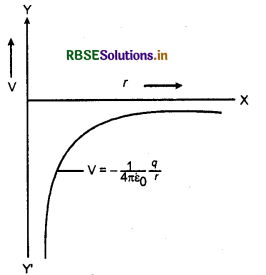
V तथा $\frac{1}{r}$ के मध्य ग्राफ

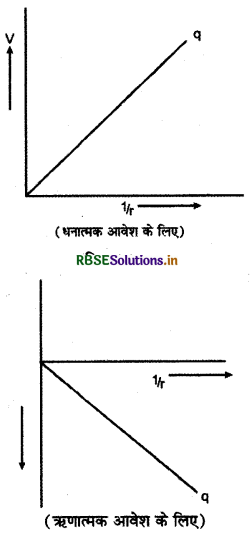
क्या आप जानते हैं

• किसी आवेश का अपने स्थान पर विद्युत विभव ज्ञात नहीं है। यह अनन्त माना गया है।
• विद्युत् विभव, विद्युत् क्षेत्र की विशेषता (characteristics) है, इस बात का कोई तात्पर्य (meaning) नहीं है कि कोई आवेशित वस्तु विद्युत् क्षेत्र में रखी गयी है या नहीं।

C पर परिणामी विभव
V = V₁ + V₂
= 0.9 + 0.6
= 1.5 वोल्ट

वैद्युत द्विध्रुव के कारण किसी बिन्दु पर विद्युत विभव (Potential at a Point due to electric dipole):
माना 2l लम्बाई के एक वैद्युत द्विध्रुव के मध्य-बिन्दु O से r दूरी पर स्थिति बिन्दु P पर विभव ज्ञात करना है।
वैद्युत द्विध्रुव आघूर्ण |$\overrightarrow{\mathrm{P}}$| = q × 2l
P = q × 2l

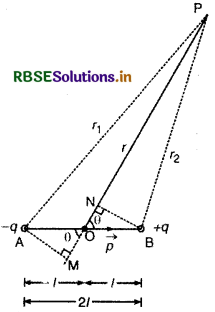
चित्र में,
cos θ = $\frac{\mathrm{OM}}{\mathrm{OA}}=\frac{\mathrm{OM}}{l}$
∴ OM = l cos θ
∴ दूरी MP = OM + OP
= OP + OM = r + l cos θ
∴ दूरी r₁ = AP ≈ MP = (r + l cos θ)
इसी प्रकार, r₂ = BP ≈ NP = (r - l cos θ)
∴ -q आवेश के कारण P पर उत्पन्न विभव
V₁ = $-\frac{1}{4 \pi \varepsilon_0} \frac{q}{r_1}$
और + q के कारण P पर उत्पन्न विभव
V2 = + $\frac{1}{4 \pi \varepsilon_0} \frac{q}{r_2}$

P पर परिणामी विभव
V = V₁ + V₂

(i) यदि बिन्दु P अक्षीय (axial) स्थिति में है, तो
θ = 0 ∴ cos θ = 1
अतः V = $\frac{1}{4 \pi \varepsilon_0} \frac{p}{\left(r^2-l^2\right)}$
दीर्घ दूरियों के लिए r >> l ∴ r² >>> l²
अतः l² को r² की तुलना में छोड़ने पर,

(ii) यदि बिन्दु P निरक्षीय (equatorial) स्थिति में स्थित है, तो
θ = 90° ∴ cos θ = 0
अतः V = 0
अर्थात् वैद्युत द्विध्रुव की निरक्षीय (equatorial) स्थिति में विद्युत् विभव शून्य होता है।

महत्वपूर्ण बिन्दु

• यह बात याद रखने योग्य है कि विद्युत् द्विध्रुव के कारण अधिक दूरी के लिए विद्युत् विभव $\frac{1}{r^2}$ के अनुसार परिवर्तित (variation) होता है, जबकि बिन्दु आवेश के कारण विद्युत् विभव $\frac{1}{r}$ के अनुसार परिवर्तित होता है।
• किसी विद्युत् द्विध्रुव के कारण विभव केवल दूरी r पर ही निर्भर नहीं करता, बल्कि वह स्थिति सदिश $\vec{r}$ व द्विध्रुव आघूर्ण $\vec{p}$ के बीच के कोण पर भी निर्भर करता है।
• विद्युत् द्विध्रुव आघूर्ण सदिश के परितः विभव में अक्षीय सममिति (axial symmetry) होती है। यदि O को नियत रखा जाये और स्थिति सदिश (position vector) को द्विध्रुव आघूर्ण सदिश के परितः (around) घूर्णन (rotation) कराया जाये तो परिणामी शंकु (resultant cone) के बिन्दुओं पर समान विभव होगा।

आकिक उदाहरण
वैद्युत द्विध्रुव के कारण वैद्युत विभव के आंकिक उदाहरण के लिए
प्रयुक्त सूत्र
1. अक्षीय स्थिति पर
V = $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{p}{r^2}$ वोल्ट

2. निरक्षीय स्थिति पर
V = 0
प्रयुक्त इकाईयाँ
V – वोल्ट

प्रयुक्त नियतांक
$\frac{1}{4 \pi \varepsilon_0}$ = 9 × 10⁹N.m²/C²

बिन्दु आवेश समूह के कारण किसी बिन्दु पर विद्युत् विभव (Potential at a Point due to Group of Point Charges)
माना n बिन्दु आवेश q₁, q₂, q₃,......, q_n बिन्दु P से क्रमशः r₁, r₂, r₃,........,r_n. दूरियों पर स्थित हैं और इन सभी आवेशों के कारण बिन्दु P पर परिणामी विभव ज्ञात करना है।

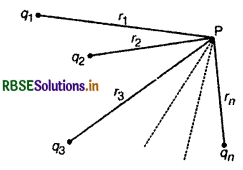
q₁ आवेश के कारण बिन्दु P पर उत्पन्न विद्युत् विभव
V₁ = $\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r_1}$

इसी प्रकार अन्य आवेशों के कारण P पर उत्पन्न विभव

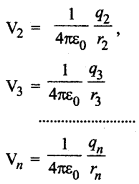
विद्युत् विभव अदिश राशि है, अतः P पर इन सभी विभवों का बीजगणितीय योग (algebraic sum) ही परिणामी विभव प्रदान करेगा।

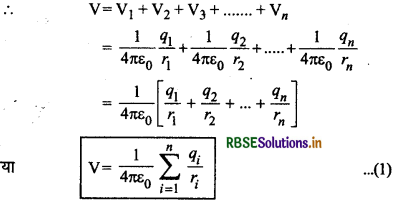
विद्युत् विभव पर आधारित आंकिक
उदाहरण के लिए
1. प्रयुक्त सूत्र,
(a) V = $\frac{W}{q}$
(b) बिन्दु आवेश के कारण विद्युत् विभव
V = $\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}$
(c) विद्युत् आवेश समूह के कारण किसी बिन्दु पर विद्युत् विभव
V = $\frac{1}{4 \pi \varepsilon_0} \cdot \sum_{i=1}^n \frac{q_i}{r_i}$

2. प्रयुक्त इकाईयाँ
q-कूलॉम, कार्य-जूल, विद्युत विभव-वोल्ट या जूल/कूलॉम

विद्युत प्रवणता के रूप में विद्युत् क्षेत्र (Electric Field as a Gradient of Electric)
माना एक बिन्दु आवेश + q बिन्दु O पर रखा है और इससे r दूरी पर बिन्दु P पर विद्युत् विभव V एवं (r - dr) दूरी पर स्थित बिन्दु Q पर विभव (V + dv) है।

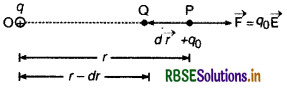
यदि एक अत्यन्त सूक्ष्म परीक्षण आवेश (very small test charge) q को P से Q तक ले जाने में कृत कार्य dw है, तो
(V + dv) - V = $\frac{d \mathrm{~W}}{q_0}$
या dV = $\frac{d \mathrm{~W}}{q_0}$ .........(1)
P बिन्दु पर स्थित + q₀ आवेश पर लगने वाला बल
$\vec{F}$ = q₀$\vec{E}$ (OP दिशा में)
∴ इस बल के विरुद्ध (against) d $\vec{r}$ विस्थापन (displacement) देने में अर्थात् P से Q तक q₀ आवेश को ले जाने में कृत कार्य
dW = $\vec{F} \cdot d \vec{r}$
= F.dr. cos 180° = -F.dr
परन्तु F = q₀E
dW = -q₀E.dr
या $\frac{d \mathrm{~W}}{q_0}$= -E.dr

समी. (1) व (2) से, dV = -E.dr
या E = - $\frac{d \mathrm{~V}}{d r}$ ..(3)

"अर्थात् किसी बिन्दु पर विद्युत् क्षेत्र की तीव्रता (electric field intensity) उस बिन्दु पर ऋणात्मक विभव प्रवणता (potential gradient) के बराबर होती है।" ऋण चिह्न यह दर्शाता है कि विद्युत् क्षेत्र $\vec{E}$ की दिशा सदैव उच्च (higher) विभव से निम्न (lower) विभव की ओर अर्थात् विभव के घटने की दिशा में (in decreasing directon) होती है। विभव प्रवणता एक सदिश राशि है जिसकी दिशा विद्युत् क्षेत्र $\vec{E}$ की विपरीत दिशा में अर्थात् विभव बढ़ने (increasing potential) की दिशा में होती है।

विद्युत् क्षेत्र व विद्युत् विभव में सम्बन्ध
$\overrightarrow{\mathrm{E}}=-\frac{d \mathrm{~V}}{\overrightarrow{d r}}$
या dV = $\overrightarrow{-\mathrm{E}} \cdot \overrightarrow{d r}$

उपरोक्त समीकरण को बिन्दु $\overrightarrow{r_1}$ व $\overrightarrow{r_2}$ के मध्य समाकलन करने पर,

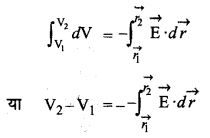
जहाँ, बिन्दु $\overrightarrow{r_1}$ व $\overrightarrow{r_2}$ पर विद्युत् विभव क्रमशः V₁ व V₂, हैं। यदि हम बिन्दु को अनन्त पर मानें, तो V₁ = 0 और $\overrightarrow{r_2} = \vec{r}$ लेने पर
V$(\vec{r})=-\int_{\infty}^r \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d r}$

क्या आप जानते हैं
1.किसी एकसमान आवेशित गोलीय खोल (spherical shell) के बाहर स्थित किसी बिन्दु पर आवेशित कोश के कारण विभव
V = $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r}$ (r ≥ R)
जहाँ q = गोलीय खोल पर समस्त आवेश
R = गोलीय कोश की त्रिज्या है।

2. खोल के भीतर विभव नियत रहता है और यह खोल के पृष्ठ के विभव के बराबर होता है
V = $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{R}$

3. E = -$\frac{d \mathrm{~V}}{d r}$ समरूप व असमरूप (uniform and non-uniform) क्षेत्र दोनों के लिए सत्य है।

समविभव पृष्ठ (Equi-potential Surface):
"ऐसा पृष्ठ जिसके प्रत्येक बिन्दु पर विद्युत् विभव समान होता है, समविभव पृष्ठ कहलाता है।" समविभव पृष्ठ की विशेषताएँ-विभवान्तर की परिभाषा के अनुसार किन्हीं दो बिन्दुओं के मध्य विभवान्तर उस कार्य के बराबर होता है जो एकांक धनावेश को निम्न विभव के बिन्दु से उच्च विभव के बिन्दु तक ले जाने में करना पड़ता है अर्थात् A व B बिन्दुओं के मध्य विभवान्तर
V_B - V_A = W_AB
यदि A व B दोनों बिन्दु एक समविभव पृष्ठ पर स्थित हैं,
तो V_B = V_A
W_AB = V_B - V_A = 0
अर्थात् “समविभव पृष्ठ पर किन्हीं दो बिन्दुओं के मध्य परीक्षण आवेश को एक बिन्दु से दूसरे बिन्दु तक ले जाने में कोई कार्य नहीं किया जाता है।" समविभव पृष्ठ के किन्हीं भी दो बिन्दुओं के बीच कोई विभवान्तर नहीं होता।

एकांक धनावेश को किसी समविभव पृष्ठ पर एक सूक्ष्म विस्थापन वा देने में किया गया कार्य
dW = $\overrightarrow{\mathrm{E}} \cdot d \vec{l}$ = E dl cos θ = 0
∴ cos θ = 0 ⇒ θ = 90°, अर्थात् $\overrightarrow{\mathrm{E}} \perp d \vec{l}$
स्पष्ट है कि विद्युत् क्षेत्र सदैव समविभव पृष्ठ के लम्बवत् होता है।
एक बिन्दु आवेश के कारण इससे दूरी पर उत्पन्न विभव
V = $\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}$ ....(1)
स्पष्ट है कि यदि r का मान नियत हो जाये, तो v का मान भी नियत (constant) हो जायेगा।

समविभव पृष्ठ की कुछ आकृतियाँ (Shapes of Some Equipotential Surface):
यदि समीकरण (1) से एक विलगित (isolated) बिन्दु आवेश को केन्द्र मानकर समकेन्द्रीय (concentric) गोलीय पृष्ठ खींचे जायें तो प्रत्येक गोलीय पृष्ठ समविभव पृष्ठ होगा [चित्र (a)]।

X-दिशा के अनुदिश (along) समरूप (uniform) विद्युत् क्षेत्र $\vec{E}$ में X-अक्ष के लम्बवत् (perpendicular) समतल पृष्ठ (plane surface) समविभव पृष्ठ होंगे [चित्र (b)] ।

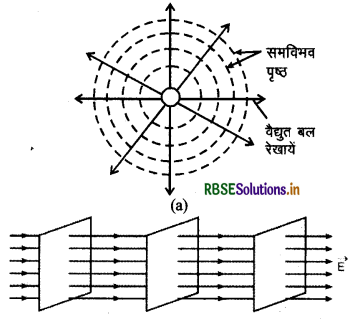
एक वैद्युत द्विध्रुव के कारण समविभव चित्र (a) एवं समान प्रकृति एवं परिमाण के आवेश युग्म के कारण समविभव पृष्ठ चित्र (b) में प्रदर्शित हैं।

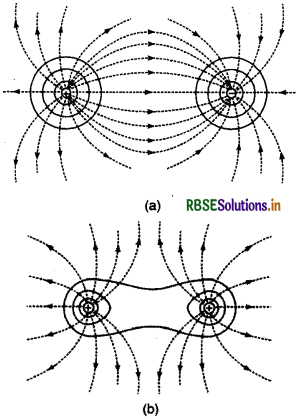
आवेश समूह की वैद्युत स्थितिज ऊर्जा (Electric Potential Energy of a System of Charges)
किन्हीं दो अथवा दो से अधिक आवेशों को अनन्त से एक-दूसरे के समीप लाकर निकाय की रचना करने में किया गया कार्य उन आवेशों से बने निकाय (system) में स्थितिज ऊर्जा के रूप में एकत्र हो जाता है। इस संचित (stored) ऊर्जा को ही निकाय की वैद्युत स्थितिज ऊर्जा कहते हैं। इसे U से व्यक्त करते हैं।

अतः “दो या दो से अधिक बिन्दु आवेशों के किसी निकाय की वैद्युत स्थितिज ऊर्जा उस कार्य के बराबर होती है जो उन आवेशों को अनन्त से परस्पर निकट लाकर निकाय की रचना करने में किया जाता
(a) दो आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा-माना दो आवेशों के निकाय में q₁ व q₂ आवेश r दूरी पर क्रमशः A व B पर स्थित हैं (चित्र)।
+q₁ के कारण बिन्दु B पर उत्पन्न विभव

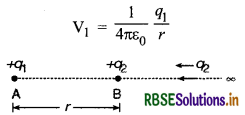
चूँकि किसी बिन्दु पर विद्युत् विभव उस कार्य के बराबर होता है जो एकांक धनावेश को अनन्त से उस बिन्दु तक लाने में करना पड़ता
अतः + q₂ आवेश को अनन्त से B बिन्दु तक लाने में किया गया कार्य अर्थात् दोनों आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा
U = W = V₁q₂
= $\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r}$ × q₂
U = $\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r}$ ..........(1)
यदि दोनों आवेश समान प्रकृति (equal nature) के हैं, तो U का मान धनात्मक होगा और यदि एक आवेश धनात्मक एवं दूसरा ऋणात्मक है, तो U का मान ऋणात्मक होगा, अत: U का मान निकालते समय आवेशों के मान चिह्न सहित (proper sign) रखने चाहिए।

(b) दो से अधिक आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा-n आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा उस कार्य के बराबर होती है जो निकाय के सभी आवेशों को अनन्त से उनकी स्थिति तक लाने में करना पड़ता है।
पहले आवेश q₁ को अनन्त से उसकी स्थिति P₁$(\overrightarrow{r_1})$ तक लाने में कोई कार्य नहीं करना पड़ेगा क्योंकि शेष सभी आवेश अनन्त पर होंगे, अतः पहले आवेश के आने का विरोध नहीं होगा।
W₁ = 0

जब दूसरा आवेश q₂ उसकी स्थिति P₂ $(\overrightarrow{r_2})$ तक लाते हैं, तो पहला आवेश q₁ उसके आने का विरोध करेगा। अतः q₂ को लाने में कृत कार्य
W₂ = (q₁ के कारण P₂ स्थिति में विभव) × q₂
= $\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r_{12}} \cdot q_2=\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r_{12}}$

जब तीसरा आवेश q₃ अनन्त से P₃ ($\overrightarrow{r_3}$) तक लाते हैं, तो कृत कार्य
W₃ = (q₁ व q₂ के कारण P₃ पर विभव) × q₃

इसी प्रकार अन्य आवेशों को लाने में कृत कार्य ज्ञात करके उन्हें जोड़ने पर,
U = $\frac{1}{4 \pi \varepsilon_0} \sum_{\text {सभी युग्म }} \frac{q_j q_k}{r_{j k}}$

इस योग को ज्ञात करने में हमें आवेशों के प्रत्येक युग्म का एक बार ही प्रयोग करना पड़ता है अतः उक्त समीकरण को निम्न प्रकार लिख सकते हैं
U = $\frac{1}{2} \sum_{j=1}^n \sum_{\substack{k=1 \\ j \neq k}}^n \frac{1}{4 \pi \varepsilon_0} \frac{q_j q_k}{r_{j k}}$ .....(3)

यहाँ $\frac{1}{2}$, का गुणा इसलिए करना पड़ रहा है क्योंकि इस योग में आवेशों के प्रत्येक युग्म को दो बार लेते हैं। उदाहरण के लिए जब j = 1, k = 2 और j = 2, k = 1, लेने पर आवेशों का एक ही युग्म दो बार (q₁q₂ और q₂q₁) आता है। हमें एक युग्म केवल एक ही बार प्रयोग करना है, अतः $\frac{1}{2}$ का प्रयोग अत्यन्त आवश्यक है।

महत्वपूर्ण बिन्दु
1. स्थितिज ऊर्जा विन्यास (configuration) की वर्तमान अवस्था का अभिलाक्षणिक गुण (characteristics property) होता है, यह इस बात पर निर्भर नहीं करता कि इस विन्यास को किस प्रकार प्राप्त किया गया है।

आकिक उदाहरण
आवेश समूह की विद्युत् स्थितिज ऊर्जा पर आधारित आंकिक
उदाहरण के लिए
प्रयुक्त सूत्र

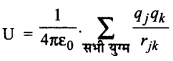
प्रयुक्त इकाईयाँ
U - जूल
प्रयुक्त नियतांक
$\frac{1}{4 \pi \varepsilon_0}$ = 9 × 10⁹N-m²/C²

बाह्य विद्युत क्षेत्र में आवेशों की स्थितिज ऊर्जा (Potential Energy of Charges in an External Electric Field)
आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा के लिए हम सूत्र प्राप्त कर चुके हैं जिसमें विद्युत् क्षेत्र के स्रोत (source) अर्थात् आवेशों की स्थितियों (positions) को भी ध्यान में रखा गया था। अब हमें बाहरी विद्युत् क्षेत्र में किसी आवेश की वैद्युत स्थितिज ऊर्जा ज्ञात करनी है। यहाँ विद्युत् क्षेत्र $\overrightarrow{\mathrm{E}}$ उत्पन्न करने वाले आवेश अज्ञात (unknown) हैं।

बाहरी विद्युत् क्षेत्र ($\overrightarrow{\mathrm{E}}$) एवं किसी बिन्दु पर विद्युत् विभव (V) दोनों प्रेक्षण बिन्दु की स्थिति बदलने पर बदल सकते हैं। यदि किसी बिन्दु P पर विद्युत् विभव V(r) है, जहाँ $\vec{r}$ बिन्दु P की स्थिति वेक्टर है, तो विभव की परिभाषा के अनुसार एकांक धनावेश को अनन्त से P बिन्दु तक लाने में किया गया कार्य V जूल होगा।
अतः किसी आवेश १ को अनन्त से P बिन्दु तक लाने में कृत कार्य
=q.V($\vec{r}$)
यही कार्य आवेश में उसकी वैद्युत स्थितिज ऊर्जा के रूप में संचित (stored) हो जायेगा।
अत: आवेश q की किसी बाहरी क्षेत्र $\vec{E}$ में बिन्दु P($\vec{r}$) पर वैद्युत स्थितिज ऊर्जा = q.V($\vec{r}$)

किसी बाह्य क्षेत्र में दो आवेशों के निकाय की स्थितिज ऊर्जा (Potential Energy of a system of two charges in an External Electric Field)
माना दो आवेश q₁ तथा q₂ किसी बाह्य विद्युत् क्षेत्र में क्रमशः $\overrightarrow{r_1}$ व $\overrightarrow{r_2}$ स्थितियों पर स्थित हैं। हमें इस बाह्य क्षेत्र (external field) में दोनों आवेशों के निकाय की स्थितिज ऊर्जा ज्ञात करनी है। इसके लिए सर्वप्रथम हम आवेश q₁ को अनन्त से $\overrightarrow{r_1}$ तक लाते हैं, इस चरण (step) में किया गया कार्य q₁V($\overrightarrow{r_1}$) है।

अब आवेश q₂ को $\overrightarrow{r_2}$ तक लाने में किए जाने वाले कार्य पर विचार करते हैं। इस चरण में केवल बाह्य क्षेत्र E के विरुद्ध ही नहीं कार्य होता, बल्कि q₂ के कारण क्षेत्र के विरुद्ध भी कार्य करना होता है। अतः

q₂ पर बाह्य क्षेत्र (external field) के विरुद्ध किया गया कार्य = q₂ V($\overrightarrow{r_2}$)
आवेश q₂ पर q₁ के कारण क्षेत्र के विरुद्ध किया गया कार्य
= $\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r_{12}}$
(r₁₂ आवेशों q₁ तथा q₂ के बीच की दूरी है।)

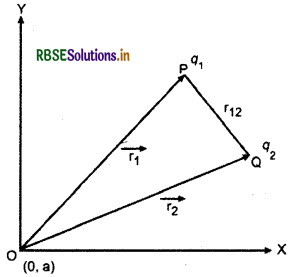
क्षेत्रों के लिए अध्यारोपण सिद्धान्त (principle of superposition) द्वारा हम q₂ पर दो क्षेत्रों (E तथा q₁ के कारण क्षेत्र) के विरुद्ध किए गए कार्यों को जोड़ते हैं, अतः
q₂ को $\overrightarrow{r_2}$ तक लाने में किया गया कार्य
= q₂V ($\overrightarrow{r_2}$) + $\frac{q_1 q_2}{4 \pi \varepsilon_0 r_{12}}$
अतः निकाय की स्थितिज ऊर्जा = विन्यास (configuration) के निर्माण में किया गया कार्य
∴ W = U = q₁ V($\overrightarrow{r_1}$) + q₂V ($\overrightarrow{r_2}$) + $\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r_{12}}$

चालक स्थिर-वैद्युतिकी (Electrostatics of Conductors):
चालक (conductors) वे पदार्थ हैं जिनसे होकर धारा का प्रवाह (flow of charge) अर्थात् आवेश का प्रवाह हो जाता है। सभी धात्विक पदार्थ चालक होते हैं। इनकी चालकता (conductivity) का कारण यह है कि सभी चालकों में आवेश वाहकों अर्थात् मुक्त इलेक्ट्रॉनों (free electrons) की बड़ी संख्या मौजूद रहती है। चालक स्थिर-वैद्युतिकी के कुछ महत्वपूर्ण तथ्य निम्नलिखित हैं
(a) चालक के अन्दर विद्युत् क्षेत्र शून्य होता है-माना एक चालक ABCD किसी बाह्य विद्युत् क्षेत्र $\overrightarrow{\mathrm{E}}_{\mathrm{ext}}$ में रखा है (चित्र)। चालक के मुक्त इलेक्ट्रॉनों पर बाह्य क्षेत्र

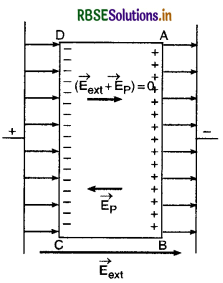
की विपरीत दिशा में E_ext बल लगेगा अतः वे चालक के पृष्ठ AB से CD की ओर गति करने लगेंगे और CD किनारे पर एकत्र (collect) हो जायेंगे। फलस्वरूप AB किनारा समान परिमाण से धनावेशित हो जायेगा। इन आवेशों को प्रेस्ति आवेश (induced charges) कहते हैं। ये प्रेरित आवेश चालक के अन्दर एक वैद्युत क्षेत्र $\overrightarrow{\mathrm{E}}_{\mathrm{p}}$, उत्पन्न करते हैं जो बाह्य क्षेत्र $\overrightarrow{\mathrm{E}}_{\mathrm{ext}}$ का विरोध करता है और इलेक्ट्रॉनों की गति का भी विरोध करता है, अतः इलेक्ट्रॉनों का प्रवाह तुरन्त रुक जाता है, जैसे ही E$\overrightarrow{\mathrm{E}}_{\mathrm{p}}$, का परिमाण $\overrightarrow{\mathrm{E}}_{\mathrm{ext}}$ के परिमाण के बराबर हो जाता है, चालक के अन्दर नेट विद्युत् क्षेत्र $\left(\vec{E}_{e x t}+\vec{E}_P\right)$ = 0 हो जाता है।
अर्थात् E_ext - E_p = 0, क्योंकि $\overrightarrow{\mathrm{E}}_{\mathrm{ext}}$ व $\overrightarrow{\mathrm{E}}_{\mathrm{P}}$ की दिशाएँ विपरीत हैं।

(b) स्थिर अवस्था में चालक के अन्दर कोई अतिरिक्त आवेश नहीं होता है-किसी उदासीन (neutral) चालक के प्रत्येक लघु आयतन (small element) अथवा पृष्ठीय अवयव (surface element) में धनात्मक तथा ऋणात्मक आवेश समान मात्रा में होते हैं। जब किसी चालक को आवेशित किया जाता है, तो स्थैतिक अवस्था में अतिरिक्त (excess) आवेश केवल उसके पृष्ठ पर विद्यमान (present) रहता है। यह तथ्य गाउस के नियम से स्पष्ट हो जाता है।

यदि चालक के भीतर किसी स्वेच्छ (arbitrary) आयतन V पर विचार करें, तो आयतन V को परिबद्ध (bound) करने वाले बन्द पृष्ठ S पर वैद्युत क्षेत्र शून्य होगा (क्योंकि चालक के अन्दर E = 0) अतः बन्द पृष्ठ से निर्गत वैद्युत फ्लक्स शून्य होगा। फलस्वरूप गाउस के प्रमेय के अनुसार पृष्ठ द्वारा परिबद्ध आवेश शून्य होगा। यह परिणाम चालक के अन्दर लिये गये प्रत्येक आयतन अवयव के लिए सत्य होगा, अतः चालक के अन्दर स्थैतिक अवस्था (static position) में कोई अतिरिक्त आवेश नहीं होता है। अर्थात् इस तथ्य को इस बात से भी समझाया जा सकता है कि चालक के अन्दर नेट विद्युत् क्षेत्र शून्य होता है।
अतः $\overrightarrow{\mathrm{E}}$ = 0
∴ $\oint \overrightarrow{\mathrm{E}} d \overrightarrow{\mathrm{S}}$ = 0 (गाउस प्रमेय से)
या $\oint \overrightarrow{\mathrm{E}} d \overrightarrow{\mathrm{S}}=\frac{\mathrm{Q}}{\varepsilon_0}$ जो कि शून्य है।
∴ Q = 0
अतः चालक के अन्दर नेट आवेश शून्य होता है।

(c) आवेशित चालक के पृष्ठ पर प्रत्येक बिन्दु पर स्थिर-वैद्युत क्षेत्र अभिलम्बवत् होना चाहिए-स्थिर-वैद्युत स्थितियों के अन्तर्गत चालक के पृष्ठ पर आवेश का पुनर्वितरण (redistribution of charges) हो जाता है इसलिए आवेश का प्रवाह रुक जाता है। अतः पृष्ठ के अनुदिश (along) विद्युत् क्षेत्र का घटक (component) शून्य होना चाहिए अर्थात्

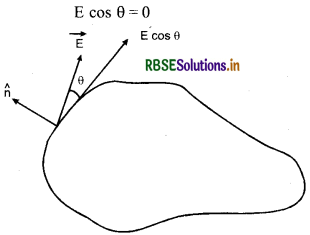
जहाँ θ पृष्ठ पर स्पर्शी (tangent) एवं विद्युत् क्षेत्र के मध्य कोण है।
चूँकि E ≠ 0 अत: cos θ = 0
θ = 90°
अर्थात् विद्युत् क्षेत्र $\vec{E}$ चालक के पृष्ठ के लम्बवत् होना चाहिए । (चित्र)।

(d) चालक के समस्त आयतन में स्थिर-वैद्युत विभव नियत रहता है तथा इसका मान इसके पृष्ठ पर भी समान (भीतर के बराबर) होता है-परिणाम (a) व (c) के आधार पर चालक के भीतर विद्युत् क्षेत्र की तीव्रता शून्य होती है (E = 0) और इसका पृष्ठ के अनुदिश कोई स्पर्श रेखीय (tangential) घटक नहीं होता है। अतः इसके भीतर अथवा पृष्ठ पर किसी छोटे परीक्षण आवेश को गति कराने में कोई कार्य नहीं होता है। इससे यह निष्कर्ष (conclusion) निकलता है कि चालक के अन्दर या पृष्ठ पर किन्हीं दो बिन्दुओं के मध्य विभवान्तर शून्य होता है अर्थात् प्रत्येक बिन्दु पर विभव समान होता है।

(e) आवेशित चालक के पृष्ठ पर विद्युत् क्षेत्र- आवेशित चालक के पृष्ठ (surface) के निकट उत्पन्न विद्युत् क्षेत्र की तीव्रता
$\overrightarrow{\mathrm{E}}=\frac{\sigma}{\varepsilon_0} \cdot \hat{n}$
जहाँ σ, आवेश का पृष्ठ घनत्व (surface density) है एवं n , पृष्ठ की लम्ब दिशा में एकांक वेक्टर है।
चित्र के अनुसार एक छोटा बेलन (cylinder) जिसका अनुप्रस्थ परिच्छेद (cross-sectional area) as काफी कम हो और थोड़ा हिस्सा पृष्ठ के अन्दर तथा थोड़ा पृष्ठ के बाहर हो, मान लेते हैं। पृष्ठ का आवेश घनत्व σ है। आवेशित चालक के अन्दर E = 0 होता है।

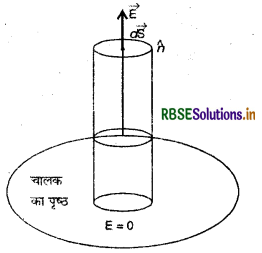
का पृष्ठ
चित्र पृष्ठ के बाहर पृष्ठ के लम्बवत् विद्युत् क्षेत्र की तीव्रता E है। बेलनाकार पृष्ठ से केवल बाहरी परिच्छेद (outer cross-section) से फ्लक्स निर्गत होता है। अति सूक्ष्म (very small) क्षेत्रफल dS के लिए विद्युत् क्षेत्र E को नियत मान लेते हैं अतः
विद्युत् फ्लक्स = ± E.(dS)

जो कि σ > 0 के लिए धनात्मक एवं σ < 0 के लिए ऋणात्मक होगा। चूँकि बेलनाकार पृष्ठ (cylindrical surface से परिबद्ध (bound) आवेश = σ.dS ∴ गाउस प्रमेय के अनुसार, E.d S = $\frac{\sigma d \mathrm{~S}}{\varepsilon_0}$ ⇒ E = $\frac{\sigma}{\varepsilon_0}$
∴ विद्युत् क्षेत्र पृष्ठ के लम्बवत् है अतः $\vec{E}=\frac{\sigma}{\varepsilon_0} \hat{n}$ जो कि σ > 0 के लिए σ के दोनों चिह्नों के लिए सही है। अत: σ > 0 के लिए विद्युत् क्षेत्र पृष्ठ के लम्बवत् बहिर्मुखी (outward) है और σ < 0 के लिए पृष्ठ के लम्बवत् अन्तर्मुखी (inward)

स्थिरवैद्युत परिरक्षण (Electrostatic Shielding)
“आकाश (space) के एक निश्चित क्षेत्र को बाह्य विद्युत् क्षेत्र (external electric field) से सुरक्षित रखने की घटना को ही स्थिरवैद्युत परिरक्षण (shielding) कहते हैं।" हम जानते हैं कि आवेशित चालक के अन्दर विद्युत् क्षेत्र शून्य होता है। अत: संवेदनशील (sensitive) उपकरणों को बाह्य विद्युत् क्षेत्र से सुरक्षित रखने के लिए उन्हें खोखले चालक के अन्दर बन्द कर दिया जाता है। ऐसे खोखले चालकों को फैराडे के खोल (Faraday's Cages) कहते हैं।

उन्हें पृथ्वी से सम्बन्धित करना आवश्यक नहीं है। बरसात में तूफान (thunder) के समय जब आकाशीय बिजली (lightning) का प्रकोप होता है, तो उस समय खुले मैदान की अपेक्षा कार या बस के अन्दर ही रहना अधिक सुरक्षित रहता है। बस या कार का आवरण (cases) वैद्युत परिरक्षण प्रदान करता है। मूल तथ्य (fundamental fact) यह है कि किसी कोटर के अन्दर विद्युत् क्षेत्र शून्य होता है, उसका आकार या आकृति जो भी रहे और चालक पृष्ठ पर चाहे जितना आवेश हो। इसका अर्थ यह हुआ कि बाहर चाहे जो भी आवेश एवं विद्युत् क्षेत्र का विन्यास रहे, किसी चालक के अन्दर कोई कोटर (cavity) बाहरी वैद्युत प्रभाव से मुक्त रहता है। (चित्र)

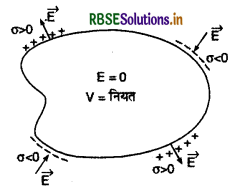
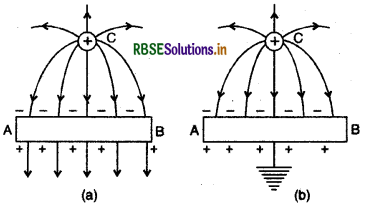
भूसम्पर्कित (earthing) चालक AB भी विद्युत् क्षेत्र के विरुद्ध पर्दे का कार्य कर सकता है। उदाहरण के लिए, चित्र (a) में जब AB को पृथ्वी से सम्बन्धित नहीं किया जाता है तो C पर धनात्मक आवेश के कारण विद्युत् क्षेत्र AB के परे भी जारी रहता है, लेकिन जब AB को भूसम्पर्कित कर दिया जाता है तो प्रेरित (induced) धनावेश पृथ्वी में चला जाता है और विद्युत् क्षेत्र AB के परे (beyond) नहीं जाता है, वह AB के प्रथम पृष्ठ पर ही समाप्त हो जाता है [चित्र (b)]। इसीलिए उच्च वोल्टेज वाले जनरेटर को ऐसे खोल (casing) में बन्द करते हैं जो भूसम्पर्कित होता है। .

परावैद्युत तथा ध्रुवण (Dielectrics and Polarisation):
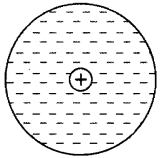
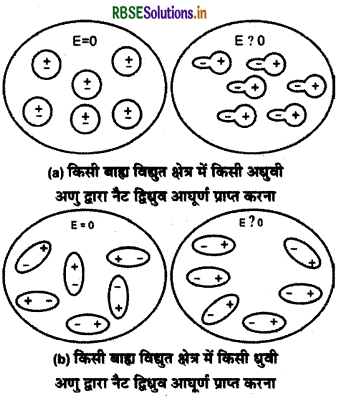
हम जानते हैं कि परमाणु विद्युतः उदासीन होता है। उसका समस्त धनावेश नाभिक में निहित (contain) रहता है और ऋणावेश नाभिक के परितः वितरित (distributed) इलेक्ट्रॉनों के रूप में होता है। दोनों आवेश परिमाण में समान होते हैं। इन दोनों आवेशों के गुरुत्व केन्द्र (centre of gravity) समान भी हो सकते हैं और भिन्न-भिन्न भी हो सकते हैं। यदि दोनों के केन्द्र समान हैं तो परमाणु अथवा अणु अधुवी (non-polar) कहलायेगा और केन्द्र यदि भिन्न हैं तो ध्रुवी (polar) कहलायेगा। अधुवी परावैद्युत-“ऐसा परावैद्युत (dielectric) जिसके परमाणओं और अणुओं में धनात्मक एवं ऋणात्मक आवेशों के गुरुत्व केन्द्र समान होते हैं, अध्रुवी परावैद्युत कहलाता है।"

इस प्रकार अध्रुवी परावैद्युत पदार्थ के परमाणु अथवा अणुओं में धन एवं ऋण आवेशों का उनके केन्द्रों के परितः (around) वितरण सममित होता है (चित्र 2-26)। ऋण एवं धन आवेशों के केन्द्रों के मध्य शून्य दूरी होने के कारण इन परमाणुओं अथवा अणुओं का वैद्युत द्विध्रुव आघूर्ण भी शून्य होता है। ट्रॉन्सफार्मर के तेल में अध्रुवीय अणु होते हैं इसलिए ट्रॉन्सफार्मर का तेल अच्छा परावैधुत होता है।

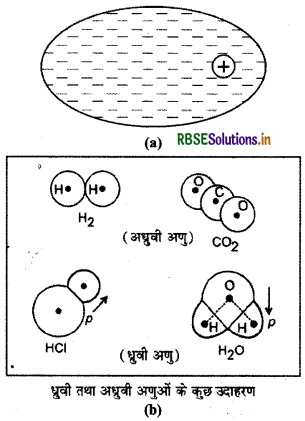
ध्रुवी परावैद्युत-“ऐसे परावैद्युत जिनके परमाणु अथवा अणुओं में धन एवं ऋण आवेशों के गुरुत्व केन्द्र भिन्न (different) होते हैं, ध्रुवी परावैद्युत कहलाते हैं।" अतः ध्रुवी परावैद्युत के परमाणुओं अथवा अणुओं में धन एवं ऋण आवेशों का उनके केन्द्रों के परितः वितरण सममिति (symmetry) में नहीं होता है (चित्र 2:27)। इस प्रकार दोनों आवेशों के केन्द्रों के मध्य एक निश्चित दूरी होने के कारण इन परमाणुओं अथवा अणुओं का एक निश्चित वैद्युत द्विध्रुव आघूर्ण भी होता है। NH₃, HCl, H₂O CO₂ इत्यादि के अणु ध्रुवी अणुओं की श्रेणी में आते हैं। जल के अणु का एक स्थायी (permanent) द्विध्रुव माघूर्ण 6 × 10^-28 Cm की कोटि का होता है।

वास्तव में अणुओं में आवेश का वितरण असममित (asymmtrical) होता है। उदाहरण के लिए, एक आयनिक अणु में एक परमाणु से दूसरे परमाणु में इलेक्ट्रॉन स्थानान्तरित हो जाते हैं। फलस्वरूप अणु धनात्मक एवं ऋणात्मक आयनों के भिन्न स्थितियों में होने के कारण ध्रुवी हो जाता है और एक स्थायी द्विध्रुव आघूर्ण रखता है।

विद्युत् क्षेत्र में अधुवी परमाणु का ध्रुवण ((Polarisation of Non-polar Atom in Electric Field):
जब एक अधूवी परमाणु किसी विद्युत् क्षेत्र में रखा जाता है तो इसका नाभिक क्षेत्र की दिशा में थोड़ा विस्थापित हो जाता है और ऋणावेशित इलेक्ट्रॉनों पर विद्युत् क्षेत्र की विपरीत दिशा में बल लगता है जिससे उनका केन्द्र क्षेत्र की विपरीत दिशा में थोड़ा विस्थापित हो जाता है (चित्र 2-28)। इस कारण प्रत्यानयन बल (restoring force) उत्पन्न हो जाता है जो इलेक्ट्रॉनों को पुनः उनकी पूर्व स्थिति (previous position) में लाने का प्रयास करता है। जब यह प्रत्यानयन बल विद्युत् क्षेत्र द्वारा आवेशों पर लगने वाले खिंचाव बल के बराबर हो जाता है तो सन्तुलन की स्थिति (position of equilibrium) आ जाती है और परमाणु ध्रुवित (polarised) हो जाता है।

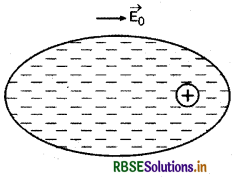
इस प्रकार परावैद्युत परमाणुओं में आवेशों के विस्थापन के कारण उनमें खिंचाव (stretch) उत्पन्न होने की घटना ध्रुवण कहलाती है।
स्पष्ट है कि परमाणुओं में खिंचाव उत्पन्न होने के कारण उनके धन एवं ऋण आवेशों के केन्द्र भिन्न हो जाने से उनमें द्विध्रुव आघूर्ण उत्पन्न हो जाता है।

परावैद्युत गुटके का ध्रुवण (Polarisation of Dielectric Slab):
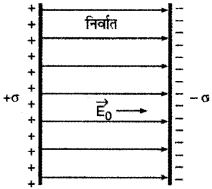
माना एक समान्तर प्लेट संधारित्र की प्लेटों को एक बैटरी द्वारा आवेशित किया जाता है। प्लेटों के मध्य निर्वात है और यदि आवेश का पृष्ठ घनत्व ±σ है तो प्लेटों के मध्य उत्पन्न विद्युत् क्षेत्र की तीव्रता (चित्र)
E₀ = $\frac{\sigma}{\varepsilon_0}$

माना अब अध्रुवी परमाणुओं वाला एक परावैद्युत गुटका (dielectric slab) प्लेटों के मध्य रख दिया जाता है (चित्र)। जैसे ही गुटका प्लेटों के मध्य रखा जाता है, इसके अणु ध्रुवित हो जाते हैं। फलस्वरूप गुटके का बायाँ फलक (face) AB - q_i एवं दायाँ फलक CD + q_i आवेश व्यक्त (represent) करने लगता है।

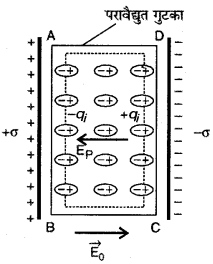
बिन्दुवत् (pointed) रेखाओं से व्यक्त परावैद्युत के अन्दर कोई नेट आवेश नहीं होता है। परावैद्युत गुटके के फलकों (faces) पर आवेश -q_i: एवं +q_i प्रेरित आवेश (induced charges) कहलाते हैं। इन प्रेरित आवेशों के कारण परावैद्युत गुटके के अन्दर एक विद्युत् क्षेत्र $\overrightarrow{\mathrm{E}_{\mathrm{P}}}$, उत्पन्न हो जाता है जिसकी दिशा CD फलक (face) से AB फलक की ओर होती है। स्पष्ट है कि $\overrightarrow{\mathrm{E}_{\mathrm{P}}}$ की दिशा $\overrightarrow{\mathrm{E}_{0}}$ की दिशा के विपरीत होती है, अतः परावैद्युत के अन्दर परिणामी विद्युत् क्षेत्र
E = E₀ - E_p ...(2)

इस प्रकार परावैद्युत गुटके को एक विद्युत् क्षेत्र में रखने पर विद्युत् क्षेत्र की तीव्रता कम हो जाती है और विद्युत् क्षेत्र E को “विद्युत् क्षेत्र का घटा हुआ मान" (reduced value of the electric field) कहते हैं।
(a) परावैद्युत नियतांक (Dielectric Constant):
“लगाये गये विद्युत् क्षेत्र की तीव्रता एवं संधारित्र की प्लेटों के मध्य परावैद्युत माध्यम (dielectric medium) रखने पर घटे हुए (reduced value) विद्युत् क्षेत्र की तीव्रता के अनुपात को ही परावैद्युत माध्यम का परावैद्युत नियतांक कहते हैं।" इसे सापेक्ष वैद्युतशीलता (relative permittivity) या विशिष्ट प्रेरित धारिता (specific inductive capacity) भी कहते हैं और इसे K से व्यक्त करते हैं। अतः
K = $\frac{\mathrm{E}_0}{\mathrm{E}}$ ....(3)
K का मान सदैव 1 से बड़ा होता है।

(b) ध्रुवण घनत्व (Polarisation Density):
“परावैद्युत गुटके को विद्युत् क्षेत्र में रखने पर उसके प्रति एकांक आयतन (per unit volume) में प्रेरित द्विध्रुव आघूर्ण को ध्रुवण घनत्व कहते हैं।" इसे P से व्यक्त करते हैं। यदि एक परमाणु का प्रेरित द्विध्रुव आघूर्ण p हो और एकांक आयतन में परमाणुओं की संख्या N हो तो ध्रुवण घनत्व
P = Np ...(4)
यदि संधारित्र की प्रत्येक प्लेट का क्षेत्रफल A हो और प्लेटों के मध्य दूरी d हो, तो
परावैद्युत गुटके का आयतन = A.d
चूंकि परावैद्युत गुटके के फलकों पर + q_i एवं -q_i आवेश प्रेरित होते हैं अतः पूरे गुटके का तुल्य (equivalent) द्विध्रुव आघूर्ण
= q_id
∴ ध्रुवण घनत्व की परिभाषा से,
P = $\frac{q_i \cdot d}{\mathrm{~A} \cdot d}=\frac{q_i}{\mathrm{~A}}$
∴ $\frac{q_i}{\mathrm{~A}}$ = σ_p = ध्रुवण आवेश पृष्ठ घनत्व
P = σ_p ....(5)

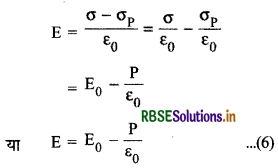
अतः संधारित्र की प्लेटों के मध्य परावैद्युत गुटका (dielectric slab) रखने पर घटे हुए विद्युत् क्षेत्र की तीव्रता

(c) वैद्युत प्रवृत्ति (Electric Susceptibility):
किसी परावैद्युत गुटके का ध्रुवण घनत्व घटे हुए विद्युत् क्षेत्र की तीव्रता के अनुक्रमानुपाती होता है और निम्न सूत्र से प्राप्त होता है
P = χε₀E ....(7)

इसमें नियतांक x को परावैद्युत गुटके की वैद्युत प्रवृत्ति कहते हैं। यह विमाहीन नियतांक (dimensionless constant) है।
समी. (7) से P का मान समीकरण (6) में रखने पर,
E = E₀ - $\frac{\chi \varepsilon_0 \mathrm{E}}{\varepsilon_0}$ = E₀ - χ_E
या E₀ = E + χE
E = E (1 + χ) ....(8)
या $\frac{\mathrm{E}_0}{\mathrm{E}}$ = (1 + χ) ..........(9)
अब समी. (3) व (8) से,
K = (1 + χ) ....(10)

(d) परमाण्विक ध्रुवणता (Atomic Polarisability):
प्रेरित आवेशों से उत्पन्न वैद्युत द्विध्रुव आघूर्ण बाह्य वैद्युत क्षेत्र के अनुक्रमानुपाती होता है और ताप पर निर्भर नहीं करता है। इसके अतिरिक्त प्रेरित वैद्युत द्विध्रुव आघूर्ण $\vec{p}$ की दिशा $\vec{E}$ के समान्तर होती है। एक एकल ध्रुवित परमाणु का प्रेरित द्विध्रुव आघूर्ण $\vec{p}$ = ε₀α $\vec{E}$ से दिया जाता है।

अनुक्रमानुपाती नियतांक α को परमाण्विक ध्रुवणता कहते हैं। α का SI मात्रक m³ है।
ज्यादातर परमाणुओं के लिए a का मान 10^-29 m³ से 10^-30 m³ की कोटि का होता है जो कि परमाणु के आयतन की कोटि होती है।

संधारित्र तथा धारिता (Capacitor and Capacitance)
धारिता की अभिधारणा (Concept of Capacity):
धारिता शब्द का अर्थ है 'धारण करने की क्षमता', अतः किसी चालक की वैद्युत धारिता का अर्थ उसके द्वारा वैद्युत आवेश धारण करने की क्षमता (ability to hold electric charge) से है। एक निश्चित सीमा के बाद यदि हम किसी बर्तन में कोई द्रव भरते हैं तो वह फैलने लगता है। इसी प्रकार जब एक निश्चित सीमा के बाद किसी चालक को आवेश दिया जाता है तो उसका विसर्जन (discharge)

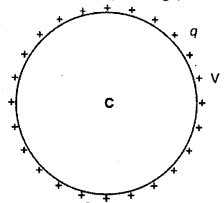
वातावरण में होने लगता है। जिस प्रकार किसी बर्तन में डाला गया द्रव उसके गुरुत्वीय तल को बढ़ाता है, ठीक उसी प्रकार किसी चालक को दिया गया आवेश उसके वैद्युत तल अर्थात् विद्युत् विभव को बढ़ाता है। किसी चालक को जितना अधिक आवेश दिया जाता है, उसका विभव भी उतना ही अधिक बढ़ता है अर्थात् “किसी चालक पर उपस्थित आवेश उसके विभव के अनुक्रमानुपाती होता है।"
q ∝ V
या q = CV ...........(1)
जहाँ C एक नियतांक है, जिसे चालक की वैद्युत धारिता कहते हैं।
इस प्रकार चालक की वैद्युत धारिता एक नियतांक होती है। इसका मान चालक की आकृति, क्षेत्रफल, चारों ओर के माध्यम तथा पास में रखे अन्य चालकों की उपस्थिति पर निर्भर करता है।
∴ C = $\frac{q}{V}$ ...(2)

अर्थात् “किसी चालक की धारिता चालक को दिये गये आवेश एवं उससे होने वाली विभव वृद्धि के अनुपात के बराबर होती है।"
पुनः C = $\frac{q}{V}$ से,
यदि V = 1 वोल्ट तो C = q
अर्थात् "किसी चालक की धारिता उस आवेश के तुल्य है जो उसके विभव में एक वोल्ट का परिवर्तन कर दे।"
मात्रक-चूँकि C = $\frac{q}{V}$

या 1 फैरड = 1 कूलॉम/वोल्ट
धारिता का मात्रक 'फैरड' एक बहुत बड़ा मात्रक है, अतः प्रचलन में इससे छोटे मात्रक 'माइक्रो फैरड' (μF) एवं 'पिको फैरड' (pF) प्रयोग में लाये जाते हैं। फैरड से इनका सम्बन्ध निम्नलिखित है
1μF = 10^-6F एवं 1p F = 10^-12F
धारिता के मात्रक फैरड' की परिभाषा निम्न प्रकार की जा सकती है
∴ C = $\frac{q}{V}$
यदि q = 1 C, V= 1 वोल्ट तो C = 1 F

"अर्थात् यदि किसी चालक को 1 कूलॉम आवेश देने पर उसके विभव में एक वोल्ट की वृद्धि हो जाती है तो चालक की धारिता 1 फैरड होगी।"
विमीय सूत्र-चूँकि
C = $\frac{q}{\mathrm{~V}}=\frac{q}{\mathrm{~W} / q}=\frac{q^2}{\mathrm{~W}}=\frac{i^2 t^2}{\mathrm{~W}}$
∴ C का विमीय सूत्र = $\frac{\left[\mathrm{A}^2 \mathrm{~T}^2\right]}{\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2}\right]}$
= [M^-1L^-2T⁴A²]

चालक की धारिता को प्रभावित करने वाले कारक (Fac tors Affecting Capacity of a Conductor)
किसी चालक की धारिता निम्नलिखित कारकों पर निर्भर करती है

• चालक के क्षेत्रफल (area) पर-चालक का क्षेत्रफल बढ़ाने पर आवेश का पृष्ठ घनत्व (σ = q/A) कम हो जाता है, अतः चालक के पृष्ठ पर विद्युत् विभव कम हो जायेगा; फलस्वरूप चालक की धारिता बढ़ जायेगी।
• आवेशित चालक के समीप अन्य चालक की उपस्थिति (presence of other conductors) पर-किसी आवेशित चालक के समीप यदि कोई अन्य आवेश रहित चालक रखा जाता है, तो आवेशित चालक का विभव कम हो जाता है; फलस्वरूप चालक की धारिता बढ़ जाती है।
• चालक के चारों ओर के माध्यम (medium around conductors) पर-चालक की सतह पर यदि वायु में विभव V है, तो K परावैद्युतांक (dielectric constant) वाला माध्यम चालक के परितः रखने पर उसका विभव V/K रह जायेगा, अतः धारिता K गुनी हो जायेगी।

विलगित गोलाकार चालक की धारिता (Capacity of an Isolated spherical Conductor)
माना R त्रिज्या का एक गोलाकार चालक K परावैद्युतांक वाले माध्यम में रखा है। जब इस गोले को + q आवेश दिया जाता है तो यह आवेश गोले के पृष्ठ पर समान रूप से वितरित हो जाता है और फलस्वरूप गोले के पृष्ठ पर विभव V उत्पन्न हो जाता है। गोले का पृष्ठ समविभव पृष्ठ (equi- potential surface) की भाँति व्यवहार करता है अतः

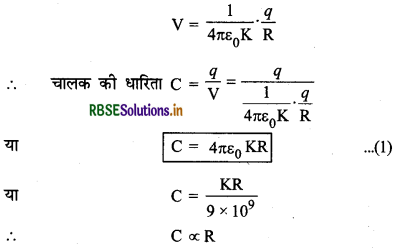
अर्थात् किसी गोलाकार चालक की धारिता उसकी त्रिज्या के अनुक्रमानुपाती होती है।

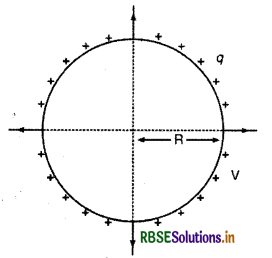
यदि चालक वायु में रखा हो, तो K = 1
C₀ = 4πε₀R ...(2)
C₀ = $\frac{\mathrm{R}}{9 \times 10^9}$

महत्वपूर्ण बिन्दु
1 बड़ा संधारित्र लघु विभव (V) पर बड़े आवेश Q के बड़े परिमाण | को परिबद्ध कर सकता है।

आकिक उदाहरण
गोलाकार चालक की धारिता पर आधारित आंकिक
उदाहरण के लिए
प्रयुक्त सूत्र
C = 4πε₀a

प्रयुक्त इकाई
C- फैरड

प्रयुक्त नियतांक
$\frac{1}{4 \pi \varepsilon_0}$ = 9 × 10⁹N-m²/C²

आवेशित चालक की ऊर्जा (Energy of a Charged Conductor)
"किसी चालक को आवेशित करने में जो कार्य किया जाता है, वही आवेशित चालक की ऊर्जा कहलाती है।"
जब किसी चालक को आवेश दिया जाता है तो प्रारम्भ में चालक को आवेश का पहला भाग देने में कोई कार्य नहीं करना पड़ता है क्योंकि उस आवेश का कोई विरोध नहीं होता है। इसके बाद जैसे-जैसे आवेश के शेष भाग दिये जाते हैं, तो चालक पर पहले से ही मौजूद आवेश दिये जाने वाले आवेशों का विरोध करते हैं, अतः बाद में दिये जाने सभी आवेशों को देने में इसी प्रतिकर्षण के विरुद्ध कार्य (work done against repulsion) करना पड़ता है। स्पष्ट है कि चालक को आवेश देने में कार्य करना पड़ता है और किसी चालक को आवेश देने में किये गये सम्पूर्ण कार्य को ही आवेशित चालक की ऊर्जा कहते हैं।
माना किसी चालक की धारिता C है और उसे + Q आवेश देने से उसका विभव V हो जाता है, तो
V = $\frac{Q}{C}$
इस स्थिति में चालक को यदि dQ आवेश दिया जाये, तो कृत कार्य
dW = V.dQ
अतः चालक को कुल q आवेश देने में किया गया कार्य अर्थात् आवेशित चालक की ऊर्जा

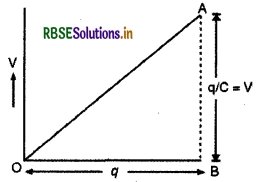
वैकल्पिक विधि-माना किसी चालक की धारिता C फैरड है तथा उसे कूलॉम आवेश देने पर उसकी प्लेटों के बीच विभवान्तर V वोल्ट स्थापित होता है, तब
V = $\frac{q}{C}$
$\frac{1}{C}$, दिये गये संधारित्र के लिए एक नियतांक है। अत: Vव के बीच ग्राफ एक सरल रेखा (straight line) होगी। संधारित्र को qआवेश देने में किया गया कार्य v - ग्राफ के नीचे 4 = 0 से q=q के बीच घिरे क्षेत्रफल के बराबर होगा। यह क्षेत्रफल एक समकोण त्रिभुज OAB है। ΔOAB का आधार OB = q है एवं ऊँचाई BA = V = q/c है। अतः संधारित्र में संचित (stored) स्थितिज ऊर्जा

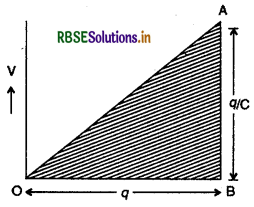
U = ΔOAB का क्षेत्रफल

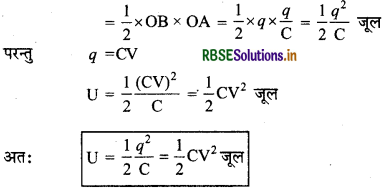
नोट:
किसी आवेशित चालक के अन्दर संचित ऊर्जा वैद्युत क्षेत्र (electric field) के रूप में रहती है। यदि आवेशित करने वाला स्रोत (बैटरी) आवेश को एक निश्चित विभव पर प्रवाहित करता है, तो आवेशित करने वाले स्रोत द्वारा कृत कार्य W = q.V होगा, जबकि आवेशित चालक में संचित ऊर्जा U = $\frac{1}{2}$q.V होगी या हम कह सकते हैं कि किसी वस्तु को आवेशित करने में 50% ऊर्जा ऊष्मा के रूप में क्षय (decay) होती है।

आकिक उदाहरण
आवेशित चालक की ऊर्जा पर आधारित आंकिक उदाहरण के लिए
प्रयुक्त सूत्र
U = $\frac{1}{2} \frac{q^2}{\mathrm{C}}=\frac{1}{2} \mathrm{CV}^2=\frac{1}{2} q \mathrm{~V}$
प्रयुक्त इकाई
U - जूल

दो सम्बद्ध आवेशित चालकों में आवेशों का पुनर्वितरण (Sharing of Charges between Two Conductors Connecting Together)
माना C₁, C₂, धारिता के दो चालक A व B हैं। इन्हें q₁ व q₂ आवेश देने पर इनके विभव V₁ व V₂, हो जाते हैं। इनकी ऊर्जाएँ क्रमशः U₁ व U₂ हैं।

जब इन चालकों को किसी पतले संयोजक तार (connecting wire) द्वारा जोड़ देते हैं, तो अधिक विभव वाले चालक से कम विभव वाले चालक पर आवेश का स्थानान्तरण (transfer) तब तक होता रहेगा जब तक दोनों के विभव समान नहीं हो जाते। इसी समान विभव (V) को उभयनिष्ठ विभव (common potential) कहते हैं। दूसरे शब्दों में, चालकों को जोड़ने पर आवेशों का पुनर्वितरण (redistribution) हो जाता है, यद्यपि आवेश की कुल मात्रा q₁ + q₂ ही रहती है।

प्रारम्भ में
q₁ = C₁V₁
एवं q₂ = C₂V₂

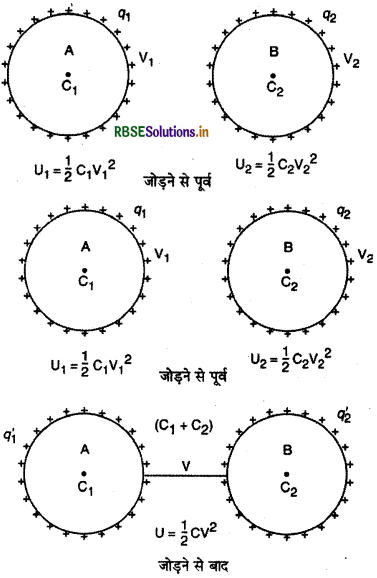
(i) उभयनिष्ठ विभव (Common Potential):
यदि संयोजक तार की धारिता नगण्य (negligible) मान लें, तो पूरे संयोजन की धारिता C = (C₁ + C₂) होगी।

(ii) पुनर्वितरण के बाद (after redistribution) प्रत्येक चालक पर आवेश-चालकों को जोड़ने के बाद आवेशों के पुनर्वितरण के पश्चात् चालक A व B पर आवेश क्रमशः
q'₁ = C₁V
और q'₂ = C₂V
$\frac{q_1^{\prime}}{q_2^{\prime}}=\frac{\mathrm{C}_1}{\mathrm{C}_2}$ ......(2)

(iii) ऊर्जा का ह्रास (Loss of Energy):
चालकों को जोड़ने के पश्चात् चालकों की वैधुत स्थितिज ऊर्जा कुछ कम हो जाती है, अतः ऊर्जा में कमी ΔU = जोड़ने के पहले कुल ऊर्जा - जोड़ने के बाद कुल ऊर्जा
जोड़ने से पहले (before contact), पहले चालक की विद्युत् स्थितिज ऊर्जा
= $\frac{1}{2}$C₁V₁²
दूसरे चालक की विद्युत् स्थितिज ऊर्जा
= $\frac{1}{2}$C₂V₂²

∴ जोड़ने से पहले दोनों चालकों की कुल स्थिति ऊर्जा
U = $\frac{1}{2}$(C₁V₁² + C₂V₂²)

दोनों चालकों को जोड़ने (after contact) पर संयुक्त धारिता (C₁ + C₂) तथा उभयनिष्ठ विभव (common potential) V हो जाता है, अतः दोनों चालकों की कुल स्थितिज ऊर्जा

(i) यदि V₁ = V₂ तो (V₁ ~ V₂) = 0
ΔU = 0

अर्थात् जब दोनों चालकों के विभव समान होते हैं, तो ऊर्जा में कोई कमी नहीं होती है क्योंकि इस स्थिति में उन्हें जोड़ने पर आवेशों का पुनर्वितरण नहीं होता है।
(ii) जब V₁ ≠ V₂ तो (V₁ ~ V₂)² > 0
∴ ΔU > 0
अर्थात् ऊर्जा में कमी होगी। ऊर्जा में यह कमी (loss of energy) चालकों के मध्य आवेश का पुनर्वितरण (sharing of charges) के कारण होती है। आवेश का प्रवाहब संयोजक तार से होकर होता है, अतः संयोजक तार के प्रतिरोध के विरुद्ध (against the resistance of connecting wire) आवेश के प्रवाहित होने में किया गया कार्य ऊष्मा में बदल जाता है। यही ऊर्जा में कमी का कारण है।

आकिक उदाहरण
दो सम्बद्ध (connected) आवेशित चालकों में आवेशों के पुनवितरण (sharing) पर आधारित आंकिक उदाहरण के लिए
प्रयुक्त सूत्र
(1) उभयनिष्ठ विभव (common potential)
V = $\frac{C_1 V_1+C_2 V_2}{C_1+C_2}$

(2) पुनर्वितरण के बाद आवेश (charge after sharing)
$\frac{q_1^{\prime}}{q_2^{\prime}}=\frac{\mathrm{C}_1}{\mathrm{C}_2}$

(3) ऊर्जा हास (energy loss)
ΔU = $\frac{\mathrm{C}_1 \mathrm{C}_2\left(\mathrm{~V}_1 \sim \mathrm{V}_2\right)^2}{2\left(\mathrm{C}_1+\mathrm{C}_2\right)}$

प्रयुक्त इकाई
विभव -वोल्ट
ऊर्जा - जूल

संधारित्र एवं उसका सिद्धान्त (Capacitor and its Principle)
“वह युक्ति (device) जिसमें चालक के आकार को बिना बदले उसकी धारिता बढ़ायी जा सकती है, संधारित्र कहलाती है।" किसी चालक को q आवेश देने पर यदि उसका विभव V हो जाता है, तो उसकी धारिता
C = $\frac{q}{V}$

स्पष्ट है कि यदि किसी प्रकार आवेश q के लिए विभव का मान V से कम हो जाये, तो चालक की धारिता C बढ़ जायेगी। इसी विचार से संधारित्र की खोज हुई। संधारित्र का सिद्धान्त (principle) निम्नलिखित तीन पदों में समझा जा सकता है
(i) माना किसी चालक A को आवेश देने पर उसका विभव V हो जाता है, तो उसकी धारिता
C = $\frac{q}{V}$ ....(1)
(ii) अब यदि चालक A के पास इसी प्रकार का दूसरा अनावेशित चालक B लाया जाये, तो प्रेरण (induction) द्वारा उसका आवेशन (charging) चित्र (b) की भाँति होगा।

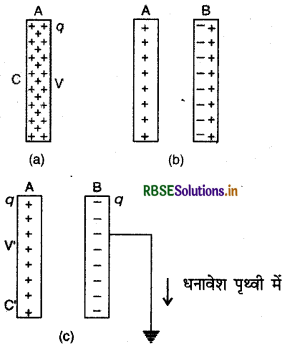
(iii) अब यदि चालक B को पृथ्वी से सम्बन्धित कर दिया जाये, तो उसका समस्त धनावेश पृथ्वी में चला जायेगा। इस नवीन स्थिति में यदि चालक A का विभव V' हो, तो A की धारिता

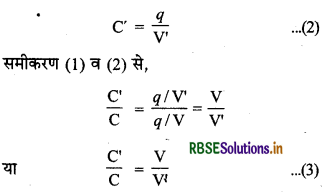
परन्तु V' = चालक A के आवेश के कारण विभव + चालक B के आवेश के कारण उत्पन्न विभव,
या V' = V - V"

इसी समीकरण से स्पष्ट है कि
V > V'
∴ समी. (3) से, C' > C
अर्थात् “जब एक आवेशित चालक के पास दूसरा अनावेशित एवं पृथ्वी से सम्बन्धित चालक लाया जाता है तो पहले चालक की धारिता बढ़ जाती है।" यही संधारित्र का सिद्धान्त है।
इस प्रकार उक्त सिद्धान्त से स्पष्ट है कि संधारित्र में दो पृथक्कित धात्वीय प्लेटें (separated metallic plates) होती हैं जिसमें एक को आवेश दिया जाता है और दूसरी को भूसम्पर्कित कर देते हैं। जब प्लेटों के मध्य किसी परावैद्युत माध्यम की जगह वायु होती है तो उसे वायु संधारित्र कहते हैं।

नोट-नियत धारिता के संधारित्र का प्रतीक =

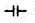
जबकि परिवर्ती धारिता के संधारित्र का प्रतीक =

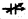
गोलाकार संधारित्र की धारिता (Capacity of Spherical Capacitor):
गोलाकार संधारित्र की रचना चित्र में दिखायी गई है। इसमें दो समकेन्द्रीय (concentric) गोलीय प्लेटें A व B होती हैं। बाहरी प्लेट B को पृथ्वी से सम्बन्धित किया जाता है और भीतरी प्लेट A को +q आवेश दिया जाता है। बाहरी गोले पर प्रेरण द्वारा उत्पन्न धनात्मक आवेश पृथ्वी में चला जाता है और केवल ऋणात्मक आवेश रह जाता है। अतः

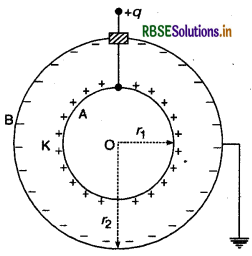
भीतरी गोले पर उत्पन्न विभव
V = V₁ + V₂
जहाँ V₁ = भीतरी गोले के + q आवेश के कारण उत्पन्न विभव
= +$\frac{1}{4 \pi \varepsilon_0 K} \frac{q}{r_1}$
और V₂ = बाहरी गोले के - q आवेश के कारण उत्पन्न विभव
= -$\frac{1}{4 \pi \varepsilon_0 K} \frac{q}{r_2}$

चूंकि बाहरी गोला पृथ्वी से सम्बन्धित है अतः इसका विभव शून्य होगा।
∴ दोनों गोलों के मध्य विभवान्तर
=V - 0 = V
∴ संधारित्र की धारिता

समीकरण (1) से स्पष्ट है कि गोलाकार संधारित्र की धारिता निम्न प्रकार बढ़ायी जा सकती है

• गोलों की त्रिज्याएँ r₁ व r₂ बढ़ाकर, लेकिन यह संधारित्र के सिद्धान्त के विरुद्ध है, अतः त्रिज्याएँ बढ़ाकर धारिता नहीं बढ़ायी जाती है।
• C ∝ K अर्थात् दोनों गोलों के मध्य अधिक परावैद्युतांक (dielectric constant) वाला परावैद्युत माध्यम (dielectric medium) रखकर धारिता बढ़ायी जा सकती है।
• C ∝ $\frac{1}{\left(r_2-r_1\right)}$ अर्थात् दोनों गोलों के मध्य दूरी घटाकर धारिता बढ़ाई जा सकती है।

बेलनाकार संधारित्र (Cylindrical Capacitor)
बेलनाकार संधारित्र की रचना संलग्न चित्र में प्रदर्शित है। इसके P तथा Q दो समाक्षीय (coaxial) खोखले (hollow) बेलनाकार चालक होते हैं जिनके बीच में कोई परावैद्युत माध्यम भरा रहता है। बाह्य बेलन Q का सम्बन्ध पृथ्वी से कर दिया जाता है।

माना आन्तरिक (internal) बेलन P, जिसकी त्रिज्या a तथा लम्बाई l है, की प्रति इकाई लम्बाई में (per unit length) आवेश वितरण λ है। प्रेरण द्वारा बाहरी बेलन Q जिसकी त्रिज्या (b) है, के आन्तरिक पृष्ठ पर प्रति एकांक लम्बाई पर आवेश – λ तथा बाह्य पृष्ठ पर आवेश + λ होगा। बेलन Q पृथ्वी से जुड़ा है अतः इसके बाह्य पृष्ठ (outer surface) पर मुक्त धनावेश पृथ्वी से आने वाले इलेक्ट्रॉनों से निरावेशित हो जाता है। इस प्रकार Q पर प्रति एकांक लम्बाई पर केवल (-λ) आवेश शेष रह जाता है।

दोनों बेलनों के बीच उनकी अक्ष से r दूरी पर स्थित बिन्दु A पर विद्युत् क्षेत्र की तीव्रता
E = $\frac{1}{2 \pi \varepsilon_0 \cdot \varepsilon_r} \frac{\lambda}{r}$ .........(1)

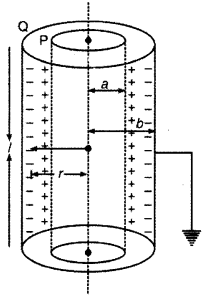
जहाँ ε_r, दोनों बेलनों के बीच भरे माध्यम (medium) की आपेक्षिक विद्युत्शीलता (relative permittivity) है।
E = $\frac{-d \mathrm{~V}}{d r}$ या dV = - Edr

अतः बेलनों P तथा Q के बीच विभवान्तर

समान्तर प्लेट संधारित्र (Parallel Plate Condensor):
इस संधारित्र में धातु की दो आयताकार प्लेटें एक ही आकार की होती हैं जो एक-दूसरे के आमने-सामने चित्र के अनुसार परस्पर समान्तर रखी होती हैं। दोनों प्लेटें विद्युत्रोधी स्टैण्डों (insulated stands) पर लगी रहती हैं और दोनों के मध्य K परावैद्युतांक वाला कोई परावैद्युत माध्यम होता है। एक प्लेट को आवेश दिया जाता है और दूसरी को भूसम्पर्कित (earthing) कर देते हैं।

माना प्रत्येक प्लेट का क्षेत्रफल A मीटर² है तथा उनके बीच की दूरी d मीटर है। माना कि प्लेट X को हम + q कूलॉम आवेश देते हैं। प्रेरण द्वारा उसके सामने वाली प्लेट Y के भीतरी तल पर -q कूलॉम आवेश तथा बाहरी तल पर + q कूलॉम आवेश उत्पन्न हो जायेगा। चूँकि प्लेट Y पृथ्वी से जुड़ी है, अतः इसके बाहरी तल का+q कूलॉम आवेश पृथ्वी में चला जायेगा। इस प्रकार प्लेटों X व Y पर बराबर तथा विपरीत आवेश होंगे। प्लेट X से चलने वाली सभी विद्युत् बल रेखाएँ प्लेट Y पर पहुँचेंगी तथा किनारों को छोड़कर बीच में विद्युत् क्षेत्र सभी जगह एकसमान (uniform) होगा।

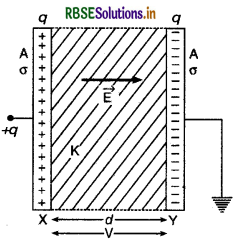
दोनों प्लेटों पर आवेश का पृष्ठ घनत्व (surface density) σ = $\frac{q}{A}$ जहाँ A प्लेटों का क्षेत्रफल है।
यदि प्लेटों के मध्य दूरी उनके विस्तार (extent) की तुलना में नगण्य (negligible) हो तो उनके मध्य विद्युत् क्षेत्र की तीव्रता
E = $\frac{\sigma}{\varepsilon_0 \mathrm{~K}}$

जहाँ ε₀ = निर्वात की विद्युत्शीलता यदि प्लेटों के मध्य विभवान्तर V एवं दूरी d हो तो

समी. (1) से स्पष्ट है कि समान्तर प्लेट संधारित्र की धारिता निम्न प्रकार बढ़ायी जा सकती है

• C ∝ A अर्थात् प्लेटों का क्षेत्रफल बढ़ाकर संधारित्र की धारिता बढ़ायी जा सकती है, लेकिन यह संधारित्र के सिद्धान्त के विरुद्ध है, अतः क्षेत्रफल बढ़ाकर संधारित्र की धारिता नहीं बढ़ायी जाती है।
• C ∝ K, अर्थात् प्लेटों के मध्य अधिक परावैद्युतांक वाला परावैद्युत माध्यम रखकर संधारित्र की धारिता बढ़ायी जा सकती है।
• C ∝ $\frac{1}{d}$ अर्थात् प्लेटों के मध्य दूरी घटाकर संधारित्र की धारिता बढ़ायी जा सकती है।

प्लेटों के मध्य आंशिक रूप से परावैद्युत माध्यम होने पर समान्तर प्लेट संधारित्र की धारिता (Capacitance of Parallel Plate Capacitor when Partially Filled with Dielectric Substance)
माना समान्तर प्लेट संधारित्र की प्लेटों के मध्य दूरी d है और उनके मध्य K परावैद्युतांक (dielectric constant) एवं t मोटाई (thickness) का परावैद्युत माध्यम आंशिक (partially) रूप से रखा है। प्लेटों के मध्य वायु वाले क्षेत्र में विद्युत् क्षेत्र की तीव्रता $\overrightarrow{\mathrm{E}}_0$ एवं परावैद्युत माध्यम में $\vec{E}$ है। दोनों प्लेटों पर आवेश का पृष्ठ घनत्व

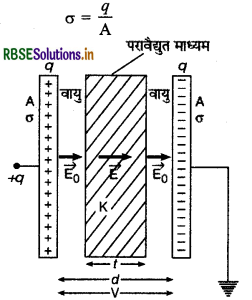
यदि प्लेटों के मध्य दूरी उनके विस्तार की तुलना (comparison to their extent) में नगण्य हो तो
E₀ = $\frac{\sigma}{\varepsilon_0}$ और E =$\frac{\sigma}{\varepsilon_0 K}$

विभवान्तर की परिभाषा से प्लेटों के मध्य विभवान्तर
V = + 1C आवेश को ऋण प्लेट से धन प्लेट तक ले जाने में किया गया कार्य
= + 1C आवेश को (d - t) दूरी वायु (air)में + t दूरी परावैद्युत माध्यम (dielectric medium) में ले जाने में कृत कार्य
= E₀ (d - t) + E.t

विशेष स्थितियाँ
(i) यदि प्लेटों के मध्य केवल वायु है तो t = 0
∴ C₀ = $\frac{\mathrm{A} \varepsilon_0}{(d-0)+0}$
या C₀ = $\frac{\mathrm{A} \varepsilon_0}{d}$

(ii) यदि प्लेटों के मध्य केवल परावैद्युत माध्यम है तो t = d

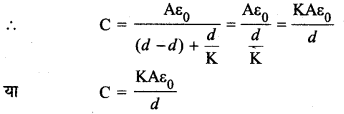
(iii) यदि प्लेटों के मध्य भिन्न-भिन्न (different) परावैद्युतांकों के n माध्यम रखे हों जिनकी मोटाइयाँ क्रमशः t₁, t₂,.........., t_n हो तो
d = (t₁ + t₂ +........+ t_n)

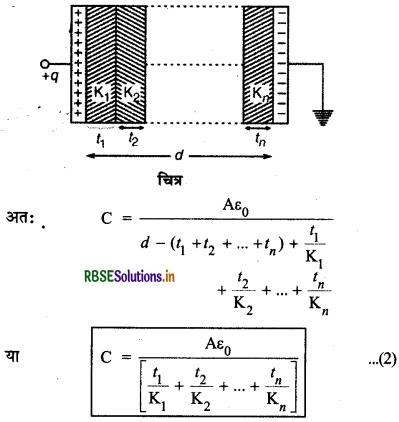
(iv) जब प्लेटों के बीच 1 मोटाई की धातु की कोई पट्टी हो तो
K = ∞
अतः समीकरण (1) से,
C = $\frac{\mathrm{A} \varepsilon_0}{(d-t)+\frac{t}{\infty}}=\frac{\mathrm{A} \varepsilon_0}{d-t}$

क्या आप जानते हैं

• यदि हम बैटरी को हटा (disconnect) लें और किसी आवेशित समान्तर पट्ट संधारित्र के प्लेटों के बीच परावैद्युत् की शीट (dielectric plate) रखें तो विद्युत् क्षेत्र का मान घट जाता है, शीट के बीच विभवान्तर का मान (V = E/d) घट जाता है, प्लेटों के मध्य संचित ऊर्जा (U) घट जाती है, आवेश का मान अपरिवर्तित रहता है।
• यदि संधारित्र की प्लेटों के मध्य चालक पदार्थ भर दिया जाए तो इसकी धारिता अनन्त हो जाएगी क्योंकि पहली प्लेट से सम्बद्ध समस्त आवेश चालकीय पदार्थ के द्वारा पृथ्वी में चला जाएगा।
• जो पदार्थ आसानी से ध्रुवित हो जाते हैं उनकी विद्युत् प्रवृत्ति (electric susceptibility) उच्च होती है।

आकिक उदाहरण
समान्तर प्लेट संधारित्र की धारिता पर आधारित आंकिक उदाहरण के लिए प्रयुक्त सूत्र

• C = $\frac{\mathrm{KA} \varepsilon_0}{d}$
• C = $\frac{\mathrm{A} \varepsilon_0}{\left(d-t+\frac{t}{\mathrm{~K}}\right)}$

प्रयुक्त इकाई
C - फैरड
प्रयुक्त नियतांक
ε₀ = 8.86 × 10^-12C²N^-1m^-2

धारिता पर परावैधुत का प्रभाव (Influence of Dielectric on Capacitance):
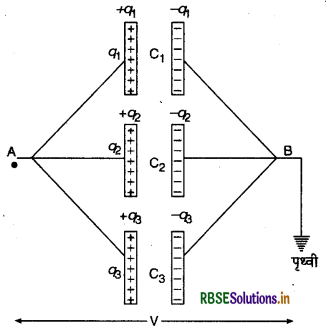
फैराडे ने संधारित्र की धारिता पर परावैद्युत माध्यम के प्रभाव का प्रायोगिक अध्ययन किया। उन्होंने चित्र में प्रदर्शित व्यवस्था के

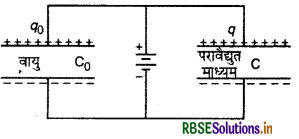
अनुसार दो समान आकार के संधारित्र एक ही बैटरी से जोड़े। एक संधारित्र की प्लेटों के मध्य उन्होंने सामान्य ताप एवं दाब (N.T.P) पर वायु ली और दूसरे की प्लेटों के मध्य कोई परावैद्युत अर्थात् कुचालक (insulator) पदार्थ लिया। दोनों संधारित्रों पर एकत्र हुए आवेशों क्रमशः qo एवं 4 की माप की तो उन्होंने पाया कि
q = Kq₀
जहाँ K दूसरे संधारित्र की प्लेटों के मध्य भरे माध्यम का परावैद्युतांक है। चूंकि दोनों संधारित्र एक ही बैटरी से जुड़े हैं, अतः दोनों की प्लेटों के मध्य विभवान्तर (V) समान होगा। अतः वायु संधारित्र की धारिता
C₀ = $\frac{q_0}{\mathrm{~V}}$
और परावैद्युत युक्त संधारित्र की धारिता

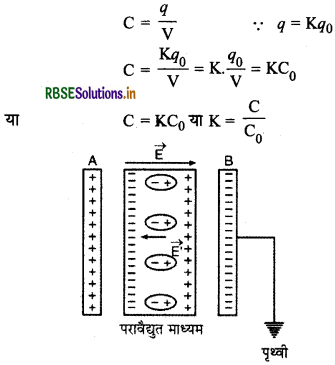
"अर्थात् परावैद्युत युक्त संधारित्र की धारिता (C) एवं वायुसंधारित्र की धारिता (C) के अनुपात को ही प्रयुक्त माध्यम (medium in use) का परावैद्युतांक कहते हैं।"
परावैद्युत माध्यम भरने से संधारित्र की धारिता बढ़ने का कारण निम्न प्रकार समझा जा सकता है

यदि किसी संधारित्र की प्लेटों को आवेशित किया जाये तो उनके मध्य विभवान्तर उत्पन्न हो जाता है। अब यदि इन आवेशित प्लेटों के मध्य कोई परावैद्युत माध्यम रख दिया जाये तो उसके अन्दर एक आंतरिक विद्युत् क्षेत्र उत्पन्न हो जाता है। इस विद्युत् क्षेत्र के कारण माध्यम के अणुओं का ध्रुवीकरण (polarisation) हो जाता है अर्थात् उनके धनात्मक एवं ऋणात्मक आवेशों के केन्द्र अलग-अलग हो जाते हैं। अणुओं का ध्रुवण चित्र में दर्शाया गया है। इस परावैद्युत माध्यम का संधारित्र की धनात्मक प्लेट की ओर वाला फलक ऋणावेशित एवं विपरीत फलक धनावेशित हो जाता है। फलस्वरूप संधारित्र की प्लेटों के मध्य परावैद्युत माध्यम के अन्दर एक विद्युत् क्षेत्र $\vec{E'}$ उत्पन्न हो जाता है जो संधारित्र की प्लेटों के कारण उत्पन्न विद्युत् क्षेत्र $\vec{E}$, के विपरीत होता है। अतः परावैद्युत के कारण प्लेटों के मध्य प्रभावी विद्युत् क्षेत्र कम (E – E') हो जाता है जिससे प्लेटों के मध्य विभवान्तर (E = -ΔV/Δx) भी कम हो जाता है फलस्वरूप संधारित्र की धारिता (C = q/V) बढ़ जाती है।

नोट-परावैद्युत सामर्थ्य (Dielectric Strength) वह अधिकतम विद्युत् क्षेत्र जिसे कोई परावैद्युत माध्यम बिना भंजन के सहन कर सकता है, उस माध्यम की 'परावैद्युत सामर्थ्य' कहलाती है। प्रत्येक परावैद्युत की एक अभिलाक्षणिक (characteristic) परावैद्युत सामर्थ्य होती है; वायु के लिए तो यह लगभग 3 × 10⁶ Vm^-1 है। किसी संधारित्र के लिए बिना किसी क्षरण (leakage) के अत्यधिक मात्रा में आवेश को संचित (stored) करने के लिए उसकी धारिता इतनी उच्च होगी कि उनके बीच विभवान्तर अथवा विद्युत् क्षेत्र उसकी भंजन सीमा (break| down limit) से अधिक न हो।

वैद्युत् विस्थापन (Electric Displacement) प्रेरित आवेश घनत्व (Induced charge density)

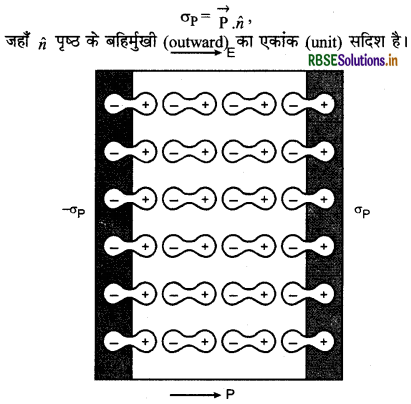
चित्र में दर्शायी गयी प्लेटों के मध्य परावैद्युत रखने पर दाहिने पृष्ठ पर प्रेरित आवेश घनत्व धनात्मक तथा बाएँ पृष्ठ पर प्रेरित आवेश घनत्व ऋणात्मक आता है।
अतः विद्युत क्षेत्र,
$\overrightarrow{\mathrm{E}} . \hat{n}=\frac{\sigma-\overrightarrow{\mathrm{P}} \cdot \hat{n}}{\varepsilon_0}$
(ε₀$\overrightarrow{\mathrm{E}}+\overrightarrow{\mathrm{P}}$)n̂ = σ .............(1)

∴ परावैद्युत् रखने पर कुल आवेश घनत्व (σ - σ_p) रह जाता है,
राशि (ε₀$\overrightarrow{\mathrm{E}}+\overrightarrow{\mathrm{P}}$) को वैद्युत् विस्थापन कहते हैं, इसे D द्वारा निरूपित करते हैं।
D = ε₀$\overrightarrow{\mathrm{E}}+\overrightarrow{\mathrm{P}}$} ............(2)

अतः समीकरण (1) से,
$\vec{D}$.n̂ = σ
$\vec{D}$ व $\vec{E}$ के परिणामों की तुलना करने पर,
$\frac{\mathrm{D}}{\mathrm{E}}=\frac{\sigma \varepsilon_0}{\sigma-\sigma_{\mathrm{P}}}$ = ε₀K
अतः D = ε₀KE ...........(4)
P =D - ε₀E ....(5)
या P = ε₀(K- 1)E ...(6)
परन्तु P = χ_eE ...(7)

जहाँ χ_e = परावैद्युत् का स्थिर अभिलक्षण है इसे परावैद्युत् माध्यम की वैद्युत् प्रवृत्ति कहते हैं।
समीकरण (6) व (7) से,
χ_e = ε₀(K - 1)

संधारित्रों का संयोजन (Combination of Capacitors)
संधारित्रों का श्रेणी संयोजन (Series Combination of Capacitors)
इसमें एक संधारित्र की दूसरी प्लेट दूसरे संधारित्र की पहली प्लेट से, दूसरे की दूसरी प्लेट तीसरे की पहली प्लेट से तथा इसी प्रकार शेष सभी को जोड़ दिया जाता है (चित्र 2-45)। संयोजन की पहली प्लेट को आवेश दिया जाता है और अंतिम प्लेट को भूसम्पर्कित कर दिया जाता है।

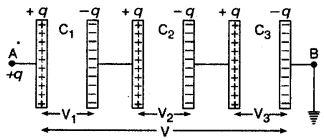
चित्र 2.45 यदि पहले संधारित्र की पहली प्लेट को + q आवेश दिया जाये तो । प्रेरण द्वारा सभी संधारित्रों की सभी प्लेटों पर एक समान आवेश q होगा, चाहे संधारित्र की धारिता कुछ भी हो। धारिताओं के मान अलग-अलग होने के कारण सभी संधारित्रों की प्लेटों के विभवान्तर अलग-अलग होंगे। यदि पूरे संयोजन का विभवान्तर V हो तो
V = V₁ + V₂ + V₃ ...(1)

चूंकि प्रत्येक संधारित्र पर आवेश समान है अतः
q = C₁V₁ = C₂V₂ = C₃V₃
V₁ = $\frac{q}{\mathrm{C}_1}$ V₂ = $\frac{q}{\mathrm{C}_2}$ V₃ = $\frac{q}{\mathrm{C}_3}$

यदि संयोजन की तुल्य धारिता C मान लें तो
V = $\frac{q}{C}$
अब समी. (1) में विभवान्तरों के मान रखने पर,
$\frac{q}{\mathrm{C}}=\frac{q}{\mathrm{C}_1}+\frac{q}{\mathrm{C}_2}+\frac{q}{\mathrm{C}_3}$
या $\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}$

इसी प्रकार जितने भी संधारित्र होंगे, सभी उक्त सूत्र की भाँति जुड़ जायेंगे। ..
∴ $\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\ldots .+\frac{1}{\mathrm{C}_n}$ .........(2)

स्मरणीय तथ्य-जिनसे आंकिक प्रश्नों को हल करने में सहायता मिलती है

• संयोजन के प्रत्येक संधारित्र पर संचित आवेश समान होगा।
• परिणामी धारिता जोड़ी जाने वाली सभी धारिताओं में न्यूनतम धारिता से भी कम होती है, अत: बड़ी धारिताओं से छोटी धारिता प्राप्त करने के लिए इस संयोजन का उपयोग किया जाता है।
• यदि समान 'धारिता C₁, के n संधारित्र श्रेणीबद्ध किये जायें तो तुल्य धारिता C = $\frac{\mathrm{C}_1}{n}$
• ∴ V = $\frac{q}{C}$ और q नियत है, अत: V ∝ $\frac{1}{C}$
  ∴ V₁ : V₂ : V₃ = $\frac{1}{\mathrm{C}_1}: \frac{1}{\mathrm{C}_2}: \frac{1}{\mathrm{C}_3}$
• पुनः चूँकि U = $\frac{1}{2} \frac{q^2}{\mathrm{C}}$ और q नियत है, अतःः
  U ∝ $\frac{1}{C}$
• ∴ U₁ : U₂ : U₃ = $\frac{1}{\mathrm{C}_1}: \frac{1}{\mathrm{C}_2}: \frac{1}{\mathrm{C}_3}$

संधारित्रों का पार्श्वक्रम संयोजन (Parallel Combination of Capacitors)
इस संयोजन में सभी संधारित्रों की पहली प्लेटें एक संधि A व दूसरी प्लेटें दूसरी संधि B के मध्य जोड़ दी जाती हैं। पहली संधि A को + q आवेश दिया जाता है और संधि B को भूसम्पर्कित कर दिया जाता है।
चूँकि सभी संधारित्र संधियों A व B के मध्य जुड़े होते हैं अतः सबका विभवान्तर (V) समान होता है। संधि A को दिया गया आवेश + q धारिताओं के अनुसार तीनों संधारित्रों में बँट जाता है।
∴ q = q₁ + q₂ + q₃ ..........(1)

चूँकि सभी संधारित्रों का विभवान्तर समान (V) है। अतः
q₁ = C₁V, q₂ = C₂V, q₃ = C₃V

यदि संयोजन की तुल्य धारिता C हो तो
q = CV

समी. (1) में आवेशों के मान रखने पर,
CV = C₁V + C₂V + C₃V
या C = C₁ + C₂ + C₃

इसी प्रकार अन्य सभी धारिताएँ जुड़ जायेंगी।
C = C₁ + C₂ +...... + C_n ...(2)

स्मरणीय तथ्य
जिनसे आंकिक प्रश्नों को हल करने में सहायता मिली है

• इस संयोजन में सभी संधारित्रों का विभवान्तर समान होता है।
• चूँकि इस संयोजन में सभी धारिताएँ यथावत् (proper place) जुड़ जाती हैं, अतः छोटी धारिताओं से बड़ी धारिता प्राप्त करने के लिए इस संयोजन (combination) का प्रयोग किया ज्ञाता है।
• यदि समान धारिता C₁, के n संधारित्र समान्तर क्रम में जोड़े जायें तो तुल्य धारिता
  C = nCT
• चूँकि q = CV और V नियत है ∴ q ∝ C
  q₁ : q₂ : q₃ = C₁ : C₂ : C₃
• चूँकि U = $\frac{1}{2}$CV² और V नियत है ∴ U ∝ C
  ∴ U₁ : U₂ : U₃ = C₁ : C₂ : C₃

आंकिक उदाहरण
संधारित्र के श्रेणी व समान्तर संयोजन पर आधारित आंकिक उदाहरण के लिए प्रयुक्त सूत्र
(1) श्रेणीक्रम $\frac{1}{\mathrm{C}_s}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}$
(2) समान्तर क्रम
C_p = C₁ + C₂ + C₃
प्रयुक्त इकाई
C-फैरड

संधारित्र में संचित ऊर्जा (Stored Energy in Capacitor) संधारित्र को आवेशित करने में किया गया कार्य ही आवेशित संधारित्र की ऊर्जा कहलाती है। यदि आवेशित संधारित्र की एक प्लेट के आवेश को दूसरी प्लेट तक ले जाया जाये तो संधारित्र अनाविष्ट (uncharged) हो जायेगा। इस क्रिया में जितनी ऊर्जा प्राप्त होगी, वही आवेशित संधारित्र की ऊर्जा होगी।

माना कि संधारित्र का प्रारम्भिक विभवान्तर V है और अनाविष्ट होने पर इसका अन्तिम विभवान्तर शून्य होगा। उक्त क्रिया में संधारित्र का औसत विभवान्तर
= $\frac{0+V}{2}=\frac{V}{2}$
यदि संधारित्र पर आवेश q हो तो इस आवेश को एक प्लेट से दूसरी प्लेट तक ले जाने में किया गया कार्य अर्थात् संधारित्र की ऊर्जा
U = W = आवेश × औसत विभवान्तर

चूँकि वायु संधारित्र (air capacitor) की धारिता और विद्युत् क्षेत्र की तीव्रता

चूँकि संधारित्र का आयतन
प्लेटों का क्षेत्रफल × उनके मध्य दूरी
= A.d
∴ $\frac{\mathrm{U}}{\mathrm{Ad}}=\frac{1}{2}$ε₀E²

एकांक आयतन में संचित ऊर्जा ।
= $\frac{1}{2}$ε₀E²
या u = $\frac{1}{2}$ε₀E² .....(2)
u को ऊर्जा घनत्व भी कहते हैं।

V - q के बीच ग्राफ

संधारित्र की प्लेटों के बीच परावैद्युत पदार्थ की पट्टी प्रवेश करायी जाने पर संधारित्र की ऊर्जा में परिवर्तन- वायु संधारित्र के लिए जिसकी धारिता Co, आवेश 40 तथा प्लेटों के बीच विभवान्तर Vo है, तब संधारित्र की ऊर्जा
U₀ =$\frac{1}{2}$C₀V₀² = $\frac{1}{2} \frac{q_0^2}{\mathrm{C}_0}$
(i) माना संधारित्र को आवेशित करने के पश्चात् उसकी प्लेटों के बीच बैटरी जुड़ी रहती है। तब प्लेटों के बीच विभवान्तर V, नियत रहता है। अब प्लेटों के बीच परावैद्युत पदार्थ रखने पर संधारित्र की धारिता C₀ से बढ़कर KC हो जाती है, अतः संधारित्र द्वारा संचित ऊर्जा
U₀ = $\frac{1}{2}$C₀V₀² = $\frac{1}{2}$(KC₀)V₀² = KU₀
अर्थात् संधारित्र की ऊर्जा बढ़ जाती है।

(ii) यदि संधारित्र को आवेशित करने के पश्चात् बैटरी हटा दी जाती है तब K परावैद्युतांक वाले पदार्थ की पट्टी प्लेटों के बीच रखी जाती है, तब संधारित्र पर संचित आवेश 40 ही बना रहता है। इस दशा में संधारित्र की ऊर्जा
U = $\frac{1}{2} \frac{q_0^2}{\mathrm{C}}=\frac{1}{2} \frac{q_0^2}{\mathrm{KC}_0}=\frac{\mathrm{U}_0}{\mathrm{~K}}$
अर्थात् संधारित्र की ऊर्जा घट जाती है।

संधारित्रों का व्हीटस्टोन सेतु संयोजन (Wheatstone's Bridge Combination of Capacitors):
इसमें 5 संधारित्र होते हैं, C₁, C₂, C₂, व C₄ धारिता के चार संधारित्र एक बन्द परिपथ ABCDA बनाते हैं जबकि C₅, धारिता का पाँचवाँ | संधारित्र एक विकर्ण भुजा BD में जुड़ा रहता है तथा V विभवान्तर का स्रोत दूसरे विकर्ण AC के सिरों के बीच जोड़ा जाता है। विभवान्तर का स्रोत लगाने पर संधारित्र आवेश का संचय करने लगते हैं। विशेष स्थिति में, जब बिन्दुओं B व D के विभव समान हो जाते हैं तो विकर्ण (diagonal) भुजा BD में आवेश का प्रवाह नहीं होता अर्थात् धारिता C₅ प्रभावहीन हो जाती है। इस दशा में व्हीटस्टोन सेतु सन्तुलित अवस्था में कहा जाता है। तुल्य परिपथ चित्र (b) में प्रदर्शित हैं।

इस स्थिति में C₁ व C₂, श्रेणीक्रम में हैं तथा प्रत्येक पर आवेश q₁ है, C₃, व C₄ भी श्रेणीक्रम में हैं, इनमें से प्रत्येक पर आवेश q₂ है।


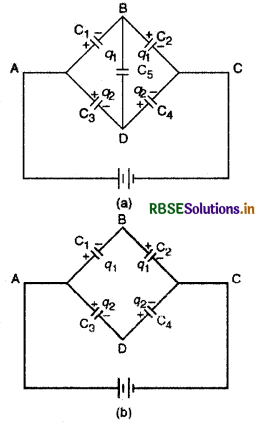
यही व्हीटस्टोन सेतु के सन्तुलन का प्रतिबन्ध है।

आकिक उदाहरण
संधारित्रों के व्हीटस्टोन सेतु पर आधारित आंकिक प्रश्नों के लिए प्रयुक्त सूत्र
$\frac{C_1}{C_2}=\frac{C_3}{C_4}$
प्रयुक्त इकाई- C-फैरड

→ स्थिर-वैद्युत स्थितिज ऊर्जा में परिवर्तन-बिन्दुओं B व A के मध्य वैद्युत स्थितिज ऊर्जा में परिवर्तन उस न्यूनतम कार्य के तुल्य है जो बाह्य बल द्वारा धन परीक्षण आवेश को बिना त्वरण के A से B तक ले जाने में किया जाता है।
ΔU = U_B - U_A = W_AB

→ विद्युत् विभव-किसी बिन्दु पर विद्युत विभव उस कार्य के बराबर है जो एकांक धनावेश को अनन्त से उस बिन्दु तक लाने में करना पड़ता है।
V = $\frac{\mathrm{W}}{q_0}$

→ विभवान्तर-किन्हीं दो बिन्दुओं के मध्य विभवान्तर उस कार्य के तुल्य है जो एकांक धनावेश को निम्न विभव के बिन्दु से उच्च विभव के बिन्दु तक ले जाने में करना पड़ता है।
V_B - V_A = W_AB

→ बिन्दु आवेश एवं आवेश समूह के कारण विद्युत् विभव--बिन्दु आवेश के कारण है दूरी पर विद्युत् विभव
V = $\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}$
आवेश समूह के कारण किसी बिन्दु पर उत्पन्न विभव
V = $\frac{1}{4 \pi \varepsilon_0} \sum_{i=1}^n \frac{q_i}{r_i}$

→ वैद्युत द्विध्रुव के कारण किसी बिन्दु पर उत्पन्न विभव-द्विध्रुव की अक्ष से θ दिशा में r दूरी पर विद्युत् विभव
V = $\frac{1}{4 \pi \varepsilon_0} \frac{p \cos \theta}{\left(r^2-l^2 \cos ^2 \theta\right)}$
जहाँ 2l वैद्युत द्विध्रुव की प्रभावी लम्बाई है।
दीर्घ दूरियों के लिए V = $\frac{1}{4 \pi \varepsilon_0} \frac{p}{r^2}$

→ विभव प्रवणता एवं विद्युत् क्षेत्र की तीव्रता में सम्बन्ध-किसी बिन्दु पर विद्युत् क्षेत्र की तीव्रता उस बिन्दु पर ऋणात्मक विभव प्रवणता के बराबर होती है।
∴ E = -$\frac{d \mathrm{~V}}{d r}$

→ समविभव पृष्ठ-ऐसा पृष्ठ जिसके प्रत्येक बिन्दु पर विद्युत् विभव समान होता है, समविभव पृष्ठ कहलाता है।

→ ध्रुवी एवं अधुवी परावैद्युत-"ऐसा परावैद्युत जिसके परमाणुओं अथवा अणुओं में धनात्मक एवं ऋणात्मक आवेशों के गुरुत्व केन्द्र समान होते हैं, अध्रुवी परावैद्युत कहलाता है।" "ऐसे परावैद्युत जिसके परमाणुओं अथवा अणुओं में धन एवं ऋण आवेशों के गुरुत्व केन्द्र भिन्न होते हैं, ध्रुवी परावैद्युत कहलाते हैं।"

→ परावैद्युत नियतांक-वायु संधारित्र की प्लेटों के मध्य लगाये गये विद्युत् क्षेत्र की तीव्रता एवं संधारित्र की प्लेटों के मध्य पावैद्युत माध्यम रखने पर घटे हुए विद्युत् क्षेत्र की तीव्रता के अनुपात को ही परावैद्युत माध्यम का परावैद्युत नियतांक कहते हैं।
$\frac{E_0}{E}$ = K

→ वैद्युत धारिता-किसी चालक की धारिता उस आवेश के तुल्य है जो उसके विभव में एक वोल्ट का परिवर्तन कर दे।
C = $\frac{q}{V}$
इसका मात्रक फैरड है।

→ गोलाकार चालक की धारिता-यदि गोलाकार चालक की त्रिज्या R हो और चालक K परावैधुतांक वाले माध्यम में रखा हो तो उसकी धारिता
C = 4πε₀K.R

→ संधारित्र-संधारित्र वह युक्ति है जिसमें चालक के आकार को बिना बदले उसकी धारिता बढ़ाई जा सकती है।

→ गोलाकार संधारित्र की धारिता-यदि बाहरी गोले की त्रिज्या व भीतरी गोले की त्रिज्या r हो और दोनों के मध्य मौजूद माध्यम का परावैद्युतांक K हो तो
C = $\frac{4 \pi \varepsilon_0 \mathrm{~K} \cdot r_1 r_2}{\left(r_2-r_1\right)}$

→ बेलनाकार संधारित्र की धारिता-बाह्य पृष्ठ की त्रिज्या (b), आन्तरिक पृष्ठ की त्रिज्या (a) तथा बेलन की लम्बाई (l) हो तथा संधारित्र की बाहरी प्लेट को भूसम्पर्कित (earthed) किया जाये तो
C = $\frac{2 \pi \varepsilon_0 \varepsilon_r l}{\log _e[b / a]}$या C =$\frac{2 \pi \varepsilon_0 \varepsilon_r l}{2 \cdot 303 \log _{10}[b / a]}$

→ समान्तर प्लेट संधारित्र की धारिता
(i) यदि प्लेटों के अन्दर K परावैद्युतांक वाला माध्यम है तो
C = $\frac{\mathrm{KA} \varepsilon_0}{d}$
(ii) वायु संधारित्र की धारिता
C₀ = $\frac{\mathrm{A} \varepsilon_0}{d}$
(ii) प्लेटों के मध्य यदि t मोटाई एवं K परावैद्युतांक का माध्यम आंशिक रूप से रखा हो तो
C = $\frac{\mathrm{A} \varepsilon_0}{(d-t)+\frac{t}{\mathrm{~K}}}$

→ संधारित्रों का श्रेणी संयोजन-संधारित्रों के श्रेणी संयोजन की तुल्य धारिता यदि C हो तो
$\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}+\ldots . .+\frac{1}{\mathrm{C}_n}$

→ संधारित्रों का समान्तर संयोजन-समान्तर संयोजन की तुल्य धारिता
C = C₁ + C₂ +......+ C_n

→ विद्युत् विभव V = $\frac{\mathrm{W}}{q_0}$

→ किसी बिन्दु पर बिन्दु आवेश के कारण विद्युत् विभव
V = $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r}$

→ विद्युत् आवेश समूह के कारण किसी बिन्दु पर विद्युत् विभव
V = $\frac{1}{4 \pi \varepsilon_0} \cdot \sum_{i=1}^n \frac{q_i}{r_i}$

→ वैद्युत् द्विध्रुव के कारण किसी बिन्दु पर विद्युत् विभव
V = $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{p \cos \theta}{\left(r^2-l^2 \cos ^2 \theta\right)}$

→ वैद्युत् द्विध्रुव की अक्षीय रेखा पर स्थित बिन्दु पर विभव
V = $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{p}{r^2}$ वोल्ट

→ वैद्युत् द्विध्रुव की निरक्षीय स्थिति पर विभव
V = 0

→ विभव प्रवणता, E = -$\frac{d \mathrm{~V}}{d r}$

→ विद्युत् क्षेत्र व विद्युत् विभव में सम्बन्ध
V$(\vec{r})=-\int_{\infty}^r \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d r}$

→ दो आवेशों के निकाय की वैद्युत् स्थितिज ऊर्जा
U = $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q_1 q_2}{r}$

→ आवेश समूह की विद्युत् स्थितिज ऊर्जा

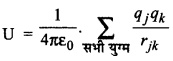
→ संधारित्र की प्लेटों के मध्य परावैद्युत् गुटका रखने पर घटे हुए विद्युत् क्षेत्र की तीव्रता
E = E₀ - $\frac{\mathrm{P}}{\varepsilon_0}$

→ वैद्युत् प्रवृत्ति तथा परावैद्युत् नियतांक में सम्बन्ध
K = 1 + χ

→ धारिता, C = $\frac{Q}{V}$

→ विलगित गोलाकार चालक की धारिता
C = 4πε₀R

→ आवेशित चालक की ऊर्जा
U = $\frac{1}{2}$CV² = $\frac{1}{2}$qV = $\frac{1}{2}\frac{q^2}{\mathrm{C}}$

→ दो सम्बद्ध आवेशित चालकों में आवेश का पुनर्वितरण

• उभयनिष्ठविभव V = $\frac{\mathrm{C}_1 \mathrm{~V}_1+\mathrm{C}_2 \mathrm{~V}_2}{\mathrm{C}_1+\mathrm{C}_2}$
• ऊर्जा का ह्यस ΔU = $\frac{C_1 C_2}{2\left(C_1+C_2\right)}$(V₁ ~ V₂)

→ गोलाकार संधारित्र की धारिता
C = $\frac{4 \pi \varepsilon_0 r_1 r_2}{\left(r_2-r_1\right)}$

→ बेलनाकार संधारित्र की धारिता
C = $\frac{2 \pi \varepsilon_0 \varepsilon_r l}{2.303 \times \log _{10}(b / a)}$

→ प्लेटों के मध्य आंशिक रूप से परावैद्युत् माध्यम होने पर समान्तर प्लेट संधारित्र की धारिता
C = $\frac{\mathrm{A} \varepsilon_0}{\left(d-t+\frac{t}{\mathrm{~K}}\right)}$

→ परावैद्युत् का धारिता पर प्रभाव
K = $\frac{\mathrm{C}}{\mathrm{C}_0}$

→ संधारित्रों का श्रेणी संयोजन
$\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\ldots+\frac{1}{\mathrm{C}_n}$

→ संधारित्रों का समान्तर संयोजन
C = C₁ + C₂ + ....+ C_n

→ संधारित्र के प्रति एकांक आयतन में संचित ऊर्जा
u = $\frac{1}{2}$ε₀E²

→ संधारित्र के व्हीटस्टोन सेतु सन्तुलन की शर्त
$\frac{C_1}{C_2}=\frac{C_3}{C_4}$

→ ध्रुवण (Polarisation):
परावैद्युत् परमाणुओं में आवेशों के विस्थापन के कारण उनमें खिंचाव उत्पन्न होने की घटना ध्रुवण कहलाती है।

→ प्रेरित आवेश (Induced charges):
परावैद्युत् गुटके के फलकों पर आया आवेश।

→ संरक्षी (Conservative):
पथ पर निर्भर न होकर केवल बिन्दुओं की स्थिति पर।

→ विविक्त (Discrete):
पृथक्

→ प्रवणता (Gradient):
दूरी के साथ तत्व की मात्रा में परिवर्तन ।

→ वायु संधारित्र (Air capacitor):
समान्तर प्लेट संधारित्र की प्लेटों के मध्य वायु होना।

→ परावैद्युतांक (Dielectric constant):
आरोपित विद्युत् क्षेत्र की तीव्रता तथा संधारित्र की प्लेटों के मध्य परावैद्युत् रखने पर विद्युत् क्षेत्र की तीव्रता के मान के अनुपात को परावैधुतांक कहते हैं।

→ वैद्युत् विभव (Electricpotential):
एक भौतिक राशि है जो वस्तुओं के मध्य आवेश के प्रवाह को नियन्त्रित करती है।

→ धारिता (Capacity):
किसी चालक के द्वारा आवेशों की संचय क्षमता।

→ परावैद्युत पदार्थ (Dielectric):
वे अचालक होते हैं जो आसानी से ध्रुवित हो सकते हैं।