RBSE Class 12 Physics Notes Chapter 12 परमाणु

These comprehensive RBSE Class 12 Physics Notes Chapter 12 परमाणु will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 12 Notes परमाणु

→ थॉमसन का परमाणु मॉडल-इसके अनुसार प्रत्येक परमाणु 10^-10 m त्रिज्या का एक धनावेशित ठोस गोला होता है जिसमें परमाणु का सम्पूर्ण धनावेश एवं द्रव्यमान समान रूप से वितरित रहता है। ऋणावेशित इलेक्ट्रॉन इस गोले में जगह-जगह ठीक उसी प्रकार धंसे रहते हैं जिस प्रकार तरबूज में उसके बीज।

→ परमाणु का रदरफोर्ड मॉडल

• परमाणु का समस्त धनावेश एवं द्रव्यमान एक बहुत छोटी जगह (10^-14 m से 10^-15 m व्यास) पर केन्द्रित रहता है जिसे नाभिक कहते हैं।
• नाभिक के परितः इलेक्ट्रॉन वृत्तीय कक्षाओं में चक्कर लगाते हैं।
• इलेक्ट्रॉनों का कुल ऋणावेश नाभिक के धनावेश के बराबर होता है।

→ कमियाँ

• यह परमाणु के स्थायित्व की व्याख्या नहीं कर सका।
• यह परमाणुओं के रेखीय स्पेक्ट्रम की व्याख्या नहीं कर सका।

 

→ बोर का परमाणु मॉडल

• इलेक्ट्रॉन नाभिक के परितः कुछ विशिष्ट कक्षाओं में ही घूम सकते हैं जिन्हें विकिरण रहित कक्षाएँ कहते
• स्थायी कक्षाओं के लिए कोणीय संवेग का मान $\frac{h}{2 \pi}$ का पूर्ण गुणज होता है।
• बाहर से ऊर्जा देने पर परमाणु उत्तेजित होता है और 10^-8 सेकण्ड के बाद पुनः अपनी मूल अवस्था को वापस लौटता है तथा शोषित ऊर्जा का फोटॉनों के रूप में उत्सर्जन करता है।

→ गणितीय सूत्र
(i) नाभिक का आकार-नाभिक से निकटतम पहुँच की a-कण की दूरी
r₀ = $\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{Z} e^2}{\mathrm{~K}}$

(ii) बोर मॉडल में वीं कक्षा की ऊर्जा
E_n = $-\frac{\mathrm{Z}^2 \mathrm{R} c h}{n^2}$

हाइड्रोजन परमाणु के लिए, Z = 1 .
E_n = $-\frac{\mathrm{R} c h}{n^2}$

(iii) θ प्रकीर्णन कोण पर प्रकीर्णित a-कणों की संख्या
N ∝ $\frac{1}{\sin ^4\left(\frac{\theta}{2}\right)}$
$\frac{N_1}{N_2}=\left[\frac{\sin \theta_2 / 2}{\sin \theta_1 / 2}\right]^4$

(iv) संघट्ट प्राचल-a-कण के वेग सदिश की नाभिक से लम्बवत् दूरी, जबकि वह नाभिक से बहुत दूर हो, संघट्ट प्राचल कहलाती है। इसका सूत्र -
b = $\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Z} e^2 \cot \left(\frac{\phi}{2}\right)}{\mathrm{K}}$
जहाँ Φ प्रकीर्णन कोण है।

(v) बोर की त्रिज्या-
r_n = $\frac{\varepsilon_0 h^2}{\pi m Z e^2}$.n²
हाइड्रोजन परमाणु के लिए, Z = 1 और पहली कक्षा के लिए,
n = 1.
r₁ = $\frac{\varepsilon_0 h^2}{\pi m e^2}$
अतः r_n = n².r₁
= n² × 0.529 Å

(vi) स्थायी कक्षा में इलेक्ट्रॉन की चाल
v_n = $\frac{Z e^2}{2 \varepsilon_0 h n}$
एवं v_n = $\frac{Z}{n}$ × 2.18 × 10⁶ms^-1

(vii) स्थायी कक्षा में इलेक्ट्रॉन की ऊर्जा
E_n = $-\frac{\mathrm{Z}^2}{n^2}\left[\frac{e^4 m}{8 \varepsilon_0^2 h^2}\right]$
या E_n = $-\frac{\mathrm{Z}^2}{n^2}$ × 13.6 eV
हाइड्रोजन परमाणु के लिए, Z = 1
E_n = $-\frac{136}{n^2}$ev

→ परमाणुओं के विविक्त ऊर्जा स्तर-परमाणुओं के ऊर्जा स्तर विविक्त एवं सुनिश्चित होते हैं। विभिन्न तत्वों के परमाणुओं के ऊर्जा स्तर भिन्न-भिन्न होते हैं अतः उनके स्पेक्ट्रम भी भिन्न-भिन्न होते हैं।

→ कुछ परिभाषाएँ

• न्यूनतम ऊर्जा वाली अवस्था को परमाणु की मूल अवस्था कहते हैं।।
• बाहर से दी गई ऊर्जा अवशोषित करके परमाणु जिन उच्च ऊर्जा अवस्थाओं में जाता है, उन्हें उत्तेजित अवस्थाएँ कहते हैं।
• परमाणु को उत्तेजित करने के लिए आवश्यक ऊर्जा को उत्तेजन ऊर्जा कहते हैं और इसे इलेक्ट्रॉन वोल्ट में व्यक्त करने पर इसके आंकिक मान को उत्तेजन विभव कहते हैं।
• परमाणु को आयनित करने के लिए आवश्यक ऊर्जा को आयनन ऊर्जा एवं ev में व्यक्त इसके आंकिक मान को आयनन विभव कहते हैं।

→ हाइड्रोजन स्पेक्ट्रम के लिए बोर का सूत्र- हाइड्रोजन स्पेक्ट्रम में मिलने वाली सभी श्रेणियों के लिए तरंगदैर्ध्य का मान बोर के सूत्र से प्राप्त किया जा सकता है
$\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]$

→ हाइड्रोजन स्पेक्ट्रम में श्रेणियाँ-हाइड्रोजन स्पेक्ट्रम में निम्नलिखित पाँच श्रेणियाँ मिलती हैं
(i) लाइमन श्रेणी :
$\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{1^2}-\frac{1}{n_2^2}\right]$
जहाँ n₂ = 2, 3, 4, 5, ...

(ii) बामर श्रेणी :
$\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{n_2^2}\right]$
जहाँ n₂ = 3, 4, 5, 6, ...

(iii) पाशजन श्रेणी
$\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{3^2}-\frac{1}{n_2^2}\right]$
जहाँ n₂ = 4, 5, 6, 7, .......

(iv) ब्रेकेट श्रेणी
$\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{4^2}-\frac{1}{n_2^2}\right]$
जहाँ n₂ = 5, 6, 7, 8,...

(v) फुण्ड श्रेणी :
$\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{5^2}-\frac{1}{n_2^2}\right]$
जहाँ n₂ = 6, 7, 8, 9, ...

→ स्पेक्ट्रम के प्रकार-स्पेक्ट्रम मूलतः दो प्रकार के होते हैं

• उत्सर्जन स्पेक्ट्रम-जब स्रोत से उत्सर्जित प्रकाश को सीधे प्रिज्म पर डालकर उसका स्पेक्ट्रम प्राप्त करते हैं तो इस स्पेक्ट्रम को उत्सर्जन स्पेक्ट्रम कहते हैं।
• अवशोषण स्पेक्ट्रम-जब प्रकाश को किसी अवशोषक माध्यम से गुजारकर स्पेक्ट्रम प्राप्त करते हैं तो प्राप्त स्पेक्ट्रम अवशोषण स्पेक्ट्रम कहलाता है।
  उक्त दोनों प्रकार के स्पेक्ट्रम तीन-तीन प्रकार के होते हैं-अविरत स्पेक्ट्रम, रेखीय स्पेक्ट्रम, बैण्ड स्पेक्ट्रम।

→ निकटतम पहुँच की दूरी
r₀ = $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{2 Z e^2}{\mathbf{K}}$

→ संघट्ट प्राचल b = $\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Z e^2(\cot (\theta / 2))}{\mathrm{K}}$

→ इलेक्ट्रॉन का कोणीय संवेग
mvr = $\frac{n h}{2 \pi}$

→ बोर की त्रिज्या
r_n = $\frac{\varepsilon_0 h^2}{\pi m Z e^2}$.n²
r_n = n²r₁ जहाँ r₁ = $\frac{\varepsilon_0 h^2}{\pi m e^2}$

सामान्य रूप से,
r_n = $\frac{n^2}{Z}$ × 0.528 Å

→ स्थायी कक्षा में इलेक्ट्रॉन की चाल
V_n = $\frac{n h}{2 \pi m r_n}=\frac{Z e^2}{2 \varepsilon_0 h n}$
सामान्य रूप से,
V_n = $\frac{\mathrm{Z}}{n}$ × 2.18 × 10⁶ms^-1
या V_n = $\frac{1}{137} \cdot \frac{c}{n}$ (हाइड्रोजन परमाणु के लिए)

→ इलेक्ट्रॉन की स्थितिज ऊर्जा
U = $-\frac{1}{4 \pi \varepsilon_0}\frac{\mathrm{Z} e^2}{r_n}$

→ इलेक्ट्रॉन की गतिज ऊर्जा
K = $\frac{1}{8 \pi \varepsilon_0} \frac{\mathrm{Z} e^2}{r_n}$

→ इलेक्ट्रॉन की कुल ऊर्जा :
E_n = $-\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Z e^2}{2 r_n}$
या E_n = $-\frac{136}{n^2}$ev (हाइड्रोजन परमाणु के लिए)

→ अवशोषित अथवा उत्सर्जित विकिरण की तरंगदैर्ध्य .

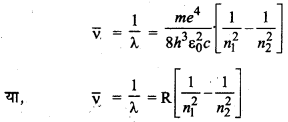
जहाँ v̄ तरंग संख्या एवं R-रिडबर्ग नियतांक है।

→ उत्सर्जित फोटॉन का तरंगदैर्ध्य
λ = $\frac{h c}{\Delta \mathrm{E}}$
या λ = $\frac{1.24 \times 10^4}{\Delta \mathrm{E}(\mathrm{eV})}$Å

→ इलेक्ट्रॉन के संक्रमण से nवीं कक्षा से निम्न कक्षा में जाने पर कुल स्पेक्ट्रम रेखाओं की संख्या
N = $\frac{n(n-1)}{2}$

→ परमाणु की विभिन्न ऊर्जा स्तरों की ऊर्जाएँ
E_n = $\frac{-\mathrm{R} h c}{n^2}$,n = 1, 2, 3, ....

→ हाइड्रोजन स्पेक्ट्रम की विभिन्न श्रेणियों के लिए रिडबर्ग का सूत्र
$\frac{1}{\lambda}=\mathrm{R}=\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]$
लाईमन श्रेणी के लिए n₁ = 1, n₂ = 2, 3, 4, ......
बामर श्रेणी के लिए n₁ = 2, n₂ = 3, 4, 5, ......
पाश्चन श्रेणी के लिए n₁ = 3, n₂ = 4, 5, 6, ......
ब्रैकेट श्रेणी के लिए n₁ = 4, n₂ = 5, 6, 7, ......
फुण्ड श्रेणी के लिए n₁ = 5, n₂ = 6, 7, 8, ......

→ मूल अवस्था (Ground State):
जब इलेक्ट्रॉन प्रथम कक्षा (n = 1) में होता है तो इस कक्षा से संबंधित इलेक्ट्रॉन की ऊर्जा न्यूनतम होगी तथा इलेक्ट्रॉन मूल अवस्था में होता है।

→ उत्तेजित अवस्था (Excited state):
ऊर्जा अवशोषित करने के पश्चात् इलेक्ट्रॉन प्रथम कक्षा (n = 1) से उच्च कक्षाओं (n = 2, 3, .....) में जाता है। जब इलेक्ट्रॉन उच्च कक्षा में जाता है तो परमाणु उत्तेजित अवस्था में कहलाता है।

→ मेसर (Maser):
लेसर द्वारा प्रकाश का अतितीव्र, एकवर्णी कलासम्बद्ध तथा संकीर्ण पुंज प्राप्त किया जाता है। मेसर द्वारा ऐसा ही पुंज प्रकाश अदृश्य सूक्ष्म तरंगों (microwaves) का प्राप्त होता है। इसलिए लेसर को प्रकाशीय मेसर (optical maser) भी कहते हैं।

→ ऊर्जित परमाणु (Energised atom):
सामान्यतः प्रत्येक परमाणु अपनी निम्नतम ऊर्जा अवस्था में रहता है जब उसे बाहर से किसी प्रकार उपयुक्त ऊर्जा मिल जाती है तो वह निम्नतम ऊर्जा-स्तर को छोड़कर किसी उच्च ऊर्जा स्तर वाली अवस्था में चला जाता है तब परमाणु ऊर्जित कहा जाता है।

→ संक्रमण (Transition):
परमाणु का एक ऊर्जा अवस्था से दूसरी ऊर्जा-अवस्था में जाना संक्रमण (transition) कहलाता है तथा इसे ऊर्जा स्तर आरेख में उन दो अवस्थाओं के बीच तीर खींचकर दिखाया जाता है।

→ निम्नतम तरंगदैर्ध्य संस्तब्ध (minimum wavelength cut off):
निम्नतम तरंगदैर्ध्य संस्तब्ध से यह प्रदर्शित होता है कि कुछ इलेक्ट्रॉनों की 'सम्पूर्ण' गतिज ऊर्जा लक्ष्य के किसी परमाणु से 'एक ही बार' टकराने से x-किरण विकिरण में बदल जाती है।

→ हाइड्रोजन सम परमाणु (Hydrogen equivalent atom):
वे परमाणु हैं जिनमें धनआवेश +Ze युक्त नाभिक और एकल इलेक्ट्रॉन होता है जहाँ z प्रोटॉन संख्या है। हाइड्रोजन परमाणु, एकधन आयनित हीलियम, द्वित-आयनित लीथियम इत्यादि हाइड्रोजन सम परमाणुओं के उदाहरण हैं।