RBSE Class 12 Physics Notes Chapter 10 तरंग-प्रकाशिकी

These comprehensive RBSE Class 12 Physics Notes Chapter 10 तरंग-प्रकाशिकी will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 10 Notes तरंग-प्रकाशिकी

→ तरंगाग्र-वह तल जिसमें मौजूद प्रत्येक कण समान कला में दोलन करता है अर्थात् समान कला में दोलन करने वाले कणों की निधि तरंगाग्र कहलाती है। तरंगाग्र निम्न तीन प्रकार के होते हैं

• गोलाकार तरंगाग्र,
• बेलनाकार तरंगाग्र,
• समतल तरंगाग्र।

→ हाइगेन्स का तरंग सिद्धान्त

• स्रोत से ऊर्जा का स्थानान्तरण तरंगों के रूप में होता है। समान कला में दोलन करने वाले कणों की निधि तरंगाग्र कहलाती है।
• तरंगाग्र पर खींची गई लम्बवत् रेखा तरंग संचरण की दिशा व्यक्त करती है। इसी को किरण कहते हैं।
• तरंगाग्र पर स्थित प्रत्येक कण द्वितीयक तरंगिकाओं के स्रोत की भाँति कार्य करता है और ये द्वितीयक तरंगिकाएँ तरंग की चाल से ही

→ प्रकाश में डॉप्लर प्रभाव

• जिस प्रकार ध्वनि तरंगों में डॉप्लर प्रभाव परिलक्षित होता है उसी प्रकार प्रकाश-तरंगों में भी डॉप्लर प्रभाव देखा जाता है।
• प्रकाश में डॉप्लर प्रभाव केवल स्रोत एवं प्रेक्षक के मध्य सापेक्ष वेग पर निर्भर करता है, न कि इस बात पर कि दोनों में कौन गतिशील है।
• डॉप्लर विस्थापन
  Δλ = \(\frac{v}{c}\)λ या v = \(\frac{\Delta \lambda}{\lambda}\)c.

 

→ अध्यारोपण का सिद्धान्त
(i) जब दो तरंगें अध्यारोपण करती हैं तो परिणामी तरंग का विस्थापन दोनों तरंगों के अलग-अलग विस्थापनों के सदिश योग के बराबर होता है अर्थात्
\(\vec{y}=\overrightarrow{y_1}+\overrightarrow{y_2}\)

(ii) अध्यारोपण में निम्नलिखित तीन स्थितियाँ सम्भव हैं
(a) जब समान आवृत्ति की दो तरंगें दो कला सम्बद्ध स्रोतों से एक ही दिशा में चलकर अध्यारोपण करती हैं तो 'व्यतिकरण' की घटना घटित होती है।
(b) जब लगभग समान आवृत्ति की दो तरंगें एक ही दिशा में चलकर अध्यारोपण करती हैं तो 'विस्पन्द' बनते हैं।
(c) जब समान आवृत्ति एवं समान आयाम की दो तरंगें विपरीत दिशाओं से आकर अध्यारोपण करती हैं तो 'अप्रगामी तरंगें' बनती हैं।

→ कला सम्बद्ध स्त्रोत-ऐसे स्रोत जिनके मध्य कलान्तर समय के साथ नियत रहता है, कला सम्बद्ध स्रोत कहलाते हैं।

→ व्यतिकरण
(i) जब समान आवृत्ति की दो तरंगें दो कला सम्बद्ध स्रोतों से एक ही दिशा में चलकर अध्यारोपण करती हैं तो अध्यारोपण के क्षेत्र में परिणामी तीव्रता में उतार-चढ़ाव उत्पन्न होने की घटना 'व्यतिकरण' कहलाती है।

(ii) जिन स्थानों पर परिणामी तीव्रता दोनों तरंगों की तीव्रताओं के योग से अधिक होती है, वहाँ पर होने वाले व्यतिकरण को 'रचनात्मक व्यतिकरण' कहते हैं और जिन स्थानों पर परिणामी तीव्रता दोनों तरंगों की तीव्रताओं के योग से कम होती है, वहाँ पर होने वाले व्यतिकरण को "विनाशी व्यतिकरण' कहते हैं।

(iii) परिणामी तरंग का आयाम
A = \(\sqrt{a^2+b^2+2 a b \cos \phi}\) और परिणामी तीव्रता
I = I₁ + I₂ + 2\(\sqrt{\mathrm{I}_1 \mathrm{I}_2}\) cos Φ
जहाँ Φ के दोनों तरंगों के मध्य कलान्तर है।

(iv) रचनात्मक व्यतिकरण के लिए,
कलान्तर Φ = 0, 2π, 4π, ...., 2nπ
या पथान्तर Δx =0, λ, 2λ, ....., nλ
जहाँ n = 0, 1, 2, 3, ......
तो I_max = I₁ + I₂ + 2\(\sqrt{\mathrm{I}_1 \mathrm{I}_2}\)

(v) विनाशी व्यतिकरण के लिए,
कलान्तर Φ = 1, 3π, S5π, ....., (2n - 1)π
या पथान्तर Δx = 2/2, 3/2, 52/2, ...., (2n - 1)λ/2
जहाँ n = 1, 2, 3, 4, ....
तो I_min = I₁ + I₂ -2\(\sqrt{\mathrm{I}_1 \mathrm{I}_2}\)

(vi) व्यतिकरण के दौरान
औसत तीव्रता I_av = \(\frac{I_{\max }+I_{\min }}{2}\) = I₁ + I₂
इस प्रकार व्यतिकरण की घटना में ऊर्जा संरक्षण के नियम का पालन होता है।

(vii) (a) केन्द्रीय दीप्त फ्रिज से nवीं दीप्त फ्रिन्ज की दूरी
x_n = \(\frac{\mathrm{D} n \lambda}{2 d}\) = nβ
जहाँ β, फ्रिन्ज की चौड़ाई एवं 2d दोनों स्लिटों के मध्य दूरी है।

(b) केन्द्रीय दीप्त फ्रिज से nवीं अदीप्त फ्रिन्ज की दूरी
x_n = \(\frac{\mathrm{D}\left(n-\frac{1}{2}\right) \lambda}{2 d}\) = (n - \(\frac{1}{2}\))β
(c) फ्रिन्ज की चौड़ाई
β = \(\frac{Dλ}{2d}\)

→ विवर्तन:

• प्रकाश के मार्ग में मौजूद किसी रुकावट के किनारों से प्रकाश-तरंगों की रुकावट का छाया की ओर मुड़ जाना ही प्रकाश का विवर्तन कहलाता है।
• विवर्तन के लिए सबसे महत्वपूर्ण शर्त यह है कि रुकावट का आकार तरंगों के तरंगदैर्ध्य की कोटि का होना चाहिए।
• एकल रेखा-छिद्र के प्रयोग में निम्निष्ठों की कोणीय स्थितियाँ
• θ = m\(\frac{λ}{e}\)
• जहाँ m = 0, प्रधान उच्चिष्ठ के लिए है।
  निम्निष्ठों के लिए m = 1, 2, 3, 4, ....
• प्रधान उच्चिष्ठ की रैखिक चौड़ाई = \(\frac{2 f \lambda}{e}\)
• विवर्तन को दो वर्गों में विभाजित किया गया है
  (a) फ्रेनल विवर्तन
  (b) फ्रॉनहॉफर विवर्तन।

→ प्रकाशिक उपकरणों की विभेदन क्षमता एवं विभेदन सीमा:
(i) किसी प्रकाशिक उपकरण द्वारा दो समीपवर्ती वस्तुओं के प्रतिबिम्बों को अलग करने की क्षमता को विभेदन क्षमता कहते हैं।

(ii) किसी प्रकाशिक यन्त्र की विभेदन सीमा दो बिन्दु वस्तुओं के बीच उस न्यूनतम कोणीय दूरी के बराबर होती है जब उनके प्रतिबिम्ब प्रकाशिक यन्त्र द्वारा ही विभेदित होते हैं।

(iii) विभेदन क्षमता

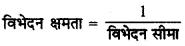
(iv) दूरदर्शी की विभेदन सीमा = \(\frac{1.22 \lambda}{d}\)
(v) सूक्ष्मदर्शी की विभेदन सीमा

→ प्रकाश का ध्रुवण:

• प्रकाश तरंग द्वारा तरंग संचरण की दिशा के परितः प्रकाश वेक्टर के दोलनों की सममिति में कमी प्रदर्शित करना ही प्रकाश का ध्रुवण कहलाता है।
• ध्रुवण की घटना ही यह सिद्ध करती है कि प्रकाश-तरंगों की प्रकृति अनुप्रस्थ होती है।
• वह तल जिसमें कम्पन होते हैं, कम्पन तल कहलाता है और वह तल जिसमें कोई कम्पन नहीं होता है, ध्रुवण तल कहलाता है।
• कम्पन तल एवं ध्रुवण तल परस्पर लम्बवत् होते हैं।
• वह आपतन कोण जिस पर किसी पारदर्शी माध्यम पर आपतित प्रकाश का परावर्तित भाग पूर्णतः समतल ध्रुवित होता है, ध्रुवण कोण कहलाता है।
• ब्रूस्टर के नियमानुसार पारदर्शी माध्यम का अपवर्तनांक ध्रुवण कोण की स्पर्शज्या के बराबर होता है अर्थात्
  μ = tan i_p
• ध्रुवण कोण पर आपतन की अवस्था में परावर्तित एवं अपवर्तित किरणें परस्पर लम्बवत् होती हैं।
• किसी पोलेरॉइड से निर्गत प्रकाश की तीव्रता
  I = I₀ cos²θ
  यदि आपतित प्रकाश अध्रुवित है तो
  I = \(\frac{1}{2}\)I₀

→ प्रकाश में डाप्लर प्रभाव
Δλ = \(\frac{v}{c}\)λ

→ व्यतिकरण में
(a) परिणामी आयाम
A = \(\sqrt{a^2+b^2+2 a b \cos \phi}\)
(a) परिणामी तीव्रता
I = I₁ + I₂ + 2\(\sqrt{I_1 I_2}\) cos Φ
(c) महत्तम तीव्रता
I_max = 4I₀
(d) औसत तीव्रता
I^R = I₁ + I₂

→ व्यतिकरण में तीव्रता का कलान्तर के साथ परिवर्तन
I^R = 4I₀ cos²\(\frac{\phi}{2}\)

→ यंग का प्रयोग
(a) केन्द्रीय दीप्त फ्रिज से दीप्त फ्रिन्जों की स्थिति
x_n = \(\frac{\mathrm{D} n \lambda}{2 d}\)

(b) दीप्त व अदीप्त फ्रिन्जों की चौड़ाई
β = \(\frac{\mathrm{D} \lambda}{2 d}\)

(c) केन्द्रीय दीप्त फ्रिन्ज से अदीप्त फ्रिन्जों की दूरी
x_n = \(\frac{\mathrm{D}\left(n-\frac{1}{2}\right) \lambda}{2 d}\)

(d) महत्तम व निम्नतम तीव्रताओं का अनुपात
\(\frac{\mathrm{I}_{\max }}{\mathrm{I}_{\min }}=\frac{\left(a_1+a_2\right)^2}{\left(a_1-a_2\right)^2}\)

→ दीप्त व अदीप्त फ्रिज की कोणीय फ्रिज चौड़ाई
θ = \(\frac{\lambda}{2 d}\)

→ एकल स्लिट के लिए विवर्तन
(a) सभी निम्निष्ठों के लिए
e sin θ =+ mλ

(b) प्रधान उच्चिष्ठ की रैखिक चौड़ाई
= \(\frac{2 f \lambda}{e}\)

→ फ्रेनल दूरी
Z_F = \(\frac{e^2}{\lambda}=\frac{d^2}{\lambda}\)

→ विभेदन क्षमता

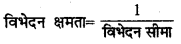
→ दूरदर्शी की विभेदन सीमा = \(\frac{1 \cdot 22 \lambda}{d}\)

→ सूक्ष्मदर्शी की विभेदन सीमा = \(\frac{1 \cdot 22 \lambda}{d}\)
d_{न्यून} = \(\frac{1.22 \lambda}{2 n \sin \beta}\)

→ ब्रूस्टर का नियम
μ = tan i_p

→ मैलस का नियम
I = I₀ cos²θ

→ कला (phase):
किसी तरंग के विस्थापन समीकरण में sine या cosine के कोणांक को कला कहते हैं। विस्थापन समीकरण y = a sin ω में पद व कला है।

→ कलान्तर (Phase difference):
दो तरंगों की कलाओं के अन्तर को कलान्तर कहते हैं।

→ पथान्तर (path difference):
किसी बिन्दु पर पहुँचने वाली दो तरंगों के पथों की लम्बाइयों के अन्तर को उस बिन्दु पर तरंगों के बीच पथान्तर कहते हैं।

→ कला सम्बद्धता (Coherence):
दो प्रकाश तरंगों के बीच कला सम्बन्ध, आकाश में समय के साथ तथा स्थिति के साथ परिवर्तित हो सकता है। यदि दो प्रकाश तरंगों के बीच कला सम्बन्ध नियत रहता है तो इस गुण को कला सम्बद्धता कहते हैं।

→ फ्रिन्ज दृश्यता (Fringe Visibility):
फ्रिन्ज दृश्यता की मदद से कला सम्बद्धता के बारे में जानकारी, व व्यतिकरण में फ्रिन्ज का विपर्यास प्राप्त किया जा सकता है।

→ वायु चकती (Airy Discs):
किसी वृत्ताकारी द्वारक पर प्रकाश के विवर्तन के कारण एक अभिसारी लेन्स किसी वस्तु की बिन्दु छाया नहीं बनाता अपितु यह एक चमकीली चकती का निर्माण करता है जिसे वायु चकती कहते हैं।

→ विभेदन सीमा (Resolution Limit):
हमारी आँख केवल उन्हीं वस्तुओं को पृथक-पृथक देख पाती है जो आँख पर \(\frac{1}{60}\) डिग्री या 1 मिनट या उससे अधिक का कोण बनाती है या जिनके बीच की कोणीय दूरी एक मिनट या उससे अधिक होती है। 1 मिनट का वह न्यूनतम कोण आँख की 'विभेदन सीमा' कहलाता है।

→ फ्रेनेल दूरी (Fresnel Distance):
वह न्यूनतम दूरी है जो कोई किरण पुंज अपने रेखीय पथ से विचलित होने से पूर्व चलता है।

→ दीर्घ वृत्त धुवित प्रकाश (Elliptically polarised light):
यदि विद्युत क्षेत्र E का शीर्ष दीर्घवृत्ताकार पथ में विस्थापित होता है तो प्रकाश दीर्घवृत्त ध्रुवित कहलाता है।