RBSE Class 12 Maths Notes Chapter 9 अवकल समीकरण

These comprehensive RBSE Class 12 Maths Notes Chapter 9 अवकल समीकरण will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 9 Notes अवकल समीकरण

प्रस्तावना (Introduction)
जब हमें भौतिकी, अभियांत्रिकी, रसायनिक क्रियाओं में किसी सिद्धान्त को गणितीय भाषा के रूप में प्रतिपादित करना होता है तो हमें निम्न प्रकार के समीकरण प्राप्त होते हैं-

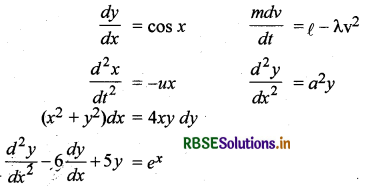
इस प्रकार के उपर्युक्त समीकरण जिनमें फलन (या फलनों) के अवकलन विद्यमान होते हैं, अवकल समीकरण कहलाते हैं। अवकल समीकरणों का प्रयोग प्रायः जीव विज्ञान, रसायन विज्ञान, मानव
विज्ञान, भौतिक विज्ञान, भू-विज्ञान आदि विभिन्न क्षेत्रों में किया जाता है।

अवकल समीकरण (Differential Equations)
एक ऐसी समीकरण जिसमें स्वतन्त्र चर (x), आश्रित चर (y) तथा उसके अवकलज विद्यमान हों, अवकल समीकरण कहलाती है।
जैसे \(\frac{d y}{d x}\) + y = cos x
\(\frac{d y}{d x}\) = tan x
\(\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}\) + 12y = e^x

 

साधारण एवं आंशिक अवकल समीकरण (Ordinary And Partial Differential Equations):
अवकल समीकरण सामान्यतया दो प्रकार के होते हैं

• साधारण अवकल समीकरण
• आंशिक अवकल समीकरण।

(i) साधारण अवकल समीकरण-वे अवकल समीकरण, जिनमें केवल एक ही स्वतन्त्र चर हो, साधारण अवकल समीकरण कहलाते हैं।
उदाहरणार्थ

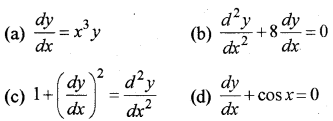
(ii) आंशिक अवकल समीकरण-वे अवकल समीकरण, जिनमें एक से अधिक स्वतन्त्र चर हों, आंशिक अवकल समीकरण कहलाते हैं।
उदाहरणार्थ
(a) x \(\frac{\partial z}{\partial x}+y \frac{\partial z}{\partial y}\)=n z
(b) \(\frac{\partial^{2} z}{\partial x^{2}}+\frac{\partial^{2} z}{\partial y^{2}}\)
इत्यादि।
प्रस्तुत अध्याय में हम केवल सांधारण अवकल समीकरणों का ही विस्तार से अध्ययन करेंगे।

टिप्पणी :

• साधारण अवकल समीकरण को प्रायः अवकल
• समीकरण भी कहते हैं।

अवकल समीकरण की कोटि तथा घात (Order And Degree of A Differential Equation):
अवकल समीकरण की कोटि (Order of a Differential Equation):
किसी अवकल समीकरण की कोटि उस अवकल समीकरण में सम्मिलित स्वतंत्र चर के सापेक्ष आश्रित चर के उच्चतम कोटि के अवकल की कोटि द्वारा परिभाषित होती है। अर्थात् एक दी गई अवकल समीकरण में विद्यमान उच्चतम अवकलन की कोटि को ही उस अवकल समीकरण की कोटि कहते हैं। अर्थात् इसमें यह देखना आवश्यक होता है कि आश्रित चर का अधिकतम कितनी बार अवकलन हुआ है।

उदाहरणार्थ

• \(\frac{d y}{d x}\) = e^x की कोटि एक है क्योंकि आश्रित चर y का अधिकतम अवकलन एक बार ही हुआ है।
• अवकल समीकरण \(\frac{d^{2} y}{d x^{2}}+\frac{7 d y}{d x}\) + 12 y = e^3x की कोटि दो है क्योंकि आश्रित चर) का अधिकतम अवकलन दो बार हुआ है।
• अवकल समीकरण \(\left(\frac{d y}{d x}\right)^{3}+6 \frac{d y}{d x}\) + 10y = 0 की कोटि 1 है क्योंकि आश्रित चर y का अधिकतम अवकलन एक बार ही हुआ है। टिप्पणी : छात्र यहाँ पर ध्यान दें कि उदाहरण
• में अवकलन समीकरण की कोटि 3 नहीं है, क्योंकि आश्रित चर का अधिकतम अवकलन एक बार ही है लेकिन की घात 3 है।

अवकल समीकरण की घात (Degree of Differential Equation)
किसी अवकल समीकरण की घात उस अवकल समीकरण में विद्यमान उच्चतम कोटि के अवकल गुणांक की घात के बराबर होती है जबकि अवकल गुणांक भिन्नात्मक घातों तथा करणी चिह्नों से स्वतंत्र हो । अर्थात् यहाँ यह ध्यान देना होगा कि किसी दी गई अवकल समीकरण की घात ज्ञात करने से पूर्व उस अवकल समीकरण को परिमेय तथा पूर्ण बीजीय बनाना आवश्यक है।

उदाहरणार्थ
\(\frac{d^{3} y}{d x^{3}}\) + 2\(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}-\frac{d y}{d x}\) + y = 0 की बात एक है क्योंकि इस समीकरण में उपस्थित अधिकतम अवकलन \(\frac{d^{3} y}{d x^{3}}\) है जो \(\left(\frac{d^{3} y}{d x^{3}}\right)^{1}\) के रूप में लिखा जा सकता है, इसलिये इस अवकल समीकरण की घात 1 तथा कोटि 3 है।

\(\left(\frac{d y}{d x}\right)^{2}\) + 5 \(\frac{d y}{d x}\) - sin² y = 0 की घात 2 है क्योंकि इस समीकरण में उपस्थित अधिकतम अवकलन (\(\frac{d y}{d x}\))है जिस पर घात 2 लगी हुई है इसलिए इस अवकल समीकरण की घात 2 तथा कोटि 1 है।

(ii) अवकल समीकरण \(\left[1+\left(\frac{d y}{d x}\right)^{3}\right]=\left(\frac{d^{2} y}{d x^{2}}\right)^{2 / 3}\) की घात ज्ञात करने से पहले इसे सरल करने पर \(\left[1+\left(\frac{d y}{d x}\right)^{3}\right]^{3}=\left[\left(\frac{d^{2} y}{d x^{2}}\right)^{2 / 3}\right]^{3}=\left(\frac{d^{2} y}{d x^{2}}\right)^{2}\) जिससे स्पष्ट है कि उपर्युक्त अवकल समीकरण की घात दो होगी, क्योंकि उच्चतम अवकलन 4 की घात दो है।

\(\frac{d y}{d x} \)+ cos \(\left(\frac{d y}{d x}\right)\) = 0
उपर्युक्त समीकरण \(\frac{d y}{d x} \) में बहुपद समीकरण नहीं है और इस प्रकार के अवकल समीकरण की घात को परिभाषित नहीं किया जा सकता है।

टिप्पणी :

• चर x तथा y को परिमेय या पूर्णबीजीय बनाना आवश्यक नहीं है। केवल अवकलनों के सन्दर्भ में ही अवकल समीकरण को परिमेय तथा पूर्ण बीजीय बनाकर घात ज्ञात करनी चाहिए।
• किसी अवकल समीकरण की कोटि एवं घात (यदि परिभाषित हो) हमेशा धनात्मक पूर्णांक होते हैं।

अवकल समीकरण का हल (व्यापक एवं विशिष्ट हल) Isolution of A Differential Equation (General And Particular Solution)
किसी अवकल समीकरण का हल अथवा समाकलन उसमें प्रयुक्त स्वतन्त्र तथा आश्रित चरों में सम्बन्ध है जिसमें कोई भी अवकल गुणांक न हो तथा यह सम्बन्ध एवं इससे प्राप्त अवकल गुणांक दिये हुये अवकल समीकरण को सन्तुष्ट करते हैं।

अवकल समीकरण का हल जिसे हम पूर्ण हल, पूर्ण समाकल या पूर्ण पूर्वज भी कहते हैं क्योंकि यह अवकल समीकरण उसी से उत्पन्न एक सम्बन्ध होता है। जैसे

• y = tanx + c, अवकल समीकरण \(\frac{d y}{d x} \) = sec²x का हल है।
• y = log cos x + c, अवकल समीकरण \(\frac{d y}{d x} \) - tanx का हल है।

व्यापक, विशिष्ट एवं विचित्र हल (General, Particular and Singular Solution)
व्यापक हल (General Solution)
(i) यदि किसी अवकल समीकरण के हल में यदि उसकी कोटि के बराबर स्वेच्छ अचर हो तो वह हल व्यापक हल कहलाता है।
लाता है। जैसे \(\frac{d y}{d x}=\frac{1}{x^{2}}\) का व्यापक हल y= -\(\frac{1}{x}\) + C; है।

(ii) विशिष्ट हल (Particular Solution) यदि किसी अवकल समीकरण के व्यापक हल में प्रयुक्त अचरों को स्वेच्छ मान देने पर प्राप्त हल विशिष्ट हल कहलाता है, जैसे
\(\frac{d y}{d x}=\frac{1}{x^{2}}\) के व्यापक हल
y = -\(\frac{1}{x}\) + C में C = 3 रखने पर
y= -\(\frac{1}{x}\) + 3 विशिष्ट हल है।

(iii) विचित्र हल (Singular Solution):
किसी अवकल समीकरण का वह हल जो उसके व्यापक हल में स्वेच्छ अचर को विशिष्ट मान देने से प्राप्त नहीं होता है, उसको अवकल समीकरण का विचित्र हल (Singular Solution) कहते हैं। विचित्र हल में स्वेच्छ अचर नहीं होता है।

व्यापक हल से अवकल समीकरणों का निर्माण (Formation Of Differential: Equations From General Solution)
एक दी गई समीकरण जो किसी वक्र कुल से सम्बन्धित हो, से एक अवकल समीकरण के निर्माण का तात्पर्य एक ऐसी समीकरण प्राप्त करना है जिसका हल दी गई समीकरण में हो । यदि दी गई समीकरण में एक स्वेच्छ अचर हो तो हम उस समीकरण का एक बार अवकलन करके दोनों समीकरणों से स्वेच्छ अचर लुप्त करते हैं।
इसी प्रकार यदि दी गई समीकरण में दो स्वेच्छ अचर हों तो हम उस समीकरण का दो बार अवकलन कर उन तीन समीकरणों से दो स्वेच्छ अचर को लुप्त करते हैं। इस प्रकार प्राप्त की गई अवकल समीकरण की कोटि स्वेच्छ अचरों की संख्याओं के तथा घात किसी स्वेच्छ अचर की उच्चतम घात के तुल्य होती है।

टिप्पणी
किसी वक्र कुल को निरूपित करने वाले अवकल समीकरण की कोटि उतनी ही होती है जितने उस वक्र कुल के संगत समीकरण में स्वेच्छ अचर होते हैं। यह विधि अग्रांकित दृष्टान्तीय उदाहरणों से स्पष्ट हो जायेगी।

प्रथम कोटि एवं प्रथम घात के अवकल समीकरणों को हल करने की विधियाँ (Methods Of Solving First Order, First Degree Differential Equations):
प्रथम कोटि एवं प्रथम घात की अवकल समीकरण का व्यापक रूप
\(\frac{d y}{d x}\) = f(x, y) ....(1)

होता है, जहाँ पर f (x, y), चर x तथा y का कोई फलन है। समीकरण (1) वक्र के किसी बिन्दु पर स्पर्श रेखा के ढाल और उस बिन्दु के आयतीय निर्देशांकों के बीच एक सम्बन्ध को प्रदर्शित करता है। इस प्रकार की अवकल समीकरण निम्न रूप में भी व्यक्त की जा सकती
Mdx + Ndy = 0 ........(2)
जहाँ M तथा N, x तथा y के फलन या अचर हैं। वैसे तो हर अवकल समीकरण को हल नहीं किया जा सकता है। फिर भी गणितज्ञों जॉन बरनौली (John Bernoulli) एवं लियोनार्ड आयलर (Leonard Euler) के अनुसार यदि अवकल समीकरण निम्नलिखित मानक रूपों में से किसी भी एक रूप की हो तो उस समीकरण का हल ज्ञात करना सम्भव होता है।

• अवकल समीकरण जिसमें चर तथा y को पृथक्-पृथक् किया जा सके, ऐसे समीकरण चरों को पृथक् करने वाली समीकरण कहलाते हैं।
• अवकल समीकरण जो चरों को पृथक् करने वाली समीकरण में बदली जा सके।
• अवकल समीकरण जो समघात रूप की हो।
• अवकल समीकरण जिसको समघात रूप में बदला जा सके।
• अवकल समीकरण जो रैखिक अवकल समीकरण के रूप में हो।
• ऐसे समीकरण जिनको रैखिक अवकल समीकरण के रूप में बदला जा सके।

पृथक्क रणीय चर वाले अवकल समीकरण (Differential Equations with Variables Separable)
एक विधि से यदि समीकरण (2) निम्न रूप में व्यक्त की जा सके
f(x)dx + Φ(y)dy = 0 .....(3)
तो यहाँ पर यह कहा जा सकता है कि चर x या y पृथक्-पृथक् हो गये हैं। ऐसी स्थिति में समीकरण (3) के प्रत्येक पद का अलग-अलग समाकलन करने पर हमें प्राप्त होता है।
∫f(x)dx + ∫Φ(y)dy = C
जहाँ C कोई स्वेच्छ अचर है।
यह विधि निम्न उदाहरणों से स्पष्ट हो जायेगी।

→ वह समीकरण जिसमें स्वतन्त्र चर के सापेक्ष आश्रित चर के अवकलज सम्मिलित हों, अवकल समीकरण कहलाता है।

→ किसी अवकल समीकरण में उपस्थित अवकल गुणांक की उच्चतम कोटि को अवकल समीकरण की कोटि या क्रम कहते हैं।

→ किसी अवकल समीकरण की घात अवकल समीकरण में सम्मिलित अवकल गुणांक की उच्चतम घात होती है जबकि अवकल समीकरण अवकल गुणांकों के बहुपद में प्रदर्शित हो।

→ प्रथम कोटिं एवं प्रथम घात के अवकल समीकरण में स्वतन्त्र चर (x), आश्रित चर (y) तथा प्रथम कोटि का अवकल गुणांक \(\frac{d y}{d x}\) सम्मिलित होता है। इस प्रकार के समीकरण को निम्न प्रकार व्यक्त किया जाता है
\(\frac{d y}{d x}\)= F(x, y) .....(i)
या \(\frac{d y}{d x}=\frac{h(x, y)}{g(x, y)}\) ...........(ii)
जहाँ h (.x, y) तथा y (x, y), x तथा y के फलन हैं।

→ प्रथम कोटि एवं प्रथम घात के अवकल समीकरणों को हल करने की प्रमुख तीन विधियाँ हैं

• चरों का पृथक्करण
• समघात अवकल समीकरण
• रैखिक अवकल समीकरण

→ चरों के पृथक्करण की विधि का प्रयोग तब किया जाता है जब y के पद dy के साथ तथा x के पद dx के साथ चले जाएँ।

→ यदि f.x, y) तथा g (x, y) शून्य घात के समघात फलन हैं तो \(\frac{d y}{d x}\) = f(x, y) तथा \(\frac{d y}{d x}\) = g(x, y) को समघातीय अवकल समीकरण कहते हैं।

→ \(\frac{d y}{d x}\) - Py = Q, जहाँ P तथा Q अचर या.x के फलन हैं तो इसे प्रथम कोटि की रैखिक अवकल समीकरण कहते हैं । जिसका हल
y (IF) = ∫(IF)Qdx + C होता है जहाँ
IF = e^∫Pdx