RBSE Class 12 Maths Notes Chapter 8 समाकलनों के अनुप्रयोग

These comprehensive RBSE Class 12 Maths Notes Chapter 8 समाकलनों के अनुप्रयोग will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 8 Notes समाकलनों के अनुप्रयोग

प्रस्तावना (Introduction):
गणित की शाखा ज्यामिति में हमने त्रिभुजों, आयतों, समलम्ब चतुर्भुजों एवं वृत्तों आदि विभिन्न ज्यामितीय आकृतियों के क्षेत्रफल ज्ञात करने के सूत्रों का अध्ययन किया है। वास्तविक जीवन की अनेक समस्याओं के लिये गणित के अनुप्रयोग में इस प्रकार के सूत्र मूल होते हैं। ज्यामिति के इन सूत्रों के माध्यम से हम विभिन्न वक्रों द्वारा घिरे क्षेत्रों का क्षेत्रफल सरलता से ज्ञात नहीं कर सकते हैं। इसके लिये हमें समाकलन गणित की कुछ संकल्पनाओं की आवश्यकता होगी।

पिछले अध्याय में हमने योगफल की सीमा के रूप में निश्चित समाकलनों का परिकलन करते समय वक्र y = f(x), कोटियों x = a, x = b एवं x-अक्ष से घिरे क्षेत्रफल को ज्ञात करने का अध्ययन किया है। यहाँ पर हम साधारण वक्रों के अन्तर्गत, सरल रेखाओं एवं वृत्तों, परवलयों तथा दीर्घवृत्तों (केवल मानकरूप) की चापों के बीच घिरे क्षेत्रफल को ज्ञात करने के लिये समाकलनों के एक विशिष्ट अनुप्रयोग का अध्ययन करेंगे। क्षेत्रंकलन को सरलता से ज्ञात करने के लिये क्षेत्र का कच्चा चित्र (rough sketch) बना लेना चाहिये जिससे समाकलन की सीमाओं तथा अक्षों के सापेक्ष वक्र की सममिति का निर्धारण करने में सुविधा रहती है । वक्रों से परिबद्ध क्षेत्र का कच्चा चित्र बनाने के लिये वक्रों की पहचान एवं उनका अनुरेखण करना आवश्यक होता है।

क्षेत्रकलन (Quardrature):
परिभाषा–समतल क्षेत्र का क्षेत्रफल ज्ञात करने की क्रिया को क्षेत्रकलन कहते हैं।

काय वक्रों का क्षेत्रफल (Areas of Cartesian Curves):
कार्तीय वक्र y = f(x), x-अक्ष तथा कोटि x = a, x = b द्वारा घिरे हुए क्षेत्र का क्षेत्रफल है :
क्षेत्रफल (Area) = \(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{b}\) y dx

उपपत्ति (Proof) माना किसी वक्र PQ का समीकरण y = (x) है, जहाँ f (x) प्रान्त [a, b] में x का वास्तविक एकमानी (single. valued) एवं संतत फलन है।
चित्रानुसार हमें क्षेत्र PRSQP का क्षेत्रफल ज्ञात करना है।

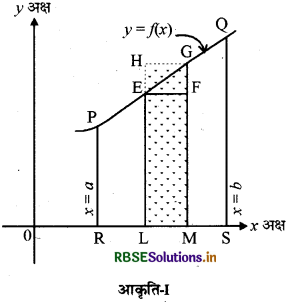
माना वक्र पर कोई बिन्दु E(x, y) है तथा G(x + δx, y + δy) इसका समीपवर्ती बिन्दु है। माना EL तथा GMक्रमशः E तथा G की कोटियां हैं। E से GM पर लम्ब EF तथा G से LE को बढ़ाकर लम्ब GH खींचने
पर
LM = OM - OL = (x + δx)- x = δx
तथा GF = MG - MG = (y + δy) - y (∵ MF = LE = y)
= δy माना, (क्षेत्रफल RLEPR) = A
अब यदि x में δx की वृद्धि के फलस्वरूप जो क्षेत्रफल में वृद्धि होगी, उसे यदि δA से प्रदर्शित करें तो, δA = (क्षेत्रफल ELMGE) अतः चित्रानुसार,

(आयत ELMF का क्षेत्रफल) < (क्षेत्रफल ELMGE) < (आयत HLMG का क्षेत्रफल)
⇒ (y, δx) < δA < (y + δy) . δx
⇒ y < \(\frac{\delta \mathrm{A}}{\delta x}\) < (y + δy)

जब G → E, तब δx → 0 तथा y + δy → y

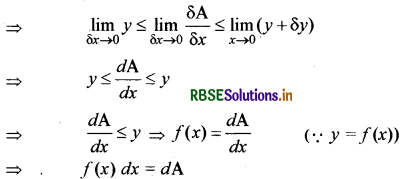
दोनों पक्षों का x के सापेक्ष x = a तथा x = b सीमाओं के बीच समाकलन करने पर,
\(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{b} d \mathrm{~A}=[\mathrm{A}]_{a}^{b}\)
= (क्षेत्रफल A जब x = b) - (क्षेत्रफल A जब x = a)
= (क्षेत्रफल PRSQP) - (0)
= क्षेत्रफल PRSQP

\(\int_{a}^{b}\)f(x)dx = वक्र y= (x), x-अक्ष तथा कोटियों x = a तथा x = b से परिबद्ध क्षेत्रफल।
क्षेत्रफल PRSQP = \(\int_{a}^{b}\)f(x)dx = \(\int_{a}^{b}\)ydx
उपरोक्त विधि से यह भी सिद्ध किया जा सकता है कि वक्र x = Φ(y), y-अक्ष तथा भुज y = c एवं y = d से परिबद्ध क्षेत्रफल
PQRSP = \(\int_{c}^{d}\)Φ(y)dy = \(\int_{c}^{d}\)xdy
∴ y-अक्ष से परिबद्ध क्षेत्रफल = \(\int_{c}^{d}\)xdx
किसी वक्र का क्षेत्रकलन ज्ञात करते समय निम्नलिखित बिन्दुओं को ध्यान में रखना चाहिये

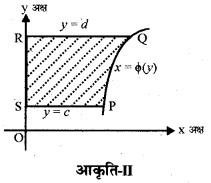
1. यदि चर्चित वक्र की स्थिति x-अक्ष से नीचे है , तब y=fx)<0 और इसलिए दिए हुए वक्र,x-अक्ष एवं कोटियाँ x= a, x = b से घिरे क्षेत्र का क्षेत्रफल ऋणात्मक हो जाता है। परन्तु हम क्षेत्रफल के केवल संख्यात्मक मान की ही चर्चा करते हैं। इसलिए यदि क्षेत्रफल ऋणात्मक है तो हम इसके निरपेक्ष मान अर्थात् \(\left|\int_{a}^{b} f(x) d x\right|\) को लेते हैं।

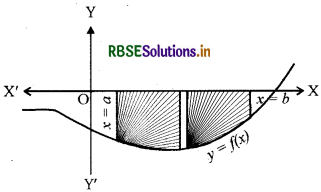
2. कई बार ऐसा भी होता है कि वक्र का कुछ भाग x-अक्ष के ऊपर है तथा कुछ भाग x-अक्ष के नीचे है। जैसा आकृति में दर्शाया गया है

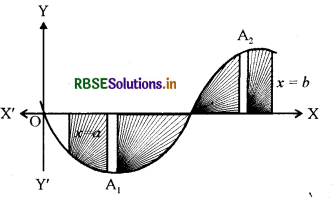
यहाँ A₁ <0 तथा A₂> 0 है, इसलिए वक्र y = f(x), x-अक्ष एवं कोटियों x = a तथा x = b से घिरे क्षेत्र का क्षेत्रफल A सूत्र A = |A₁| + A₂, द्वारा प्राप्त किया जाता है।
3. यदि वक्र किसी निर्देशी अक्ष या किसी रेखा के प्रति सममित हो, तो किसी एक सममित भाग का क्षेत्रफल ज्ञात करके उसको सममित भागों की कुल संख्या से गुणा करके अभीष्ट क्षेत्रफल ज्ञात करते हैं।

किसी समतल वक्र के लिये क्षेत्रफल की गणना करने का व्यावहारिक नियम (Behaviour Rule of Area Calculation For Plane Curves):

• दिये गये वक्र की एक रफ आकृति खींचिये।
• उस क्षेत्र का निर्माण कीजिये जिसके क्षेत्रफल की गणना हमें करनी है।
• क्षेत्र के लिये निश्चित समाकल इस प्रकार निर्धारित कीजिये कि समाकल्य की सीमायें (Limits) इस प्रकार चुनी जायें कि परतंत्र चर (Independent Variables) पूरे क्षेत्र में विचरित हो।
• उपर्युक्त पद के निर्धारण के अनुसार निश्चित समाकलन का मान ज्ञात करते हैं जो कि वक्र का अभीष्ट क्षेत्रफल होता है।
• वक्र अनुरेखण में रेखा, वृत्त, परवलय, दीर्घवृत्त एवं अति परवलय का ज्ञान अति आवश्यक है जिनका अध्ययन छात्र कक्षा-11 में कर चुके हैं। लेकिन इस अध्याय में इसकी आवश्यकता को ध्यान में रखते हुए पुनः संक्षिप्त में इनका वर्णन यहाँ पर किया जा रहा है।

रेखा और वक्रों की प्रकृति
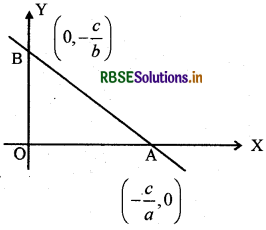
1. सरल रेखा ax + by + c = 0
x = 0, y = \(\frac{-c}{b}\)
y = 0, y = \(\frac{-c}{a}\)

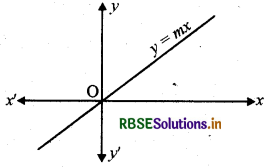
2. मूल बिन्दु से गुजरने वाली रेखा y = mx

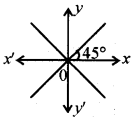
3. मूल बिन्दु से गुजरने वाली रेखा जिसका रूप है y = ±x

4. y-अक्ष के समान्तर x = a दूरी पर

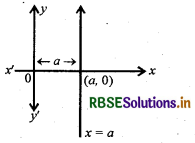
5. x-अक्ष के समान्तर y = b दूरी पर

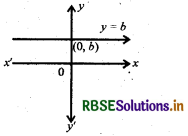
6. उस वृत्त का समीकरण जिसका केन्द्र (0, 0) और त्रिज्या a है
x² + y² = a²

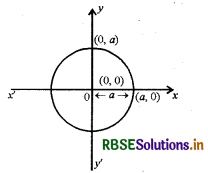
7. वृत्त का व्यापक समीकरण x² + y² + 2gx +2fy + c = 0 में केन्द्र (-g, -f) = केन्द्र
(-x के गुणांक का \(\frac{1}{2}\), -y के गुणांक का \(\frac{1}{2}\)) तथा त्रिज्या \(\sqrt{g^{2}+f^{2}-c}\)

8. परवलय y² = 4ax
शीर्ष: (0,0)
नाभि: (a , 0)
नियता का समीकरण :x =-a
अक्ष का समीकरण :y = 0
नाभिलम्ब की लम्बाई : 4a

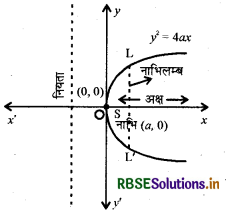
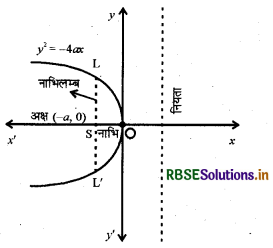
9. परवलय y = -4ax
शीर्ष: (0,0)
नाभि: (-a,0)
नियता का समीकरण :x = a
अक्ष का समीकरण :y = 0
नाभिलम्ब की लम्बाई : 4a

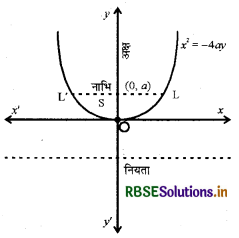
10. परवलय x² = 4ay
शीर्ष : (0,0)
नाभि : (0, a)
नियता का समीकरण :y=-a
अक्ष का समीकरण :x = 0
नाभिलम्ब की लम्बाई : 4a

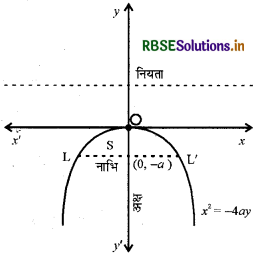
11. परवलय x² = -4ay
शीर्ष : (0,0)
नाभि : (0, -a)
नियता का समीकरण :y = a
अक्ष का समीकरण :x = 0
नाभिलम्ब की लम्बाई : 4a .

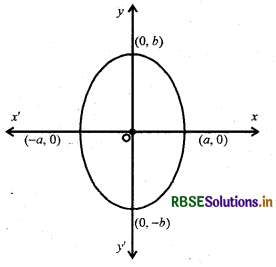
12. दीर्घवृत्त \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, a > b

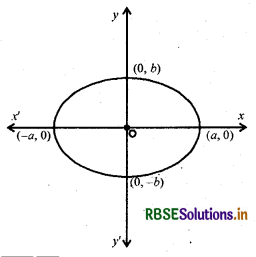
दीर्घवृत्त का दूसरा रूप
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, b > a

एक वक्र एवं एक रेखा से घिरे क्षेत्र का क्षेत्रफल (The Area of The Region Bounded By A Curve And A Line):
इस उपपरिच्छेद में, हम एक रेखा और एक वृत्त, एक रेखा और एक परवलय तथा एक रेखा और एक दीर्घवृत्त से घिरे क्षेत्र का क्षेत्रफल ज्ञात करेंगे। उपरोक्त चर्चित वक्रों के समीकरण केवल प्रामाणिक रूप में ही अध्ययन किए जाएंगे क्योंकि अन्य रूपों वाले समीकरण का उपयोग इस पाठ्यपुस्तक के अध्ययन क्षेत्र से बाहर है।

दो कार्तीय वक्रों से परिबद्ध क्षेत्रफल (Area Bounded By Two Cartesian Curves)
संलग्न चित्र में छायांकित भाग दो कार्तीय वक्रों y = f(x) और y = g(x) तथा दो रेखाओं (कोटियों) x = a और x = b के मध्य परिबद्ध क्षेत्र के क्षेत्रफल को दर्शाता है।

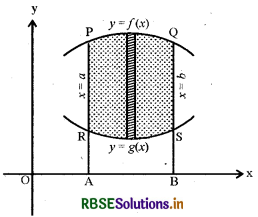
इस परिबद्ध क्षेत्र का क्षेत्रफल = क्षेत्रफल APQBA

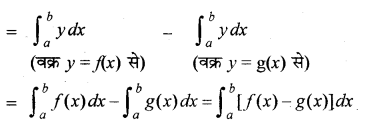
नोट : वक्र x =f(y) और x = g(y) तथा रेखाओं y = c और y = d से परिबद्ध क्षेत्र का क्षेत्रफल

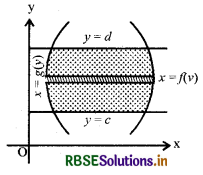
= \(\int_{c}^{d}\)[f (y)-g(y)]dy

विशेष स्थितियाँ:
स्थिति I : जब दोनों वक्र दो बिन्दुओं पर प्रतिच्छेद करते हों तथा उनका उभयनिष्ठ क्षेत्रफल इन बिन्दुओं के बीच स्थित हो।

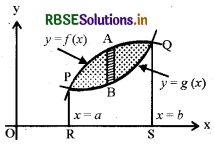
यदि वक्र y = f(x) तथा y=g(x) दो बिन्दुओं P(x = a) तथा Q(x = b) पर प्रतिच्छेद करते हों तथा उनका उभयनिष्ठ क्षेत्रफल P एवं के मध्य स्थित हो, तो उभयनिष्ठ क्षेत्रफल = क्षेत्रफल PBQAP

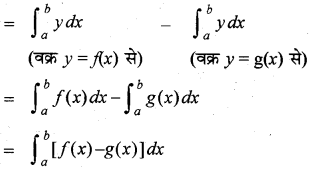
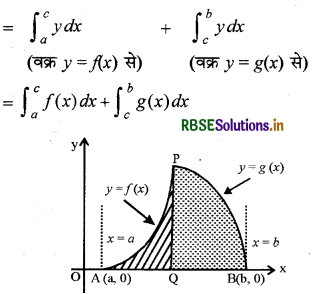
स्थिति II : जब दोनों वक्र एक बिन्दु पर प्रतिच्छेद करते हों तथा उनके बीच का क्षेत्रफल :-अक्ष से परिबद्ध हो। माना वक्र y = f(x) तथा y = g(x) बिन्दु P(x = c) पर प्रतिच्छेद करते हैं। माना वक्र y = f(x), x-अक्ष को बिन्दु A (a, 0) तथा वक्र y = g(x), x-अक्ष को बिन्दु B(b, 0) पर मिलते हैं । वक्रों तथा xअक्ष से परिबद्ध अभीष्ट क्षेत्रफल = (क्षेत्रफल AQPA) + (क्षेत्रफल QBPQ)

→ वक्र y = f(x), x-अक्ष एवं रेखाओं x = a व x = b से घिरे क्षेत्र का क्षेत्रफल \(\int_{0}^{b}\) y dx = \(\int_{0}^{b}\) f(x) dx

→ वक्र x = g(y), y-अक्ष एवं रेखाओं y = c, y = d से घिरे क्षेत्र का क्षेत्रफल = \(\int_{c}^{d}\) x dy = \(\int_{c}^{d}\) g(y) dy

→ दो वक्रों y = f(x), y = g(x) एवं रेखाओं x = a, x = b के मध्य घिरे क्षेत्र का क्षेत्रफल = \(\int_{a}^{d}\)[f(x)- g(x)] dx, जहाँ [a, b] में f(x) ≥ g(x)

→ यदि [a, c] में f(x) ≥ g(x) एवं [a, b] में f(x) ≤ g(x) a < c < b तो क्षेत्रफल = \(\int_{a}^{c}\)[f(x) - g(x)] dx + \(\int_{b}^{c}\)g(x) - f(x)] dx