RBSE Class 12 Maths Notes Chapter 8 Application of Integrals

These comprehensive RBSE Class 12 Maths Notes Chapter 8 Application of Integrals will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 8 Notes Application of Integrals

Introduction:
To find the area of various geometrical figures By formulae such as the area of triangles, rectangles, squares, quadrilaterals and circles.
By such formulae, we cannot find the areas enclosed by curves but by using integrals we can find such areas.
In the previous chapter, we have studied to find the area bounded by the curve y = / (x), the ordinates x = a, x = b and x - axis, while calculating definite integral as the limit of a sum.
Here, in this chapter, we shall study a specific application of integrals to find the area enclosed by simple curves, area between lines and arcs of circles, parabolas and ellipses.    '

Area under Simple Curves
In the figure shown below, y = f(x) is a curve. For finding the area bounded by the curve y = f(x), x-axis and

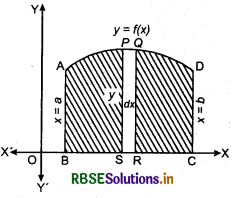
the ordinates x = a and x = b, we think of the area under the curve as composed of lines number of very thin vetical strips. Consider an arbitrary strip PQRS of height y and width dx, then area of this strip dA = ydx. This area is called the elementary area which is located at an arbitrary position within the region which is specified by some value of x between a and b.

Total area A of the region between x-axis, ordinates x = a, x = b and the curve y =/(x), will be the result of adding up elementary areas of thin strips. So,
A = \(\int_{a}^{b}\) dA = \(\int_{a}^{b}\) y dx = \(\int_{a}^{b}\) f(x) dx
Similarly,-for finding the area bounded by the curve x = g(y), y-axis and lines y = c and y = d, we divide the area under the curve as composed as large number of very thin horizontal strips as shown in figure below.

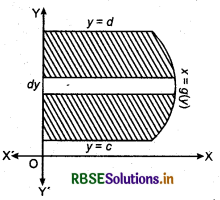
If this area is denoted by A, then
A = \(\int_{c}^{d}\) xdy = \(\int_{c}^{d}\) g(y) dy
Here, we consider horizontal strip.

Remark:
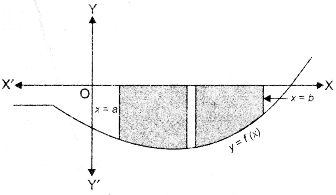
If the position of the curve under consideration is below the x-axis, then since f(x) < 0 from x = a to x = b as shown below, the area bounded by the curve, x-axis and the ordinates x = a, x = b come out to be negative. But, it is only the numerical value of the area which is taken into consideration. Thus, if the area is negative, we take its absolute value, i.e., |\(\int_{a}^{b}\)f(x)dx|

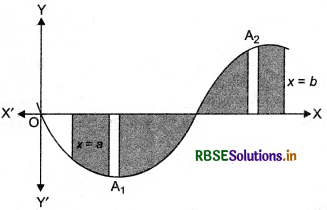
Generally, it may happen that some portion of the curve is above x-axis and some is below the x-axis as shown below. Here, A₁ < 0 and A₂ >0. Therefore, the area
A bounded by the curve y = f(x), x-axis and the ordinates xa and xb is given by A 

The Area of the Region Bounded by a Curve and a Line:
With the above learnt method, we can find the area of the region bounded by a line and a circle, a line and a parabola, a line and an ellipse. Equations of above mentioned curves will be in their standard forms only as the cases in the other forms go beyond the scope of this textbook. 

Area Between Two Curves
(i) Let y = f(x) and y = g(x) are two curves, which intersect each other at .t = a and x = b as shown in figure. For finding the area between the two curves, we take a vertically thin strip whose length is f(x) - g(x)] and breadth is dx, then area of this vertical strip is :

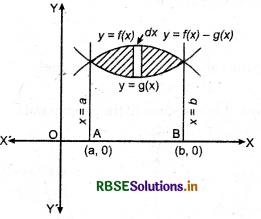
dA = [f(x) - g(x)] dx
And, the total area between the two curves is taken as:
A = \(\int_{a}^{b}\)[f(x)-g(x)]dx
We can also find the area between two curves as :
A = [area bounded by y = f(x), j-axis and the lines x = a, x = b] - [area bounded by y = g(x), x-axis and the lines x - a, x = b]
A = \(\int_{a}^{b}\)f(x) dx - \(\int_{a}^{b}\)g(x) dx = \(\int_{a}^{b}\)a[f(x)-g(x)] dx where f(x) ≥ g(x) in [a, b].

(ii) In interval [a, b],f(x) > g(x)
If c be any point between a and b(a< c<b), where both the curves intersect each other as shown in figure, then the area of the regions bounded by curves can be obtained as : 

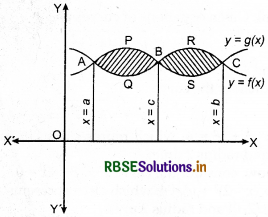
Required area = Area of region APBQA + Area of region BSCRB
= \(\int_{a}^{c}\)[f(x)-g(x)] dx + \(\int_{c}^{b}\)[g(x) - f(x)] dx
∴ f(x) ≥ g(x) in [a, c] and f(x) < g(x) in [c, b] where a< c < b.

→ The area of the region bounded by the curve y = f(x), x-axis and the lines x = a and x = b is given by the formula:
Area = \(\int_{a}^{b}\) y dx = \(\int_{a}^{b}\)f(x) dx

→ The area of the region bounded by the curve x = y-axis and the lines y = c, y = d is given by the formula:
Area = \(\int_{c}^{d} \)g(x) \(\int_{c}^{b}\)(y) dy

→ The area of the region enclosed between two curves y = f(x), y g(x) and the lines x = a, x = b is given by the formula:
Area \(\int_{a}^{b}\)|f(x) - g(x)|dx where f(x) ≥ g(x) in [a, b].