RBSE Class 12 Maths Notes Chapter 7 समाकलन

These comprehensive RBSE Class 12 Maths Notes Chapter 7 समाकलन will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 7 Notes समाकलन

परिचय (Introduction):
यदि हम समाकलन गणित (Integral Calculus) के इतिहास का अध्ययन करें तो हमें ज्ञात होगा कि इसकी खोज समतल में रेखाओं तथा वक्रों (Curves) द्वारा परिबद्ध (bounded) समतल क्षेत्रों के क्षेत्रफलों को ज्ञात करने के लिए की गई थी। इसकी धारणा ऐसी श्रेणी के योगफल की सीमा पर आधारित थी जिसमें पदों की संख्या अनन्त थी और प्रत्येक पद शून्य की अग्रसर था। इसका अध्ययन इस दृष्टि से हम अध्याय-8 में करेंगे। बाद में यह देखा गया कि समाकलन की प्रक्रिया (Process of Integration), अवकलन (Differentiation) की प्रतिलोम (Inverse) प्रक्रिया है।

अवकलन गणित में हमें दिये गये फलन का अवकलन गुणांक या अवकलन ज्ञात करना होता है, जबकि समाकलन गणित में हमें वह फलन ज्ञात करना होता है जिसका अवकल गुणांक दिया होता है। अतः वह प्रक्रिया (Process) जिसके द्वारा किसी दिये हुए फलन f(x) से वह फलन माना F(x), ज्ञात करना जिसका अवकल गुणांक \(\frac{d}{d x}\){F (x)} = फलन f(x) हो, समाकलन (Integration) कहलाती है। स्पष्टतः समाकलन की यह प्रक्रिया अवकलन की प्रतिलोम प्रक्रिया है तथा इसे प्रति-अवकलन (Anti-derivatives) भी कहते हैं, अर्थात् यदि
\(\frac{d}{d x}\){F(x)} = f(x)

तो F(x), दिये हुए फलन (x) का x सापेक्ष समाकलन कहलाता है। इसे संकेतन रूप (Symbolically) में निम्न प्रकार से व्यक्त किया जाता है-fx)dx = F(x) जहाँ पर संकेत (जो कि अंग्रेजी अक्षर S, जिसका प्रयोग योग के लिए किया जाता है, का एक बढ़ा हुआ रूप है) का प्रयोग समाकलन के लिए किया जाता है तथा dr में अक्षर x, उस चर (Variable) को व्यक्त करता है जिसके सापेक्ष हमें समाकलन करना है फलन (x) जिसका हमें. समाकलन करना होता है, उसे समाकल्य (Integrand) कहते हैं तथा F(x) की समाकल (Integral) कहते हैं। अतः

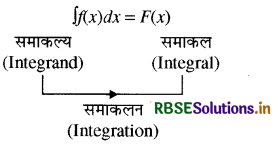
उदाहरणार्थ

• चूँकि \(\frac{d}{d x}\)(sin x) = cos x ∴ ∫cos xdx = sin x
• चूँकि \(\frac{d}{d x}\)(tan x) = sec² x ∴ ∫sec²xdx = tan x
• \(\frac{d}{d x}\left(\frac{x^{5}}{5}\right)\) = x⁴ ∴∫x⁴dx = \(\frac{x^{5}}{5}\)
• \(\frac{d}{d x}\left(\frac{e^{3 x}}{3}\right)\) = e^3x = \(\frac{e^{3 x}}{3}\)

 

समाकलन-अचर (The Constant of Integration):
हम जानते हैं कि किसी भी अचर फलन का अवकल गुणांक शून्य होता है। अर्थात्
\(\frac{d}{d x}\)(c) = 0, जहाँ c एक अचर फलन है।
अब यदि तब \(\frac{d}{d x}\){F(x)} = f(x)
तब \(\frac{d}{d x}\){F(x) + c} = \(\frac{d}{d x}\){F(x)} + \(\frac{d}{d x}\)(c)
= f(x) + 0
= f(x)
अतः समाकलन की परिभाषा से
∫f(x) dx = F(x) + c

यहाँ पर c, समाकलन-अचर (The Constant of Integration) कहलाता है तथा चर x से स्वतंत्र (Independent) होता है। c के अलग-अलग मान रखने पर दिये हुये फलन (x) के भिन्नभित्र समाकल प्राप्त होते हैं जिनमें केवल अचर पद का ही अन्तर होता है। अतः F(x) + c, फलन f(x) का व्यापक समाकल कहलाता है।

व्यापक समाकल में c निश्चित नहीं होता। c की अनिश्चितता के कारण यह अनिश्चित समाकल (Indefinite Integral) भी कहलाता है।

उदाहरणार्थ
(i) चूँकि \(\frac{d}{d x}\)(tan x + c) = sec²x
∴ ∫sec²x dx = tan x + c

(ii) चूंकि \(\frac{d}{d x}\)(e^x + c) = e^x
∴ ∫e^xdx = e^x + c

(iii) चूँकि \(\frac{d}{d x}\)(sin x + c) = cos x
∴ ∫cos x dx = sin x + c

टिप्पणी :
छात्रों को अनिश्चित समाकलन की प्रत्येक समस्या में समाकलन की प्रक्रिया के अन्त में समाकलन-अचर लिखने का अभ्यास होना चाहिए। यह समाकलन की प्रक्रिया के बाद अन्त में जोड़ा जाता है। सुविधा के लिए हम इसे बार-बार नहीं लिखते। |

समाकलन के प्रमेय (Theorems on Integration):
प्रमेय-1 : यदि समाकलन-अचर हटा दिया जाये, तो
\(\frac{d}{d x}\)[∫f(x)dx] = f(x)

उपपत्ति : माना कि
\(\frac{d}{d x}\){F(x)} = f(x) ....(1)

तो समाकलन की परिभाषानुसार
∫f(x)dx = {F(x) + c} ..............(2)

जहाँ c एक अचर है।
समीकरण (2) के दोनों पक्षों का x के सापेक्ष अवकलन करने पर
\(\frac{d}{d x}\)[∫f(x)dx] = \(\frac{d}{d x}\){F(x) +c}
= \(\frac{d}{d x}\){F(x)} +\(\frac{d}{d x}\)(c)
= f(x) + 0 [समी. (i) से]
\(\frac{d}{d x}\)[∫f(x)dx] = f(x)
इस प्रमेय से यह सिद्ध होता है कि समाकलन की प्रक्रिया, अवकलन की प्रतिलोम (Inverse) प्रक्रिया है।

प्रमेय-2 एक अचर तथा फलन के गुणनफल का समाकल उस अचर तथा फलन के समाकल के गुणनफल के बराबर होता है, अर्थात्
∫kf(x)dx = k∫f(x)dx
जहाँ k अचर है।

उपपत्ति-अवकलन गणित के प्रमेय से हम जानते हैं कि
\(\frac{d}{d x}\)[k∫f(x)dr] = k\(\frac{d}{d x}\)[∫f(x)dx]
= kf(x) [प्रमेय 1 से]
अतः समाकलन की परिभाषानुसार
∫kf(x)dx = k∫f(x)dx

प्रमेय-3
∫{f₁(x) ± f₂(x)}dx = ∫f₁(x)dx ± ∫f₂(x)dx
अर्थात् दो फलनों के योग व अन्तर का समाकल उनके समाकलों के योग व अन्तर के बराबर होता है।

उपपत्ति
माना ∫f₁(x)dx = Φ₁(x) ....(1)
तथा ∫f₂(x)dx = Φ₂(x) ....(2)
अतः
\(\frac{d}{d x}\)Φ₁(x) = f₁(x) तथा \(\frac{d}{d x}\)(x) = Φ₂(x) = f₂(x)
∴ \(\frac{d}{d x}\){Φ₁(x) ± Φ₂(x)} = \(\frac{d}{d x}\)Φ₁(x) + \(\frac{d}{d x}\)Φ₂(x)
= f₁(x) + f₂(x)

समाकलन करने पर
Φ₁(x) ± Φ₂(x) = ∫{f₁(x) ± f₂(x)}dx
या ∫f₁(x)dx ± ∫f₂(x)dx = ∫{f₁(x) ± f₂(x)}dx [समीकरण (1) व (2) से]
इस प्रमेय को परिमित संख्या के पदों के समाकल के लिए भी प्रयोग कर सकते हैं।
∴ ∫{f₁(x) ± f₂(x) ± f₃(x)} ± ......... ± f_n(x)}dx
= ∫f₁(x)dx ± ∫f₂(x)dx ± ∫f₃(x)dx ±...... ± ∫f_n(x)dx
इस प्रकार समाकलन संक्रिया परिमित संख्या के पदों पर बंटित होती है।

टिप्पणी

• इस प्रमेय को पद प्रति पद समाकलन का नियम कहते हैं।
• इस नियम का अनन्त पदों के योग के समाकल पर लागू होना आवश्यक नहीं है।

व्यापीकरण
∫af₁(x)dx ± ∫bf₂(c)dx= a∫f₁(x)dx ± b∫f₁(x)dx

समाकलन के मानक सूत्र (Standard Formulae of Integration):
अवकलन गणित के मानक सूत्रों में केवल मात्र परिभाषा का प्रयोग करने से ही समाकलन के लिये अनेक संगत सूत्र प्राप्त किये जा सकते हैं। ऐसा निम्न सारणी में दर्शाया गया है :

अवकलज सूत्र	संगत समाकल सूत्र
\(\frac{d}{d x}\)(c) = 0, c अचर है	∫0 d x=c  अचर
(xn) = nxn-1, n ≠ 0 या \(\frac{d}{d x}\left(\frac{x^{n+1}}{n+1}\right)\) = xn, n ≠ -1	∫nxn-1 dx = xn + c, n ≠ 0 ∫xn dx =  \(\frac{x^{n+1}}{n+1}\) + c, n ≠ -1
\(\frac{d}{d x}\)(log|x|) = \(\frac{1}{n}\), n ≠ 0	∫\(\frac{1}{x}\)dx = log|x| + c, x ≠ 0
\(\frac{d}{d x}\)(ex) = ex	∫ex dx = ex + c
\(\frac{d}{d x}\left(\frac{a^{x}}{\log _{e} a}\right)\) = ax, a > 0, a ≠ 1	∫ax dx =  \(\frac{a^{x}}{\log _{e} a}\) + c = ax logae + c, a > 0, a ≠ 1
\(\frac{d}{d x}\)(sinx) = cos x  जहाँ x रेडियन में है।	∫cos x dx = sin x + c जहाँ x रेडियन में है।
\(\frac{d}{d x}\)(-cos x) = sin x	∫sin x dx = -cos x + c
\(\frac{d}{d x}\)(tan x) = sec2x	∫sec2x dx = tan x + c
\(\frac{d}{d x}\)(-cotx) = cosec2x = csc2x	∫cosec2x dx = ∫csc2x dx = -cot x + c
\(\frac{d}{d x}\)(sec x) = sec x tan x	∫sec x tan x dx = sec2 x + c
\(\frac{d}{d x}\)(-cosec x) = cosec x cot x	∫cosec x cct x dx = - cosec x + c
\(\frac{d}{d x}\)(sin hx) = cos hx	∫cos hx dx = sin hx + c
\(\frac{d}{d x}\)(cos hx) = sin hx	∫sin hx dx = cos hx + c
\(\frac{d}{d x}\)(tan hx) = sech2x	∫sech2x dx = tan hx + c
\(\frac{d}{d x}\)(-coth x) = cosech2x	∫cosech2x dx = - cot hx + c
\(\frac{d}{d x}\)(-sech x) = sec hx tan hx	∫sec hx tan hx dx = -sec hx + c
\(\frac{d}{d x}\)(-cosec hx) = cosec hx cot hx	∫cosec hx cot hx dx = -cosec hx + c
\(\frac{d}{d x}\)(sin-1x) = (arcsin x) = \(\frac{1}{\sqrt{1-x^{2}}}\), (|x| < 1)	∫\(\frac{1}{\sqrt{1-x^{2}}}\) dx = sin-1 x + c = arcsin x + c, (|x| < 1)
\(\frac{d}{d x}\)(-cos-1x) = (-arccos x) = -\(\frac{1}{\sqrt{1-x^{2}}}\)	∫-\(\frac{1}{\sqrt{1-x^{2}}}\)dx = -cos-1 x + c
\(\frac{d}{d x}\)(tan-1x) = (-arctan x) = \(\frac{1}{1+x^{2}}\)	∫\(\frac{1}{1+x^{2}}\)dx = tan-1x + c = arctan x + c
\(\frac{d}{d x}\)|x| = x ≠ 0	∫\(\frac{|x|}{x}\), dx = |x| + c, (x ≠ 0)

टिप्पणी: ऊपर दिये गये हर सूत्र में समाकलन-अचर (Constant of Integration) c जोड़ा जाना चाहिये।
संक्षिप्त रूप : cosec x = csc x . arcsin = sin^-1 इत्यादि।

समाकलन की विधियाँ (Methods of Integration):
पिछले अध्याय में हमने ऐसे समाकलनों की चर्चा की थी, जो कुछ फलनों के अवकलजों से सरलतापूर्वक प्राप्त किये जा सकते हैं। यह विधि निरीक्षण पर आधारित थी। इसमें ऐसे फलन F की खोज की जाती है जिसका अवकलज f है। इससे f के समाकलन की प्राप्ति होती है। कई फलन ऐसे होते हैं जिनका समाकलन सीधे तौर से नहीं किया जा सकता है। ऐसे फलनों को हम पहले आदर्श रूप में बदलते हैं ताकि उनका समाकलन गत अध्याय के अनुसार किया जा सके। मुख्यतः निम्न विधियों की सहायता से दिये हुए समाकलन को आदर्श रूप में बदला जा सकता ह

• प्रतिस्थापन द्वारा समाकलन (Integration by Substitution)
• आंशिक भिन्नों में वियोजन द्वारा समाकलन (Integration by Resolution into Partial Fraction)
• खण्डशः समाकलन (Integration by Parts)

प्रतिस्थापन द्वारा समाकलन (Integration by Substitution)
इस विधि में समाकलन के लिये दिये हुए फलन में उचित प्रतिस्थापन (Substitution) से स्वतंत्र चर (Independent Variable) को नये चर में परिवर्तित करके समाकल (Integral) को मानक रूप में लाया जाता है। इसके पश्चात् पहले अनुच्छेद में बताये अनुसार मानक सूत्रों का प्रयोग करके समाकलन किया जाता है। इस दशा में नीचे दिया गया प्रमेय काफी लाभदायक सिद्ध होगा।

प्रमेय (Theorem) : यदि ∫f(x)dx चर x को संबंध x = (t) द्वारा चर t में बदला जाये, तब
∫f(x)dx = ∫f{Φ(t)} Φ'(t)dt
जहाँ Φ'(t) = {Φ(t)
उपपत्ति-माना I = ∫f (x)dx
तब परिभाषा से \(\frac{d I}{d t}\) = f(x)
अब यदि x = Φ(t) हो, तो \(\frac{d x}{d t}\) = Φ'(t) ...(3)
पुन: \(\frac{d I}{d t}=\frac{d I}{d x} \cdot \frac{d x}{d t}\)
= f(x).Φ'(t) [समी. (2) व (3) से]
अतः समाकलन की परिभाषा से
I = ∫f(x) Φ'(t) dt
अर्थात् ∫f(x)dx = ∫f{Φ(t)}Φ'(t)dt

टिप्पणी:
उपर्युक्त प्रमेय से यह स्पष्ट है कि समाकलन की प्रतिस्थापन विधि में समाकल्य (Integrand) को ऐसे दो गुणनखण्डों में तोड़ना होता है कि उनमें से एक गुणनखण्ड किस फलन का अवकल गुणांक हो, दूसरा गुणनखण्ड उसके पदों में व्यक्त किया जा सके। हम इसे निम्न उदाहरणों से स्पष्ट करेंगे।

त्रिकोणमितीय सर्व-समिकाओं के उपयोग द्वारा समाकलन (Integration using Trigonometric Identities) त्रिकोणमितीय फलनों के सूत्र का संकलन ।

• sin 2A = 2sin A cos A
• cos 2A = cos²A - sin²A = 2cos²A - 1 = 1 - 2 sin²A
• sin 2A = \(\frac{2 \tan \mathrm{A}}{1+\tan ^{2} \mathrm{~A}}\)
• cos 2A = \(\frac{1-\tan ^{2} \mathrm{~A}}{1+\tan ^{2} \mathrm{~A}}\)
• tan 2A = \(\frac{2 \tan \mathrm{A}}{1+\tan ^{2} \mathrm{~A}}\)
• sin 3A = 3sin A - 4sin³A
• cos 3A = 4cos³A - 3cos A
• tan 3A = \(\frac{3 \tan \mathrm{A}-\tan ^{3} \mathrm{~A}}{1-3 \tan ^{2} \mathrm{~A}}\)
• sin(- A) = - sin A, cos (- A) = cos A
• tan(- A) = - tan A
• 2 sin A cos B = sin (A + B) + sin (A - B)
• 2 cos A sin B = sin (A + B) - sin (A - B)
• 2 cos A cos B = cos (A + B) + cos (A - B)
• 2 sin A sin B = cos (A - B) - cos (A + B)

कुछ विशिष्ट फलनों के समाकल (Integrals of Some Particular Functions):
इस परिच्छेद में हम निम्नलिखित महत्वपूर्ण समाकलन सूत्रों की व्याख्या करेंगे और बहुत से दूसरे संबंधित प्रामाणिक समाकलनों को ज्ञात करने में उनका प्रयोग करेंगे।

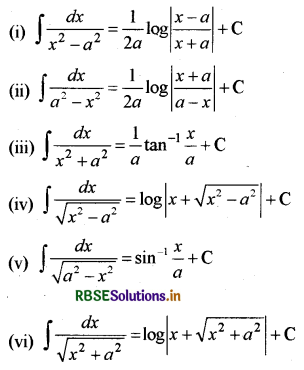
अब हम उपर्युक्त परिणामों को सिद्ध करते हैं।

(i) हम जानते हैं कि

(ii) ∫\(\frac{d x}{a^{2}-x^{2}}=\frac{1}{2 a} \log \left|\frac{x+a}{a-x}\right|\)+ C

(iii) x = a tan θ रखने पर
dx = a sec θ dθ और tan^-1\(\left(\frac{x}{a}\right)\) = θ
इसलिये

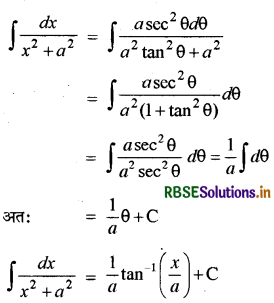
(iv) x = a sec θ रखने पर dx = a sec θ tan θ dθ इसलिये
इसलिये

(v) माना x =a sin θ dx = a cosθ dθ
इसलिये

(vi) x = a tan θ dx = a sec²θ dθ
इसलिये

इन प्रामाणिक सूत्रों के प्रयोग से अब हम कुछ और सूत्र प्राप्त करते हैं जो कि अनुप्रयोग की दृष्टि से उपयोगी हैं और इनका प्रयोग दूसरे समाकलनों का मान ज्ञात करने के लिये किया जाता है।

(vi) समाकलन ∫\(\frac{d x}{a x^{2}+b x+C}\) अथवा ∫\(\frac{d x}{\sqrt{a x^{2}+b x+\mathrm{C}}}\)
ज्ञात करने के लिये हम
ax² + bx + c = a[x² + \(\frac{b}{a}\) x + \(\frac{c}{a}\)]
= a\(\left[\left(x+\frac{b}{2 a}\right)^{2}+\left(\frac{c}{a}-\frac{b^{2}}{4 a^{2}}\right)\right]\) लिखते हैं।

अब x + \(\frac{b}{2 a}\) = 1 को मानते हैं dx = dt एवं \(\frac{c}{a}-\frac{b^{4}}{4 a^{2}}\) = ±k² लिखते हुये हम पाते हैं कि \(\left(\frac{c}{a}-\frac{b^{2}}{4 a^{2}}\right)\) के चिह्न पर निर्भर करते हुये यह समाकलन \(\frac{1}{a} ∫\frac{d t}{t^{2} \pm k^{2}}\) अथवा \(\frac{1}{\sqrt{a}}\) ∫\(\frac{d t}{\sqrt{t^{2} \pm k^{2}}}\) में परिवर्तित हो जाता है और इस प्रकार से इसका मान सूत्र लगाकर ज्ञात किया जा सकता है।

(vii) ∫\(\frac{p x+q}{a x^{2}+b x+\mathrm{C}}\) dx , अथवा ∫\(\frac{(p x+q)}{\sqrt{a x^{2}+b x+C}}\) dx जहाँ p, q, a, b, c अचर हैं, के प्रकार के समाकलन ज्ञात करने के लिये हम ऐसी दो वास्तविक संख्यायें A और B ज्ञात करते हैं ताकि
px + q = A\(\frac{d}{d x}\)(ax² +bx+C) + B = A(2ax + b) + B, A तथा B, ज्ञात करने के लिये हम दोनों पक्षों से x के गुणांकों एवं अचरों को समान करते हैं। A तथा B के ज्ञात हो जाने पर समाकलन ज्ञात प्रामाणिक रूप में परिवर्तित हो जाता है।

आंशिक भिन्नों द्वारा समाकलन (Integration By Partial Fractions):
परिमेय बीजीय फलन (Rational Algebraic Functions)

• यदि f(x) तथा g(x) दो x के बहुपद फलन हों तो भिन्न f(x)/ g(x), x का परिमेय बीजीय फलन कहलाती है। उदाहरणार्थ
  \(\frac{x^{2}-x+1}{x^{3}+x^{2}-5 x}\), \(\frac{x^{3}}{x^{2}+8 x-12}\)
  \(\frac{4 x+1}{(x-2)^{2}(x+3)}\) इत्यादि
• यदि किसी परिमेय बीजीय भिन्न में अंश की धात हर की घात से कम हो तो ऐसी भिन्न परिमेय वास्तविक भिन्न (Rational Proper Fraction) कहलाती है और यदि अंश की घात हर की घात के बराबर या ज्यादा हो तो वह परिमेय विषम भिन्न (Rational Improper Fraction) कहलाती है। उपर्युक्त भिन्न में पहली तथा तीसरी परिमेय वास्तविक भिन्न है और दूसरी परिमेय विषम भिन्न है चूँकि यहाँ पर अंश की घात हर की घात से ज्यादा है।

परिमेय बीजीय फलनों का समाकलन (Integration of Rational Algebaric Functions):
यदि परिमेय बीजीय फलन एक विषम भिन्न (Improper Fraction) हो तो हर का अंश में भाग देते हैं। यह भाग तब तक चलता रहता है जब तक कि शेषफल की घात हर की घात से कम न हो जाये । इसको बहुपद (Polynomial) तथा वास्तविक भिन्न (Proper Fraction) के योग के रूप में व्यक्त किया जा सकता है।

उदाहरणार्थ
\(\frac{x^{3}}{x^{2}+8 x+12}\) = (x - 8) + \(\frac{52 x+96}{x^{2}+8 x+12}\)
यहाँ पर बहुपद का आसानी से समाकलन किया जा सकता है। वास्तविक भिन्न का समाकलन करने हेतु इसे आंशिक भिन्नों (Partial Fractions) में वियोजित कर प्रत्येक भिन्न का समाकलन किया जाता है।

वास्तविक भिन्न को आंशिक भिन्नों में वियोजित करने के नियम (Rules of Resolving a Proper Fraction into Partial Fractions)
स्थिति 1 : जब हर में बिना पुनरावृत्ति के एक-घातीय गुणनखण्ड (Liner Factor) हो (When there are non-repeated linear factor in denominator)
उदाहरणाथ \(\frac{\mathrm{F}(x)}{(x+a)(x+b)(x+c)} \equiv \frac{\mathrm{A}}{x+a}+\frac{\mathrm{B}}{x+b}+\frac{\mathrm{C}}{x+c}\)
जहाँ A, B, C अचर अज्ञात राशियाँ हैं, जिनका मान ज्ञात करना है। लघु विधि (Short Method) इस विधि में अचर राशियों के मान, दाहिने पक्ष में मानी गई भिन्नों का लघुत्तम समापवर्त्य (L.C.M.) लेकर दोनों पक्षों के अंशों को बराबर रखने पर प्राप्त समीकरण में क्रमानुसार x = a, b, c, ..... रखकर प्राप्त किये जा सकते हैं।

स्थिति 2 : जब हर में पुनरावृत्ति वाले रैखिक खण्ड हों (When there are repeated liner factors in denominator)
उदाहरणार्थ
\(\frac{\mathrm{F}(x)}{(a x+b)^{n}}=\frac{\mathrm{A}_{1}}{a x+b}+\frac{\mathrm{A}_{2}}{(a x+b)^{2}}+\ldots \ldots \ldots \ldots+\frac{\mathrm{A} n}{(a x+b)^{n}}\)
जहाँ A₁, A₂, .....A_n अचर अज्ञात राशियाँ हैं, जिनका मान ज्ञात करना है।

स्थिति 3 : जब हर में बिना पुनरावृत्ति के द्विघात खण्ड हों (When there are non-repeated quadratic factors in denominator) हर में बिना पुनरावृत्ति के (ax² + bx + c) के रूप में द्विघात खण्ड (Quadratic factors) हों तो आंशिक भिन्न को अग्र प्रकार से वियोजित करते हैं
उदाहरणार्थ \(\frac{F(x)}{(x+a)\left(x^{2}+b x+c\right)} \equiv \frac{A}{x+a}+\frac{B x+C}{x^{2}+b x+c}\)
जहाँ A, B, C अचर अज्ञात राशियाँ हैं, जिनका मान ज्ञात करना है।

स्थिति 4 :
जब हर में पुनरावृत्ति वाले द्विघात खण्ड हों (When there are repeated quadratic factors in denominator) हर में पुनरावृत्ति वाले (ax² + bx + c)ⁿ के रूप में द्विघात खण्ड के संगत n आंशिक भिन्नों का निम्न रूप का समूह होता है।
\(\frac{\mathrm{F}(x)}{\left(a x^{2}+b x+c\right)^{n}}=\frac{\mathrm{A}_{1} x+\mathrm{B}_{1}}{a x^{2}+b x+c}+\frac{\mathrm{A}_{2} x+\mathrm{B}_{2}}{\left(a x^{2}+b x+c\right)^{2}}+\ldots \ldots \ldots+\frac{\mathrm{A}_{n} x+\mathrm{B} n}{\left(a x^{2}+b x+c\right)^{n}}\)
जहाँ A₁, A₂, ....., A_n, B₁, B₂, .... B_n, अचर अज्ञात राशियाँ हैं, जिनका मान ज्ञात करना है।

उदाहरणार्थ
\(\frac{\mathrm{F}(x)}{(x+a)\left(x^{2}+b x+c\right)^{2}} \equiv \frac{\mathrm{A}}{(x+a)}+\frac{\mathrm{B} x+\mathrm{C}}{x^{2}+b x+c}+\frac{\mathrm{D} x+\mathrm{E}}{\left(x^{2}+b x+c\right)^{2}}\)
जहाँ A, B, C, D, E अचर अज्ञात राशियाँ हैं, जिनका मान ज्ञात करना है।
उपर्युक्त चारों क्रमों को निम्न तालिका में दिया जा रहा है

परिमेय फलन का रूप	आंशिक भिन्न का रूप
\(\frac{p x+q}{(x-a)(x-b)}\), a ≠ b	\(\frac{A}{x-a}+\frac{B}{x-b}\)
\(\frac{p x+q}{(x-a)^{2}}\)	\(\frac{A}{x-a}+\frac{B}{x-b}\)
\(\frac{p x^{2}+q x+r}{(x-a)(x-b)(x-c)}\)	\(\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c}\)
\(\frac{p x^{2}+q x+r}{(x-a)^{2}(x-b)}\)	\(\frac{A}{x-a}+\frac{B}{(x-a)^{2}}+\frac{C}{(x-b)}\)
\(\frac{p x^{2}+q x+r}{(x-a)\left(x^{2}+b x+c\right)}\)	\(\frac{A}{x-a}+\frac{B x+C}{x^{2}+b x+c}\)

खंडशः समाकलन (Integration By Parts)
पिछले अनुच्छेदों में हमने फलनों के योगफल (sum) तथा व्यवकलन (difference) का समाकलन (integration) किया। कुछ फलनों के गुणनफल का समाकलन प्रतिस्थापन विधि से किया। यहाँ हम फलनों के गुणनफल का समाकलन खण्डशः समाकलन (integration by parts) के नियम से करेंगे।
खण्डशः समाकलन का नियम (Rule of Integration by Parts): कथन : यदि तथा v, x के दो फलन हैं, तो
If u and v are two functions of x, then
∫u.v dx = u∫v dx - ∫{\(\frac{d u}{d x}\)(∫vdx)}dx

प्रमाण : यदि u₁ तथा u₂, x के दो फलन हों, तब अवकलन के नियम से हम जानते हैं कि
\(\frac{d}{d x}\)(u₁.u₂ = u₁\(\frac{d u_{2}}{d x}\) + u₂\(\frac{d u_{1}}{d x}\) .......... (1)
(1) के दोनों पक्षों का x के सापेक्ष समाकलन करने पर

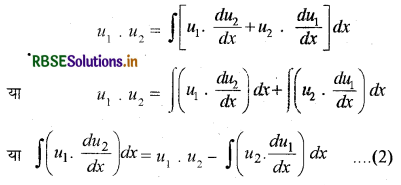
अब मान लो कि u₁ = u तथा \(\frac{d u_{2}}{d x}\) = v, अर्थात् u₂ = ∫v dx
अतः (2) से
∫u.v ak = x ∫v dx - ∫{\(\frac{d u}{d x}\)∫vdx}dx ............(3)
अब यदि पहले फलन को ४ व दूसरे फलन को v से व्यक्त करें तो उपर्युक्त खण्डशः समाकलन नियम को शब्दों में निम्न प्रकार सेव्यक्त कर सकते हैं : दो फलनों के गुणनफल का समाकलन = प्रथम फलन x द्वितीय फलन का समाकलन - [प्रथम फलन का अवकलन - द्वितीय फलन का समाकलन] उपर्युक्त नियम की सहायता से किये गये समाकलन को खण्डशः समाकलन (Integration by parts) कहते हैं।

खण्डशः समाकलन के लिये कुछ महत्वपूर्ण बिन्दु (Some Important Points for Integration by Parts)
(a) खण्डशः समाकलन विधि की सबसे बड़ी सफलता प्रथम व द्वितीय फलन के सही चुनाव पर निर्भर करती है।
(b) फलनों का चुनाव इस प्रकार किया जाना चाहिये कि द्वितीय फलन का समाकल आसानी से ज्ञात किया जा सके।

फलनों के चुनने का कोई व्यापक नियम नहीं है फिर भी हमें निम्न बिन्दु ध्यान में रखने चाहिये :

• यदि समाकल्य चर (x) की घात तथा चरघातांकी या त्रिकोणमितीय फलनों का गुणनफल हो तो चरघातांकों या त्रिकोणमितीय फलन को द्वितीय फलन लेना चाहिए।
• अकेले प्रतिलोम त्रिकोणमितीय फलन या लघुगणकीय फलनों के समाकलन के लिए इकाई 1 को द्वितीय फलन लेकर समाकलन करना चाहिए।
• खण्डशः समाकलन करते समय कई बार दायीं ओर (RHS) को समाकल मूलरूप में या चिह्न परिवर्तन के साथ या उसके गुणन के रूप में पुनः आ जाये, तब ऐसी स्थिति में पक्षान्तरण कर समाकलन करना चाहिये।
• आवश्यकतानुसार खण्डशः समाकलन का सूत्र एक से अधिक बार प्रयोग में लिया जा सकता है।

नोट-फलनों का चुनाव हम, शब्द 'ILATE' में, पहले आने वाले फलन को प्रथम फलन व बाद में आने वाले फलन को द्वितीय फलन चुन सकते हैं। जहाँ

• I - (Inverse trigonometrical functions) प्रतिलोम त्रिकोणमितीय फलनों (sin^-1x, cos^-1x, tan^-1x इत्यादि) के लिए है।
• L - (Logarithmic functions) लघुगणकीय फलनों (log x, log(x² + a) इत्यादि) के लिए है।
• A - (Algebraic functions) बीजीय फलनों (x, x+1, 2x, x इत्यादि) के लिए है।
• T - (Trigonometrical functions) त्रिकोणमितीय फलनों (sin x, cos x, tan x इत्यादि) के लिए है।
• E - (Exponential functions) चरघांताकीय फलनों (a^x,e^x, 2^x, 10x, 3^-x इत्यादि) के लिए है।

खण्डशः समाकल विधि को अब हम कुछ उदाहरणों से स्पष्ट करेंगे।

• ∫e^x{f(x) + f'(x)}dx
• ∫{f(log x) + f'(log x)}dx
• ∫{xf'(x) + f(x)}dx प्रकार के समाकलन जहाँ f'(x) = \(\frac{d}{d x}\)f(x)

(i) माना = ∫e^x{f(x) + f'(x)}dx

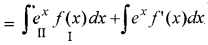
केवल प्रथम समाकल का को दूसरा फलन लेकर खण्डशः समाकलन करने पर
= f(x)∫e^xdx - ∫{\(\frac{d}{d x}\)f(x).∫e^xdx}dx + ∫e^xf(x)dx + C
= f(x)e^X - ∫f(x)e^xdx + ∫e^xf'(x)dx + C
या I = e* f (x) + C

(ii) माना I = ∫{f (log x) + f"(log x)}dx
माना log x =t
x = e ⇒ dx = e^x dt
I = ∫e {f(t) + f"(1)}dt = e' f(t)+C [भाग (i) से]
= xf (log x) + C

(iii) माना I = ∫{xf'(x) + f(x)}dx
= ∫xf'(x)dx + ∫f(x)dx
केवल प्रथम समाकल का x को दूसरा फलन खण्डशः
= x∫f'(x)dx - ∫{\(\frac{d}{d x}\)(x)∫f'(x)dx}dx + ∫f(x)dx + C
= xf(x) - ∫{1.f(x)}dx + ∫f(x)dx + C
= xf(x) - ∫f(x)dx + ∫f(x)dx + C
= xf(x) + C

कुछ अन्य प्रकार के समाकलन (Integrals of some more types)
यहाँ हम खण्डशः समाकलन विधि पर आधारित कुछ विशिष्ट प्रकार के प्रामाणिक समाकलनों की चर्चा करेंगे जैसे कि
(i) ∫\(\sqrt{x^{2}-a^{2}}\)dx
(ii) ∫\(\sqrt{x^{2}+a^{2}}\)dx
(ii) ∫\(\sqrt{a^{2}-x^{2}}\)dx
अब हम उपर्युक्त परिणामों को सिद्ध करते हैं।
(i) माना
I = ∫\(\sqrt{x^{2}-a^{2}}\)dx
अचर फलन 1 को द्वितीय फलन मानते हुये और खण्डशः समाकलन द्वारा हम पाते हैं

इसी प्रकार दूसरे दो समाकलनों में अचर फलन 1 को द्वितीय
फलन लेकर एवं खण्डशः समाकलन विधि द्वारा हम पाते हैं।
(ii) ∫\(\sqrt{x^{2}+a^{2}}\) dx = \(\frac{1}{2}\) x \(\sqrt{x^{2}+a^{2}}\) + \(\frac{a^{2}}{2}\)log|x + \(\sqrt{x^{2}+a^{2}}\)| + C

(ii) ∫\(\sqrt{a^{2}-x^{2}}\) dx = \(\frac{1}{2}\) x \(\sqrt{a^{2}-x^{2}}\)-\(\frac{a^{2}}{2}\) sin^-1 \(\frac{x}{a} \) + C
विकल्पत : समाकलनों (i), (ii) और (ii) में क्रमशःx = a sec θ , x = a tan θ और x = a sin θ, प्रतिस्थापन करने पर भी इन समाकलनों को ज्ञात किया जा सकता है।

निश्चित समाकलन (Definite Integrals):
अभी तक हमने अनिश्चित समाकलनों के बारे में अध्ययन किया है और कुछ विशिष्ट फलनों के समाकलनों सहित अनिश्चित समाकलनों को ज्ञात करने की कुछ विधियों पर चर्चा की है। इस परिच्छेद में हम किसी फलन के निश्चित समाकलन का अध्ययन करेंगे।

परिभाषा (Definition): यदि [F(x)] = f(x) तथा a व b, स्वतंत्र चर x के दो मान हों, तो
\(\int_{a}^{b}\)f(x) dx = \([\mathrm{F}(x)]_{a}^{b}\) = F(b) - F(a)
को a तथा b सीमाओं के बीच f(x) का निश्चित समाकल (Definite Integral) कहते हैं । यहाँ a को समाकल की निम्न सीमा (Lower limit) तथा b को उच्च सीमा (Upper limit) कहते हैं । अन्तराल (a, b) को समाकलन परिसर (range of integration) कहते हैं ।

यहाँ ध्यान देने योग्य है कि, यदि
∫f(x) dx = F(x) + C हो तो
\(\int_{a}^{b}\) f(x) d x = \([\mathrm{F}(x)+\mathrm{C}]_{a}^{b}\)
= {F(b) + C} - {F(a) + C}
= F(b) - F(a)

अतः किसी फलन का निश्चित समाकल एक निश्चित संख्या होती है। निश्चित समाकलन का मान स्वेच्छ अचर C पर निर्भर नहीं करता अर्थात् अद्वितीय (unique) होता है।

योगफल की सीमा के रूप में निश्चित समाकलन (Definite Integral as the limit of a sum)
परिभाषा (Definition) : यदि f(x) अन्तराल [a, b] में परिभाषित, कोई वास्तविक मानों का सतत फलन (real valued continuous function) हो और अन्तराल [a, b] को n बराबर भागों में बिन्दुओं a+h, a + 2h, ...a + (n-1)h द्वारा विभाजित किया जाये जिसमें प्रत्येक भाग की लम्बाई h हो, तो ।
\(\int_{a}^{b}\)f(x) dx = \(\lim _{h \rightarrow 0}\)h[f(a) + f(a+h) + f(a +2h) +...+ f{a(n-1)h}]
जहाँ n → ∞ तथा nh = b - a ⇒ h = \(\frac{b-a}{n}\)
इस परिभाषा के प्रयोग से निश्चित समाकल के मान ज्ञात करने की विधि को प्रथम सिद्धान्त से समाकलन या आदितः (ab - initio) समाकलन या संकलन से समाकलन कहते हैं।

समाकलन गणित का मूल प्रमेय (Fundamental Theorem of Integral Calculus):
कथन (Statement) : यदि f (x) अन्तराल [a, b] में परिभाषित है एक वास्तविक (real valued) सतत फलन (continuous function) हो तथा f (x) का समाकलन (integral) यदि F(x) हो अर्थात् ∫f(x)dx = F(x) तो,
\(\int_{a}^{b}\) f(x) d x=[F(x)]_{a}^{b} = F(b) - F(a)
= \(\lim _{h \rightarrow 0}\)h[f(a) + f(a+h) + f(a - 2h) + ..+ f{a + (n-1)h}]
F(b) - F(a) निश्चित समाकल का मान कहलाता है और यह अद्वितीय (unique) होता है।

उपपत्ति (Proof):
माना f(x) चित्रानुसार [a, b] में परिभाषित एक ' वास्तविक (real valued) एवं सतत फलन (continuous function)

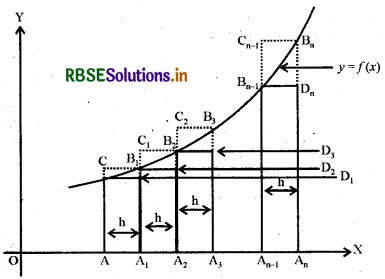
अन्तराल [a, b] को 'n' समान अन्तरालों (h लम्बाई के) में विभाजित करने पर
AA₁ = OA_n - OA
या AA₁ + A₁A₂ + A₂A₃ + ... +A_n-1A_n = b - a

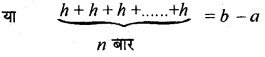
या nh = b - a ⇒ h = \(\frac{b-a}{n}\)
माना y = f(x)
अतः जब x = a, y = f (a)
∴ x = a पर y = f(a)
अतः चित्रानुसार बिन्दु B के निर्देशांक [a, f(a)] होंगे अर्थात्
AB = f (a) इसी प्रकार
A₁B₁ =f (a+h);
A₂B₂ = fa+2h);
A₃B₃ = f (a + 3h); ....; A_n-1B_n-1 = f(a + (n-1)h)
तथा A_nB_n = f (a + nh)
अतः चित्रानुसार, माना छायांकित आयताकार पट्टिकाओं, जो कि वक्र के नीचे हैं, के क्षेत्रफलों का योगफल A, लें तो
Δ₁= आयत AA₁D₁B+ आयत A₁A₂D₂B₁ + आयत A₂A₃D₃B₂ +.....+ आयत A_n-1A_nD_nB_n-1
= (AA₁)(AB)+(A₁A₂)(A₁B₁) + (A₂A₃)(A₂B₂) +...+ (A_n-1A_n)(A_n-1B_n-1)
= hf (a) + hf (a + h) + hf (a + 2h) +...+hf (a + \(\overline{n-1}\)h)
= h[f(a) + f(a +h) + f(a +21) +....+ f(a + \(\overline{n-1}\)h)]
उपर्युक्त क्षेत्रफल वक्र y = f (x), x अक्ष तथा दो कोटियों x = a,x = b से परिबद्ध क्षेत्रफल AA_nB_nBA से कम होगा। अतः उपर्युक्त विवेचना से स्पष्ट है कि A का मान Δ₁ से ज्यादा तथा Δ₂ से कम होगा
Δ₁ < Δ < Δ₂
पुनः Δ₂ - Δ₁ = hf(a + nh)- hf(a)
= hf(b) - hf(a) {∵nh = b - a}
= h[f(b) - f(a)]
यहाँ हम स्पष्ट रूप से देख सकते हैं कि जब आयताकार पट्टिकाओं की चौड़ाई ‘h', अत्यधिक अल्प होगी अर्थात् h → θ तो Δ₁, और Δ₂, का मान Δ के अत्यधिक निकट होगा। अर्थात्

जो यह दर्शाता है कि निश्चित समाकल को योगफल सीमा के रूप में व्यक्त कर सकते हैं।

टिप्पणी : उपर्युक्त सूत्रों को निम्न प्रकार से भी व्यक्त कर सकते हैं :
(i) \(\int_{a}^{b}\) f(x) dx = \(\lim _{n \rightarrow \infty}\)h[f(a)+ f(a+h)+...+...+f(a + \(\overline{n-1}\)h)]]
जहाँ h = \(\frac{b-a}{n}\) (स्पष्ट है कि, जब n → ∞, h → 0)

(ii) \(\int_{a}^{b}\) f(x) dx = \(\lim _{n \rightarrow \infty}\)h[f (a+h) + f(a + 2h) +...+f(a+nh)]
जहाँ h = \(\frac{b-a}{n}\)
प्रथम सिद्धान्त से समाकलन का मान ज्ञात करने के लिये उपर्युक्त में से किसी भी सूत्र का प्रयोग कर सकते हैं।

कुछ महत्वपूर्ण परिणाम (Some important results)
(i) n प्राकृत संख्याओं का योग
\(\sum_{r=1}^{n}\)r = 1 + 2 + 3 +.....+ n = \(\frac{n(n+1)}{2}\)

(ii) n प्राकृत संख्याओं के वर्गों का योग
\(\sum_{r=1}^{n}\)r = 1² + 2² + 3² ...... + n² = \(\frac{n(n+1)(2 n+1)}{6}\)

(ii) n प्राकृत संख्याओं के घनों का योग
\(\sum_{r=1}^{n}\)r = 1³ + 2³ + 3³ .....n³ = \(\left[\frac{n(n+1)}{2}\right]^{2}\)

(iv) n विषम प्राकृत संख्याओं का योग
\(\sum_{r=1}^{n}\)r = 1 + 3 + 5 +....(2n - 1) = n²

(v) समान्तर श्रेणी के n पदों का योग
a + (a + d) + (a + 2d) + .... + {a+ (n-1)d} = \(\frac{n}{2}\)[2a + (n-1)d]

(vi) गुणोत्तर श्रेणी के n पदों का योग
a + ar + ar² +.... + ar^n-1 = \(\frac{a\left(r^{n}-1\right)}{r-1}\), r ≠ 1

कलन की आधारभूत प्रमेय (Fundamental Theorem of Calculus):
क्षेत्रफल फलन (Area Function)
हमने \(\int_{a}^{b}\)f(x) dx को वक्र y = f(x), x- अक्ष एवं कोटियों x = a तथा x = b से घिरे क्षेत्र के क्षेत्रफल के रूप में परिभाषित किया है। माना कि [a, b] में x.कोई बिन्दु है तब \(\int_{a}^{b}\)f(x) dx आकृति में छायांकित क्षेत्र के क्षेत्रफल को निरूपित करता है । इस छायांकित क्षेत्र का क्षेत्रफल x के मान पर निर्भर है। दूसरे शब्दों में, इस छायांकित क्षेत्र का क्षेत्रफल x का एक फलन है। हम x के इस फलन को A (x) से निर्दिष्ट करते हैं । इस फलन A (x) को हम क्षेत्रफल फलन कहते हैं अर्थात्
A(x) = \(\int_{a}^{b}\)f (x) dx ....(1)
इस परिभाषा पर आधारित प्रथम आधारभूत प्रमेय और द्वितीय आधारभूत प्रमेय निम्न प्रकार है, इनकी उत्पत्ति इस पाठ्यक्रम की सीमा के बाहर है।

प्रमेय-1 समाकलन गणित की प्रथम आधारभूत प्रमेय (First Fundamental Theorem of Integral Calculus):
मान लीजिये कि बन्द अन्तराल [a,b] पर एक सतत फलन है और A (x) क्षेत्रफल फलन है। तब सभी x ∈ [a, b] के लिये A (x) = f(x)

समाकलन गणित की द्वितीय आधारभूत प्रमेय (Second Fundamental Theorem of Integral Calculus)
यहाँ पर हम एक महत्वपूर्ण प्रमेय की व्याख्या करते हैं जिसकी सहायता से हम प्रति अवकलज का उपयोग करते हुए निश्चित समाकलनों का मान ज्ञात करते हैं।

प्रमेय-2 मान लीजिये कि बन्द अन्तराल [a, b] पर एक सतत फलन है और /का प्रति अवकलज F है।
तब \(\int_{a}^{b}\)f(x) dx = \([f(x)]_{a}^{b}\) = F(b) - F(a)

प्रतिस्थापन द्वारा निश्चित समाकलनों का मान ज्ञात करना (Evaluation Of Definite *Intégrals By Substitution)
यदि दिये हुये फलन का समाकल प्रतिस्थापन द्वारा ज्ञात करना हो, तो समाकल की सीमाओं को नई प्रतिस्थापित चर राशि के अनुसार बदल लेना चाहिये ऐसा करने से पहले वाली चर राशि का नये समाकल से कोई संबंध नहीं रहता है।

निश्चित समाकलनों के कुछ गुणधर्म (Some Properties of Definite Integrals)
P₁: \(\int_{a}^{b}\)f(x) dx = \(\int_{a}^{b}\)f(t)

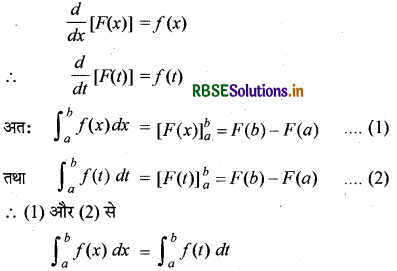
अतः निश्चित समाकल में यदि समाकल की सीमाएं (limits) समान रहें, तो चर (variables) राशि के प्रतीक को बदलने पर इसके मान में कोई परिवर्तन नहीं होता।

P₂ : \(\int_{a}^{b}\) f(x) dx = -\(\int_{a}^{b}\) f(x) dx विशिष्टतया \(\int_{a}^{a}\)f(x) dx = 0
उपपत्ति :
माना = \(\frac{d}{d x}\)[P(x)] = f (x)

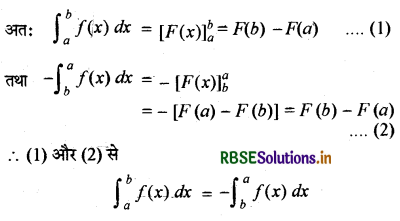
यहां हम प्रेक्षित करते हैं कि यदि a = b, तब \(\int_{a}^{a}\)f(x) dx = 0
अतः निश्चित समाकल की सीमाओं को परस्पर बदलने पर समाकल के मान का चिह्न बदल जाता है।

P₃: \(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{c}\) f(x) dx + \(\int_{c}^{b}\) f(x) dx
उपपत्ति :
माना = \(\frac{d}{d x}\)[F(x)] = f(x)

P₄: \(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{b}\) f(a + b - x) dx
उपपत्ति :
R.H.S. \(\int_{a}^{b}\) f(a + b - x) dx
मान लीजिए a+ b - x = t
तब 0 + 0 - dx = dt
dx = - dt
जब x = a तब t= b और जब x = b तब tra
\(\int_{a}^{b}\) f(a+b-x) dx = -\(\int_{b}^{a}\) f(t) dt

= \(\int_{a}^{b}\)f(t)dt P₂, से
= \(\int_{a}^{b}\)f(x)dx P₁ से
अतः R.H.S. = L.H.S.

P₅ :\(\int_{o}^{a}\) f(x) dx = \(\int_{o}^{a}\) f(a-x) dx
उपपत्ति : यदि R.H.S. के समाकल में a -x = 1 रखें, तो dx = dt तथा,
जब x = 0, t = a और जब x = a, t = 0

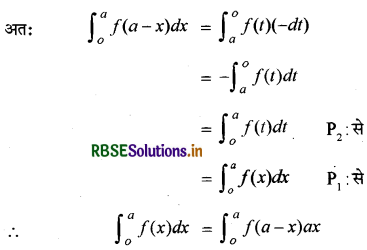
P₆ : \(\int_{-a}^{a}\) f(x) dx = {2 \(\int_{0}^{a}\)f(a - x)dx
यदि f (x) सम (even) फलन हो
=0, यदिfr) विषम (odd) फलन हो
उपपत्ति : यदि f(-x) = f(x) हो, तो फलन f (x) सम (even) कहलाता है, तथा यदि f(-x)=-f(x) हो, तो फलन f (x) विषम (odd) कहलाता है।

P₃ के अनुसार
\(\int_{-a}^{a}\) f(x) dx = \(\int_{-a}^{0}\) f(x) dx + \(\int_{0}^{a}\) f(x) dx
(∵ -a < 0 < a). ....(1)
अब R.H.S. प्रथम समाकल में x = -1 रखें तो x = -dt
तथा, जब x = 0, t = 0 और जब x = -a, t = a

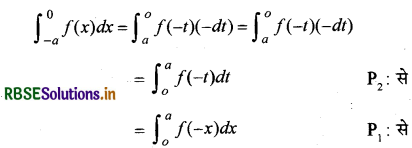
स्थिति 1.
जब f(x) सम फलन हो, अर्थात् f(-x) =f(x) तब
\(\int_{-a}^{o}\) f(x) dx = \(\int_{0}^{a}\) f(x) dx ....(2)
∴ (1) और (2) से
\(\int_{-a}^{o}\) f(x) dx = \(\int_{0}^{a}\) f(x) dx + \(\int_{0}^{a}\) f(x) dx = 2\(\int_{0}^{a}\)f(x) dx

स्थिति 2.
जब f(x) विषम फलन हो, अर्थात् f(-x) = -f(x),
तब


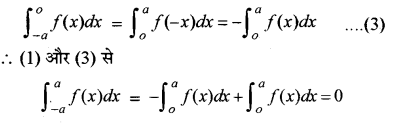
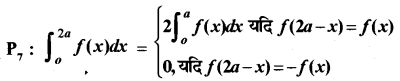
उपपत्ति : P₃ के अनुसार
\(\int_{0}^{2 a^{\prime}}\) f(x) dx = \(\int_{0}^{a^{\prime}}\) f(x) dx + \(\int_{a}^{2 a^{\prime}}\) f(x) dx....(1)
अब दाहिने पक्ष के द्वितीय समाकल में x = 2a - t में रखें, तो dx =-dt तथा,
जब x = 2a, t = 0 और जब x = a, t = a
∴ \(\int_{a}^{2 a}\) f(x) dx = \(\int_{a}^{0}\) f(2 a-t)(-dt) = -\(\int_{a}^{0}\) f(2a-t) dt
= \(\int_{0}^{a}\)(2a-t)dx P₂, से
= \(\int_{0}^{a}\)(2a-x)dx P₁, से

स्थिति 1.
जब f (2a -x) =f(x) हो, तब
\(\int_{a}^{2 a}\) f(2 a-x) dx = \(\int_{0}^{a}\) f(x) dx ....(2) ..
(1) और (2) से
\(\int_{a}^{2 a}\) f(x) dx =\(\int_{0}^{a}\) f(x) d x+ \(\int_{0}^{a}\) f(x) dx = 2\(\int_{0}^{a}\) f(x) dx

स्थिति 2.
जब f(2a -x) = -f(x) हो, तब
\(\int_{a}^{2 a}\) f(x) dx = \(\int_{0}^{a}\)-f(x) dx = -\(\int_{0}^{a}\) f(x) dx ....(3)
(1) और (3) से
\(\int_{a}^{2 a}\) f(x) dx = \(\int_{0}^{a}\) f(x) dx - \(\int_{0}^{a}\) f(x) dx = 0

→ माना df (x) = F(x) तब ∫F(x)dx = f(x) + C, समाकलन, अवकलन की प्रतिलोम प्रक्रिया है। यहाँ C समाकलन अचर है।

→ ∫(F(x)+ g(x))dx = ∫f(x) dx + ∫g(x) dx

→ ∫kf(x) dx = k∫f(x) dx + C

→ कुछ मानक समाकलन
∫xⁿdx = \(\frac{x^{n+1}}{n+1}\) + C, n ≠ -1

→ ∫\(\frac{1}{x}\)dx = log |x| + C

→ ∫dx = x + C

→ ∫cos x dx = sin x + C

→ ∫sinx dx = -cosx+C

→ ∫tan x dx = log |sec x| + C = - log|cos x|+C

→ ∫cot x dx = log |sin x| + C

→ ∫secx dx = log|sec x + tan x| + C
= log\(\left|\tan \left(\frac{\pi}{4}+\frac{\pi}{2}\right)\right|\) + C

→ ∫cosec x dx = log|cosec x-cot x| + C
= log tan\(\left| \frac{\pi}{2}\right|\) + C

→ ∫sec²x dx= tanx+C

→ ∫cose²x dx = -cotx+C

→ ∫sec x tan x dx = secx+C

→ ∫cosec x cot x dx =-cosec x+C

→ ∫e^xdx = e^x + C

→ ∫a^x dx = \(\frac{a^{x}}{\log a}\) + C

→ ∫\(\frac{1}{1+x^{2}}\)dx = sin^-1x + C

→ ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\)dx = sin^-1\(\left(\frac{x}{a}\right)\) + C

→ ∫\(\frac{1}{1+x^{2}}\) dx = tan^-1x + C

→ ∫\(\frac{1}{a^{2}+x^{2}}\) dx = \(\frac{1}{a}\) tan^-1\(\left(\frac{x}{a}\right)\) + C
= -\(\frac{1}{a}\) cot^-1\(\left(\frac{x}{a}\right)\) + C

→ ∫\(\frac{1}{x \sqrt{x^{2}-1}}\)dx = sec^-1x + C = -cosec^-1x + C

→ ∫\(\frac{1}{x \sqrt{x^{x}-a^{2}}}\) dx = \(\frac{1}{a}\) sec^-1\(\left(\frac{x}{a}\right)\) + C

→ समाकलन की विधियाँ-

• प्रतिस्थापन द्वारा समाकलन
• खण्डशः समाकलन
• बीजीय फलनों के आंशिक भिन्नों द्वारा समाकलन

→ ∫u . v dx = u∫v dx = ∫{\(\frac{d u}{d x}\)∫vdx}dx

→ ∫e^x[f(x) + f'(x)]dx = e^xf(x)+C

→ कुछ विशिष्ट समाकलन
∫\(\frac{1}{a^{2}+x^{2}}\)dx = \(\frac{1}{a}\)tan^-1\(\left(\frac{x}{a}\right)\) + C

→ ∫\(\frac{1}{x^{2}-a^{2}}\)dx = \(\frac{1}{2a}\)log\(\left|\frac{x-a}{x+a}\right|\) + C

→ ∫\(\frac{1}{\sqrt{a^{2}+x^{2}}}\) dx = log |x + \(\sqrt{a^{2}+x^{2}}\)| + C

→ ∫\(\frac{1}{a^{2}-x^{2}}\) dx = \(\frac{1}{2 a}\)log \(\left|\frac{a+x}{a-x}\right|\) + C

→ ∫\(\frac{1}{\sqrt{x^{2}-a^{2}}}\) dx = log \(\left|x+\sqrt{x^{2}-a^{2}}\right|\) + C

→ ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\) dx = sin^-1\(\left(\frac{x}{a}\right)\) + C

→ ∫\(\sqrt{a^{2}-x^{2}}\) dx = \(\frac{1}{2}\) x \(\sqrt{a^{2}-x^{2}}\)+\(\frac{a^{2}}{2}\) sin^-1\(\left(\frac{x}{a}\right)\) + C

→ ∫\(\sqrt{x^{2}-a^{2}}\) dx = \(\frac{1}{2}\) x \(\sqrt{x^{2}-a^{2}}-\frac{a^{2}}{2}\) log|x + \(\sqrt{x^{2}-a^{2}}\)| + C

→ ∫\(\sqrt{a^{2}+x^{2}}\) dx = \(\frac{1}{2}\) x \(\sqrt{a^{2}+x^{2}}+\frac{a^{2}}{2}\) log|x + \(\sqrt{a^{2}+x^{2}}\)| + C

→ ∫\(\frac{1}{a x^{2}+b x+C}\)dx प्रकार के समाकलन

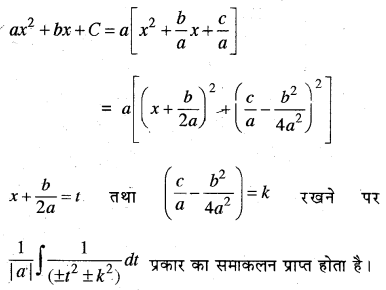
→ ∫\(\frac{p x+q}{a x^{2}+b x+c}\)dx प्रकार का समाकलन
यहाँ p(x) + q = A. \(\frac{d}{d x}\)(ax² + bx + c) + B
= A (2ax + b) + B
A एवं B के मान ज्ञात कर
∫\(\frac{p x+q}{a x^{2}+b x+c}\) dx = ∫\(\frac{\mathrm{A}(2 a x+b)+\mathrm{B}}{a x^{2}+b x+c}\) dx

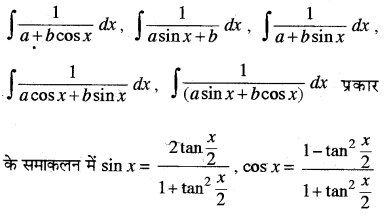
तथा tan\(\frac{x}{2}\) = t रखने पर हल किया जाता है।

→ ∫\(\frac{1}{a+b \sin ^{2} x}\) dx, ∫\(\frac{1}{a \sin ^{2} x+b}\), ∫\(\frac{1}{a \cos ^{2} x+b}\) dx ∫\(\frac{1}{a+b \cos ^{2} x}\) d x ∫\(\frac{1}{a^{2} \sin ^{2} x+b^{2} \cos ^{2} x}\) dx x में cos² x से अंश व हर में भाग देकर tan x = x या cot x = z. प्रतिस्थापित करते हैं और समाकलन करते हैं।

→ \(\frac{P(x)}{Q(x)}\) विषम परिमेय फलन है तो \(\frac{P(x)}{Q(x)}\) = T(x) + \(\frac{P_{1}(x)}{Q(x)}\) जहाँ T(x), x में एक बहुपद है और \(\frac{P_{1}(x)}{Q(x)}\) एक उचित परिमेय फलन है। ∫\(\frac{P(x)}{Q(x)}\)dx का मान ज्ञात करना है जहाँ \(\frac{P(x)}{Q(x)}\) एक उचित फलन है। \(\frac{P(x)}{Q(x)}\) का आंशिक भिन्नों में नियोजन करते हैं।

परिमेय फलन-आंशिक भिन्न

→ निश्चित समाकलन : यदि ∫f(x)dx = F(x) तो
\(\int_{a}^{b}\) f(x) dx = \([\mathrm{F}(x)]_{a}^{b}\) = F(b) – F(a)
a = निम्न सीमा b = उच्च सीमा

→ योगफलन की सीमा के रूप में निश्चित समाकलन
\(\lim _{n \rightarrow \infty}\) S_n = \(\int_{a}^{b}\) f(x) dx = \(\lim _{h \rightarrow 0}\) h
[f(a) + f(a+h) + f(a+2h) +.... + f(a + (n-1)h]
जहाँ h = \(\frac{b-a}{n}\) जब h → 0 तब h → ∞

→ निश्चित समाकलन के गुणधर्म

• \(\int_{a}^{b}\)f(x)dx = \(\int_{a}^{b}\)f(z)dz
• \(\int_{a}^{b}\)f(x)dx = -\(\int_{b}^{a}\)f(x)dx
• \(\int_{a}^{b}\)f(x)dx = \(\int_{a}^{c}\)f(x)dx + \(\int_{c}^{a}\)f(x)dx
• \(\int_{0}^{a}\)f(x)dx = \(\int_{0}^{a}\)f(a - x)dx
• \(\int_{a}^{b}\)f(x)dx = \(\int_{a}^{b}\)f(a + b - x)dx
• \(\int_{0}^{2a}\)f(x)dx = \(\int_{0}^{a}\)f(x)dx + \(\int_{0}^{a}\)f(2a - x)dx
• \(\int_{0}^{2a}\)f(x)dx = 2\(\int_{0}^{a}\)f(x)dx यदि f(2a - x) = f(x)
• \(\int_{0}^{2a}\)f(x)dx = 0 यदि f(2a - x) = -f(x)
• \(\int_{-a}^{a}\) f(x) dx = 2 \(\int_{0}^{a}\) f(x) dx , यदि f समाफलन अर्थात् f(-x) = f(x)
• \(\int_{-a}^{a}\) f(x) dx = 0 यदि } f एक विषम फलन हैं अर्थात् f(-x) = f(x)