RBSE Class 12 Maths Notes Chapter 7 Integrals

These comprehensive RBSE Class 12 Maths Notes Chapter 7 Integrals will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 7 Notes Integrals

Introduction:
Name 'integral' has its origin in the process of summation and the word 'to integrate' literally means, 'to find the sum of Differential Calculus is centred on the concept of the derivative. The original motivation for the derivative was the problem of defining tangent lines to the graphs of functions and calculating the slope of such lines. Integral Calculus is motivated by the problem of defining and calculating the area of the region bounded by the graph of the functions.

The development of integral calculus arises out of the efforts of solving the problems of the following types :
(a) the problem of finding a function whenever its derivative is given,
(b) the problem of finding the area bounded by the graph of a function under certain conditions.
These two problems lead to the two forms of the integrals, e.g., indefinite and definite integrals, which together constitute the Integral Calculus.

Integration as an Inverse Process of Differentation:
Integration is the inverse provess of differentiation. Instead of differentiating a function, we are given the derivative of a function and asked to find its primitive, i.e., the original function. Such a process is called integration or anti differentiation.
Primitive or Anti-derivative
If Φ(x) = f(x), then Φ(x) is called primitive or anti-derivative of f(x).

For example, primitive or anti-derivative of x² because \(\frac{x^{3}}{3}\), because
\(\frac{d}{d x}\left(\frac{x^{3}}{3}\right)=\frac{3 x^{2}}{3}\) = x²

Now, let primitive or anti-derivative of/(x) is Φ(x) and C is any constant. Then
\(\frac{d}{d x}\)[Φ(x) + C} = Φ'(x) = f(x) [Φ'(x) = f(x)]
Φ(x) is also primitive or anti-derivative of f(x).

Nate : If a function f(x) has a primitive or anti¬derivative> then it has infinitely many primitive or anti-derivative because in Φ(x) + C, C is a constant and it may take any value.
For example, \(\frac{x^{3}}{3}, \frac{x^{3}}{3}\) + 1, \(\frac{x^{3}}{3}\) + 2, ............. etc. are primitive or anti-derivative of x² where C = 0, 1, 2, ..............etc.

 

Indefinite Integral:
Let f is any function of x. Then all primitive or anti-derivative is called the indefinite integral of f(x). Indefinite integral is denoted by symbol ∫f(x) dx.
The symbol ∫f(x) dx is read as "indefinite integral of f(x) with respect to x.
Thus,
\(\frac{d}{d x}\)(F(x) + C) = f(x) ⇔ ∫ f(x)dx = F(x) + C
where F(x) is primitive (anti-derivative) off(x) and C is any arbitrary constant.

Basic Definitions
(a) Integrand: The function which is integrated is called the integrand.
(b) Integral: The function obtained after integration of a function is called the integral.
(c) Integration : The process of finding integral of a function is called integration.
For example, If F{x) and f(x) are two function such that
\(\frac{d}{d x}\)F(x) = f(x)
i.e.,f{x) is the differential coefficient of F(x), then f(x) is integrand and F(x) is integral and process of finding f(x) is called integration.

Symbols/Terms/Phrases	Meaning
∫f(x) dx	Integral of f with respect to x
f(x) in ∫ f(x) dx	Integrand
x in ∫f{x) dx	Variable of integration
Integrate	Find the integral
An integral off	A function F such that F’ (x) = fix)
Integration	The process of finding the integral
Constant of Integration	Any real number C, considered as constant function

Some Standard Results
We know the formulae for the derivatives of many functions, corresponding integral are given below :

Derivative	Integration (Anti-derivative)
\(\frac{d}{d x}\)\(\left(\frac{x^{n+1}}{n+1}\right)\) = xn n ≠ -1	∫xn dx = \(\frac{x^{n+1}}{n+1}\) + C, n ≠ -1
\(\frac{d}{d x}\)logex = \(\frac{1}{x}\), x > 0	∫\(\frac{1}{x}\)dx = loge |x| + C [∵ x > 0]
\(\frac{d}{d x}\)(ex) = ex	∫ex dx = ex + C
\(\frac{d}{d x}\left(\frac{a^{x}}{\log _{e} a}\right)\) = ax	∫ax dx = \(\frac{a^{x}}{\log _{e} a}\) + C
\(\frac{d}{d x}\)(cos x) = - sin x dx	∫ sin x dx = - cos x + C
\(\frac{d}{d x}\)(sin x) = cos x dx	∫ cos x dx = sin x + C
\(\frac{d}{d x}\)(tan x) – sec2 x dx	∫sec2 x dx = tan x + C
\(\frac{d}{d x}\)(cot x) = - cosec2x	∫cosec2 x dx = - cot x + C
\(\frac{d}{d x}\)(sec x) = sec x tan x dx	∫sec x tan x dx = sec x + C
\(\frac{d}{d x}\)(cosec x) = -cosec x cot x	∫cosec x cot x dx = - cosec x + C
\(\frac{d}{d x}\)(sin-1x) = \(\frac{1}{\sqrt{1-x^{2}}}\)	∫\(\frac{1}{\sqrt{1-x^{2}}}\)dx = sin-1x + C
\(\frac{d}{d x}\)(cos-1x) = -\(\frac{1}{\sqrt{1-x^{2}}}\)	∫-\(\frac{1}{\sqrt{1-x^{2}}}\)dx = cos-1x + C
\(\frac{d}{d x}\)(tan-1x) = \(\frac{1}{1+x^{2}}\)	∫\(\frac{1}{1+x^{2}}\)dx = tan-1x + C
\(\frac{d}{d x}\)(cot-1x) = -\(\frac{1}{1+x^{2}}\)	∫-\(\frac{1}{1+x^{2}}\)dx = cot-1x + C
\(\frac{d}{d x}\)(sec-1x) = \(\frac{1}{x \sqrt{x^{2}-1}}\)	∫\(\frac{1}{x \sqrt{x^{2}-1}}\)dx = sec-1x + C
\(\frac{d}{d x}\)(cosec-1x) = -\(\frac{1}{x \sqrt{x^{2}-1}}\)	∫-\(\frac{1}{x \sqrt{x^{2}-1}}\)dx = cosec-1x + C

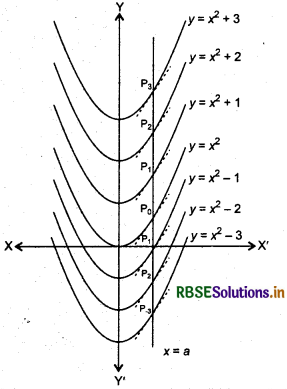
Geometrical Interpretation of Indefinite Integral
∫f[x) dx = F(x) + C = y (say)
y = F(x) + C represents a family of curves. By giving different values of C, we get different members of family. These members can be denoted by shifting any of the curves parallel to itself.

For example,
Let f(x) = 2x, then
∫f(x) dx = x² + C
where C is an arbitrary constant.
Let us consider the graph of y = ∫ f(x) dx
i.e., the graph of y = x² + C ...(i)
Equation (i) is the equation of a family of curves. For different values of C, we will get the equation of different members of this family of curves.
Case I: For C = 0, the curve is
y = x² + 0 or y = x²
This is a parabola having vertex (0, 0) and axis y-axis and is drawn upward.

Case II: For C = 1, the curve is y = x² + 1
This is a parabola having vertex (0,1) and axis y-axis and is drawn upward.

Case III: For C = 2, the curve is y = x² + 2
This is a parabola having vertex (0, 2) and axis y-axis and is drawn upward.

Case IV: For C = -1, the curve is y = x² -1
This is a parabola having vertex (0, -1) and axis y-axis and is drawn upward.
Similarly, we can get different members of the family of curves y = x² + C for different values of C.

The graphs of these curves have been shown in the figure below.

Some Properties of Indefinite Integral:
Property 1. Differentiation and integration are inverse process to each other.
i.e \(\frac{d}{d x}\)∫f(x)dx = f'(x)
and ∫f'(x) dx = f(x) + C, where C is any constant which is called constant of integration.
Proof:
Let anti-derivative of f is F
i.e., \(\frac{d}{d x}\)F(x)dx = f(x)
Then ∫f(x)dx = F(x) + C
∴ \(\frac{d}{d x}\)∫f(x) dx = \(\frac{d}{d x}\)(F(x) + C) = \(\frac{d}{d x}\)(F(x)) = f(x)
We see that f'(x) = \(\frac{d}{d x}\)f(x)
∴∫f'(x)dx = f(x) + C,
where C is any constant which is called constant of integration.

Property 2:
The integral of the product of a constant and a function is equal to the product of the constant and the integral of the function.
i.e., ∫kf(x) dx = k ∫f(x) dx, where k is a constant.
Proof:
\(\frac{d}{d x}\)∫kf(x) dx = k\(\frac{d}{d x}\)∫f(x) dx = kf(x)
and \(\frac{d}{d x}\)[k∫f(x) dx] = k \(\frac{d}{d x}\)∫f(x) dx = kf(x)
∴ ∫k f(x) dx = k∫f(x) dx

Property 3:
(A) The integral of the sum of two function is equal to the sum of the integrals of the two functions.
i.e., ∫[f(x) + g(x)] dx = ∫f(x) dx + ∫g(x) dx
(B) The integral of the difference of two function is equal to the difference of the integrals of the two functions.
i.e., ∫[f(x) - g(x)] dx = ∫f(x) dx - ∫g(x) dx
Proof: (A) {∫ [fix) + g(x)]dx} = f(x) + g(x) ...(1)
Again, \(\frac{d}{d x}\)[∫f(x) dx + ∫g(x) dx]
= \(\frac{d}{d x}\)∫f(x) dx + \(\frac{d}{d x}\)∫g(x) dx
= f(x) + g(x) ...(2)
From (1) and (2), derivative of functions are same.
Hence, ∫ [f(x) + g(x)] dx = ∫f(x) dx + ∫g(x) dx
Similarly, (B) can be proved.

Generalization: The above results can be generalized to the form:
∫[k₁f₁(x) ± k₂f₂(x) ... ± k_nf_n{x)} dx = k₁∫f₁(x) dx ± k₂∫f₂(x) dx... ±f_n∫f_n(x) dx

Property 4 :
Two indefinite integrals with the same derivative lead to the same family of curves and so they are equivalent.
Proof:
Let f and g are two functions such that
= \(\frac{d}{d x}\)∫f(x)dx = \(\frac{d}{d x}\)∫g(x)dx
or = \(\frac{d}{d x}\)[∫f(x) dx - ∫g(x) dx] = 0
∴ ∫f(x) dx - ∫g(x) dx = C
where C is a real number
or ∫f(x) dx = ∫g(x) dx + C
Hence, family of curves ∫f(x) dx + C₁ and ∫g(x) dx + C₂ are identical where C₁ and C₂ are real numbers.
∴ ∫f(x) dx and ∫g(x) dx are equivalent.

Integration by Inspection:
To find an antiderivative of a given function, we search initiative for a function whose derivative is the given function. The search for the requisite function for finding an antiderivative is known as integration by the method of inspection.

Comparison between Differentiation and integration

Differentiation	Integration
(i) It is an operation on functions.	(i) It is also an operation on functions.
(ii) For any constant k1, k2, ………., kn = k1\(\frac{d}{d x}\)f1(x) ± k2\(\frac{d}{d x}\)f2(x) ± ….. ± kn\(\frac{d}{d x}\)fn(x)	(ii) For any constant k1, k2, ………., kn ∫[k1f1(x) ± k2f2(x) ... ± knfn{x)} dx = k1∫f1(x) dx ± k2∫f2(x) dx... ±fn∫fn(x) dx
(iii) Some functions are not differentiable.	(iii) Some functions are also not integrable.
(iv) The derivative of a function, if it exists, is unique.	(iv) The integral of a function is not unique.
(v) If a polynomial function F is differentiated, the result is a polynomial whose degree is 1 less than the degree of polynomial function F.	(v) If a polynomial function F is integrated the result is a polynomial whose degree is 1 more than the degree of polynomial function F.
(vi) We can obtain a derivative at a point.	(vi) Integral of a function may be obtained over an interval in which function is defined.
(vii) The derivative of a function has a geometrical meaning, namely, the slope of the tangent to the corresponding curve at a point.	(vii) The indefinite integral of a function represents geometrically, a family of curves placed parallel to each other having parallel tangents at the points of intersection of the curves of the family with the lines perpendicular to the axis representing the variable of integration.
(viii) The derivative is used for finding some physical quantities like the velocity of a moving body when the distance travelled at any time t is known.	(viii) The integral is also used for finding some physical quantities like distance travelled when the velocity at time t is known.
(ix) Differentiation is a process involving limits.	(ix) Integration is also a process involving limits.
(x) Differentiation is the inverse process of integration.	(x) Integration is the inverse process of differentiation.

Methods of Integration:
In previous section, we discussed integrals of those functions which were readily obtainable from derivatives of some functions. It was based on inspection. This method is not very suitable for many functions. Hence, we need to develop additional methods for finding the integrals by reducing them into standard forms. We have the following methods of integration:

• Integration by substitution
• Integration by partial fraction
• Integration by parts

Integration by Substitution
Integrals of certain functions cannot be obtained directly if they are not in the standard forms, but they may be reduced to standard forms by proper substitution. The method of finding an integral by reducing it to standard form by a proper substitution is called integration by substitution.

Some functions which are integrated by substitution
(i) Integrals of the form If (ax ±b)dx
Let I = ∫f (ax ± b) dx
Putting ax ± b = t
Differentiating both sides with respect to x, we get
adx = dt
or dx = \(\frac{1}{a}\) dt
Substituting ax±b = t and dx = \(\frac{1}{a}\) dt in I, we get
I = ∫f(ax ± b) dx
= \(\frac{1}{a}\)∫f(t)dt = \(\frac{1}{a}\)F(t) + C
= \(\frac{1}{a}\)F(ax ±b) + C

(ii) Integrals of the form ∫f{Φ(x)} Φ'(x) dx
If Φ(x) is a continuously differentiable function, then we substitute
Φ(x) = t and Φ'(x) dx = dt
This substitution reduces the above integral to ∫(f) dt. After evaluating this integral we substitute back the value of f.

(iii) Integrals of the form ∫\(\int \frac{\phi^{\prime}(x)}{f\{\phi(x)\}}\)dx
Putting Φ(x) = t
Differentiating both sides with respect to x, we get <|y'(x)dx = dt
Φ'(x)dx = dt
Then, \(\int \frac{\phi^{\prime}(x)}{f\{\phi(x)\}}=\int \frac{d t}{f(t)}\)
After evaluating this integral we substitute back the value of t.

Remark : Method of integration by substitution is also used in other methods of integration like integration by parts and integration by partial function.

Integration by substitution of some important trigonometric functions
Now, we discuss some important integrals involving trigonometric functions and their standard integrals using substitution technique. These will be used later without reference.

See the integrals of the following trigonometric functions with respect to x:
(i) ∫tan x dx = ∫\(\frac{\sin x}{\cos x}\)dx
Putting cos x = t
Then - sin x dx = dt
or sin x dx = - dt
∫\(\frac{\sin x}{\cos x}\)dx = -∫\(\frac{1}{t}\) dt = - log |t| + C
= - log |cos x| + C
Thus, ∫tan x dx = - log |cos x| + C
⇒ ∫tan x dx = log |sec x| + C

(ii) ∫cot x dx = dt
Putting sin x = t
Then, cos x dx = dt
∫\(\frac{\cos x}{\sin x}\)dx = -∫\(\frac{1}{t}\) dt = log |t| + C
= log |sin x| + C
Thus, ∫cot xdx = log |sin x| + C

(iii) ∫sec x dx = ∫\(\frac{\sec x(\sec x+\tan x)}{\sec x+\tan x}\)dx
[Multiplying numerator and denominator by (sec x + tan x)]
= ∫\(\frac{\sec ^{2} x+\sec x \tan x}{\sec x+\tan x}\)dx
Putting sec x + tan x = t
Then, (sec x tan x + sec²x) dx = dt
∴ ∫\(\frac{\sec ^{2} x+\sec x \tan x}{\sec x+\tan x}\)dx = ∫\(\frac{d t}{t}\)
= log |t| + C
= log |sec x + tan x| + C
∴ ∫sec xdx = log |sec x + tan x| + C

(iv) ∫cosec xdx = ∫\(\frac{{cosec} x({cosec} x+\cot x)}{{cosec} x+\cot x}\)dx
[Multiplying numerator and denomiantor by (cosec x + cot x)]
= ∫\(\frac{{cosec}^{2} x+{cosec} x \cot x}{{cosec} x+\cot x}\)
Putting cosec x + cot x = t
Then (- cosec x cot x - cosec²x) dx = df
or - (cosec x cot x + cosec²x) dx = dt
or (cosec x cot x + cosec²x) dx = - dt
= - log | t | + C
= - log |cosec x + cot x| + C
= -log
[Multiplying numerator and denominator by (cosec x - cot x)]
= -log\(\left|\frac{{cosec}^{2} x-\cot ^{2} x}{{cosec} x-\cot x}\right|\) + C
= -log\(\left|\frac{1}{{cosec} x-\cot x}\right|\) + C (∵ cosec²x - cot²x = 1)
= log |cosec x - cot x| + C
∴ ∫cosec x dx = log |cosec x- cotx| +C

Integration Using Trigonometric Identities
In this section, we use known trigonometric identities to find the integral. When the integrand involves some trigonometric functions, we use the following trigonometric identities:

• sin²x = \(\frac{1-\cos 2 x}{2}\)
• cos²x = \(\frac{1+\cos 2 x}{2}\)
• sin (A + B) + sin (A - B) = 2 sin A cos B
• sin (A + B) - sin (A - B) = 2 cos A sin B
• cos (A + B) + cos (A - B) = 2 cos A cos B
• cos (A - B) - cos (A + B) = 2 sin A sin B
• sin³x = \(\frac{3 \sin x-\sin 3 x}{4}\)
• cos³x = \(\frac{\cos 3 x+3 \cos x}{4}\)

Integrals of some Particular Functions
In this section, we introduce some important formulae of integrals and apply them to evaluate many other integrals:

Expression	Substitution
(A) x2 + a2	x = a tan θ or a cot θ
(B) x2 - a2	x = a sec θ or a cosec θ
(C) a2 - x2	x = a sin θ or a cos θ
(D) \(\sqrt{\frac{a-x}{a+x}}\) or \(\sqrt{\frac{a+x}{a-x}}\)	x = a cos 2θ

Theorem:
(i) ∫\(\frac{1}{x^{2}+a^{2}}\)dx = \(\frac{1}{a}\)tan^-1\(\frac{x}{a}\) + C
Proof:
We now prove the above results.
Putting x = a tan θ
Then dx = a sec²θ
and tan θ = x/a
or θ = tan^-1x/a

(ii) ∫\(\frac{1}{x^{2}-a^{2}}\)dx = \(\frac{1}{2 a}\) log \(\left|\frac{x-a}{x+a}\right|\) + C
Proof:

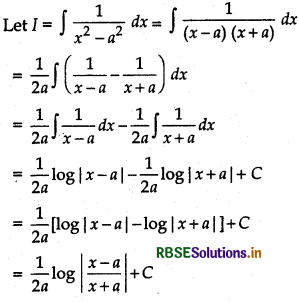
Alter: I = ∫\(\frac{1}{x^{2}-a^{2}}\)dx
Putting x = a sec θ
Then dx = a sec θ tan θ dθ
and sec θ = \(\frac{x}{a}\)
θ = sec^-1\(\frac{x}{a}\)

(iii) ∫\(\frac{1}{a^{2}-x^{2}}\) d x = \(\frac{1}{2 a}\) log\( \left|\frac{a+x}{a-x}\right|\) + C
Proof:

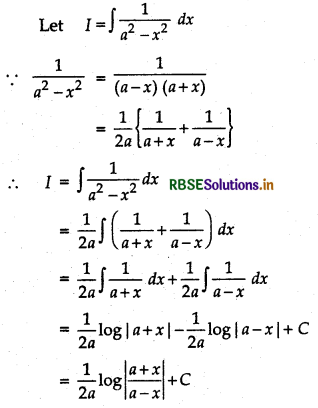
(iv) ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\) dx = sin^-1\(\left(\frac{x}{a}\right)\) + C
Proof:
Let I = ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\)dx
Putting x = a sin θ
Then dx = a cos θ dθ
and sin θ = \(\frac{x}{a}\)
or θ = sin^-1\(\frac{x}{a}\)

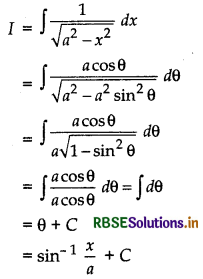
Similarly, by making substitution x = a cos θ, we get
∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\)dx = -cos^-1\(\frac{x}{a}\) + C

(v) ∫\(\frac{1}{\sqrt{a^{2}+x^{2}}}\) dx = log |x + \(\sqrt{a^{2}+x^{2}}\)| + C
Proof:
Let I = ∫\(\frac{1}{\sqrt{a^{2}+x^{2}}}\)dx
Putting x = atan θ
Then dx = a sec² θ dθ
and tan θ = \(\frac{x}{a}\)
or θ = tan^-1\(\frac{x}{a}\)

(vi) ∫\(\frac{1}{\sqrt{x^{2}-a^{2}}}\) dx = log |x + \(\sqrt{x^{2}-a^{2}}\)| + C
Proof:
Let I = ∫\(\frac{1}{\sqrt{x^{2}-a^{2}}}\)dx
Putting x = atan θ
Then dx = a sec θ tan θ dθ
and tan θ = \(\frac{x}{a}\)
or θ = tan^-1\(\frac{x}{a}\)

Integration by Partial Fractions
Let P(x) and Q(x) are two polynomials in x and degree of P(x) is less than that of Q(x) [Q(x) ≠ 0] then \(\frac{P(x)}{Q(x)}\) is called proper rational function. If degree of P(x) Q(x) is more than the degree Q(x) and Q(x) ≠ 0 then \(\frac{P(x)}{Q(x)}\) is called improper rational function. The imporper rational functions can be reduced to the proper function by long division process.

Thus, if is improper, then
\(\frac{P(x)}{Q(x)}\) = T(x) + \(\frac{P(x)}{Q(x)}\)
where T(x) is a polynomial in x and is a proper rational function.

If \(\frac{P(x)}{Q(x)}\) is a proper rational function then for finding the value of ∫\(\frac{P(x)}{Q(x)}\)dx we factonse Q(x) and wnte the integral as a sum of simple rational functions. This method is known as partial fraction decomposition.

The given table below indicates the types of simpler partial fractions that are to be associated with various kind of rational functions.

Form of the rational functions	Form of the partial Function
\(\frac{p x+q}{(x-a)(x-b)}\), a ≠ b	\(\frac{A}{x-a}+\frac{B}{x-b}\)
\(\frac{p x+q}{(x-a)^{2}}\)	\(\frac{A}{x-a}+\frac{B}{x-b}\)
\(\frac{p x^{2}+q x+r}{(x-a)(x-b)(x-c)}\)	\(\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c}\)
\(\frac{p x^{2}+q x+r}{(x-a)^{2}(x-b)}\)	\(\frac{A}{x-a}+\frac{B}{(x-a)^{2}}+\frac{C}{(x-b)}\)
\(\frac{p x^{2}+q x+r}{(x-a)\left(x^{2}+b x+c\right)}\)	\(\frac{A}{x-a}+\frac{B x+C}{x^{2}+b x+c}\)

where x² + bx + c cannot be factorised further. A, B and C are real numbers. After determining the value of A, B and C, we integrate the given function.

Integration by parts:
Integration by parts means the integration of products of two functions. If u and v are any two differentiable functions of a single variable *, then by the product rule of differentiation, we have
\(\frac{d}{d x}\)(u v) = u \(\frac{d v}{d x}\) + v \(\frac{d u}{d x}\) .......(1)

Integrating both sides of equation (1) w. r. t. x, we get

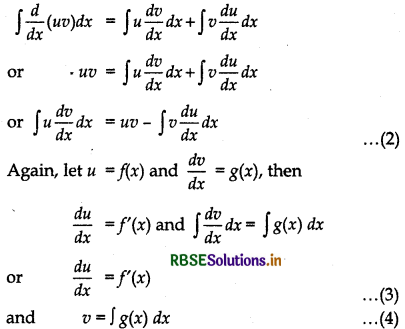
From equation (2), (3) and (4), we get
∫f(x).g(x) dx = f(x) ∫g(x)dx - ∫[∫g(x)dxf'(x)]dx i.e., ∫f(x) g(x) dx = f(x)∫g(x) dx - ∫[f'(x)∫g(x)dx]dx ...........(5)
Let f is the first function and g is the second function, then formula (5) may be stated as follow :
"The integral of the product of two functions = (first function) × (integral of the second function) - Integral of [(differential coeficient of the first function) × (integral of the second function)]"

In other words, if f₁(x) and f₂(x) are two functions and f'₁(x) is the differential coefficient of f₁(x) w. r. t. x, then,
∫f₁(x). f₁(x)dx = f₁(x) ∫f₂(x)dx - ∫[f'₁(x) ∫f₂(x)dx]dx

Remark 1.
Proper choice of first and second function : To evaluate integration of product of two functions, we take the first function which one of the two functions is not directly integrable (e.g., log x, sin^-1x, tan^-1x etc.) and the remaining function is taken as the second function. If in the integral both the functions are easily integrable, then the first function is chosen in such a way that the derivative of the function is a simple function and the function thus obtained under the integral sign is easily integrable than the original function.

Remark 2.
Integration by parts is not applicable to product of functions in all cases. For example, the method of integration by parts does not work for Jsin*2d*. The reason is that there does not exist function whose derivative is sin x².

Remark 3.
If the integral be a single function, take 1 as the second function.

Remark 4.
Usually, if any function is a power of x or a polynomial in x, then we take it as the first function. However, in case where other function is inverse trigonometric function or logarithmic function, then we take them as first function.
I - Inverse trigonometric functions (sin^-1x, cos^-1x, tan^-1x etc.)
L - Logarithmic functions
A - Algebraic functions
T - Trigonometric functions
E - Exponential functions

Integrals of Some More Types:
Here, we will prove three special types of standard integrals based on the technique of integration by parts
(i) ∫\(\sqrt{x^{2}-a^{2}}\) dx
(ii) ∫\(\sqrt{x^{2}+a^{2}}\) dx
(iii) ∫\(\sqrt{a^{2}-x^{2}}\) dx

Theorem:
(i) ∫\(\sqrt{x^{2}-a^{2}}\) dx = \(\frac{1}{2}\) x \(\sqrt{x^{2}-a^{2}}\) - \(\frac{a^{2}}{2}\) log \(\left|x+\sqrt{x^{2}-a^{2}}\right|\) + C
Proof:

(ii) ∫\(\sqrt{x^{2}+a^{2}}\) dx = \(\frac{1}{2}\) x \(\sqrt{x^{2}+a^{2}}\) + \(\frac{a^{2}}{2}\) log \(\left|x+\sqrt{x^{2}+a^{2}}\right|\) + C
Proof:

(iii) ∫\(\sqrt{a^{2}-x^{2}}\) dx = \(\frac{1}{2}\) x \(\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\) sin^-1 \(\frac{x}{a}\) + C
Proof:

Remarks:
Integrals
(i) ∫\(\sqrt{x^{2}-a^{2}}\) dx
(ii) ∫\(\sqrt{x^{2}+a^{2}}\) dx
(iii) ∫\(\sqrt{a^{2}-x^{2}}\) dx are also evaluated by the method of substitution.
Let I = ∫\(\sqrt{x^{2}-a^{2}}\) dx
Put x = a sec θ
dx = a sec θ tan dθ
= ∫ \(\sqrt{a^{2} \sec ^{2} \theta-a^{2}}\) a sec θ tan θ dθ
= ∫ a \(\sqrt{\left(\sec ^{2} \theta-1\right)}\) a sec θ tan θ dθ
= a² ∫\(\sqrt{\tan ^{2} \theta}\) sec θ tan θ dθ
= a² ∫ tan θ sec θ tan θ dθ
= a² ∫ sec θ tan² θ dθ
= a²∫ sec θ (sec² θ -1) dθ
= a²∫ sec θ sec²θ dθ - a²∫sec θ dθ
I = a²I₁ - a² log |sec θ + tan θ| + C₁

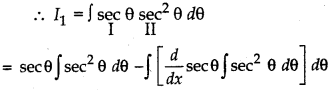
= sec θ tan θ - ∫sec θ tan θ tan θ dθ + C₂
= sec θ tan θ - ∫sec θ tan² θ dθ + C₂
= sec θ tan θ - ∫sec θ (sec² θ -1) dθ + C₂
= sec θ tan θ - ∫sec θ sec² θ dθ + ∫ sec θ dd + C₂
= sec θ tan θ - + log | sec θ + tan θ | + C₂
or I₁ + I₂ = sec θ tan θ + log |sec θ + tan θ| + C₂
or 2I₁ = sec θ tan θ + log |sec θ tan θ| + C₂
or I₁ = \(\frac{1}{2}\) sec θ tan θ + \(\frac{1}{2}\) log | sec θ + tan θ | + \(\frac{C_{2}}{2}\)

Putting the value of I₂ in equation (1), we get

(ii) I = ∫\(\sqrt{x^{2}+a^{2}}\) dx
Let x = a tan θ, θ = tan^-1\(\frac{x}{a}\)

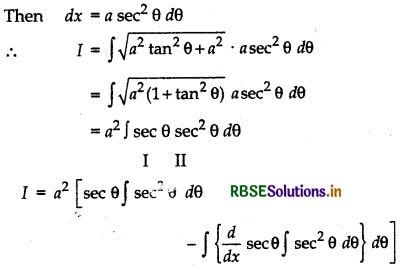
= a² sec θ tan θ - a² ∫ sec θ tan θ.tan θ dθ
= a² sec θ tan θ - a² ∫ sec θ tan² θ dθ
= a² sec θ tan θ - a² ∫ sec θ (sec² θ - 1) dθ
= a² sec θ tan d - a² j sec θ sec²θ dθ + a² sec θ dθ
I = a² sec θ tan θ -1 + a² log |sec θ + tan θ| + C₁
or I + I = a² sec θ tan d + a² log |sec θ + tan θ | + C₁
or 2I = a² sec θ tan d + a² log |sec θ + tan θ| + C₁

(iii) Let I = ∫\(\sqrt{a^{2}-x^{2}}\) dx

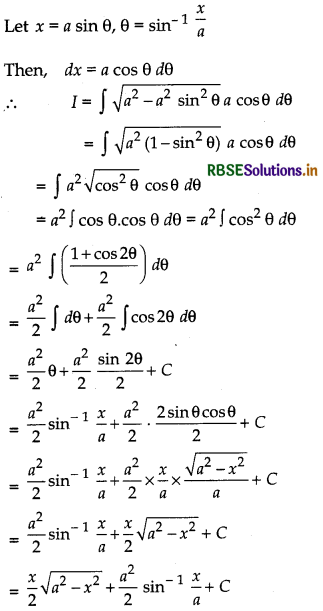
Definite Integral:
Indefinite integral of any function is not unique because by putting different values of constant in it, we can get different values of integral. The definite integral of an}? function has a unique value. If f(x) is any function, then its definite integral is denoted by \(\int_{a}^{b}\)f(x) dx, where b is upper limit and a is lower limit. Hence, when we integrate any function within two limits, then it is called definite integral.
Let ∫f(x) dx = F(x) + C ...(1)
(Indefinite integral of the function) Now, putting upper limit b in place of the variable
∫f(x) dx = F(b) + C ...(2)
Now, putting lower limit a in place of the variable
∫f(x) dx = F{a) + C ...(3)
Substracting equation (3) from equation (2), we get
\(\int_{a}^{b}\)f(x) dx = [F(b) + C) - [F(a) + C]
= m-m
The arbitrary constant disappers in evaluation of the value of the definite integral.
Definite integral can also be represented as :
\(\int_{a}^{b}\)f(x) dx = [F(x)fa = F(b) - F(a)
[Here, F(x) is an anti-derivative : F(x) \(\frac{d}{d x}\) f(x) = f(x)]
Definite integral also be represented as the limit of a sum.
Let f be continuous function defined in the closed inverval [a, b] and F(x) be an antiderivative of f(x) then, definite integral of f(x) in closed interval [a, b] is denoted by \(\int_{a}^{b}\)f(x) dx
and \(\int_{a}^{b}\)f(x)dx = \([F(x)]_{a}^{b} \)= F(b) - F(a)
where a and b are the lower and upper limits of the integral. This definite integral has a unique value.

Definite integral as the limit of a sum
Let f be a continuous function defined in close interval [a, b]. Assume that all the values taken by the function are non-negative, so the graph of the function is a curve above the x-axis.

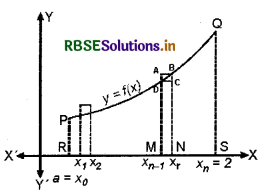
The definite integral \(\int_{a}^{b}\)f(x)dx is the area bounded by the curve y = f(x), the ordinates x = a, x = b and the x-axis. To evaluate this area, consider the region PRSQP between this curve, x-axis and ordinates x = a and x = b.

Divide the interval [a, b] into n equal sub intervals denoted by [x₀, x₁], [x₁; x₂], ............... [x_r-1, x_r], ............ [x_n-1, x_n] n. Let width of each sub - interval is h where x₀ = a, x₁ = a + h, x₂ = a + 2h ..........., x_r = a + rh and x_n = b = a + nh ⇒ n = \(\frac{b-a}{h}\)

We note that as n → ∞ h → ∞
The region PRSQP is the sum of n sub-regions.
Clearly, area of rectangle (MNCD) < area of region (MNBDM) < area of rectangle (MNBA). ...(1)
If h → 0 all the three areas shown in (1) become nearly equal to each other.
If S_n and S_n' denote the sum of areas of all lower rectangle and upper rectangles raised over sub-intervals [x_r-1, x_r] for r = 1,2,....... n respectively, then

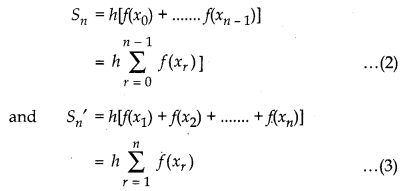
Here, at a = x0 length of rectangle is f(x₀) and breadth of rectangle is h.
∴ Area of lower rectangle = f(x₀) × h = hf(x₀)
And at point x₁ length of rectangle is f(x₂) and breadth of rectangle is h.

Area of upper rectangle = f(x₁) ≠ h = hf(x₁)
For any arbitrary sub-interval [x_r-1 x_r], we have S_n < (MNBDM) area of region (MNBDM) < S_n' ...(4)

As n → ∞ strips become narrower and narrower. It is assumed that the limiting values of S_n and S_n' are same in both cases and the common limiting value is the required area under the curve.

Symbolically, we write

The above expression (6) is known as the definition of definite integral as the limit of sum.
Some useful results for direct applications :
(i) Sum of n natural numbers
Σn = 1 + 2 + 3+ ... (n-1) + n = \(\frac{n(n+1)}{2}\)

(ii) Sum of square of n natural numbers
Σn² = 1² + 2² + 3² + ... n² = \(\frac{1}{6}\)n(n +1) (2n + 1)

(iii) Sum of cube of n natural numbers
Σn³ = 1³ + 2³ + 3³ + ... n³ = \(\left[\frac{n(n+1)}{2}\right]^{2}\)

(iv) Sum of n terms of A.P.
a + (a + d) + (a + 2d) +... a + (n - 1 )d = \(\frac{n}{2}\)[2a + (n - 1)d]

(v) Sum of n terms of G.P.
a + ar + ar² + ... + ar^n-1 = \(\frac{a\left(r^{n}-1\right)}{(r-1)}\) when r > 1

(vi) sin a + sin (a + h) + sin (a + 2h) +....+ sin [a + (n - 1 )h]

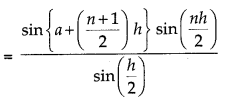
(vii) cos a + cos (a + h) + cos (a + 2h) +...+ cos [(a + (n - 1 )h]

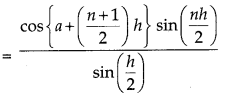
Remark :
The value of the definite integral of a function over any particular interval depends on the function and the interval, but not on the variable of integration that we choose to represent the independent variable. If the independent variable is denoted by t or u instead of x, we simply write the integral as \(\int_{a}^{b}\) f(t)dt or \(\int_{a}^{b}\)f(u)du instead of \(\int_{a}^{b}\)f(x)dx. Hence, the variable of integration is called a dummy variable.

Fundamental Thorem of Calculus
Area function : Integral \(\int_{a}^{b}\) f(x) dx represent the area of the region bounded by the curve y = f(x), the ordinate x = a and x = b and x-axis.
Let x be a given point [a, b]. Then \(\int_{a}^{b}\) f(x) dx represent the area of the shaded region A(x).

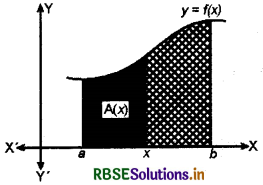
Clearly, f(x) > 0 ∀ x ∈ [a, b]
The area of shaded region depends upon the value of x.
In other words the area of shaded region is a function of x. If A(x) represent the area of shaded region, then
A(x) = \(\int_{a}^{x}\)f(x) dx
Two basic fundamental theorems have been given here which are based on the area of shadéd region. The parts of these theorems are beyond the scope of this book.

First fundamental theorem of integral calculus
Theorem 1.
Let f be a continuous function of the closed interval [a, b] and let A(x) be the area function. Then, A'(x) f(x) for all x ∈ [a1 b]

Second fundamental theorem of integral calculus
Theorem 2.
Letf be continuous function defined on the closed interval [a, b] and F be an antiderivative off.
Then, \(\int_{a}^{x}\)f(x) dx = [F(x)]_{a}^{b} = F(b) - F(a)
In other words \(\int_{a}^{b}\)f(x) dx = (Value of the anti-derivative F off at the upper limit b) - (Value of the same anti-derivative at the lower limit a)

Remarks:
(1) Second fundamental theorem of integral calculus is very useful, because it gives us a method for calculating the definite integral more easily.
(il) In \(\int_{a}^{b}\)f(x) dx, the function f needs to be well defined and continuous in [a, bi.

Evaluation of Definite Integrals by Substitution
To evaluate definite integral, by substitution method, the following steps could be needed for evaluating the value of \(\int_{a}^{b}\) f(x) dx.
Step 1. Consider the integral without limits and substitute, y = f(x) or x = g{y) to reduce the given integral to a known form.
Step 2. Integrate the new integrand w.r.t. the new variable without mentioning the constant of integration.
Step 3. Resubstitute for the new variable and write the answer in terms of the original variable.
Step 4. Find the values of answers obtained in (3) at the given limits of integral and find the difference of the values at the upper and lower limits.

Remark:
After performing steps 1 and 2, there is no need of step 3. Here, the integral will be kept in the new variable itself, and the limits of the integral will accordingly be changed so that we can perform the last step.

Some Properties of Definite Integrals
Here, we define properties of definite integral by theorems. These theorems will be useful in evaluating the definite integrals more easily.

Theorem 1:
\(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{b}\) f(t) dt
Proof: :
Let ∫f(x) dx = F(x)
Then ∫(f) dt = F(t)

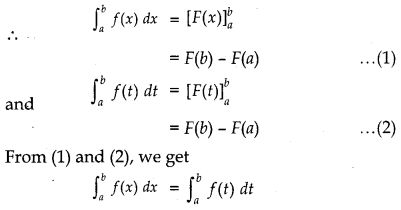
From (1) and (2), we get
\(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{b}\) f(t) dt
i.e., integration is independent of the change of variable.

Theorem 2:
\(\int_{a}^{b}\) f(x) dx =-\(\int_{b}^{a}\) f(x) dx
Proof :
Let ∫f(x) = F(x)

From (1) and (2), we get
\(\int_{a}^{b}\) f(x) dx =-\(\int_{b}^{a}\) f(x) dx
i.e., if the limits of a definite integral are interchanged then its value changes by minus sign only.

Theorem 3:
\(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{c}\) f(x) dx + \(\int_{c}^{b}\) f(x) dx a, b, c are real number and a< c < b.
Proof :
Let ∫f(x) dx = F(x)

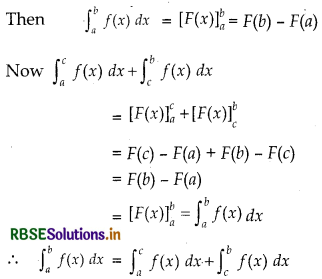
Remark :
The above property can be generalized the following form:
If a < c₁< c₂, , < c_n < b then
\(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{c_{1}}\) f(x) dx + \(\int_{c_{1}}^{c_{2}}\) f(x) dx + .......... + \(\int_{c_{2}}^{c_{3}}\) f(x) dx + .... + \(\int_{c_{n}}^{b}\) f(x) dx

Theorem 4 :
\(\int_{a}^{b}\)f(x) dx = \(\int_{a}^{b}\) f(a+b-x) dx
Proof:
Putting a + b- x = t ⇒ -dx = dt
⇒ dx = - dt
When x = a, then t = a + b- a = b and when x = b, then t = a + b - b = a

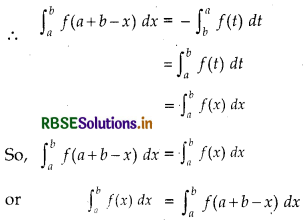
Theorem 5:
If f(x) is a continuous function defined in [0, a], then
\(\int_{0}^{a}\) f(x) = \(\int_{0}^{a}\) f(a-x) dx
Proof:
In \(\int_{0}^{a}\)(a -x)dx putting a - x = t
⇒ - dx = dt ⇒ dx = - dt
When x = 0, then t = a
When x = a, then t = 0

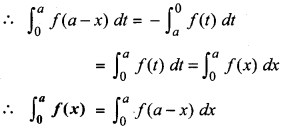
Theorem 6:
If f(x) is a continuous function defined in [0, a), then:
\(\int_{0}^{2 a}\) f(x) dx = \(\int_{0}^{a}\) f(x) d x+\(\int_{0}^{a}\) f(2a - x) dx
Proof:
\(\int_{0}^{2 a}\) f(x) d x=\(\int_{0}^{a}\) f(x) d x+\(\int_{0}^{2 a}\) f(x) d x
[From theorem (3)]
Putting t = 2a - x in second integral of R.H.S.
dt = - dx
⇒ - dt = dx
When x = a, then t = 2a - a = a
When x = 2a, then t = 2a - 2a = 0
∴ Second integral of R.H.S.

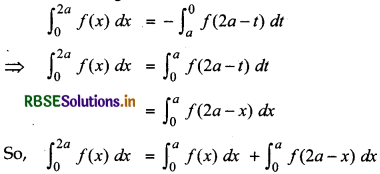
Theorem 7:
If f(x) is a continuous function defined in [0,2a], then:

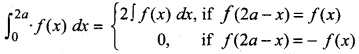
Proof:
If f(2a - x) = f(x), then from (1)

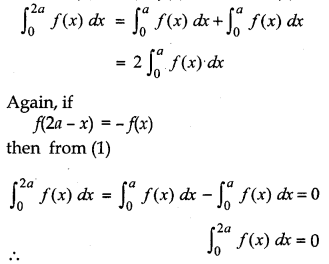
Theorem 8:
If f(x) is a continuous function defined in [- a, a], then:
(1) \(\int_{-a}^{a}\) f(x) dx = 2 \(\int_{0}^{a}\) f(x) dx
If f(x) is an even function i.e., a f(-x) = f(x)
(2) \(\int_{-a}^{a}\) f(x) dx = 0 = o
If f(x) is an odd function i.e.,
f(- x) = -f(x) [From theorem (3)]
Proof:
\(\int_{-a}^{a}\) f(x) dx = \(\int_{-a}^{0}\) f(x) dx + \(\int_{0}^{a}\) f(x) dx .............(1)
Putting t = - x in first integral of R.H.S.
dt = - dx ⇒ - dt = dx
When x = - a, then t = a
When x = 0, then t = 0 (∵ x = - t)

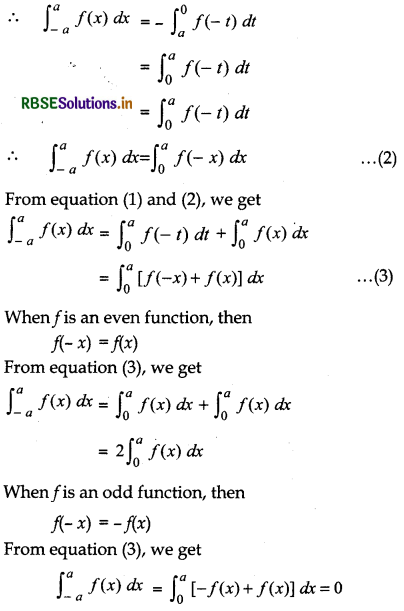
→ If differential coefficient of F(x) is fix), then F(x) is called antiderivative or primitive of f(x).
i.e., F'(x) = f(x)
If C is any arbitrary constant,
\(\frac{d}{d x}\)[F(x) + C] = F'(x) = f(x)
Similarly, if F(x), fix) is anti-derviative (primitive) of fix), then F(x) + C also be anti-derivative of f(x).
Let F(x) = f(x). Then we write f(x) dx = F(x) + C.
These integrals are called indefinite integrals or general integrals, C is called constant of integration. All these integrals differ by a constant.

→ Differentiation and integration are inverse process of each other, i.e.,
\(\frac{d}{d x}\)∫(x) dx = f(x)
and ∫f' (x) dx = f(x) + C

→ Indefinite integrals with same derivatives belong to the same family of curves and so they are equivalent.

→ Process of integrating of any function is called integration.

→ Integration of some standard function are given below:
∫xⁿdx = \(\frac{x^{n+1}}{n+1}\) + C, n ≠ -1

→ ∫\(\frac{1}{x}\)dx = log |x| + C

→ ∫dx = x + C

→ ∫cos x dx = sin x + C

→ ∫sinx dx = -cosx+C

→ ∫tan x dx = log |sec x| + C = - log|cos x|+C

→ ∫cot x dx = log |sin x| + C

→ ∫secx dx = log|sec x + tan x| + C
= log\(\left|\tan \left(\frac{\pi}{4}+\frac{\pi}{2}\right)\right|\) + C

→ ∫cosec x dx = log|cosec x-cot x| + C
= log |tan\(\frac{\pi}{2}\)| + C

→ ∫sec²x dx= tanx+C

→ ∫cose²x dx = -cotx+C

→ ∫sec x tan x dx = secx+C

→ ∫cosec x cot x dx =-cosec x+C

→ ∫e^xdx = e^x + C

→ ∫a^x dx = \(\frac{a^{x}}{\log a}\) + C

→ ∫\(\frac{1}{1+x^{2}}\)dx = sin^-1x + C

→ ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\)dx = sin^-1\(\left(\frac{x}{a}\right)\) + C

→ ∫\(\frac{1}{1+x^{2}}\) dx = tan^-1x + C

→ ∫\(\frac{1}{a^{2}+x^{2}}\)dx = \(\frac{1}{a}\) tan^-1\(\left(\frac{x}{a}\right)\) + C
= -\(\frac{1}{a}\) cot^-1\(\left(\frac{x}{a}\right)\) + C

→ ∫\(\frac{1}{x \sqrt{x^{2}-1}}\)dx = sec^-1x + C = -cosec^-1x + C

→ ∫\(\frac{1}{x \sqrt{x^{x}-a^{2}}}\) dx = \(\frac{1}{a}\) sec^-1\(\left(\frac{x}{a}\right)\) + C

→ ∫\(\frac{1}{a^{2}+x^{2}}\)dx = \(\frac{1}{a}\)tan^-1\(\left(\frac{x}{a}\right)\) + C

→ ∫\(\frac{1}{x^{2}-a^{2}}\)dx = \(\frac{1}{2a}\)log\(\left|\frac{x-a}{x+a}\right|\) + C

→ ∫\(\frac{1}{\sqrt{a^{2}+x^{2}}}\) dx = log |x + \(\sqrt{a^{2}+x^{2}}\)| + C

→ ∫\(\frac{1}{a^{2}-x^{2}}\) dx = \(\frac{1}{2 a}\)log \(\left|\frac{a+x}{a-x}\right|\) + C

→ ∫\(\frac{1}{\sqrt{x^{2}-a^{2}}}\) dx = log |x +  \(\sqrt{x^{2}-a^{2}}\)| + C

→ ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}}\) dx = sin^-1\(\left(\frac{x}{a}\right)\) + C

→ ∫\(\sqrt{a^{2}-x^{2}}\) dx = \(\frac{1}{2}\) x \(\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\) sin^-1\(\left(\frac{x}{a}\right)\) + C

→ ∫\(\sqrt{x^{2}-a^{2}}\) dx = \(\frac{1}{2}\) x \(\sqrt{x^{2}-a^{2}}-\frac{a^{2}}{2}\) log|x + \(\sqrt{x^{2}-a^{2}}\)| + C

→ ∫\(\sqrt{a^{2}+x^{2}}\) dx = \(\frac{1}{2}\) x \(\sqrt{a^{2}+x^{2}}+\frac{a^{2}}{2} \)log|x + \(\sqrt{a^{2}+x^{2}}\)| + C

→ Integration by parts is the integral of products of two functions. If f(x) and g(x) are any two differentiable functions of a single variable x, then
∫f(x)g(x)dx = f(x)∫g(x)dx
"The integral of the product of two functions = (first function) × (integral of the second function) - Integral of [(differential coefficient of the first function) × integral of the second function)]"

Remark 1.
The per choice of the first and second function: In the product of two functions if one of the two functions is not directly integrable (e.g., log x, sin^-1 x, tan^-1x etc.) We take it as the first function and the remaining function is taken as the second function. If both the functions are easily integrable, then the first function is chosen in such a way that the derivative of the function is a simple function and the function thus obtained under the integral sign is easily integrable than the original function.

Remark 2.
Integration by parts is not applicable to product of function in all cases. For example, the method does not work for ∫sin x² dx. The reason is that there does not exist any function whose derivative is sin x².

Remark 3.
Usually, if any function is a polyno¬mial in. x, then we take it as the first function. However, in cases where other function is inverse trigonometric function or logarithmic function, then we take them as first function.

We can also choose the first function of the function which comes first in the word ILATE, where 

• I - Inverse trigonometric function (sin^-1 x, cos ^-1 x, tan^-1x)
• L - Logarithmic functions
• A - Algebraic functions
• T - Trigonometric functions
• E - Exponential functions

→ Let f be continuous function defined on the closed interval [a, b] and F(x) be an anti-derivative of f(x) then definite integral of/(x) in closed interval [a, b] is denoted by
\(\int_{a}^{b}\)f(x) dx = \([F(x)]_{a}^{b}\) = F(b) - F(a)

→ Properties of definite integral are as follows, which will be useful in evaluating the definite integrals more easily.
(i) \(\int_{a}^{b}\)f(x)dx = \(\int_{a}^{b}\)f(t)dt
i.e., integration is independent of the change of variable.

(ii) \(\int_{a}^{b}\)f(x)dx = -\(\int_{b}^{a}\)f(x)dx
i.e., the limits of a definite integral are interchanged then its value changes by minus sign only.

(iii) \(\int_{a}^{b}\)f(x)dx = \(\int_{a}^{c}\)f(x)dx + \(\int_{c}^{a}\)f(x)dx
where a, b, c are real numbers and a < c < b.

This property can be generalized into the following form:
If a < c₁ < c₂ < c₃ ... < c_n < b, then
\(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{c_{1}}\) f(x) dx + \(\int_{c_{1}}^{c_{2}}\) f(x) dx + \(\int_{c_{2}}^{c_{3}}\) f(x) dx + ..................... + \(\int_{c_{n}}^{b} \)f(x) dx

(iv) \(\int_{0}^{a}\)f(x)dx = \(\int_{0}^{a}\)f(a - x)dx

(v) \(\int_{-a}^{a}\) f(x) dx = 2 \(\int_{0}^{a}\) f(x) dx , if f(-x) = f(x) i.e f is even

(vi) \(\int_{-a}^{a}\) f(x) dx = 0 if f(-x) = f(x) i.e f is odd

(vii) \(\int_{0}^{2a}\)f(x)dx = 2\(\int_{0}^{a}\)f(x)dx if f(2a - x) = f(x)

(viii) \(\int_{0}^{2a}\)f(x)dx = 0 if f(2a - x) = -f(x)

(ix) \(\int_{0}^{2a}\)f(x)dx = \(\int_{0}^{2a}\){f(x) + f(2a - x)}dx

(x) \(\int_{a}^{b}\)f(x)dx = \(\int_{a}^{b}\)f(a + b - x)dx

(xi) \(\int_{a}^{b}\)f(x)dx = (b - a)\(\int_{0}^{1}\)f{(b - a)x + a}dx

→ Definite integral as the limit of a sum is define as : If f is a continuous function defined on closed interval [a, b] and interval [a, b] divided into n equal sub-interval width as each sub-interval is h, where
a < a + h < a + 2h < a + 3h... < a + (n - 1)h < b,
Then \(\int_{a}^{b}\)f(x)dx
= \(\lim _{h \rightarrow 0}\)h[f(a)+f(a + h)+f(a + 2h) + ... +f{a + (n - 1)}h]
Where, h = \(\frac{b-a}{n}\)