RBSE Class 12 Maths Notes Chapter 6 अवकलज के अनुप्रयोग

These comprehensive RBSE Class 12 Maths Notes Chapter 6 अवकलज के अनुप्रयोग will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 6 Notes अवकलज के अनुप्रयोग

भूमिका (Introduction):
विज्ञान एवं अभियांत्रिकी के साथ-साथ सामाजिक विज्ञान, अर्थशास्त्र
और कई क्षेत्रों में अवकलज के विस्तृत अनुप्रयोग हैं । इस अध्याय में हम अवकलज के कुछ अनुप्रयोगों पर विचार करेंगे जो कि निम्न हैं

• राशियों के परिवर्तन की दर प्राप्त करने में,
• किसी बिन्दु पर स्पर्श रेखा एवं अभिलम्ब का समीकरण ज्ञात करने में
• वर्धमान एवं ह्रासमान फलनों का अन्तराल ज्ञात करने में एवं
• फलन का अधिकतम और न्यूनतम मान ज्ञात करने में किया जाता है।

राशियों के परिवर्तन की दर (Rate of Change of Quantities)
माना s एक राशि है जो समय t के साथ परिवर्तित होती है, तब समय t में लघु परिवर्तन δt होने पर राशि s में लघुपरिवर्तन δs है तब s में प्रति इकाई समय औसत परिवर्तन की दर \(\frac{\delta s}{\delta t}\) है तथा समय t के सापेक्ष s में क्षणिक परिवर्तन की दर निम्न प्रकार से
\(\lim _{\delta t \rightarrow 0} \frac{\delta s}{\delta t}=\frac{d s}{d t}\)
अतः समय t के सापेक्ष s में परिवर्तन की दर \(\frac{d s}{d t}\) है।
यदि v तथा r दोनों समय t के फलन हों तो
\(\frac{d v}{d t}=\frac{d v}{d r} \cdot \frac{d r}{d t}\)
अर्थात् \(\frac{d v}{d r}=\frac{d v / d t}{d r / d t}\)
अतः r के सापेक्ष v में परिवर्तन की दर ज्ञात करने के लिए t के सापेक्ष v व r में परिवर्तन की दर ज्ञात करके किया जा सकता है।

 

वर्धमान और ह्रासमान फलन ( Increasing And Decreasing Function):
वर्धमान फलन (Increasing Function)
एक फलन f(x) खुला अन्तराल (Open Interval) (a, b) में वर्धमान कहलाता है, यदि
x₁ < x₂ ⇒ f(x₁) < f(x₂), ∀ x₁, x₂ ∈ (a, b)

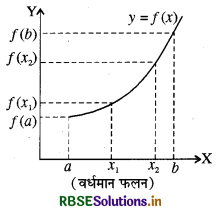
ह्रासमान फलन (Decreasing Function)
एक फलन f(x). खुला अन्तराल (Open Interval) (a, b) में ह्रासमान, फलन कहलाता है, यदि x₁ < x₂ ⇒ f(x₁) > f(x₂), ∀ x₁, x₂, ∈ (a, b)

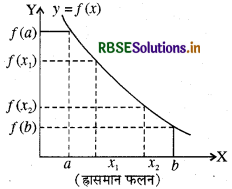
अचर फलन (Constant Function):
एक फलन f(x) खुला अन्तराल (a, b) में अचर फलन है यदि
f(x) = C, x ∈ (a, b), C एक अचर है।

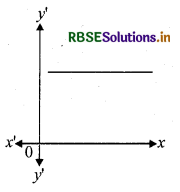
प्रमेय (Theorem)
माना कि एक वास्तविक अवकलनीय फलन f(x) खुला अन्तराल (a, b) में परिभाषित है, तो

• f(x) > 0 ∀ x ∈ (a, b) ⇒ f(x) खुला अन्तराल (a, b) में वर्धमान फलन है।
• fox) < 0 ∀ x ∈ (a, b) ⇒ f(x) अन्तराल (a, b) में ह्रासमान फलन है।
• f(x) = 0, ∀ x ∈ (a, b) ⇒ f(x), अन्तराल (a, b) में अचर फलन है।

प्रमाण
(i) f(x) > 0
⇒ f(x + h) - f(x) तथा h के चिह्न समान हैं, h के प्रत्येक छोटे मान के लिए
f(x) = \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

⇒ f(x + h) > f(x), जब h धनात्मक है
तथा f(x + h) < f(x), जब h ऋणात्मक है। ∴ x + h > x ⇒ f(x + h) > f(x), जब h > 0
x + h < x ⇒ f(x + h) < f(x), जब h <0
⇒ खुला अन्तराल (a, b) में वर्धमान है।

(ii) f(x) < 0 ⇒ f(x + h) - f(x) तथा h के चिह्न विपरीत हैं, h के प्रत्येक छोटे मान के लिए ∴ x + h > x ⇒ f(x + h) < f(x), जब h > 0
तथा x + h < x = f(x + h) > f(x), जब h < 0
⇒ fखुला अन्तराल (a, b) पर ह्रासमान है।

स्पर्श रेखा (Tangent Line):
मान लीजिए किसी वक्र y = f(x) पर कोई दो बिन्दु P(x, y) तथा Q(x + h, y + b) हैं। P तथा Q को मिलाओ।

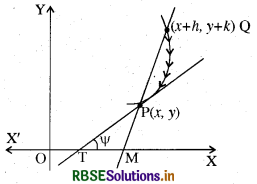
जब बिन्दु Q वक्र के अनुदिश (along the curve) P की ओर अग्रसर होता है तो जीवा PQ किसी निश्चित रेखा (मान लो PT) की ओर अग्रसर होगी। "PQ की सीमान्त स्थिति (limiting position) जब Q → P अर्थात् सरल रेखा PT बिन्दु P पर वक्र की स्पर्श रेखा ( tangent) कहलाती है।

अवकलज \(\left(\frac{d y}{d x}\right)\) का ज्यामितीय अर्थ (Geometrical Interpretation of The Derivative) \(\left(\frac{d y}{d x}\right)\)
मान लीजिए किसी वक्र y = f(x) पर P(x, y) कोई बिन्दु है तथा इसके बहुत समीप कोई अन्य बिन्दु Q(x + δx, y + δy) है जहाँ δx तथा δy अति लघु हैं। Q को P से मिलाकर इस प्रकार बढ़ाओ कि जीवा PQ, x-अक्ष को T' पर काटे। बिन्दु P तथा Q से x-अक्ष पर PM तथा QN लम्ब डालो और P से QN पर PR लम्ब डालो।

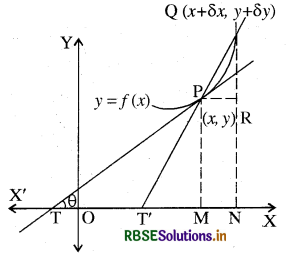
तब \(\frac{\delta y}{\delta x}=\frac{Q R}{P R}\) = tan QPR
= tan PT'X
= उस कोण की स्पर्श ज्या (tangent)

जो जीवा PQ, x-अक्ष से बनाती है।
\(\lim _{\delta x \rightarrow 0} \frac{\delta y}{\delta x}=\lim _{\delta x \rightarrow 0}\) tan PT'X
अब जैसे-जैसे δx शून्य की ओर अग्रसर होता है, Q भी P की ओर अग्रसर होगा और अन्त में जीवा PQ वक्र के P बिन्दु पर स्पर्श रेखा PT बन जाती है तथा कोण PT'X (जो जीवा PQ, xअक्ष से बनाती है) कोण PTX (जो स्पर्श रेखा PT, x-अक्ष से बनाती है) के बराबर हो जाता है।
∴ \(\frac{d y}{d x}=\lim _{\delta x \rightarrow 0} \frac{\delta y}{\delta x}=\lim _{Q \rightarrow P}\)tan ∠PT'X = tan ∠PTX

अर्थात् अवकल गुणांक \(\left(\frac{d y}{d x}\right)\) उस कोण की स्पर्शज्या (trigonometrical tangent) है जो वक्र y = f(x) के किसी बिन्दु P(x, y) पर खींची हुई स्पर्श रेखा x-अक्ष की दिशा के साथ बनाती है। साधारणतया यह कोण PTX, θ से प्रदर्शित किया जाता है।
अतः \(\frac{d y}{d x}\) = tan θ
उस कोण की स्पर्शज्या को जो बिन्दु P पर खींची गई स्पर्श रेखा x-अक्ष के साथ बनाती है। सामान्यतः बिन्दु P पर वक्र की प्रवणता (gradient) कहलाते हैं।

स्पर्श रेखाएँ और अभिलम्ब (Tangents and Normal)
इस अनुच्छेद में हम अवकलन के प्रयोग से किसी वक्र के एक बिन्दु पर स्पर्श रेखा और अभिलम्ब के समीकरण ज्ञात करेंगे।
(A) स्पर्श रेखा का समीकरण (Equation of the Tangent)
निर्देशांक ज्यामिति से हम जानते हैं कि बिन्दु (x₁, y₁) से गुजरने वाली सरल रेखा का समीकरण जिसकी प्रवणता m हो, होता
y - y₁ = m(x - x₁) अब स्पर्श रेखा के लिए सामान्य संकेतन में,
m = tan θ = \(\frac{d y}{d x}\)

अत: वक्र y = f(x) के बिन्दु P(x₁, y₁) पर स्पर्श रेखा का अभीष्ट समीकरण
(y - y₁) = \(\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right)}\)(x - x₁)
या (y - y₁) = f'(x₁, y₁) (x - x₁)

विशेष स्थितियाँ-
(i) यदि वक्र के किसी बिन्दु (x₁, y₁) पर स्पर्श रेखा y-अक्ष के समान्तर हो तो
\(\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right)}\) = 0
विलोमतः यदि वक्र के किसी बिन्दु (x₁, y₁) पर \(\frac{d y}{d x}\) = 0 हो तो उस बिन्दु पर स्पर्श रेखा x-अक्ष के समान्तर होगी।

(ii) यदि वक्र के किसी बिन्दु (x₁, y₁) पर स्पर्श रेखा y-अक्ष के समान्तर (या x-अक्ष पर लम्बवत्) हो, तो
\(\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right)}\) = ∞
या \(\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right)}=\frac{1}{0}\)
विलोमतः यदि वक्र के किसी बिन्दु (x, y) पर \(\frac{d y}{d x}\) = 0, तब उस बिन्दु पर स्पर्श रेखा y-अक्ष के समान्तर होती है। अर्थात् x-अक्ष पर लम्बवत् होती है।

(B) अभिलम्ब का समीकरण (Equation of the Normal)
अभिलम्ब-वक्र के किसी बिन्दु पर अभिलम्ब वह सरल रेखा है जो उस बिन्दु से गुजरती है तथा वक्र के उस बिन्दु पर खींची गई स्पर्श रेखा पर लम्ब है।

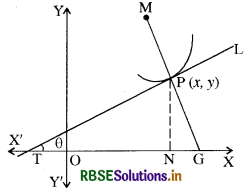
हम जानते हैं कि बिन्दु P(x₁, y₁) पर स्पर्श रेखा का झुकाव
m = \(\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right)}\)

अतः बिन्दु (x, y) पर लम्ब रेखा का झुकाव माना
m = -\(\frac{1}{\frac{d y}{d x}}=\frac{-d x}{d y}\)

अतः वक्र के बिन्दु P(x, y) पर अभिलम्ब का समीकरण
y - y₁ = -\(\left(\frac{d x}{d y}\right)_{\left(x_{1}, y_{1}\right)}\)(x - x₁)
या (y - y₁)\(\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right.}\) + (x - x₁) = 0

Note:
यदि दो वक्र y = f₁(x) और y = f₂(x) किसी बिन्दु P पर एक-दूसरे को काटते हैं तब P पर स्पर्श रेखाओं के मध्य कोण को P पर वक्रों के मध्य कोण द्वारा परिभाषित करते हैं। यदि P पर स्पर्श रेखाओं की प्रवणता \(\left(\frac{d y}{d x}\right)_{1}\), और \(\left(\frac{d y}{d x}\right)_{2}\) हो तो दोनों वक्रों के मध्य प्रतिच्छेदन कोण Φ है तो
tan Φ = \(\pm \frac{\left(\frac{d y}{d x}\right)_{1}-\left(\frac{d y}{d x}\right)_{2}}{1+\left(\frac{d y}{d x}\right)_{1}\left(\frac{d y}{d x}\right)_{2}}\)
यदि Φ = \(\frac{\pi}{2} \)हो तो \(\left(\frac{d y}{d x}\right)_{1}\left(\frac{d y}{d x}\right)_{2}\) = -1

अवकलज, त्रुटि तथा निकटतममान (Differentials, Errors and Approximation)
हम जानते हैं कि y का x के सापेक्ष अवकलज \(\frac{d y}{d x}\) होता है जो
अनुपात \(\frac{\Delta y}{\Delta x}\) का सीमान्त मान है जब Δx → 0, \(\frac{d y}{d x}\) एक प्रतीक है, दो अलग-अलग राशियों का अनुपात नहीं है, फिर भी हम इस अनुच्छेद में प्रतीक dy तथा dx का अर्थ इस तरीके से देते हैं कि प्रतीक का मौलिक अर्थ भागफल के अनुरूप हो जाता है, dx तथा dy अवकलज कहलाते हैं।

हम जानते हैं कि सीमान्त अवस्था में जब Δx → 0, तो
\(\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\frac{d y}{d x}\)

\(\frac{d y}{d x} \)से \(\frac{\Delta y}{\Delta x}\) का मान एक बहुत छोटी राशि h से इस प्रकार भिन्न रहता है कि h → 0 जब Δx → 0
∴ \(\frac{\Delta y}{\Delta x}=\frac{d y}{d x}\) + h, जहाँ h → 0 जब Δx → 0
⇒ Δy = \(\frac{d y}{d x}\)Δx + h(Δx)
चूँकि h Δx एक बहुत ही छोटी राशि है, जिसे नगण्य मान सकते हैं।
Δy = \(\frac{d y}{d x}\)Δx, निकटतम हम इस सूत्र का प्रयोग अनाश्रित चर x में अल्प परिवर्तन के संगत आश्रित चर y में अल्प परिवर्तन की गणना करने में कर सकते हैं। x में त्रुटि Δx को x में निरपेक्ष त्रुटि कहते हैं, \(\frac{\Delta x}{x}\) को x में आपेक्षिक त्रुटि कहते हैं तथा \(\frac{\Delta x}{x}\) × 100 को x में प्रतिशत त्रुटि कहते हैं।

टिप्पणी:
Δy = \(\frac{d y}{d x}\)Δx + hΔx, चूँकि h Δx बहुत सूक्ष्म है, इसलिए Δy का मुख्यमान \(\frac{d y}{d x}\)Δx है जो y का अवकलज कहलाता है तथा इसे Δy से प्रदर्शित किया जाता है अर्थात्
dy = \(\frac{d y}{d x}\)Δx
Δy सन्निकटतः dy के बराबर है। अत: Δy = \(\frac{d y}{d x}\)Δx

(उच्चतम और निम्नतम (Maxima and Minima)
इस अनुच्छेद में, हम विभिन्न फलनों के उच्चतम और निम्नतम मानों की गणना करने में अवकलज की संकल्पना का प्रयोग करेंगे, वास्तव में हम एक फलन के आलेख के वर्तन बिन्दुओं को (Turning Points) को ज्ञात करेंगे और इस प्रकार उन बिन्दुओं को ज्ञात करेंगे जिन पर आलेख स्थानीय अधिकतम (या न्यूनतम) पर पहुँचता है। ऐसे बिन्दुओं का ज्ञान ग्राफ खींचने में बहुत उपयोगी होता है। इसके अलावा हम एक फलन का निरपेक्ष उच्चतम मान (Absolute maximum value) और निरपेक्ष न्यूनतम मान (Absolute minimum value) भी ज्ञात करेंगे।

हम एक फलन y = f(x) के परिमित अन्तराल [a, b] में आरेख पर स्थित बिन्दुओं A, P, Q, R, S तथा B की कोटियों पर विचार करते हैं।

बिन्दु P एवं R के लघु सामीप्य (Small neighbourhood) में इन बिन्दुओं की कोटियाँ अधिकतम हैं, जबकि Q एवं s के लघु सामीप्य में इन बिन्दुओं की कोटियाँ न्यूनतम हैं, A की कोटि सबसे कम एवं B की कोटि सबसे अधिक हैं। बिन्दु P, Q, R, S पर खींची गई वक्र की स्पर्श रेखाएँ x अक्ष के समान्तर हैं।

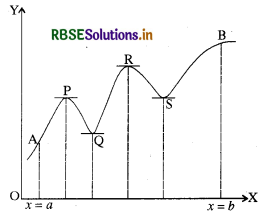
बिन्दु P एवं R को फलन के उच्चिष्ठ बिन्दु (points of maxima) तथा बिन्दु Q एवं S को फलन के निम्निष्ठ बिन्दु (points of minima) कहते हैं एवं इनकी कोटियाँ फलन के क्रमशः उच्चिष्ठ एवं निम्निष्ठ मान कहलाती हैं। उच्चिष्ठ एवं निम्निष्ठ बिन्दुओं को फलन के चरम बिन्दु (Extreme points) भी कहते हैं।

(1) परिभाषाएँ (Definitions)
(i) सापेक्ष उच्चिष्ठ एवं निम्निष्ठ मान (Relative maximum and minimum value) : फलन f(x) का मान बिन्दु x = C पर सापेक्ष उच्चिष्ठ कहलाता है यदि फलन (x) का मान x = C के अल्प प्रतिवेश के प्रत्येक बिन्दु पर f(c) से छोटा है अर्थात्
f(x) ≤ f(c), ∀ x ∈ (c - 1, C + h)

जहाँ h एक धनात्मक अल्प राशि है। इसी प्रकार फलन f(x) का मान x = c पर सापेक्ष निम्निष्ठ कहलाता है यदि फलन f(x) का मान x = C के अल्प प्रतिवेश के प्रत्येक बिन्दु पर fc) से बड़ा है अर्थात्
f(x) 2 fC), ∀ x ∈ (c - h, C + h) सापेक्ष उच्चिष्ठ मान को सामान्यतः उच्चिष्ठ या अधिकतम तथा सापेक्ष निम्निष्ठ मान को सामान्यतः निम्निष्ठ या न्यूनतम मान कहते हैं।

(ii) निरपेक्ष उच्चिष्ठ एवं निम्निष्ठ मान (Absolute maximum and minimum value)
फलन f(x) का मान प्रान्त D में बिन्दु x = c पर निरपेक्ष उच्चिष्ठ या निरपेक्ष अधिकतम (greatest) कहलाता है, यदि f(x) = f(c), ∀ x ∈ D तथा फलन f(x) का मान प्रान्त D में बिन्दु x = C पर निरपेक्ष निम्निष्ठ या निरपेक्ष न्यूनतम (least) कहलाता है यदि f(x) > f(c), ∀ x ∈D

टिप्पणी
किसी प्रान्त में फलन के उच्चिष्ठ एवं निम्निष्ठ मान एक से अधिक हो सकते हैं परन्तु प्रान्त में निरपेक्ष अधिकतम या निरपेक्ष न्यूनतम मान केवल एक ही होता है। एक उच्चिष्ठ मान, निम्निष्ठ मान से कम हो सकता है इसी प्रकार एक निम्निष्ठ मान, उच्चिष्ठ मान से अधिक हो सकता है। फलन के उच्चिष्ठ एवं निम्निष्ठ मान को चरम मान भी कहते हैं।

(2) फलन के चरम मान के लिए आवश्यक प्रतिबन्ध (Necessary Condition for the extreme value of a function)
प्रमेय : यदि f(x) एक अवकलनीय फलन है तो x = c पर f(x) के चरम मान होने के लिए आवश्यक है कि f(c) = 0 इसी प्रकार से यदि f(c) फलन f(x) का सापेक्ष निम्निष्ठ मान है, तो भी f(c) = 0 होता है।

टिप्पणी
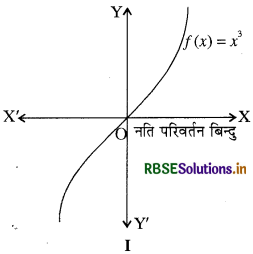
फलन f(x) के x = c पर उच्चिष्ठ या निम्निष्ठ मान विद्यमान होने के लिए f'(c) = 0 केवल आवश्यक प्रतिबन्ध है परन्तु पर्याप्त नहीं है। उदाहरण के लिए यदि हम f(x) = x³ लें तब x = 0 पर (0) = 0 परन्तु (0) फलन का चरम मान नहीं है, क्योंकि जब x > 0 → f(x) > f(0) तथा जब x < 0 = f(x) < f(0)
अतः 10) न तो उच्चिष्ठ है और न निम्निष्ठ।

(3) फलन के चरम मान के लिए पर्याप्त प्रतिबन्ध (Sufficient condition for the extreme value of a function)
प्रमेय :
(i) x = c पर फलन f(x) का उच्चिष्ठ मान विद्यमान होगा, यदि f'(c) = 0 तथा f''(c) < 0 (ii) x = C पर फलन f(x) का निम्निष्ठ मान विद्यमान होगा, यदि f(c) = 0 तथा f"(c) > 0

टिप्पणी
यदि x = C पर फलन (x) के लिए f(c) = 0; f"(c) = 0 परन्तु f"(c) ≠ 0 तो यह बिन्दु नति परिवर्तन बिन्दु (Point of inflexion) कहलाता है।

(4) प्रमेय 1 (प्रथम अवकलज परीक्षण):
मान लीजिए कि एक फलन f किसी विवृत्त अन्तराल I पर परिभाषित है। मान लीजिए कि f अन्तराल I में स्थित क्रांतिक बिन्दु c पर संतत है। तब

• x के बिन्दु c से होकर बढ़ने के साथ-साथ, यदि f'(x) का चिह्न धन से ऋण में परिवर्तित होता है अर्थात् यदि बिन्दु c के बायीं ओर और उसके पर्याप्त निकट के प्रत्येक बिन्दु पर f'(x) > 0 तथा c के दायीं ओर और पर्याप्त निकट के प्रत्येक बिन्दु पर f'(x) < 0 हो तो c स्थानीय उच्चतम एक बिन्दु है।
• x के बिन्दु c से होकर बढ़ने के साथ-साथ यदि f'(x) का चिह्न ऋण से धन में परिवर्तित होता है, अर्थात् यदि बिन्दु c के बायीं ओर और उसके पर्याप्त निकट के प्रत्येक बिन्दु पर f(x) < 0 तथा c के दायीं ओर और उसके पर्याप्त निकट के प्रत्येक बिन्दु पर f(x) > 0 हो तो c स्थानीय निम्नतम बिन्दु है।
• x के बिन्दु c से होकर बढ़ने के साथ यदि f(x) का चिह्न परिवर्तित नहीं होता है, तो c न तो स्थानीय उच्चतम बिन्दु है और न स्थानीय निम्नतम बिन्दु। वास्तव में, इस प्रकार के बिन्दु को नति परिवर्तन बिन्दु (Point of Inflection) कहते हैं।

टिप्पणी
यदि c फलन f का एक स्थानीय उच्चतम बिन्दु है तो f(c) फलन का स्थानीय उच्चतम मान है। इसी प्रकार, यदि c फलन का एक स्थानीय निम्नतम बिन्दु है, तो f(c) फलन का स्थानीय निम्नतम मान है। आकृतियाँ I और II प्रमेय 1 की ज्यामितीय व्याख्या करती हैं।

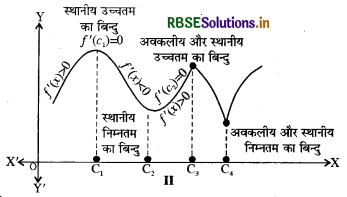
(5) फलन के उच्चिष्ठ एवं निम्निष्ठ के गुण (Properties of maxima and minima of a function):
यदि f(x) एक संतत फलन है और उसका ग्राफ खींचा जा सके तो निम्नलिखित गुण सरलता से देखे जा सकते हैं

• फलन f(x) के दो समान मानों के मध्य कम से कम एक उच्चिष्ठ या निम्निष्ठ मान अवश्य होता है।
• उच्चिष्ठ व निम्निष्ठ मान एकान्तर क्रम में विद्यमान होते हैं।
• f(x) का चिह्न धन से ऋण होता है जब f(x) उच्चिष्ठ बिन्दु से गुजरता है तथा जब f(x) का चिह्न ऋण से धन होता है तो f(x) निम्निष्ठ बिन्दु से गुजरता है।
• यदि किसी बिन्दु के दोनों तरफ f(x) का चिह्न नहीं बदलता है तो वह बिन्दु नति परिवर्तन बिन्दु होता है।
• उच्चिष्ठ एवं निम्निष्ठ बिन्दु पर f(x) = 0 होने से, उस बिन्दु पर स्पर्श रेखा x-अक्ष के समान्तर होती है।
• यदि किसी बिन्दु पर f(x) का मान उच्चिष्ठ (निम्निष्ठ) हो, तो उस बिन्दु पर \(\frac{1}{f(x)}\) [f(x) ≠ 0] का मान निम्निष्ठ (उच्चिष्ठ) होता है।

(6) उच्चिष्ठ तथा निम्निष्ठ ज्ञात करने की क्रियाविधि (Working rule to find maxima and minima)

• दिये गये फलन को y = f(x) के रूप लिखिए तथा \(\frac{d y}{d x}\) ज्ञात कीजिए।
• समीकरण \(\frac{d y}{d x}\) = 0 को हल कीजिए, माना हल x = a₁, a₂, a₃...... हैं।
• \(\frac{d^{2} y}{d x^{2}}\) ज्ञात करके प्रत्येक बिन्दु x = a₁, a₂, a₃...... पर इसका मान ज्ञात कीजिए।
• यदि x = a₁, पर \(\frac{d^{2} y}{d x^{2}}\) < 0 ही तो x = a₂, फलन का उच्चिष्ठ बिन्दु है, तथा यदि x = a₁, पर \(\frac{d^{2} y}{d x^{2}}\) > 0 तो x = a₁, फलन का निम्निष्ठ बिन्दु है। \(\frac{d^{2} y}{d x^{2}}\) = 0 होने की स्थिति में आगे अवकलन कीजिए।
  • \(\frac{d^{3} y}{d x^{3}}, \frac{d^{4} y}{d x^{4}}\) ........ आदि ज्ञात कीजिए जब तक कि x = a₁, पर मान अशून्य हो।
  • यदि अशून्य होने वाला अवकल गुणांक विषम क्रम का है, जैसे \(\frac{d^{3} y}{d x^{3}}, \frac{d^{5} y}{d x^{5}}\) .......... तो x = a₁, पर फलन न तो उच्चिष्ठ है और न निम्निष्ठ है।
  • यदि अशून्य होने वाला अवकल गुणांक सम क्रम का है जैसे \(\frac{d^{4} y}{d x^{4}}, \frac{d^{6} y}{d x^{6}}\), ....... तो वही स्थिति होगी जो \(\frac{d^{2} y}{d x^{2}}\) ≠ 0 होने के साथ होती है। इसी प्रकार अन्य बिन्दुओं x = a₁, a₂, a₃ ........ पर परीक्षण करते हैं।

→ परिवर्तन की दर-यदि एक राशि y एक दूसरी राशि x के सापेक्ष किसी नियम y = f(x) को संतुष्ट करते हुए परिवर्तित होती है तो \(\frac{d y}{d x}\) (या f'(x)) x के सापेक्ष y में परिवर्तन की दर को निरूपित करता है।

→ अवकलज-यदि y = f(x), (a, b) में अवकलनीय फलन है तब
\(\frac{d y}{d x}=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0}\) \(\frac{f(x+\Delta x)-f(x)}{\Delta x}\) = f'(x)
⇒ \(\frac{d y}{d x}\) = f'(x)
⇒ dy = f'(x) dx
यहाँ Δx को निरपेक्ष त्रुटि, \(\frac{\Delta x}{x}\) को सापेक्षिक त्रुटि एवं \(\frac{\Delta x}{x}\) × 100 को प्रतिशत त्रुटि कहते हैं।

→ स्पर्श रेखा एवं अभिलम्ब

• बिन्दु (x, y) पर स्पर्श रेखा की प्रवणता = \(\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right)}\)
• बिन्दु (x, y,) पर वक्र की स्पर्श रेखा का समीकरण y - y₁ = \(\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right)}\) (x - x₁)
• बिन्दु (x₁, y₁) पर अभिलम्ब की प्रवणता = -\(\frac{1}{\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right)}}\)
• बिन्दु (x₁, y₁) पर अभिलम्ब का समीकरण
  y - y₁ = -\(\frac{1}{\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right)}}\) (x - x₁)

→ वर्धमान ह्रासमान फलन
(a) एक फलन f अन्तराल [a, b] में वर्धमान है यदि [a, b] में x₁ < x₂ ⇒ f(x₁) < f(x₂), सभी x₁, x₂, ∈ (a, b) के लिए तब हम कहेंगे कि (a, b) में f(x) वर्धमान है यदि ∀ x ∈ (a, b), f'(x) > 0
(b) एक फलन , अन्तराल [a, b] में ह्रासमान है यदि [a, b] में x₁ > x₂ ⇒ f(x₁) < f(x₂) सभी x₁, x₂, ∈ (a, b) के लिए तब हम कहेंगे कि (a, b) में f(x) ह्रासमान है यदि ∀ x ∈ (a, b), के लिए f'(x) > 0 हो।

→ उच्चतम एवं निम्नतम
(a) फलन f के प्रान्त में एक बिन्दु c जिस पर या तो f(c) = 0 या f अवकलनीय नहीं है, f का क्रांतिक बिन्दु कहलाता है।
(b) प्रथम अवकलज परीक्षण-माना कि एक विवृत अन्तराल I पर फलन f परिभाषित है। माना I में एक क्रान्तिक बिन्दु c पर फलन संतत है तब

• जब x बिन्दु c के बायीं ओर से दायीं ओर बढ़ता है तब f(x) का चिह्न धन से ऋण में परिवर्तित होता है तब c स्थानीय उच्चतम बिन्दु कहलाता है।
• जब x बिन्दु के बायीं ओर से दायीं ओर बढ़ता है तब f(x) का चिह्न ऋण से धन में परिवर्तित होता है तब c स्थानीय निम्नतम का एक बिन्दु है।
• जब x बिन्दु c के बायीं ओर से दायीं ओर बढ़ता है तब f(x) परिवर्तित नहीं होता तब c नति परिवर्तन बिन्दु है।

(c) द्वितीय अवकलज परीक्षण-माना कि एक अन्तराल I पर f एक परिभाषित फलन है और C ∈ I तथा f c पर लगातार दो बार अवकलनीय है तब

• यदि f(c) = 0 और f"(c) < 0 तब x = c स्थानीय उच्चतम का एक बिन्दु है। f का स्थानीय उच्चतम मान f(c) है।
• यदि f(c) = 0 और f(c) > 0 तब x = c स्थानीय निम्नतम का एक बिन्दु है। का स्थानीय निम्नतम मान f(c) है।
• यदि f(c) = 0 और f(c) = 0 तो यह परीक्षण असफल रहता है।