RBSE Class 12 Maths Notes Chapter 5 सांतत्य तथा अवकलनीयता

These comprehensive RBSE Class 12 Maths Notes Chapter 5 सांतत्य तथा अवकलनीयता will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 5 Notes सांतत्य तथा अवकलनीयता

प्रस्तावना ( Introduction):
पिछली कक्षा में हम फलनों की सीमा तथा बहुपदीय फलनों एवं
त्रिकोणमितीय फलनों का अवकलन करना सीख चुके हैं। इस अध्याय में हम सातत्य (Continuity), अवकलनीयता (Differentiability).791 57cto reefeath Hitamente at महत्त्वपूर्ण संकल्पनाओं को प्रस्तुत करेंगे। यहाँ हम प्रतिलोम त्रिकोणमितीय फलनों का अवकलन करना भी सीखेंगे। यहाँ पर हम कुछ नये प्रकार के फलनों को प्रस्तुत कर रहे हैं, जिनको चरघातांकी (Exponential) और लघुगणकीय (Logarithmic) फलन कहते हैं।

फलन की सततता या सातत्य (Continuity of A Function):
मान लीजिये कि f वास्तविक संख्याओं के किसी उपसमुच्चय में परिभाषित एक वास्तविक फलन है और मान लीजिये कि f के प्रान्त में a एक बिन्दु है। तब बिन्दु a पर संतत है, यदि
\(\lim _{x \rightarrow a}\) f(x) = f(a)
विस्तृत रूप से यदि x = a पर बायीं सीमा, दायीं सीमा और फलन के मान का यदि अस्तित्व (existence) है और ये सभी एक-दूसरे के बराबर हों, तो x = a पर फलन संतत कहलाता है।

याद कीजिये कि यदि x = a पर बायें पक्ष तथा दायें पक्ष की सीमायें संपाती हैं तो इनके उभयनिष्ठ मान को हम x = a पर फलन की सीमा कहते हैं । इस प्रकार हम सातत्य की परिभाषा को एक अन्य प्रकार से भी व्यक्त कर सकते हैं जो कि इस प्रकार से एक फलन x = a पर संतत है, यदि फलन x = a पर परिभाषित है और यदि x = a पर फलन का मान x = a पर फलन की सीमा के बराबर है। यदि x = a पर फलन संतत नहीं है तो हम कहते हैं कि a पर f असंतत (Discontinuous) है तथा a को f का एक असांतत्य का बिन्दु (Point of Discontinuity) कहते हैं।

इसको हम निम्न प्रकार से भी परिभाषित कर सकते हैंकिसी फलन f(x) का लेखा चित्र (Graph) खींचने पर जो वक्र प्राप्त होता है वह इस प्रकार हो कि किसी बिन्दु x = a पर टूटता न हो तो फलन f(x) उस बिन्दु पर संतत (Continuous) कहलाता है। इसके विपरीत यदि किसी बिन्दु पर फलन f(x) का लेखाचित्र टूट जाता है, तो उस बिन्दु को फलन का असांतत्य बिन्दु (Point of Discontinuity) कहते हैं।

यदि कोई फलन f(x) किसी अन्तराल (a, b) के प्रत्येक बिन्दु पर संतत हो तो उस फलन को अन्तराल (Interval) (a, b) में संतत कहते हैं। सातत्य को ज्यामितीय रूप से समझने के लिए निम्नलिखित आरेखों पर (0, 2):विचार करते हैं

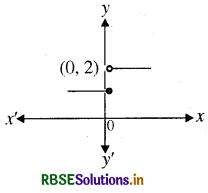
(1) फलन f(x) = 1, यदि x ≤ 0
= 2, यदि x > 0
का आरेख निम्न प्रकार है यह फलन वास्तविक रेखा के प्रत्येक बिन्दु पर परिभाषित है। x = 0 के बायें फलन के (0, 2), बायें तथा दायें पक्ष की सीमायें क्रमशः 1 तथा 2 हैं। बायें - तथा दायें फलन की सीमायें समान संपाती नहीं हैं। अतः x = 0 पर फलन संतत नहीं है।

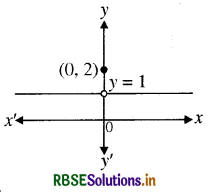
(2) फलन f(x) = 1 यदि x ≠ 0
= 2, यदि x = 0
यह फलन भी प्रत्येक बिन्दु पर परिभाषित है। x = 0 पर दोनों ही, बायें तथा दायें पक्ष की सीमायें 1 के बराबर हैं। किन्तु x = 0 पर फलन का मान 2 है जो कि दायें और बायें पक्ष की सीमाओं के उभयनिष्ठ मान के बराबर नहीं है। यह एक दूसरा उदाहरण है जिसमें x = 0 पर फलन संतत नहीं है।

→ फलन के किसी बिन्दु पर सातत्य (Continuity of A Function At A Point):
फलन f.x) अपने प्रान्त के किसी बिन्दु x = a पर संतत होगा
यदि
(i) \(\lim _{x \rightarrow a}\) f(x) = f(a) विद्यमान हो तथा
(ii) \(\lim _{x \rightarrow a^{-}}\) f(x) = \(\lim _{x \rightarrow a^{+}}\) f(x) = f(a) = f (a - 0)
= f (a + 0) = f (a)
⇒ \(\lim _{h \rightarrow 0}\) f(a - h) = \(\lim _{h \rightarrow 0}\)(a + h) = f (a)
अर्थात् बायीं सीमा = दायीं सीमा = a पर फलन का मान

 

(संतत फलन (Continuous Function):
यदि कोई फलन अपने प्रान्त के प्रत्येक बिन्दु पर संतत है तो उसे संतत फलन कहते हैं। निम्नलिखित फलन अपने संगत प्रान्त में सदैव संतत होते हैं

• अचर फलन : f(x) = c
• तत्समक फलन : f(x) = x
• मापांक फलन : f(x) = |x| = x, x ≥ 0
  = -x, x < 0
• बहुपद फलन : f(x) = a₀xⁿ + a₁x^n-1 + a₂x^n-2 + .... +a_n
• त्रिकोणमितीय फलन : sinx, cosx, .......
• चरघातांकी फलन : f(x) = a^x
• लघुगणकीय फलन : f(x) = log_ex, log_ax
• परिमेय फलन : \(\frac{f(x)}{g(x)}\), g(x) ≠ 0
• प्रतिलोम त्रिकोणमितीय फलन : sin^-1x, cos^-1x, ........
• अतिपरवलय फलन : f(x) = sinhx, coshx, tanhx

असंतत फलन (Discontinuous Function):
यदि कोई फलन अपने प्रान्त में कम से कम एक बिन्दु पर संतत नहीं है तो उसे असंतत फलन कहते हैं। जैसे

• \(\frac{1}{x}\), x = 0 पर असंतत
• tanx, secx, x = ±\(\frac{\pi}{2}\), ± \(\frac{3 \pi}{2}\) पर असंतत
• (cotx, cosecx, x = 0, ± π, ± 2π पर असंतत
• sin\(\frac{1}{x}\), cos\(\frac{1}{x}\)x = 0 पर असंतत
• e^1/x, x = 0 पर असंतत
• [x], (महत्तम पूर्णांक फलन) प्रत्येक पूर्णांक पर असंतत
• x - [x], (अपूर्णांश फलन) प्रत्येक पूर्णांक पर असंतत

→ संतत फलन के गुणधर्म (Properties of Continuous Function)
(1) यदि f(x) या g(x) दो ऐसे वास्तविक फलन हैं जो एक वास्तविक संख्या a के लिए संतत हैं तब निम्नलिखित फलन भी उस वास्तविक संख्या a के लिए संतत होंगे

• f(x) + g(x), x = a पर संतत है
• f(x) - g(x), x = a पर संतत है
• f(x) . g(x), x = a पर संतत है
• f(x) जहाँ पर c अचर है, x = a पर संतत है।

(2) यदि f(x) तथा (x) दो संतत फलन हैं तो \(\frac{f(x)}{g(x)}\) उन बिन्दओं g(x) पर संतत होगा, जिन पर g(x) ≠ 0
(3) यदि f(x) तथा g(x) दो संतत फलन हैं तो उनका संयुक्त फलन (gof)(x) भी संतत फलन होगा।

→ अवकलनीयता (Differentiability):
यदि y = fix) कोई संतत फलन है तो x = a पर फलन अवकलनीय होगा यदि फलन के वक्र के उस बिन्दु पर स्पर्श रेखा खींची जा सकती हो। इसके विपरीत हम इसे इस प्रकार कह सकते हैं कि फलन f(x) बिन्दु x = a पर अवकलनीय नहीं होगा यदि वक्र के इस बिन्दु पर अंसतत (टूटा हुआ हो) या इस बिन्दु पर वक्र की दिशा में कोणीय परिवर्तन हो रहा हो।
अतः हम कह सकते हैं कि f(x) बिन्दु P पर अवकलनीय है, यदि और केवल यदि बिन्दु P पर एक अद्वितीय स्पर्श रेखा का अस्तित्व हो अर्थात् वक्र P पर कोणीय बिन्दु न हो।

→ किसी बिन्दु पर दायां अवकलज का मान (Value of Right Derivative At A Point):
बिन्दु x = a पर फलन f(x) का दायां अवकलज का मान Rf'(a) = \(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\) h > 0 होता है।

→ किसी बिन्दु पर बायां अवकलज का मान (Value Of Left Derivative At A Point):
बिन्दु x = a पर फलन f(x) का बायाँ अवकलज का मान Lf"(a)
= f'(a - 0) = \(\lim _{h \rightarrow 0} \frac{f(a-h)-f(a)}{-h}\) h > 0 होता है।

→ x = a पर फलन की अवकलनीयता (Differentiability Of Function At x = a)
★ कोई फलन f(x), x = a पर अवकलनीय तब होगा जबकि उसके दायें अवकलज का मान, बायें अवकलज के मान के बराबर होगा। अर्थात् Rf'(a) = Lf' (a)
⇒ f'(a + 0) = f"(a - 0)
⇒ \(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}=\lim _{h \rightarrow 0} \frac{f(a-h)-f(a)}{-h}\)
यदि Rf'(a) ≠ Lf'(a)
तब f(x), x = a पर अवकलनीय नहीं होगा। कोई फलन संवृत अन्तराल (Closed Interval) [a, b] में अवकलनीय (differentiable) कहलाता है यदि फलन अन्तराल (a, b) के प्रत्येक बिन्दु पर अवकलनीय (differentiable) हो, साथ ही 'a' तथा 'b' पर भी अवकलनीय हो । इस प्रकार फलन विवृत्त अन्तराल (Open Interval) (a, b) में अवकलनीय (differentiable) कहलाता है यदि यह (a, b) के प्रत्येक बिन्दु पर अवकलनीय है।

→ महत्त्वपूर्ण परिणाम (Important Results)

• प्रत्येक अवकलनीय फलन संतत होता है।
• लेकिन प्रत्येक संतत फलन अवकलनीय हो यह आवश्यक नहीं है। जैसे-मापांक फलन f(x) = |x|, x = 0 पर संतत है, लेकिन अवकलनीय नहीं।
• यदि कोई फलन संतत नहीं है तो वह निश्चित रूप से अवकलनीय नहीं होता है।
• अवकलनीय फलनों का योग, अन्तर, गुणनफल, भागफल तथा संयुक्त फलन भी सदैव अवकलनीय ही होता है।
• प्रत्येक बहुपदीय, चरघातांकी तथा अचर फलन वास्तविक रेखा पर सदैव अवकलनीय होते हैं।
• लघुगणकीय फलन, त्रिकोणमितीय फलन तथा प्रतिलोम त्रिकोणमितीय फलन अपने प्रान्त पर अवकलनीय होते हैं।

→ अवकलन के मूल प्रमेय (Fundamental Theorems On Differentiation)
(1) किसी भी अचर राशि का अवकलज शून्य होता है अर्थात्
(2) एक अचर राशि तथा किसी फलन के गुणनफल का अवकल गुणांक उस अचर राशि तथा फलन के अवकलज का गुणनफल होता है।
अर्थात् \(\frac{d}{d x}\)[af(x)] = a\(\frac{d}{d x}\)[f(x)] = af"(x)
अतः (अचर राशि × फलन) का अवकलज = अचर राशि × फलन का अवकलज

फलनों के बीजीय योगफल का अवकलज, इन फलनों के अवकलजों के बीजीय योग के बराबर होता है।
अर्थात् \(\frac{d}{d x}\)(u + y + w +....) = \(\frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}\)+ ..........
जहाँ u, y, w, ........ सभी x के फलन हैं तथा जिनका पृथक् पृथक् अवकल गुणांक ज्ञात किया जा सकता है।

टिप्पणी-यदि विभिन्न फलन + अथवा - चिन्हों से सम्बन्धित हो, तो सम्पूर्ण फलन का अवकल गुणांक प्रत्येक फलन के अलग
अलग अवकल गुणांक को उचित चिन्ह सहित रखकर तथा योग करने पर प्राप्त होता है
\(\frac{d}{d x}\)(u ± y ± w ±....) = \(\frac{d u}{d x}±\frac{d v}{d x}±\frac{d w}{d x}\)± ..........

(4) दो फलनों के गुणनफल का अवकलज माना कि u तथा v, x के फलन हैं जिनका पृथक्-पृथक् अवकल गुणांक ज्ञात किया जा सकता है।
माना कि y = u.v
तब \(\frac{d y}{d x}\) = u . \(\frac{d v}{d x}\) + v. \(\frac{d u}{d x}\)
अर्थात् \(\frac{d}{d x}\)(u . v) = u .\(\frac{d v}{d x}\) + v . \(\frac{d u}{d x}\)
अतः दो फलनों के गुणनफल का अवकलज = (प्रथम फलन) × (द्वितीय फलन का अवकलज) + (द्वितीय फलन) × (प्रथम फलन का अवकलज) है टिप्पणी-दो फलनों में से किसी भी एक को प्रथम फलन माना जा सकता है।

व्यापकीकरण-उपरोक्त परिणाम में दो से अधिक फलनों के गुणनफल का अवकलज भी निम्न सूत्र द्वारा ज्ञात किया जाता है।
\(\frac{d}{d x}\)(u, v, w, z ......) = (v. w. z.....) \(\frac{d u}{d x}\) + (u, w, z, ......) \(\frac{dv}{d x}\) + (u, v, z, .......)\(\frac{dw}{d x}\) + ..........

नियम-प्रथम फलन के अवकल गुणांक से शेष सभी फलनों के गुणनफल को गुणा कर दें। फिर द्वितीय फलन के अवकल गुणांक से. शेष सभी फलनों के गुणनफल को गुणा कर दें। इस प्रकार एक-एक करके सभी फलनों के अवकल गुणांकों को शेष फलनों के गुणनफल से गुणा करते जायें तथा इन पदों के बीच योग (+) का चिन्ह रखते जायें तो अभीष्ट अवकल गुणांक ज्ञात हो जाता है।

(5) दो फलनों के भागफल का अवकल गुणांक
मान लो कि y = \(\frac{u}{v}\) है, यहाँ पर u, v चर x के फलन हैं।

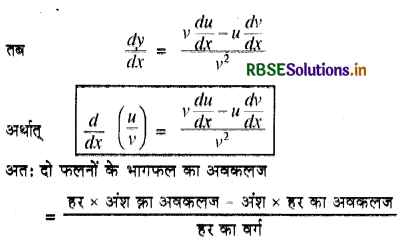
→ महत्त्वपूर्ण फलनों के अवकलज (Derivatives of Important Functions)

• \(\frac{d}{d x}\)(xⁿ) = nx^n-1
• \(\frac{d}{d x}\)(e^x) = e^x
• \(\frac{d}{d x}\)(a^x) = a^x log_e a
• \(\frac{d}{d x}\)(log_ex) = \(\frac{1}{x}\)
• \(\frac{d}{d x}\)(log_ax) = \(\frac{1}{x \log _e a}\)
• \(\frac{d}{d x}\)(sin x) = cos x
• \(\frac{d}{d x}\)(cos x) = -sin x
• \(\frac{d}{d x}\)(tan x) = sec²x
• \(\frac{d}{d x}\)(cot x) = - cosec²x
• \(\frac{d}{d x}\)(sec x) = sec x tan x
• \(\frac{d}{d x}\)(cosec x) = -cosec x cot x
• \(\frac{d}{d x}\)(sin^-1x) = \(\frac{1}{\sqrt{1-x^2}}\)
• \(\frac{d}{d x}\)(cos^-1x) = -\(\frac{1}{\sqrt{1-x^2}}\)
• \(\frac{d}{d x}\)(tan^-1x) = \(\frac{1}{1+x^2}\)
• \(\frac{d}{d x}\)(cot^-1x) = -\(\frac{1}{1+x^2}\)
• \(\frac{d}{d x}\)(sec^-1x) = \(\frac{1}{1+x^2}\)
• \(\frac{d}{d x}\)(cosec^-1x) = -\(\frac{1}{1+x^2}\)

टिप्पणी-उपरोक्त परिणामों से स्पष्ट है कि जो फलन co शब्द से प्रारम्भ हो रहे हैं, उनका अवकलज ऋणात्मक एवं अन्य सभी धनात्मक।

→ फलन के फलन का अवकलज (Derivative of A Function of A Function):
माना कि y = f(u) तथा u = Φ(x) अर्थात् y, u का फलन है और प, स्वयं x का फलन है। यह भी माना कि x में कोई वृद्धि δx के संगत u में वृद्धि δu है और u में वृद्धि δu के संगत y में वृद्धि δy हो, तब

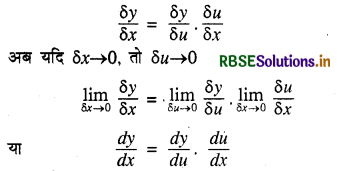
→ व्यापकीकरण
y = f(u), u = Φ(v), v = Ψ(w),
w = f(x) तो
\(\frac{d y}{d x}=\frac{d y}{d u} \cdot \frac{d u}{d v} \cdot \frac{d v}{d w} \cdot \frac{d w}{d x}\)

→ लघु विधि (Shortest Method):
इस विधि से अवकल गुणांक ज्ञात करने के लिए हम प्रत्येक परतंत्र चर का उसके स्वतंत्र चर के सापेक्ष अवकलज उस समय तक ज्ञात करते हैं जब तक कि हमें \(\frac{d x}{d x}\) प्राप्त न हो जाये। तत्पश्चात् इन सभी परिणामों को गुणा कर अभीष्ट अवकल गुणांक प्राप्त करते हैं।
उदाहरणार्थ-y = cos log x² का x के सापेक्ष अवकल गुणांक ज्ञात करने के लिए सर्वप्रथम y का चर, log x² के सापेक्ष अवकल गुणांक ज्ञात कीजिये जो कि -sin log x² है, फिर log x² का चर x² के सापेक्ष अवकल गुणांक ज्ञात कीजिये जो कि , है, अन्त में x² का चर x के सापेक्ष अवकल गुणांक ज्ञात कीजिये जो कि 2x है। अब इन तीनों अवकल गुणांकों का गुणनफल ही y का x के सापेक्ष अभीष्ट अवकल गुणांक होगा। अर्थात् y = cos log. x²
तो 4 = - sin log_e x² × \(\frac{1}{x^2}\) × 2x
= \(\frac{-2}{x}\) sin log_e x²
\(\frac{d}{d x}\)(cos log_e x²) = \(\frac{-2}{x}\)sin log_ex²

→ अस्पष्ट फलनों के अवकलज (Derivatives of Implicit Functions):
(i) स्पष्ट फलन (Explicit Function)
यदि किसी समीकरण में x तथा y दोनों चर हों तथा इसमें y को x के (या x को y के) फलन के रूप में स्पष्ट रूप से व्यक्त किया जा सके तो y को x का (या x को y का) स्पष्ट फलन कहते हैं।

(ii) अस्पष्ट फलन (Implicit Function)
यदि किसी समीकरण में x तथा y दोनों चर हों तथा इसमें y को x के फलन के रूप (या x को y के फलन के रूप) में स्पष्ट रूप में व्यक्त
नहीं किया जा सके तो ऐसे फलनों को अस्पष्ट फलन कहते हैं।

क्रिया विधि (Working Method)
(1) y को x का फलन मानकर समीकरण f(x, y) = 0 के प्रत्येक पद का x के सापेक्ष अवकलन कीजिये।
\(\frac{d y}{d x}\) के पदों को एकत्रित करके \(\frac{d y}{d x}\)का मान ज्ञात करते हैं।

→ त्रिकोणमितीय रूपान्तरण के प्रयोग से अवकलज (Differentiation By Using Trigonometrical Transformation):
कभी-कभी त्रिकोणमितीय रूपान्तरण से फलन सरलतम रूप में प्राप्त हो जाता है फिर उसका अवकलन गुणांक आसानीपूर्वक ज्ञात किया जा सकता है। साधारणतया यह रूपान्तरण प्रतिलोम त्रिकोणमितीय फलनों में बहुत उपयोगी रहता है। निम्नलिखित त्रिकोणमितीय एवं प्रतिलोम त्रिकोणमितीय सूत्र रूपान्तरण करने में बहुत सहायक होते हैं।

• sin 2x = 2 sin x cos x
• cos 2x = cos²x - sin²x= 2 cos²x-1 = 1 - 2 sin²x
• sin 2x = 2tan.x
• cos 2x = \(\frac{2 \tan x}{1+\tan ^2 x}\)
• tan 2x = \(\frac{1-\tan ^2 x}{1+\tan ^2 x}\)
• sin 3x = 3 sin x - 4 sin³x
• cos 3x = 4 cos³x - 3 cos x
• tan 3x = \(\frac{3 \tan x-\tan ^3 x}{1-3 \tan ^2 x}\)
• sin^-1x ± sin^-1y = sin^-1[x\(\sqrt{1-y^2}\) ± y\(\sqrt{1-x^2}\)]
• cos^-1x ± cos^-1y = cos^-1[xy ± \(\sqrt{1-y^2}\)\(\sqrt{1-x^2}\)]
• tan^-1x + tan^-1y = tan^-1\(\left(\frac{x+y}{1-x y}\right)\)
• tan^-1 - tan^-1 = tan^-1\(\left(\frac{x-y}{1+x y}\right)\)
• sin^-1x + cos^-1x = \(\frac{\pi}{2},\)
• sec^-1x + cosec^-1x = \(\frac{\pi}{2}\), tan^-1x + cot^-1x = \(\frac{\pi}{2}\)
• sin^-1(sin x) = sin (sin^-1x) = x
• cos^-1(cos x) = cos (cos^-1x) = x
• tan^-1(tan x) = tan (tan^-1x) = x

हम यहाँ पर कुछ महत्त्वपूर्ण प्रतिस्थापन (Substitutions) दे रहे हैं, जिनका उपयोग अवकलन करने में किया जा सकता है :

• व्यंजक - प्रतिस्थापन :
• \(\sqrt{a^2-x^2}\) x = a sin θ या x = a cos θ
• \(\sqrt{a^2+x^2}\) x= a tan θ या x = a cot θ
• \(\sqrt{x^2-a^2}\) = a sec θ या x = a cosec θ
• \(\sqrt{\frac{a-x}{a+x}}\) या \(\sqrt{\frac{a+x}{a-x}}\) x = a cos 2θ या x = a cos θ
• \(\sqrt{\frac{a^2-x^2}{a^2+x^2}}\) या \(\sqrt{\frac{a^2+x^2}{a^2-x^2}}\) = a² cos 2θ या x² = a² cos θ

→ चरघातांकी तथा लघुगणकीय फलन (Exponential And Logarithmic Functions):
चरघातांकी फलन-यदि a कोई वास्तविक संख्या इस प्रकार हो कि f(x) = a जहाँ a > 0, a ≠ 1, तब फलन f(x) = a को चरघातांकी फलन कहते हैं जिसका प्रान्त वास्तविक संख्याओं का समुच्चय R होता है और परिसर, समस्त धनात्मक वास्तविक संख्याओं का समुच्चय होता है। अर्थात्
प्रान्त (Domain) = R (वास्तविक संख्याओं का समुच्चय)
परिसर (Range) = R+ (धनात्मक वास्तविक संख्याओं का समुच्चय)
जब a = e तब फलन f(x) = a = f(x) = ex इस फलन को प्राकृतिक चरघातांकी फलन (natural exponential function) कहते

अतः f(x) = er प्राकृतिक चरघातांकी फलन लघुगणकीय फलन-यदि a > 0, a + 1 एक वास्तविक संख्या हो तब a = b
तब x, आधार a पर b का लघुगणक कहलाता है तथा इसे प्रतीक log_ab = x से निरूपित करते हैं।
यदि a = 10 अर्थात् आधार 10 हो तो log₁₀z को साधारण लघुगणक कहते हैं तथा यदि आधार e हो तो log_ex को प्राकृतिक लघुगणक कहते हैं।

अतः f(x) = log_ex या log x जो कि प्राकृतिक लघुगणक है। लघुगणक के लिये निम्न सूत्रों को प्रमाणित किया जा सकता है

• log (xy) = log x + log y
• log\(\left(\frac{x}{y}\right)\) = log x - log y
• logx = n log x
• log_ax x log_xa = 1 (या log_ax = \(\frac{1}{\log _x a}\))
• log_ee = 1 तथा log_e1 = 0
• आधार परिवर्तन का मान सूत्र
  log_aP = \(\frac{\log _b p}{\log _b a}\) या log_ap x log_ba = log_bp
• x के सापेक्ष e^x का अवकलज - ही होता है अर्थात् \(\frac{d}{d x}\)e^x = e^x
• x के सापेक्ष log x का अवकलज = होता है अर्थात्
  \(\frac{d}{d x}\)(log xy) = \(\frac{1}{x}\)
• x = _alog_ax = _elog e^x
• x^m = _alog_ax^m = _am log_ax

→ लघुगणकीय अवकलन (Logarithmic Differentiation)
जब दिया गया फलन [f(x)]^Φ(x) के रूप का हो तब ऐसे फलनों का अवकलन करने के लिए हम सर्वप्रथम फलनों का लघुगणक (Logarithm) लेते हैं और फिर इससे प्राप्त परिणाम का अवकलन करते हैं अतः इस विधि को लघुगणकीय अवकलन कहते हैं। जब कभी भी फलन में चर राशियाँ घात में आयें या फलन जटिल गुणनखण्डों का गुणनफल हो, तब भी इस विधि का प्रयोग बहुत उपयोगी सिद्ध होता है।
माना कि y = u^v, जहाँ u तथा v, x के फलन हैं। दोनों पक्षों का
लघुगणक लेने पर log_ey = log_eu^v = y log_eu
अब दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

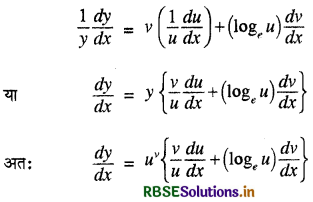
सावधान (Caution) → y = x^x + (cos x)^x + x^{log x} प्रकार के फलनों में सीधा लघुगणक लेना सम्भव नहीं है जबकि कभीकभी छात्र असावधानी से निम्न प्रकार लिख लेते हैं
log_ey = x log_ex + x log_ecos x + log x. log x

जो कि नितान्त गलत है क्योंकि
log_e(a + b) ≠ log_ea + log_eb
ऐसे फलनों में विविध पदों का अवकलन गुणांक अलग-अलग ज्ञात करना पड़ता है। यह निम्न उदाहरणों से और अधिक स्पष्ट हो जायेगा

→ फलनों के प्राचलिक रूपों के अवकलज ( Derivatives of Functions In Parametric Forms):
प्राचलिक समीकरण (Parametric Equations) जब x तथा y दोनों किसी तीसरी चर राशि के पदों में व्यक्त किये जाते हैं, जैसे यदि x = f(t), y = Φ(t) हो तो चर राशि t को प्राचल कहते हैं तथा इस प्रकार के समीकरण प्राचलिक समीकरण (Parametric Equation) कहलाते हैं।

ऐसे समीकरण में \(\frac{d y}{d x}\) का मान उनमें प्रयुक्त प्राचल का विलोप (Eliminate) कर अवकलन करने से प्राप्त किया जा सकता है। किन्तु कभी-कभी विलोपन कठिन होता है तब ऐसी स्थिति में हम का मान जब '\(\frac{d y}{d x}\)' प्राचल हो तो निम्न सूत्र से ज्ञात कर सकते हैं

अतः x के सापेक्ष y का अवकल गुणांक, प्राचल के सापेक्ष y और x के अवकल गुणांक का भागफल होता है।

→ द्वितीय कोटि का अवकलज (Second Order Derivative):
कुछ भौतिक एवं ज्यामितीय अवधारणा के लिए हमें द्वितीय कोटि के अवकलज के मान की आवश्यकता होती है। हम पहले ही अध्ययन कर चुके हैं कि यदि y, x का एक अवकलनीय फलन है, तो हम इसका अवकलज \(\frac{d y}{d x}\) ज्ञात कर सकते हैं जो कि इसका प्रथम कोटि का अवकलज कहलाता है।

अब यदि \(\frac{d y}{d x}\) जो कि पुनः x का एक अवकलनीय फलन है, तो हम.इसका भी अवकलज \(\frac{d}{d x}\left(\frac{d y}{d x}\right)\) ज्ञात कर सकते हैं जो कि y का x के सापेक्ष द्वितीय कोटि का अवकलज कहलाता है और इसे \(\frac{d^2 y}{d x^2}\) द्वारा निरूपित किया जाता है।
यदि y = f(x) है, तो द्वितीय कोटि के अवकलज को D²(y), y₂, y" तथा f'(x) द्वारा भी निरूपित किया जाता है।

→ माध्यमान प्रमेय (Mean Value Theorem):
फ्रेंच गणितज्ञ माइकेल रोल (1652-1719) ने बीजगणित में समीकरण के मूल ज्ञात करने के लिए एक महत्त्वपूर्ण प्रमेय का प्रतिपादन किया था जिसे बाद में अवकलन में भी काम में लिया गया। इस प्रमेय के विकसित रूप का अध्ययन रोल प्रमेय के नाम से किया जाता है। लाग्रांज माध्यमान प्रमेय एवं कई अन्य प्रमेय इस प्रमेय पर आधारित हैं। यहाँ (A) रोल प्रमेय एवं (B) लाग्रांज प्रमेय के प्रयोगों का अध्ययन करेंगे

(A) रोल प्रमेय (Rolle's Theorem)
मान लीजिये कि एक वास्तविक फलन f संवृत अन्तराल [a, b] में इस प्रकार परिभाषित है कि

• f संवृत अन्तराल [a, b] में संतत् है,
• f विवृत अन्तराल (a, b) में अवकलनीय है, तथा
• f(a) = f(b) तो विवृत अन्तराल (a, b) में कम से कम एक बिन्दु c इस प्रकार विद्यमान होगा कि f(c) = 0

रोल प्रमेय का ज्यामितीय अर्थ (Geometrical Interpretation of Rolle's Theorem):

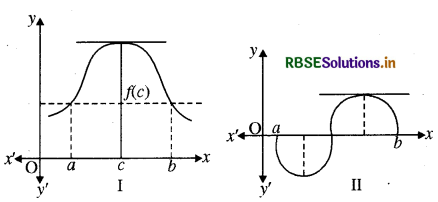
उपरोक्त आकृति I और II में कुछ ऐसे विशिष्ट फलनों के आलेख दिये गये हैं, जो रोल के प्रमेय की परिकल्पना को संतुष्ट करते हैं। ध्यान दीजिये कि a और b के मध्य स्थित वक्र के बिन्दुओं पर स्पर्श रेखा की प्रवणता पर क्या घटित होता है। इनमें से प्रत्येक आलेख में कम से कम एक बिन्दु पर प्रवणता शून्य हो जाती है। रोल के प्रमेय के कथन का यही दावा है, क्योंकि y = f(x) के आलेख के किसी बिन्दु पर स्पर्श रेखा की प्रवणता कुछ अन्य नहीं है अपितु उस बिन्दु पर f(x) का अवकलज होता है। अर्थात् ज्यामितीय रूप में रोल प्रमेय का रूप निम्न प्रकार परिभाषित किया जा सकता है

यदि एक वास्तविक फलन (x) का आलेख बिन्दु x = a एवं x = b पर संतत है तथा इन बिन्दुओं के मध्य के आलेख के प्रत्येक बिन्दु पर स्पर्श रेखा खींची जा सकती है, बिन्दु x = a एवं बिन्दु x = b पर कोटियाँ समान हैं तो वक्र पर उक्त बिन्दुओं के मध्य कम से कम एक बिन्दु इस प्रकार विद्यमान होगा जिस पर खींची गई स्पर्श रेखा x-अक्ष के समान्तर होगी।" यदि रोल प्रमेय की तीनों शर्तों में से एक भी संतुष्ट न हो, तो रोल प्रमेय लागू नहीं होगी।

(B) लाग्रांज का माध्यमान प्रमेय (Lagrange's Mean Value Theorem)
मान लीजिये कि एक वास्तविक फलन संवृत अन्तराल [a, b] में इस प्रकार परिभाषित है कि

• f संवृत अन्तराल [a, b] में संतत है।
• f विवृत अन्तराल (a, b) में अवकलनीय है। तो विवृत अन्तराल (a, b) में कम से कम एक बिन्दु c ऐसा विद्यमान होगा कि f'(c) = \(\frac{f(b)-f(a)}{b-a}\)

लाग्रांज के माध्यमान प्रमेय का ज्यामितीय अर्थ (Geometrical Interpretation of Lagrange’s Mean Value Theorem)
फलन y = f(x) का आलेख आकृति IInd में दिया गया है। हम पहले ही f(c) की व्याख्या वक्र y = f(x) के बिन्दु (c, f (c)) पर खींची गई स्पर्श रेखा की प्रवणता के रूप में कर चुके हैं।

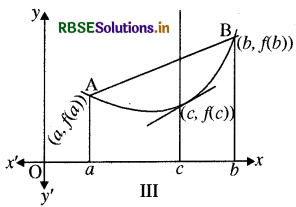
अब हम आकृति III में छेदक AB रेखा का झुकाव ज्ञात करेंगे।

अर्थात् जीवा AB की प्रवणता वक्र के x = c बिन्दु पर खींची स्पर्श रेखा की प्रवणता के बराबर होती है अतः लाग्रांज माध्यमान प्रमेय का ज्यामितीय अर्थ निम्न हैमान लीजिये कि एक वास्तविक फलन f(x), संवृत अन्तराल [a, b] में इस प्रकार परिभाषित है कि वक्र y = f(x) अन्तराल [a, b] में संतत है तथा अन्तराल (a, b) के प्रत्येक बिन्दु पर स्पर्श रेखा खींची जा सकती है तो (a, b) में कम से कम एक बिन्दु x = c अवश्य विद्यमान होगा जहाँ वक्र पर खींची गई स्पर्श रेखा अन्तराल के सिरों को मिलाने वाली जीवा के समान्तर होगी।

लाग्रांज माध्यमान प्रमेय का दूसरा रूप (Another form of Lagrange's Mean Value Theorem)
यदि लाग्रांज प्रमेय में b = a + h, h > 0, c = a + θh लें जहाँ 0 < θ < 1 तो c ∈ (a, b) = a + θh ∈ (a, a + h) लाग्रांज प्रमेय निम्नलिखित रूप ले लेती है :
यदि वास्तविक फलन f(x) अन्तराल [a, a + h] में इस प्रकार परिभाषित है कि

• f संवृत अन्तराल [a, a + h] में संतत है,
• f विवृत अन्तराल (a, a + h) में अवकलनीय है,

तो 0 एवं 1 के मध्य कम से कम एक वास्तविक संख्या 0 इस प्रकार विद्यमान होगी कि
f(a + h) = f(a) + h f' (a + θh)
टिप्पणी-इस प्रमेय के लिए प्रतिबंध f(a) = f(b) आवश्यक नहीं है। यह f(a) = f(b) के लिए भी मान्य है तथा इस अवस्था में यह प्रमेय रोल प्रमेय में परिवर्तित हो जाती है।

→ सातत्य-एक फलन y = f(x), एक अन्तराल में संतत कहलाता है यदि x के प्रत्येक मान के लिए विद्यमान हो।

→ किसी बिन्दु पर फलन का सातत्य-एक फलन f(a) एक बिन्दु a पर संतत कहलाता है, यदि
\(\lim _{x \rightarrow a^{-}}\) f(x), \(\lim _{x \rightarrow a^{+}}\) f(x) एवं (a) विद्यमान हो और \(\lim _{x \rightarrow a^{-}}\) f(x) = \(\lim _{x \rightarrow a^{+}}\) f(x) = f(a)
यदि फलन x = a पर संतत नहीं है तो x = a पर फलन असंतत कहलाता है।

→ यदि f एवं g, x = a पर संतत फलन हो तो

• f ± g भी x = a पर संतत है।
• f. g भी x = a पर संतत है।
• \(\frac{f}{g}\) भी x = a संतत है यदि g(a) # 0
• cf भी x = a पर संतत है जहाँ c अचर है।
• |f| भी x = a पर संतत फलन है।

→ सभी अचर फलन, बीजीय फलन, तत्समक फलन, लघुगणकीय फलन, चरघातांकी फलन, त्रिकोणमितीय फलन एवं प्रतिलोम त्रिकोणमितीय फलन अपने प्रान्त में सदैव संतत होते हैं।

→ कुछ महत्त्वपूर्ण अवकलन

• \(\frac{d}{d x}\)(xⁿ) = nx^n-1
• \(\frac{d}{d x}\)(e^x) = e^x
• \(\frac{d}{d x}\)a^x = a^x log a
• \(\frac{d}{d x}\)log_ex = \(\frac{1}{x}\)
• \(\frac{d}{d x}\)log_ax = \(\frac{1}{x \cdot \log _6 a}\)
• \(\frac{d}{d x}\)sin x = cos x
• \(\frac{d}{d x}\)cos x = - sin x
• \(\frac{d}{d x}\)tan x = sec²x
• \(\frac{d}{d x}\)cot x = -cosec²x
• \(\frac{d}{d x}\)sec x = sec x tan x
• \(\frac{d}{d x}\)(cosec x) = – cosec x cotx
• \(\frac{d}{d x}\)(sin^-1x) = \(\frac{1}{\sqrt{1-x^2}}\)
• \(\frac{d}{d x}\)(cos^-1x) = -\(\frac{1}{\sqrt{1-x^2}}\)
• \(\frac{d}{d x}\)(tan^-1x) = \(\frac{1}{1+x^2}\)
• \(\frac{d}{d x}\)(cot^-1x) = -\(\frac{1}{1+x^2}\)
• \(\frac{d}{d x}\)(sec^-1x) = \(\frac{1}{x \sqrt{x^2-1}}\)
• \(\frac{d}{d x}\)(cosec^-1x) = -\(\frac{1}{x \sqrt{x^2-1}}\)

→ अवकलन के मूलभूत नियम

• \(\frac{d}{d x}\)[k f(x)] = k \(\frac{d}{d x}\)f(x)
• \(\frac{d}{d x}\)[f(x) ± g(x)] = \(\frac{d}{d x}\) f(x) ± \(\frac{d}{d x}\) g(x)
• \(\frac{d}{d x}\)(u, v) = u \(\frac{d v}{d x}\) + v \(\frac{d u}{d x}\)
• \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^2}\)
• (fog)'(x) = [f'(g(x))] × g'(x)
• यदि y = [f(x)]^g(x) तब \(\frac{d y}{d x}\) = y[log f(x), g'(x) + \(\frac{g(x)}{f(x)}\)f'(x)]
• यदि x = f(t) और y = g(t) तब \(\frac{d y}{d x}=\frac{d y / d t}{d x / d t}\)
• यदि u एवं v, x के फलन हों तो \(\frac{d u}{d v}=\frac{d u / d x}{d v / d x}\)

→ रोल प्रमेय-यदि f(x) एक वास्तविक मान फलन है जो कि संवृत अन्तराल [a, b] में परिभाषित है तथा

• यह संवृत अन्तराल [a, b] में संतत है।
• यह विवृत अन्तराल (a. b) में अवकलनीय है।
• f(a) = f(b) तब (a, b) में कम-से-कम एक बिन्दु c ∈ (a, b) ऐसा होगा ताकि f'(c) = 0

→ लाग्रांज माध्यमान प्रमेय
यदि f(x) एक वास्तविक मान फलन है जो कि संवृत अन्तराल [a, b] में इस प्रकार परिभाषित है तथा

• यह संवृत अन्तराल [a, b] में संतत है
• यह विवृत अन्तराल (a, b) में अवकलनीय है तब (a, b) में कम से कम एक बिन्दु c इस प्रकार विद्यमान होगा कि f'(c) = \(\frac{f(b)-f(a)}{(b-a)}\)