RBSE Class 12 Maths Notes Chapter 4 सारणिक

These comprehensive RBSE Class 12 Maths Notes Chapter 4 सारणिक will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 4 Notes सारणिक

(परिचय (Introduction):
निम्नलिखित समीकरण निकाय पर विचार कीजिये :
a₁x + b₁y = c₁
a₂x + b₂y = c₂
इन समीकरणों को
$\left[\begin{array}{ll} a_1 & b_1 \\ a_2 & b_2 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} c_1 \\ c_2 \end{array}\right]$
के रूप में व्यक्त कर सकते हैं। अब इन समीकरणों का निकाय का अद्वितीय हल है अथवा नहीं इसको a₁b₂ - a₂b₁ संख्या द्वारा ज्ञात किया जाता है। (स्मरण कीजिये कि यदि $\frac{a_1}{a_2} \neq \frac{b_1}{b_2}$ या a₁b₂ - b₁a_2s ≠ 0, है तो समीकरणों के निकाय का हल अद्वितीय होता है) यह संख्या a₁b₂ - a₂b₁ जो समीकरणों के निकाय के अद्वितीय हल ज्ञात करती है, वह आव्यूह A = $\left[\begin{array}{ll} a_1 & b_1 \\ a_2 & b \end{array}\right]$ से सम्बन्धित है और इसे A का सारणिक या det A कहते हैं।
अतः A = $\left|\begin{array}{ll} a_1 & b_1 \\ a_2 & b_2 \end{array}\right|$

• इस सारणिक में दो स्तम्भ तथा दो पंक्ति हैं, अतः इसे दो क्रम का सारणिक कहते हैं।
• इसी प्रकार तीन, चार .......... इत्यादि क्रम के सारणिक भी प्राप्त किये जा सकते हैं।

टिप्पणी

• किसी समीकरण निकाय को अद्वितीय हल करने के लिए निकाय में जितने चर हों उतने ही समीकरणों की आवश्यकता होती है। अतः किसी भी सारणिक में पंक्ति एवं स्तम्भों की संख्या सदैव समान होती है।
• एक मैट्रिक्स को अव्युत्क्रमणीय मैट्रिक्स कहते हैं। यदि
  |A| = 0 अर्थात् मैट्रिक्स से सम्बन्धित सारणिक का मान शून्य हो।

→ सारणिक की परिभाषा (Definition of Determinants)
माना A = [a_ij] एक n क्रम की वर्ग मैट्रिक्स है, तब एक अद्वितीय संख्या (Unique number) |a_ij| मैट्रिक्स A की सारणिक कहलाती है और इसे सारणिक A या |A| 'से प्रकट करते हैं।

→ सारणिक का मान (Value of Determinants)|
(i) एक क्रम की सारणिक का मान
माना A = [a] एक क्रम की वर्ग मैट्रिक्स है, तब सारणिक A = |A| = a, सारणिक का मान स्वयं संख्या ही है।
उदाहरणार्थ-यदि A = [5] हो, तब सारणिक A = |A| = [5] = 5 यदि A = [-3] हो, तब सारणिक A = |A| = |-3| = -3
टिप्पणी-उपर्युक्त उदाहरणों से सारणिक एवं मापांक में अन्तर स्पष्ट है। अतः एक क्रम की सारणिक को मापांक नहीं समझना चाहिए।

(ii) द्वितीय क्रम की सारणिक का मान
माना A = $\left[\begin{array}{ll} a_1 & b_1 \\ a_2 & b_2 \end{array}\right]$ एक द्वितीय क्रम की वर्ग मैट्रिक्स है, तब सारणिक A = |A| = $\left|\begin{array}{ll} a_1 & b_1 \\ a_2 & b_2 \end{array}\right|$ = a₁ |b₂| - b₁ |a₂| = a₁b₂ - a₂b₁, सारणिक A का मान है। अतः |A| = अग्रग विकर्ण के अवयवों का गुणा-पिछले विकर्ण के अवयवों का गुणा यहाँ a,,b,a, व b, सारणिक के अवयव कहलाते हैं। द्वितीय क्रम की सारणिक में कुल 22 = 4 अवयव होते हैं। इनमें a₁b₁: a₂b₂ दो पंक्तियाँ तथा a₁a₂, : b₁b₂, दो स्तम्भ हैं अतः a₁b₂, - a₂b₁, सारणिक का प्रसार कहलाता है। इसके निम्न उदाहरण दिये जा रहे हैं

उदाहरण 1.
$\left|\begin{array}{cc} 1 & 3 \\ -2 & 7 \end{array}\right|$ का मान ज्ञात कीजिये।
हल:
$\left|\begin{array}{cc} 1 & 3 \\ -2 & 7 \end{array}\right|$ = (1) (7) - (-2) (3) = 7 + 6 = 13

 

उदाहरण 2.
$\left|\begin{array}{cc} i^4 & 1 \\ -1 & 1 \end{array}\right|$ का मान ज्ञात कीजिये।
हल:
$\left|\begin{array}{cc} i^4 & 1 \\ -1 & 1 \end{array}\right|$ = i⁴ × 1 - (-1) × 1
= 1 × 1 - (-1) × 1 = 1 + 1 [:: i² = - 1]
= 2

(iii) तृतीय क्रम की सारणिक का मान
माना A = $\left[\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right]$ एक, तृतीय क्रम की वर्ग मैट्रिक्स है,
तब [A] से सम्बन्धित सारणिक

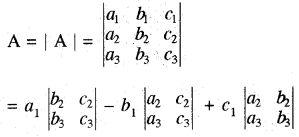
= a₁(b₂c₃ - b₃c₂) - b₁(a₂c₃ - a₃c₂) + c₁(a₂b₃ - a₃b₂) ....(1)
= a₁b₂c₃ - a₂b₃c₂ - b₁a₂c₃ + b₁a₃c₂ + c₁a₂b₃ - c₁a₃b₂
= (a₁b₂c₃ + b₁c₂a₃ + c₁a₂b₃) - (a₃b₂c₁ + b₃c₂a₁ + c₃a₂b₁) ....(2)
यहाँ संख्या के a₁,b₁,c₁: a₂,b₂.c₂, a₃,b₂.c₃, सारणिक के अवयव कहलाते हैं, तृतीय क्रम की सारणिक में कुल = 3² = 9 अवयव होते हैं। अवयव a₁,b₁,c₁: a₂,b₂.c₂, a₃,b₂.c₃, क्रमशः प्रथम, द्वितीय तथा तृतीय पंक्ति बनाते हैं। जबकि अवयव a₁,a₂a₃; b₁,b₂,b₃, c₁, c₂,c₃; क्रमशः प्रथम, द्वितीय तथा तृतीय स्तम्भ बनाते हैं। a,,b,,, अग्रग विकर्ण के अवयव और abs.c, पिछले विकर्ण के अवयव हैं। समीकरण (2) का दायाँ पक्ष, सारणिक की प्रथम पंक्ति से सारणिक का प्रसार कहलाता है।

तृतीय क्रम की सारणिक के प्रसार का नियम (Rule Of Expansion Of III Order Determinant)

• प्रथम पंक्ति के अवयवों को एकान्तर क्रम से धनात्मक तथा ऋणात्मक चिह्न लगाकर लिखें।
• इन चिह्नों सहित अवयवों को, द्वितीय क्रम की उन सारणिकों से क्रमशः गुणा करें जो उस पंक्ति व स्तम्भ का दमन (Suppress) करने पर प्राप्त होती है जिसमें यह अवयव स्थित है।
• इन गुणनफलों का योग, तृतीय क्रम को सारणिक का मान होता है।

उदाहरणार्थ:
सारणिक $\left|\begin{array}{lll} 1 & 2 & 0 \\ 2 & 3 & 1 \\ 3 & 0 & 2 \end{array}\right|$ का मान ज्ञात कीजिये।
हल:

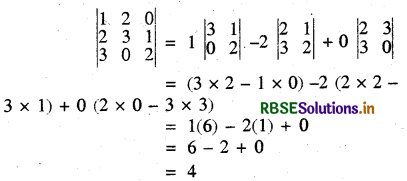
मैट्रिक्स व सारणिक में अन्तर (Difference. Between Matrix And Determinant):

• मैट्रिक्स संख्याओं का एक सुव्यवस्थित रूप है एवं उसका कोई संख्यात्मक मान नहीं होता है जबकि सारणिक का मान एक निश्चित मान (संख्यात्मक) होता है।
• मैट्रिक्स किसी भी क्रम की हो सकती है जबकि सारणिक में पंक्तियों एवं स्तम्भों की संख्या बराबर होती है।
• मैट्रिक्स की पंक्तियों को स्तम्भों एवं स्तम्भों को पंक्तियों से बदलने पर एक नई मैट्रिक्स प्राप्त होती है, जबकि ऐसा करने पर सारणिक के मान में कोई परिवर्तन नहीं होता है, जिसे हम आगे सिद्ध करेंगे।

तृतीय क्रम की सारणिक का मान ज्ञात करने का सारूस चित्र (Sarrus Diagram):

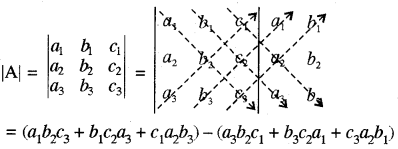
टिप्पणी : सारूस चित्र से सारणिक का मान ज्ञात करने के लिए उपर्युक्त चित्रानुसार तीन अग्रणी विकर्णों (Leading diagonals) के अवयवों के गुणन के योग में से, तीन पिछले विकर्णों के अवयवों के गुणन के योग को घटाते हैं।

उदाहरणार्थ

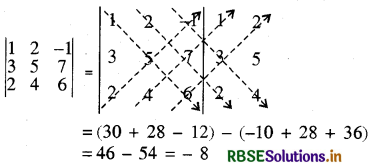
सारणिक का प्रसार (Expansion of Determinants):
वर्ग आव्यूह A = [a_ij]_3×3, के सारणिक पर विचार करते हैं। जहाँ

|A| = a₁₁$\left|\begin{array}{ll} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right|$ - a₁₂$\left|\begin{array}{ll} a_{21} & a_{23} \\ a_{31} & a_{33} \end{array}\right|$ + a₁₃$\left|\begin{array}{ll} a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right|$
a₁₁ के आगे (-1)¹⁺¹ = + होगा
a₁₂ के आगे (-1)¹⁺² = - होगा
a₁₃ के आगे (-1)¹⁺³ = + होगा

द्वितीय पंक्ति (R₂) के अनुदिश प्रसरण
|A| = -a₂₁$\left|\begin{array}{ll} a_{12} & a_{13} \\ a_{32} & a_{33} \end{array}\right|$ + a₂₂$\left|\begin{array}{ll} a_{11} & a_{13} \\ a_{31} & a_{33} \end{array}\right|$ - a₂₃$\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{31} & a_{32} \end{array}\right|$
a₂₁ आगे (-1)²⁺¹ = - होगा
a₂₂ के आगे (-1)²⁺² = + होगा
a₂₃ के आगे (-1)²⁺³ = - होगा

तृतीय पंक्ति (R₃) के अनुदिश प्रसरण
|A| = a₃₁$\left|\begin{array}{ll} a_{12} & a_{13} \\ a_{22} & a_{23} \end{array}\right|$ - a₃₂$\left|\begin{array}{ll} a_{11} & a_{13} \\ a_{21} & a_{23} \end{array}\right|$ + a₃₃$\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|$
a₃₁ के आगे (-1)³⁺¹ = + होगा
a₃₂ के आगे (-1)³⁺² = - होगा
a₃₃ के आगे (-1)³⁺³ = + होगा
इसी प्रकार C₁, C₂, C₃, के अनुदिश प्रसरण करने पर समान परिणाम प्राप्त होता है।

टिप्पणी:

• सारणिक का विस्तार किसी भी पंक्ति या स्तम्भ के अनुसार किया जा सकता है।
• सारणिक के प्रसार का यह नियम किसी भी क्रम की सारणिक के लिए सत्य है।
• सारणिक का मान शीघ्र प्राप्त करने के लिए इसका प्रसार उस पंक्ति या स्तम्भ के अनुसार करें, जिसके अधिकतम अवयव शून्य हों।
• सारणिकों का प्रसरण करते समय (-1)^i+j से गुणा करने के स्थान पर हम (i + j) के सम या विषम होने के अनुसार +1 या -1 से गुणा कर सकते हैं।

सारणिक के गुणधर्म (Properties of Determinants):
गुणधर्म 1.
यदि किसी सारणिक में समस्त पंक्तियों को स्तम्भों में और स्तम्भों की पंक्तियों में बदल दें, तो सारणिक के मान में कोई अन्तर नहीं होता है।
उपपत्ति-माना

प्राप्त होता है।
Δ₁, को प्रथम स्तम्भ के अनुदिश प्रसरण करने पर हम प्राप्त करते
Δ₁ = a₁(b₂c₃ - c₂b₃) – a₂(b₁c₃ - b₃c₁ ) + a₃(b₁c₂ - b₂c₁)
अतः Δ = Δ₁

टिप्पणी

• उपर्युक्त व्याख्या से स्पष्ट है कि यदि A एक वर्ग आव्यूह है तो det (A) = det(A') जहाँ A', A का परिवर्त आव्यूह है।
• चूँकि किसी सारणिक की पंक्तियों और स्तम्भों को परस्पर बदलने पर सारणिक का मान अपरिवर्तित रहता है, अतएव जो गुण हम किसी सारणिक की पंक्तियों के लिए सिद्ध करेंगे वही गुण सारणिक के स्तम्भों के लिए भी सत्य होंगे।

उदाहरण : Δ = $\left|\begin{array}{ccc} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{array}\right|$ के लिए गणधर्म 1 का सत्यापन कीजिए।
हल:
सारणिक का प्रथम पंक्ति के अनुदिश प्रसरण करने पर -
Δ = 2 (0 - 20) + 3 (-42 - 4) + 5 (30 - 0) = - 28
पंक्तियों एवं स्तम्भों को परस्पर परिवर्तित करने पर
Δ₁ = $\left|\begin{array}{ccc} 2 & 6 & 1 \\ -3 & 0 & 5 \\ 5 & 4 & -7 \end{array}\right|=2\left|\begin{array}{cc} 0 & 5 \\ 4 & -7 \end{array}\right|-(-3)\left|\begin{array}{cc} 6 & 1 \\ 4 & -7 \end{array}\right|+5\left|\begin{array}{lc} 6 & 1 \\ 0 & 5 \end{array}\right|$
= 2 (0 - 20) + 3 (-42 - 4) + 5 (30 - 0)
= - 28
स्पष्टतः Δ = Δ₁
अतः गुणधर्म 1 सत्यापित हुआ।

गुणधर्म 2.
यदि एक सारणिक की कोई भी दो पंक्तियों (या स्तम्भों) को परस्पर परिवर्तित कर दिया जाता है तब सारणिक का संख्यात्मक मान वही रहता है, किन्तु उसका चिह्न बदल जाता है।
उपपत्ति-माना कि
Δ = $\left|\begin{array}{lll} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array}\right|$
प्रथम पंक्ति के अनुदिश प्रसरण करने पर हम पाते हैं
Δ = a₁(b₂c₃ - b₃c₂) - a₂(b₃c₁ - b₃c₁) + a₃(b₁c₂ - b₂c₁)

पहली और तीसरी पंक्तियों को परस्पर परिवर्तित करने
अर्थात् R₁ ↔ R₃, से प्राप्त नया सारणिक
Δ₁ = $\left|\begin{array}{lll} c_1 & c_2 & c_3 \\ b_1 & b_2 & b_3 \\ a_1 & a_2 & a_3 \end{array}\right|$
है। इसे तीसरी पंक्ति के अनुदिश प्रसरण करने पर
Δ₁ = a₁(c₂b₃ - b₂c₃) - a₂(c₁b₃ - c₃b₁) + a₃(b₂c₁ - b₁c₂)
= - [a₁(b₂c₃ - b₃c₂) - a₂(b₁c₃ - b₃c₁) + a₃(b₁c₂ - b₂c₁)
प्राप्त होता है। यह स्पष्ट है कि Δ = -Δ₁
इसी प्रकार हम किन्हीं दो स्तम्भों को परस्पर परिवर्तित करके उक्त परिणाम को सत्यापित कर सकते हैं।

टिप्पणी-हम सारणिक की दो आसन्न पंक्तियों (स्तम्भों) को परस्पर बदलें अथवा किन्हीं दो स्तम्भों (पंक्तियों) को परस्पर बदलें, तो सारणिक के मान का चिह्न बदल जाता है। सारणिक का यह एक बहुत महत्त्वपूर्ण गुण है।

उदाहरण :
Δ = $\left|\begin{array}{ccc} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{array}\right|$ के लिए गुणधर्म 2 का सत्यापन कीजिए।
हल:
Δ = $\left|\begin{array}{ccc} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{array}\right|$ = 2(0 - 20) + 3(-42 - 4) + 5(30 - 0)
= -40 - 138 + 150 = -28
R₂ ↔ R₃
Δ₁ = $\left|\begin{array}{ccc} 2 & -3 & 5 \\ 1 & 5 & -7 \\ 6 & 0 & 4 \end{array}\right| = 2\left|\begin{array}{cc} 5 & -7 \\ 0 & 4 \end{array}\right|-(-3)\left|\begin{array}{cc} 1 & -7 \\ 6 & 4 \end{array}\right|+5\left|\begin{array}{ll} 1 & 5 \\ 6 & 0 \end{array}\right|$
= 2 (20 - 0)+ 3 (4 + 42) + 5 (0 - 30)
= 40 + 138 - 150 = 28
अतः Δ = -Δ₁

गुणधर्म 3.
यदि एक सारणिक की कोई दो पंक्तियाँ (अथवा स्तम्भ) समान हैं (सभी संगत अवयव समान हैं), तो सारणिक का मान शून्य होता हैं
उपपत्ति-यदि हम सारणिक Δ की समान पंक्तियों (या स्तम्भों) को परस्पर परिवर्तित कर देते हैं तो Δ का मान परिवर्तित नहीं होता है।
तब गुणधर्म (2) के अनुसार Δ का चिह्न बदल जाता है। इसलिए
Δ= - Δ
2Δ = 0 ∴ Δ = 0 आइये हम उपर्युक्त गुणधर्म का एक उदाहरण के द्वारा सत्यापन करते हैं।

उदाहरणार्थ Δ = $\left|\begin{array}{lll} 3 & 2 & 3 \\ 2 & 2 & 3 \\ 3 & 2 & 3 \end{array}\right|$ का मान ज्ञात कीजिये।
हल:
पहली पंक्ति के अनुदिश प्रसरण करने पर हम प्राप्त करते हैं कि
Δ = 3(6 - 6) - 2(6 - 9) + 3(4 - 6)
= 0 - 2(-3) + 3(-2) = 6 - 6 = 0
यहाँ पर R₁, और R₂, समान हैं।

गुणधर्म 4.
यदि एक सारणिक के किसी एक पंक्ति (अथवा स्तम्भ) के प्रत्येक अवयव को एक अचर राशि K से गुणा करते हैं तो उसका मान भी K से गुणित हो जाता है।
उपपत्ति-माना कि Δ = $\left|\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right|$
इसकी प्रथम पंक्ति के अवयवों को K से गुणा करने पर प्राप्त सारणिक Δ₁, है तो
Δ₁ = $\left|\begin{array}{ccc} K a_1 & K b_1 & K c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right|$
प्रथम पंक्ति के अनुदिश प्रसरण करने पर, हम प्राप्त करते हैं कि
Δ₁ = Ka₁(b₂c₃ - b₃c₂) - Kb₁(a₂c₃ - c₂a₃) + Kc₁(a₂b₃ - b₂a₃)
= K[a₁(b₂c₃ - b₁c₂) - b₁(a₂c₃ - c₂a₃) + c₁(a₂b₁₃ - b₂a₃)]
= KΔ
अतः $\left|\begin{array}{ccc} K a_1 & K b_1 & K c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right|=\mathbf{K}\left|\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right|$

टिप्पणी

• इस गुणधर्म के अनुसार, हम एक सारणिक की किसी एक पंक्ति या स्तम्भों से सार्व उभयनिष्ठ गुणनखण्ड बाहर निकाल सकते हैं।
• यदि एक सारणिक की किन्हीं दो पंक्तियों (या स्तम्भों) के संगत अवयव समानुपाती (उसी अनुपात में) है, तब उसका मान शून्य होता है।

उदाहरण 1.
Δ = $\left|\begin{array}{ccc} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ K a_1 & K a_2 & K a_3 \end{array}\right|$ = 0 (पंक्तियाँ R₂, व R₃, समानुपाती हैं)

उदाहरण 2.
सारणिक $\left|\begin{array}{ccc} 102 & 18 & 36 \\ 1 & 3 & 4 \\ 17 & 3 & 6 \end{array}\right|$ का मान ज्ञात कीजिये।
हल:
माना कि

गुणधर्म 5.
यदि एक सारणिक की एक पंक्ति या स्तम्भ के कुछ या सभी अवयव दो (या अधिक) पदों के योगफल के रूप में व्यक्त हों तो सारणिक को दो (या अधिक) सारणिकों के योगफल के रूप में व्यक्त किया जा सकता है।

उदाहरणतया

= दायाँ पक्ष
इसी प्रकार दूसरी पंक्तियों व स्तम्भों के लिए हम गुणधर्म (5) का सत्यापन कर सकते हैं।

गुणधर्म 6.
यदि एक सारणिक के किसी पंक्ति या स्तम्भ के प्रत्येक अवयव में, दूसरी पंक्ति या स्तम्भ के संगत अवयवों के समान गुणजों को जोड़ दिया जाता है तो सारणिक का मान वही रहता है। अर्थात् यदि हम R_i → R_i + kR_j, या C_i = C_i, + kC_j, का प्रयोग करें तो सारणिक का मान वही रहता है।
उपपत्ति-माना कि

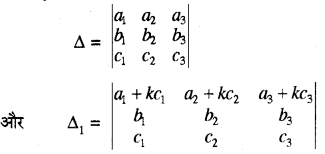
जहाँ Δ₁ संक्रिया R₁ → R₁ + kR₃, का प्रयोग करने पर यहाँ हम तीसरी पंक्ति (R₃) के अवयवों को अचर k से गुणा करके और उन्हें पहली पंक्ति (R₁) के संगत अवयवों में जोड़ते
इस प्रक्रिया को हम संकेतन के रूप में निम्न प्रकार से लिखते
R₁ → R₁ + kR₃
अब पुनः Δ₁ = $\left|\begin{array}{lll} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array}\right|+\left|\begin{array}{ccc} k c_1 & k c_2 & k c_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array}\right|$
(गुणधर्म 5 के द्वारा)
= Δ + 0 (जबकि R₁, और R₃, समानुपाती हैं)
अतः Δ = Δ₁

टिप्पणी
(i) यदि सारणिक Δ में R_i → kR_i, या C_i → KC_i, के प्रयोग से
प्राप्त सारणिक Δ₁, है, तो Δ₁, = KΔ
(ii) यदि एक साथ R_i → R_i + kR_j जैसी संक्रियाओं का एक से अधिक बार प्रयोग किया गया हो तो ध्यान देना चाहिए कि पहली संक्रिया से प्रभावित पंक्ति का अन्य संक्रिया में प्रयोग नहीं होना चाहिये। ठीक इसी प्रकार की टिप्पणी स्तम्भों की संक्रियाओं में
प्रयोग की जाती है।

गुणधर्म 7.
यदि Δ(x) = $\left|\begin{array}{l} \mathrm{R}_1 \\ \mathrm{R}_2 \\ \mathrm{R}_3 \end{array}\right|$ तृतीय कोटि का एक सारणिक है तथा यह x का फलन है तब

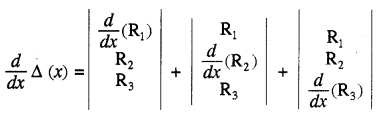
उदाहरणार्थ : यदि Δ(x) = $\left|\begin{array}{ccc} x & 1 & 2 \\ 0 & x^2 & 1 \\ 1 & 1 & x^3 \end{array}\right|$ तब
Δ'(x) = $\left|\begin{array}{ccc} 1 & 0 & 0 \\ 0 & x^2 & 1 \\ 1 & 1 & x^3 \end{array}\right|+\left|\begin{array}{ccc} x & 1 & 2 \\ 0 & 2 x & 0 \\ 1 & 1 & x^3 \end{array}\right|+\left|\begin{array}{ccc} x & 1 & 2 \\ 0 & x^2 & 1 \\ 0 & 0 & 3 x^2 \end{array}\right|$

टिप्पणी

• |A^T| = |A|
• |kA| = kⁿ |A|, यदि A एक n क्रम का वर्ग आव्यूह है।
• A = diag (a₁a₂ .... a_n) = |A| = a₁a₂ .... a_n
• |AB| = |A||B|
• |AB| = |BA|
• |Aⁿ| = |A|ⁿ; n ∈ N

त्रिभुज का क्षेत्रफल (सारणिक रूप में) (Area of A Triangle In Determinant Form)
यदि किसी त्रिभुज के शीर्षों के निर्देशांक क्रमशः (x₁, y₂), (x₂, y₂) तथा (x₃, y₃) हों, तो निर्देशांक ज्यामिति से हमें ज्ञात है कि त्रिभुज का क्षेत्रफल का सूत्र निम्न होता है

A= 2 [(2 - yy) + x_(73 - Y५) + xz(v! - y)]
चूँकि क्षेत्रफल एक धनात्मक संख्या होती है, अतएव उपर्युक्त व्यंजक का निरपेक्ष मान ही त्रिभुज का क्षेत्रफल होगा। तीन संरेख बिन्दुओं से बने त्रिभुज का क्षेत्रफल शून्य होगा अतः समीकरण (1) से

जो कि बिन्दुओं A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) के समरेख होने का अभीष्ट प्रतिबन्ध है।

उपसारणिक और सहखण्ड (Minor And Cofactor):
इस अनुच्छेद में हम उपसारणिकों और सहखण्डों का प्रयोग करके सारणिकों के प्रसरण का विस्तृत रूप लिखना सीखेंगे। उपसारणिक-एक सारणिक के दिये गये अवयव की पंक्ति एवं स्तम्भ के दमन (Suppress) करने पर जो शेष सारणिक प्राप्त होती है वह उस अवयव की उपसारणिक कहलाती है।

उदाहरणार्थ
Δ = $\left|\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right|$
सारणिक के अवयव a₂, द्वितीय पंक्ति तथा प्रथम स्तम्भ में है। यदि Δ में द्वितीय पंक्ति व प्रथम स्तम्भ को छोड़ दिया जाये तो शेष सारणिक निम्न प्राप्त होगी

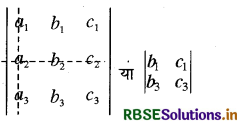
जो अवयव a₂, की उपसारणिक है।

इसी प्रकार Δ के अवयव c₃ की उपसारणिक

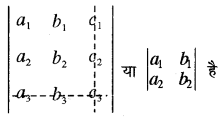
इस प्रकार व्यापक रूप में किसी n × n क्रम की सारणिक में 1वीं पंक्ति एवं jवें स्तम्भ के प्रतिच्छेदन पर स्थित अवयव as की उपसारणिक, वीं पंक्ति एवं 5वें स्तम्भ का दमन करने पर शेष बची हुई (n - 1) × (n - 1) क्रम की सारणिक होगी। सारणिक के किसी भी अवयव a_ij, से सम्बन्धित उपसारणिक को सामान्यतया उसके संगत बड़े अक्षर M_ij, से प्रकट करते हैं। जैसे अवयव a₁₁ की उपसारणिक को M₁₁ से तथा अवयव a₁₂ की उपसारणिक को M₁₂ से प्रकट करते हैं।

उदाहरणार्थ
सारणिक $\left|\begin{array}{cc} -5 & 3 \\ 4 & 6 \end{array}\right|$ में अवयव 4 की उपसारणिक |3| होगी
सारणिक $\left|\begin{array}{ccc} 1 & -6 & 5 \\ 7 & 3 & 2 \\ -1 & -3 & 6 \end{array}\right|$ में अवयव 5 की
उपसारणिक $\left|\begin{array}{cc} 7 & 3 \\ -1 & -3 \end{array}\right|$ एवं अवयव 7 की

उपसारणिक $\left|\begin{array}{ll} -6 & 5 \\ -3 & 6 \end{array}\right|$ होगी।

उदाहरण : सारणिक Δ = $\left|\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right|$ में अवयव 6 का उपसारणिक ज्ञात कीजिए।
हल:
अवयव 6 का उपसारणिक = M₂₃ = $\left|\begin{array}{ll} 1 & 2 \\ 7 & 8 \end{array}\right|$
= 8 - 14
= - 6

सहखण्ड-किसी भी सारणिक में iवीं पंक्ति एवं jवें स्तम्भ के प्रतिच्छेदन पर स्थित अवयव a_ij का सहखण्ड A_ij = (-1) ^{i + j} उपसारणिक
A_ij = (-1) ^{i + J}M_ij, जहाँ पर a_ij का उपसारणिक M_ij है।
M_ij जब i + j सम संख्या है।
M_ij जब i + j विषम संख्या है।

उदाहरणार्थ-Δ = $\left|\begin{array}{ccc} 7 & 4 & -1 \\ -2 & 3 & 0 \\ 1 & -5 & 2 \end{array}\right|$ हो, तब
अवयव 7 का सहखण्ड = (-1)¹⁺¹$\left|\begin{array}{cc} 3 & 0 \\ -5 & 2 \end{array}\right|$
= 6 - 0 = 6

अवयव 5 का सहखण्ड = (-1)³⁺²$\left|\begin{array}{cc} 7 & -1 \\ -2 & 0 \end{array}\right|$
= -(0 - 2) = 2

अवयव 4 का सहखण्ड = (-1)¹⁺²$\left|\begin{array}{cc} -2 & 0 \\ 1 & 2 \end{array}\right|$
= -(-4) = 4

टिप्पणी
(i) शीघ्र गणना के लिए 2 व 3 क्रम की सारणिक में सह-खण्डों के चिह्न संगत स्थिति के अनुसार निम्न प्रकार होते हैं,

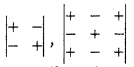
(ii) सारणिक में किसी अवयव की स्थिति के अनुसार पंक्ति एवं स्तम्भ का योग सम या विषम होने के अनुसार ही सम्बन्धित उपसारणिक एवं सह-खण्ड के चिह्न समान या विपरीत होंगे।

आव्यह के सहखंडज और व्युत्क्रम (Adjoint And Inverse of A Matrix)
पिछले अध्याय में हमने एक आव्यूह के व्युत्क्रम का अध्ययन किया है। इस अनुच्छेद में हम एक आव्यूह के व्युत्क्रम के अस्तित्व के लिए शर्तों की भी व्याख्या करेंगे। A^-1 ज्ञात करने के लिए पहले हम एक आव्यूह का सहखंडज परिभाषित करेंगे। आव्यूह का सहखंडज (Adjoint of a Matrix)

परिभाषा-एक वर्ग आव्यूह A = [a_ij] का सहखंडज आव्यूह [A_ij] के परिवर्त के रूप में परिभाषित है, जहाँ A_ij, अवयव a_ij का सहखंड है। आव्यूह A के सहखंडज को adjA के द्वारा व्यक्त करते हैं।

उदाहरणार्थ-आव्यूह A = $\left[\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right]$ का सहखंडज ज्ञात कीजिये।
हल:
A₁₁ = 4, A₁₂ = -3
A₂₁ = -2, A₂₂ = 1
adj A = $\left[\begin{array}{ll} \mathrm{A}_{11} & \mathrm{~A}_{12} \\ \mathrm{~A}_{21} & \mathrm{~A}_{22} \end{array}\right]^{\prime}=\left[\begin{array}{cc} 4 & -3 \\ -2 & 1 \end{array}\right]^{\prime}$
adj A = $\left[\begin{array}{cc} 4 & -2 \\ -3 & 1 \end{array}\right]$

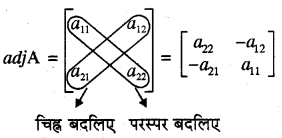
टिप्पणी- 2 × 2 कोटि के वर्ग आव्यूह A = $\left[\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right]$ का

सहखंडज adjA, a₁₁ और a₂₂ को परस्पर बदलने एवं a₁₂ और a₂₁ के चिह्न परिवर्तित कर देने से भी प्राप्त किया जा सकता है। जैसा नीचे दर्शाया गया है

प्रमेय 1 :
यदि A कोई n कोटि का आव्यूह है तो,
A(adjA) = (adjA) A = |A|I, जहाँ I, n कोटि का तत्समक आव्यूह है।
उपपत्ति:
माना कि A = $\left[\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right]$ है तब

adjA = $\left[\begin{array}{lll} A_{11} & A_{21} & A_{31} \\ A_{12} & A_{22} & A_{32} \\ A_{13} & A_{23} & A_{33} \end{array}\right]$
क्योंकि एक पंक्ति या स्तम्भ के अवयवों का संगत सहखंडों की गुणा का योग |A| के समान होता है अन्यथा शून्य होता है।
|A| = $\left|\begin{array}{ll} 2 & 3 \\ 4 & 1 \end{array}\right|$ = 2 - 12 = -10 ≠ 0

प्रमेय 2 : यदि A तथा B दोनों एक ही कोटि के व्युत्क्रमणीय आव्यूह हों तो AB तथा BA भी उसी कोटि के व्युत्क्रमणीय आव्यूह होते हैं।

प्रमेय 3 : आव्यूहों के गुणनफल का सारणिक उनके क्रमशः सारणिकों के गुणनफल के समान होता है। अर्थात् |AB| = |A B| जहाँ A तथा B समान कोटि के वर्ग आव्यूह हैं।

टिप्पणी-हम जानते हैं कि

चूंकि यहाँ पर R,, R, तथा R, में से |A| को उभयनिष्ठ लिया गया है।
अर्थात् |(adjA)| |A| = |A|³(1) = |A|³
अर्थात् (adjA) = A²
व्यापक रूप से, यदि n कोटि का एक वर्ग आव्यूह A हो तो
|adjA| = |A|^n-1 होगा।

इस प्रकार
A(adjA) = $\left|\begin{array}{ccc} \mathrm{A} & 0 & 0 \\ 0 & |\mathrm{~A}| & 0 \\ 0 & 0 & \mid \mathrm{A} \end{array}\right|$ = |A| = $\left|\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right|$
A(adjA) = |A|I इसी प्रकार, हम दर्शा सकते हैं कि
(adjA)A = |A| I अतः A(adjA) = (adjA)A = |A| I सत्यापित है।

अव्युत्क्रमणीय आव्यूह (Singular Matrix) यदि किसी वर्ग आव्यूह A का सारणिक |A| = 0 हो, तो आव्यूह A अव्युत्क्रमणीय आव्यूह कहलाती है।

उदाहरणार्थ A = $\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right]$
एक अव्युत्क्रमणीय आव्यूह है क्योंकि
|A| = $\left|\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right|$ = 1(45 – 48) -2(36 - 42) + 3(32 - 35) = -3 + 12 -9 = 0

व्युत्क्रमणीय आव्यूह (Non-singular Matrix)
यदि किसी वर्ग आव्यूह A का सारणिक |A| ≠ 0 हो, तो आव्यूह A व्युत्क्रमणीय आव्यूह कहलाती है।

उदाहरणार्थ A = $\left[\begin{array}{ll} 2 & 3 \\ 4 & 1 \end{array}\right]$ एक व्युत्क्रमणीय आव्यूह है क्योंकि
$\left|\begin{array}{ll} 2 & 3 \\ 4 & 1 \end{array}\right|$ = 2 - 12 = - 100

प्रमेय 4 : एक वर्ग आव्यूह A के व्युत्क्रम का अस्तित्व है यदि और केवल यदि A व्युत्क्रमणीय आव्यूह है।
उपपत्ति-माना कि n कोटि का व्युत्क्रमणीय आव्यूह A है और n कोटि का तत्समक आव्यूह I है। तब n कोटि के एक वर्ग आव्यूह B का अस्तित्व इस प्रकार हो ताकि AB = BA = I
अब AB = I है तो |AB = |I| या |A B| = 1 (क्योंकि |I| = 1, |AB| = |A| |B|)

इससे प्राप्त होता है |A| ≠ 0. अतः A व्युत्क्रमणीय है। विलोमतः माना कि A व्युत्क्रमणीय है। तब A ≠ 0
अब A(adj A) = (adj A) A = |A| = I (प्रमेय 1)
या A ($\frac{1}{|\mathrm{~A}|}$adj A) = ($\frac{1}{|\mathrm{~A}|}$adj A) A = I
या AB = BA = 1, जहाँ B = $\frac{1}{|\mathrm{~A}|}$adj A
अतः A के व्युत्क्रम का अस्तित्व है और A^-1 = $\frac{1}{|\mathrm{~A}|}$

सारणिकों और आव्यूहों के अनुप्रयोग (Appli Cations of Determinants And Matrices)
इस अनुच्छेद में हम सारणिकों तथा आव्यूहों का अनुप्रयोग दो या तीन चर राशियों वाले रैखिक समीकरण निकाय को हल करने के बारे में अध्ययन करेंगे। संगत निकाय-निकाय संगत कहलाता है यदि इसके हलों (एक या अधिक) का अस्तित्व होता है। असंगत निकाय-निकाय असंगत कहलाता है यदि इसके किसी भी हल का अस्तित्व नहीं होता है। इस अध्याय में हम अद्वितीय हल के समीकरण निकाय तक ही सीमित रहेंगे।

आव्यूह के व्युत्क्रम द्वारा रैखिक समीकरणों के निकाय का हल (Solution of A System of Linear Equations Using Inverse of A Matrix)
हम रैखिक समीकरणों के निकाय को आव्यूह समीकरण के रूप में व्यक्त करते हैं और आव्यूह के व्युत्क्रम का प्रयोग करके उसे हल करते हैं।

निम्नलिखित समीकरण निकाय पर विचार कीजिए
a₁x + b₁y + c₁z = d₁
a₂x + b₂y + c₂z = d₂
a₃x + b₃y + c₃z = d₃

मान लीजिए A = $\left[\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right]$ , X = $\left[\begin{array}{l} x \\ y \\ z \end{array}\right]$ और B =$\left[\begin{array}{l} d_1 \\ d_2 \\ d_3 \end{array}\right]$

तब समीकरण निकाय AX = B के रूप में निम्नलिखित प्रकार से व्यक्त की जा सकती है
$\left[\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right]\left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\left[\begin{array}{l} d_1 \\ d_2 \\ d_3 \end{array}\right]$
स्थिति I
यदि A एक व्युत्क्रमणीय आव्यूह है तब इसके व्युत्क्रम का अस्तित्व है। अतः AX = B से हम इस प्रकार से लिख सकते हैं
A^-1(AX) = A^-1B
या (A^-1 से पूर्व गुणन के द्वारा) (A^-1A)
X = A^-1B (साहचर्य गुणन द्वारा)
या IX = A^-1B
या X = A^-1B
यह आव्यूह समीकरण दिए गए समीकरण निकाय का अद्वितीय हल प्रदान करता है क्योंकि एक आव्यूह का व्युत्क्रम अद्वितीय होता है। समीकरणों के निकाय के हल करने की यह विधि आव्यूह विधि कहलाती है।

स्थिति II
यदि A एक अव्युत्क्रमणीय आव्यूह है तब |A| = 0 होता है।
इस स्थिति में हम (adj A) B ज्ञात करते हैं।
यदि (adj A) B ≠ 0, (O शून्य आव्यूह है), तब कोई हल नहीं होता है और समीकरण निकाय असंगत कहलाती है।
यदि (adj A) B = 0, तब निकाय संगत या असंगत होगी क्योंकि निकाय के अनंत हल होंगे या कोई भी हल नहीं होगा।

→ n कोटि के प्रत्येक वर्ग आव्यूह A = [a_ij] को एक संख्या (वास्तविक या सम्मिश्र) द्वारा संबंधित कर सकते हैं जिसे वर्ग आव्यूह का सारणिक कहते हैं। इसे |A| या det (A) या Δ के द्वारा निरूपित करते हैं।

→ आव्यूह A = [a₁₁]_1×1 का सारणिक |a₁₁|_1×1 = a₁₁ के द्वारा दिया जाता है।

→ आव्यूह A = $\left[\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right]$ का सारणिक |A| = $\left[\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right]$ = a₁₁a₂₂ - a₁₂₂₁

→ तृतीय क्रम का सारणिक Δ = $\left|\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right|=a_1\left|\begin{array}{ll} b_2 & c_2 \\ b_3 & c_3 \end{array}\right|-b_1\left|\begin{array}{ll} a_2 & c_2 \\ a_3 & c_3 \end{array}\right|+c_1\left|\begin{array}{ll} a_2 & b_2 \\ a_3 & b_3 \end{array}\right|$

→ |A'| = |A| जहाँ A' = A का परिवर्त है।

→ यदि हम दो पंक्तियों या स्तम्भों को परस्पर बदल दें तो सारणिक का चिह्न बदल जाता है।

→ यदि सारणिक की कोई दो पंक्ति या स्तम्भ समान या समानुपाती हों तो सारणिक का मान शून्य होता है।

→ यदि हम एक सारणिक की एक पंक्ति या स्तम्भ के अचर k से गुणा कर दें तो सारणिक का मान k गुना हो जाता है।

→ यदि A = [a_ij]_n×n, तो |kA| = kⁿ|A|

→ (x₁, y₁), (x₂, y₂) और (x₃, y₃) शीर्षों वाली त्रिभुज का क्षेत्रफल
Δ = $\frac{1}{2}\left|\begin{array}{lll} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array}\right|$

→ दिए गए आव्यूह A के सारणिक के एक अवयव a_ij का उपसारणिक वीं पंक्ति और jवां स्तम्भ हटाने से प्राप्त सारणिक होता है और इसे M_ij द्वारा व्यक्त किया जाता है।

→ a_ij का सहखण्ड A_ij = (-1)^i+j M_ij द्वारा व्यक्त किया जाता है।

→ A के सारणिक का मान |A| = a₁₁A₁₁ + a₁₂A₁₂ + a₁₃A₁₃ है और इसे एक पंक्ति या स्तम्भ के अवयवों और उनके संगत सहखण्डों के गुणनफल का योग करके प्राप्त किया जाता है।

→ यदि एक पंक्ति (या स्तम्भ) के अवयवों और अन्य दूसरी पंक्ति (या स्तम्भ) के सहखण्डों की गुणा कर दी जाए तो उनका योग शून्य होता है, जैसे
a₁₁A₂₁ + a₁₂A₂₂ + a₁₃A₂₃ = 0

→ यदि A = $\left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|$ के सहखण्डन adjA = $\left|\begin{array}{lll} \mathrm{A}_{11} & \mathrm{~A}_{21} & \mathrm{~A}_{31} \\ \mathrm{~A}_{12} & \mathrm{~A}_{22} & \mathrm{~A}_{32} \\ \mathrm{~A}_{13} & \mathrm{~A}_{23} & \mathrm{~A}_{33} \end{array}\right|$ होता है, जहाँ a_ij का सहखण्ड A_ij है।

→ A (adj A) = (adj A) A = |A| I, जहाँ A, n कोटि का वर्ग आव्यूह है।

→ यदि कोई वर्ग आव्यूह क्रमशः अव्युत्क्रमणीय या व्युत्क्रमणीय कहलाता है यदि |A| = 0 या |A| ≠ 0

→ A A^-1 = A^-1A = I

→ (A^-1)^-1 = A

→ A^-1 = $\frac{1}{(\mathrm{~A})}$(adj A)→ यदि a₁x + b₁y + c₁z = d₁
a₂x + b₂y + C₂z = d₂
a₃x + b₃y + c₃z = d₃
तब इन समीकरणों को AX = B के रूप में लिखा जा सकता है
जहाँ A = $\left[\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right]$. X = $\left[\begin{array}{l} x \\ y \\ z \end{array}\right]$ और B = $\left[\begin{array}{l} d_1 \\ d_2 \\ d_3 \end{array}\right]$

→ समीकरण AX = B का अद्वितीय हल X = A^-1B द्वा

रा दिया जाता है जहाँ |A| ≠ 0

→ समीकरणों का निकाय संगत या असंगत होता है यदि इसके हल का अस्तित्व है या नहीं।

• AX = B में (i) यदि |A| ≠ 0 तो अद्वितीय हल का अस्तित्व है।
• यदि |A| = 0 और (adj A) B ≠ 0 तो किसी हल का अस्तित्व नहीं है।
• यदि |A| = 0 और (adj A) B = 0 तो निकाय संगत या असंगत होती है।