RBSE Class 12 Maths Notes Chapter 4 Determinants

These comprehensive RBSE Class 12 Maths Notes Chapter 4 Determinants will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 4 Notes Determinants

Introduction:
In this chapter, we shall study determinants up to order three only with real entries. Also, we will study various properties of determinants, minors, cofactors and applications of determinants in finding the area of triangle, adjoint and inverse of a square matrix, consistency and inconsistency of system of linear equations and solution of linear equations in two or three variables using inverse of a matrix.

Determinant:
To every square matrix A = [a_ij] of order n, we can associate a number (real or complex) called determinant of the square matrix A, where a_ij = (i, j)^th element of A.
This may be thought of as a function which associated each square matrix with a unique number (real or complex), if M is the set of square matrices, K is the set of number (real or complex) and/: M → K is defined by f(A) = k, where A e M and ke K, then f(A) is called the determinant of A. It is also denoted by |A| or det A or ΔA.

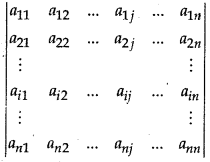
Remarks:

• For a matrix A, |A| is read as determinant of A and not modulus of A.
• Only square matrices have determinants.

Determinants of a Matrix of order 1:
Let A = [a] be the matrix of order 1, then determinant of A is defined to be equal to a.

Determinants of a Matrix of Order 2:
Let A = \(\left[\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right]_{2 \times 2}\) be a matrix of order 2 × 2, then determinant of A is defined as:
det A = |A| = Δ = \(\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|\)
= a₁₁a₂₂ - a₂₁a₁₂

Example 1:
Let's evaluate: \(\left|\begin{array}{rr} 3 & 7 \\ 8 & -4 \end{array}\right|\)
We have, \(\left|\begin{array}{rr} 3 & 7 \\ 8 & -4 \end{array}\right|\) = {3 × (-4)} - {8 × 7}
= 12 - 56 = -68

 

Example 2.
Let's show that:
\(\left|\begin{array}{lr} \sin 10^{\circ} & -\cos 10^{\circ} \\ \sin 80^{\circ} & \cos 80^{\circ} \end{array}\right|\) = 1
We have, L.H.S = \(\left|\begin{array}{lr} \sin 10^{\circ} & -\cos 10^{\circ} \\ \sin 80^{\circ} & \cos 80^{\circ} \end{array}\right|\)
= {sin 10° × cos 80°} - {sin 80° × (-cos 10°)}
= sin 10° cos 80° + sin80° cos 10°
= sin(10° + 80°) = sin 90° = 1

Determinants of a Matrix of Order 3:
Determinants of a matrix of order 3 can be determined by expressing it in terms of 2 order determinants. This is known as expansion of a determinant along a row (or a column). There are six ways of expanding a determinant of order 3. 3 ways corresponding to each of three rows (R₁, R₂ and R₃) and three corresponding to each of three columns (C₁, C₂ and C₃) giving the same value as shown below.
Consider the determinant of square matrix A = [a_ij]_3×3
i.e., A = \(\left[\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right]\)
Expansion along first row (R₁)

Step 1 : Multiply first element a₁₁ of R₁ by (-1)⁽¹⁺¹⁾ [(-1)^{[sum of suffixes in a₁₁]} and the second order determinant obtained by deleting the element of first row (R₁) and first column (C₁) of |A| as an lies in R₁ and C₁,
i.e (-1)⁽¹⁺¹⁾a₁₁\(\left|\begin{array}{ll} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right|\)

Step 2 : Multiply 2nd element a₁₂ of R₁ by (-1)⁽¹⁺²⁾ [(-1)^{[sum of suffixes in a₁₂]} and the second order determinant obtained by deleting elements of first row (R₁) and second column (C₂) of | A | as a₁₂ lies in R₁ and C₂,
i.e (-1)⁽¹⁺²⁾a₁₁\(\left|\begin{array}{ll} a_{21} & a_{23} \\ a_{31} & a_{33} \end{array}\right|\)

Step 3 : Multiply third element a₁₃ of Rx by (-1)⁽¹⁺³⁾ [(-1)^{sum of suffixes in a₁₃]} and the second order determinant obtained by deleting elements of first row (R₁) and third column (C₃) of | A | as a₁₃ lies in R₁ and C₃,
i.e (-1)⁽¹⁺³⁾a₁₁\(\left|\begin{array}{ll} a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right|\)

Step 4: Now, the expansion of determinant of A, that is, | A j written as sum of all three terms obtained in steps 1, 2 and 3 above is given by
det A = | A | = (-1)⁽¹⁺¹⁾a₁₁\(\left|\begin{array}{ll} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right|\) + (-1)⁽¹⁺²⁾a₁₁\(\left|\begin{array}{ll} a_{21} & a_{23} \\ a_{31} & a_{33} \end{array}\right| \)+ (-1)⁽¹⁺³⁾a₁₁\(\left|\begin{array}{ll} a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right|\)
or |A| = a₁₁(a₂₂a₃₃ - a₃₂a₂₃) - a₁₂(a₂₁a₃₃ - a₃₁a₂₃) + a₁₃(a₂₁a₃₂ - a₃₁a₂₂)
= a₁₁a₂₂a₃₃ - a₁₁a₃₂a₂₃ - a₁₂a₂₁a₃₃ + a₁₂a₃₁a₂₃ + a₁₃a₂₁a₃₂ - a₁₃a₃₁a₂₂

Note: We shall apply all four all four steps together.

Expansion along second row (R₂)

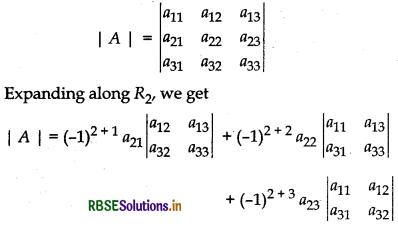
= - a₂₁ (a₁₂a₃₃ - a₃₂a₁₃) + (a₁₁a₃₃ - a₃₁a₁₃) - a₂₃(a₁₁a₃₂ - a₃₁a₁₂)
|A| = -a₂₁a₁₂a₃₃ + a₂₁a₃₂a₁₃ + a₂₂a₁₁a₃₃ - a₂₂a₃₁a₁₃ - a₂₃a₁₁a₃₂ + a₂₃a₃₁a₁₂
= a₂₂a₁₁a₃₃ - a₂₃a₁₁a₃₂ - a₂₁a₁₂a₃₃ + a₂₃a₃₁a₁₂ + a₂₁a₃₂a₁₃ - a₂₂a₃₁a₁₃ ........(2)

Expansion along first column (C₁)

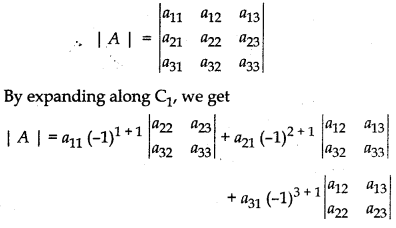
= a₁₁(a₂₂a₃₃ - a₃₂a₂₃) - a₂₁(a₁₂a₃₃ - a₃₂a₁₃) + a₃₁(a₁₂a₂₃ - a₂₂a₁₃)
|A| = a₁₁a₂₂a₃₃ - a₁₁a₃₂a₂₃ - a₂₁a₁₂a₃₃ + a₂₁a₃₂a₁₃ + a₃₁a₁₂a₂₃ - a₃₁a₂₂a₁₃
|A| = a₁a₂₂a₃₃ - a₁₁a₃₂a₂₃ - a₂₁a₁₂a₃₃ + a₃₁a₂₂a₁₃ + a₃₁a₁₂a₂₃ - a₃₁a₂₂a₁₃
|A| = a₁₁a₂₂a₃₃ - a₁₁a₃₂a₂₃ - a₂₁a₁₂a₃₃ - a₃₁a₂₂a₁₃ + a₃₁a₁₂a₂₃ + a₂₁a₃₂a₁₃ ..........(3)
Clearly, from (1), (2) and (3) value of |A| are equal. Hence, expanding a determinant along any row or column gives same value.

Remarks

• For easier calculations, we shall expand the determinant along that row or column which contains maximum number of zeros.
• While expanding, instead of multiplying by (-1)^i+j we can multiply by + 1 or - 1 according as (i + j) is even or add.

Value of a determinant of order third:
To find value of determinant of order 3 or more following definitions are essential.
(i) Minor of in |A| : In determinant |A|, minor of a_ij can be obtained by removing ith row and jth column (from a_ij). Remaining determinant is called minor of a_ij and is denoted by M_ij.

(ii) Cofactors of a_ij in |A| : Cofactors of a_ij in |A| are denoted by C_ij. Thus
C_ij = (-1)^i+jM_ij

Properties of Determinants:
In the previous section, we have learnt how to expand the determinants. In this section, we will study some properties of determinants which simplifies its evaluation by obtaining maximum number of zero in a row or a column. These properties are true for determinants of any order. However, we shall restrict ourselves upto determinants of order 3 only.

Property 1.
The value of the determinant remains unchanged if the rows and columns are interchanged.
Proof:
Let Δ = \(\left|\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array}\right|\)
Expanding along first column, we get
Δ = a₁\(\left|\begin{array}{ll} b_{2} & c_{2} \\ b_{3} & c_{3} \end{array}\right|\) - b₁\(\left|\begin{array}{ll} a_{2} & c_{2} \\ a_{3} & c_{3} \end{array}\right|\) + c₁\(\left|\begin{array}{ll} a_{2} & b_{2} \\ a_{3} & b_{3} \end{array}\right|\)
= a₁(b₂c₃ - c₂b₃) - b₁(a₂c₃ - c₂a₃) + c₁(a₂b₃ - b₂a₃)... (ii)

By interchanging rows and columns of Δ
Δ' = \(\left|\begin{array}{lll} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{array}\right|\)

Expanding along first column, we get
Δ' = a₁\(\left|\begin{array}{ll} b_{2} & b_{3} \\ c_{2} & c_{3} \end{array}\right|\) - b₁\(\left|\begin{array}{ll} a_{2} & a_{3} \\ c_{2} & c_{3} \end{array}\right|\) + c₁\(\left|\begin{array}{ll} a_{2} & a_{3} \\ b_{2} & b_{3} \end{array}\right|\)
= a₁(b₂c₃ - c₂b₃) - b₁(a₂c₃ - c₂a₃) + c₁(a₂b₃ - b₂a₃) ..........(ii)

From (i) and (ii) Δ' = Δ
Corollary: For any square matrix A
|A'| = |A|

Property 2.
If any two rows (or columns) of a determinant are interchanged then sign of determinant changes.
Proof:
Let Δ = \(\left|\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array}\right|\)
Interchanging first and third rows, the new determinant obtained is
Δ' = \(\left|\begin{array}{lll} a_{3} & b_{3} & c_{3} \\ a_{2} & b_{2} & c_{2} \\ a_{1} & b_{1} & c_{1} \end{array}\right|\)

Expanding along first column, we get
Δ' = a₃\(\left|\begin{array}{ll} b_{2} & c_{2} \\ b_{1} & c_{1} \end{array}\right|\) - a₂\(\left|\begin{array}{ll} b_{3} & c_{3} \\ b_{1} & c_{1} \end{array}\right|\) + a₁\(\left|\begin{array}{ll} b_{3} & c_{3} \\ b_{2} & c_{2} \end{array}\right|\)
= a₃(b₂c₁ - b₁c₂) - a₂(b₃c₁ - b₁c₃) + a₁(b₃c₂ - b₂c₃)
= -a₁(b₂c₃ - b₃c₂) + a₂(b₁c₃ - b₃c₁) - a₃(b₁c₂ - b₂c₁)
= -[a₁(b₂c₃ + b₃c₂) - a₂(b₁c₃ + b₃c₁) - a₃(b₁c₂ + b₂c₁)
∴ Δ' = Δ
[Δ = a₁(b₂c₃ + b₃c₂) - a₂(b₁c₃ + b₃c₁) - a₃(b₁c₂ + b₂c₁]
i.e \(\left|\begin{array}{lll} a_{3} & b_{3} & c_{3} \\ a_{2} & b_{2} & c_{2} \\ a_{1} & b_{1} & c_{1} \end{array}\right|=-\left|\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array}\right|\)

Property 3.
If any two rows (or columns) of a determinant are identical (all corresponding elements are same), then value of determinant is zero.
Proof:
Let determinant
Δ = \(\left|\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{1} & b_{1} & c_{1} \\ a_{3} & b_{3} & c_{3} \end{array}\right|\)
Here, first and second rows are identical.
If we interchange the identical rows (or columns) of the determinant A then A does not change. However by property 2, it follows that A has changed its sign.
Δ = \(\left|\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{1} & b_{1} & c_{1} \\ a_{3} & b_{3} & c_{3} \end{array}\right|\) = -Δ
⇒ Δ = -Δ ⇒ Δ + Δ = 0
⇒ 2Δ =0
∴ Δ = 0
Similarly, we can prove it for two identical columns.

Property 4.
If each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets multiplied by k.
Proof:
Let Δ = \(\left|\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array}\right|\) and Δ' be the determinant obtained by multiplying the element of the first row by k, then

Corollary: For any square matrix of order n
n|kA| = KN |A|

Remarks:
1. By this property we can take out any common factor from any one row or any one column of a given determinant.

2. If corresponding elements of any two rows (or columns) of a determinant are proportional (in the same ratio), then its value is zero. Thus,
Δ = \(\left|\begin{array}{ccc} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ K a_{1} & K a_{2} & K a_{3} \end{array}\right|\) (rows R₁ and R₂ are proportional)

Property 5.
If some or all elements of a row or column of a determinant are expressed As sum of two (or more) terms, then the determinant can be expressed as sum of two (or more) determinants.
Proof:
Let Δ = \(\left|\begin{array}{lll} a_{1}+\alpha & b_{1} & c_{1} \\ a_{2}+\beta & b_{2} & c_{2} \\ a_{3}+\gamma & b_{3} & c_{3} \end{array}\right|\)
Expanding Δ along the first column, we get

This rule can be expressed in general form.

Property 6.
If to each element of any row or column of a determinant, the equimultiples of corresponding elements of other row (or column) are added, then value of determinant remains same, i.e., the value of determinant remains same if we apply the operation R_i → R_i + kR_j or C_i → C_i + KC_j
Proof: Let
Δ = \(\left|\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array}\right|\)
If multiplying second column of determinant Δ by l and third column by m and then added in first column the obtained determinant is Δ', then

[In second and third determinants, first and second columns are respectively identical to first and third column. Thus, their value will be zero.]
= \(\left|\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array}\right|\) = Δ

Remarks:

• If Δ is the determinant obtained by applying R_i → kR_i or C_j → kC_j to the determinant Δ, then Δ = KΔ.
• If more than one operation like R_i → R_i + kR_j is done in one step, care should be taken to see that a row that is affected in one operation should not be used in another operation. A similar remark applies to column operations.

Area of A Triangle:
In earlier classes, we have studied that if (x₁ y₁), (x₂, y₂) and (x₃ y₃) are vertices of any triangle then its area can be find by following expression:
= \(\frac{1}{2}\)[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

This expression can be expressed in determinant form as:
Δ = \(\frac{1}{2}\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|\) ........(1)

Conditions of collinearity of three points :
If three points A, B and C whose coordinates are respectively (x₁ y₁), (x₂, y₂) and (x₃ y₃) and all the three points are collinear then area of triangle formed by three points will be zero. Thus, by
Δ = \(\frac{1}{2}\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|\) = 0
⇒ \(\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|\) = 0 ..........(2)

Equation of a line passing through two given L points:
Let Ax₁ y₁) and B(x₂, y₂) are two points and P(x, y) is any point on the line joining these points. Thus, points A, B and
\(\left|\begin{array}{ccc} x & y & 1 \\ x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \end{array}\right|\) = 0
Note: Since, area is a positive quantity, so we always take absolute value of determinant.

Minor And Cofactors:
Definition 1: Minor of an element a_ij of a determinant is the determinant obtained by deleting its rn row and fcolumn in which element a_ij lies. Minor of an element is denoted by M_ij.
Note: Minor of an element of a determinant of order (n > 2) is a determinant of order n - 1.

Definition 2 : Cofactor of an element a_ij, denoted by is defined by A_ij is defined by
A_ij = (-1)^i+j; M_ij, where is minor of a_ij

Note: If elements of a row (or column) are multiplied with cofactors of any other row (or column), then their sum is zero. For example,

Similarly, we can try for other rows and columns.

Adjoint And Inverse of A Matrix:
In the previous chapter, we have studied inverse of a matrix. In this section, we shall discuss the condition for existence of inverse of a matrix.
To find inverse of a matrix A, i.e., A^-1 we shall first define adjoint of a matrix.

Adjoint of a Matrix:
The adjoint of a square matrix A = [a_ij]nxn is defined as the transpose of the matrix [A_ij]MXn, where, A_ij is the cofactor of the element a_ij. Adjoint of the matrix A is denoted by adj A.

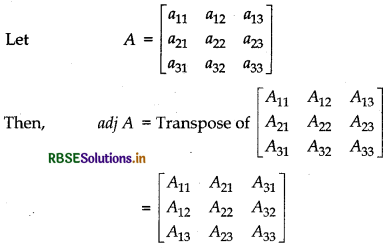
Remarks:
For a square matrix of order 2, given by
A = \(\left[\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right]\)

The adj A can also be obtainted by interchanging a₁₁ and a₁₂ and by changing signs of a₁₂ and a₂₁ i.e.,

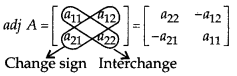
Example: Let's find adj A for A = \(\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\)
Answer:
A = \(\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\)
Then, |A| = \(\left|\begin{array}{ll} a & b \\ c & d \end{array}\right|\)

Cofactors of |A| are :
A₁₁ = (-1)¹⁺¹M₁₁ = d
A₁₂ = (-l)¹⁺²M₁₂ = -c
A₂₁ = (-1)²⁺¹M₂₁ = -b
A₂₂ = (-1)²⁺²M₂₂ = a

Matrix formed by the cofactors of |A| is
B(say) = \(\left[\begin{array}{ll} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array}\right]=\left[\begin{array}{cc} d & -c \\ -b & a \end{array}\right]\)
∴ adj A = Transpose of matrix B
⇒ adj A = \(\left[\begin{array}{ll} A_{11} & A_{21} \\ A_{12} & A_{22} \end{array}\right]=\left[\begin{array}{cc} d & -b \\ -c & a \end{array}\right]\)

Theorem 1.
If A be any square matrix of order h, then A (adj A) = (adj A) A = |A|I where I is the identity matrix of order n.
Proof:
Let

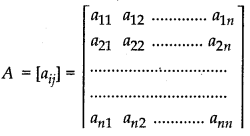
If a_ij is cofactor of A_ij, then
(adj.A)_ij = A_ij, ∀ i, j = 1, 2, ........... n
Again, A and adj A, both an square matrices of order n.
Thus, A(adj A) and (adj A) exists and their order will be n.

∴ A (adj A) = |A| I_n or A(adj A) = |A| I
Since Σa_ijA_ij = |A| When i = j
Σa_ijA_ij = 0 When i ≠ j
Similarly, we can prove that (adjA)A = |A| I_n
Thus A(adj A) = (adj. A)A = |A| I_n

Singular Matrix
A square matrix A is said to be singular if |A| = 0.
For example: If A = \(\left[\begin{array}{cc} 5 & 10 \\ 2 & 4 \end{array}\right]\)Then |A| = \(\left|\begin{array}{cc} 5 & 10 \\ 2 & 4 \end{array}\right|\)
= (5 × 4) - (2 × 10) = 20 - 20 = 0
Thus, matrix A is singular matrix.

Non-Singular Matrix:
A square matrix A is said to be non-singular if |A| ≠ 0. For example: if A = \(\left[\begin{array}{ll} 3 & 7 \\ 2 & 5 \end{array}\right]\), then
|A| = \(\left|\begin{array}{ll} 3 & 7 \\ 2 & 5 \end{array}\right|\)
|A| = (3 × 5) - (2 × 7) = 15 - 14 = 1 ≠ 0
Thus, matrix A is non-singular matrix.

Theorem 2.
If A and B are non-singular matrices of the same order, then AB and BA are also non-singular matrices of the same order.

Theorem 3.
The determinant of the product of matrices is equal to product of their respective determinants, that is, |AB| = |A| |B|, where A and B are square matrices of the same order
Remarks
We know that (adj A) A = |A|I

In general, if A is a square matrix of order n, then |adj(A)| = |A|^n-1.

Inverse of a Matrix
A square matrix of order n is invertible if there exists a square matrix B of the same order such that AB = In = BA.
In such a case we can say that the inverse of A is B and we write A^-1 = B.

Theorem 1.
The inverse of a square matrix exists if |A| ≠ 0.
Proof :
Let A be a matrix of order n and its inverse matrix B will of order n, then
AB = I 1
But |AB| = |A| . |B| = |I| = I
Thus |A| ≠0
Again if |A| ≠ 0 then
A\(\frac{({adj} A)}{|A|}=\frac{({adj} A) A}{|A|}\) = I
Thus B = \(\frac{{adj} A}{|A|}\) or A^-1 (Here B = A^-1)
i. e. AB = BA = I
Thus, B inverse matrix of A exists whereas |A| ≠ 0iff |A| ≠ 0.

Theorem 2.
The inverse of non-singular matrix is unique.
Proof :
Let matrix A is a non-singular matrix of order n. B and C are its invertible matrices.
Now AB = BA = I and AC = CA = f
AC = I ⇒ B(AC) = BI = B ...(i)
and BA = I ⇒ (BA)C = CI = C ...(ii)
but B(AQ = (BA)C
(By associativity of multiplication of matrices)
From (i) and (ii), B = C
Thus, invertible matrix has unique inverse.

Theorem 3.
Reversal law of inverse : If A and B are two square matrices of order n and are invertibe then
(AB)^-1 = B^-1A^-1
where A^-1 and B^-1 are inverse of A and B respectively.
Proof :
A^-1 and B^-1 are inverse matrices of A and B respectively, then
(AB) (B^-1A^-1) = A(BB^-1)A^-1
= AIA^-1 (∵ BB^-1 = 1)
By associativity of multiplication of matrices
= AA^-1 (∵ AI = A)
= I ...(1)
Similarly
(B^-1A^-1) (AB) = B^-1(A^-1A)B
= B^-1IB (∵A^-1A = 1)
By associativity of multiplication of matrices = B-1B (-.IB = B)
= 1 ...(2)
From (1) and (2), we get
(AB)^-1 = B^-1A^-1

Corollary:
(A₁A₂ ............ A_n)^-1 = A_n^-1A_n^-1.......... A₂^-1A₁^-1

Theorem 4.
Cancellation law: If A,B and C are square matrices of order n and A is a non-singular matrix, then
(i) AB = AC => B = C (Left cancellation law)
(ii) BA = CA =>B = C (Right cancellation law)
Proof: Since, A is a non-singular matrix, so A-1 exists.
AB = AC
⇒ A^-1(AB) = A^-1(AC)
⇒ (A^-1aA)B = (A^-1A)C [∵ A^-1(AB) = (A^-1A)B
A^-1(AC) = (A^-1A)C
By associativity of multiplication of matrices
⇒ IB=IC (∵ A^-1A = I)
⇒ B = C (∵ IB = B and IC = C)
Again BA = CA
⇒ (BA)A^-1 = (CA)A^-1 [∵ (BA)A^-1 = B(AA^-1)
(CA)A^-1 = C(AA^-1)
By associativity of multiplication of matrices]
⇒ B(AA^-1) = C(AA^-1)
⇒ BI = CI (∵ AA^-1 = 1)
⇒ B = C (∵ BI = B and Cl = C)

Theorem 5.
If matrix A is invertible then show that transpose of A is also invertible and (A')^-1 = (A^-1)'.
Proof:
Let A is an invertible matrices of order n, then
∵ |A| ≠ 0
∵ |A'| = |A| ≠ 0
i.e., A' is also invertible,
Now AA^-1 = A^-1A = I
⇒ (AA^-1)' = (A^-1A)' = r
⇒ (A^-1)'A' =A'(A^-1A) = I [∵ (AB)' = B'A' and I' = I
AB = BA = I => B^-1 = A]
Thus (A')^-1 =(A^-1)'

Theorem 6.
If matrix A is invertible and symmetric, then A-1 is also symmetric.
Proof:
A is an invertible symmetric matrix, then A' = A .
Again, we know that
(A^-1)' = (A')^-1
∴ (A^-1)' = A^-1 [∵ A' = A]
Thus, A^-1 is also symmetric.

Theorem 7.
If A and B are two invertible matrices of same order then show that
(adj AB) = (adj B) (adj A)
Proof:
A and B are invertible matrices of same order, then
|A| ≠ 0 and |B| ≠ 0
∴ |AB| = |A||B| ≠ 0
Thus, (AB)^-1 exists.

Thus, adj (AB) = (adj B) (adj A)

Theorem 8.
For any sqaure matrix A, prove that (adj A)' = adj A'
Proof :
Let A be a sqaure matrix of order n. Then (adj A)' and adj A' will be matrices of order n and (i, j)th element of (adj A)'
= (i, j)th element of (adj A)
= Cofactor of (i, j)th element of A
= Cofactor of (j, j)th element of A'
= (i, j)th element of (adj A')
Thus, (adj A)' = (adj A').

Theorem 9.
If A be a non-singular matrix of order tt then show that
|adjA| = |A|^n-1.
Proof:
∵ A (adj A) = |A| I
⇒ |A (adj A) | = |A| |I| (∵ A = B ⇒ |A| = |B|)
⇒ |A| |adjA| = |A|ⁿ |I| [∵ |kI| = kⁿI]
⇒ |A| |adj A| = |A|ⁿ
⇒ |adjA| = |A|^n-1 [∵ |I| = I]
Thus, |adjA| = |A|^n-1.

Theorem 10.
If matrix A is non-singular matrix of order n, then show that
adj (adjA) = |A|^n-2A .
Proof:
We know that for any non-singular matrix B.
B(adj B) = |B|I
Let B = adj A
Then (adj A) [adj (adj A)] = |adj A| I
⇒ (adj A) [adj (adj A)] = | A |^n-1I [∵ (adjA) = |A|^n-1]
⇒ A(adj A) [adj (adj A)] = |A|^n-1A [∵ AI_n = A]
⇒ |A| [adj (adj A)] = |A|^n-1A [∵ A (adj A) = |A| I]
⇒ [adj (adj A)] = | A |^n-2A

Corollary: If matrix A is a non-singular matrix of order n, then
| adj (adj A) | = |A|^(n-1)2
Proof:
∵ adj (adj A) |A|^n-2 (By Theorem 10)
⇒ |adj (adj A)| = || A |^n-2A|
⇒ |adj (adj A)| = | A |^n(n-2) |A| (∵ |kA| = kⁿ|A|)
⇒ |adj (adjA)| =A^{n2-2K + 1} (|A|^n(n-2) A| = | A |^{n2-2K + 1}]
⇒ |adj (adj A)| =A^(n-1)2

Theorem 11.
If product of two non-singular matrix is zero matrix then show that both are singular matrices.
Proof :
Let A and B are two non-singular matrices of order n and AB = O (zero matrix)
If possible, let B be a non-singular matrix. Thus, B-1 exists. .
Now AB = O
⇒ (AB)B^-1 = OB^-1
[Post multiplying both sides by B^-1]
⇒ A(BB^-1) = OB^-1 = O
[By associativity of multiplication of matrices
and OB^-1 = B^-1O = O]
⇒ AI_n = O
⇒ A = O [∵ AI_n = OA]
But, A is non-singular matrix so, B is singular matrix. Again, if possible A is a matrix so A-1 exists.
Now AB = O => A^-1(AB) = A^-1O
[Pre-multiplying both sides by A^-1]
⇒ (A^-1A)B = O
[By associtivity of multiplication of matrices]
⇒ I_nB = O [∵ A^-1A = I_n]
⇒ B = O [∵ I_nB = BI_n = B]
But A is non-singular matrix so B is singular matrix.

Theorem 12.
If A is non-singular matrix then show that
|A^-1| = |A^-1|, i.e., A^-1 = \(\frac{1}{|A|}\)
Proof:
| A | ≠ 0
Thus, A^-1 exists and
AA^-1 = I = A^-1A
⇒ |AA^-1| = |I |
⇒ |A| |A^-1| = 1 [∵ |AB| = |A| |B| and |I| = 1]
⇒ |A^-1| = \(\frac{1}{|A|}\) [∵ |A| ≠ 1]

Steps for finding the inverse of a square Matrix
To find inverse of matrix, following steps are used :
Step 1: Find determinant value of given matrix.
Step 2 : Replace each element of matrix by their cofactors and get cofactors matrix.
Step 3 : Find transpose of matrix obtained in step 2. Now, we get adj A.
Step 4 : Matrix obtained in step 3 is divided by determinant value of matrix. Thus, the matrix so obtained is the inverse of the given matrix.

Applications of Determinants And Matrices:
In this section, we shall discuss application of determinants and matrices for solving the system of linear equations in two or three variable and for checking the consistency of the system of linear equations.

Consistent system: A system of equation is said to be consistent if its solution (one or more) exists.
Inconsistent system : A system of equation is said to be inconsistent if its solution does not exist.

Solution of system of linear equation using inverse of a matrix
Let us express the system of linear equation as matrix equations and solve them using inverse of the matrix. Consider the system of equation
a₁x + b₁y + c₁z = d₁
a₂x + b₂ c₂z = d₂
a₃x + b₃y + c₃z = d₃

Let A = \(\left[\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array}\right]\) X = \(\left[\begin{array}{l} x \\ y \\ z \end{array}\right]\)and B = \(\left[\begin{array}{l} d_{1} \\ d_{2} \\ d_{3} \end{array}\right]\)

Then, the system of equation can be written as, AX = B i.e.,
\(\left[\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array}\right]\left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\left[\begin{array}{l} d_{1} \\ d_{2} \\ d_{3} \end{array}\right]\)

Case I : If A is non-singular matrix, then its inverse exists. Now .
or AX = B
or A^-1(AX) = A^-1B (Pre-multiplyingby A^-1)
or (A^-1A) X = A^-1B (By associative property)
or IX = A^-1B
or X = A^-1B.
This matrix equation provides unique solution for the given system of equation as inverse of matrix is unique. This method of solving system of equation is known as matrix method.

Case II: If A is a singular matrix, then |A| = 0.
In this case, we calculate (adj A) B
If (adj A) B ≠ 0 (0 being zero matrix), then solution does not exist and the solution of equation is called inconsistent.
If (adj A) B = 0, then system may be either consistent or inconsistent according as the system have either infinitely.

→ A determinant is defined as a (mapping) function from the set of square matrices to the set of real numbers.

→ Every square matrix A is associated with a number, called its determinant. Determinant is denoted by det (A) or |A| or A.

→ Expanding a determinant along any row or column gives same value. For easier calculations, we shall expand the determinant along that row or column which contains maximum number of zeros.

→ The value of the determinant remains unchanged if its rows and columns are interchanged.

→ If any two rows (or columns) of a determinant are interchanged, then sign of determinant changes.

→ If any two rows (or columns) of a determinant are iddentical (all corresponding elements are same), then value of determinant is zero.

→ If each elemment of a row (or column) of a determinant is multiplied by a constant k, then its value gets multiplied by k.

→ If some or all elements of a row or column of a determinant are expressed as sum of two (or morre) terms, then the determinant can be exprressed as sum of two (or more) determinants.

→ If each element of a row (or column) of a determinant is zero, then its value is zero.

→ Let (x₁, y₁), (x₂, y₂), and (x₃, y₃) be the vertices of a triangle, then
Area of triangle = -[x₁(y₂ - y₃) + x₂ ( y₃ - y₁) + x₃ (y₁ - y₂)]
Δ = \(\frac{1}{2}\left|\begin{array}{lll} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array}\right|\)

→ Area is a positive quantity, we always take the absolute value of the determinant.

→ The area of the triangle formed by three collinear points is zero.

→ Minor of an element of a_ij determinant is the determinant obtained by deleting its ith row and jth column in-which element a_ij lies.

→ Minor of an element a_ij is denoted by M_ij

→ Minor of an element of a determinant of order n (n > 2) is determinant of order n - 1.

→ If the minors are multiplied by the proper signs we get cofactors.

→ The cofactor of the element a_ij is A_ij (= (- 1)^1+jM_ij).

→ The signs to be multiplied are given by the rule.

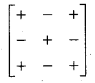
→ Adjoint of a matrix is the transpose of the matrix formed by the cofactors of the given matrix.

→ adj A = Transpose of \(\left|\begin{array}{lll} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \end{array}\right|=\left|\begin{array}{lll} A_{11} & A_{21} & A_{31} \\ A_{12} & A_{22} & A_{32} \\ A_{13} & A_{23} & A_{33} \end{array}\right|\)

→ A square matrix A is said to be singular if |A| =0.

→ A square matrix A is said to be non-singular if |A| ≠ 0.

→ A square matrix A is invertible if and only if A is non-singular matrix.

→ A system of equations is said to be consistent if its solution (one or more) exists.

→ A system of equations is said to be inconsistent if its solution does not exist.

→ Let the system of equations be :
a₁x + b₁y + c₁z = d₁
a₂x + b₂y + c₂z = d₂
a₃x + b₃y + c₃z = d₃

Let A = \(\left[\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right]\), X = \(\left[\begin{array}{l} x \\ y \\ z \end{array}\right]\) and B = \(\left[\begin{array}{l} d_1 \\ d_2 \\ d_3 \end{array}\right]\)

Then, the system of equations can be written as, AX = B, i.e.
\(\left[\begin{array}{lll} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array}\right]\left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\left[\begin{array}{l} d_1 \\ d_2 \\ d_3 \end{array}\right]\)

For a square matrix A in matrix equation AX = B

• |A| ≠ 0, there exists unique solution
• |A| = 0 and (adj A) B ≠ 0, then there exists no solution.
• |A| = 0 and (adj A) B = p, then system may or may not be consistent.