RBSE Class 12 Maths Notes Chapter 3 आव्यूह

These comprehensive RBSE Class 12 Maths Notes Chapter 3 आव्यूह will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 3 Notes आव्यूह

भूमिका (Introduction)):
सर्वप्रथम जे.जे. सिल्वेस्टर ने मैट्रिक्स शब्द का प्रयोग किया तथा गणितज्ञ आर्थर कैली (Arthur Cayley) ने समीकरणों को हल करते समय मैट्रिक्स विषय की खोज की थी तथा उन्होंने 1858 में आव्यूह सिद्धान्त का विकास किया। आव्यूह सिद्धान्त की सहायता से बीजगणित, रेखागणित, सांख्यिकी, अर्थशास्त्र, भौतिक विज्ञान, रसायन विज्ञान आदि की समस्याओं का हल हम आसानी से प्राप्त कर सकते हैं। रेखीय समीकरण निकाय (System of Linear Equations) के हल में मैट्रिक्स का सबसे महत्त्वपूर्ण उपयोग होता है। नेटवर्क एवं गुप्त वार्ताओं को एक स्थान से दूसरे स्थान तक प्रेषित करने में भी इसका विशेष महत्त्व है। हम प्रस्तुत अध्याय में आव्यूह तथा आव्यूह बीजगणित (Matrix Algebra) के बारे में विस्तार से अध्ययन करेंगे।

मैट्रिक्स की परिभाषा (Definition Of Matrix):
आव्यूह संख्याओं या फलनों का एक आयताकार क्रम-विन्यास है। इन संख्याओं या फलनों को आव्यूह के अवयव अथवा प्रविष्टियाँ कहते हैं। आव्यूह को हम अंग्रेजी वर्णमाला के बड़े (Capital) अक्षरों A, B, C द्वारा व्यक्त करते हैं एवं मैट्रिक्स के अन्तर्गत आने वाली संख्याओं को निम्न प्रकार के किसी भी कोष्ठक में बन्द करके लिख सकते हैं
\(\left(\begin{array}{cc} 6 & 5 \\ -4 & 3 \\ 0 & 7 \end{array}\right) \quad\left[\begin{array}{cc} 6 & 5 \\ -4 & 3 \\ 0 & 7 \end{array}\right] \quad\left\|\begin{array}{cc} 6 & 5 \\ -4 & 3 \\ 0 & 7 \end{array}\right\|\)
यहाँ पर हम आव्यूह के लिए बड़े कोष्ठक [ ] का प्रयोग करेंगे। क्षैतिज रेखा में लिखी हुई संख्याएँ पंक्ति (Row) तथा ऊर्ध्वाकार रेखा में लिखी संख्याएँ स्तम्भ (Column) कहलाती हैं।

आव्यूह के कुछ अन्य उदाहरण निम्नलिखित हैं

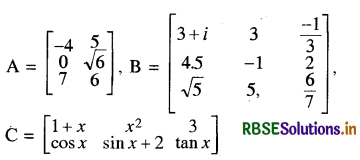
उपर्युक्त उदाहरणों में क्षैतिज रेखायें आव्यूह की पंक्तियाँ (Rows) और ऊर्ध्व रेखायें आव्यूह के स्तम्भ (Column) कहलाते हैं। इस प्रकार A में 3 पंक्तियाँ तथा 2 स्तम्भ हैं और B में 3 पंक्तियाँ तथा 3 स्तम्भ जबकि C में 2 पंक्तियाँ तथा 3 स्तम्भ हैं।
आव्यूह का संख्यात्मक मान नहीं होता है। यह तो केवल एक क्रम विन्यास है।

मैट्रिक्स का क्रम (Order of A Matrix):
m पंक्तियों तथा n स्तम्भों वाले किसी आव्यूह को m × n कोटि (order) का आव्यूह अथवा केवल m × n आव्यूह कहते हैं। अतएव आव्यूहों के उपर्युक्त उदाहरणों के संदर्भ में A, एक 3 × 2 आव्यूह, B एक 3 × 3 आव्यूह तथा C एक 2 × 3 आव्यूह है। हम यहाँ पर देखते हैं कि A में 3 × 2 = 6 अवयव और B तथा C में क्रमशः 9 तथा 6 अवयव हैं।

सामान्यतः किसी m × n आव्यूह का निम्नलिखित आयताकार क्रम-विन्यास होता है।

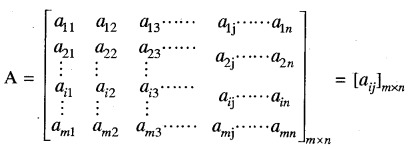
1 ≤ i ≤ m, 1 ≤ j ≤ n जहाँ i, j ∈ N

इसमें a₁₁ ah₁₂, ......... a_mn. आव्यूह के अवयव कहलाते हैं। इसमें m पंक्तियाँ व n स्तम्भ हैं। a₁₂, का अनुबन्ध 12 बताता है कि यह अवयव प्रथम पंक्ति तथा दूसरे स्तम्भ का है। a_ij का अनुबन्ध इस बात को इंगित करता है कि यह अवयव iवीं पंक्ति एवं jवें स्तम्भ का है। संक्षेप में इसे हम [a_ij]_m×n के रूप से प्रदर्शित करते हैं। m × n कोटि के प्रत्येक आव्यूह की प्रत्येक पंक्ति में n अवयव एवं प्रत्येक स्तम्भ में m अवयव होते हैं।

नोट

• मैट्रिक्स का क्रम लिखने में पहले पंक्तियों की संख्या तथा बाद में स्तम्भों की संख्या लिखी जाती है।
• आव्यूह के अवयव लिखते समय इसके मध्य ',' (comma) नहीं लगाते हैं।
• हम इस अध्याय में ऐसे आव्यूहों पर विचार करेंगे जिनके अवयव वास्तविक संख्याएँ हैं अथवा वास्तविक मानों को ग्रहण करने वाले फलन हैं।

 

मैट्रिक्स के विभिन्न प्रकार (Various Types of Matrix)
इस अनुच्छेद में हम विभिन्न प्रकार के आव्यूहों की परिचर्चा करेंगे
(1) पंक्ति मैट्रिक्स (Row Matrix) एक मैट्रिक्स, पंक्ति मैट्रिक्स कहलाता है, यदि उसमें केवल एक ही पंक्ति हो। उदाहरण के लिए
A = [a b c]_1×3
B = [\(\frac{-3}{2}\) √6 5 2]_1×4

(2) स्तम्भ मैट्रिक्स (Column Matrix):
एक मैट्रिक्स, स्तम्भ मैट्रिक्स कहलाता है, यदि उसमें केवल एक ही स्तम्भ हो।
उदाहरण के लिए
A = \(\left[\begin{array}{c} 0 \\ \sqrt{5} \\ -2 \\ 3 \end{array}\right]_{4 \times 1}\)

B = \(\left[\begin{array}{c} 0 \\ \sqrt{5} \\ -2 \\ 3 \end{array}\right]_{4 \times 1}\)

(3) वर्ग मैट्रिक्स (Square Matrix):
एक मैट्रिक्स जिसमें पंक्तियों की संख्या स्तम्भों की संख्या के समान होती है, एक वर्ग मैट्रिक्स कहलाता है। अतः एक m × n मैट्रिक्स, वर्ग मैट्रिक्स कहलाता है, यदि m = n और उसे कोटि 'n' का वर्ग मैट्रिक्स कहते हैं। उदाहरण के लिए
A = \(\left[\begin{array}{ccc} 1 & 2 & 3 \\ 3 & -2 & 1 \\ 4 & 2 & 1 \end{array}\right]_{3 \times 3}\)
एक 3 कोटि का वर्ग मैट्रिक्स है। व्यापक रूप से इसे A = [a_ij]_m×n से व्यक्त करते हैं। अवयव a₁₁, a₂₂, a₃₃ ......, a_nn अग्रग विकर्ण के अवयव कहलाते हैं । अग्रग विकर्ण के अवयवों का योग आव्यूह का अनुरेख (Trace of the Matrix) कहलाता है।

(4) शून्य मैट्रिक्स (Zero Matrix)
एक मैट्रिक्स, शून्य मैट्रिक्स अथवा रिक्त मैट्रिक्स कहलाता है यदि इसके सभी अवयव शून्य होते हों। इसे 0 से व्यक्त करते हैं। . उदाहरण के लिए
\(\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]\) = 0_2×3

\(\left[\begin{array}{ll} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array}\right]\) = 0_3×2

(5) विकर्ण मैट्रिक्स (Diagonal Matrix):
एक ऐसा वर्ग मैट्रिक्स जिसके अग्रग विकर्ण (Leading diagonal) या मुख्य-विकर्ण के अवयवों को छोड़कर शेष सभी अवयव शून्य हों, उसे विकर्ण मैट्रिक्स कहते हैं। उदाहरण के लिए
A = \(\left[\begin{array}{lll} 5 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 3 \end{array}\right]_{3 \times 3}\)

B = \(\left[\begin{array}{ll} 1 & 0 \\ 0 & 5 \end{array}\right]_{2 \times 2}\)

(6) इकाई मैट्रिक्स (Unit Matrix)
एक ऐसा विकर्ण मैट्रिक्स जिसके अन्तर्गत विकर्ण के सभी अवयव इकाई एक (1) के बराबर हों, उसे इकाई मैट्रिक्स कहते हैं। उदाहरण के लिए

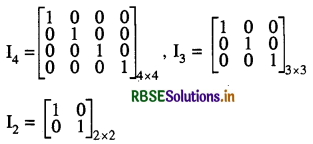
(7) अदिश मैट्रिक्स (Scalar Matrix):
ऐसा विकर्ण मैट्रिक्स जिसके अग्रग विकर्ण (मुख्य विकर्ण) के । सभी अवयव समान हों, अदिश मैट्रिक्स कहलाता है। उदाहरण के लिए
A = [5]_1×1,
B = \(\left[\begin{array}{cc} \sqrt{5} & 0 \\ 0 & \sqrt{5} \end{array}\right]_{2 \times 2}\)
C = \(\left[\begin{array}{lll} x & 0 & 0 \\ 0 & x & 0 \\ 0 & 0 & x \end{array}\right]_{3 \times 3}\)
क्रमशः कोटि 1, 2 तथा 3 के अदिश मैट्रिक्स हैं।

टिप्पणी
प्रत्येक अदिश मैट्रिक्स विकर्ण मैट्रिक्स है तथा प्रत्येक इकाई मैट्रिक्स विकर्ण मैट्रिक्स तथा अदिश मैट्रिक्स है। परन्तु प्रत्येक विकर्ण मैट्रिक्स तथा अदिश मैट्रिक्स इकाई मैट्रिक्स नहीं है।

(8) त्रिभुजाकार मैट्रिक्स (Triangular Matrix):
(a) ऊपरी त्रिभुजाकार मैट्रिक्स (Upper Triangular Matrix)-ऐसा वर्ग मैट्रिक्स A = [a_ij]_m×n, जिसमें a_ij = 0 जबकि i > j, अर्थात् अग्रग विकर्ण के नीचे के सभी अवयव शून्य हों, ऊपरी त्रिभुजाकार मैट्रिक्स कहलाती है। उदाहरण के लिए

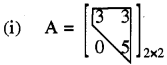
यह एक 2 × 2 क्रम की ऊपरी त्रिभुजाकार मैट्रिक्स है।

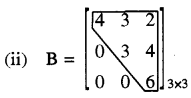
यह एक 3 × 3 क्रम की ऊपरी त्रिभुजाकार मैट्रिक्स है।

(b) निम्न त्रिभुजाकार मैट्रिक्स (Lower Triangular Matrix)-ऐसा वर्ग मैट्रिक्स A = [a_ij]_m×n जिसमें a_ij = 0 जबकि i < j अर्थात् अग्रग विकर्ण के ऊपर के सभी अवयव शून्य हों, निम्न त्रिभुजाकार मैट्रिक्स कहलाती है। उदाहरण के लिए

यह एक 2 × 2 क्रम की निम्न यह एक 3 × 3 क्रम की निम्न त्रिभुजाकार मैट्रिक्स है। त्रिभुजाकार मैट्रिक्स है।

टिप्पणी-विकर्ण मैट्रिक्स ऊपरी तथा निम्न त्रिभुजाकार दोनों मैट्रिक्स होती हैं। क्योंकि मुख्य विकर्ण के नीचे तथा ऊपर वाले अवयव शून्य होते हैं।

आव्यूहों की समानता (Equality of Matrices)
दो आव्यूह A = [a_ij] तथा B = [b_ij] समान कहलाते हैं, यदि
(i) वे समान कोटियों के हों, तथा
(ii) A का प्रत्येक अवयव, B के संगत अवयव के समान हो, अर्थात् i तथा j के सभी मानों के लिए a_ij = b_ij हों।
उदाहरण के लिए
\(\left[\begin{array}{ll} 5 & 3 \\ 0 & 2 \end{array}\right] \)तथा \(\left[\begin{array}{ll} 5 & 3 \\ 0 & 2 \end{array}\right]\)
समान आव्यूह हैं किन्तु \(\left[\begin{array}{ll} 3 & 5 \\ 0 & 2 \end{array}\right]\) तथा \(\left[\begin{array}{ll} 5 & 3 \\ 0 & 2 \end{array}\right]\) समान आव्यूह नहीं हैं। प्रतीकात्मक रूप में, यदि दो आव्यूह A तथा B समान हैं, तो हम इसे A = B लिखते हैं।

आव्यूहों का योग (Addition of Matrices):
जब दो आव्यूह A = [a_ij] तथा B = [b_ij] समान क्रम m × n के हों, तो उनके योग का आव्यूह उनके संगत अवयवों का योग करने पर प्राप्त होता है, जिसे A + B से प्रदर्शित किया जाता है तथा इस प्रकार प्राप्त आव्यूह का क्रम भी m xn ही होता है। अतः यदि A = [a_ij]_m×n तथा B = [b_ij]_m×n हों, तो इनके योग को निम्न प्रकार परिभाषित किया जाता है, अर्थात्
A + B = [a_ij]_m×n + [b_ij]_m×n
= [a_ij + b_ij]_m×n
या A + B = [c_ij]_m×n
जहाँ पर [c_ij] = [a_ij + b_ij]

उदाहरणार्थ-यदि A = \(\left[\begin{array}{lll} -2 & 5 & 7 \\ -4 & 2 & 3 \end{array}\right]\) तब A + B = \(\left[\begin{array}{ccc} 6 & -10 & -8 \\ 5 & 3 & 4 \end{array}\right]\)

टिप्पणी
दो असमान क्रम भी आव्यूहों का योग अपरिभाषित है। अतः एक ही क्रम के आव्यूहों को जोड़ सकते हैं। अर्थात् आव्यूहों का योग ज्ञात करने के लिए उनका क्रम समान होना आवश्यक है। दो आव्यूहों का योग एक द्विचर संक्रिया (Binary Operation) होती है।
दो आव्यूहों का व्यवकलन-जब दो आव्यूह A तथा B समान क्रम के हों तो इनका व्यवकलन A-B से निरूपित होता है तथा इसे A के अवयवों में से B के संगत अवयवों को व्यवकलन कर प्राप्त करते हैं। A-B का क्रम वही होता है जो क्रम A व B का होता है।

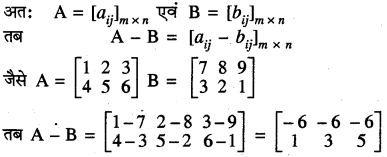
आव्यूह योग के गुणधर्म (Properties of Matrix Addition)
आव्यूह में योग संक्रिया निम्न गुणधर्मों का पालन करती है

• क्रम विनिमेयता (Commutativity) : A + B = B + A.
• साहचर्यता (Associativity) : A + (B + C) = (A + B) + C
• योज्य तत्समक आव्यूह (Additive Identity Matrix) शून्य आव्यूह O योज्य तत्समक आव्यूह कहलाती है क्योंकि A + O = A = O + A
• योज्य प्रतिलोम आव्यूह (Additive Inverse) : मैट्रिक्स । A का योज्य प्रतिलोम (-A) होता है अतः
  A + (-A) = 0 = (-A) + A
• निरसन नियम (Cancellation Law) यदि A, B तथा C तीनों आव्यूह योग के लिए अनुकूलनीय हों, अर्थात् तीनों ही आव्यूह समान क्रम के हों तो
  A + B = A + C = B = C (वाम निरसन नियम)
  B + A =C + A = B = C (दक्षिण निरसन नियम)

Note : दो आव्यूहों का व्यवकलन क्रमविनिमेय एवं साहचर्य नहीं होता।

आव्यूह का अदिश से गुणा (Multiplication of Matrix By A Scalar):
यदि A = [a_ij]_m×n क्रम का एक आव्यूह है तथा k एक अदिश है तो इनके गुणनफल को हम kA से प्रदर्शित करते हैं, जो अदिश k से A के प्रत्येक अवयव को गुणा करने पर प्राप्त होता है। अर्थात् KA = [ka_ij]_m×n

उदाहरणार्थ

आव्यूह का ऋण आव्यूह (Negative of a Matrix)
किसी आव्यूह A का ऋण आव्यूह -A से निरूपित होता है। हम -A को -A = (-1) A द्वारा परिभाषित करते हैं। उदाहरणार्थ-यदि आव्यूह A = \(\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\), तो -A को हम निम्न प्रकार से प्राप्त कर सकते हैं
-A = (-1)A = (-1)\(\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]=\left[\begin{array}{ll} -a & -b \\ -c & -d \end{array}\right]\)

एक आव्यूह के अदिश गुणन के गुणधर्म | (Properties of Scalar Multiplication of A Matrix):
यदि A = [a_ij] तथा B = [b_ij] समान कोटि m x n वाले दो आव्यूह हों तो इनके योग में अदिश गुणनफल बंटन नियम का पालन करता है अर्थात् यदि k कोई स्वेच्छ अदिश है, तो
(A + B) = kA + kB

यदि k तथा । अदिश हो तथा A = [a_ij]_m×n , आव्यूह हो, तो
(k + l)A = KA + lA

प्रमाण
(i) माना कि A = [a_ij]_m×n, तथा B = [b_ij]_m×n
A + B = [a_ij + b_ij]_m×n
k (A + B) = k[a_ij + b_ij]_m×n
= [ka_ij + kb_ij]_m×n
= [ka_ij]_m×n + [kb_ij]_m×n
= k[a_ij]_m×n + k[b_ij]_m×n
= ka + kb
अत: k(A + B) = KA + kB

(ii) यदि A = [a_ij]_m×n तथा k और l अदिश हैं तब
(k + D) A = (k + D) [a_ij]_m×n
= [(k + 1) a_ij]_m×n
= [ka_ij]_m×n+ [l_ij]_m×n
= k[a_ij]_m×n + l[a_ij]_m×n
=KA + IA
अत: (k + D) A = KA + IA

आव्यूहों का गुणा (Multiplication Of Matrices)
हम आव्यूहों के गुणन को निम्नलिखित तरह से परिभाषित करते हैं दो आव्यूहों A तथा B का गुणनफल परिभाषित होता है, यदि A में स्तम्भों की संख्या, B में पंक्तियों की संख्या के समान होती है। मान लीजिये कि A = [a_ij] एक m × n कोटि का आव्यूह है और B = [b_ij] एक n × p कोटि का आव्यूह है तब आव्यूहों A तथा B का गुणनफल एक m × p कोटि का आव्यूह C होता है। आव्यूह C का (i,k) वाँ अवयव C. प्राप्त करने के लिए हम A की वीं पंक्ति और B के वें स्तम्भ को लेते हैं और फिर उनके अवयवों का क्रमानुसार गुणन करते हैं। उसके बाद इन सभी गुणनफलों का योगफल ज्ञात कर लेते हैं।
यदि A = [a_ij]_m×n, B = [b_ij]_n×p

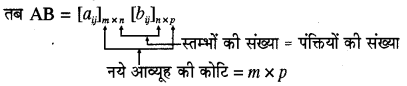
उदाहरण के लिए

तो AB जात ज्ञात कीजिये।
हल:

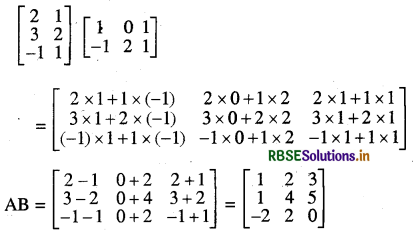
टिप्पणी

• आव्यूह गुणन AB में आव्यूह A को पूर्व पद तथा आव्यूह B को उत्तर पद कहते हैं।
• यदि आव्यूह A व B में गुणनफल AB व BA दोनों अनुकूलनीय हों तो भी यह आवश्यक नहीं है कि AB = BA हो। आव्यूह AB सामान्यतया आव्यूह BA से भिन्न होते हैं।
• यदि AB परिभाषित है तो यह आवश्यक नहीं कि BA भी परिभाषित हो।
• यदि A और B दोनों ही समान कोटि के वर्ग आव्यूह हैं, तो AB तथा BA दोनों परिभाषित होते हैं।

आव्यूह गुणन के गुणधर्म (Properties Of Matrix Multiplication):
(i) क्रम विनिमेयता (Commutativity):
सामान्यतः आव्यूह गुणन क्रम विनिमेय नियम का पालन नहीं करता है अर्थात् AB ≠ BA

Note:
समान कोटि के विकर्ण आव्यूह का गुणन क्रम विनिमेय होता है। जैसे A = \(\left[\begin{array}{ll} 1 & 0 \\ 0 & 2 \end{array}\right]\) B = \(\left[\begin{array}{ll} 3 & 0 \\ 0 & 4 \end{array}\right]\) तो AB = BA = \(\left[\begin{array}{ll} 3 & 0 \\ 0 & 8 \end{array}\right]\)

(ii) साहचर्यता (Associativity):
यदि आव्यूह A, B तथा C इस प्रकार हैं कि उनके निम्न गुणनफल परिभाषित हों तो
(AB) C = A(BC)

(iii) बंटनता (Distributivity)
आव्यूहों का गुणा योग के सापेक्ष बंटन नियम का पालन करता है, जैसे

• AB + C) = AB + AC [बायां बंटन नियम]
• (A + B)C = AC + BC [दायां बंटन नियम]

जबकि आव्यूह A, B तथा C इस प्रकार हों कि प्रयुक्त सभी गुणा सम्भव हो।

(iv) गुणन तत्समक अवयव (Multiplicative Identity Element):
आव्यूह गुणन में इकाई आव्यूह ही गुणन तत्समक अवयव कहलाता है।
अर्थात् AI_n = I_nA = A

(v) शून्य भाजक (Zero divisors)
यदि दो अशून्य आव्यूह A तथा B का गुणा एक शून्य आव्यूह हो तो A तथा B शून्य भाजक कहलाते हैं।

उदाहरणार्थ

नोट:

• दो वास्तविक संख्याओं a तथा b के लिए, यदि ab = 0 है तो या तो a = 0 या b = 0 या दोनों 0 होते हैं किन्तु आव्यूहों के लिए यह अनिवार्यतः सत्य नहीं होता। यह उपर्युक्त उदाहरण से स्पष्ट
• दो विकर्ण आव्यूहों का गुणनफल भी एक विकर्ण आव्यूह होता है
  तथा diag (a₁, a₂, .... a_n) x diag (b₁ b₂, b₃ .... b_n) = diag (a₁b₁ a₂b₂ a₃b₃ .... a_nb_n)
• दो अदिश आव्यूहों का गुणन भी अदिश आव्यूह होता है।
• दो त्रिभुजाकार आव्यूहों का गुणन भी एक त्रिभुजाकार आव्यूह । होता है।
• A² = A . A, A³ = AAA = A²A
  इसी प्रकार Aⁿ = AA .... A (n बार)
• A^m Aⁿ = A^m+n
• (A^m)ⁿ = A^mn = (Aⁿ)^m
• I^m = I
• यदि A एक n कोटि का आव्यूह है तो A° = I
• (A + B)² = A² + B² + AB + BA
• (A - B)² = A² + B² - AB - BA
• (A + B) (A - B) = A² - B² - AB + BA
• (A - B) (A + B) = A² - B² + AB - BA
• यदि A = diag (λ₁, λ₂ ........λ_n)
  = A = diag(λ₁ⁿ, λ₂ⁿ ........λ_nⁿ), ∀ n ∈ N

आव्यूह का परिवर्त (Transpose of A Matrix):
यदि किसी आव्यूह A की पंक्तियों और स्तम्भों को परस्पर बदल दिया जाये तो इस प्रकार प्राप्त नई आव्यूह को मूल आव्यूह A की परिवर्त आव्यूह कहते हैं और इसे A' या A^T से निरूपित करते हैं,
अर्थात् A^T = [a_ij]_m×n जहाँ A = [a_ij]_m×n

उदाहरणार्थ

आव्यूहों के परिवर्त के गुणधर्म (Properties of Transpose of Matrices)
यदि A और B दो ऐसे क्रम के आव्यूह हैं, जिनका योग और गुणा सम्भव हो तो

• (A^T)^T = A
• (kA)^T = kA^T जहाँ k कोई अचर है।
• (A + B)^T = A^T + B^T
• (AB)^T = B^TA^T
• (A₁A₂......A_n)^T = A_n^T ..... A ^TA,^T
• (Aⁿ)^T = (A^T)ⁿ, n ∈ N

सममित तथा विषम सममित आव्यूह (Symmetric and Skew Symmetric Matrix)
सममित आव्यूह (Symmetric Matrix)
एक वर्ग मैट्रिक्स A, सममित मैट्रिक्स कहलाती है यदि और केवल यदि

• A' = A, जहाँ A', A की परिवर्त मैट्रिक्स है। या
• a_ij = a_ji ∀ i, j

उदाहरणार्थ
\(\left[\begin{array}{cc} 6 & -7 \\ -7 & 8 \end{array}\right]\) तथा \(\left[\begin{array}{lll} a & h & g \\ h & b & f \\ g & f & c \end{array}\right]\)
क्रमशः 2 × 2 व 3 × 3 की सममित मैट्रिक्स है।

टिप्पणी:
AA' तथा A A सममित मैट्रिक्स होती है।

विषम सममित मैट्रिक्स (Skew Symmetric Matrix):
एक वर्ग मैट्रिक्स A, विषम सममित मैट्रिक्स कहलाती है, यदि और केवल यदि

• A' = - A या
• a_ij = -a_ij जब i ≠ j
  = 0 जब i = j

उदाहरणार्थ
\(\left[\begin{array}{cc} 0 & -5 \\ 5 & 0 \end{array}\right]\) तथा \(\left[\begin{array}{ccc} o & h & g \\ -h & o & f \\ -g & -f & o \end{array}\right]\)
क्रमशः 2 × 2 व 3 × 3 क्रम की विषम सममित मैट्रिक्स है।

टिप्पणी
विषम सममित मैट्रिक्स के अग्रग विकर्ण के सभी अवयव शून्य होते हैं।

प्रमेय-1.
वास्तविक अवयवों वाले किसी वर्ग आव्यूह A के लिए A + A' एक सममित आव्यूह तथा A - A' एक विषम सममित आव्यूह होते हैं।
उपपत्ति-माना कि B = A + A' तब
B' = (A + A) = A' + (A')' [∵ (A + B)' = A' + B']
= A' + A [∵ (A') = A]
= A + A' [∵ A + B = B + A]
= B
B = A + A' एक सममित आव्यूह है। अब माना कि
C = A - A' C' = (A - A') = A' – (A)' [∵ (A - B) = A' = B']
C' = A' - A [:: (A') = A]
C' = - (A - A)
= - C [∵ A - A' = C]
अतः C = A - A'
एक विषम सममित आव्यूह है।

प्रमेय-2.
किसी वर्ग आव्यूह को एक सममित तथा एक विषम सममित आव्यूहों के योगफल के रूप में व्यक्त किया जा सकता है।
उपपत्ति
माना कि A एक वर्ग आव्यूह है। हम इसको निम्न प्रकार लिख सकते हैं
A = \(\frac{1}{2}\) (A + A') + \(\frac{1}{2}\) (A - A')
प्रमेय 1 के अनुसार (A + A') एक सममित आव्यूह और (A - A) एक विषम आव्यूह है।
∵ किसी आव्यूह A के लिए, (KA) = kA' होता है।
अतः इससे निष्कर्ष निकलता है कि \(\frac{1}{2}\)(A + A') सममित आव्यूह तथा \(\frac{1}{2}\)(A - A') विषम सममित आव्यूह है। अतः किसी वर्ग आव्यूह को एक सममित तथा एक विषम सममित आव्यूहों के योगफल के रूप में व्यक्त किया जा सकता है।

उदाहरणार्थ
आव्यूह A = \(\left[\begin{array}{ccc} 1 & 1 & -1 \\ 2 & 0 & 3 \\ 3 & -1 & 2 \end{array}\right]\) को एक सममित आव्यूह तथा एक विषम सममित आव्यूह के योगफल के रूप में व्यक्त कीजिये।
हल:
यहाँ पर A' = \(\left[\begin{array}{ccc} 1 & 2 & 3 \\ 1 & 0 & -1 \\ -1 & 3 & 2 \end{array}\right]\) मान लीजिये

अतः P = \(\frac{1}{2}\) (A + A') एक सममित आव्यूह है। अब मान लीजिये

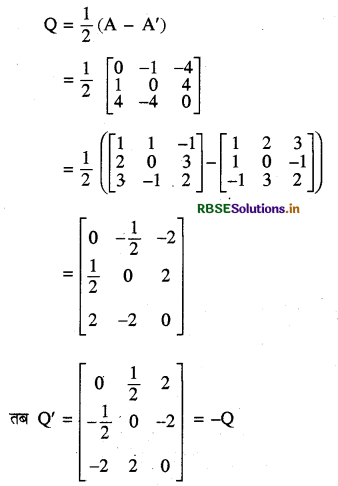
अतः Q = \(\frac{1}{2}\) (A - A') एक विषम सममित आव्यूह है।

अतः आव्यूह A एक सममित आव्यूह तथा एक विषम सममित आव्यूह के योगफल के रूप में व्यक्त किया गया है।

Note

• यदि A एक सममित आव्यूह है तो Aⁿ भी एक सममित आव्यूह है।
• यदि A एक सममित आव्यूह है तो KA भी एक सममित आव्यूह है।
• यदि A एक विषम सममित आव्यूह है तो Aⁿ एक सममित आव्यूह होगा तथा A²ⁿ⁺¹ एक विषम सममित आव्यूह होगा।
• A और B दो सममित आव्यूह है तो A + B, A - B, AB + BA भी सममित आव्यूह होंगे।

आव्यूह पर प्रारम्भिक संक्रिया (आव्यूह रूपांतरण) [Elementary Operation (Transformation) of A Matrix]:
किसी आव्यूह पर छः प्रकार की संक्रियायें (रूपान्तरण) की जाती हैं, जिनमें से तीन पंक्तियों तथा तीन स्तम्भों पर होती हैं, जिन्हें प्रारम्भिक संक्रियायें या रूपान्तरण कहते हैं। यदि यह रूपान्तरण पंक्तियों पर किया जाये तो पंक्ति रूपान्तरण कहलाता है और यदि यह रूपान्तरण स्तम्भों पर किया जाये तो स्तम्भ रूपान्तरण कहलाता है। हम मैट्रिक्स के प्रारम्भिक रूपान्तरण में निम्न संक्षिप्त संकेत काम में लेंगे
(i) R_i ↔ R_j, i वीं पंक्ति एवं 5 वीं पंक्ति के विनिमेय को व्यक्त करता है। इसी प्रकार C_i ↔ C_j वें तथा j वें स्तम्भों के विनिमेय को व्यक्त करता है।

(ii) i वीं पंक्ति के प्रत्येक अवयव को k, जहाँ k ≠ 0 से गुणा करने को R_i → kR_j द्वारा निरूपित करते हैं। इसी प्रकार 1 वें स्तम्भ के प्रत्येक अवयव को k, जहाँ k ≠ 0 से गुणा करने को C₂ → kC₂, द्वारा निरूपित करते हैं। जैसे A = \(\left[\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right]\) पर C₂ → \(\frac{1}{2}\)C₂, करने पर \(\left[\begin{array}{ll} 1 & 1 \\ 3 & 2 \end{array}\right]\) प्राप्त होगा।

(iii) i वीं पंक्ति के अवयवों में j, वीं पंक्ति के संगत अवयवों को k से गुणा करके जोड़ने को R_i → R_i + kR_j, से निरूपित करते हैं। इसी प्रकार स्तम्भ संक्रिया को C_i,→C_i, + kC_j से निरूपित करते हैं। जैसे A = \(\left[\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right]\) पर R₂ → R₂ - 2R₁, प्रयोग करने पर \(\left[\begin{array}{ll} 1 & 1 \\ 3 & 2 \end{array}\right]\) प्राप्त होता है।

इसी प्रकार A = \(\left[\begin{array}{ccc} 1 & 1 & 1 \\ 2 & 5 & 7 \\ 2 & 1 & -1 \end{array}\right]\) पर R₂ → R₂ - 2R₁, का प्रयोग करने पर हमें आव्यूह \(\left[\begin{array}{ccc} 1 & 1 & 1 \\ 0 & 3 & 5 \\ 2 & 1 & -1 \end{array}\right]\) प्राप्त होता है।

व्युत्क्रमणीय आव्यूह ( Invertible Matrices):
परिभाषा
यदि A, कोटि m का एक वर्ग आव्यूह है और यदि एक अन्य वर्ग आव्यूह का अस्तित्व इस प्रकार है, कि AB = BA = I, तो B को आव्यूह A का व्युत्क्रम आव्यूह कहते हैं और इसे A-1 द्वारा निरूपित करते हैं। ऐसी दशा में आव्यूह A व्युत्क्रमणीय कहलाता है।
उदाहरण के लिए, माना A = \(\left[\begin{array}{ll} 2 & 3 \\ 1 & 2 \end{array}\right]\) तथा B = \(\left[\begin{array}{cc} 2 & -3 \\ -1 & 2 \end{array}\right]\) दो आव्यूह हैं।

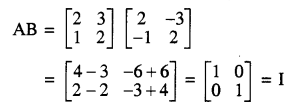
और साथ ही BA = \(\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\) = I है अत: B आव्यूह, A का व्युत्क्रम है।
दूसरे शब्दों में, B = A^-1 तथा A आव्यूह B का व्युत्क्रम है,
अर्थात्
A = B^-1

टिप्पणी

• किसी आयताकार (Rectangular) आव्यूह का व्युत्क्रम आव्यूह नहीं होता है, क्योंकि गुणनफल AB तथा BA के परिभाषित होने और समान होने के लिए, यह अनिवार्य है कि A तथा B समान कोटि के वर्ग आव्यूह हों।
• यदि B, आव्यूह A का व्युत्क्रम है, तो A, आव्यूह B का व्युत्क्रम होता है।
• (A^-1)^-1 = A
• (A^T)^-1 = (A^-1)T
• (Aⁿ)^-1 = (A^-1)n
• adj (A^-1) = (adjA)^-1
• (A^-1) = A
• A = deag (a₁ a₂ ..... a_n)
  = A^-1 = deag (a₁^-1 a₂^-1 ..... a_n^-1)
• यदि A एक सममित आव्यूह है तो A^-1 भी सममित आव्यूह होगा। यदि A एक विकर्ण आव्यूह है तो A^-1 भी विकर्ण आव्यूह होगा। यदि A एक अदिश आव्यूह है तो A^-1 भी एक अदिश आव्यूह होगा।
• यदि A एक त्रिभुजाकार आव्यूह है तो A^-1 भी एक त्रिभुजाकार आव्यूह होगा।
• AB = AC ⇔ B = C ⇔ A ≠ 0

प्रमेय-3. [व्युत्क्रम आव्यूह की अद्वितीयता (Uniqueness of Inverse)]
किसी वर्ग आव्यूह का व्युत्क्रम आव्यूह, यदि उसका अस्तित्व है तो अद्वितीय होता है।
उपपत्ति-माना कि A = [a] कोटि m का, एक वर्ग आव्यूह है। यदि सम्भव हो, तो माना कि B तथा C आव्यूह A के दो व्युत्क्रम आव्यूह हैं, अब हम दिखायेंगे कि B = C है
∵ आव्यूह A का व्युत्क्रम B है।
∵ AB = BA = I ......(1)
∵ आव्यूह A का व्युत्क्रम C भी है।
∵AC = CA = I ........ (2)
अब B = BI = B(AC) = (BA)C = IC = C

प्रमेय-4.
यदि A तथा B समान कोटि के व्युत्क्रमणीय आव्यूह हों तो (AB)^-1 = B^-1A^-1
उपपत्ति
एक व्युत्क्रमणीय आव्यूह की परिभाषा से हम इस प्रकर से लिख सकते हैं
(AB)(AB)^-1 = I
या A^-1 (AB) (AB)^-1 = A^-1I
[A^-1 का दोनों पक्षों से पूर्वगुणन करने पर
या (A^-1A) B (AB)^-1 = A^-1 (∵ A^-1I = A^-1)
IB (AB)^-1 = A^-1(∵ A^-1A = I)
या B(AB)^-1 = A^-1
(∵ IB = B)
B^-1B (AB)^-1 = B^-1A^-1
B^-1 का दोनों पक्षों से पूर्वगुणन करने पर] या I(AB)^-1 = B^-1A^-1 (∵ B^-1B = I)
अतः (AB)^-1 = B^-1A^-1

प्रारम्भिक संक्रियाओं द्वारा एक आव्यूह का व्युत्क्रम (Inverse of A Matrix By Elementary Operations):
यदि हमें आव्यूह A का प्रारम्भिक रूपांतरण से व्युत्क्रम (inverse) निकालना हो तो हमें निम्न विधि का पालन करना चाहिए :
1. A को निम्न प्रकार लिखियेपंक्ति रूपान्तरण के लिए A = IA स्तम्भ रूपान्तरण के लिए A = AI

2. अब इस समीकरण में वाम पक्ष में केवल A पर और दक्षिण पक्ष में पूर्व (या उत्तर) गुणज I पर प्रारम्भिक पंक्ति (या स्तम्भ) रूपांतरण तब तक करते रहना चाहिए जब तक कि वाम पक्ष में मैट्रिक्स A, I में परिवर्तित न हो जाए। यदि इस प्रकार दक्षिण पक्ष में I, B में परिवर्तित हो जाता है, तो अब समीकरण का निम्न रूप
होगा
I = BA (या I = AB)

3. मैट्रिक्स B, मैट्रिक्स A का अभीष्ट व्युत्क्रम है। टिप्पणी-उस दशा में जब A = IA (A = AI) पर एक या अधिक प्रारम्भिक पंक्ति (स्तम्भ) संक्रियाओं के करने पर यदि बायें पक्ष के आव्यूह A की एक या अधिक पंक्तियों के सभी अवयव शून्य हो जाते हैं तो A^-1 का अस्तित्व नहीं होता है।

→ फलनों या संख्याओं का एक आयताकार क्रम विन्यास, आव्यूह कहलाता है।

→ m पंक्तियों एवं n स्तम्भों वाले आव्यूह को m × n कोटि का आव्यूह कहते हैं।
A_m×n = A = [a_ij]_m×n

→ यदि किसी आव्यूह में एक ही पंक्ति हो तो उसे पंक्ति आव्यूह कहते हैं।

→ यदि किसी आव्यूह में एक ही स्तम्भ हो तो उसे स्तम्भ आव्यूह कहते हैं।

→ यदि किसी आव्यूह में सभी अवयव शून्य हो तो उसे शून्य आव्यूह कहते हैं।

→ यदि किसी आव्यूह में पंक्तियों एवं स्तम्भों की संख्या समान हो तो उसे वर्ग आव्यूह कहते हैं।

→ यदि किसी वर्ग आव्यूह के अग्रग विकर्ण के सभी अवयव एक (1) हो तथा अन्य सभी अवयव शून्य हो, इकाई या तत्समक आव्यूह कहते हैं।

→ दो आव्यूहों का योग एवं व्यवकलन तभी होगा जब दोनों आव्यूह एक ही क्रम में हों।

→ दो आव्यूहों का गुणन तभी होगा जब प्रथम आव्यूह में स्तम्भों की संख्या द्वितीय आव्यूह में पंक्तियों की संख्या के बराबर हो।

→ KA = k [a_ij] = [k (a_ij)], जहाँ k अचर है।

→ - A = (-1) A

→ A - B = A + (-B)

→ A + B = B + A

→ (A + B) + C = A + (B + C), जहाँ A, B तथा C समान कोटि के आव्यूह हैं।

→ k (A + B) = KA + kB, जहाँ k अचर है।

→ (k + 1) A = kA + IA, जहाँ k व । अचर हैं।

→ यदि A = [a_ij]_m×n तथा B = [b_jk]_n×p, तो AB = C = [C_ik]_m×p , जहाँ c_ik = \(\sum_{j=1}^n\)a_ijb_jk

→ A (BC) = (AB)C

→ A (B + C) = AB + AC

→ (A + B) C = AC + BC

→ यदि A = [a_ij]_m×n, तो A' या A^T = [a_ji]_n×m

→ (A') = A

→ (KA) = KA'

→ (A ± B) = A' ± B'

→ (AB)' = B'A'

→ यदि A' = A तो A एक सममित आव्यूह है।

→ यदि A' = - A है तो A एक विषम सममित आव्यूह है।

→ किसी भी वर्ग आव्यूह को एक सममित एवं एक विषम सममित आव्यूह के रूप में निरूपति किया जा सकता है।

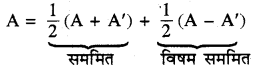
→ आव्यूहों पर प्रारम्भिक संक्रियाएँ निम्नलिखित हैं

• R_i ↔ R_j या C, ↔ C_j
• R_i → KR_i या C_i → KC_i
• R_i → R_i + kR_j या C_i → C_i + KC_j

→ यदि A तथा B दो वर्ग आव्यूह हैं, इस प्रकार AB = BA = I, तो A का व्युत्क्रम आव्यूह B है जिसे A^-1 द्वारा निरूपित करते हैं आव्यूह B का व्युत्क्रम A है।