RBSE Class 12 Maths Notes Chapter 3 Matrices

These comprehensive RBSE Class 12 Maths Notes Chapter 3 Matrices will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 3 Notes Matrices

Introduction:
The term 'matrix' (Latin for 'Womb', derived from Mater - Mother) was coined by James Joseph Sylverter in 1850, who understood a matrix as an object giving rise to a number of determinant today called minor.'
In 1857, Arthus Cayley develped the properties of matrices as a pure algebraic structure. The knowledge of matrices is necessary in various branches of mathematics. Matrices are not only used as a representation of the coefficients in system of linear equations, but utility of matrices far exceeds that use.

Matrix notation and operations are used in electronic spreadsheet programs for personal computer, which in turn is used in different areas of business and science like budgeting, sales projection, cost estimation, analysing the results of an experiment etc. Also, many physical operations such as magnification, rotation and reflection through a plane can be represented mathematically by matrices. Matrices are also used in cryptography. This mathematical tool is not only used in certain branches of sciences, but also in genetics, economics, sociology, modem psychology and industrial management. In this present chapter, we shall learn about matrices and shall confine ourselves to the study of basic laws of matrix algebra.

Definition and Notation:
A matrix is an ordered rectangular array of numbers or functions. The members or functions are called the elements or the entries of the matrix. The elements can be real numbers, complex numbers, polynomials or even more general functions.

 

Notation of a Matrix
Generally, we denote matrix by capital letters A, B, C, X, Y, Z, ..................... and elements or entries by small letters with numbers in suffix.
The elements of the matrix are written within the symbols [ ] or () or ∥ ∥.

The following are some examples of matrices:

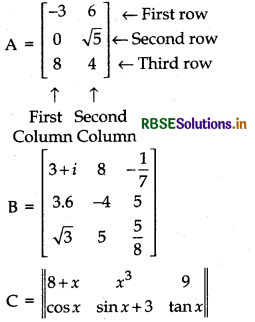
In the above examples, the horizontal lines of elements are said to constitute, rows of the matrix and the vertical lines of elements are said to constitute, columns of the matrix, Thus, A has 3 rows and 2 columns, B has 3 rows and 3 columns while C has 2 rows and 3 columns.

Order of A Matrix:
A matrix having m rows and n columns is called a matrix of order m × n or simply m × n matrix (read as m by n matrix).

A set of mn numbers (real or imaginary) arranged in the form of a rectangular array of m rows and n columns is called m × n matrix.
A_{m × n} matrix is usually written as

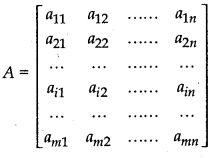
In compact form the above matrix is represented by
A = [a_ij]_{m × n} or A = [a_ij].
a₁₁, a₂₂, ........... a_mn are known as the elements of the matrix A. The element a_ij belongs to i_th row and j_th column and is called the (i, j)_th element of the matrix A. Thus, in the element a- the first subscript i always denoted the number of row and the second subscript j, number of column in which the element occurs.

For example (i):
\(\left[\begin{array}{ccc} 2 & -3 & 11 \\ 3 & 7 & 9 \end{array}\right]\) is a matrix having 2 rows and 3 columns. So, its a matrix of order 2 × 3
\(\left[\begin{array}{cccc} 15 & 7 & 70 & 25 \\ 16 & 6 & 55 & 24 \\ 10 & 13 & 31 & 11 \end{array}\right]\) is a matrix having 3 rows and 4 columns. So, its a matrix of order 3 × 4
\(\left[\begin{array}{rrr} i & 3 & -1 \\ 7 & -1 & 3 \\ 5 & 10 & 3 \end{array}\right]\) is a matrix having 3 rows and 3 columns. So, its a matrix of order 3 × 3

(ii) Construct a 3 × 3 matrix A = [a_ij], whose elements are given by : a_ij = i² + j²
Answer:
We can write A = [a_ij]_{3 × 3} as
Here a_ij = i² + j²
Now, a₁₁ = 1² + 1² = 2
a₁₂ = 1² + 2² = 5
a₁₃ = 1² + 3² = 10
a₂₁ = 2² + 1² = 5
a₂₂ = 2² + 2² = 8
a₂₃ = 2² + 3² = 13
a₃₁ = 3² + 1² = 10
a₃₂ = 3² + 2² = 13
a₃₃ = 3² + 3² = 18

Now, putting a₁₁, a₂₁, .................. a₃₃ in matrix A
A = \(\left[\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{22} \end{array}\right]=\left[\begin{array}{ccc} 2 & 5 & 10 \\ 5 & 8 & 13 \\ 10 & 13 & 18 \end{array}\right]\)

Note:

• We shall follow the notation, namely A = [a_ij]_{m × n} to indicate that A is a matrix of order m × n.
• We shall consider only those matrices whose elements are real numbers or functions taking real values.

Types of Matrices:
Here, we shall discuss different types of matrices.
1. Rectangular Matrix : A matrix in which number of rows are not equal to number of columns, is called rectangular matrix.
There are two types of rectangular matrix :
(i) Horizontal Matrix : A matrix in which number of columns are greater than number of rows is called horizontal matrix.

Example: \(\left[\begin{array}{ccc} 3 & 7 & 8 \\ 9 & 10 & 15 \end{array}\right]\)
Here, number of columns = 3 and number of rows = 2

(ii) Vertical Matrix : A matrix in which number of rows are greater than number of columns, is called vertical matrix.
Example: \(\left[\begin{array}{lll} a & b & c \\ e & f & g \\ l & m & n \\ q & r & s \end{array}\right]\)
Here, number of rows = 4 and number of columns = 3

2. Square Matrix : A matrix in which the number of rows are equal to the number of columns, is said to be square matrix. Thus, m x n matrix is said to be a square matrix where m = n and is known as a square matrix of order V.
Example: \(\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\) is square matrix of order 2 × 2
\(\left[\begin{array}{lll} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{array}\right]\) is square matrix of order 3 × 3

3. Diagonal Matrix :
A, square matrix A = [a_ij]_{m × n} is called a diagonal matrix, if all the elements excepts those in the leading diagonal, are zero, i.e., a_ij = 0 for all i ≠ j. A diagonal matrix of order n × n having d₁, d₂, ................ d_n as diagonal element is denoted by
diag [d₁, d₂, ...................... d_n]
Example: \(\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{array}\right]\) is a diagonal matrix, to be denoted by
A = diag [1,2,3]

4. Row Matrix:
A matrix having only one row is called a row matrix.
Example: A = [-\(\frac{1}{2}\) √5 2 3]_1×4 is a row matrix of order 1 × 4.

5. Column Matrix:
A matrix having only one column is called column matrix.
A = \(\left[\begin{array}{l} 3 \\ 7 \\ 8 \end{array}\right]\) is a column matrix of order 3 × 1

6. Scalar Matrix:
A diagonal matrix is said to be a scalar matrix if its diagonal elements are equal, that is, a square matrix A = [a_ij]_{m × n} is called a scalar matrix if

• a_ij = 0 for all i ≠ j and
• a_ij = c for all i = j, where c ≠ 0

are scalar matrices of order 1,2 and 3 respectively.

7. Identity or Unit Matrix :
A square matrix in which elements in the diagonal are all 1 and rest are all zero is called an identity matrix. In other words, a square matrix A = [a_ij] is called an identity or unit matrix if

• a_ij = 0 for all i ≠ j and
• a_ij = 1 for all i = j

The identity matrix of order rt is denoted by I_n.
Example: [1], \(\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right],\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\)
are identity matrices of order 1, 2, 3 respectively.

8. Null Matrix or Zero Matrix:
A matrix is said to be null matrix or zero matrix if all its elements are zero.
Example: [0], \(\left[\begin{array}{ll} 0 & 0 \\ 0 & 0 \end{array}\right],\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right],\left[\begin{array}{ll} 0, & 0 \end{array}\right]\) are all zero matrices.

9. Triangular Matrix
(i) Upper Triangular Matrix: A square matrix A = [a_ij] is called an upper triangular matrix if = 0 for all i > j matrix.
Example: A = \(\left[\begin{array}{llll} 1 & 2 & 4 & 3 \\ 0 & 3 & 2 & 4 \\ 0 & 0 & 1 & 8 \\ 0 & 0 & 0 & 7 \end{array}\right]\) is an upper triangular matrix.

(ii) Lower Triangular Matrix : A square matrix A = [a_ij] is called a lower triangular matrix if a_ij = 0 for all i < j.
Thus, in a lower triangular matrix all elements above the main diagonal are zero.
Example: A = \(\left[\begin{array}{lll} 1 & 0 & 0 \\ 2 & 7 & 0 \\ 3 & 5 & 8 \end{array}\right]\) is a lower triangular matrix of order 3.

A triangular matrix A = [ai_ij]_{n × n} is called a strictly triangular if a_ij = 0 for all i = 1, 2......... n

10. Sub-matrix:
If some row and columns are deleted from a matrix, then remaining matrix is called sub-matrix of given matrix.
Example: A = \(\left[\begin{array}{lll} 5 & 6 & 1 \\ 3 & 2 & 8 \\ 7 & 4 & 5 \end{array}\right]\)
It first row and first column is deleted then we get, \(\left[\begin{array}{ll} 2 & 8 \\ 4 & 5 \end{array}\right]\) which is sub-matrix of given matrix.

11. Comparable Matrices :
Two matrices A and B are said to be comparable if they are of same order.
Example: A = \(\left[\begin{array}{lll} 3 & 4 & 2 \\ 1 & 2 & 6 \end{array}\right] \)B = \(\left[\begin{array}{lll} 2 & 1 & 5 \\ 4 & 1 & 7 \end{array}\right]\)
Here A and B are comparable matrices, since their order is 2 × 3 (same).

Equality of Matrices
Two matrices A = [a_ij] and B = [b_ij] are said to be equal if

• they are of the same order.
• each element of A is equal to the corresponding element of B. i.e., a_ij = b_ij for all i and j.

Example: \(\left[\begin{array}{ll} 2 & 3 \\ 0 & 1 \end{array}\right]\) and \(\left[\begin{array}{ll} 2 & 3 \\ 0 & 1 \end{array}\right]\) are equal matrices but \(\left[\begin{array}{ll} 3 & 2 \\ 0 & 1 \end{array}\right]\) and \(\left[\begin{array}{ll} 2 & 3 \\ 0 & 1 \end{array}\right]\) are not equal matrices.

Symbolically we write equal matrix as A = B and for not equal matrix as A ≠ B.

Operations of Matrices:
Now, we shall discuss some operations on matrices- addition and subtraction on matrices, multiplication of a matrix by a scalar and multiplication of matrices.

Addition of Matrices:
Let A and B be two matrices, each of order m × n. Then their sum A + B is a matrix of order m × n and is obtained by adding the corresponding elements of A and B.
Example:
If A = \(\left[\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{array}\right]\) is a 2 × 3 matrix and B = \(\left[\begin{array}{lll} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{array}\right]\) is another 2 × 3 matrix. Then, we define
A + B = \(\left[\begin{array}{lll} a_{11}+b_{11} & a_{12}+b_{12} & a_{13}+b_{13} \\ a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23} \end{array}\right]\)

In general, if A = [a_ij] and B = [b_ij] are two matrices of the same order, say m × n. Then, the sum of the two matrices A and B is defined as a matrix C = [c_ij]_{m × n} where c_ij + b_ij, for all possibe values of i and j.

Note:
We emphasise that if A and B are not of the same order, then A + B is not defined. For example, if A = \(\left[\begin{array}{ll} 2 & 8 \\ 1 & 0 \end{array}\right]\), B = \(\left[\begin{array}{lll} 1 & 3 & 6 \\ 4 & 0 & 9 \end{array}\right]\), then A + B is not defined.

Multiplication of a Matrix by a Scalar:
If A = [a_ij]_{m × n} is a matrix of order m × n and k is a scalar then their product is shown by kA which is obtained by multiplying each element of A by k. i.e.,
kA = [ka_ij]

Negative of a Matrix:
The negative of a matrix is denoted by - A. A = (- 1)A.
Example:

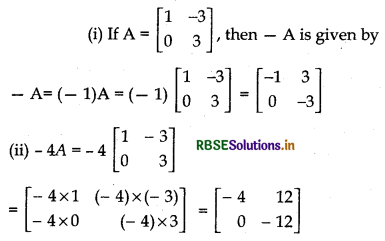
Subtraction of Matrices:
For two martices A and B of the same order, the subtracting of matrix B from matrix A is denoted by A - B = A + (-B) i.e.,
A - B = [a_ij]_{m × n} - [b_ij]_{m × n}
where A = [a_ij]_{m × n}
and B = [b_ij]_{m × n}
= [a_ij - b_ij]_{m × n}

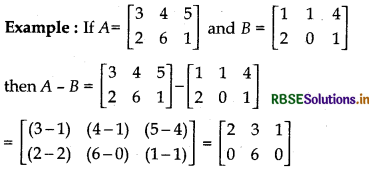
Properties of Matrices Addition:
1. Commutative Property: If A and B are two matrices of the same order, then their sum is commutative, i.e.,
A + B = B + A
Proof: Let A = [a_ij - b_ij]_{m × n} and B = [b_ij - b_ij]_{m × n}
So, two matrices are suitable for addition, then
A + B = [a_ij - b_ij]_{m × n} + [b_ij]_{m × n}
= [a_ij + b_ij]_{m × n}
By definition of addition of matrices
= [b_ij + a_ij]_{m × n}
(∵ a_ij and b_ij are number. Thus their addition is communtative)
= [b_ij]_{m × n} + [a_ij]_{m × n}
(By definition of addition of matrices)
= B + A
Thus, A + B - B + A
1. e., Sum of two matrices is commutative.

2. Associative Property:
If A B and C are three matrices of order m × n, then their sum is associative, i.e.,
(A + B) + C = A + (B + C)
Proof : Let A = [a_ij]_{m × n}; B = [b_ij]_{m × n}; C = [c_ij]_{m × n}
(A + B) + C =([a_ij]_{m × n} + [b_ij]_{m × n}) + [c_ij]_{m × n}
= [a_ij + b_ij]_{m × n} + [c_ij]_{m × n} (By definition of addition)
= [(a_ij + b_ij) + [c_ij]_{m × n} (By definition of addition)
= [a_ij + (b_ij + [c_ij)]_{m × n} (∵ a_ij, b_ij, [c_ij, are numbers whose sum is commutative)
= [a_ij]_{m × n} + [b_ij + c_ij]_{m × n} (By definition of addition of two matrices)
= [a_ij]_{m × n} + [b_ij]_{m × n} + [c_ij]_{m × n}
= A + (B + C)
(A + B) + C = A + (B + C)
Thus, sum of three matrices is associative.

3. Existence of Additive Identity :
If order of matrix A is m × n and also the order of matrix O is m × n, then
A + O = A = O + A
It means matrix O_{m × n} is additive identity.
Proof:
Let A = [a_ij]_{m × n}
A + O = [a_ij]_{m × n} + [O_ij]_{m × n}
= [a_ij + O]_{m × n} = [a_ij]_{m × n} = A
and O + A = [O + ai_ij]_{m × n} = [a_ij]_{m × n} = A

4. Existence of Additive Inverse :
For each matrix A there exist matrix - A of same order such that A + (- A) = O, where O is null matrix.
Then - A is called additive inverse of A or negative of A.
Proof : Let A = [a_ij]_{m × n} then - A = - [a_ij]_{m × n}
Thus, A + (- A) = [a_ij]_{m × n} + [- a_ij]_{m × n}
= [a_ij + (-a_ij]_{m × n} (By definition of addition of matrices)
= [a_ij - a_ij]_{m × n} = [0]_{m × n} = O_{m × n}

Example : If A = \(\left[\begin{array}{ll} 2 & 3 \\ 4 & 5 \end{array}\right]_{2 \times 2}\) then -A = \(\left[\begin{array}{ll} 2 & 3 \\ 4 & 5 \end{array}\right]=\left[\begin{array}{ll} -2 & -3 \\ -4 & -5 \end{array}\right]\)
Thus, \(\left[\begin{array}{ll} -2 & -3 \\ -4 & -5 \end{array}\right]\) is called the additive inverse of \(\left[\begin{array}{ll} 2 & 3 \\ 4 & 5 \end{array}\right]\)

5. Cancellation Laws :
If A, B, C are matrices of the same order, then A + B = A + C ⇒ B = C,
Proof :
We have A + B = A + C ...(i)
Adding - A to both sides, we get
- A + (A + B) = - A + (A + C)
By associativity, we get
(- A + A) + B = (- A + A) + C
⇒ O + B = O + C
[Since, O is the additive identity]
B = C [∵ O + B = B, O + C = C By additive identity definition]

Properties of Scalar Multiplication of a Matrix:
Property 1.
In the addition of matrices, scalar multiplication follows distributive law, i.e., if k is an arbitrary scalar, then
k(A. + B) = kA + kB
Proof: Let A = [a_ij]_{m × n} and B = [b_ij]_{m × n}
∵ A + B=[a_ij + b_ij]_{m × n}
k(A + B) = k[a_ij + b_ij]_{m × n}„ = [ka_ij + kb_ij]_{m × n}
= [ka_ij]_{m × n} + [kb_ij]_{m × n} = k[a_ij]_{m × n} + k[b_ij]_{m × n}
= kA + kB

Property 2.
It k and l are scalars and A = [a_ij]_{m × n} is matrix, then
(k + l)A =kA + IA
Proof:
A = [a_ij]_{m × n} and k and l are scalars, then
(k + l)A = (k + l) [a_ij] = [(k + l)a_ij]
= [ka_ij] + [la_ij]
= k[a_ij] + l[a_ij] = kA + IA
Thus, (k + l)A = kA + lA

Property 3.
If k and 1 are scalars and A = [a_ij]_{m × n} is - matrix, then
(i) (kl)A = l(lA) = l(kA)
(ii) (- k)A = - (kA) = k(- A)
(iii) IA = A
(iv) (- 1)A = - A .
Proof :
(i) Since, k and l are scalars, so kl is also scalar then (kl) A also a matrix of order m × n. So, k(lA) and l(kA) are martices of order rn x n.
Thus, (kl)A and k(lA) are two matrices of same order m × n such that
(i) [(kl)A]_ij = (kl) a_ij
(By the definition of scalar multiplication)
⇒ [(kl)A]_ij =k(la_ij) (By associative multiplication)
⇒ [(kl)A]_ij = k(lA)_ij
(By definition of scalar multiplication)
⇒ [(kl)A]_ij = [k(lA)]_ij
(By definition of scalar multiplication where i = 1, 2, ..............., m and j = 1, 2,..n)
Thus, by definition of equality of matrices (kl)A = k(lA)

Similarly, we can prove that
(kl)A = k(lA) = l(kA)

(ii) Putting l = -1 in (kl) A = k(lA) = l(kA)
(- k)A = k(- A) = - (kA)

(iii) Putting k = -1 in (- k) A = k(- A) = - (kA)
-1(-1)A =(-1)(-A)
= - (- 1.A) = 1A = A
∴ 1A = A

(iv) Putting k = 1 in (- k) A = k(~ A) = - (kA)
(-1) A = 1(- A) = - (1A) = - A
∴ (- 1)A = - A

Multiplication of Matrices:
The product of two matrices A and B is defined if the number of columns of A is equal to the number of rows of B.
In other words, for multiplication of two matrices A and B, the number of columns in A should be equal to the number of rows in B. Further more, for getting the elements of the product matrix, we take the rows of A and columns of B, multiply them element-wise and take the sum.
Let A = [a₁, a₂, .................. a_n] be a row matrix and B = \(\left[\begin{array}{c} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \end{array}\right]\) be a column matrix. Then we define
AB = a₁b₁ + a₂b₂ + ......... + a_nb_n

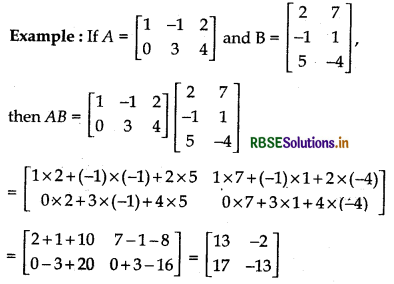
Using the product of a row matrix and a column matrix, let us now define the multiplication of any two matrices.
If A = (a_ij]_{m × n} and B =[b_ij]_{n × p} are two marices of orders m × n and n × p respectively, then their product AB is the matrix of order m x p and is defined as
(AB)_ij = (ith row of A) (jth column of B) for all i = 1,2, .... m and j = 1,2, ................... p

Note: If A and B are two matrices such that AB exists, then BA may or may not exist.

Properties of Matrix Multiplication
1. Commutative Property:
Matrix multiplication is not commutative in general. .
Proof :
Let A and B be two matrices such that AB exists then it is quite possible that BA may not exits and vice-versa. Similarly, if AB and BA both exists, then they may not be equal.

2. Associative Property :
Matrix multiplication is associative i.e., (AB)C = A(BC) whenever both sides are defined.
Proof:
Let A = [a_ij]_{m × n} = [b_jk]_{n × p} and C = [c_kl]_{p × q} are of order m × n, n × p and p × q matrices.

3. Distributive Property :
Matrix multiplication is distributive over matrix addition, i.e., if A, B and C matrices are such that AB, AC and BC are defined, then
(i) A(B + Q =AB+ AC
(ii) (A + B)C =AC + BC
Proof:
(i) Let A = [a_ij]_{m × n}, B = [b_jk]_{n × p} and C = [c_jk]_{n × p} are three matrices, then B + C is defined whose order is n x p
Thus, A(B + C) will be oder m × p.
∵ AB and AC both are of same order m × p.
∴ AB + AC is of order also.
So, A(B + Q and AB + AC are of same order such that their corresponding elements are equal.

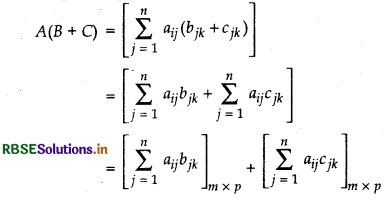
= AB + AC
Thus, A(B + C) = AB + AC
Similarly, (A + B)C = AC + BC

4. Existence of Multiplicative Identity :
For each square matrix A, there exists an identity matrix of same order such that
IA = AI = A
Proof :
Let A = [a_ij]_{n × n}, is a square matrix of order n × n and I is a matrix of order n × n matrix also. I is such that n

Thus, matrices AI and A are such that their corresponding elements are equal.
Thus AI = A ...(ii)
From (i) and (ii)
IA = A = AI.

Property 5. If the product of two matrices is a zero metrix it is not necessary that one of the matrices is a zero matrix.

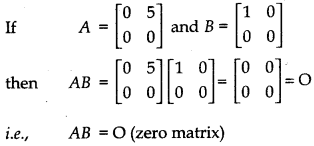
i.e., AB = O (zero matrix) whereas neither A nor B is zero matrix.

6. Cancellation Law :
Generally, multiplication of matrices does not follow cancellation law
Proof:
Let

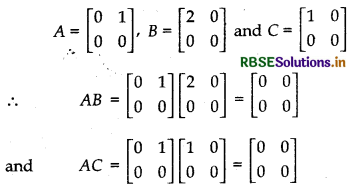
i.e., AB = AC, but B ≠ C
So, here cancellation law is not executed.

7. Product of a Matrix with a Null Matrix:
The product of the matrix with a null matrix is always a null matrix, then
A_{m × n}O_{n × p} = O_{m × p}
and O_{p × m}A_{m × n} = O_{p × n}
Proof :
Let A = [a_ij]_{n × n} and O_{n × p} = [b_ij]_{n × p}, where by - O, for all i and ;, then A_{m × n} O_{n × p} will be of order m × p
[∵ b_ij = O for all i and j]
Thus, A_{m × n}O_{n × p} and O_{m × p} are two matrices such that their corresponding elements are equal.
Thus, A_{m × n}O_{n × p} = O_{m × p}
Similarly, we can prove O_{p × m}A_{m × n} = O_{p × n}

If two matrics A and B are such that their product AB = O, then it does not necessarily imply that BA = O (zero matrix).
Example:

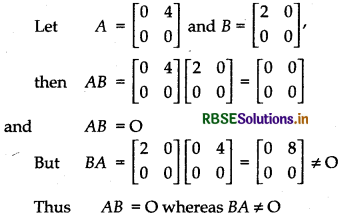
Positive Integral Powers of a Square Matrix:
For any square matrix, we define
(i) A¹ = A and (ii) Aⁿ⁺¹ = AⁿA, where n is positive integers, (n ∈ N).
It is clear from the above definitions that A² = AA; A³ = A²A = (AA)A etc.
Similarly A^mAⁿ = A^m+n
and (A^m)ⁿ = A^mn, where m, n ∈N

Matrix Polynomial:
If f(x) = a₀Aⁿ + a₁x^n-1 + a₂x^n-2 + .......... + a_n-1x + a_n is a polynomial and A is a square matrix of
order n. Then
f(A) = a₀Aⁿ + a₁A^n-1 + a₂A^n-2 + ............ + a_n-1A + a_nI_n
is called a matrix polynomial
Example: If f{x) = x³ + 3x² - 3x + 2 be a polynomial and is a square matrix, then
f(A) = A³ + 3A² - 3A + 21 is a matrix polynomial.

Theorem 1.
If A and B are two matrices of same order, then
(A + B)² = A² + AB + BA + B² When AB = BA then (A + B)² = A² + 2AB + B²
Proof:
Let A and B are two matrices of same order n.
Thus, (A + B) is a square matrix of order n
Now, (A + B)² = (A + B) (A + B)
= A(A + B) + B(A + B) (By distributive law)
= AA + AB + BA + BB (By distributive law)
= A² + AB + BA + B²
Thus (A + B)² = A² + AB + BA + B² ...(i)

Special case: When AB = BA, then
(A + B)² = A² + AB + BA + B² [From(i)]
= A² + AB + AB + B² (∵ AB = BA)
= A² + 2AB + B²
Thus (A + B)² = A² + 2AB + B²

Theorem 2.
If A and B are two matrices of same order, then
(A + B) (A - B) = A² - AB + BA - B² when
AB = BA, then (A + B) (A - B) = A²- B²
Proof:
(A + B) (A - B) = A(A - B) + B(A - B) (By law of distribution)
= AA -AB + BA - BB (By law of distribution)
= A² - AB + BA - B²
Thus, (A + B) (A - B) = A² - AB + BA - B² ...(i)

Special case: When AB = BA then,
(A + B) (A - B) = A² - AB + AB - B², From (i)
= A² - B² (∵ AB = BA)
Therefore, (A + B) (A - B) = A² - B²

Transpose of A Matrix:
Definition: If A = [a_ij] be an m × n matrix, then the matrix obtained by interchanging the rows and columns of A is called the transpose of A. Transpose of the matrix A is denoted by A' or (A^T).
In other words, if A = [a_ij]_{m × n}, then A' = [a_ij]_{n × m}.

Properties of Transpose of the Matrices
Here are the following properties of transpose of matrices without proof. These may be varified by taking suitable examples.
For any matrices A and B of suitable orders, we have

• (A')' = A
• (kA)' = kA (where k is any constant)
• (A + B)' = A' + B'
• (AB)' = B'A'

Symmetric And Skew-Symmetric Matrices:
Symmetric matrix :
A square matrix A = |n,,] is called a symmetric matrix, if a_ij = a_ji for all i,j.
Example :
(i) Matrix A = \(\left[\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 2 & 5 \\ 1 & 5 & -2 \end{array}\right]\) is symmetric, because a₁₂ = -1= a₂₁, a₁₃ = 1 = a₃₁ a₂₃ = 5 = a₃₂ i.e., a_ij = a_ji for all i, j. It follows from the definition of a symmetric matrix that A is symmetric, if
a_ij = a_ji for all i, j
⇒ (A)_ij = (A')_ij for ail i, j
⇒ A = A''
(i) Matrix A = \(\left[\begin{array}{lll} a & h & g \\ h & b & f \\ g & f & c \end{array}\right]\) is a symmetric matrix as A = A'

(iii) Matrix B = \(\left[\begin{array}{ccc} 2+i & 1 & 3 \\ 1 & 2 & 3+2 i \\ 3 & 3+2 i & 4 \end{array}\right]\) is a symmetric matrix because B' = B

Skew-Symmetric Matrix :
A sqaure matrix A = [a_ij] is a skew symmetric matrix if A' = - A, that is a_ij = -a_ji or a_ij values of i and j.
Example: (i) Matrix A = \(\left[\begin{array}{ccc} 0 & 2 & -3 \\ -2 & 0 & 5 \\ 3 & -5 & 0 \end{array}\right]\) is skew - symmetric, because
a₁₂ = 2, a₂₁ = -2 ⇒ a₁₂ = -a₂₁
a₁₃ = -3, a₃₁ = 3 ⇒ a₁₃ = -a₃₁
and a₂₃ = 5, a₃₂ = -5 ⇒ a₂₃ = -a₃₂

It follows from the definition of a skew-symmetric matrix that A is skew-symmetric iff
⇒ a_ij = - a_ij for all i, j
⇒ (A)_ij = “ (A')_ij for all i, j
⇒ A = - A'
Thus, a square matrix A is a skew-symmetric matric if A' = -A.

(ii) Matrix A = \(\left[\begin{array}{ccc} 0 & 2 i & 3 \\ -2 i & 0 & 4 \\ -3 & -4 & 0 \end{array}\right]\), B = \(\left[\begin{array}{ccc} 0 & -3 & 5 \\ 3 & 0 & 2 \\ -5 & -2 & 0 \end{array}\right]\) are skew-symmetric matrices because A' = - A and B' = - B.
Now, we are going to prove some results of symmetric and skew-symmetric matrices.

Theorem 1.
For any square matrix A with real number entries, A + A' is a symmetric matrix and A - A' is a skew- symmetric matrix.
Proof:
Let B = A + A', then
B' = (A + A')'
- A' + (A')' [As (A + B)' = A' + B']
= A' + A [As (A')' = A]
= A + A' [As A +B = B + A]
= B
Therefore B = A + A' is a symmetric matrix.
Now let C = A - A'
C'= (A - A')' = A' - (A')'
= A' - A = -(A - A') = -C
Therefore C = A - A' is skew-symmetric matrix.

Theorem 2.
Any square matrix can be expressed as the sum of a symmetric and a skew-symmetric matrix.
Proof:
Let A be a square matrix, then we can write
A= \(\frac{1}{2}\)(A + A') + \(\frac{1}{2}\)(A - A')
From the Theorem 1, we know that (A + A') is a symmetric matrix and (A - A') is a skew symmetric matrix.
Since, for any matrix A, (kA)' = kA', it follows that \(\frac{1}{2}\) (A + A') is a symmetric matrix and \(\frac{1}{2}\) (A - A') is a skew symmetric matrix. Thus, any square matrix can be expressed as the sum of the symmetric and a skew symmetric matrix.

Elementary Operations On Matrix
There are six operations (transformations) on a matrix, three of which are due to rows and three due to columns, which are known as elementary operations or transformations.
(i) The interchange of any two rows or two columns:
Symbolically the interchange of i^th and j^th rows is denoted by R_i ↔ R_j and interchange of i^th and j^th column is denoted bY C_i ↔ C_j

Example: Applying R₁ ↔ R₂ to \(\left[\begin{array}{rrr} 1 & 2 & 1 \\ -1 & \sqrt{3} & 1 \\ 5 & 6 & 7 \end{array}\right]\), we get \(\left[\begin{array}{rrr} -1 & \sqrt{3} & 1 \\ 1 & 2 & 1 \\ 5 & 6 & 7 \end{array}\right]\)

(ii) The multiplication of the elements of any row or column by a non zero number : Symbolically, the multiplication of each element of the i^th row by k, where k ≠ 0 is denoted by R_i → k R_i.
The corresponding column operation is denoted by C_j → kC_j

Example: Applying C₃ → \(\frac{1}{7}\)C₃ to \(\left[\begin{array}{rrr} 1 & 2 & 1 \\ -1 & \sqrt{3} & 1 \end{array}\right]\), we get \(\left[\begin{array}{ccc} 1 & 2 & \frac{1}{7} \\ -1 & \sqrt{3} & \frac{1}{7} \end{array}\right]\)

(iii) The addition to the elements of any row or colum, the corresponding elements of any other row or column multiplied by any non zero number : Symbolically, the addition to the elements of i^th row, the corresponding elements of j^th row multiplied by k is denoted by R_i → R_i + kR_j
The corresponding column operation is denoted by C_i → C_i + kC_j

Example: Applying R₂ → R₂ - 2R₁ to \(\left[\begin{array}{rr} 1 & 2 \\ 2 & -1 \end{array}\right]\), we get \(\left[\begin{array}{rr} 1 & 2 \\ 0 & -5 \end{array}\right]\)

Invertible Matrices:
Definition : If A is a square matrix of order m and if there exists another square matrix B of the same order m, such that AB = BA = I, then B is called the inverse matrix of A and it is denoted by A^-1. In that case A is said to be invertible.

Example: Let A = \(\left[\begin{array}{ll} 2 & 3 \\ 1 & 2 \end{array}\right]\) and B = \(\left[\begin{array}{ll} 2 & 3 \\ 1 & 2 \end{array}\right]\) be two matrices.

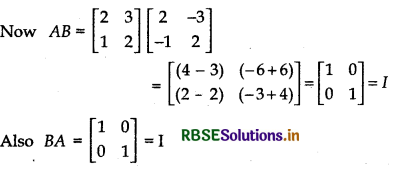
Thus, B is the inverse of A,in other words B = A^-1 and A is inverse of B, i.e., A = B^-1

Note:

• A rectangular matrix does not possess inverse matrix, since for products BA and AB to be defined and to be equal, it is necessary that matrices A and B should be square matrices of the same order.
• If B is the inverse of A, then A is also inverse of B.

Theorem 3.
(Uniqueness of inverse) Inverse of a square matrix, if it exists, is unique.
Proof :
Let A = [a_ij] be a square matrix of order m. If possible, let B and C be two inverses of A. We shall show that B = C.
Since, B is the inverse of A
AB = BA = I ...(1)
Since, C is also the inverse of A
AC = CA = I ...(2)
Thus B = BI = B(AC)
= (BA)C = IC = C

Theorem 4.
If A and B are invertible matrices of the same'order, then (AB)^-1 = B^-1 A^-1.
Proof :
From the definition of inverse of a matrix, we have (AB) (AB)^-1 = 1 ‘
or A^-1 (AB) (AB)^-1 = A^-1I (Pre multiplying both sides by A^-1)
or (A^-1A) B (AB)^-1 = A^-1(sine A^-1I = A^-1)
or IB (AB)^-1 = A^-1
or B(AB)^-1 = A^-1
or B^-1B (AB)^-1 = B^-1 A^-1
or I (AB)^-1 = B^-1 A^-1
Hence (AB)^-1 = B^-1 A^-1

Inverse of a Matrix by Elementary Operations
Let X, A and B be matrices of the same order such that X = AB. In order to apply a sequence of elementary row operations on the matrix equation X = AB,we will apply these row operations simultaneously on X and on the first matrix A of the product AB on RHS.

Similarly, in order to apply a sequence of elementary column operations on the matrix equation X=AB, we will apply, these operations simultaneously on X and on the second matrix B of the product AB on R.H.S

In view of the above discussion, we canclude that if A is a matrix such that A^-1 exists, then to find A^-1 using elementary row operations, write A = IA and apply a sequence of row operation on A = IA till we get, I = BA. The matrix B will be the inverse of A. Similarly, if we wish to find A^-1 using column oprations, then write A = A I and apply a sequence of column of operations on A = A I till we get, I = AB.

Remark:
In case, after applying one or more elementary row (column) operations on A = IA (A = AI), if we obtain all zeros in one or more rows of the matrix A on L.H.S., then A^-1 does not exist.

→ A matrix is an ordered rectangular arrray of numbers (may be real or complex) or functions.

→ Elements or entries of the mattrix are the numbers or functions in the array.

→ Rows of matrix are the horizontal lines of elements.

→ Columns of matrix are the vertical lines of elements.

→ Order of a Matrix:
If a matrix has "m" rows and "n" columns, then order of the matrix is m × n.
The total numbers of elements in the matrix of m × n will be mn.
Any point (x, y) in a plane can be represented in the matrix format as below :
P = [x, y] or \(\left[\begin{array}{l} x \\ y \end{array}\right]\)

→ Types of a Matrix
Column Matrix

• A matrix having only one column and any number of rows.
• General Form: A = [a_ij]_m×1, order of the matrix is m × 1.

→ Row Matrix

• A matrix having only one row and any number of columns.
• General Form = A = [a_ij]_1×n order of the matrix is 1 × n.

→ Square Matrix

• A matrix of order m × n, such that m = n
• General Form = A = [a_ij]_m×m, order of the matrix is m.

→ Diagonal Matrix

• A square matrix is said to be a diagonal matrix, if all its non-diagonal elements zero.
• General = A = [b_ij]_m×m, order of the matrix is m where b_ij = 0, if i = j;

→ Scalar Matrix

• A diagonal matrix is said to be a scalar matrix if its diagonal elements are equal.
• General Form = A = [b_ij]_m×m, order of the matrix is m where b_ij = 0, if i ≠ j and b_ij = 1, if i = j

→ Zero Matrix
A matrix is said to be zero matrix or null matrix if all its elements are zero and is denoted by O.

→ Equal Matrices
Two matrices are said to be equal if:

• they are of the same order
• each element of A is equal to the corresponding element of B.

→ Operation on Matrices
Addition of Matrices

• The sum of matrices A + B is defined only if matrices A and B are of same order.
• If A = [a_ij]_m×n and B = [b_ij]_m×n then, A + B = [a_ij + b_ij]_m×n

→ Properties of Addition of Matrices
Let A = [a_ij], B = [b_ij] and C = [c_ij] are three matrices of order m × n.

Commutative Law
A + B = B + A

Associative Law
(A+ B) + C = A + (B + C)

Existence of Additive Identity
A zero matrix (O) of order m × n (same as of A), is additive identity, if A + 0 = A = 0 + A

Existence of Additive Inverse
If A is a square matrix, then the matrix (- A) is called additive inverse, if A + (- A) = 0 = (- A) + A
- A is the additive inverse of A or negative of A.

Cancellation Law
A + B = A + C ⇒ B = C (Left cancellation law)
B + A = C + A ⇒ B = C (Right cancellation law)

Subtraction of Matrices
Let A and B be two matrices of the same order, then subtraction of matrices, A - B, is defined as A - B = [a_ij - b_ij]_m×n, where A = [a_ij]_m×n, B = [b_ij]_m×n.

→ Multiplication of Matrices
Multiplication of a Matrix by a Scalar
Let A = [a_ij]_m×n be a matrix and k be any scalar. Then, the matrix obtained by multiplying each element of A by k is called the scalar multiple of A by k and is denoted by kA, given as kA = [ka_ij]_m×n

→ Properties of Scalar Multiplication :
If A and B are matrices of order m × n, then

• k(A + B) = kA + kB)
• (k₁ + k₂)A = k₁A + k₂A
• k₁k₂A = k₁ (k₂A) = k₂(k₁A)
• (-k) A = - (kA) = k (- A) also called as negative of a matrix.

Multiplication of Two Matrices
If A = [a_ij] of order m × n and B = [b_ij] of order n × p then the product C = [c_ij] will be a matrix of the order m × p.

Note:

• If AB is defined, then BA need not be defined.
• If A, B are respectively m × n, k × 1 matrices, then both AB and BA are defined if and only if n = k and 1 = m.
• If the product of two matrices is a zero matrix, it is not necessary that one of the matrices is a zero matrix.

→ Properties of Multiplication of Matrices
Let A = [a_ij], B = [b_ij] and C = [c_ij] are three matrices of order m x n.

• Commutative Law
  AB ≠ BA
• Associative Law
  (A B) C = A (BC)
• Distributive Law
  • A (B + C) = AB + AC
  • (A + B) C - AC + BC, whenever both sides of equal-ity are defined.

→ Existence of Multiplicative Identity
For every square matrix A, there exists an identity matrix of same order such that IA = AI = A

→ Cancellation Law
If A is non-singular matrix, then

• AB = AC ⇒ B = C (Left cancellation law)
• BA = CA ⇒ B = C (Right cancellation law)
• AB = 0, does not necessarily imply that A = 0 or B = 0 or both A and B = 0

→ Transpose of a Matrix
Let A = [a_ij]_m×n be a matrix of order m × n. Then, the n × m a matrix obtained by interchanging the rows and columns of A is called the transpose of A and is denoted by A' or AT.

→ Properties of Transpose

• (A')' = A
• (A + B)' = A' + B'
• (AB)' = B' A'
• (kA)' = kA'
• (AN)' = (A')N
• (ABC)' = C'B' A'
• A square matrix A = [a_ij] is said to be symmetric if A' = A

Note:

• If A is symmetric then, [a_ij] = [a_ij]
• If A is skew-symmetric then, [a_ij] = - [a_ij]
• All the diagonal elements of a skew-symmetric matrix are zero.

→ Elementary Operation (Transformation) of a Matrix

• There are six operations (transformation) on a matrix, three of which are due to rows and three due to columns.
• Interchanging any two rows (or columns), denoted by R_i ⇔ R_j or C_i ⇔ C_j

→ Invertible Matrices
If A is a square matrix of order m, and if there exists another square matrix B of the same order m, such that AB - BA = I, then B is called the inverse matrix of A and it is denoted by A^-1. In that case A is said to be invertible.