RBSE Class 12 Maths Notes Chapter 2 Inverse Trigonometric Functions

These comprehensive RBSE Class 12 Maths Notes Chapter 2 Inverse Trigonometric Functions will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 2 Notes Inverse Trigonometric Functions

Introduction:
We know that sin θ, cos θ, tan θ etc., are called trigonometrical circular functions, in which θ has a fixed value for every function.
If sin θ = x, then x - sin θ
Term sin^-1 x, which expresses angle θ as x, is called inverse circular function.
We know that, to find inverse function f^-1 of any function f, it is necessary for a function f to be one-one onto or bijective.

We studied that trigonometric functions are not one-one and onto over their natural domain and ranges and hence their inverses do not exist. In this chapter, we will study about the restrictions on domains and ranges of trigonometric functions which ensure the existence of their inverses and observe their behaviour through graphical representations. Besides, some elementary properties will also be discussed.

The inverse trigonometric functions play an important role in calculus as they serve to define many integrals. The concepts of inverse trigonometric functions is also used in science and engineering.

 

Basic Concepts:
We have studied trigonometric functions, which are defined as follows :

• sine function, i.e., sin: R → (-1, 1]
• cosine function, i.e., cos : R → [- 1,1]
• tangent function, i.e., tan: R - {x: x = (2n + 1) \(\frac{\pi}{2}\)n ∈ Z] → Z
• cotangent function, i.e., cot: R - {x: x = rπ, n ∈ Z} → R
• secant function, i.e.r sec: R - [x : x = (2n + 1) \(\frac{\pi}{2}\), n ∈ Z} → R - (- 1, 1)
• cosecant function, i.e., cosec : R - {x : x = rπ, n ∈ Z} → R - (-1, 1)

Inverse of a Function :
If f: X → Y such that f(r) = y is one-one and onto, then we can define a unique function g : Y → X such that g(y) = x, where x ∈ X and y = f(x), y ∈ Y. Here, the domain of g = range of f and the range of g = domain of f. The function# is called the inverse of f and is denoted by f^-1. Further, g is also one-one and onto and inverse of g is f. Thus, g^-1 = (f^-1)^-1 = f. We also have
(f^-1of) (x) = f^-1a (f(x)) = f^-11(y) = x
and (fof^-1)(y) = f(f^-1(y)) = f(x) = y

Inverse of Sine Function :
Since, the domain of sine function is the set of all real numbers and range is the closed interval [-1, 1]. If we restrict its domain to \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\), then it becomes one-one and onto with range [-1, 1]. Actually, sine function restricted to any of the intervals etc. is one-one and its range is [-1, 1], We of sine function in each of these intervals. We denote the inverse of sine function by sin^-1 (arc sine function). Thus, sin -1 is a function whose domain is [-1,1] and range could be any of the internals \(\left[\frac{-3 \pi}{2}, \frac{-\pi}{2}\right],\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\) or \(\left[\frac{\pi}{2}, \frac{3 \pi}{2}\right]\) and so on. Corresponding to each such interval, we get a branch of the function sin^-1

Principal Value Branch of sin^-1 :
The branch with range \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\) is called the principal value branch, whereas other intervals as range give different branches of sin^-1. When we refer to the function sin^-1 we take it as the function whose domain is [-1, 1] and range is \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)

We write sin^-1: [-1, 1] → \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)

From the definition of the inverse functions, it follows that sin (sin^-1x) = x if -1 < x < 1 and sin^-1(sin x) = x if
-\(\frac{\pi}{2}\) ≤ x ≤ \(\frac{\pi}{2}\) In other words, if y = sin^-1 x, then sin y = x.

Graph of sin^-1x :
(i) We know that if y = f(x) is an invertible function, then x = f^-1(y). Thus, the graph of sin^-1 function can be obtained from the graph of original function by interchanging x and y axes, i.e., if (a, b) is a point on the graph of sine function, then (b, a) becomes the corresponding point on the graph of inverse of sine function. Thus, the graph of the function y = sin^-1 x can be obtained from the graph of y = sin x by interchanging x and y-axes. The graphs of y = sin x and y = sin-1 x are shown in (a) and (b). The dark portion of the graph of y = sin^-1 x represent the principal value branch.


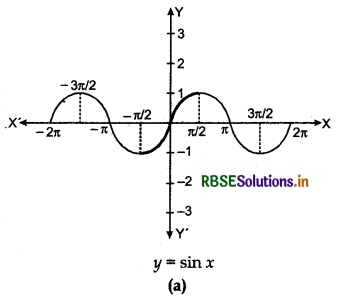
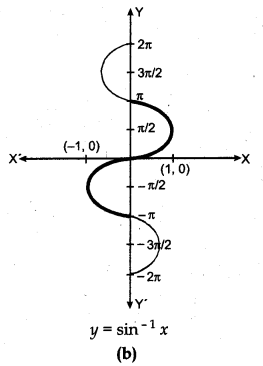
Inverse of Cosine Function cos^-1 and its Principal Value Branch:
Like sine function, the cosine function is a function whose domain is the set of all real numbers and range is the set [-1, 1]. If we restrict the domain of cosine function to [0, π], then it becomes one-one and onto with range [-1, 1]. Actually, cosine function restricted to any of the intervals [- π, 0], [0, π], [π, 2π] etc., is bijective with range as [- 1, 1]. We can therefore, define the inverse of cosine function in each of these intervals. We denote the inverse of the cosine function by cos^-1 (arc cosine function). Thus, cos^-1 is a function whose domain is [- 1, 1] and range could be any of the intervals [- π, 0], [0, π], [π, 2π] etc. Corresponding to each such interval, we get a branch of the function cos^-1.

Principal Value Branch of cos^-1:
The branch with range [0, π] is called the principal value branch of the function cos^-1. We write
cos^-1: [-1, 1] → [0, π]
The graph of the function given by y = cos^-1 x can be drawn in the same way as dicussed about the graph of y = sin^-1 x. The graphs of y = cos x and y = cos^-1 x are given in (a) and (b).

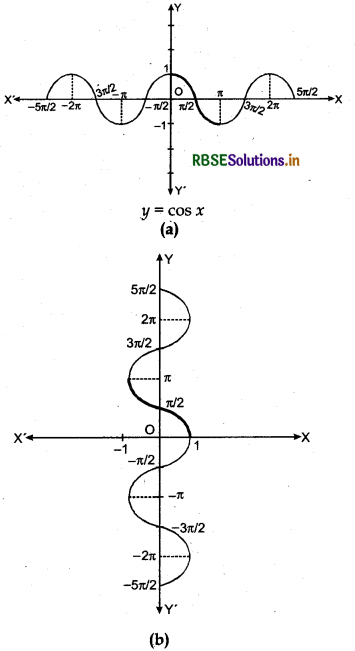
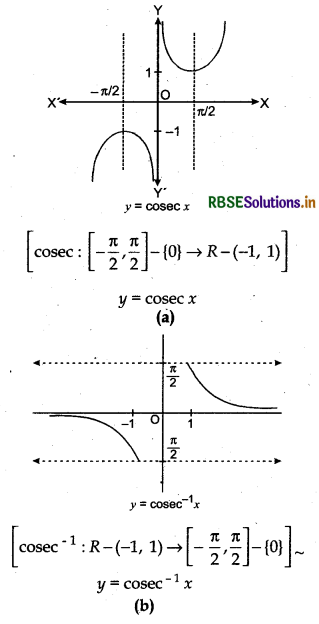
Graph of cosec^-1 x :
Function f: [- π/2, π/2] - {0} → (- ∞, - 1] ∪ [1, ∞) is derfined such that f(x) = cosec x which is one-one onto (since its domain is restricted). Thus, it is invertible. Then its inverse cosec^-1 x is a function whose doman is (- ∞, -1] ∪ [1, ∞) and range is [- π/2, π/2] - {0}.

Graph of y - cosec x and y = cosec^-1 x are given in following figures:

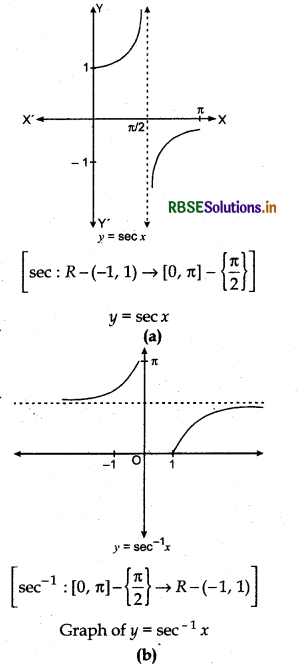
Graph of sec^-1 x :
Function f: [0, π] - [π/2] → (- ∞, - 1] ∪ [1, ∞) is defined such that f(x) = sec x which is one-one onto. Thus, it is invertible (since its domain is restricted). Its inverse sec^-1 x is a function whose decimals (- ∞, - 1] ∪ [1, ∞) and range is [0, π] - [π/2].

Following figures show the graph of y = sec x and y = sec^-1 x.

Graph of tan^-1x:
We know that f(x) = tan x is called function whose domain is set
{x : x ∈ R and x ≠ (2n + 1)\(\frac{\pi}{2}\), n ∈ Z}
and range is R. Thus, tan function is not defined for odd multiples of \(\frac{\pi}{2}\) i.e., \(\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}\), etc. and also not one-one onto. If we restrict its domain then tan^-1 function become one-one onto. If we take \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) as domain of tan^-1 function then it is defined as f : \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) → R or tan : \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) → R
whose range is R and it is one-one onto.

Actually, tangent function restricted to any of the intervals \(\left(-\frac{3 \pi}{2},-\frac{\pi}{2}\right),\left(-\frac{\pi}{2}, \frac{\pi}{2}\right),\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\) bijective and its range is R. Thus, tan^-1 can be defined as a function whose domain is R and range could be any of the intervals \(\left(-\frac{3 \pi}{2},-\frac{\pi}{2}\right),\left(-\frac{\pi}{2}, \frac{\pi}{2}\right),\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\) and so on. These intervals give different branches of the function tan^-1. The branch with range \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\) is called the principal

tan^-1 : R → \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)

The graph of the function y = tan x and y = tan^-1 x are given in (a) and (b).

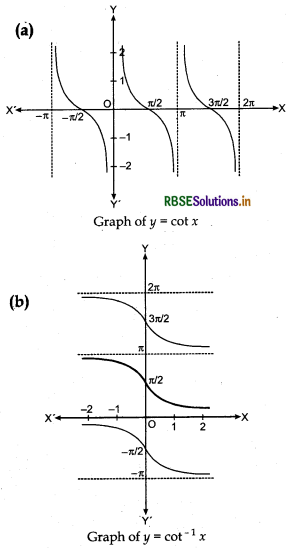
Graph of cot^-1 x :
We know that domain of the cot function (cotangent function) is the set {x : x ∈ R and x ≠ nπ, n ∈ Z} and range is R. It means that cotangent function is not defined for integral multiples of π. If we restrict the domain of cotangent function to (0, π), then it is bijective and its range as R. In fact, cotangent function restricted to any of the intervals (-π, 0), (0, π), (π, 2π) etc., is bijective and its range is R. Thus cot^-1 can be defined as a function whose domain is the R and range as any of the intervals (- π, 0), (0, π), (π, 2π) etc. These intervals give different branches of the function cot^-1. The fimction with range (0, π) is called the principal value branch of the function cot^-1. We thus have
cot^-1 : R → (0, π)

The graphs of y = cot x and y = cot^-1 x are given in (a) and (b)

To Remember :
The following table gives the inverse trigonometric function (principal value branches) along with their domains and ranges.

Note :

• sin^-1 x should not be confused with (sin x)^-1. In fact (sin x)^-1 ≠ \(\frac{1}{\sin x}\) and similarly for other trigonometric functions.
• Whenever no branch of an inverse trigonometric functions is mentioned, we mean the principal value branch of that function.
• The value of an inverse trigonometric functions lies in the range of principal value of that inverse trigonometric functions.

Properties Of Inverse Trigonometric Functions:
In this section, we will study various properties of inverse trigonometric functions and prove them by theorems.
We know that y = sin^-1 x then x = sin y, if x = sin y then y = sin^-1 x

Theorem 1.
Prove that:
(i) sin^-1(sin x) = x, x ∈ \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\)
(ii) cos^-1 (cos x) = x, x ∈ [0, π]
(iii) tan (tan x) = x, x ∈ \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
(iv) cot^-1 (cot x) = x, x ∈ (0, π)
(v) sec^-1 (sec x) = x, x ∈ [0, π] - \(\left\{\frac{\pi}{2}\right\}\)
(vi) cosec^-1 (cosec x) = x, x ∈ \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) - {0}
Proof:
(i) Let sin x = y, where x ∈ \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\)
Then sin^-1y = x
Thus, sin^-1 (sin x) = x (∵ y = sin x)
Hence Proved.

(ii) Let cos x = y, where x ∈ [0, π]
Then cos^-1y = x
Thus, cos^-1 (cos x) = x (∵ y = cos x)
Hence Proved.

(iii) Let tan x = y, where x ∈ \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
Then tan^-1y = x
Thus, tan^-1(tan x) = x (∵ y = tan x)
Hence Proved.

(iv) Let cot x = y, where x ∈ (0, π)
Then cot^-1y = x
Thus, cot^-1(cot x) = x (∵ y = cot x)
Hence Proved.

(v) Let sec x = y, where x ∈ [0, π] - \(\left\{\frac{\pi}{2}\right\}\)
Then sec^-1y = x
Thus, secs^-1(sec x) = x (∵ y = sec x)
Hence Proved.

(vi) Let cosec x = y, where x ∈ \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) - {0}
Then cosec^-1y = x
Thus, cosec^-1(cosec x) = x (∵ y = cosec x)
Hence Proved.

Theorem 2.
Prove that:
(i) sin (sin^-1x) = x,x ∈ [-1,1]
Proof:
Let sin^-1x = θ, where x ∈ [-1, 1]
Then sin θ = x
Thus, sin (sin^-1x) = x (∵ θ = sin^-1x)
Hence Proved

(ii) cos (cos^-1x) = x, x ∈ [-1,1]
Proof:
Let cos^-1x = θ, where x ∈ [- 1, 1]
Then cos θ = x
Thus, cos (cos^-1 x) = x (∵ θ = cos^-1x)
Hence Proved.

(iii) tan (tan^-1x) = x, x ∈ R
Proof:
Let tan^-1x = 0, where x ∈ R
Then tan 0 = x
Thus, tan (tan^-1x) = x (∵ θ = tan^-1x)
Hence Proved.

(iv) sec (sec^-1x) = x, x ∈ R - (-1, 1)
Proof:
Let sec^-1x = 0, where x ∈ R - (- 1, 1)
Then sec θ = x
Thus, sec (sec^-1x) = x (∵ θ = sec^-1x)
Hence Proved.

(v) cot (cot^-1x) = x, x ∈ R
Proof:
Let cot^-1x = 0, where x ∈ R
Then cot θ = x
Thus, cot (cot^-1x) = x (∵ θ = cot^-1x)
Hence Proved.

(vi) cosec (cosec^-1x) = x, x ∈ R - (-1,1)
Proof:
Let cosec^-1x = 0, where x ∈ R - (-1, 1)
Then cosec θ = x
Thus, cosec (cosec^-1x) = x (∵ θ = cosec^-1x)
Hence Proved.

Theorem 3.
Prove that:
(i) sin^-1\(\left(\frac{1}{x}\right)\) = cosec^-1x, (x ≥ 1 or x ≤ -1)
Proof:
Let sin^-1\(\left(\frac{1}{x}\right)\) = θ (∵ -1 ≤ \(\frac{1}{x}\) ≤ 1)
⇒ sin θ = \(\frac{1}{x}\) ⇒ cosec θ = x
⇒ θ = cosec^-1x
Thus, sin^-1\(\left(\frac{1}{x}\right)\) = cosec^-1x (∵ θ = sin^-1\(\frac{1}{x}\))

(ii) cos^-1\(\left(\frac{1}{x}\right)\) = sec^-1x, (x ≥ 1 or x ≤ -1)
Proof:
Let cos^-1\(\left(\frac{1}{x}\right)\) = θ (∵ -1 ≤ \(\frac{1}{x}\) ≤ 1)
⇒ cos θ = \(\frac{1}{x}\) ⇒ sec θ = x
⇒ θ = sec^-1x
Thus, cos^-1\(\left(\frac{1}{x}\right)\) = sec^-1x (∵ θ = cos^-1\(\frac{1}{x}\))

(iii) tan^-1\(\left(\frac{1}{x}\right)\) = cot^-1x, (x > 0)
Proof:
Let tan^-1\(\left(\frac{1}{x}\right)\) = θ
tan θ = \(\left(\frac{1}{x}\right)\)
⇒ cot θ = x
⇒ θ = cot^-1x
Thus, tan^-1\(\left(\frac{1}{x}\right)\) = cot^-1x (θ = tan-^-1\(\frac{1}{x}\)
Hence Proved.

Note:
(i) cosec^-1\(\left(\frac{1}{x}\right)\) = sin^-1x, x ∈ [1, -1]
Proof:
Let cosec^-1\(\left(\frac{1}{x}\right)\) = θ ⇒ cosec θ = \(\frac{1}{x}\)
⇒ sin θ = x ⇒ θ = sin^-1x
Thus, cosec^-1\(\left(\frac{1}{x}\right)\) = sin^-1x
Hence Proved

(ii) sec^-1\(\left(\frac{1}{x}\right)\) = cos^-1x, x ∈ [1, -1]
Proof:
Let sec^-1\(\left(\frac{1}{x}\right)\) = θ ⇒ sec θ = \(\frac{1}{x}\)
⇒ cos θ = x ⇒ θ = cos^-1x
Thus, sec^-1\(\left(\frac{1}{x}\right)\) = cos^-1x
Hence Proved.

(iii) cot^-1\(\left(\frac{1}{x}\right)\) = tan^-1x, x > 0
⇒ tan θ = x ⇒ θ = tan^-1x
Thus, cot^-1\(\left(\frac{1}{x}\right)\) = tan^-1x
Hence Proved

Theorem 4.
Prove that
(i) sin^-1 (-x) = - sin^-1 x, x ∈ [-1,1]
Proof:
Let sin^-1(- x) = θ ⇒ - x = sinθ
⇒ x = - sin θ => x = sin (- θ)
⇒ - θ = sin^-1x ⇒ θ = - sin^-1x
Thus, sin^-1(- x) = - sin^-1x [∵ θ = sin^-1(-x)]
Hence Proved.

(ii) tan^-1 (- x) = - tan x, x ∈ R
Proof:
Let tan^-1(- x) = θ ⇒ - x = tan θ
⇒ x = - tan θ ==> x = tan (- θ)
⇒ θ = - tan^-1x
Thus, tan^-1 (- x) = - tan^-1x [ ∵ θ = tan^-1(- x)]
Hence Proved.

(iii) cosec^-1(- x) = - cosec^-1 x, |x| > 1
Proof:
Let cosec^-1(-x) = θ ⇒ -x = cosec θ
⇒ x = - cosec θ ⇒ x = cosec (- θ)
⇒ θ = - cosec ^-1x
Thus, cosec^-1(- x) = - cosec^-1x [∵ θ = cosec^-1(-x)]
Hence Proved.

Theorem 5.
Prove that:
(i) cos^-1(- x) = \(\frac{\pi}{2}\) - cos^-1x, x ∈ [-1,1]
Proof:
Let cos^-1(-x) = θ ⇒ -x = cos θ
⇒ x = - cos θ ⇒ x = cos (π - θ)
⇒ cos^-1x = π - θ ⇒ θ = π - cos^-1x
Thus, cos^-1(- x) = π - cos^-1x [∵ θ = cos^-1(- x)]
Hence Proved.

(ii) sec^-1(- x) = \(\frac{\pi}{2}\) - sec^-1x, |x| > 1
Proof:
Let sec^-1(- x) = θ ⇒ - x = sec θ
⇒ x = - sec θ ⇒ x = sec (π - θ)
⇒ sec^-1 x = π - θ ⇒ θ = π - sec^-1x
Thus, sec^-1 (- x) = π - sec^-1x
Hence Proved.

(iii) cot^-1(-x) = \(\frac{\pi}{2}\) - cot^-1x, x ∈ R
Proof:
Let cot^-1(- x) = θ ⇒ - x = cot θ
⇒ x = - cot θ ⇒ x = cot (π - θ) ⇒ θ = π - cot^-1x
⇒ cot^-1 x = π - θ ⇒ θ = π - cot^-1x
Thus, cot^-1 (- x) = π - cot^-1x
Hence Proved.

Theorem 6.
Prove that:
(i) sin^-1 + cos^-1 = \(\frac{\pi}{2}\), x ∈ [-1, 1]
Proof:
Let sin^-1x = θ ⇒ -x = cos θ
⇒ x = - sin θ ⇒ x = cos (\(\frac{\pi}{2}\) - θ)
⇒ cos^-1x = \(\frac{\pi}{2}\) - θ
⇒ cos^-1x = \(\frac{\pi}{2}\) - sin^-1θ [∵ θ = sin^-1x]
Thus, sin^-1 + cos^-1 = \(\frac{\pi}{2}\)
Hence Proved.

(ii) tan^-1(- x) + cot^-1x = \(\frac{\pi}{2}\), x ∈R
Proof:
Let tan^-1x = θ
⇒ - x = cosec θ
⇒ x = - sec θ ⇒ x = sec (\(\frac{\pi}{2}\) - θ)
⇒ sec^-1x = \(\frac{\pi}{2}\) - θ
⇒ sec^-1x = \(\frac{\pi}{2}\) - tan^-1θ [∵ tan^-1(x) = θ]
Thus, tan^-1(- x) + cot^-1x = \(\frac{\pi}{2}\)
Hence Proved.

(iii) cot^-1(-x) = \(\frac{\pi}{2}\) - cot^-1x, x ∈ R
Proof:
Let cosec^-1(- x) = θ⇒ - x = cosec θ
⇒ x = cosec θ ⇒ x = cosec (\(\frac{\pi}{2}\) - θ)
⇒ sec^-1x = \(\frac{\pi}{2}\) - θ
⇒ cosec^-1x = \(\frac{\pi}{2}\) - sec^-1θ [∵ tan^-1(x) = θ]
Thus, sec^-1(- x) + cot^-1x = \(\frac{\pi}{2}\)
Hence Proved.

Theorem 7.
Prove that:
(i) tan^-1x + tan^-1y = tan^-1\(\left(\frac{x+y}{1-x y}\right)\), if xy < 1
Proof:
Let tan^-1x = θ and tan^-1y = Φ
⇒ tan θ = x and tan Φ = y
⇒ tan(θ + Φ) = \(\frac{\tan \theta+\tan \phi}{1-\tan \theta \tan \phi}\)
⇒ θ + Φ = tan^-1\(\left(\frac{\tan \theta+\tan \phi}{1-\tan \theta \tan \phi}\right)\)
Thus, tan^-1x + tan^-1y = tan^-1\(\left(\frac{x+y}{1-x y}\right)\)
Hence Proved.

(ii) tan^-1x - tan^-1y = tan^-1\(\left(\frac{x-y}{1+x y}\right)\), if xy > -1
Proof:
Let tan^-1x = θ and tan^-1y = Φ
⇒ tan θ = x and tan Φ = y
⇒ tan(θ - Φ) = \(\frac{\tan \theta-\tan \phi}{1+\tan \theta \tan \phi}\)
⇒ θ - Φ = tan^-1\(\left(\frac{\tan \theta-\tan \phi}{1+\tan \theta \tan \phi}\right)\)
Thus, tan^-1x - tan^-1y = tan^-1\(\left(\frac{x-y}{1+x y}\right)\)
Hence Proved.

Note:
If tan^-1x + tan^-1y = tan^-1\(\left(\frac{x+y}{1-x y}\right)\)
tan^-1x + tan^-1(-y) = tan^-1\(\left(\frac{x-y}{1+x y}\right)\)
Thus, tan^-1x - tan^-1y = tan^-1\(\left(\frac{x-y}{1+x y}\right)\)

(iii) 2 tan^-1x = tan^-1\(\left(\frac{2 x}{1-x^{2}}\right)\), if |x| < 1
Proof:
Let x = tan θ ⇒ θ = tan^-1x

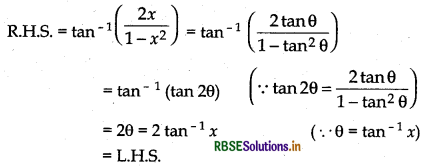
Thus, 2 tan^-1x = tan^-1\(\left(\frac{2 x}{1-x^{2}}\right)\)
Hence Proved.

Note: If, we put y = x in
tan^-1x + tan^-1y = tan^-1\(\left(\frac{x+y}{1-x y}\right)\)
Then, tan^-1x + tan^-1x = tan^-1\(\left(\frac{x+x}{1-x x}\right)\)
∴ 2tan^-1x = tan^-1\(\left(\frac{2 x}{1-x^{2}}\right)\)

Theorem 8.
Prove that:
(i) 2tan^-1x = sin^-1\(\left(\frac{2 x}{1+x^{2}}\right)\), |x| ≤ 1
Proof:
Let tan^-1x = θ
Then, x = tan θ

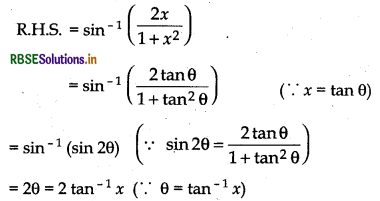
Thus, 2tan^-1x = sin^-1\(\left(\frac{2 x}{1+x^{2}}\right)\)

(ii) 2tan^-1x = cos^-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\), x ≥ 0
Proof:
Let x = tan θ

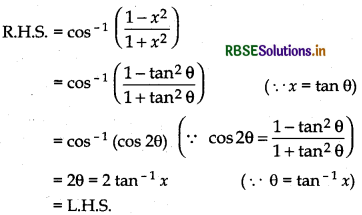
Thus, 2tan^-1x = sin^-1\(\left(\frac{2 x}{1+x^{2}}\right)\)
Hence Proved.

Theorem 9.
Prove that
2 sin^-1x = sin^-1[2x\(\sqrt{1-x^{2}}\)], - \(\frac{1}{\sqrt{2}}\) ≤ x ≤ \(\frac{1}{\sqrt{2}}\)
Proof:
Let sin^-1x = θ ⇒ sin θ = x
∵ sin 2θ = 2 sin θ cos θ
= 2 sin θ\(\sqrt{1-\sin ^{2} \theta}\)
⇒ 2θ = sin^-1(2sinθ \(\sqrt{1-\sin ^{2} \theta}\))
Thus, 2 sin^-1x = sin^-1(2x\(\sqrt{1-x^{2}}\))
Hence Proved.

Theorem 10.
Prove that:
2 cos^-1x = cos^-1(2x² - 1), 0 < x < 1
Proof:
Let cos^-1x = θ ⇒ x = cos θ
∵ cos 2θ = 2 cos² θ - 1 = (2x² - 1)
⇒ 2θ = cos^-1(2x² - 1)
2 cos^-1x = cos^-1(2x² -1)
Hence Proved.

Theorem 11.
Prove that:
3 sin^-1x = sin^-1(3x - 4x³), ∀ x ∈ \(\left[-\frac{1}{2}, \frac{1}{2}\right]\)
Proof:
Let sin^-1x = θ ⇒ x = sin θ
sin 3θ = 3 sin θ - 4 sin3 θ
sin 3θ = (3x - 4x³) (∵ x = sin θ)
⇒ 3θ = sin^-1(3x - 4x³) (∵ θ = sin^-1x)
Thus, 3 sin^-1 x = sin^-1 (3x - 4x³)

Theorem 12.
Prove that:
3 cos^-1x = cos^-1(4x³ - 3x), x ∈ [\(\frac{1}{2}\), 1]
Proof:
Let cos^-1x = θ ⇒ x = cos θ (∵ cos 3θ = 4 cos³θ - 3 cos θ)
⇒ cos 3θ = (4x³ - 3x) (∵ cos θ = x)
⇒ 3θ = cos^-1(4x³ - 3x)
Thus, 3 cos^-1x = cos^-1(4x³ - 3x) (∵ θ = cos^-1x)

Theorem 13.
Prove that:
(i) sin^-1x + sin^-1y = sin^-1[x\(\sqrt{\left(1-y^{2}\right)}\) + y\(\sqrt{\left(1-x^{2}\right)}\)] xy < 0, x²+ y² > 1
Proof:
Let sin^-1x = θ and sin^-1y = Φ
Then sin θ = x and sin Φ = y
∵ sin (θ + Φ) = sin θ cos Φ + cos θ sin Φ

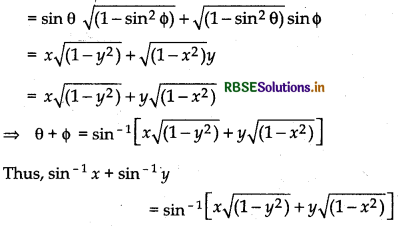
Hence Proved.

(ii) sin^-1x - sin^-1y = sin^-1[x\(\sqrt{\left(1-y^{2}\right)}\) - y\(\sqrt{\left(1-x^{2}\right)}\)] xy > 0, and x² + y² > 1
Proof:
Let sin^-1x = θ and sin^-1y = Φ
Then sin θ = x and sin Φ = y
∵ sin (θ + Φ) = sin θ cos Φ + cos θ sin Φ

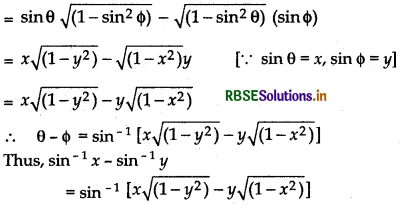
Hence Proved.

(iii) cos^-1x + cos^-1y = cos^-1[xy - \(\sqrt{\left(1-x^{2}\right)\left(1-y^{2}\right)}\)], x ≥ -1, y < 1 and x + y ≥ 0
Proof:
Let cos^-1x = θ and cos^-1y = Φ
Then cos θ = x and cos Φ = y
∵ cos (θ + Φ) = cos θ cos Φ + sin θ sin Φ

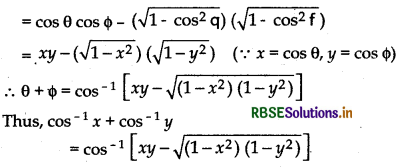
Hence Proved.

(iv) cos^-1x - cos^-1y = cos^-1[xy + \(\sqrt{\left(1-x^{2}\right)\left(1-y^{2}\right)}\)] x ≥ -1, y ≤ 1 and x - y ≤ 0
Proof:
Let cos^-1x = θ and cos^-1y = Φ
Then cos θ = x and cos Φ = y
∵ cos (θ - Φ) = cos θ cos Φ - sin θ sin Φ

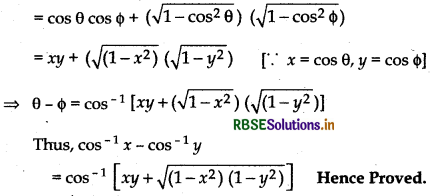
Theorem 14.
Prove that:
sin^-1x = cos^-1\(\sqrt{1-x^{2}}\)

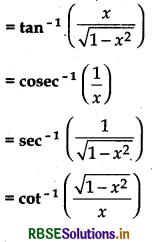
Proof:
Let sin^-1x = θ Then x = sin θ ............(1)

Theorem 15.
Prove that
cos^-1x = sin^-1-1x

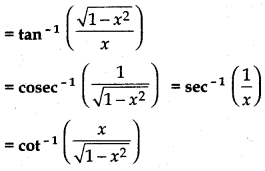
Proof:
Let cos^-1x = θ
⇒ cos θ = x

Theorem 16.
Prove that:

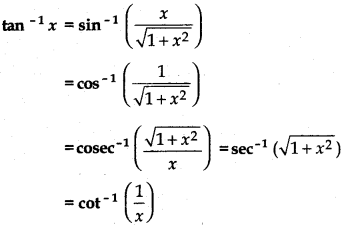
Proof:
Let tan^-1x = θ
∴ tan θ = x = \(\frac{x}{1}\)

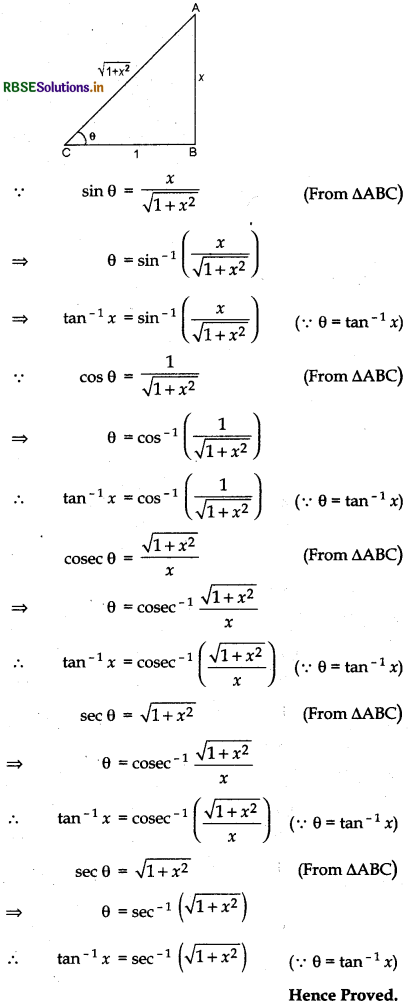
Note:
tan^-1 x = θ
⇒ x = tan θ
∴ sec θ = \(\sqrt{1+\tan ^{2} \theta}\)
Let x = tan θ ⇒ θ = tan^-1x
∴ sec θ = \(\sqrt{1+x^{2}}\)
⇒ θ = sec^-1\(\left(\sqrt{1+x^{2}}\right)\)
tan^-1x = sec^-1\(\left(\sqrt{1+x^{2}}\right)\) (∵ θ = tan^-1x)
cot θ = \(\frac{1}{\tan q}=\frac{1}{x}\)
θ = cot^-1\(\left(\frac{1}{x}\right)\)
∴ tan^-1x = cot^-1\(\left(\frac{1}{x}\right)\) (∵ θ = tan^-1x)

Theorem 17.
Prove that:
cot^-1x ± cot^-1y = cot^-1\(\frac{x y \mp 1}{y \pm x}\)
Proof:
Let cot^-1x = θ and cot^-1y = Φ
Then cot θ = x and cot Φ = y

Hence Proved.

Theorem 18.
prove that:
(i) 3tan^-1x = tan^-1\(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right) \cdot\left(-\frac{1}{\sqrt{3}}<x<\frac{1}{\sqrt{3}}\right)\)
Proof:
Let tan^-1x = θ then tan θ = x

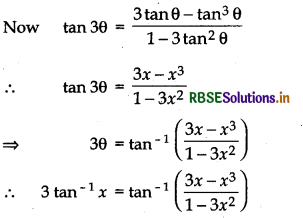
Hence Proved.

(ii) 3 cot^-1x = cot^-1\(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\)
Proof:
Again, cot^-1x = θ then cot θ = x

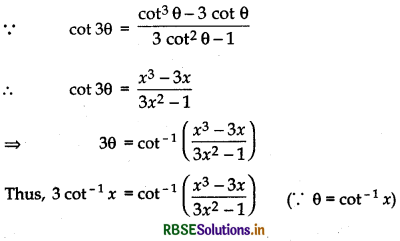
Function	Domain	Range
y = sin-1 x iff x = sin y	- 1 ≤ x ≤ 1,	\(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\)
y = cos-1x iff x = cos y	-1 ≤ x ≤ 1	[0, π]
y = tan-1 x iff x = tan y	- ∞ < c < ∞	\(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
y = cot-1x iff x = cot y	-∞ < x < ∞	[0, π]
y = cosec-1 x iff x = cosec y	(-∞, - 1] ∪ [1, ∞)	[-\(\frac{\pi}{2}\), 0) ∪  (0, \(\frac{\pi}{2}\)]
y = sec-1 x iff x = sec y	(-∞, - 1] ∪ [1, ∞]	[0, \(\frac{\pi}{2}\))  ∪ (\(\frac{\pi}{2}\), π]

Note:

• sin^-1x and tan^-1x are increasing functions in their domain,
• cos^-1x and cot^-1x are decreasing functions in their domain.

Property I:

• sin^-1x + cos^-1x = π/2, for all x ∈ [-1, 1]
• tan^-1x + cot^-1x = π/2, for all x ∈ R
• sec^-1x + cosec^-1x= π/2, for all x ∈ (-∞, - 1] ∪ [1, ∞)

Property II:

• sin^-1\(\left(\frac{1}{x}\right) \)= cosec^-1x, for all x ∈ (-∞, 1] ∪ [1, ∞)
• cos^-1\(\left(\frac{1}{x}\right) \) = sec^-1x, for all x ∈ (-∞, 1] ∪ [1, ∞)
• tan^-1\(\left(\frac{1}{x}\right) \) = cot^-1x, for x > 0
  = -π + cot^-1x, for x < 0
• cosec^-1(-x) = -cosec^-1x for all x ∈ R (-∞, -1) ∪ [1, ∞)

Property III:

• cos^-1(- x) = π - cos^-1 (x), for all x ∈ [-1, 1]
• sec^-1(- x) = π - sec^-1x, for all x ∈ (- ∞, -1] ∪ [1, ∞)
• cot'^-1(- x) = π - cot^-1x, for all x ∈ R
• sin^-1(- x) = - sin^-1(x), for all x ∈ [-1, 1]
• tan^-1(- x) = - tan^-1x, for all x ∈ R
• cosec^-1(- x) = - cosec^-1x, for all x ∈ R (-∞ -1) ∪ [1, ∞)

Property IV:

• sin (sin^-1 x) = x, for all x ∈ [-1,1]
• cos (cos^-1 x) = x, for all x ∈ [-1,1]
• tan (tan^-1 x) = x, for all x ∈ R
• cosec (cosec^-1x) = x, for all x ∈ (-∞ - 1] ∪ [1, ∞)
• sec (sec^-1 x) = x, for all x ∈ (-∞, -1] ∪ [1, ∞)
• cot (cot^-1x) = x, for all x ∈ R