RBSE Class 12 Maths Notes Chapter 13 प्रायिकता

These comprehensive RBSE Class 12 Maths Notes Chapter 13 प्रायिकता will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 13 Notes प्रायिकता

भूमिका (Introduction):
पूर्व की कक्षाओं में हमने प्रायिकता को किसी यादृच्छिक परीक्षण की घटनाओं के घटित होने की अनिश्चितता की माप के रूप में पढ़ा था। हमने रूसी गणितज्ञ ए.एन. कौल्मोग्रोब (1903-1987) द्वारा प्रतिपादित अभिगृहितीय दृष्टिकोण का उपयोग किया था और प्रायकिता को परीक्षण के परिणामों पर परिभाषित फलन के रूप में निरूपित किया था। वहाँ हमने अभिप्रयोग, घटनायें एवं उनके प्रकार (सरल घटनायें, मिश्र घटनायें, स्वतंत्र घटनायें, आश्रित घटनायें, परस्पर अपवी घटनायें आदि.....) का विश्लेषणात्मक अध्ययन किया था। प्रस्तुत अध्याय में हम किसी घटना की सप्रतिबंध प्रायिकता (Conditional Probability) के बारे में विचार करेंगे, जबकि किसी अन्य घटना के घटित होने की सूचना हमारे पास हो, तथा इस महत्त्वपूर्ण अवधारणा की सहायता से बेज़-प्रमेय (Bayes' theorem) प्रायिकता का गुणन नियम तथा स्वतंत्र घटनाओं के बारे में अध्ययन करेंगे। हम यहाँ पर यादृच्छिक चर (Random Variable) और इसका ग्रायिकता बंटन, यादृच्छिक चर का माध्य, प्रसरण आदि का अध्ययन करेंगे। अध्याय के अन्तिम अनुभाग में हम एक महत्त्वपूर्ण असंतत प्रायिकता बंटन (Discrete Probability Distribution) के बारे में भी

सप्रतिबंध प्रायिकता (Conditional Probability)
* परिभाषा-यदि E तथा F किसी यादृच्छिक परीक्षण के प्रतिदर्श समष्टि से सम्बन्धित दो घटनाएँ हैं, तो F के घटित होने की सूचना पर, E की प्रायिकता अग्रलिखित सूत्र से प्राप्त होती है
P(E|F) = \(\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{F})}\), जबकि P(F) ≠ 0
इसी प्रकार P(F|E) = \(\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{E})}\) जबकि P(F) ≠ 0

 

सप्रतिबंध प्रायिकता के गुण (Properties of Conditional Probability):
माना कि E तथा F किसी प्रतिदर्श समष्टि S की दो घटनाएँ हैंगुण 1 P(S|F) = P(F|F) = 1

गुण 2 यदि A और B प्रतिदर्श समष्टिS की कोई दो घटनाएँ हैं और F एक अन्य घटना इस प्रकार है कि P(F) ≠ 0, तब
P[(A ∪ B)|F] = P(A|F) + P(B|F) - P[A ∩ B)|F] विशेष रूप से, यदि A और B परस्पर अपवर्जी घटनाएँ हों, तो
P[(A ∪ B)|F] = P(A|F) + P(B|F) हम जानते हैं कि

जब A तथा B परस्पर अपवर्जी हों तो P(A ∩ B|F) = 0
= P(A ∪ B|F) = P(A|F) + P(BIF)

अतः जब A तथा B परस्पर अपवर्जी घटनाएँ हों, तो
P(A ∪ B) = P(A|F) + P(B|F)

गुण 3 P(E' |F) = 1 - P(E|F)
गुण 1 से हमें ज्ञात है कि
⇒ P(S|F) = 1 = P[(E ∪ E')[F] = 1 क्योंकि S = E ∪ E'
⇒ P(E|F) + P(E|F) = 1 क्योंकि E तथा E' परस्पर अपवर्जी घटनाएँ हैं
अतः P(E|F) = 1 – P(E|F)
आइए अब कुछ उदाहरण लें।

प्रायिकता का गुणन नियम (Multiplication Theorem on Probability):
सप्रतिबंध प्रायिकता की परिभाषा से हम जानते हैं कि घटना F के दिये जाने पर घटना E की सप्रतिबंध प्रायिकता को P(EF) द्वारा लिखते हैं और इसे निम्न प्रकार से ज्ञात करते हैं :

समीकरण (1) और (2) को मिलाने से हमें प्राप्त होता है कि
P(EF) = P(E) P(FE) = P(F).P(E|F) जबकि P(E) ≠ 0 और P(F) ≠ 0
P(EF) को P(EF) द्वारा भी व्यक्त करते हैं
P(EF) = P(E).P(F|E) = P(F).P(E|F) जब P(E) ≠ 0, P(F) ≠ 0
उपरोक्त परिणाम को 'प्रायिकता का गुणन नियम' कहते हैं।

विशेष स्थितियाँ
(1) जब घटनायें E, F तथा G हैं तब
P(E ∩ F ∩ G) = P(E).P(FIE).P(G|E ∩ F)
या P(EFG) = P(E).P(F|E).P(G|EF)
जब घटनायें E तथा F स्वतंत्र घटनायें हैं अर्थात् किसी एक घटना के घटित होने पर दूसरी घटना पर कोई प्रभाव नहीं पड़ेगा।
अतः P(E|F) = P(E)
एवं P(FE) = P(F)

अतः उपर्युक्त प्रमेय से,
P(EF) = P(E).P(F)
तथा P(EFG) = P(E).P(F).P(G)

व्यापक रूप में P(EFGH....) = P(E).P(F).P(G)P(H)

टिप्पणी

• दो घटनाओं E तथा F को पराश्रित (dependent) कहते हैं, यदि वे स्वतंत्र न हों अर्थात् यदि P(E ∩ F) ≠ P(E).P(F)
• यदि दो ऐसी स्वतंत्र घटनाएँ घटती हैं जिनकी प्रायिकता शून्येतर है, तो वह परस्पर अपवर्जी नहीं हो सकती हैं। विलोमतः यदि दो शून्येतर प्रायिकता वाली परस्पर अपवर्जी घटनाएँ घटती हैं, तो वह स्वतंत्र नहीं हो सकती हैं।
• दो यादृच्छिक परीक्षण स्वतंत्र कहलाते हैं, यदि प्रत्येक घटना युग्म E और F के लिए, जहाँ E पहले परीक्षण से तथा F दूसरे परीक्षण से संबंधित हैं. घटनाओं E तथा F के एक साथ घटित होने की प्रायिकता, जब दोनों परीक्षण सम्पन्न किए जाएँ, प्रायिकता P(E) और P(F) के गुणनफल के बराबर होती हैं, जिनका परिकलन दोनों परीक्षणों के आधार पर अलग-अलग किया जाता है। अर्थात् P(E ∩ F) = P(E).P(F)
• तीन घटनाओं A, B और C को स्वतंत्र कहा जाता है यदि और केवल यदि
  P(A ∩ B) = P(A) P(B)
  P(A ∩ C) = P(A) P(C)
  P(B ∩ C) = P(B) P(C)
  और P(A ∩ B ∩ C) = P(A) P(B) P(C)

यदि उपरोक्त में से कम से कम एक भी शर्त सत्य नहीं होती है तो दी गई घटनाओं को स्वतंत्र नहीं कहा जाता है।

एक प्रतिदर्श समष्टि का विभाजन (Partition of A Sample Space):
घटनाएँ E₁, E₂, ...E_n, प्रतिदर्श समष्टि S के विभाजन को निरूपित करती हैं यदि वे पूर्णतः युग्मतः असंयुक्त हैं, समग्र हैं तथा उनकी प्रायिकता शून्येतर है।

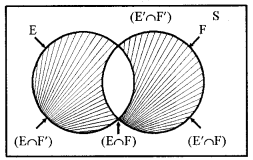
उदाहरणतः हम देखते हैं कि कोई घटना E और उसकी पूरक घटना E' प्रतिदर्श समष्टि S का विभाजन है क्योंकि E ∩ E' = और EUE' = S.
वेन आरेख चित्र से हम आसानी से प्रेक्षण कर सकते हैं कि यदि E और F किसी प्रतिदर्श समष्टि S के संगत कोई दो घटनाएँ हैं, तो {E F, E F} समुच्चय E का एक विभाजन है। समुच्चय {E' ∩ F, E ∩ F, E ∩ F'} समुच्चय E ∪ F का एक विभाजन है और समुच्चय {E ∩ F', E ∩ F E ∩ F E ∩ F} संपूर्ण प्रतिदर्श S का एक विभाजन है।

सम्पूर्ण प्रायिकता की प्रमेय (Theorem of Total Probability):
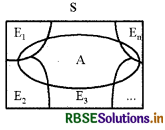
माना कि {E₁, E₂, ...E_n} किसी प्रतिदर्श 'S', का एक विभाजन है अर्थात् E₁, E₂, ...E_n, परस्पर अपवर्जी और निःश्शेष घटनायें हैं। माना A एक ऐसी घटना है जिसकी प्रायिकता शून्येतर है तब
P(A) = P(E) P(A|E₁) + P(E) P(A|E₂) + .... + P(E) P(A|E_n)
= \(\sum_{j=1}^{n}\)P(E_j)P(A|E_j)

प्रमाणः-दिया गया है कि E₁, E₂, ...E_n, प्रतिदर्श समष्टि S का एक विभाजन है :
∴ S = E₁ ∪ E₁ ∪..... ∪ E_n .....(1)
और E_i ∩ E_j = Φ,∀ i, ≠ j = 1, 2, ..... n

हम जानते हैं कि किसी घटना A के लिए

A = A ∩ S
= A ∩ (E₁ ∪ E₂ ∪ .... ∪ E_n)
= (A ∩ E₁) (A ∩ E₂) ....(A ∩ E_n)
साथ ही A ∩ E_i, और A ∩ E_i, क्रमशः समुच्चयों E_i, और E_i,के

उपसमुच्चय हैं जो i ≠ j के लिए असंयुक्त है इसलिए i ≠ j, i,j= 1, 2 ....,n के लिए ARE, और ARE भी असंयुक्त
∴ P(A) = P[(A ∩ E₁) ∪ (A ∩ E₂) ∪ .... ∪ (A ∩ E_n)]
= P(A ∩ E₁) + (A ∩ E₂) + .... + (A ∩ E_n)

अब हम
P(A ∩ E_i) = P(E_i) P(A|E_j)
क्योंकि
P(E.) ≠ 0 ∀ i = 1, 2, ...., n

प्रायिकता के गुणन नियम द्वारा हम जानते हैं कि
इसलिए P(A) = P(E₁) P(A|E₁) + P(E₂) P(A|E₂) + .... + P(E_n) P(AE_n)
या P(A) = \(\sum_{j=1}^{n}\)P(E_j)P(A|E_j)

बेज़ प्रमेय (Bayes' Theorem):
प्रसिद्ध गणितज्ञ जॉन बेज़ ने प्रतिलोम प्रायिकता ज्ञात करने की समस्या का समाधान सप्रतिबंध प्रायिकता के उपयोग द्वारा किया है। उनके द्वारा बनाया गया सूत्र 'बेज़-प्रमेय' के नाम से जाना जाता है जो उनकी मृत्योपरांत 1763 में प्रकाशित हुआ था। बेज़-प्रमेय के कथन व प्रमाण को आगे दिया गया है।

कथन (Statement)
यदि E₁, E₂,...., E_n, अरिक्त घटनाएँ हैं जो कि प्रतिदर्श समष्टि S के विभाजन का निर्माण करती हैं अर्थात् E₁, E₂,....,E_n, युग्मतः असंयुक्त हैं और E₁ ∪ E₂,.... ∪ E_n = S और A कोई ऐसी घटना है जिसकी प्रायिकता शून्येतर है, तो

टिप्पणी :
बेज़-प्रमेय के अनुप्रयोग में निम्नलिखित का उपयोग करते हैंयहाँ पर घटनाओं E₁, E₂,...., E_n को परिकल्पनाएँ (hypotheses) कहते हैं।

P(E_i) को परिकल्पना E_j, की पूर्वकालीन (a prior) प्रायिकता कहते हैं। सप्रतिबंध प्रायिकता P(EA) को परिकल्पना E की उत्तरकालीन (a posteriori) प्रायिकता कहते हैं। बेज़ प्रमेय को कारणों की प्रायिकता का सूत्र भी कहा जाता है। बेज़-प्रमेय की विविध परिस्थितियों में उपयोगिता है। इनमें से कुछ को निम्नलिखित उदाहरणों में स्पष्ट किया गया है।

यादृच्छिक चर और इसके प्रायिकता बंटन (Random Variables and its Probability Distribution)
यादृच्छिक चर (Random Variable)
एक ऐसा चर जिसका मान संयोग से निर्धारित होता है, यादृच्छिक चर कहलाता है। यहाँ पर संयोग से निर्धारित का अर्थ है कि चर के मान यादृच्छिक प्रयोग के परिणामों से निर्धारित होते हैं अर्थात् किसी यादृच्छिक प्रयोग के सम्भावित परिणाम ही यादृच्छिक चर के मान हो सकते हैं।

परिभाषा-एक यादृच्छिक चर वह फलन होता है जिसका प्रान्त किसी यादृच्छिक का प्रतिदर्श समष्टि होता है। उदाहरण के लिये एक सिक्के को दो बार अनुक्रम में उछाले जाने के परीक्षण पर विचार कीजिये। इस परीक्षण का प्रतिदर्श समष्टि है :
S = {HH, HT, TH, TT}

यदि X, प्राप्त चितों की संख्या को व्यक्त करता है तो X एक यादृच्छिक चर है और प्रत्येक परिणाम के लिए इसका मान निम्न प्रकार से दिया गया है :
X(HH) = 2, X(HT) = 1,X(TH) = 1, X(TT) = 0

एक ही प्रतिदर्श समष्टि पर एक से अधिक यादृच्छिक चर परिभाषित किए जा सकते हैं । उदाहरण के लिए माना कि Y प्रतिदर्श समष्टि S के प्रत्येक परिणाम के लिए चितों की संख्या से पटों की संख्या के घटाव को व्यक्त करता है। तब
Y(HI) = 2, Y(HI) = 0, Y(TH) = 0, Y(TT) = -2
अतः एक प्रतिदर्श समष्टि S में X और Y तो भिन्न यादृच्छिक चर परिभाषित किए गए हैं।

एक यादृच्छिक चर की प्रायिकता बंटन (Probability Distribution of A Random Variable):
किसी यादृच्छिक चर के सभी मानों एवं उनकी संगत प्रायिकताओं को लेकर प्राप्त बंटन प्रायिकता बंटन कहलाता है। इसे हम निम्नलिखित उदाहरण के माध्यम से समझने का प्रयास करेंगे। माना कि दस परिवार f₁ f₂, .....f₁₀, हैं जिनके सदस्यों की संख्या क्रमशः 3, 4, 3, 2, 5,4, 3, 6,4,5 है। यहाँ पर हम एक परिवार का चुनाव करें और उसके सदस्यों की संख्या को नोट कर X से व्यक्त कीजिए । यहाँ पर स्पष्ट है कि X एक यादृच्छिक चर है जिसे निम्न प्रकार से परिभाषित किया गया है :
X(f₁) = 3, X(f₂) = 4, X(f₃) = 3, X(f₄) = 2, X(f₅) = 5
X(f₆) = 4, X(f₇) = 3, X(f₈) = 6, X(f₉) = 4, X(f₁₀) = 5
अतः 2, 3, 4, 5, 6 में से X कोई भी मान ले सकता है। अब X का मान 2 होगा जबकि परिवार f₄ को चुना गया हो। X का मान 3 हो सकता है जब f₁, f₃, f₇ में से किसी प्रकार परिवार को चुना जाए। इसी प्रकार :
X = 4, जब परिवार f₂f₆ या f₉, को चुना जाएगा
X = 6, जब परिवार f₅ या f₁₀ को चुना जाएगा
और X = 6, जब परिवार को चुना जाएगा चूँकि हमने माना है कि प्रत्येक परिवार का चुना जाना समसंभाव्य है, इसलिए परिवार के चुने जाने की प्रायिकता \(\frac{1}{10}\) है।
अतः X का मान 2 होने की प्रायिकता \(\frac{1}{10}\)
हम इसे इस प्रकार से लिख सकते हैं :
P(X = 2) = \(\frac{1}{10}\)

इसी प्रकार से

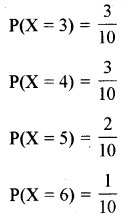
इस प्रकार का विवरण जिसमें यादृच्छिक चर के साथ उसकी संगत प्रायिकताओं को लिखा जाता है, को यादृच्छिक चर X की प्रायिकता बंटन कहते हैं। व्यापकतः एक यादृच्छिक चर X की प्रायिकता बंटन को निम्न प्रकार से परिभाषित किया जाता है-

परिभाषा : किसी यादृच्छिक चर X की प्रायिकता बंटन संख्याओं की निम्नलिखित प्रणाली (निकाय) होती है
X: x₁, x₂, ..... x_n.
P(X) : P₁, P₂. ..... P_n,
जहाँ p_i>0, \(\sum_{i=1}^{n}\)P_i = 1, i = 1, 2, ...., n
वास्तविक संख्याएँ x₁, x₂, ..... x_n. यादृच्छिक चर X के संभव मान (मूल्य) हैं और p_i(i = 1, 2, .....n) यादृच्छिक चर X का मान x होने की प्रायिकता है अर्थात् P(X = x_i) = P_i,

यादृच्छिक चर का माध्य (Mean of a Random Variable):
परिभाषा—माना कि X एक यादृच्छिक चर है जिसके संभावित मान x₁, x₂, ..... x_n, की क्रमशः प्रायिकता P₁, P₂. ..... P_n है। X का माध्य, जिसे µ से व्यक्त करते हैं संख्या \(\sum_{i=1}^{n}\)x_iP_i, द्वारा प्राप्त होती है अर्थात् ४ का माध्य, चर X, के संभावित मानों का भारित औसत होता है, जब प्रत्येक मान को उसकी संगत प्रायिकता से भारित किया गया हो। यादृच्छिक चर X के माध्य को X की प्रत्याशा (Expectation) भी कहते हैं जिसे E(X) से व्यक्त करते हैं अतः

E(X) = µ = \(\sum_{i=1}^{n}\)x_iP_i = x₁P₁ + x₂P₂ + ..... + x_nP_n, अन्य शब्दों में यादृच्छिक चर X का माध्य या प्रत्याशा X के सभी संभावित मानों का
उनकी संगत प्रायिकताओं के गुणन का योग होता है।

यादच्छिक चर का प्रसरण (Variance of A Random Variable):
परिभाषा यदि X एक यादृच्छिक चर है जिसके संभावित मूल्य x₁, x₂, ..... x_n, की संगत प्रायिकताओं p(x₁), p(x₂), .... p(x_n) के साथ विद्यमान हैं।

माना कि µ = E(X), X का माध्य है। X का प्रसरण Var(X) या σ द्वारा निरूपित, को निम्न प्रकार से परिभाषित किया जाता है :
σ_x² = Var(X) = \(\sum_{i=1}^{n}\)(x_i - µ)²p(x_i)
ऋणेतर संख्या
σ_x = \(\sqrt{{Var}}(\mathrm{X})=\sqrt{\sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2} p\left(x_{i}\right)}\)
को यादृच्छिक चर X का मानक विचलन (standard deviation) कहते हैं।

यादृच्छिक चर का प्रसरण ज्ञात करने का अन्य सूत्र हम जानते हैं कि

बरनौली परीक्षण (Bernoulli Trials):
परिभाषा—एक यादृच्छिक प्रयोग के परीक्षणों को बरनौली परीक्षण कहते हैं यदि वे अग्रलिखित शर्तों को संतुष्ट करते हैं :

• परीक्षणों की संख्या निश्चित (परिमित) होनी चाहिए।
• परीक्षण स्वतंत्र होने चाहिए
• प्रत्येक परीक्षण के तथ्यतः दो ही परिणाम होने चाहिए, सफलता या असफलता
• किसी परिणाम की प्रायिकता प्रत्येक परीक्षण में समान रहनी चाहिए। उदाहरण के तौर पर एक पासे को 30 बार उछालना 30 बरनौली परीक्षणों की स्थिति है, जिसमें प्रत्येक परीक्षण का परिणाम सफलता (माना कि. सम संख्या प्रकट होना) या असफलता (विषम संख्या प्रकट होना) है और सभी 30 उछालों में सफलता की प्रायिकता (p) एक समान है। निःसन्देह पासे की उत्तरांतर उछालें स्वतंत्र प्रयोग होते हैं। यदि पासा न्याय्य है और इसके छः फलकों पर छः संख्याएँ 1 से 6 तक लिखी

गई है तो p = \(\frac{1}{2}\) सफलता की और q = 1 - p = \(\frac{1}{2}\) असफलता की प्रायिकता है।

द्विपद बंटन (Binomial Distribution):
माना कि p तथा व किसी घटना E की एक परीक्षण में क्रमशः सफलता और असफलता की प्रायिकता है, इस घटना के स्वतंत्र, पुनरावर्त बरनौली अभिप्रयोगों पर विचार करें, यदि n स्वतंत्र परीक्षणों में x सफल परीक्षण है तब (n-x) परीक्षण असफल होंगे तब इन परीक्षणों की प्रायिकता ⁿC_xp^xq^n-x द्वारा दी जाती है तथा इस परिणाम को द्विपद बंटन कहते हैं।

उपपत्ति-माना कि एक अभिप्रयोग में एक घटना की सफलता की प्रायिकता p और असफलता की प्रायिकता q है, यदि इस अभिप्रयोग को n बार दोहराया जाये तो घटना की सफलता की संख्या 0, 1, 2, 3, 4, ......n हो सकती है। अब, यादृच्छिक रूप से चयनित x परीक्षणों में सभी के सफलता की प्रायिकता
=p.p.p.p.p.........(x बार)
= p^x

पुनःn स्वतंत्र पुनरावर्त परीक्षणों में शेष परीक्षण असफल होंगे अतः (n-x) परीक्षणों के सभी में असफलताओं की प्रायिकता
=q.q.q.q.q.........(n - x) बार
= q^n-x

अब n सफलताओं और (n-x) असफलताओं की प्रायिकता
= p^x.q^n-x

परन्तु स्वतंत्र पुनरावर्त परीक्षणों में से सफलताओं को ⁿC द्वारा चुना जा सकता है। अर्थात् x सफलतायें ⁿC_x, विविध क्रमों से प्राप्त हो सकती हैं जो कि सभी परस्पर अपवर्जी होंगी अतः प्रायिकता के योग प्रमेय से n परीक्षणों में 'x' सफलताओं की अभीष्ट प्रायिकता
p(x) = ⁿC_xq^n-xp^x,
या p(X = x) = ⁿC_xq^n-xp^x
जहाँ पर x = 0, 1, ............. n
और q = 1 - p
इस p(x) को द्विपद बंटन का प्रायिकता फलन कहते हैं। एक nबरनौली परीक्षणों और प्रत्येक परीक्षण में सफलता की प्रायिकता P वाले द्विपद बंटन को B(n, p) से व्यक्त करते हैं।

→ घटना F के घटित होने पर, घटना E की प्रतिबन्धित प्रायिकता P(E/F) से व्यक्त करते हैं तथा
P (E|F) = \(\frac{P(E \cap F)}{P(F)}\), P(F) ≠ 0

→ 0 ≤ P (EF) ≤ 1

→ P(E' |F) = 1 – P(E|F)

→ P((E ∪ F)|G) = P(E|G) + P(F|G) - P((E ∩F)|G)

→ P(E ∩ F) = P(E) P(F|E), P(E) ≠ 0
P(E ∩ F) = P(F). P(EF), F(F) ≠ 0

→ यदि E तथा F दो स्वतन्त्र घटनाएँ हैं तब
P(E ∩ F) = P(E), P(F) . P(EF) = P(E), P(F) ≠0
.. P(F|E) = P(F), P(E) ≠ 0

→ यदि {E₁, E₂.....E_n} प्रतिदर्श समष्टि S का एक विभाजन है और प्रत्येक घटना E₁, E₂,....E_n की प्रायिकता शून्येतर है। यदि A प्रतिदर्श समष्टि S के संगत एक घटना है, तब
P(A) = P(E) P(A|E₁) + P(E,) P(A|E₂) + .... + P(E) P (A|E_n)
= \(\sum_{j=1}^{n}\)P(E_j) P(A|E_j)

→ यदि E₁, E₂.....E_n, अरिक्त घटनाएँ हैं जो कि प्रतिदर्श समष्टि S के विभाजन का निर्माण करती हैं अर्थात् E₁, E₂.....E_n, युग्मत: असंयुक्त है और E₁ ∪ E₂ ∪ ..... ∪ E_n = S तथा A कोई ऐसी घटना है जिसकी प्रायिकता शून्येतर है, तब
P(E_i/A) = \(\frac{\mathrm{P}\left(\mathrm{E}_{i}\right) \mathrm{P}\left(\mathrm{A} \mid \mathrm{E}_{i}\right)}{\Sigma \mathrm{P}\left(\mathrm{E}_{j}\right) \mathrm{P}\left(\mathrm{A} \mid \mathrm{E}_{j}\right)}\)

→ वह फलन जिसका प्रान्त किसी यादृच्छिक परीक्षण का प्रतिदर्श समष्टि होता है, यादृच्छिक चर कहलाता है।

→ यदि X एक यादृच्छिक चर है जिसमें संभावित मान x₁, x₂.....x_n, की प्रायिकताएँ क्रमशःp₁, p₂.....p_n हैं तो X का प्रायिकता वितरण है
im-9
जहाँ p_i > 0. \(\sum_{i=1}^{n}\)p_i, = 1, 1 = 1, 2, 3.....
तब X का माध्य µ निम्न प्रकार परिभाषित है
= \(\sum_{i=1}^{n}\)x_ip_i =E (X)
µ को X की प्रत्याशा भी कहते हैं।

→ X का प्रसरण Var(X) या σ²_x द्वारा व्यक्त करते हैं तथा
σ²_x = Var (X) = \(\sum_{i=1}^{n}\)(x_i - µ) p(x_i)
σ²_x = E (X - µ)²
तथा ऋणेतर संख्या
σ_x = \(\sqrt{{Var}(\mathrm{X})}=\sqrt{\sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2} p\left(x_{i}\right)}\)
को यादृच्छिक चर X का मानक विचलन कहते हैं।

→ Var(X) =E (X²) - [E(X)]²

→ एक यादृच्छिक प्रयोग के परीक्षणों को बरनौली परीक्षण कहा जाता है, यदि

• परीक्षणों की संख्या n परिमित हो।
• परीक्षण स्वतन्त्र हो ।
• प्रत्येक परीक्षण के केवल दो ही परिणाम अर्थात् सफलता या असफलता हो।
• किसी परिणाम की प्रायिकता प्रत्येक परीक्षण में समान हो।

→ बरनौली परीक्षण B (n, p), P (X = x) = ⁿC_x,p^xq^n-x, x = 0, 1, .... n (q = 1 - p).