RBSE Class 12 Maths Notes Chapter 13 Probability

These comprehensive RBSE Class 12 Maths Notes Chapter 13 Probability will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 13 Notes Probability

Introduction:
In earlier classes, we have studied the probability as a measure of uncertainty of events in a random experiment. Also axiomatic approach formulated by Russian Mathematician A.N. Kolmogorov (1903-1987) have been disscussed. In this chapter, we shall discuss the important concept of conditional probability of an event given that another event has occured, which will be helpful in understanding the Baye's theorem, multiplication rule of probability and independence of events. In the end of this chapter we will study an important discrete probability distribution which is known as Binomial distribution.

Meaning of Probability:
'Probability' or similar words we often use in our daily life as :
Today storm may come or this year least hope that Gaurav will be passed. These statements shows uncertainity. Mathematical measure of this uncertainity is called probability.
Example : If a coin is tossed then out of head and tail which one appear on top ? Its pre-estimation is not possible because both cases are equally, likely in such cases, we find what is the probability to get a specific result.

Conditional Probability:
If E and F are two events associated with a random experiment, then the probability of combined occurence of events E and F whereas event F has al¬ready occured, is multiplication of their probability. i.e., P(E ∩ F) = F(E).P\(\left(\frac{F}{E}\right)\)
Let, for any experiment sample space is S and its two events are E and F.
Let event E has happened and P(E) ≠ 0.
Since E ⊂ S and event E has happen so all elements of S cannot occur, only those elements of S occur which are exist in E. Thus, in this case reduced sample space will be E. Again, all elements of event E cannot occur, but elements of F which exit in E can occur. Set of these elements is F ∩ E or (E ∩ F).

Thus, probability of event F when event E has already happened p\(\left(\frac{F}{E}\right)\) means to find probability of E ∩ F whereas sample space is S.

Similarly, probability of event E when event F has already occurred is given by following formula :

 

Properties of Conditional Probability:
1. Let E and F are two events of a sample space S, then

2. If A and B are two events of a sample S and F is another event such that P(F) ≠ 0, then
P[(A ∪ B)/F] = P(A/F) + P(B/F) - P[(A ∩ B)/F]

Specially, if A and B are two mutually exclusive events then
P[(A ∪ B)/F] = P(A/F) + P(B/F) - P[A ∩ B)/F]

Specially, if A and B are two mutually exclusive events then
P[(A ∪ B)/F] = P(A/F) + P(B/F)

We know that
P[(A ∪ B)/F) = \(\frac{P[(A \cup B) \cap F]}{P(F)}\)
= \(\frac{P[(A \cap F) \cup(B \cap F)]}{P(F)}\)

By distribution law of union over intersection of

When A and B are mutually exclusive,
P[(A ∩ B)/F] = 0
⇒ P[(A ∪ B)/F] = P(A/F) + P(B/F)

Thus, when A and B are mutually events, then
P\(\left(\frac{A \cup B}{F}\right)\) = P(A/F) + P(B/F)

3. P(E'/F) = 1 - P(E/F)
We know that
P(S/F) = 1
⇒ P[E ∪ F)/F] = 1 [∵ S = E ∪ F]
⇒ P(E/F) + P(E'/F) = 1 [∵ E and F are mutuallly exclusive events]
Thus, P(E'/F) = 1 - P(E/F)

Multiplication Theorem on Probability:
Let E and F be two events associated with a sample space S, then the set E ∩ F denotes the happening of two events E and F.
Example:
In the test of drawing second card after one, we can find probability of compound events a king and a queen. To find probability of event EF use conditional probability which is denoted by P(E/F) and is written as :
P(E/F) = \(\frac{P(E \cap F)}{P(F)}\), P(F) ≠ 0
or P(E ∩ F) = P(F) - P(E/F) ...(i)

Similarly if event E is given then probability of F with condition is expressed as P\(\left(\frac{F}{E}\right)\) and can be written as:
P\(\left(\frac{F}{E}\right)=\frac{P(E \cap F)}{P(E)}\)
Joining two conditions (i) and (ii)
P(E ∩ F) = P(F).P\(\left(\frac{F}{E}\right)\) = P(E).P\(\left(\frac{F}{E}\right)\)
whereas P(E) ≠ 0 and P(F) ≠ 0
Above result is known as multiplication law of probability.

Multiplication Rule of Probability for more than two Events :
Let E, F and G are three events of sample space S then

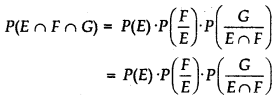
Thus, the multiplication rule of probability can be extended for four or more events.

Independent Events:
If A and B are two events such that the probability of occurrence of one of them is not affected by occur¬rence of the other. Such events are called independent events.
Two events A and B are said to be independent, if =P(A), provided P(B) * 0
P\(\left(\frac{A}{B}\right)\) = P(A), provided P(B) ≠ 0
and P\(\left(\frac{B}{A}\right)\) = P(B), provided P(A) ≠ 0

By multiplication theorem of probability
P\(\left(\frac{A}{B}\right)\) = P(A)P\(\left(\frac{B}{A}\right)\)

If A and B are independent events, then
P(A ∩ B) = P(A) P(B)

Note : Three events A, B and C are said to be mutually independent if
P(A ∩ B)=P(A). P(B)
P(B ∩ C) =P(B). P(C)
P(A ∩ C) = P(A). P(C)
and P(A ∩ B ∩ C) = P(A). P(B). P(C)
If at least one of the above is not true for three events, we say that the events are not independent.

Bayes’ Theorem:
Suppose, we have two bags A and B. Bag A contains 3 blue and 5 black balls and Bag B contains 6 red and 7 yellow balls. One ball is drawn at random from one of the bags. We can find the probability of selecting any of the bags (i.e. \(\frac{1}{2}\)) or probability of drawing a ball of a particular colour (say blue) from a particular bag (say Bag A). In other words, we can find the probability that the ball drawn is of a particular colour, if we are given the bag from which the ball is drawn. But, can we find the probability that the ball drawn is from a particular bag (say Bag B), if the colour of the ball drawn is given ? Here, we have to find the reverse probability of Bag B to be selected when an event occured after it is known.

Famous mathematician, John Bayes1 solved the problem of finding reverse probability by using conditional probability. The formula developed by him is known as 'Bayes theorem' which was published posthu¬mously in 1763. Before stating and proving the Bayes' theorem, let us first take up a definition and some preliminary results.

Partition of a sample space:
A set of events E₁, E₂, ..., E_n represents partition of a sample space S, if

• E_i ∩ E_j = Φ, i ≠ j, i, j = 1, 2, 3, ...........n
• E₁ ∪ E₂ ∪ E₃ ∪ ... ∪ E_n = S and
• P(E_i) > 0, ∀ i = 1, 2, 3, ..., n

In other words, the events E₁, E₂, ..., E_n represent a partition of the sample space S if they are pairwise disjoint, exhaustive and have non-zero probabilities.

Example :
Any non-empty event E and its complement £' form a partition of the sample space S.
∵ E ∩ E'= Φ
and E ∪ E' = S

Theorem of total probability:
Statement:
Let E₁, E₂, ..., E_n be a partition of the sample space S, and suppose that each of the events E₁, E₂, ..., E_n has non-zero probability of occurrence. Let A be any event associated with S, then

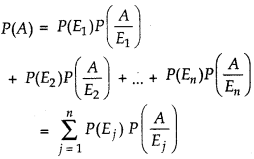
Proof :
Given that,
E₁, E₂, ..., E_n is a partition of sample space S.
E_i ∩ E_j = Φ ∀ i ≠ j, i, j = 1, 2, ..., n

We know that for any event A,
A = A ∩ S
= A ∩ (E₁ ∪ E₂∪ ... ∪ E_n)
= (A ∩ E₁) ∪ (A ∩ E₂) ∪ ... ∪ (A ∩ E_n)
Also A ∩ E_i and A ∩ E_j are respectively the subsets of E_i and E_j. We know that E_i and E_j are disjoint, for i ≠ j, therefore, A ∩ E_i and A ∩ E_j are also disjoint for all
∴ i ≠ j, i, j = 1, 2, ..., n.
∴ P(A) = P[(A n E₁) ∪ (A n E₂) ∪ ... ∪ (A ∩ E₁)]
= P(A ∩ E₁) + P(A ∩ E₂) + ... + P(A ∩ E_n)
By multiplication theorem of probability, we have

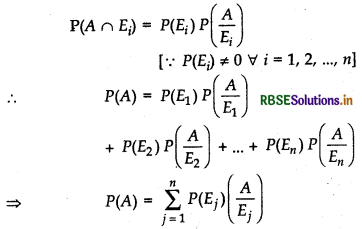
Bayes’ Theorem’s Statement:
If E₁, E₂,..., E_n are non empty events which constitute a partition of sample
space S, i.e., E₁, E₂, ..............E_n are pairwise disjoint and
E₁ ∪ E₂ ∪ ... ∪ E_n = S and A is any event of non-zero probability, then

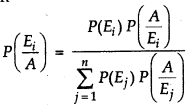
Proof:
We know that

Note :

• E₁, E₂,..., E_n are called hypotheses.
• P(E_i) is called the priori probability of hypothesis E_j and the conditional probability P(E_i/ A) is called a posteriori probability of the hypothesis E_j.

Random Variables Distributions:
A random variable is a function whose domain is sample space of any random experiment.
e.g., tossing a coin two times
Following is the sample space of this experiment:
S = {HH, HT, TH, TT}

If X denotes number of head obtained then X is a random variable and for each result its value is given as:
X(HH) = 2, X(HT) = 1, X(TH) = 1, X(TT) = 0
In one sample space, more than one random variable can be defined. Let y denotes number of heads-number of tails for each result of sample space S then
Y(HH), = 2, Y(HT) = 0, Y(TH) = 0, Y(TT) = - 2
Thus, in sample space S, X and Y are defined as two different random variable.

Probability distribution of a random variable:
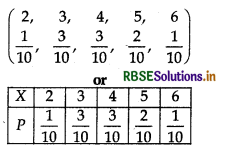
A tabular distribution gives the values of the random variable along with the corresponding probabilities is called its probability distribution. Let 10 families, whose number of families are respectively 3, 4, 3, 2, 5, 4, 3, 6, 4, 5. Thus random variable can accept any value from X, 2,3,4,5 and 6 which depends on which family is selected. Out of these 10 families, only one family is f₄ which has 2 members. Three families are such that f₁, f₃, f₅ each has 3 members. Three families are such that f₂, f₆, f₉ each has 4 members. Two families f₅ and f₁₀ are such that each has 5 members and only one family f₈ such that which has 6 members. Thus value of X will be only 2, if f₄ is selected. Since selection of each family is equally likely.

Thus probability that/4 is selected is \(\frac{1}{10}\). Again, value of random variable X will be 3, if selected family is f₄ or f₃ or f₇. It means
P(X = 2) = \(\frac{1}{10}\), P(X = 3) = \(\frac{3}{10}\), P(X = 4) = \(\frac{3}{10}\),
P(X = 5) = \(\frac{2}{10}\).P(X = 6)= \(\frac{1}{10}\)

Definition :
The probability distribution of random Variable X is system of following numbers:

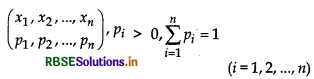
Here, possible values of random variable X are real numbers x₁ x₂, x₃ ..., x_n and p_i (i = 1,2,..., n) is probability of acception xi by random variable X. It can be shown as:

Probability distribution:
A tabular distribution given the values of the random variable along with the correspond¬ing probabilities is called its probability distribution.

Note: If X = x_i and P(X): p₁ p₂, p₃ ... p_n where p_i > 0 and \(\sum_{i=1}^{n}\)p_i = 1; i = 1,2,... n.

Meaning of a random variable:
In many problems, it is desirable to describe some feature of the random variable by mean of a single number that can be computed from its probability distribution. Few such numbers are mean, mode and median. In this section, we shall discuss mean only.
Let X be a random variable whose possible values x₁, x₂, .........,x_n occur with probabilities p₁, p₂,... p_n, respectively.

The mean of a random variable X is also called expectation of X, denoted by E(X).
E(X) = µ = \(\sum_{i=1}^{n}\)x_iE_i
= x₁p₁ + x₂p₂ +... + x_np_n
Thus, the mean of X, denoted by p, is the weighted aver-age of the possible values of X, each value being weighted by its probability with which it occurs.

Variance of a random variable:
Let X be a random variable whose possible values x₁ x₂,... x_n occur with probabilities p₁, p₂,... p_n respectively. Then the variance of X, is denoted by
var(X) or σ_x² = var(X)
= E(X - µ)² = \(\sum_{i=1}^{n}\)(x_i - µ)²P_i

The non-negative number σ_x is called the standard deviation of the random variable X.
σ_x = \(\sqrt{{Var}(X)}\)
= +\(\sqrt{\sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2} p_{i}}\)

Another formula to find the variance:
We know that,

Bernoulli Trials and Binomial Distribution:
Bernoulli trials:
The outcome of any trial is independent of the outcome of any other trial. In each of such trials, the probability of success or failure, remains constant. Such independent trials which have only two outcomes usually referred as 'success' or 'failure' are called Bernoulli trials.

Trials of a random experiment are called Bernoulli trials, if they satisfy the following conditions:

• There should be a finite number of trials.
• The trials should be independent.
• Each trials has exactly two outcomes: success or failure.
• The probability of success remains the same in each trial.

Binomial distribution:
The probability distribution of number of successes in an experiment consistiing of n Bernoulli trials may be obtained by distribution of binomial expansion of (q + p)". Hence, this distribution of number of successes X can be written as:

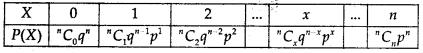
The above probability distribution is known as binomial distribution with parameters n and p, because for given values of n and p, we can find the complete probability distribution.

The probability of x successes P(X = x) is also denoted by P(x) and is given by
P(x) = ⁿC_x q^n-x p^x
x =0, 1,...., n{q = 1 - p)
This P(x) is called the probability function of the binomial distribution. A binomial distribution with n-Bernoulli trials and probability'’ of success in each trial as p, is denoted by B (n, p).

→ The conditional probability of an event A, given the occurrence of the given event B is given by:
P\(\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}\); P(B) ≠ 0
Similarly, P\(\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}\); P(B) ≠ 0

→ 0 ≤ P\(\left(\frac{A}{B}\right)\) ≤ 1, P\(\left(\frac{\bar{A}}{B}\right)\) = 1 - P\(\left(\frac{A}{B}\right)\)

→ If A and B be two events of sample space S and F be any other events such that P(F) ≠ 0, then
P{(A ∪ B)/F} = P(A/F) + P(B/F) - P\(\left(\frac{A \cap B}{F}\right)\)
Specially, if A and B are disjoint events, them
P(A ∪ B)/F) = P(A/F) + P(B/F)

→ Multiplication Theorem on Probability
P(A ∩ B) = P(A)P\(\left(\frac{B}{A}\right)\)
P(A) ≠ 0 or P(A ≠ B)
= P(B)P\(\left(\frac{A}{B}\right)\); P(B) ≠ 0.

→ If A and B be two independent events, then
P\(\left(\frac{A}{B}\right)\) = P(A),P(A) ≠ 0;
P\(\left(\frac{A}{B}\right)\) = P(A),P(B) ≠ 0;
and P(A ∩ B) = P(A)P(B).

→ Theorem of Total Probability: Let {A₁ A₂,............... A_n} be a partition of a sample space and suppose that each of A₁ A₂,............... A_n has non-zero probability. Let E be any event associated with S, then
P(E) = P(A₁)P\(\left(\frac{E}{A_{1}}\right)\) + P(A₂)P\(\left(\frac{E}{A_{2}}\right)\) + .............. + P(A_n)P\(\left(\frac{E}{A_{n}}\right)\)
= \(\sum_{i=1}^{n}\)P(A_i)P\(\left(\frac{E}{A_{i}}\right)\)

→ Bayes' Theorem : If A₁ A₂,............... A_n are events which constitute a partition of sample space, S, i.e., A₁ A₂,............... A_n are pairwise disjoint and A₁ ∪ A₂ ∪ ............... ∪ A_n = S and E be any event with non-zero probability, then
P(A_i)P\(\left(\frac{E}{A_{i}}\right) = \frac{P\left(A_{i}\right) P\left(\frac{A_{i}}{E}\right)}{\sum_{i=1}^{n} P\left(A_{i}\right) P\left(\frac{A_{i}}{E}\right)}\); i = 1, 2, 3............,n

→ A random variable is a real valued function whose domain is the sample space of a random experiment.

→ The probability distribution of a random variable X is the system of numbers:

where p_i > 0, \(\sum_{i=1}^{n}\)p_i = 1; i = 1,2, ...................,n

→ Let X be a random variable whose possible values x₁ x₂, .................. x_n occur with probabilities p₁, p₂, .............. p_n respectively.
(a) The mean of X, denoted by p, is the number \(\sum_{i=1}^{n}\)x_ip_i
The mean of a random variable X is also called the expectation of X, denoted by E(X).

(b) Variance of X = var(X) = σ_x² = E(X - µ)² = \(\sum_{i=1}^{n}\)(x_i - µ)² p_i

(c) var(X) =E(X²) - {E(X)}²
The non-negative number
σ_x = +\(\sqrt{{var}(x)}\) = +\(\sqrt{\sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2}\left(x_{i}\right)}\) is called the standard deviation of the random variable X.

→ Trials of-a random experiment are called Bernoulli trials, if they satisfy the following conditions :

• There should be a finite number of trials.
• The trials should be independent.
• Each trial has exactly two outcomes success or failure.
• The probability of success remains the same in each trial.

For Binomial distribution B{n, p), P(X = x) = ⁿC_x q^n-xp^x, x = 0,1,... n (where q = 1 - p)