RBSE Class 12 Maths Notes Chapter 12 रैखिक प्रोग्रामन

These comprehensive RBSE Class 12 Maths Notes Chapter 12 रैखिक प्रोग्रामन will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 12 Notes रैखिक प्रोग्रामन

भूमिका (Introduction):
कक्षा XI में हम दो चर राशियों वाले रैखिक असमिकाओं और रैखिक असमिकाओं के निकायों के आलेखीय निरूपण से हल निकालने के विषय में अध्ययन कर चुके हैं। गणित में कई अनुप्रयोगों में असमिकाओं/समीकरणों के निकाय सम्मिलित हैं। इस अध्याय में हम रैखिक असमिकाओं/समीकरणों के निकायों का वास्तविक जीवन की समस्याओं को हल करने में उपयोग करेंगे। एक फर्नीचर विक्रेता दो वस्तुओं जैसे पलंग और सोफासेट का व्यवसाय करता है। निवेश के लिए उसके पास रुपये 1,50,000 और रखने के लिए केवल 70 वस्तुओं के लिए स्थान है। एक पलंग पर रुपये 2,000 और एक सोफासेट पर रुपये 2,500 की लागत आती है, वह अनुमान लगाता है कि एक पलंग को बेचकर रुपये 300 और एक सोफासेट को बेचने पर रुपये 500 का लाभ कमा सकता है।

मान लीजिये कि वह सभी वस्तुओं को बेच सकता है जिनको कि वह खरीदता है तब वह जानना चाहता है कि कितने पलंग एवं सोफासेटों को खरीदना चाहिये जिससे उपलब्ध निवेश राशि पर उसका सकल लाभ अधिकतम हो। इस प्रकार की समस्याओं जिनमें सामान्य प्रकार की समस्याओं में लाभ का अधिकतमीकरण और लागत का न्यूनतमीकरण खोजने का प्रयास किया जाता है, इष्टतमकारी समस्याएँ कहलाती हैं। अतः इष्टतमकारी समस्या में अधिकतम लाभ, न्यूनतम लागत या संसाधनों का न्यूनतम उपयोग सम्मिलित है। रैखिक प्रोग्रामन समस्याएँ एक विशेष लेकिन एक महत्त्वपूर्ण प्रकार की इष्टतमकारी समस्या है और उपरोक्त उल्लिखित इष्टतमकारी समस्या भी एक रैखिक प्रोग्रामन समस्या है। उद्योग, वाणिज्य, प्रबंधन, विज्ञान आदि में विस्तृत सुसंगतता के कारण रैखिक प्रोग्रामन समस्याएँ अत्यधिक

रैखिक प्रोग्रामन समस्या और उसका गणितीय सूत्रीकरण (Linear Programming Problem And Its Mathematical Formulatic)
हम अपना विचार उपरोक्त उदाहरण के साथ प्रारम्भ करते हैं जो कि दो चर राशियों वाली समस्या के गणितीय प्रतिरूप का मार्गदर्शन करेगा।
इस उदाहरण में हमने ध्यानपूर्वक देखा कि

• व्यापारी अपनी धनराशि से पलंग या सोफासेट या दोनों खरीदकर लाभ कमा सकता है।
• उपरोक्त वस्तुओं को खरीदने के लिये उसके पास सीमित स्थान एवं अधिकतम निवेश की सीमा है। 

मान लीजिए कि वह कोई पलंग नहीं खरीदता केवल सोफासेट के खरीदने का निश्चय करता है, इसलिए वह 1,50,000 2,500 या 60 सोफासेट को खरीद सकता है। इस स्थिति में उसका सकल लाभ रुपये (500 × 60) या रुपये 30,000 होगा। मान लीजिए कि वह कोई सोफासेट न खरीदकर केवल पलंग ही खरीदने का चयन करता है। तब वह अपनी उपलब्ध रुपये 1,50,000 की राशि में 1,50,000: 2,000 अर्थात् 75 पलंग ही खरीद सकता है। परन्तु वह केवल 70 नगों को ही रख सकता है। अतः वह 70 पलंग मात्र खरीदने के लिए बाध्य होगा। जिससे सकल लाभ रुपये 70 × 300 अर्थात् रुपये 21,000 ही होगा। ऐसी और भी बहुत सारी संभावनायें हैं।

उदाहरण के लिये वह 20 सोफासेट और 50 पलंग खरीदने का चयन कर सकता है, क्योंकि उसके पास 70 वस्तुओं को रखने का स्थान उपलब्ध है। इस स्थिति में उसका कुल सकल लाभ रुपये (20 × 500 + 50 × 300) अर्थात् रुपये (10,000 + 15,000) = रुपये 25,000 इत्यादि। अतः हम ज्ञात करते हैं कि फर्नीचर व्यापारी विभिन्न चयन विधियों के द्वारा अपनी धनराशि का निवेश कर सकता है और विभिन्न निवेश योजनाओं को अपनाकर विभिन्न लाभ कमा सकेगा। अब समस्या इस बात की है कि उसे अपनी धनराशि को अधिकतम लाभ प्राप्त करने के लिए किस प्रकार निवेश करना चाहिए? इस प्रश्न का उत्तर जानने के लिये हमें समस्या का गणितीय सूत्रीकरण करने का

समस्या का गणितीय सूत्रीकरण (Mathematica Formulation of The Problem)
माना कि पलंगों की संख्या x और सोफासेटों की संख्या y है जिन्हें फर्नीचर विक्रेता खरीदता है। स्पष्टतःx तथा y ऋणेतर हैं, अर्थात् x ≥ 0 (ऋणेतर व्यवरोध) ....(1)
y ≥ 0 ....(2)

क्योंकि पलंगों और सोफासेटों की संख्या ऋणात्मक नहीं हो सकती है। विक्रेता के पास अधिकतम धनराशि (यहाँ पर रुपये 1,50,000 है) का निवेश करने का व्यवरोध है और पास रखने की अधिकतम वस्तुयें 70
गणितीय रूप में व्यक्त करने पर
2,000 x+2,500 y ≤ 1,50,000 (निवेश व्यवरोध) 
या 20x + 25y ≤ 1,500
या 4x + 5y ≤ 300 ....(3)
x + y ≤ 70 (संग्रहण व्यवरोध) ....(4) 

व्यवसायी इस प्रकार से निवेश करना चाहता है उसका लाभ z (माना) अधिकतम हो और जिसे x तथा y के फलन के रूप में निम्न प्रकार से व्यक्त किया जा सकता है
z = 300x + 500y (उद्देश्य फलन कहलाता है) दी गयी समस्या अब गणितीय रूप में परिवर्तित हो जाती है। 
z = 300x + 500y का अधिकतमीकरण कीजिये जहाँ व्यवरोध निम्नलिखित है
4x + 5y ≤ 300
x + y ≤ 70
x ≥ 0, y ≥ 0 
ऐसी समस्याओं को रैखिक प्रोग्रामन समस्या कहते हैं। अर्थात् एक रैखिक प्रोग्रामन समस्या वह समस्या है जो कि x एवं y जैसे चरों के एक रैखिक फलन z (जोकि उद्देश्य फलन कहलाता है) का इष्टतम सुसंगत/अनुकूलतम सुसंगत मान (अधिकतम या न्यूनतम मान) ज्ञात करने से संबंधित है। 

रैखिक प्रोग्रामन समस्याओं को हल करने की आलेखीय विधि (Graphical Method of Solving Linear Programming Problems)
अब हम पलंगों और सोफासेटों में निवेश की समस्या का उल्लेख करेंगे। इस समस्या को हम आरेख द्वारा हल करेंगे। रैखिक असमीकरणों के रूप प्रदत्त व्यवरोधों का आरेख खींचने पर
4x + 5y ≤ 300
x + y ≤ 70 ....(4)
y ≥ 0 इस निकाय का आरेख (छायांकित क्षेत्र) में असमीकरणों (1) से (4) तक के द्वारा नियत सभी अर्धतलों के उभयनिष्ठ बिन्दुओं से निर्मित है। छायांकित क्षेत्र में प्रत्येक बिन्दु विक्रेता को पलंगों और सोफासेटों में निवेश करने के लिए सुसंगत विकल्प प्रस्तुत करता है.। इसलिये यह क्षेत्र समस्या का सुसंगत क्षेत्र कहलाता है। जैसाकि आकृति में दिखाया गया है, इस क्षेत्र का प्रत्येक बिन्दु समस्या का सुसंगत हल कहलाता है। अतः हम निम्न को परिभाषित करते हैंसुसंगत क्षेत्र प्रदत्त समस्या के लिए एक रैखिक प्रोग्रामन समस्या के ऋणेतर व्यवरोध x, y ≥ 0 सहित सभी व्यवरोधों द्वारा नियत उभयनिष्ठ क्षेत्र संसुगत क्षेत्र (या हल क्षेत्र) कहलाता है।आकृति में क्षेत्र OCEB (छायांकित) समस्या के लिए सुसंगत क्षेत्र है। सुसंगत क्षेत्र के अतिरिक्त जो क्षेत्र है उसे असुसंगत क्षेत्र कहते हैं।

सुसंगत हल समूह सुसंगत क्षेत्र के अंतःभाग तथा सीमा के सभी बिंदु व्यवरोधों के सुसंगत हल कहलाते हैं। आकृति में सुसंगत क्षेत्र OCEB के अंत:भाग तथा सीमा के सभी बिंदु समस्या के संसुगत हल प्रदर्शित करते हैं । उदाहरण के लिए बिंदु (50, 20) समस्या का एक सुसंगत हल है और इसी प्रकार बिंदु (0, 60), (75,0) इत्यादि भी हल हैं। सुसंगत हल के बाहर का कोई भी बिंदु असुसंगत हल कहलाता है। उदाहरण के लिए बिंदु (80, 50) समस्या का असुसंगत हल है।

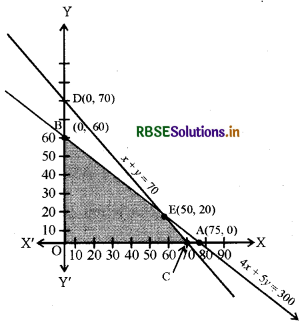
इष्टतम/अनुकूलतम(सुसंगत ) हल : सुसंगत क्षेत्र में कोई बिंदु जो उद्देश्य फलन का इष्टतम मान (अधिकतम या न्यूनतम) दे, एक इष्टतम हल कहलाता है। अब हम देखते हैं कि सुसंगत क्षेत्र OCEB में प्रत्येक बिंदु (1) से (4) तक में प्रदत्त सभी व्यवरोधों को संतुष्ट करता है और ऐसे अनंत बिंदु हैं । यह स्पष्ट नहीं है कि हम उद्देश्य फलन Z = 300x+ 500y के अधिकतम मान वाले बिंदु को किस प्रकार ज्ञात करने का प्रयास करें। इस स्थिति को हल करने के लिए हम निम्न प्रमेयों का उपयोग करेंगे जो कि रैखिक प्रोग्रामन समस्याओं को हल करने में मूल सिद्धांत (आधारभूत) है। इन प्रमेयों की उपपत्ति इस पुस्तक की विषय-वस्तु से बाहर है।

प्रमेय 1 माना कि एक रैखिक प्रोग्रामन समस्या के लिए R सुसंगत क्षेत्र (उत्तल बहुभुज) है और माना कि Z = ax + by उद्देश्य फलन है। जब Z का एक इष्टतम मान (अधिकतम या न्यूनतम) हो जहाँ व्यवरोधों से संबंधित चर x और y रैखिक असमीकरणों द्वारा व्यक्त हो तब यह इष्टतम मान संसुगत क्षेत्र के कोने (शीर्ष) पर अवस्थित होने चाहिए।

प्रमेय 2 माना कि एक रैखिक प्रोग्रामन समस्या के लिए R सुसंगत क्षेत्र है तथा Z= ar+ by उद्देश्य फलन है। यदि र परिबद्ध क्षेत्र हो तब उद्देश्य फलन Z,R में दोनों अधिकतम और न्यूनतम मान रखता है और इनमें से प्रत्येक R के कोनीय (comer) बिंदु (शीर्ष) पर स्थित होता है। उपरोक्त उदाहरण में परिबद्ध (सुसंगत) क्षेत्र के कोनीय बिंदु 0,C, E और B हैं और बिंदुओं के निर्देशांक ज्ञात करना सरल है यथा (0,0), (70, 0), (50, 20) और (0, 60) क्रमशः कोनीय बिंदु हैं। अब हमें इन बिंदुओं पर, Z का मान ज्ञात करना है। 
वह इस प्रकार है :

हम निरीक्षण करते हैं कि व्यवसायी को निवेश योजना (0, 60) अर्थात् केवल 60 सोफासेटों को खरीदने में अधिकतम लाभ होगा। इस विधि में निम्न पदों का समाविष्ट है :

• रैखिक प्रोग्रामन समस्या का सुसंगत क्षेत्र ज्ञात कीजिए और उसके कोनीय बिंदुओं (शीर्ष) को या तो निरीक्षण से अथवा दो रेखाओं के प्रतिच्छेद बिंदु को दो रेखाओं की समीकरणों को हल करके उस बिंदु को ज्ञात कीजिए। 
• उद्देश्य फलन Z= ax + by का मान प्रत्येक कोनीय बिंदु पर ज्ञात कीजिए और मान लो कि M और m, क्रमशः इन बिंदुओं पर अधिकतम तथा न्यूनतम मान प्रदर्शित करते हैं।
  • जब सुसंगत क्षेत्र परिबद्ध है,M और m,z के अधिकतम और न्यूनतम मान हैं।
  • ऐसी स्थिति में जब सुसंगत क्षेत्र अपरिबद्ध हो तो हम निम्नलिखित विधि का उपयोग करते हैं
    (a) M को Z का अधिकतम मान लेते हैं यदि x + by > M द्वारा प्राप्त अर्ध तल का कोई बिंदु सुसंगत क्षेत्र में न पड़े अन्यथा Z कोई अधिकतम मान नहीं है।
    (b) इसी प्रकार m, को Z का न्यूनतम मान लेते हैं यदि ax + by < m द्वारा प्रदत्त खुले अर्धतल और सुसंगत क्षेत्र में कोई बिंदु उभयनिष्ठ नहीं है। अन्यथा Z का कोई न्यूनतम मान नहीं है।

रैखिक प्रोग्रामन समस्याओं के भिन्न प्रकार (Different Types of Linear Programming Problems)
रैखिक प्रोग्रामन समस्याओं को निम्नलिखित भागों में बाँटा जा सकता है

• उत्पादन सम्बन्धी समस्यायें
• आहार सम्बन्धी समस्यायें
• परिवहन सम्बन्धी समस्यायें

1. उत्पादन सम्बन्धी समस्यायें रैखिक प्रोग्रामन समस्याओं के इस भाग में हम ज्ञात करते हैं कि विभिन्न उत्पादनों के कितने नग बनाने में एक निश्चित जन शक्ति उत्पादन के लिये कितनी मशीनें पर्याप्त होंगी, उत्पादन पर कितना खर्च होगा, श्रम के घंटे, माल भण्डार गोदाम में प्रत्येक उत्पादन को रखने के लिये स्थान आदि को दृष्टि में रखते हुए अधिकतम लाभ कमाया जा सके। 

2. आहार सम्बन्धी समस्यायें इस प्रकार की समस्याओं में हम ज्ञात करते हैं कि विभिन्न प्रकार के घटक/पोषक तत्व आहार में कितनी मात्रा में प्रयोग किए जाएँ जिससे उसमें सभी पोषक तत्वों की न्यूनतम आवश्यक मात्रा कम से कम लागत पर प्राप्त हो।

3. परिवहन सम्बन्धी समस्यायें इस प्रकार की समस्याओं में हम परिवहन प्रणाली को तय करते हैं जिसमें संयंत्रों/कारखानों से विभिन्न बाजारों में उत्पादनों को भेजने में परिवहन व्यय न्यूनतम हो।

→ कुछ व्यवरोधों के अन्तर्गत किसी रैखिक फलन का न्यूनतमीकरण या अधिकतमीकरण करने की विधि को रैखिक प्रोग्रामन समस्या कहते हैं। रैखिक फलन को उद्देश्य फलन कहते हैं।

→रैखिक प्रोग्रामन समस्या विभिन्न प्रकार की होती है, जैसे

• आहार सम्बन्धी समस्या
• उत्पादन सम्बन्धी समस्या
• परिवहन सम्बन्धी समस्या

→ सभी व्यवरोधों के तथा ऋणेतर चरों x > 0, y  0 के उभयनिष्ठ क्षेत्र को सुसंगत क्षेत्र (feasible region) या हल क्षेत्र कहा जाता है।

→ वे बिन्दु जो सुसंगत क्षेत्र में तथा इसकी सीमा रेखा पर होते हैं, व्यवरोधों का सुसंगत हल कहलाते हैं । सुसंगत क्षेत्र के बाहर कोई बिन्दु असुसंगत हल कहलाता है।

→ सुसंगत क्षेत्र में कोई बिन्दु जिससे उद्देश्य फलन का इष्टतमकारी मान ज्ञात होता है, उसे इष्टतमकारी हल कहते हैं।

→ प्रमेय 1: यदि एक रैखिक प्रोग्रामन समस्या के लिए R सुसंगत क्षेत्र है तथा उद्देश्य फलन Z = ax + by है । जब Z का एक इष्टतम मान (अधिकतम या न्यूनतम) हो जहाँ व्यवरोधों से सम्बन्धित चर x और y रैखिक समीकरणों द्वारा व्यक्त हो तब यह इष्टतम मान सुसंगत क्षेत्र के कोनों पर होता

→ प्रमेय 2 : यदि किसी रैखिक समस्या के लिए सुसंगत क्षेत्र र प्रतिबद्ध हो तो उद्देश्य फलन के सुसंगत क्षेत्र R में अधिकतम तथा न्यूनतम मान दोनों होते हैं । ये मान सुसंगत क्षेत्र के कोनीय बिन्दुओं पर होते हैं।

→ यदि सुसंगत क्षेत्र के दो कोनीय बिन्दुओं पर इष्टतमकारी मान समान हों तो तब इन बिन्दुओं को मिलाने वाली रेखा पर किसी भी बिन्दु के लिए उद्देश्य फलन का इष्टतमकारी मान प्राप्त होता है।

→ रैखिक प्रोग्रामन समस्या को हल करने के लिए निम्न चरण प्रयुक्त होते हैं

• रैखिक प्रोग्रामन का सुसंगत क्षेत्र ज्ञात करके उसके कोनीय बिन्दुओं को ज्ञात करते हैं।
• सुसंगत क्षेत्र के प्रत्येक कोनीय बिन्दु पर उद्देश्य फलन Z = ax + by का मान ज्ञात करते हैं । यहाँ से उद्देश्य फलन का न्यूनतम/अधिकतम मान प्राप्त करते हैं।
• यदि उच्चतम तथा न्यूनतम मान क्रमशः M तथा N हों तथा सुसंगत क्षेत्र प्रतिबन्धित हो तो M तथा N क्रमशः उद्देश्य फलन के उच्चतम तथा निम्नतम मान होते हैं।