RBSE Class 12 Maths Notes Chapter 11 त्रि-विमीय ज्यामिति

These comprehensive RBSE Class 12 Maths Notes Chapter 11 त्रि-विमीय ज्यामिति will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 11 Notes त्रि-विमीय ज्यामिति

प्रस्तावना (Introduction):
पूर्व कक्षा XI में हमने वैश्लेषिक ज्यामिति का अध्ययन द्वि-विमीय और त्रि-विमीय विषयों के परिचय में केवल कार्तीय विधि तक ही सीमित रखा है। पिछले अध्याय में हमने सदिशों की मूल संकल्पनाओं का अध्ययन किया है। यहाँ पर हम सदिशों के बीजगणित का त्रिविमीय ज्यामिति में उपयोग करेंगे। इसके उपयोग से त्रि-विमीय ज्यामिति अत्यंत सरल एवं सुरुचिपूर्ण बन जाती है। इस अध्याय में हम दो बिन्दुओं को मिलाने वाली रेखा की दिक्कोसाइन व दिक्-अनुपात का अध्ययन करेंगे और साथ ही विभिन्न स्थितियों में, अंतरिक्ष में रेखाओं और तलों के समीकरणों, दो रेखाओं, दो तलों व एक रेखा और एक तल के बीच का कोण, दो विषमतलीय रेखाओं के बीच न्यूनतम दूरी व एक तल की एक बिन्दु से दूरी के विषय में अध्ययन करेंगे। उपरोक्त परिणामों में से अधिकांश परिणामों को
सदिशों के रूप में प्राप्त करते हैं।

एक रेखा के दिक्-कोसाइन (Direction Cosines of A Line):
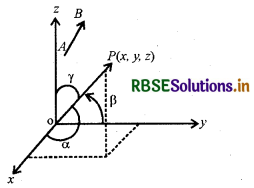
माना AB एक रेखा खण्ड है जिसे सदिश \(\overrightarrow{\mathrm{AB}}\) द्वारा प्रदर्शित किया गया है । मूल बिन्दु से \(\overrightarrow{\mathrm{AB}}\) के समान व समान्तर एक सदिश खींचो। यदि सदिश OP निर्देशांक अक्षों ox, OY तथा OZ की धनात्मक दिशाओं के साथ क्रमशः कोण α, β तथा γ बनायें तो cos α, cos β तथा cos γ को \(\overrightarrow{\mathrm{OP}}\) दिक्-कोसाइन कहते हैं । साधारणतः इनको l, m तथा n से निरूपित किया जाता है। अर्थात् l = cos α, m = cos β तथा n = cos γ। कोण α, β, तथा γ को दिक् कोण कहा जाता है तथा यह प्रतिबन्धों 0 ≤ α ≤ π, 0 ≤ β ≤ π तथा 0 ≤ γ ≤ π को सन्तुष्ट करते हैं। सदिश \(\overrightarrow{\mathrm{AB}}\) तथा \(\overrightarrow{\mathrm{OP}}\) की दिक्-कोसाइन समान होंगी क्योंकि ये सदिश समान्तर है तथा अक्षों के साथ समान कोण बनाते हैं।

टिप्पणी:
(i) सदिश \(\overrightarrow{\mathrm{PO}}\), ox, OY तथा OZ अक्षों के साथ कोण π - α, π - β, तथा π - γ बनाता है। अतः \(\overrightarrow{\mathrm{PO}}\) की दिक्-कोसाइन (दिक्-कोज्यायें) cos (r - α), cos (r - β) तथा cos (r - γ) अर्थात् - cos α, - cos β, -cos γ या - l, - m, - n, होंगी। अतः यदि l, m, n किसी रेखा की दिक्-कोसाइन हैं, तो -l, m, -n, भी उसी रेखा की दिक्कोसाइन होंगी क्योंकि हर स्थिति में आधार रेखा वही है।

(ii) चूँकि -1 ≤ cosx ≤ 1, ∀ x ∈ R, अत: l, m, n, के मान ऐसी वास्तविक संख्या होती है जो - 1 से छोटी नहीं होती तथा 1 से बड़ी नहीं होती। फलतः दिक्-कोसाइन [-1, 1] [11.3]|

निर्देशी अक्षों की दिक्-कोसाइन (Direction Cosines of A Coordinate Axes):
x-अक्ष तीनों निर्देशी अक्षों के साथ क्रमशः o, \(\frac{\pi}{2}\) एवं \(\frac{\pi}{2}\) के कोण बनाती है, अतः इनकी दिक्-कोसाइन cos 0, cos \(\frac{\pi}{2}\), cos \(\frac{\pi}{2}\) अर्थात् 1, 0, 0 होती है।

इसी प्रकार -अक्ष एवं 2-अक्ष की दिक-कोसाइन क्रमशः 0, 1, 0 तथा 0, 0, 1 होती है। अतः
x-अक्ष की दिक्-कोसाइन = 1, 0,0
y-अक्ष की दिक्-कोसाइन = 0, 1,0.
x-अक्ष की दिक्-कोसाइन = 0, 0, 1

टिप्पणी-किसी निर्देशी अक्ष के समान्तर रेखा की दिक्-कोसाइन संगत निर्देशी अक्ष की दिक्-कोसाइन के बराबर होती है।

 

रेखा की दिक्-कोसाइन में सम्बन्ध (Relation Between The Direction Cosines of a Line)
माना कि एक रेखा RS की दिक्-कोसाइन l, m, n है । मूल बिन्दु से दी गई रेखा के समान्तर एक रेखा खींचते हैं और इस पर एक बिन्दु p(x, y, z) लेते हैं । P से x-अक्ष पर लम्ब PA खींचिये जैसाकि आकृति में दिखाया गया है।
यदि OP = r से cos α = \(\frac{\mathrm{OA}}{\mathrm{OP}}=\frac{x}{r}\)
l = \(\frac{x}{r}\) ∴ l = cos α होता है।

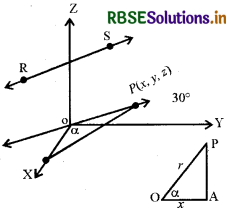
इसलिए x = lr प्राप्त होता है।
इसी प्रकार y = mr और z =nr प्राप्त होगा।
इसलिये x² + y² + z² = (lr)² + (mr)² + (nr)²
x² + y² + z² = P (l² + m² + n²)
परन्तु x² + y² + z² = r²
अतः l² + m² + n² = 1

किसी रेखा के दिक् -अनुपात (Direction Ratios of A Line)
एक रेखा के दिक्-कोसाइन के समानुपाती संख्याओं को रेखा के दिक् अनुपात (direction ratios or dr's) कहते हैं। यदि एक रेखा के दिक्-कोसाइन l, m,n व दिक्-अनुपात a, b, c हों तब किसी शून्येतर NER के लिये a = λl, b = λm और c = λn

नोट : दिक्-अनुपातों को दिक्-संख्यायें भी कहते हैं।
माना कि एक रेखा के दिक्-अनुपात a, b, c और रेखा की दिक्कोसाइन l, m, n हैं तब
\(\frac{l}{a}=\frac{m}{b}=\frac{n}{c}\) = k (माना)
यहाँ पर k एक अचर है।
इसलिये l = ak, m = bk, n = ck ....(1)
परन्तु l² + m² + n² = 1
इसलिये (ak)² + (bk)² + (ck)² = 1
या k²(a² + b² + c²) = 1
या k = ± \(\frac{1}{\sqrt{a^{2}+b^{2}+c^{2}}}\)

समीकरण (1) में मान रखने पर, रेखा की दिक्-कोसाइन (d.c.'s)
l = ± \(\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}\)
m = ±\( \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}\)
n = ± \(\frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}\)
यहाँ धन चिह्न (Positive sign) दिष्ट रेखा AB की दिक्-कोसाइन को व्यक्त करता है तथा ऋण चिह्न (Negative sign) रेखा BA की दिक्-कोसाइन को व्यक्त करता है। अतः किसी रेखा के दिक्-अनुपातों a, b, c से उसकी दिक्-कोसाइन प्राप्त करने के लिए a, b, c को \(\sqrt{a^{2}+b^{2}+c^{2}}\) से भाग देते हैं।

टिप्पणी:

• दिक्-अनुपात की संख्याएँ अद्वितीय नहीं होतीं जबकि दिक्-कोसाइन की संख्याएँ अद्वितीय होती हैं।
• a² + b² + c² = 1 जबकि l² + m² + n² = 1

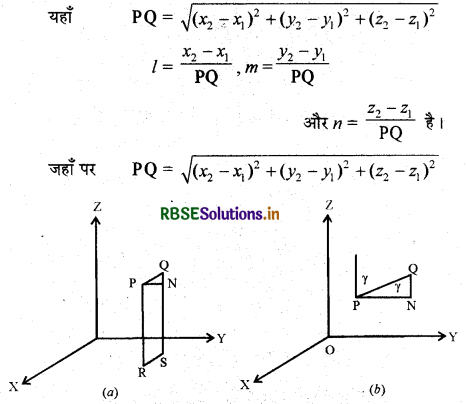
दो बिन्दुओं को मिलाने वाली रेखा की दिक्-कोसाइन (Direction Cosines of A Line Passing Through Two Points)
माना कि PQ रेखा की दिक्-कोसाइन l, m,n हैं और यह x, y तथा z-अक्ष के साथ कोण क्रमशः α, β, γ बनाती है। अब हम P तथा Q से लम्ब खींचें जो xy-तल को R तथा S पर मिलते हैं। P से एक अन्य लम्ब खींचते हैं, जो QS को N पर मिलता है। समकोण त्रिभुज PNQ में, ∠PQN = γ
जैसाकि आकृति में दिखाया गया है।
इसलिये cos γ = \(\frac{\mathrm{NQ}}{\mathrm{PQ}}=\frac{z_{2}-z_{1}}{\mathrm{PQ}}\)
इसी प्रकार cos α = \(\frac{x_{2}-x_{1}}{\mathrm{PQ}}\) और cos β = \(\frac{y_{2}-y_{1}}{\mathrm{PQ}}\)
अतः बिंदुओं P(x₁, y₁, z₁) तथा Q(x₂, y₂, z₂) को जोड़ने वाले रेखाखण्ड PQ की दिक्-कोसाइन

टिप्पणी
(i) बिन्दुओं P(x₁, y₁, z₁) तथा Q(x₂, y₂, z₂) को जोड़ने वाले रेखाखण्ड के दिक् अनुपात निम्न प्रकार से प्राप्त किये जा सकते
x₂ - x₁, y₂ - y₁, z₂ - z₁, या x₁ - x₂, y₁ - y₂, z₁ - z₂
(ii) दिक्-कोसाइन \(\frac{x_{2}-x_{1}}{\mathrm{PQ}}, \frac{y_{2}-y_{1}}{\mathrm{PQ}}, \frac{z_{2}-z_{1}}{\mathrm{PQ}}\) अर्थात् \(\frac{x_{2}-x_{1}}{\sqrt{\Sigma\left(x_{2}-x_{1}\right)^{2}}}, \frac{y_{2}-y_{1}}{\sqrt{\sum\left(x_{2}-x_{1}\right)^{2}}}, \frac{z_{2}-z_{1}}{\sqrt{\Sigma\left(x_{2}-x_{1}\right)^{2}}}\) से प्राप्त कर सकते हैं।

अंतरिक्ष में रेखा का समीकरण (Equation of a Line In Space):
कक्षा XI में द्वि-विमीय तल में रेखाओं का अध्ययन करने के पश्चात् अब हम अंतरिक्ष में एक रेखा के सदिश तथा कार्तीय समीकरणों को ज्ञात करेंगे। एक रेखा अद्वितीयतः निर्धारित होती है, यदि

• यह दिए बिंदु से दी गई दिशा से होकर जाती है, या
• यह दो दिए गए बिंदुओं से होकर जाती है।

दिये गये बिन्दु A से जाने वाली तथा दिये गये सदिश के समान्तर रेखा का समीकरण (Equation Of A Line Through A Given Point A And Parallel To A Given Vector)
समकोणिक निर्देशांक निकाय के मूल बिंदु O के सापेक्ष माना दिया गया बिन्दु A का सदिश \(\vec{a}\) है, और यह भी माना कि बिन्दु A से जाने वाली तथा दिये गये सदिश \(\vec{b}\) के समान्तर रेखा l है, माना सरल रेखा पर कोई बिन्दु P है जिसका स्थिति सदिश \(\vec{r}\), है तब AP सदिश \(\vec{b}\)के समान्तर है।

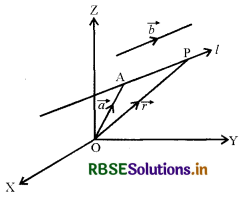
अर्थात् AP = λ\(\vec{b}\), जहाँ λ एक वास्तविक संख्या है।
परन्तु \(\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AP}}\)
अर्थात् \(\vec{r}=\vec{a}+\lambda \vec{b} \).....(1)
यहाँ P सरल रेखा पर कोई स्वेच्छ बिन्दु है इसलिये λ को भिन्न-भिन्न मान देने से रेखा पर P की भिन्न-भिन्न स्थिति प्राप्त करते हैं, अतः उपरोक्त समीकरण (1) सरल रेखा का प्राचलिक समीकरण है जिसका प्राचल (Parameter) λ है।

सदिश रूप से कार्तीय रूप व्युत्पन्न करना (Derivation of Cartesian Form from Vector Form)
मान लीजिए कि दिए गए बिंदु λ के निर्देशांक (x₁, y₁, z₁) हैं और रेखा की दिक्-अनुपात a, b, c हैं। मान लीजिए किसी बिंदु P के निर्देशांक (x, y, z) हैं। तब
\(\vec{r}\) = xî + yĵ + zk̂ ; \(\vec{a}\) = x₁î + y₁ĵ + z₁k̂
और \(\vec{b}\) = aî + bĵ + ck̂

इन मानों को समीकरण (1) में प्रतिस्थापित करके î, ĵ और k̂, के गुणांकों की तुलना करने पर हम पाते हैं कि
xî + yĵ + zk̂ = x₁î + y₁ĵ + z₁k̂ + λ(aî + bĵ + ck̂)
= xî + yĵ + zk̂ = (x₁ + λa)î + (y₁ + λb)ĵ + (z₁ + λc)k̂
अतः x = x₁ + λa,y = y₁ + λb, z = z₁ + λc ....(2)

ये रेखा के प्राचल समीकरण हैं। समीकरण (2) से प्राचल λ का विलोपन करने पर अर्थात्
\(\frac{x-x_{1}}{a}\) = λ \(\frac{y-y_{1}}{b}\) = λ \(\frac{z-z_{1}}{c}\) = λ
यह रेखा का कार्तीय समीकरण है।

टिप्पणी-यदि रेखा की दिक्-कोसाइन l, m, n हैं, तो रेखा का समीकरण है
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=\frac{z-z_{1}}{n}\)

दो दिये गये बिन्दुओं से जाने वाली रेखा का समीकरण (Equation of A Line Passing Through Two Given Points):
माना कि एक रेखा पर स्थिति दो बिंदुओं A(x₁, y₁, z₁) और B(x₂, y₂, z₂) के स्थिति सदिश क्रमशः और में हैं जैसा कि आकृति में दर्शाया गया है।

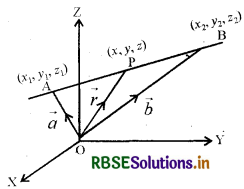
माना \(\vec{r}\) एक स्वेच्छ बिंदु P का स्थिति सदिश है । तब P रेखा पर है यदि और केवल यदि \(\overrightarrow{\mathrm{AP}}=\vec{r}-\vec{a}\) तथा \(\overrightarrow{\mathrm{AB}}=\vec{b}-\vec{a}\) संरेख सदिश हैं । इसलिए P रेखा पर स्थित है यदि और केवल यदि
\(\vec{r}-\vec{a}\) = λ(\(\vec{b}-\vec{a}\))
या \(\vec{r} = \vec{a}\) + λ(\(\vec{b}- \vec{a}\)), λ ∈ R .....(1)

जो रेखा का सदिश समीकरण है।
सदिश रूप से कार्तीय रूप व्युत्पन्न करना

जो रेखा के समीकरण का कार्तीय रूप है।

दो रेखाओं के मध्य कोण (Angle Between Two Lines):
माना कि L₁, और L₂, मूल बिन्दु से गुजरने वाली दो रेखायें हैं जिनके दिक्-अनुपात क्रमशः a₁, b₁, c₁, और a₂, b₂, c₂, हैं। यहाँ पर हमने यह भी माना है कि L₁, पर एक बिन्दु P तथा L₂, पर एक बिन्दु Q जैसा कि आकृति में दर्शाया गया है । दिये गये सदिश OP तथा 0Q पर विचार कीजिये। माना कि OP और OQ के बीच न्यून कोण θ है। याद रहे कि सदिशों OP और OQ के घटक क्रमशः a₁, b₁, c₁, और a₂, b₂, c₂, हैं। इसलिये उनके बीच का कोण θ
cos θ = \(\left|\frac{a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\right|\) द्वारा प्रदत्त है। ......(1)

पुनः sin के रूप में, रेखाओं के बीच का कोण

sin θ = \(\sqrt{1-\cos ^{2} \theta}\) से प्रदत्त है। मान रखने पर

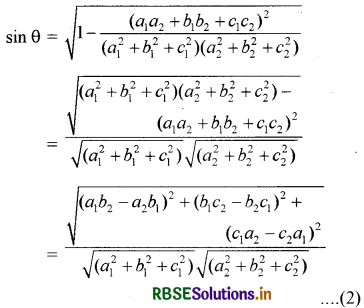
नोट : उस स्थिति में जब रेखायें L₁, और L₂, मूल बिन्दु से नहीं गुजरती हैं तो हम L₁, और L₂, के समान्तर मूल बिन्दु से गुजरने वाली रेखायें क्रमशः L₁, व L₂, लेते हैं। दिक्-कोसाइन के रूप में दो रेखाओं के मध्य कोण यदि रेखाओं L₁, और L₂, के दिक्-अनुपातों के बजाय दिक्-कोसाइन दी गई हों जैसे L₁, के लिये l₁, m₁, n₁, और L₂, के लिये l₂, m₂, n₂,

तो समीकरण (1) तथा (2) निम्नलिखित प्रारूप लेंगे-
cos θ = |l₁l₂ + m₁m₂ + n₁n₂|
क्योंकि l₁² + m₁² + n₁² = 1 = l₂² + m₂² + n₂² ....(3)

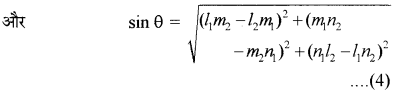
दो रेखाओं के समान्तर एवं लम्बवत् होने का प्रतिबन्ध (Conditions of parallelism and Perpendicularity of two lines)
(a) रेखाओं के समान्तर होने का प्रतिबन्ध समान्तर रेखाओं के बीच का कोण 0° होता है।
अतः \(\frac{l_{1}}{l_{2}}=\frac{m_{1}}{m_{2}}=\frac{n_{1}}{n_{2}}\) या \(\frac{a_{1}}{b_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

(b) रेखाओं के लम्बवत् होने का प्रतिबन्ध यदि रेखायें लम्बवत् हैं तो उनके मध्य कोण 90° होगा
अर्थात् cos 90° = 0 = l₁l₂, + m₁m₂ + n₁n₂ = 0
इसलिये
l₁l₂, + m₁m₂ + n₁n₂
या a₁a₂, + b₁b₂ + c₁c₂ = 0

अब हम उन दो रेखाओं के बीच का कोण ज्ञात करेंगे जिनके सदिश समीकरण दिये गये हैं। यदि उन रेखाओं \(\vec{r}=\vec{a}_{1}+λ \vec{b}_{1}\), और \(\vec{r}=\vec{a}_{2}+\mu \vec{b}_{2}\), के बीच न्यून कोण θ है।

तब cos θ = \(\left|\frac{\overrightarrow{b_{1}} \overrightarrow{b_{2}}}{\left|\overrightarrow{b_{1}}\right|\left|\overrightarrow{b_{2}}\right|}\right|\)

विशेष स्थितियाँ
(i) यदि दोनों रेखायें परस्पर लम्बवत् हैं
\(\vec{b}_{1} \vec{b}_{2}\) = 0
(ii) यदि दोनों रेखायें परस्पर समान्तर हैं
\(\overrightarrow{b_{1}}=\lambda \overrightarrow{b_{2}}\)
कार्तीय रूप में यदि रेखाओं .
\(\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}\) ............(1)
आर \(\frac{x-x_{2}}{a_{2}}=\frac{y-y_{2}}{b_{2}}=\frac{z-z_{2}}{c_{2}}\) ....(2)
के बीच का कोण θ है जहाँ रेखाएँ (1) व (2) के दिक्-अनुपात क्रमशः a₁, b₁, c₁, तथा a₂, b₂ c₂, हैं तब
cos θ = \(\left|\frac{a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\right|\)

दो रेखाओं के मध्य न्यूनतम दूरी (Shortest Distance Between Two Lines):
अंतरिक्ष में यदि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं तो उनके बीच की न्यूनतम दूरी शून्य है और अंतरिक्ष में यदि दो रेखाएँ समांतर हैं तो उनके बीच की न्यूनतम दूरी, उनके बीच लंबवत् दूरी होगी अर्थात् एक रेखा के एक बिंदु से दूसरी रेखा पर खीचा गया लंब। इसके अतिरिक्त अंतरिक्ष में, ऐसी भी रेखाएँ होती हैं जो न तो प्रतिच्छेदी और न ही समांतर होती हैं। वास्तव में ऐसी रेखाओं के युग्म असमतलीय होते हैं और इन्हें विषमतलीय रेखाएँ कहते हैं।

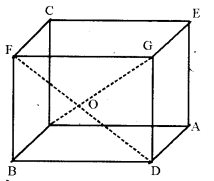
विषमतलीय रेखायें (परिभाषा)-ऐसी दो रेखायें जो न तो समान्तर हों और न परस्पर प्रतिच्छेद करती हैं, विषमतलीय रेखायें कहलाती हैं। इनके लिये ऐसा कोई समतल विद्यमान नहीं होता है जिसमें ये दोनों रेखायें विद्यमान हों।

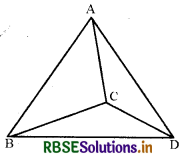
उदाहरण के लिये चित्र में OG एवं FD रेखायें विषमतलीय हैं । इसी प्रकार AG एवं FD भी विषमतलीय रेखायें हैं, चतुष्फलक ABCD में AC एवं BD, AD एवं BC,AB एवं CD विषमतलीय रेखाओं के उदाहरण हैं । ऐसा माना गया है कि समान्तर रेखायें भी अनन्त दूरी के पश्चात् मिल जाती हैं। दो रेखाओं के बीच न्यूनतम दूरी से हमारा अभिप्राय एक ऐसे रेखाखंड से है जो एक रेखा पर स्थित एक बिंदु को दूसरी रेखा पर स्थित अन्य बिंदु को मिलाने से प्राप्त हो ताकि इसकी लंबाई न्यूनतम हो । न्यूनतम दूरी रेखाखंड दोनों विषमतलीय रेखाओं पर लंब होगा।

दो विषमतलीय रेखाओं के बीच की दूरी । (Distance Between Two Skew Lines):
माना कि l₁ और l₂ दो विषमतलीय रेखाएँ हैं जिनके समीकरण निम्नलिखित हैं
\(\vec{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}\) .....(1)
और \(\vec{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}\).....(2)
रेखा l₁, पर कोई बिंदु S जिसकी स्थिति सदिश \(\vec{a}_{1}\), और l₂, पर कोई बिंदु T जिसकी स्थिति सदिश \(\vec{a}_{2}\) है, लीजिए। तब न्यूनतम दूरी सदिश का परिमाण, ST का न्यूनतम दूरी की दिशा में प्रक्षेप की माप के समान होगा। यदि l₁, और l₂, के बीच की न्यूनतम दूरी सदिश PQ है तो यह दोनों \(\vec{b}_{1}\) और \(\vec{b}_{2}\) पर लंब होंगी।

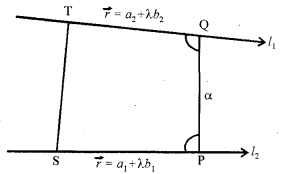
और इसकी दिशा में इकाई सदिश n̂ इस प्रकार होगा कि
n̂ = \(\frac{\vec{b}_{1} \times \vec{b}_{2}}{\left|\vec{b}_{1} \times \vec{b}_{2}\right|}\)
तब PQ = dh
जहाँ d न्यूनतम दूरी सदिश का परिमाण है। मान लीजिए \(\overrightarrow{\mathrm{ST}} \) और \(\overrightarrow{\mathrm{PQ}}\) के बीच का कोण θ है, तब

कार्तीय रूप (Cartesian Form):
रेखाओं : जबकि दोनों रेखाओं के समीकरण सममित रूप में हों।

समान्तर रेखाओं के बीच की दूरी (Distance Between Parallel Lines):
यदि दो रेखाएँ l₁, और l₂, समांतर हैं तो वे समतलीय होती हैं। माना कि दी गई रेखाएँ क्रमशः
\(\vec{r}=\vec{a}_{1}+\lambda \vec{b}\) .....(1)
और \(\vec{r}=\vec{a}_{1}+µ \vec{b}\) .......(2)
हैं, जहाँ l₁, पर बिंदु S का स्थिति सदिश \(\vec{a}_{1}\) और l₂, पर बिंदु T का स्थिति सदिश \(\vec{a}_{2}\), है जैसाकि आकृति में दर्शाया गया है।

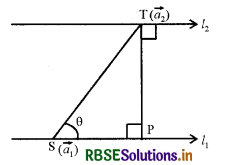
क्योंकि l₁, और l₂ समतलीय हैं। यदि बिंदु T से l₁, पर डाले गए लंब का पाद P है तब रेखाओं l₁, और l₂, के बीच की दूरी = |TP|
माना कि सदिशों \(\overrightarrow{\mathrm{ST}}\) और \(\vec{b}\) के बीच का कोण θ है। तब
\(\vec{b} \times \overrightarrow{\mathrm{ST}} \) = (\(|\vec{b}||\overrightarrow{\mathrm{ST}}|\) sin θ) n̂ ....(3)

जहाँ पर n , रेखाओं , और , के तल पर लंब इकाई सदिश है।
लेकिन \(\overrightarrow{\mathrm{ST}}=\vec{a}_{2}-\vec{a}\)_{1}

समीकरण (3) में मान रखने पर
\(\vec{b} \times\left(\vec{a}_{2}-\vec{a}_{1}\right)=|\vec{b}|\) PT n̂ (क्योंकि PT = ST sin θ)
अर्थात् \(\left|\vec{b} \times\left(\vec{a}_{2}-\vec{a}_{1}\right)\right|=\vec{b}\)|PT| .1 ∵ |n̂| = 1

इसलिए ज्ञात रेखाओं के बीच न्यूनतम दूरी
इसलिये समान्तर रेखाओं के बीच की न्यूनतम दूरी
d = \(|\overrightarrow{\mathrm{PT}}|=\left|\frac{\vec{b} \times\left(\vec{a}_{2}-\vec{a}_{1}\right)}{|\vec{b}|}\right|\) है।

समतल (Plane):
परिभाषा (Definition):
कोई पृष्ठ (Surface) एक समतल कहलाता है यदि उस पृष्ठ के किन्हीं दो बिन्दुओं को मिलाने वाली रेखा का प्रत्येक बिन्दु अर्थात् सम्पूर्ण रेखा पृष्ठ पर स्थित हो। x, y, z में प्रत्येक एक घातीय समीकरण एक समतल को निरूपित करता है। समतल का व्यापक समीकरण ax + by + cz + d = 0 होता है।

कुछ प्रमुख समतलों के समीकरण

• xy समतल का समीकरण-इस समतल पर z का मान सदैव शून्य रहता है। अतः z = 0, xy समतल का समीकरण होगा। इसी प्रकार yz समतल का समीकरण x = 0 तथा zx तल का समीकरण y = 0
• मूल बिन्दु से गुजरने वाला समतल समतल ax + by + cz + d = 0 यदि मूल बिन्दु से गुजरता है तब a.0+.b.0 + c.0 + d = 0 ⇒ d = 0 अतः अभीष्ट समतल ax + by + cz = 0 एक समतल को अद्वितीय रूप से ज्ञात किया जा सकता है यदि

निम्नलिखित में से कोई एक शर्त हमें ज्ञात हो

• समतल का अभिलंब और मूल बिंदु से समतल की दूरी ज्ञात है, अर्थात् अभिलंब रूप में समतल का समीकरण
• यह एक बिंदु से गुजरता है और दी गई दिशा के लंबवत् है।
• यह दिए गए तीन असंरेख बिंदुओं से गुजरता है।

अभिलम्ब रूप में समतल का समीकरण (Equation of A Plane In Normal Form).
एक समतल की मूल बिंदु से लंबवत् दूरी d(d ≠ 0) है जैसाकि आकृति में है। यदि \(\overrightarrow{\mathrm{ON}}\) मूल बिंदु से तल पर लंब है तथा \(\overrightarrow{\mathrm{ON}}\) के अनुदेश । मात्रक अभिलंब सदिश है तब \(\overrightarrow{\mathrm{ON}}\) = dn̂ है। माना कि समतल पर कोई बिंदु P है। इसलिए, \(\overrightarrow{\mathrm{NP}} \cdot \overrightarrow{\mathrm{ON}}\) पर लंब है।
इसलिये , \(\overrightarrow{\mathrm{NP}} \cdot \overrightarrow{\mathrm{ON}}\) = 0
माना P की स्थित सदिश ; है तो NP = \(\vec{r}\) - dn̂ (क्योंकि \(\overrightarrow{\mathrm{ON}}+\overrightarrow{\mathrm{NP}}\) = OP)

अतः समीकरण (1) में मान रखने पर
या (\(\vec{r}\) - dn̂). dn̂ = 0
या (\(\vec{r}\) - dn̂).n̂ = 0(d ≠ 0)
\(\vec{r}\).n̂ - dn̂.n̂ = 0
अर्थात् \(\vec{r}\).n̂ = d (क्योंकि n̂.n̂ = 1)....(2)
अतः समतल का सदिश समीकरण \(\vec{r}\).n̂ = d है।

कातीय रूप में समतल का समीकरण (Equation of Plane in Cartesian Form)
समतल का सदिश समीकरण \(\vec{r}\).n̂ = d

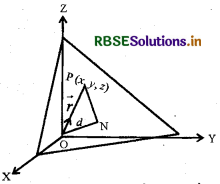
जहाँ । समतल के अभिलंब इकाई सदिश है। माना समतल पर कोई बिन्दु P(x₁, y₁, z₁) है । तब
\(\vec{OP}\) = \(\vec{r}\)= xî + yĵ + zk̂

माना n की दिक्-कोसाइन l, m, n हैं।
तब in = lî + mĵ + nk̂

समतल के सदिश समीकरण में मान रखने पर
(xî + yĵ + zk̂).d(lî + mĵ + nk̂) = d.
अर्थात् lx + my + nz =d ....(3)

यह समतल का कार्तीय समीकरण है।

टिप्पणी:
समीकरण (3) प्रदर्शित करता है कि यदि \(\vec{r}\).(aî +bî + ck̂) = d एक समतल का सदिश समीकरण है तो ax + by + cz = d समतल का कार्तीय समीकरण है जहाँ a, b तथा c समतल के अभिलंब के दिक्-अनुपात हैं।

एक दिये गये सदिश के अनुलम्ब तथा दिये गये बिन्दु से होकर जाने वाले समतल का समीकरण (Equation of A Plane Perpendicular To A Given Vector | And Passing Through A Given Point):
माना कि समतल एक बिन्दु A, जिसकी स्थिति सदिश, \(\vec{a}\) है, से जाता है और सदिश \(\vec{n}\) के अनुलम्ब है। माना कि समतल पर किसी बिन्दु P का स्थिति सदिश, \(\vec{r}\) है। जैसाकि आकृति में दर्शाया गया है। तब बिन्दु P समतल में स्थित होता है, यदि और केवल यदि AP, N पर लम्ब है।
अर्थात् \(\overrightarrow{\mathrm{AP}} \cdot \overrightarrow{\mathrm{N}}\) = 0
परन्तु \(\vec{AP} = \vec{r} - \vec{a}\)
इसलिए \((\vec{r} - \vec{a}).\vec{N}\) = 0 ............(1)

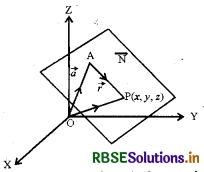
समीकरण (1) समतल का सदिश समीकरण है।
समीकरण (1) को निम्न प्रकार भी लिखा जा सकता है
\(\vec{r} \cdot \overrightarrow{\mathrm{N}}-\vec{a} \cdot \overrightarrow{\mathrm{N}}\) =0
\(\vec{r} \cdot \overrightarrow{\mathrm{N}} = \vec{a} \cdot \overrightarrow{\mathrm{N}}\)
टिप्पणी : समतल के उपरोक्त समीकरण (2) को \(\vec{r}.\vec{n}\) = d (जहाँ d = \(\vec{a}.\vec{n}\)) भी लिखा जा सकता है। इस रूप को समतल का सदिश गुणांक रूप भी कहते हैं।

कार्तीय रूप (Cartesian Form):
माना कि दिया हुआ बिंदु A(x₁, y₁, z₁) और समतल पर कोई बिंदु P(x₂, y₂, z₂) है तथा N के दिक्-अनुपात A, B तथा C हैं, तब
\(\vec{a}\) = x₁î + y₁ĵ + z₁k̂, \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\) = xî + yĵ + zk̂
और \(\vec{N}\) = Aî + Bĵ + Ck̂
अब \((\vec{r}-\vec{a}) \cdot \overrightarrow{\mathrm{N}}\) = 0
इसलिए
(x - x₁)î + (y - y₁)ĵ + (z - z₁)k̂ .(Aî + Bĵ + Ck̂) = 0
अर्थात् A(x - x₁) + B(y - y₁) + C(z - z₁) = 0

तीन असंरेखीय बिन्दुओं से होकर जाने वाले समतल का समीकरण (Equation of A Plane Passing Through Three Non Collinear Points):
माना समतल पर स्थित तीन असंरेख बिंदुओं R, S और T के स्थिति सदिश क्रमशः \(\vec{a}, \vec{b}\) और \(\vec{c}\) हैं। जैसा कि आकृति में है।

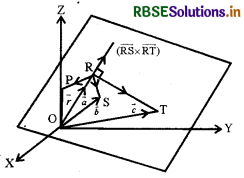
सदिश \(\overrightarrow{\mathrm{RS}}\) और \(\overrightarrow{\mathrm{RT}}\) दिए समतल में हैं । इसलिए सदिश \(\overrightarrow{\mathrm{RS}} \times \overrightarrow{\mathrm{RT}}\) बिंदुओं R, S और T को अन्तर्विष्ट करने वाले समतल पर लंब होगा। माना समतल में कोई बिंदु P का स्थिति संदिश \(\vec{r}\), है। इसलिए R से जाने वाले तथा सदिश \(\overrightarrow{\mathrm{RS}} \times \overrightarrow{\mathrm{RT}}\) पर

लंब, समतल का समीकरण \((\vec{r}-\vec{a}) \cdot(\overrightarrow{\mathrm{RS}} \times \overrightarrow{\mathrm{RT}})\) = 0 है।
या \((\vec{r}-\vec{a}) \cdot[(\vec{b}-\vec{a}) \times(\vec{c}-\vec{a})]\) = 0 ....(1)
∵ \(\overrightarrow{\mathrm{RS}}=\vec{b}-\vec{a}\)
और \(\overrightarrow{\mathrm{RT}}=\vec{c}-\vec{a}\)
यह तीन असंरेख बिंदुओं से गुजरने वाले समतल के समीकरण का सदिश प्रारूप है।

कार्तीय रूप (Cartesian Form)
मान लीजिए बिन्दुओं R, S और T के निर्देशांक क्रमशः (x₁, y₁, z₁), (x₂, y₂, z₂) और (x₃, y₃, z₃) है। मान लीजिए कि समतल पर किसी बिंदु P के निर्देशांक (x, y, z) व इसका स्थिति सदिश \(\vec{r}\) है। तब
\(\overrightarrow{\mathrm{RP}}\) = (x - x₁)î + (y - y₁)ĵ + (z - z₁)k̂
\(\overrightarrow{\mathrm{RS}}\) = (x₂ - x₁)î + (y₂ - y₁)ĵ + (z₂ - z₁)k̂
\(\overrightarrow{\mathrm{RT}}\) = (x₃ -x₁)î + (y₃ - y₁)ĵ + (z₃ - z₁)k̂
इन मानों को सदिश प्रारूप के समीकरण में प्रतिस्थापन करने पर हम पाते हैं कि
\(\left|\begin{array}{ccc} x-x_{1} & y-y_{1} & z-z_{1} \\ x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1} \end{array}\right|\) = 0
जो तीन बिंदुओं (x₁, y₁, z₁), (x₂, y₂, z₂) और (x₃, y₃, z₃) से गुजरने वाले समतल के समीकरण का कार्तीय प्रारूप है।

समतल के समीकरण का अन्तःखण्ड रूप (Intercept Form of The Equation of A Plane)
सिद्ध कीजिये कि यदि कोई समतल x,y तथा 2 अक्षों पर क्रमश: a, b तथा c लम्बाई के अन्तः खण्ड काटता है तब उस समतल का
समीकरण \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1 होता है।

माना समतल का समीकरण
Ax + By + Cz + D = 0 है .....(1)
माना समतल (1) अक्षों पर बिन्दु P Q तथा R पर इस प्रकार मिलता है कि OP = a, OQ = b तथा OR = c
अतः बिन्दुओं P, Q तथा R के निर्देशांक क्रमशः (a, 0,0), (0, b, 0) तथा (0, 0,c) होंगे। चूँकि बिन्दु P(a,0,0) समतल (1) पर स्थित है अतः ये निर्देशांक समतल के समीकरण में सन्तुष्ट कराने पर
A.a + B.0 + C.0 + D = 0
⇒ Aa + D = 0

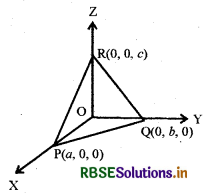
⇒ A = \(\frac{-\mathrm{D}}{a}\)

इसी प्रकार बिन्दु Q तथा R के निर्देशांक सन्तुष्ट कराने पर
Bb + D = 0 या B = \(\frac{-\mathrm{D}}{b}\)
Cc + D = 0 या C = \(\frac{-\mathrm{D}}{c}\)

A, B तथा C के मान समीकरण (1) में रखने पर
\(\frac{-\mathrm{D}}{a}\) x + \(\frac{-\mathrm{D}}{b}\) y + \(\frac{-\mathrm{D}}{c}\) z + D = 0
या \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) - 1 = 0
या \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1 ...........(2)
समीकरण (2) जो अन्त:खण्ड रूप में समतल का अभीष्ट समीकरण है।

दो दिये गये समतलों के प्रतिच्छेदन से होकर जाने वाले समतल का समीकरण (Equation of Plane Passing Through The Intersection of Two Given Planes)
हम जानते हैं कि दो समतलों का प्रतिच्छेदन सदैव एक सरल रेखा होती है। वह समतल जो दो समतलों की प्रतिच्छेदन रेखा को समादित करता है उसे दो समतलों के प्रतिच्छेदन से गुजरने वाला समतल कहते हैं। दो . सतमलों के प्रतिच्छेदन से गुजरने वाले समतलों का एक कुल होता है।

सदिश रूप

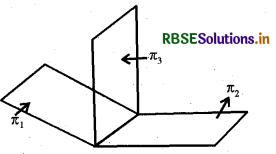
माना कि π₁, और π₂, समतल, जिनके समीकरण क्रमशः \(\vec{r} \cdot \vec{n}_{1}=d_{1}\) और \(\vec{r} \cdot \vec{n}_{2}=d_{2}\) हैं। इनके प्रतिच्छेदन रेखा पर स्थित किसी बिंदु का स्थिति सदिश इन दोनों समीकरणों को संतुष्ट करेगा। जैसाकि आकृति में दिखाया गया है।

यदि इस रेखा पर स्थित किसी बिंदु की स्थिति सदिश । है तो
\(\vec{t} \cdot \vec{n}_{1}=d_{1}\) और \(\vec{t} \cdot \vec{n}_{2}=d_{2}\)

इसीलिए λ के सभी वास्तविक मानों के लिए हम पाते हैं कि
\(\vec{t} \cdot\left(\vec{n}_{1}+\lambda \vec{n}_{2}\right)\) = d₁ + λd₂

क्योंकि । स्वेच्छ है इसलिए यह रेखा के किसी बिंदु को संतुष्ट करता है। इस प्रकार समीकरण \(\vec{r} \cdot\left(\vec{n}_{1}+\lambda \vec{n}_{2}\right)\) = d₁ + λd₂, समतल ग, को निरूपित करता है जो ऐसा है कि यदि कोई सदिश \(\vec{r}\), π₁, और π₂, के समीकरणों को संतुष्ट करता है तो वह π₃, को अवश्य संतुष्ट करेगा। अतः समतलों \(\vec{r} \cdot \vec{n}_{1}=d_{1}\) और \(\vec{r} \cdot \vec{n}_{1}=d_{1}\), के प्रतिच्छेदन रेखा से जाने वाले किसी समतल का समीकरण
\(\vec{t} \cdot\left(\vec{n}_{1}+\lambda \vec{n}_{2}\right)\) = d₁ + λd₂ है। .....(1)

कार्तीय रूप (Cartesian Form):
माना \(\vec{n}_{1}\) = A₁î + B₁ĵ + C₁k̂
\(\vec{n}_{2}\) = A₂î + B₂ĵ + C₂k̂
\(\vec{r}\) = xî + yĵ + zk̂

तो (1) का परिवर्तित रूप है।
⇒ (xî + yĵ + zk̂).(A₁î + B₁ĵ + C₁k̂ + λ(A₂î + B₂ĵ + C₂k̂)) = d₁ + λd₂
⇒ xî + yĵ + zk̂).((A₁ + λA₂)î + (B₁ + λB₂)ĵ + (C₁ + λC₂)k̂) = d₁ + λd₂
⇒ x(A₁ + λA₂) + y(B₁ + λB₂) + (C₁ + λC₂) = d₁ + λd₂
या (A₁x + B₁y + C₁z - d₁) + A(A₂x + B₂y + C₁z - d₁) = 0.....(2)
समीकरण (2) जो प्रत्येक λ के लिये दिये गये समतलों के प्रतिच्छेदन रेखा से होकर जाने वाले किसी समतल का कार्तीय समीकरण है।

दो रेखाओं का सह-तलीये होना (Co Planarity of Two Lines)
सदिश रूप (Vector Form)
माना कि दो ज्ञात रेखाओं
\(\vec{r}=\vec{a}_{1}+\lambda \vec{b}_{1}\) ....(1)
तथा  \(\vec{r}=\vec{a}_{2}+µ \vec{b}_{2}\) ....(2)
रेखा \(\vec{r}=\vec{a}_{1}+\lambda \vec{b}_{1}\), स्थिति सदिश \(\vec{a}_{1}\) वाले बिन्दु (A) से गुजरती है तथा सदिश \(\vec{b}_{1}\), के समान्तर है एवं रेखा, \(\vec{r}=\vec{a}_{2}+µ \vec{b}_{2}\) स्थिति सदिश \(\vec{a}_{1}\) वाले बिन्दु (B) से गुजरती है तथा सदिश \(\vec{b}_{2}\) के समान्तर है।
\(\overrightarrow{\mathrm{AB}}=\vec{a}_{2}-\vec{a}\)_{1}

ज्ञात रेखायें सह-तलीय हैं, यदि और केवल यदि \(\overrightarrow{\mathrm{AB}}, \vec{b}_{1}\), और \(\vec{b}_{2}\) सह-तलीय हैं, अर्थात्
\(\overrightarrow{\mathrm{AB}} \cdot\left(\vec{b}_{1} \times \vec{b}_{2}\right)\) = 0
या \(\left(\vec{a}_{2}-\vec{a}_{1}\right) \cdot\left(\vec{b}_{1} \times \vec{b}_{2}\right)\) = 0

कार्तीय रूप (Cartesian Form):
माना कि बिंदुओं A और B के निर्देशांक क्रमशः (x₁, y₁, z₁) और (x₂, y₂, z₂) हैं। मान लीजिए कि \(\vec{b}_{1}\) और \(\vec{b}_{2}\) के दिक्-अनुपात क्रमशः a₁, \(\vec{b}_{1}, \vec{c}_{1}\) तथा a₂, \(\vec{b}_{2}, \vec{c}_{2}\) हैं। तब ।
\(\overrightarrow{\mathrm{AB}}\) = (x₂ - x₁)î + (y₂ - y₁)ĵ + (z₂ - z₁)k̂
\(\vec{b}_{1}\) = a₁î + b₁ĵ + c₁k̂; और \(\vec{b}_{2}\) = a₂î + b₂ĵ + c₂k̂

ज्ञात रेखाएँ सह-तलीय हैं, यदि और केवल यदि \(\overrightarrow{\mathrm{AB}} \cdot\left(\vec{b}_{1} \times \vec{b}_{2}\right)\) = 0 जिसे निम्नलिखित कार्तीय रूप में व्यक्त कर सकते हैं
\(\left|\begin{array}{ccc} x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{array}\right|\) = 0

दो समतलों के बीच का कोण (Angle Between Two Planes)
परिभाषा:
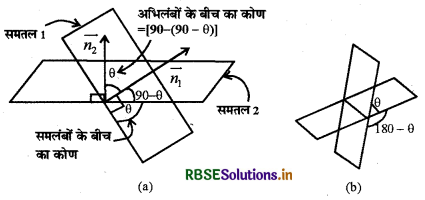
दो समतलों के बीच का कोण उनके अभिलंबों के मध्यस्थ कोण द्वारा परिभाषित है जैसाकि आकृति (a) में दर्शाया गया है कि यदि दो समतलों के बीच का कोण θ है तो 180 - θ [आकृति (b)] भी उनके बीच का कोण है। हम न्यून कोण को ही समतलों के बीच का कोण लेंगे। माना कि समतलों, \(\vec{r} \cdot \vec{n}_{1}\) = d₁, और \(\vec{r} \cdot \vec{n}_{2}\) = d₂, के बीच का कोण में है। तब किसी सार्व बिंदु से समतलों पर खींचे गए अभिलेखों के बीच का कोण θ है।
तब cos θ = \(\left|\frac{\overrightarrow{n_{1}} \cdot \overrightarrow{n_{2}}}{\left|\overrightarrow{n_{1}}\right|\left|\overrightarrow{n_{2}}\right|}\right|\)

टिप्पणी:
(i) यदि दोनों समतल परस्पर लम्बवत् हैं । यदि \(\vec{n}_{1} \cdot \vec{n}_{2}\) = 0

कार्तीय रूप (Cartesian Form)
मानाकि समतलों : A₁x + B₁y + C₁z + D₁ = 0
और A₂x + B₂y + C₂z + D₂ = 0 के बीच का कोण θ है।
तो समतलों के अभिलंब के दिक्-अनुपात क्रमशः A₁ B₁, C₁, और A₂, B₂, C₂, हैं। इसलिए
cos θ = \(|\frac{A_{1} A_{2}+B_{1} B_{2}+C_{1} C_{2}}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}} \sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}|\)

टिप्पणी

• यदि दोनों समतल परस्पर लंब हैं तब = 90° और इस तरह cos θ = 0, अत: cos θ = A₁A₂+ B₁B₂ + C₁C₂ = 0
• यदि दोनों समतल समान्तर हैं तो
  \(\frac{\mathrm{A}_{1}}{\mathrm{~A}_{2}}=\frac{\mathrm{B}_{1}}{\mathrm{~B}_{2}}=\frac{\mathrm{C}_{1}}{\mathrm{C}_{2}}\)

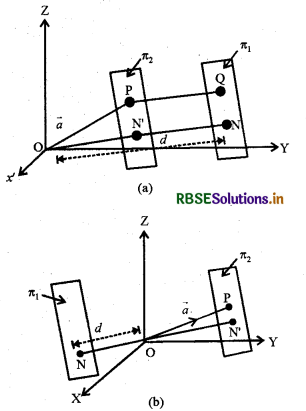
समतल से दिये गये बिन्दु की दूरी (Distance of A Point From A Plane):
एक बिन्दु P जिसका स्थिति सदिश \(\vec{a}\) और एक समतल , जिसका समीकरण \(\vec{r}\).n̂ =d जैसा आकृति में दर्शाया गया है। पुनः बिन्दु P से समतल π₁ के समान्तर समतल π₂ पर विचार कीजिये समतल स, के अभिलम्ब इकाई सदिशn है अतः इसका समीकरण
(\(\vec{r}-\vec{a}\)).n̂ = 0 है।
⇒ \(\vec{r}\).n̂ - \(\vec{a}\).n̂ = 0
⇒ \(\vec{r}\)n̂ = \(\vec{a}\).n̂
अतः मूल बिन्दु से इस समतल की दूरी
ON' = |\(\vec{a}\).n̂| है।

इसलिये P से समतल π₁, से दूरी
PQ = ON – ON'
= |d - \(\vec{a}\).n̂| है।

जो एक बिन्दु से समतल पर लम्ब की लम्बाई है। आकृति (b) के लिए हम इसी प्रकार का परिणाम स्थापित कर सकते हैं।

टिप्पणी

• यदि समतल π₂, का समीकरण \(\vec{r} \cdot \overrightarrow{\mathrm{N}}\) = d के रूप का है, जहाँ N समतल पर अभिलंब है तो लांबिक दूरी \(\frac{|\vec{a} \cdot \overrightarrow{\mathrm{N}}-d|}{|\overrightarrow{\mathrm{N}}|}\) है।
• मूल बिंदु O से समतल \(\vec{r} \cdot \overrightarrow{\mathrm{N}}\) = d की दूरी \(\frac{|d|}{|\vec{N}|}\) (क्योंकि \(\vec{a}\) = 0)

कार्तीय रूप (Cartesian Form)
माना कि दिया हुआ बिन्दु P(x₁, y₁, z₁) है जिसका स्थिति सदिश a है और दिये गये समतल का कार्तीय रूप का समीकरण Ax + By + Cz = D है।
तब \(\vec{a}\) = x₁î + y₁ĵ + z₁k̂
\(\vec{N}\) = Aî + Bĵ + Ck̂

अतः टिप्पणी (1) के द्वारा P से समतल का लम्ब की लम्बाई

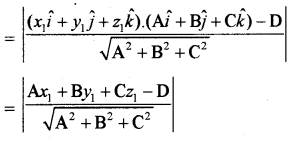
एक रेखा और एक समतल के बीच का कोण (Angle Between A Line And A Plane)
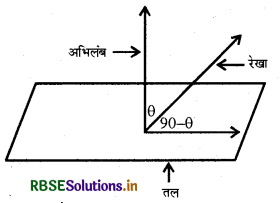
परिभाषा-एक रेखा और एक समतल के बीच का कोण, रेखा और समतल के अभिलंब के बीच के कोण का कोण (complementary angle) पूरक होता है।

सदिश रूप (Vector Form):
माना कि रेखा का समीकरण \(\vec{r}=\vec{a}+\lambda \vec{b}\) है तथा समतल का समीकरण \(\vec{r}.\vec{n}\) = d है। तब रेखा और समतल के अभिलंब के बीच का कोण 0, निम्नलिखित सूत्र द्वारा व्यक्त किया जा सकता है
cos θ = \(\left|\frac{\vec{b} \cdot \vec{n}}{|\vec{b}| \cdot|\cdot \vec{n}|}\right|\)
और इस प्रकार रेखा और समतल के बीच का कोण Φ = (90° - θ) के बराबर होगा, अर्थात्
sin Φ = sin(90° - θ) = cos θ
अर्थात् sin Φ = \(\left|\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|}\right|\) या Φ = sin^-1\(\left|\frac{\vec{b} \cdot \vec{n}}{|\vec{b}||\vec{n}|}\right|\)

→ किसी बिन्दु P का मूल बिन्दु O के सापेक्ष स्थिति सदिश \(\overrightarrow{\mathrm{OP}} = (\vec{r})\) = xî + yĵ + rk̂ होता है जहाँ P के निर्देशांक (x, y, z) हैं। \(\overrightarrow{\mathrm{OP}}\) का परिमाण = \(|\vec{r}|=\sqrt{x^{2}+y^{2}+z^{2}}\)

→ यदि \(\vec{r}\) = aî + bĵ + ck है तो \(\vec{r}\), के दिक्अनुपात a, b, c होंगे। a, b, c अक्षों पर \(\vec{r}\), के प्रक्षेप भी हैं।

→ यदि किसी सदिश \(\vec{r}\), के दिक्अनुपात a, b, c, दिक्कोज्याएँ l, m, n एवं परिमाण r हैं तो
l = \(\frac{a}{r}\), m = \(\frac{b}{r}\), n = \(\frac{c}{r}\)

→ यदि l, m तथा n किसी सदिश के दिक्कोज्याएँ हों तो l² + m² + n² = 1 तथा
\(\vec{r}=|\vec{r}| \)(lî + mĵ +nk̂)
तथा r̂ = \(\frac{\vec{r}}{|\vec{r}|}\) = iî + mĵ + nk̂

→ यदि l₁, m₁, n₁, तथा l₂, m₂, n₂, दो रेखाओं की दिक्कोज्याएँ हैं
तो cos θ = l₁l₂, m₁m₂, n₁n₂

(i) यदि रेखाएँ परस्पर लम्बवत् हों तो ..
l₁l₂ + m₁m₂ + n₁n₂ = 0

(ii) यदि रेखाएँ समान्तर हों तो
\(\frac{l_{1}}{l_{2}}=\frac{m_{1}}{m_{2}}=\frac{n_{1}}{n_{2}}\)

→ यदि दो रेखाओं के दिक्अनुपात a₁, b₁, c₁, तथा a₂, b₂, c₂ हैं
तो उनके बीच के कोण θ के लिए
cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)

(i) यदि रेखाएँ परस्पर लम्बवत् हों तो
a₁a₂ + b₁b₂ + c₁c₂ = 0

(ii) यदि रेखाएँ समान्तर हों तो
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

→ बिन्दु (\(\vec{a}\)) से जाने वाले एवं सदिश (\(\vec{b}\)) के समान्तर रेखा का समीकरण \(\vec{r}=\vec{a}+\lambda \vec{b}\) होता है। जहाँ λ अशून्य वास्तविक संख्या है।

→ कार्तीय रूप में, बिन्दु (x₁, y₁, z₁) से जाने वाली रेखा, जिसकी दिक्कोज्याएँ l, m, n हैं, का समीकरण
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=\frac{z-z_{1}}{n}\)
यदि रेखा के दिक्अनुपात a, b, c हैं तो रेखा का समीकरण
\(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\)

→ बिन्दुओं \(\vec{a}\)/(x₁, y₁, z₁) तथा \(\vec{b}\)/(x₂, y₂, z₂) से जाने वाली रेखा का समीकरण
सदिश रूप में : \(\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})\)
कार्तीय रूप में : \(\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}\)

→ यदि रेखाओं \(\vec{r}=\vec{a}_{1}+\lambda \vec{b}_{1}\) तथा \(\vec{r}=\vec{a}_{2}+\lambda \vec{b}_{2}\) के बीच न्यूनकोण θ हो, तो
cos θ = \(\left|\frac{\vec{b}_{2} \cdot \vec{b}_{2}}{\left|\vec{b}_{1} \| \vec{b}_{2}\right|}\right|\)

→ यदि \(\frac{x-x_{1}}{l_{1}}=\frac{y-y_{1}}{m_{1}}=\frac{z-z_{1}}{n_{1}}\), तथा \(\frac{x-x_{2}}{l_{2}}=\frac{y-y_{2}}{m_{2}}=\frac{z-z_{2}}{n_{2}}\) दो रेखाएँ हैं तो इनके बीच न्यूनकोण के लिए,
cos θ = |l₁l₂ + m₁m₂ + n₁n₂|

→ रेखाओं \(\vec{r}=\vec{a}_{1}+\lambda \vec{b}_{1}\) तथा \(\vec{r}=\vec{a}_{2}+\lambda \vec{b}_{2}\) के मध्य न्यूनतम \(\left|\frac{\left(\vec{b}_{1} \times \vec{b}_{2}\right) \cdot\left(\vec{a}_{2}-\vec{a}_{1}\right)}{\left|\vec{b}_{1} \times \vec{b}_{2}\right|}\right|\) होती है।

→ रेखाओं \(\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}\) तथा \(\frac{x-x_{2}}{a_{2}}=\frac{y-y_{2}}{b_{2}}=\frac{z-z_{2}}{c_{2}}\) के बीच न्यूनतम दूरी
\(\frac{\left|\begin{array}{ccc} x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{array}\right|}{\sqrt{\left(a_{1} b_{2}-a_{2} b_{1}\right)^{2}+\left(b_{1} c_{2}-b_{2} c_{1}\right)^{2}+\left(c_{1} a_{2}-c_{2} a_{1}\right)^{2}}}\) होती है।

→ समान्तर रेखाओं \(\vec{r}=\vec{a}_{1}+\lambda \vec{b}_{1} \) तथा \(\vec{r}=\vec{a}_{2}+\lambda \vec{b}_{2}\) के बीच न्यूनतम \(\left|\frac{\left(\vec{a}_{2}-\vec{a}_{1}\right) \times \vec{b}}{|\vec{b}|}\right|\) दूरी है।

→ रेखाएँ \(\vec{r}=\vec{a}_{1}+\lambda \vec{b}_{1}\) तथा \(\vec{r}=\vec{a}_{2}+\lambda \vec{b}_{2}\) एक-दूसरे को प्रतिच्छेदित करेंगी अर्थात् एक ही तल में होंगी यदि
\(\left(\vec{b}_{1} \times \vec{b}_{2}\right) \cdot\left(\vec{a}_{2} \times \vec{a}_{1}\right)\) = 0

→ मूल बिन्दु से d दूरी पर समतल का सदिश समीकरण \(\vec{r}\) . n̂ = d होता है, जहाँ n̂ समतल पर मूल बिन्दु से मात्रक अभिलम्ब सदिश है।

→ समतल का व्यापक समीकरण ax + by + cz + d = 0 होता है, जिस पर \(\vec{n}\) = aî + bî + ck̂ अभिलम्ब सदिश होता है।

→ मूल बिन्दु से d दूरी पर समतल का कार्तीय समीकरण lx + my + nz = d होता है जहाँ l, m, n समतल पर अभिलम्ब की दिक्कोज्याएँ हैं।

→ उस समतल का समीकरण जो बिन्दु \(\vec{a}\) से जाता है तथा \(\vec{n}\) पर लम्ब है, \((\vec{r}-\vec{a}) \cdot \vec{n}\) = 0

→ बिन्दु (x₁, y₁, z₁) से जाने वाली तथा A, B, C दिक्अनुपात वाली रेखा पर लम्बवत् समतल का समीकरण
A (x - x₁) + B (y - y₁) + c (z – z₁) = 0

→ तीन असरेखीय बिन्दुओं (x₁, y₁, z₁)/\(\vec{a}\) , (x₁, y₁, z₁)/\(\vec{b}\) तथा (x₃, y₃, z₃)/\(\vec{c}\) से जाने वाले समतल का सदिश व कार्तीय

समीकरण \((\vec{r}-\vec{a}) \cdot[(\vec{b}-\vec{a}) \times(\vec{c}-\vec{a})]\) = 0
तथा \(\left|\begin{array}{ccc} x-x_{1} & y-y_{1} & z-z_{1} \\ x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1} \end{array}\right|\) = 0

→ उस समतल का समीकरण जो अक्षों पर a, b तथा c के अन्त:खण्ड काटता है \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1

→ समतलों \(\vec{r} \cdot \vec{n}_{1} \) = d₁  तथा \(\vec{r} \cdot \vec{n}_{2}\) = d₂, से प्रतिच्छेदी रेखा से जाने वाले समतल का समीकरण \(\vec{r} \cdot\left(\vec{n}_{1}+\lambda \vec{n}_{2}\right)\) = d₁ + λd₂ होता है, जहाँ λ एक अशून्य वास्तविक संख्या है।

→ समतलों a₁x + b₁y + c₁z + d₁ = 0 तथा a₂x + b₂y +
c₂z + d₂ = 0 के प्रतिच्छेदी रेखा से जाने वाले समतल का समीकरण (a₁x + b₁y + c₁z + d₁) + 2 (a₂x + b₂y + c₂z + d₂) = 0

→ रेखाएँ \(\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}\) तथा \(\frac{x-x_{2}}{a_{2}}=\frac{y-y_{2}}{b_{2}}=\frac{z-z_{1}}{c_{2}}\) सहतलीय होंगी, यदि
\(\left|\begin{array}{ccc} x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{array}\right|\) = 0

→ यदि समतलों \(\vec{r}, \vec{n}_{1}\) = d₁, तथा \(\vec{r}, \vec{n}_{2}\) = d₂, के मध्य कोण θ हो तो
cos θ = \(\frac{\left|\vec{n}_{1} \cdot \vec{n}_{2}\right|}{\left|\vec{n}_{1}\right|\left|\vec{n}_{2}\right|}\)

→ रेखा \(\vec{r}=\vec{a}+\lambda \vec{b}\) तथा समतल \(\vec{r}\).n̂ = d के बीच कोण θ हो तो
sin θ = \(\frac{|\vec{b} \cdot \hat{n}|}{|\vec{b} \| \hat{n}|}\)

→ समतलों a₁x + b₁y + c₁z + d₁ = 0 तथा a₂x + b₂y + c₂z + d₂ = 0 के बीच का कोण θ हो तो
cos θ = \(\left|\frac{a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\right|\)

→ समतल \(\vec{r}\).n̂ = d से बिन्दु a की दूरी = [d - \(\vec{a}\).n̂|

→ समतल ax + by + cz + d = 0 की बिन्दु (x₁ y₁, z₁) से लम्बवत् दूरी \(\left|\frac{a x_{1}+b y_{1}+c z_{1}+d}{\sqrt{a^{2}+b^{2}+c^{2}}}\right|\)