RBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry

These comprehensive RBSE Class 12 Maths Notes Chapter 11 Three Dimensional Geometry will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 11 Notes Three Dimensional Geometry

Introduction:
We have read about basic concepts of vectors in the previous chapter. Now, we shall use vector algebra in Three Dimensional Geometry. Vector algebra makes it very easy and interesting. In this chapter we shall read about direction cosines and direction ratios of a line joining two points, equation of lines, angle between two lines, two planes and a line and a plane, shortest distance between two points. We shall represent above in vector and cartesian form.

Direction Cosines and Direction Ratios of a Line:
Direction Cosines: If a directed line L makes angles α, β and γ with positive direction of X-axis, Y-axis and Z-axis respectively, then cos α, cos β and cos γ, are called direction cosines of a line. They are denoted by Z, m and n.
Therefore, l = cos a, m = cos β and n = cos γ Also, stun of squares of directed cosines of a line is always 1,
i.e., l² + m² + n² = 1
⇒ cos²α + cos²β + cos²γ = 1.
If we reverse the direction of L, then the direction angles are replaced by their supplements, i.e., n - α, n - β and it n - γ.
Thus, the signs of the direction cosines are reversed.

• Direction cosines of a directed line are unique.
• Direction cosines of X, Y and Z axes are (1, 0, 0), (0,1,0) and (0,0,1).
• If the given line in space does not pass through the origin, then, in order to find its direction cosines, we draw a line through the origin and parallel to the given line. Now take one of the directed lines from the origin and find its direction cosines as two parallel line have same set of direction cosines.

 

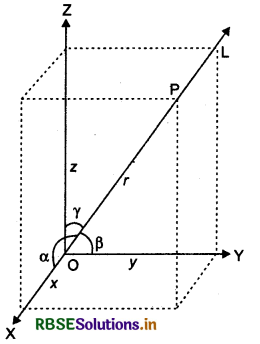
Direction Ratios :
Any three numbers which are proportional to the direction cosines of a line are called direction ratios of the line.
If l, m, n are the direction cosines and a, b, c are the direction ratios of a line, then for X * 0 and X e R,
a = λI, b = λm and c = λn
⇒ \(\frac{a}{l}\) = λ, \(\frac{b}{m}\) = λ and \(\frac{c}{n}\) = λ
⇒ \(\frac{l}{a}=\frac{1}{\lambda}\) (=k), \(\frac{m}{b}=\frac{1}{\lambda}\) (=k) and \(\frac{n}{c}=\frac{1}{\lambda}\)(=k) k is a constant.
⇒ l - ak, m = bk, n = ck
We know, l² + m² + n² = 1
⇒ a²k² + b²k² + c²k² = 1
⇒ k² [a² + b² + c²] = 1
where, depending on the desired sign of k, either a positive or a negative sign is to be taken for l, m and n.

Relation between the Direction Cosines of a Line:
Consider a line PQ with direction cosines l, m, n. Through the origin draw a line parallel to the given line and take a point R(x, y, z) on this line. From R draw a perpendicular RM on the x-axis.

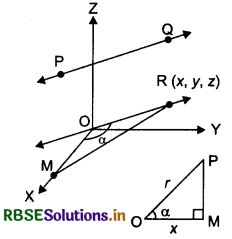
Let OR = r
In right-angled triangle OMR,
∠OMR = 90° and ∠ROM = a
∴ cos α = \(\frac{O M}{O P}=\frac{x}{r}\)
⇒ l = \(\frac{x}{r}\)
⇒ x = lr
Similarly, y = mr and z = nr
Now, OR² = x² + y² + z²
⇒ r² = (lr)² + (mr)² + (nr)²
⇒ r² = r² (l² + m² + n²)
⇒ 1 = l² + m² + n²
Thus, l² + m² + n² = 1

Direction Cosines of a Line passing Through Two Points:
We can determine the direction cosines of a line PQ passing through P(x1, y, za) and Q(x2, y2, z2) as follows :

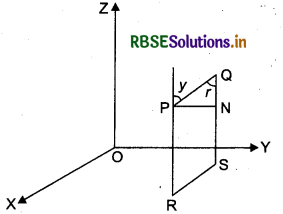
Let l,m, and n be the direction cosines of the line PQ and let it makes angles a, P and y with the x, y and z-axis, respectively.
Draw perpendiculars from P and Q to XY-plane to meet at R and S.
Draw a perpendicular from P to QS to meet at N. Now, in right-angled ΔPNQ,
∠PQN = r
∴ \(\frac{N Q}{P Q}\) = cos γ = \(\frac{z_{2}-z_{1}}{P Q}\)
Similarly,
cos α = \(\frac{x_{2}-x_{1}}{P Q}\)
and cos β = \(\frac{y_{2}-y_{1}}{P Q}\)

So, the direction cosines of the line segment joining point P(x₁, y₁ z₁) and Q(x₂, y₂, z₂) are :
\(\frac{x_{2}-x_{1}}{P Q}, \frac{y_{2}-y_{1}}{P Q}, \frac{z_{2}-z_{1}}{P Q}\)
and x₂ - x₁ y₂ - y₁ z₂ - z₁ are the direction ratios of line PQ.
where PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)
is the distance between points P and Q.

Remarks:

• The direction ratios of the line segment joining P(x₁ y₁ z₁) and Q(x₂, y₂, z₂) may be taken as :
• x₂ - x₁ y₂ - y₁ z₂ - z₁ or x₁ - x₂, y₁ - y₂, z₁ - z₂.
• Direction ratios of two parallel lines are proportional, as the two parallel lines have same set of direction cosines.
• Direction ratios of a line are not unique.

Equation of a Line in Space:
Here, in this section we shall read about vector and cartesian equation of a line in space.
A line is uniquely defined, if

• it passes through the given point and the given in space.
• it passes through two given points.

Equation of a Line through a given Point A (\(\vec{a}\)) and Parolielto given Vector \(\vec{m}\).
Let L be the line which passes through the point A, whose position vector is \(\vec{a}\) and is parallel to the vector \(\vec{b}\).

Let O be orgin. Then, \(\overrightarrow{O A}=\vec{a}\). Let \(\vec{r}\) be the position vector of an arbitrary point P on the line.


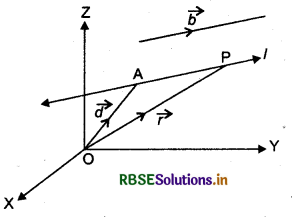
Clearly, for each value of the parameter A, this equation gives the position vector of a point P on the line.
Hence, the vector equation of a line is given by
\(\vec{r}=\vec{a}\) + λ \(\vec{b}\) .......(1)

Derivation of Cartesian Form from Vector Form:
Let the coordinates of the given point A be (x₁ y₁ z₁) and the direction ratios of the line be a, b, c. Consider the coordinates of any point P be (x, y, z). Then,
\(\vec{r}\) = xî + yĵ + zk̂
a = x₁î + y₁ĵ + z₁k̂

∵ Direction ratios of given line are a, b, c and it is parallel to the vector \(\vec{b}\)
∴ \(\vec{b}\) = aî + bĵ + ck̂

Now, vector equation of line is
\(\vec{r}=\vec{a}\) + λ\(\vec{b}\)

Substituting the values of \(\vec{a}, \vec{b}\) and \(\vec{r}\) in equation (i), we get
xî + yĵ + zk̂ =( x₁î + y₁ĵ + z₁k̂) + λ (ai + bj + ck)
⇒ xî +yĵ +zk̂ = (x₁ + λa)î + (y₁ + kb)ĵ + (z₁ + λc) k̂

Equating the coefficients of î, ĵ and k̂, we get
⇒ x = x₁ + λa, y = y₁ + kb, z = z₁ + λc

These are the parametric equations of the line.
⇒ \(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\) = λ ...(ii)

Eliminating the parameter X from (ii), we get the cartesian equation of line, whose direction ratios are a, b, c and which passing through A(x, y, z) as :
\(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\)

Equation of a Line Passing Through Two Given Points:
Vector Form :
Let \(\vec{a}\) and \(\vec{b}\) be the position vectors of two points A(x₁ y₁ z₁) and B(x₂, y₂, z₂), respectively that are lying on a line L.

If O be origin, then \(\overrightarrow{O A}=\vec{a}\) and \(\overrightarrow{O B}=\vec{b}.\)

\(\overrightarrow{A B}\) = (Position vector of B) - (Position vector of A)
= \(\vec{b} - \vec{a}\)

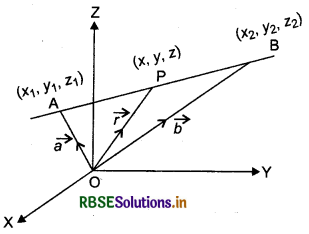
Let \(\vec{r}\) be the position vector of an arbitrary point P(x, y, z) on line L, then \(\overrightarrow{O P}=\vec{r}\)

\(\overrightarrow{A P} = \vec{r} - \vec{a}\) 
Since, \(\overrightarrow{A P}\) and \(\overrightarrow{A B}\) are collinear vectors,
\(\overrightarrow{A P}\) = λ(\(\overrightarrow{A B}\)), λ ∈ R
⇒ \(\vec{r}-\vec{a}\) = λ(\(\vec{b}-\vec{a}\))
⇒ \(\vec{r}\) = \(\vec{a}\) + λ(\(\vec{b}-\vec{a}\))

Thus, vector equation of line L, passing throughpoints A(\(\vec{a}\)) and B(\(\vec{b}\)) is
\(\vec{r} = \vec{a}\) + λ(\(\vec{b}-\vec{a}\)), x ∈ R ...(2)

Derivation of Cartesian Form from Vector Form:
We have \(\vec{r}\) = xî + yĵ + zk̂
\(\vec{a}\) = x₁î + y₁ĵ + z₁k̂
\(\vec{b}\) = x₂î + y₂ĵ + z₂k̂

Substituting these values in equation (2), we get
xî + yĵ + zk̂ = x₁î + y₁ĵ + z₁k̂ + λ(x₂ - x₁)î + (y₂ - y₁)ĵ + (z₂ - z₁)k̂]

Eliminating the like coefficients of î, ĵ, k̂, we get
x = x₁ + λ(x₂ - x₁),
⇒ x - x₁ = λ(x₂ - x₁);

y = y₁ + λ(y₂ - y₁)
⇒ y - y₁ = λ(y₂ - y₁);

z = z₁ + λ(z₂ - z₁)
⇒ z - z₁ = λ(z₂ - z₁)

On eliminating λ, we get
\(\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}\)
Which is the equation of line in cartesian form passing through the given points.

Angle Between Two Lines
(i) Let L₁ and L₂ be two lines passing through origin whose directionratios are a₁ b₁ c₁ and a₂, b₂, c₂ respectively. Let P and Q be two points on L₁ and L₂ respectively and θ be the acute angle between OP and OQ.
The angle θ between them is given by

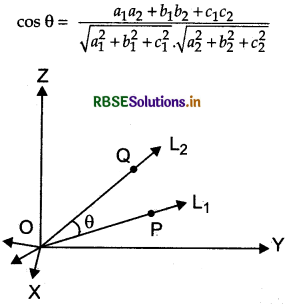
The angle between the lines in terms of sin θ is given by

Remarks:
If the lines L₁ and L₂ do not pass through the origin, we may take lines L₁ and L₂ which are parallel to L₁ and L₂ respestively and pass through the origin.

(ii) Let l₁ m₁ n₁ and l₂, m₂, n₂ be the direction-cosines of line OP and OQ respectively. If θ is the angle between these lines, then
cos θ = |l₁l₂ + m₁m₂ + n₁n₂|
(Since, l₁² + m₁² + n₁² = 1 = l₂² + m₂² + n₂²)
and sin θ = \(\sqrt{\left(m_{1} n_{2}-m_{2} n_{1}\right)^{2}+\left(n_{1} l_{2}-n_{2} l_{1}\right)^{2}+\left(l_{1} m_{2}-l_{2} m_{1}\right)^{2}}\)

(iii) Two perpendicular lines : Two lines whose direction cosines are l₁ m₁ n₁ and l₂, m₂, n₂ respectively, are mutually perpendicular
then θ = \(\frac{\pi}{2}\) ⇒ cos θ = cos\(\frac{\pi}{2}\) = 0
⇒ l₁l₂ + m₁m₂ + n₁n₂ = 0
If a₁ b₁ c₁ and a₂, b₂, c₂ are the direction-ratios of the lines, then the lines are mutually perpendicular if a₁a₂ + b₁b₂ + c₁c₂ = 0

(iv) Two parallel lines : If l₁ m₁ n₁ and l₂, m₂, n₂ are the direction-cosines of two lines and the lines are mutually parallel, then 0 = 0°
sin θ = sin 0° = 0
sin θ = \(\sqrt{\left(m_{1} n_{2}-m_{2} n_{1}\right)^{2}+\left(n_{1} l_{2}-n_{2} l_{1}\right)^{2}+\left(l_{1} m_{2}-l_{2} m_{1}\right)^{2}}\)
= 0
⇒ m₁n₂ - m₂n₁ = 0 or \(\frac{m_{1}}{m_{2}}=\frac{n_{1}}{n_{2}}\)
and n₁l₂ - n₂l₁ = 0 or \(\frac{n_{1}}{n_{2}}=\frac{l_{1}}{l_{2}}\)
⇒ \(\frac{l_{1}}{l_{2}}=\frac{m_{1}}{m_{2}}=\frac{n_{1}}{n_{2}}\)

When a₁ b₁ c₁ and a₂, b₂, c₂ are the direction-ratios of the lines then they are mutually parallel if
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

Now, we find the angle between two lines when their equations are given. If θ is the acute angle between the lines

where, a₁ b₁ c₁ and a₂, b₂, c₂ are the direction ratios of the lines (1) and (2), respectively, then
cos θ = \(\left|\frac{a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\right|\)

Shortest Distance Between Two Lines:
To find shortest distance between two lines, some definitions are essential which are expresses as :
Coplanar lines :
The lines which are in same plane are called coplanar lines. Coplanar lines are either parallel or intersecting lines.

Skew lines:
In a space there are lines which are neither intersecting nor parallel. In fact such pair of lines are non-coplanar and are called skew lines.

Line of shortest distance between two skew lines:
If l₁ and l₂ are two skew lines in space then shortest distance between them will be that line which will be perpendicular to both lines.

Shortest distance between two skew lines :
The shortest distance between two skew lines is a line segment which is an intercept on common perpendicular by these lines.

Distance Between Two Skew Lines:
Vector Form :
Let L₁ and L₂ be two skew lines with equations
L₁: \(\vec{r}=\overrightarrow{a_{1}}\)+λ \(\overrightarrow{b_{1}}\) .........(1)
L₂: \(\vec{r}=\overrightarrow{a_{2}}\)+λ \(\overrightarrow{b_{2}}\) .........(2)

Clearly, L₁ and L₂ pass through the point A and B with positions vectors \(\overrightarrow{a_{1}}\) and \(\overrightarrow{a_{2}}\) respectively and are parallel to the vectors \(\overrightarrow{b_{1}}\) and \(\overrightarrow{b_{2}}\) respectively.

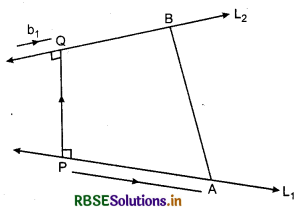
If \(\overrightarrow{P Q}\) is the shortest distance vector between L₁ and L₂, then it being perpendicular to both b₁ and b₂, the unit vector n̂ along \(\overrightarrow{P Q}\) would therefore be
n̂ = \(\frac{\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}}{\left|\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}\right|}\)
Thus \(\overrightarrow{P Q}\) = (PQ) n̂ = dn̂ where PQ = d (Shortest distance). Let θ be the angle between \(\overrightarrow{A B}\) and \(\overrightarrow{P Q}\), then
PQ = AB cos θ ...(1)

Note: If two lines intersect each other, then the shortest distance between them is zero, or

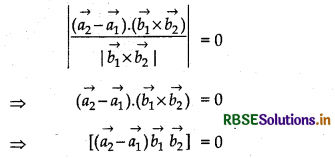
Cartersian Form: Shortest distance between the lines

Distance between Two Parallel Lines:
If two lines L₁ and L₂ are parallel, then they are coplanar. Let the lines be given by
\(\vec{r} = \overrightarrow{a_{1}}\) + λ \(\vec{b}\)
and \(\vec{r} = \overrightarrow{a_{2}}\) + λ \(\vec{b}\)

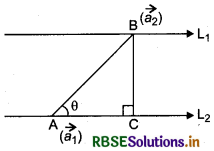
Clearly, L₁ and L₂ passes through the points A and B with position vectors \(\overrightarrow{a_{1}}\) and \(\overrightarrow{a_{2}}\) respectively and both are parallel to the vector \(\vec{b}\).

Let BC be perpendicular from B to L₁ then the shortest distance between L₁ and L₂ = BC.
Let θ be angle between \(\overrightarrow{A B}\) and \(\vec{b}\).
Then, \(\vec{b}\) × \(\overrightarrow{A B}\) = (|\(\vec{b}\)| |× AB | sin θ )n̂
where n̂ is the unit vector perpendicular to the plane of the lines L₁ and L₂.

⇒ \(\vec{b}\) × \(\left(\overrightarrow{a_{2}}-\overrightarrow{a_{1}}\right)\) = |\(\vec{b}\)| (BC)n̂, where BC = (AB) sin 0

Plane:
A plane is a surface such that if any two points are taken on it, the line segment joining them lies completely on the surface.

Normal to a Plane:
A line which is perpendicular to all lines on a plane, is called normal at plane.
All normals at plane are parallel to each other.
Any plane can be specified by many ways :

• From three non-collinear points only one plane in one side can be drawn. Thus three given points determine a specific plane.
• From origin at a given distance and perpendicular in given direction, only one plane can be drawn. Thus if normal of plane and its distance from origin is given then a specific plane is determined.
• Two concurrent line determine a specific plane.
• At a plane, one point and its normal determines a unique plane.

In the following section, vector and cartesian equation of plane will be find in different form.

Equation of a Plane in Normal Form:
Let the distance of plane ABC from origin is d. ON is normal to plane ABC from origin O and n̂ is unit normal vector along \(\overrightarrow{O N}\).
Then \(\overrightarrow{O N}\) = dn̂

Let P be any point on the plane. So, \(\overrightarrow{N P}\) is perpendicular to \(\overrightarrow{O N}\).

This is the vector form equation of the plane.

Equation of Cartesian Form
Let P(x, y, z) be any point on a plane, then
\(\overrightarrow{O P}=\vec{r}\) = x î + y ĵ + z k̂

Let direction cosines of n are l, m, n, then
n̂ = l î + m ĵ + nk̂
Since,\( \vec{r}\)n̂ = d,
(x î + y ĵ + zk̂).(l î + mĵ + nk̂) = d
⇒ lx + my + nz = d
This is the cartesian form of the plane in the normal form.

Remark:

• If distance of the plane from the origin is d and l, m, n are the direction cosines of the normal to the plane, then the foot of the perpendicular is (ld, md, nd).
• Equation lx + my + nz - d shows that if \( \vec{r}\) .(aî + bĵ + ck̂) = d is the vector equation of a plane, then ax + by+ cz = d is the cartesian equation of the plane, where a, b and c are the direction ratios of the normal to the plane.

Equation of a Plane perpendicular to a given vector and passing through a given point:
Let a plane passes through a point A with position vector \(\vec{a}\) and perpendicular to the vector \(\vec{N}\).
Let P(x, y, z) be any point on the plane whose position vector is \( \vec{r}\).
Then, point P lies on the plane if and only if \(\overrightarrow{A P}\) is perpendicular to \(\vec{N}\).
i.e., \(\overrightarrow{A P}.\vec{N}\) = 0
⇒ \((\vec{r}-\vec{a}) \cdot \vec{N}\) = 0 [∵ \(\overrightarrow{A P}=\vec{r}-\vec{a}\)]

This is the vector equation of the plane.

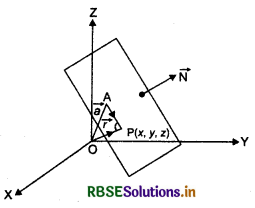
Cartesian Form of Plane:
Let the given point A(x₁ y₁ z₁) and P(x, y, z) be any point on the plane and direction ratios of \(\vec{N}\) are A, B and C, then
\(\vec{a}\) = x₁î + y₁ĵ + z₁k̂
\(\vec{r}\) = xî + yĵ + zk̂
and \(\vec{N}\) = Aî + Bĵ + Ck̂
Now \((\vec{r}-\vec{a}) \cdot \vec{N}\) = 0
[(x - x₁) î + (y - y₁) ĵ + (z - z₁)k̂].(Aî + B ĵ + Ck̂) = 0
Thus, A(x - x₁) + B(y - y₁) + C(z - z₁) = 0.

Equation of a plane passing through three non-collinear points:
Let R, Q and M be three non-collinear points on the plane with position vectors \(\vec{a}, \vec{b}\) and \(\vec{c}\) respectively. The vectors \(\overrightarrow{R Q}\) and \(\overrightarrow{R M}\) are in the given plane. Therefore, the vectors \(\overrightarrow{R Q} \times \overrightarrow{R M}\) is perpendicular to the plane containing points R, Q and M.

Let the position vector of any point P(x, y, z) is \(\vec{r}\)
The equation of the plane passing through R and perpendicular to the vector \(\overrightarrow{R Q} \times \overrightarrow{R M}\) is :
\((\vec{r}-\vec{a}) \cdot(\overrightarrow{R Q} \times \overrightarrow{R M}\) = 0
or \((\vec{r}-\vec{a}) \cdot[(\vec{b}-\vec{a}) \times(\vec{c}-\vec{a})]\) = 0 ...(1)

This is the equation of the plane in vector form.

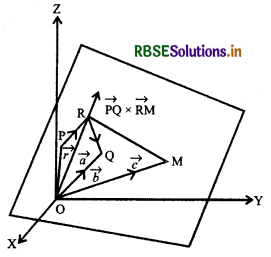
Cartesian Form of plane:
Let coordinate of point R, Q and M are (x₁ y₁ z₁), (x₂, y₂, z₂) (x₃ y₃ z₃) respectively.

Let (x, y, z) be the coordinates of any point P on the plane with position vector \(\vec{r}\), then
\(\overrightarrow{R P}\) = (x - x₁)î + (y - y₁)ĵ + (z - z₁)k̂
\(\overrightarrow{R Q}\) = (x₂ - x₁)î + (y₂ - y₁)ĵ + (z₂ - z₁)k̂
\(\overrightarrow{R M}\) = (x₃ - x₁)î + (y₃ - y₁)ĵ + (z₃ - z₁)k ̂

Substituting these values in equation (1) of the vector form and expressing it in the form of a determinant, we have
\(\left|\begin{array}{ccc} x-x_{1} & y-y_{1} & z-z_{1} \\ x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1} \end{array}\right|\) = 0
which is the equation of the plane in cartesian form passing through three non-collinear points (x₁ y₁ z₁), (x₂, y₂, z₂) (x₃ y₃ z₃).

Intercept form of the equation of a plane :
Let the general equation of the plane be :
Ax + By + Cz + D = 0(D ≠ 0) ...(1)

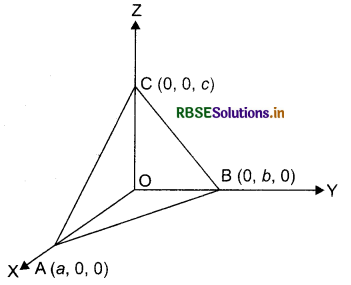
Let this plane cuts intercepts a, b, c on x, y and z-axes respectively.
So, the plane meets x, y and z axis at (a, 0, 0), (0, b, 0), (0, 0, c) respectively.
So, A.a + B.O + C.O + D = 0
⇒ An + D = 0 or A = -\(\frac{D}{a}\)
⇒ Bb + D = 0 or B = -\(\frac{D}{b}\)
⇒ Cc + D = 0 or C = -\(\frac{D}{c}\)

Putting the values of A, B, C in equation (1), we get

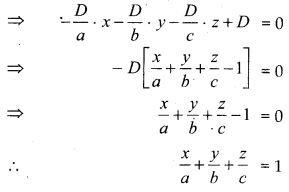
This is the required equation of the plane in the intercept form.

Plane passing through the intersection of two given planes:
Let two planes PQ and RS intersect each other at a line AB whose equations are \(\vec{r} \cdot \overrightarrow{n_{1}}\) = d₁ and \(\vec{r} \cdot \overrightarrow{n_{2}}\) = d₂ respectively. The position vector of a point lie on intersecting line AB must satisfy both equations.

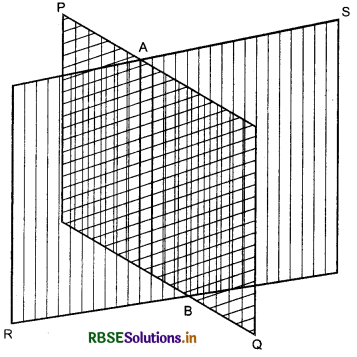
Thus, the equation of any plane passing through the intersection of planes \(\vec{r} \cdot \overrightarrow{n_{1}}\) = d₁ and \(\vec{r} \cdot \overrightarrow{n_{2}}\) = d₂
\(\left(\vec{r} \cdot \overrightarrow{n_{1}}-d_{1}\right)+\lambda\left(\vec{r} \cdot n_{2}-d_{2}\right)\) = 0
or
\(\vec{r} \vec{r}\left(\overrightarrow{n_{1}}+\lambda \overrightarrow{n_{2}}\right)=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{2}}\)

Cartesian Form of plane :
Let equations of two planes
a₁x + b₁y + c₁z + d₁ = 0 ...(1)
and a₂x + b₂y + c₂z + d₂ = 0 ... (2)

In figure, plane PQ and RS intersect in line AB. Thus, AB is a intersecting line.
∵ Planes (1) and (2) intesect in a line, then we suppose that the point (x'₁ y'₁, z'₁) lies on this line. Because this point is on the intersect line, thus its coordinate satisfy (1) and (2).
a₁x' + b₁y’ + c₁z' + d₁ = 0 ...(3)
and a₂x' + b₂y' + c₂z' + d₂ = 0 ...(4)

Multiplying equation (4) by any constant X and adding in equation (3), we get
(a₁x' + b₁y' + C₁z' + d₁) + λ(a₂x' + b₂y' + c₂z' + d₂) = 0
⇒ (a₁ + λa₂)x' + (b₁ + λb₂)y' + (c₁ + λc₂)z' + d₁ + λd₂ = 0
∴ Required plane
(a₁ + λa₂)x + (b₁ + λb₂)y + (c₁ + λc₂)z + (d₁ + λd₂) = 0 Value of λ can be find by the given condition.

Coplanarity of Two Lines:
Let two known lines are
\(\vec{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}\) ........(1)
and \(\vec{r}=\overrightarrow{a_{2}}+\lambda \overrightarrow{b_{2}}\) .....(2)

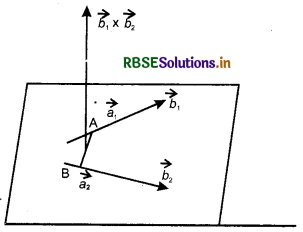
Line (1) passes through the point A, whose position vector is \(\overrightarrow{a_{1}}\) and is parallel to \(\overrightarrow{b_{1}}\)
Line (2) passes through the point B, whose position \(\overrightarrow{a_{2}}\) and is parallel to \(\overrightarrow{b_{2}}\)
∴ \(\overrightarrow{A B}=\overrightarrow{a_{2}}-\overrightarrow{a_{1}}\)

The given lines will be coplanar if and only if \(\overrightarrow{A B}\) is perpendicular to \(\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}\).
i.e \(\overrightarrow{A B}\left(\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}\right)\) = 0
⇒ \(\left(\overrightarrow{a_{2}}-\overrightarrow{a_{1}}\right) \cdot\left(\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}\right)\) = 0

Cartesian Form:
Let coordinates of points A and B are (x₁ y₁ z₁) and (x₂, y₂, z₂) respectively and direction ratios of \(\overrightarrow{b_{1}}\) and \(\overrightarrow{b_{2}}\) are a₁ b₁ c₁ and a₂, b₂, c₂ respectively.
Then \(\overrightarrow{A B}\) = (x₂ - x₁)î + (y₂ - y₁) ĵ + (z₂ - z₁) k̂
\(\overrightarrow{b_{1}}\) = a₁î + b₁ ĵ + c₁k̂
and \(\overrightarrow{b_{2}}\) = a₂î + b₂ ĵ + c₂k̂

The given lines are coplanar if and only if
\(\overrightarrow{A B} \cdot\left(\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}\right)\) = 0.

In the cartesian form it can be expressed as :
\(\left|\begin{array}{ccc} x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{array}\right|\) = 0

Angle Between Two Planes:
Definition: The angle between two planes is the angle between their normals.
Let θ be the angle between the planes P₁ \(\vec{r} \cdot \overrightarrow{n_{1}}\) = d₁ and P₂,\(\vec{r} \cdot \overrightarrow{n_{2}}\) = d₂. Then θ is the angle between the normals to the plane drawn from any common point.

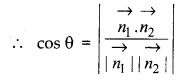
Remark:
Both planes are mutually perpendicular if \(\overrightarrow{n_{1}}, \overrightarrow{n_{2}}\) = 0 and are parallel if \(\overrightarrow{n_{1}}\) and \(\overrightarrow{n_{2}}\) are parallel.

Cartesian Form:
Let equations of two planes P₁ and P₂ are
a₁x + b₁y + c₁z + d₁ = 0
and a₂x + b₂y + c₂z + d₂ = 0

The direction ratios of the normal to the planes are a₁, b₁ c₁ and a₂, b₂, c₂ respectively.
Let θ is the angle between them. Then,

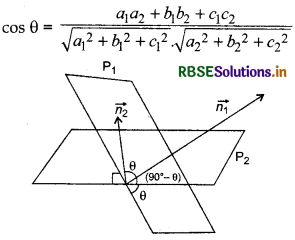
Remark:
1. If both planes are mutually perpendicular, then θ = 90°. Thus cos θ = 0. Hence
cos θ = a₁a₂ + b₁b₂ + c₁c₂ = 0.

2. Planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 are parallel, if
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

3. Equation of plane :
(a) Equation of plane parallel to plane
\(\vec{r}.\vec{n}\) = d is
\(\vec{r}.\vec{n}\) = λ
(b) Equation of plane parallel to plane ax + by + cz + d = 0 is ax + by + cz + d + λ = 0 value of λ can be determined by the given condition.

Distance of a Point from a Plane:
Vector Form:
Let a point P whose position vector is \(\vec{a}\) and a plane π₁ whose equation is \(\vec{r}\).n̂ = d.
Again, a plane π₂, through P parallel to the plane π₁

The unit vector normal to π₂ is n̂.

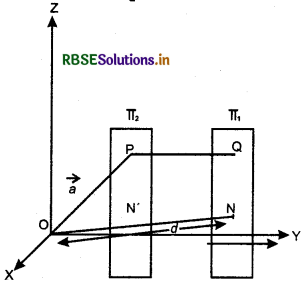
So, its equation is
(\(\vec{r}-\vec{a}\)).n̂ = 0
i.e \(\vec{r}\). n̂ = \(\vec{a}\).n̂

Hence, distance of the plane PQ from origin.
ON' = |\(\vec{a}\).n̂|
∴ Distance of the plane nx from P = | d - \(\vec{a}\).n̂|
which is the length of the perpendicular from a point to the given line.

Remark:
(1) If the equation of the plane n₂ is in the form r .N = d, where N is normal to the plane, then

Cartesian Form :
Let equation of plane be ax + by + cz + d = 0 and P is a point outside the plane whose coordinates are (x₁ y₁ z₁). The coordinates of any point A lies on the plane are (x, y, z).
Perpendicular PN is drawn on the plane from the point P outside the plane.

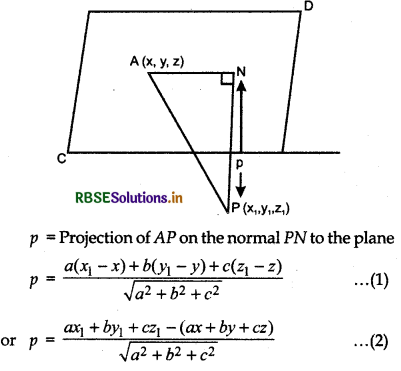
But equation of the plane ax+ by + cz + d = 0
∴ ax + by + cz = - d
Putting these values in equation (2)
p = \(\frac{a x_{1}+b y_{1}+c z_{1}+d}{\sqrt{a^{2}+b^{2}+c^{2}}}\)

∵ Distance is positive
∴ p = \(\left|\frac{a x_{1}+b y_{1}+c z_{1}+d}{\sqrt{a^{2}+b^{2}+c^{2}}}\right|\)
This is required distance.

Angle Between a Line and a Plane
Definition : The angle between a line and a plane is the complement of the angle between the line and normal to the plane.

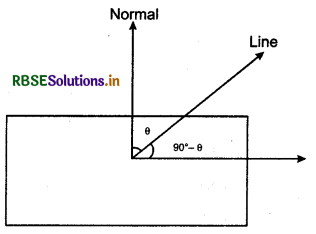
Vector form:
Let equation of line is \(\vec{r}=\vec{a}+\lambda \vec{b}\) and equation of plane is \(\vec{r}.\vec{n}\) = d. Then the angle 0 between the line and the normal to the plane is

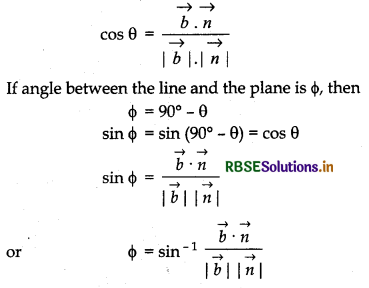
Cartesian form:
Angle between line
\(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\)
and normal to the plane Ax + By + Cz + D = 0 is 0 in such a way:
cos θ = \(\frac{a \cdot A+b \cdot B+c \cdot C}{\sqrt{a^{2}+b^{2}+c^{2}} \cdot \sqrt{A^{2}+B^{2}+C^{2}}}\)
If angle between the line and the plane is Φ, then
Φ = 90° - θ
sin Φ = sin (90° - θ) = cos θ
sin Φ = \(\frac{a \cdot A+b \cdot B+c \cdot C}{\sqrt{a^{2}+b^{2}+c^{2}} \cdot \sqrt{A^{2}+B^{2}+C^{2}}}\)

→ Shortest distance between two points P(x₁ y₁ z₁) and Q(x₂, y₂, z₂) in space is :
PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)

→ Distance of the point P (x, y, z) from origin O (0,0,0) is:
OP = \(\sqrt{x^{2}+y^{2}+z^{2}}\)

→ Let P(x₁ y₁ z₁) and Q(x₂ y₂ z₂) be two points and let R (x, y, z) be a point on PQ dividing it in the ratio
(i) internally, is given by
x = \(\frac{m x_{2}+n x_{1}}{m+n}\), y = \(\frac{m y_{2}+n y_{1}}{m+n}\), z = \(\frac{m z_{2}+n z_{1}}{m+n}\)
(ii) externally, is given by
x = \(\frac{m x_{2}-n x_{1}}{m-n}\), y = \(\frac{m y_{2}-n y_{1}}{m-n}\), z = \(\frac{m z_{2}-n z_{1}}{m-n}\)

→ The coordinates of the mid point of the line segment joining the point P(x₁ y₁ z₁) and Q(x₂ y₂ z₂) are :
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}, \frac{z_{1}+z_{2}}{2}\right)\)

→ Coordinates of the centroid of the triangle with vertices (x₁ y₁ z₁), (x₂ y₂ z₂) and (x₃ y₃ z₃) are :
\(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}, \frac{z_{1}+z_{2}+z_{3}}{3}\right)\)

→ The distance of point P (x, y, z) from x-axis, y-axis andz-axisare \(\sqrt{y^{2}+z^{2}}, \sqrt{z^{2}+x^{2}}\) and \(\sqrt{x^{2}+y^{2}}\) respectively.

→ If a line makes angle α, β and γ with axes OX, OY and OZ respectively. The cosines of these angles are the direction cosines of line, hence, cos α, cos β and cos γ are the direction cosines of the line which is respresented by l, m and n. I = cos α, m = cos β and n = cos γ and cos²α + cos²β + cos²γ = 1
⇒ l² + m² + n² = 1
(i) Direction cosines of a line joining two points P(x₁ y₁ z₁) and Q(x₂ y₂ z₂) are :
\(\frac{x_{2}-x_{1}}{p q}=\frac{y_{2}-y_{1}}{p q}=\frac{z_{2}-z_{1}}{p q}\)
where pq = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)

(ii) The direction ratios of the line segment joining two points P(x₁ y₁ z₁) and Q(x₂ y₂ z₂) are : x₂ - x₁, y₂ - y₁, z₂ - z₁

→ Direction ratios of a line are the numbers which are proportional to the direction cosines of a line. Generally, direction ratios are represented as a, b and c. If l, m, n are the direction cosines and a, b, c are the direction ratios of a line then.
l = \(\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}\); m = \(\frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}\); n = \(\frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}\)

(i) If l, m and n be the direction cosines of vector r then l² + m² + n² = 1
(ii) \(\vec{r}=|\vec{r}|\)(lî + mĵ + nk̂)
and \(\vec{r}=\frac{\vec{r}}{|\vec{r}|}\) = lî + mĵ + nk̂
(iii) Projection of vector \(\vec{r}\) on axes is |\(\vec{r}\)|, m |\(\vec{r}\)|, and n |\(\vec{r}\)| respectively.

→ The projection of line segment joining the points P(x₁ y₁ z₁) and Q(x₂ y₂ z₂) on a line having direction cosines l, m and n are
|(x₂ - x₁)l + (y₂ - y₁)m + (z₂ - z₁)n|

→ If direction cosines of two lines are l₁ m₁ n₁ and l₂, m₂, n₂ respectively then
cos θ = l₁l₂ + m₁m₂ + n₁n₂
(i) If lines are perpendicular, then
l₁l₂ + m₁m₂ + n₁n₂ = 0

(ii) If lines are parallel, then
\(\frac{l_{1}}{l_{2}}=\frac{m_{1}}{m_{2}}=\frac{n_{1}}{n_{2}}\)

→ If direction cosine of two lines are proportional to a₁, b₁ c₁ and a₂, b₂, c₂ then angle between them
cos θ = \(\frac{a_{1} b_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)
(i) If lines are perpendicular, then
a₁a₂ + b₁b₂ + c₁c₂ = 0
(ii) If lines are parallel, then
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

→ Vector equation of a line that passes through the given point \(\vec{r}\) and parallel to a given vector \(\vec{b}\) is \(\vec{r}=\vec{a}+\lambda \vec{b}\) where λ, is a non-zero real number.
(i) Cartesian equation of a line through a point (x₁ y₁ z₁) and having direction cosines l, m, n is
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=\frac{z-z_{1}}{n}\) (∵ l² + m² + n² = 1)

(ii) If direction ratios of the line is a, b, c then the equation of the line is \(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\)

→ Equation of a line passing through two points (x₁ y₁ z₁) and (x₂ y₂ z₂) is :
\(\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}\)

→ If acute angle between two lines \(\vec{r}=\vec{a}_{1}+\lambda b_{1}\) and \(\vec{r}=\vec{a}_{1}+µ b_{1}\) is θ, then
cos θ = \(\left|\frac{\overrightarrow{b_{1}} \vec{b}_{2}}{\mid \vec{b}_{1} \| \vec{b}_{2}}\right|\)

→ If \(\frac{x-x_{1}}{l_{1}}=\frac{y-y_{1}}{m_{1}}=\frac{z-z_{1}}{n_{1}}\) and \(\frac{x-x_{2}}{l_{2}}=\frac{y-y_{2}}{m_{2}}=\frac{z-z_{2}}{n_{2}}\) be two lines, then for acute angle θ
cos θ = |l₁l₂ + m₁m₂ + n₁n₂|

→ Those lines which are neither intersect nor parallel are known as non-coplanar lines. Hence both are on different planes.

→ If L₁ and L₂ be two lines in space then the line segment perpendicular to both the lines are known as shortest distance. If shortest distance line of both lines intersect at point P and Q then PQ is known as shortest distance.

→ Shortest distance between the lines \(\vec{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}\) and \(\vec{r}=\overrightarrow{a_{2}}+\mu \overrightarrow{b_{2}}\) is \(\left|\frac{\left(\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}\right) \cdot\left(\overrightarrow{a_{2}} \times \overrightarrow{a_{1}}\right)}{\left|\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}\right|}\right|\)

→ Shortest Distance between the lines \(\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}\) and \(\frac{x-x_{2}}{a_{2}}=\frac{y-y_{2}}{b_{2}}=\frac{z-z_{2}}{c_{2}}\) is:
S.D = \(\frac{\left|\begin{array}{ccc} x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{array}\right|}{\sqrt{\left(b_{1} c_{2}-c_{2} b_{1}\right)^{2}+\left(c_{1} a_{2}-c_{2} a_{1}\right)^{2}+\left(a_{1} b_{2}-b_{2} a_{1}\right)^{2}}}\)

→ Shortest Distance between the lines \(\vec{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}\) and \(\vec{r}=\overrightarrow{a_{2}}+\mu \overrightarrow{b_{2}}\) is S.D = \(\left|\frac{\left(\overrightarrow{a_{2}}-\vec{a}_{1}\right) \times \vec{b}}{|\vec{b}|}\right|\)

→ Lines \(\vec{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}\) and \(\vec{r}=\overrightarrow{a_{2}}+\mu \overrightarrow{b_{2}}\) intersect each other if
\(\left(\overrightarrow{b_{1}} \times \vec{b}_{2}\right)\left(\overrightarrow{a_{2}}-\overrightarrow{a_{1}}\right)\) = 0

→ The vector equation of a plane which is at a distance d from the origin is \(\vec{r}\) n̂ = d, where n̂ is the normal unit vector to the plane through the origin.

• General equation of a plane is ax + by + cz + d = 0
• Normal vector on plane ax + by + cz + d = 0 is \(\vec{x}\) = aî + bĵ + ck̂
• If l, m, and n be the direction cosines of normal and distance of the plane from the origin is p then normal form of plane is lx + my + nz = d.

→ Cartesian equation of a plane at a distance d from the origin is lx + my + nz = d, where l, m, n are the direction cosines of normal at plane.

→ Equation of the plane which passes through \(\vec{n}\) is \((\vec{r}+\vec{a}) \vec{n}\) = 0

→ Equation of the plane which passes through the point (x₁ y₁ z₁) and having direction cosines A, B, C and perpendicular to the line is :
A(x - x₁) + B(y- y₁) + C(z - z₁) = 0

→ Equation of the plane which passes through three non-collinear points (x₁ y₁ z₁), (x₂ y₂ z₂) and (x₃ y₃ z₃) is :
\(\left|\begin{array}{ccc} x-x_{1} & y-y_{1} & z-z_{1} \\ x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1} \end{array}\right|\) = 0

→ Equation of the plane which passes through three non-collinear points \(\vec{a}, \vec{b}\) and \(\vec{c}\) is.
\((\vec{r}-\vec{a})[\vec{b}-\vec{a}) \times(\vec{c}-\vec{a})]\) = 0

→ Equation of the plane which passes through points (a, 0, 0), (0, b, 0) and (0, 0, c) is :
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1

→ Vector equation of a plane that passes through the intersection of planes \(\vec{r} \cdot \overrightarrow{x_{1}}\) = d₁ and \(\vec{r} \cdot \overrightarrow{x_{2}}\) = d₂ is \(\vec{r}(\vec{x}+\lambda \vec{x})\) = d₁ + λ d₂, where λ is any non-zero constant.

→ Vector equation of a plane that passes through the intersection of two given planes A₁x + B₁y + C₁z + D₁ = 0 and A₂ x + B₂y + C₂z + D₂ = 0 is :

→ Lines \(\vec{r}=\vec{a}_{1}+\lambda \vec{b}_{1} \)and \(\vec{r}=\vec{a}_{2}+\lambda \vec{b}_{2}\) are coplanar if \(\left(\overrightarrow{a_{2}}-\overrightarrow{a_{1}}\right) \cdot\left(\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}\right)\)

→ Lines \(\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}\) and \(\frac{x-x_{2}}{a_{2}}=\frac{y-y_{2}}{b_{2}}=\frac{z-z_{2}}{c_{2}}\) are coplanar if \(\left|\begin{array}{ccc} x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{array}\right|\) = 0

→ (i) If θ is the angle between the planes \(\vec{r}-\overrightarrow{x_{1}}\) = d₁ and \(\vec{r}-\overrightarrow{x_{1}}\) = d₂, then cos θ = \(\frac{\left|\overrightarrow{x_{1}} \vec{x}_{2}\right|}{\left|\overrightarrow{x_{1}}\right|\left|\vec{x}_{2}\right|}\)

(ii) If θ be the angle between the lines \(\vec{r}=\vec{a}+\lambda \vec{b}\) and \(\vec{r}=\vec{x}\) = d, then
sin θ = \(\frac{|\vec{b} \hat{x}|}{|\vec{b} \| \hat{x}|}\)

→ If θ be the angle between the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0, then

• If planes are mutually perpendicular, then a₁a₂ + b₁b₂ + c₁c₂ = 0
• If planes are parallel, then \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

→ The distance of a point whose position vector is from the plane is \(\vec{a}\) from the plane \(\vec{r} \hat{x}=d \)is \(|d-\vec{a} \hat{x}|\)

→ The distance from a point (x₁ y₁ z₁) to the plane ax + by + cz + d = 0 is
\(\left|\frac{a x_{1}+b y_{1}+c z_{1}+d}{\sqrt{a^{2}+b^{2}+c^{2}}}\right|\)