RBSE Class 12 Maths Notes Chapter 10 सदिश बीजगणित

These comprehensive RBSE Class 12 Maths Notes Chapter 10 सदिश बीजगणित will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 10 Notes सदिश बीजगणित

भूमिका (Introduction):
हमें अपने दैनिक जीवन में अनेक प्रश्न मिलते हैं, जैसे कि आपकी ऊँचाई क्या है? जयपुर से आगरा की दूरी कितनी है? एक फुटबाल के खिलाड़ी को अपनी ही टीम के दूसरे खिलाड़ी के पास गेंद पहुँचाने के लिये गेंद पर किस प्रकार प्रहार करना चाहिए? क्रिकेट के खेल में खिलाड़ी को किस वेग से किस दिशा में गेंद मारनी चाहिए कि गेंद बाउण्डरी के पार चली जाये? इत्यादि। उपर्युक्त प्रकार के प्रश्नों में से कुछ प्रश्नों के उत्तर हम परिमाण के रूप में देते हैं। जबकि कुछ प्रश्नों के उत्तर देने हेतु परिमाण के साथ-साथ दिशा की भी आवश्यकता पड़ती है। इस अध्याय में हम इस प्रकार की राशियों का अध्ययन करेंगे और इनकी विभिन्न संक्रियाओं और इनके गुणधर्मों का अध्ययन करेंगे।

राशियाँ (Quantities):
हम विभिन्न प्रकार की भौतिक राशियों से भली-भाँति परिचित हैं। लम्बाई, क्षेत्रफल, समय, वेग, बल इत्यादि भौतिक राशियाँ हैं । प्रत्येक भौतिक राशि को नापा जा सकता है। राशि के नाप को उसका परिमाण (Magnitude) कहते हैं।
चाल (Speed) एवं वेग (Velocity) दो भिन्न-भिन्न भौतिक राशियाँ हैं। चाल में केवल परिमाण होता है, दिशा नहीं। लेकिन वेग में परिमाण. एवं दिशा दोनों होते हैं। जैसे-एक कार एक घण्टे में 60 किमी. की गति से पूर्व दिशा में जाती है तो '60 किमी. प्रति घण्टा' को चाल (Speed) और '60 किमी. प्रति घण्टा पूर्व की ओर' को वेग (Velocity) कहते हैं।
अतः हम भौतिक राशियों को निम्न दो भागों में बाँट सकते हैं

• अदिश राशियाँ (ScalarQuantities)
• सदिश राशियाँ (Vector Quantities)

(i) अदिश राशियाँ (Scalar Quantities) - वे भौतिक राशियाँ जिनमें केवल परिमाण होता है किन्तु किसी विशेष दिशा से सम्बन्धित नहीं होती, अदिश (Scalar) राशियाँ कहलाती हैं। जैसे-लम्बाई, आयतन, समय, तापमान, चाल, द्रव्यमान आदि अदिश राशियाँ हैं।
(ii) सदिश राशियाँ (Vector Quantities) वे भौतिक राशियाँ जिनमें परिमाण एवं दिशा दोनों होते हैं, सदिश राशियाँ कहलाती हैं । जैसे-वेग, त्वरण, बल, संवेग, आघूर्ण आदि।

 

दिष्ट रेखा खण्ड (Directed Line Segment):
एक निश्चित दिशा में खींची गई सरल रेखा के किसी खण्ड भाग को दिष्ट रेखा खण्ड कहते हैं। यदि O दिष्ट रेखा खण्ड का आरम्भिक बिन्दुव P इसका अन्तिम बिन्दु हो, तो इसे संकेत \(\overrightarrow{\mathrm{OP}}\) द्वारा प्रकट किया जाता है। दिष्ट रेखा खण्डके आरम्भिक एवं अन्तिम बिन्दुओं को आपस में नहीं बदला जा सकता है। अतः \(\overrightarrow{\mathrm{OP}}\) तथा \(\overrightarrow{\mathrm{OP}}\) दो अलग-अलग दिष्ट रेखा खण्ड हैं।

सदिश राशि का निरूपण (Representation of A Vector):
हमने यह जाना है कि सदिश राशि में परिमाण एवं दिशा AP दोनों होते हैं, अतः इसे सुविधापूर्वक एक दिष्ट रेखा खण्ड द्वारा प्रदर्शित किया जा सकता है। दिष्ट रेखा खण्ड की लम्बाई सदिश का परिमाण होगा और उस पर लगा हुआ तीर का चिन्ह इसकी दिशा होगी।

सामने दिया गया चित्र किसी सदिश का है। जिसमें लम्बाई OP उस सदिश का परिमाण है और इस पर लगा हुआ तीर का चिह्न उस सदिश दिशा को बतलाता है। इस सदिश को OP द्वारा व्यक्त किया जाता है। इसके परिमाण को |\(\overrightarrow{\mathrm{OP}}\)| या OP द्वारा व्यक्त किया जाता है। सदिश \(\overrightarrow{\mathrm{OP}}\) में सिरे O को आरम्भिक बिन्दु या मूल बिन्दु और सिरे P को अन्तिम बिन्दु या शीर्ष कहते हैं।

सदिश राशि का संकेतन (Notation of A Vector):
सदिशों को प्रायः \(\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{PQ}}, \overrightarrow{\mathrm{RS}}\)....... आदि या \(\vec{a}, \vec{b}, \vec{c}\)........ आदि द्वारा निरूपित किया जाता है।

सदिश का मापांक (Modulus of A Vector)
एक धनात्मक संख्या जो किसी सदिश राशि के परिमाण को व्यक्त करती है, उस सदिश राशि का परिमाण व्यक्त करती है। जब सदिशों को \(\vec{a}, \vec{b}, \vec{c}\) द्वारा व्यक्त किया जाता है तो इनके परिमाणों को उनके संगत अक्षरों \(\vec{a}, \vec{b}, \vec{c}\) से व्यक्त किया जाता है। अर्थात् |\(\vec{a}\)| = a, |\(\vec{b}\)| = b, |\(\vec{c}\)| = c इत्यादि अर्थात् सदिश के परिमाण को इसका मापांक कहते हैं। इसी प्रकार यदि सदिश AB को \(\vec{a}\) त से व्यक्त किया जाता है, तो इसके मापांक को |\(\overrightarrow{\mathrm{AB}}\)| = |\(\vec{a}\)| = |a| = a से व्यक्त करते हैं। किसी सदिश का मापांक सदैव धनात्मक होता है। किसी सदिश \(\overrightarrow{\mathrm{AB}}\) के लिये, |\(\overrightarrow{\mathrm{AB}}\)|=|\(\overrightarrow{\mathrm{BA}}\)| किसी सदिश का मापांक उसका निरपेक्ष मान भी होता है।

स्थिति सदिश (Position Vector):
अंतरिक्ष में मूल बिन्दु O(0, 0,0) के सापेक्ष एक ऐसा बिन्दु P लीजिये जिसके निर्देशांक (x, y, z) हैं । तब सदिश \(\overrightarrow{\mathrm{OP}}\) जिसमें O और P क्रमशः प्रारम्भिक एवं अंतिम बिन्दु हैं, O के सापेक्ष P का स्थिति सदिश कहलाता है। दूरी सूत्र का उपयोग करते हुए \(\overrightarrow{\mathrm{OP}}\) या \(\vec{r}\), का परिमाण निम्नलिखित रूप में प्राप्त होता है-

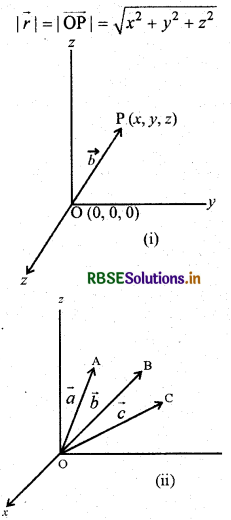
हम अपने व्यवहार में मूल बिन्दु O के सापेक्ष बिन्दुओं A, B, C इत्यादि के स्थिति सदिश क्रमशः \(\vec{a}, \vec{b}\) तथा \(\vec{c}\) से निर्दिष्ट किये जाते हैं, जैसा कि आकृति में दिखाया गया है।

दिक् कोसाइन (Directed Cosines):
एक बिन्दु P(x, y, z) का स्थिति सदिश \(\overrightarrow{\mathrm{OP}}\) अथवा \(\vec{r}\) को लीजिये, जैसा कि आकृति में दर्शाया गया है। सदिश \(\vec{r}\) द्वारा x,y एवं z-अक्ष की धनात्मक दिशाओं के साथ बनाये गये क्रमशः कोण α, β एवं γ दिशा कोण कहलाते हैं। इन कोणों के कोसाइन मान अर्थात् cos α, cos β एवं cos γ सदिश \(\vec{r}\) के दिक्-कोसाइन (Directed Cosines) कहलाते हैं, और सामान्यतः इन्हें क्रमशः l, m और n से प्रदर्शित किया जाता है।

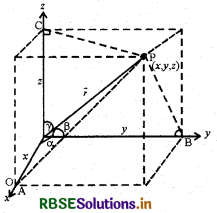
आकृति से हम देखते हैं कि ΔOAP एक समकोण त्रिभुज है।
cos α = \(\frac{x}{r}\) (r को \(\vec{r}\) के लिये प्रयोग किया गया है)

इसी प्रकार ΔOBP और ΔOCP समकोण त्रिभुज हैं । तब
cos β = \(\frac{z}{r}\) और cos γ = \(\frac{z}{r}\)
l = \(\frac{x}{r}\) ∴ x = lr

इसी तरह से y = mr और z = nr लिख सकते हैं। इस प्रकार बिन्दु P के निर्देशांकों को (lr, mr,nr) के रूप में अभिव्यक्त किया जा सकता है। दिक्-कोसाइन के समानुपाती संख्यायें lr, mr एवं nr सदिश के दिक्-अनुपात कहलाते हैं और इनको क्रमशः a, b तथा c से निर्दिष्ट किया जाता है।

सदिशी के प्रकार (Types of Vectors):
(i) शून्य सदिश (Null or Zero Vector):
ऐसा सदिश जिसका परिमाण शून्य हो, शून्य सदिश कहलाता है। शून्य सदिश का प्रारम्भिक व अन्तिम बिन्दु एक ही होता है। अतः इसकी दिशा अनिश्चित होती है, अर्थात् इसकी कोई भी दिशा हो सकती है । सभी शून्य सदिश समान होते हैं और इन्हें \(\overrightarrow{\mathrm{O}}, \overrightarrow{\mathrm{AA}}, \overrightarrow{\mathrm{BB}}\), ..... आदि से व्यक्त करते हैं।

इकाई सदिश (Unit Vector)-ऐसा सदिश जिसका परिमाण एक इकाई हो, इकाई सदिश कहलाता है। अलग-अलग दिशाओं के इकाई सदिश अलंग-अलग होते हैं। यदि सदिश \(\vec{a}\) का परिमाण a, (a ≠ 0) हो, तो \(\frac{\vec{a}}{a}\) सदिश की दिशा में इकाई सदिश होता है। इसको संकेत \(\vec{a}\) से व्यक्त करते हैं। अतः
\(\vec{a}\) = aâ, जहाँ |\(\vec{a}\)| = a
â = \(\frac{\vec{a}}{a}\), a ≠ 0
â = \(\frac{\vec{a}}{|a|}\)

(ii) सह-आदिम सदिश (Co-initial Vectors): दो या दो से अधिक सदिश जिनके प्रारम्भिक बिन्दु एक ही हों, सह-आदिम सदिश कहलाते हैं । इस चित्र में \(\overrightarrow{\mathrm{OA}}, \overrightarrow{\mathrm{OB}}\) और \(\overrightarrow{\mathrm{OC}}\) सहआदिम सदिश हैं।

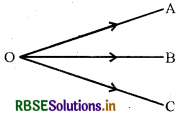
(iv) संरेख सदिश (Collinear Vectors): ऐसे सदिश जिनको निरूपित करने वाले दिष्ट रेखाखण्ड समान्तर हों, अथवा एक ही रेखा पर हों, समान्तर या संरेखीय सदिश कहलाते हैं। ये सदिशों के परिमाण या दिशाओं से प्रभावित नहीं होते। यदि \(\vec{a}\) और \(\vec{b}\) समान्तर सदिश हैं तो इन्हें \(\vec{a}\) = m\(\vec{a}\) या \(\vec{b}\) = n\(\vec{b}\) से व्यक्त कर सकते हैं, जहाँ m, n कोई अदिश राशियाँ हैं।

(v) समान सदिश (Equal Vectors)-दो या दो से अधिक सदिश समान सदिश कहलाते हैं यदि

• वे समदिश सदिश हों, तथा
• उनके परिमाण बराबर हों। यदि सदिश \(\vec{a}\) और \(\vec{b}\) समान सदिश हैं तो हम इन्हें. \(\vec{a}\) = \(\vec{b}\). से व्यक्त करते हैं।

(vi) ऋणात्मक सदिश (Negative of a Vector)-दो सदिश
एक-दूसरे के ऋण सदिश कहलाते हैं, यदि

• इनके आधार समान हों
• इनकी दिशाएँ विपरीत हों तथा
• इनके परिमाण बराबर हों।

सदिश \(\overrightarrow{\mathrm{BA}}\), सदिश \(\overrightarrow{\mathrm{AB}}\) का ऋणात्मक है और इसे \(\overrightarrow{\mathrm{BA}} = - \overrightarrow{\mathrm{AB}}\) के रूप में लिखा जाता है।

सदिशों का योगफल (Addition of Vectors):
1. योग का त्रिभुज नियम (Triangle Law of Addition)
माना कि व दो सदिश राशियाँ हैं । अन्तरिक्ष में A एक स्वेच्छागृहित बिन्दु लिया, A को प्रारम्भिक बिन्दु लेते हुये A से सदिश के समान सदिश \(\overrightarrow{\mathrm{AB}}\) के अन्तिम बिन्दु B से सदिश के समान सदिश \(\overrightarrow{\mathrm{BC}}\) खींचो, अतः \(\overrightarrow{\mathrm{AB}} = \vec{a} \overrightarrow{\mathrm{BC}} = \vec{b}\) होगा।

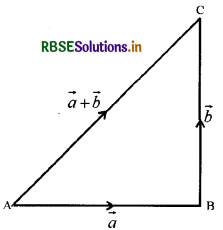
सदिश \(\overrightarrow{\mathrm{AC}}\) को सदिश \(\vec{a}\) का योगफल सदिश कहते हैं और इसे \(\vec{a}+\vec{b}\) द्वारा व्यक्त किया जाता है। यदि हम सदिश AC को सदिश : से व्यक्त करें तब \(\vec{a}+\vec{b}=\vec{c}\)
अर्थात् \(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AC}}\)

अतः यदि दो सदिश एक त्रिभुज की क्रमागत भुजाओं द्वारा प्रदर्शित किये जाते हैं तो इन दो सदिशों का योगफल, विपरीत दिशा में ली गई त्रिभुज की तीसरी भुजा द्वारा प्रदर्शित किया जायेगा। इस नियम को योग का त्रिभुज नियम (Triangle law of addition) कहते हैं।

योगका समान्तर चतुर्भुज नियम (Parallelogram Law of Addition):
माना कि व दो सदिश राशियाँ हैं। अन्तरिक्ष में O एक स्वेच्छागृहित बिन्दु लिया, O को मूल बिन्दु लेते हुए O से सदिश व सदिश के समान सदिश \(\overrightarrow{\mathrm{OA}}\) व सदिश \(\overrightarrow{\mathrm{OB}}\) खींचो, अतः \(\overrightarrow{\mathrm{OA}} = \vec{a}\) और \(\overrightarrow{\mathrm{OB}} = \vec{b}\) होगा।

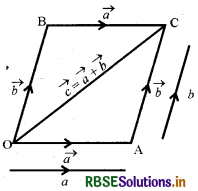
अब समान्तर चतुर्भुज OACB की रचना करो, OC समान्तर चतुर्भुज OACB का विकर्ण है। यहाँ पर \(\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{BC}}=\vec{a}\) और \(\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{AC}}=\vec{b}\) है।

अब त्रिभुज OAC में योग के त्रिभुज नियम से \(\overrightarrow{O C} = \overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}=\vec{a}+\vec{b}\)
अत: यदि दो सदिश एक समान्तर चतुर्भुज की दो संलग्न भुजाओं द्वारा प्रदर्शित किये जाते हैं, तो इन दो सदिशों का योगफल समान्तर चतुर्भुज के विकर्ण जिसका आरम्भिक बिन्दु वही है जो दिये हुये सदिशों का है, द्वारा प्रदर्शित किया जायेगा। इस नियम को सदिश योग का समान्तर चतुर्भुज नियम कहते हैं।

सदिश योगफल के गुणधर्म (Properties of Vector Addition)
गुणधर्म-1. दो सदिशों \(\vec{a}\) तथा \(\vec{b}\) के लिए
\(\vec{a}+\vec{b}=\vec{b}+\vec{a}\) (क्रमविनिमेयता)

उपपत्ति (Proof):
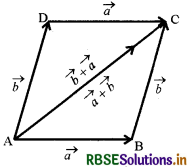
समांतर चतुर्भुज ABCD को लीजिए जैसा आकृति में दर्शाया गया है। माना \(\overrightarrow{\mathrm{AB}}=\vec{a}\) और \(\overrightarrow{\mathrm{BC}}=\vec{b}\), तब त्रिभुज ABC में त्रिभुज नियम का उपयोग करते हुए हमें प्राप्त होता, कि \(\overrightarrow{\mathrm{AC}}=\vec{a}+\vec{b}\) ............(1)

अब, क्योंकि समांतर चतुर्भुज की सम्मुख भुजाएँ समान एवं समांतर हैं, इसलिए आकृति में दर्शाये अनुसार \(\overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{BC}}=\vec{b}\) और \(\overrightarrow{\mathrm{DC}}=\overrightarrow{\mathrm{AB}}=\vec{a}\) है।

पुनः त्रिभुज ADC में त्रिभुज नियम के प्रयोग से \(\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DC}}=\vec{b}+\vec{a}\) ....(2)
अतः समीकरण (1) तथा (2) से \(\vec{a}+\vec{b}=\vec{b}+\vec{a}\)
अतः स्पष्ट है कि सदिशों का योग क्रमविनिमेय नियम का पालन करता है।

गुणधर्म-2.
तीन सदिशों \(\vec{a}, \vec{b}\) और \(\vec{c}\) के लिए  (\(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c}\))(साहचर्य गुण)

उपपत्ति (Proof): माना, सदिशों \(\vec{a}, \vec{b}\) तथा \(\vec{c}\) को क्रमशः \(\overrightarrow{\mathrm{PQ}}, \overrightarrow{\mathrm{QR}}\) एवं \(\overrightarrow{\mathrm{RS}}\) से निरूपित किया गया है जैसा कि आकृति (I) और (II) में दर्शाया गया है।

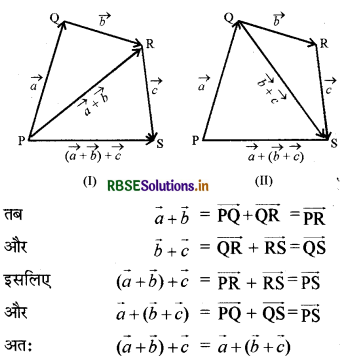
अर्थात् सदिशों का योग साहचर्य नियम का पालन करता है।

टिप्पणी-सदिश योगफल के साहचर्य गुणधर्म की सहायता से हम तीन सदिशों \(\vec{a}, \vec{b}\), तथा \(\vec{c}\) का योगफल कोष्ठकों का उपयोग किए बिना \(\vec{a}+\vec{b}+\vec{c}\) के रूप में लिखते हैं।

गुणधर्म-3.
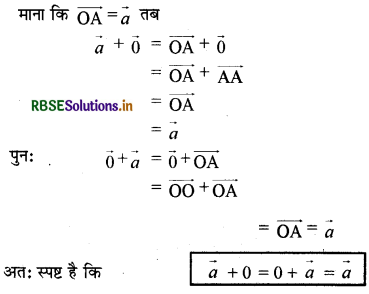
शून्य सदिश योज्य तत्समक होता है। माना कि एक सदिश है और 6 शून्य सदिश है। तब
\(\vec{a}+\overrightarrow{0}=\overrightarrow{0}+\vec{a}=\vec{a}\)
उपपत्ति (Proof):
माना कि OA = तब

एक अदिश से सदिश का गुणन (Multiplication of A Vector By At Scalar)
मान लीजिए कि \(\vec{a}\) एक दिया हुआ सदिश है और λ एक अदिश है। तब सदिश \(\vec{a}\) का अदिश λ से गुणनफल जिसे λ\(\vec{a}\) के रूप में निर्दिष्ट किया जाता है, सदिश \(\vec{a}\) का अदिश λ से गुणन कहलाता है। यहाँ पर ध्यान दीजिए कि λ\(\vec{a}\) भी सदिश के संरेख एक सदिश है। λ के मान धनात्मक अथवा ऋणात्मक होने के अनुसार λ\(\vec{a}\) की दिशा, \(\vec{a}\) के समान अथवा विपरीत होती है। λ\(\vec{a}\) का परिमाण \(\vec{a}\) के परिमाण का |λ| गुणा होता है, अर्थात्

एक सदिश के घटक (Components of A Vector):
आइये, बिंदुओं A(1,0, 0), B(0, 1,0).और C(0, 0, 1) को क्रमशः x-अक्ष, y-अक्ष एवं z-अक्ष पर लेते हैं । तब स्पष्टतः
|OA] = 1, |OB| = 1 और |OC| = 1
सदिश \(\overrightarrow{\mathrm{OA}}, \overrightarrow{\mathrm{OB}}\) और \(\overrightarrow{\mathrm{OC}}\) जिनमें से प्रत्येक का परिमाण 1 है, क्रमशः ox, OY और OZ अक्षों के अनुदिश मात्रक सदिश कहलाते हैं और इनको क्रमशः î, ĵ और k̂ द्वारा निर्दिष्ट किया जाता है।

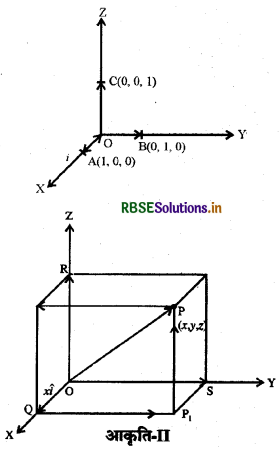
अब एक बिंदु P(x, y, z) का स्थिति सदिश लेते हैं, \(\overrightarrow{\mathrm{OP}}\) जैसा कि आकृति II में दर्शाया गया है। माना कि बिंदु P₁, से तल XOY पर खींचे गए लंब का पाद बिंदु P₁ है। इस प्रकार हम देखते हैं कि P₁,P, z-अक्ष के समांतर है । क्योंकि î, ĵ एवं k̂ क्रमशः x,y एवं z-अक्ष के अनुदिश मात्रक सदिश हैं और P के निर्देशांकों की परिभाषा के अनुसार हम पाते हैं कि \(\overrightarrow{\mathrm{P}_1 \mathrm{P}}=\overrightarrow{\mathrm{OR}}\) = zk̂ , इसी प्रकार \(\overrightarrow{\mathrm{QP}_1}=\overrightarrow{\mathrm{OS}}\) = yĵ और \(\overrightarrow{\mathrm{OQ}}\) = xî , इस प्रकार हम पाते हैं कि
\(\overrightarrow{\mathrm{OP}_1}=\overrightarrow{\mathrm{OQ}}+\overrightarrow{\mathrm{QP}_1}\) = xî + yĵ
और \(\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OP}_1}+\overrightarrow{\mathrm{P}_1 \mathrm{P}}\) = xî + yĵ + zk̂ इस प्रकार O के सापेक्ष P का स्थिति सदिश OP (अथवा ;).
= xî + yî + zk̂ के रूप में प्राप्त होता है।

किसी भी सदिश का यह रूप घटक रूप कहलाता है । यहाँ x,y एवं z, \(\vec{r}\) के अदिश घटक कहलाते हैं और xî, yĵ एवं zk̂ क्रमागत अक्षों के अनुदिश ; के सदिश घटक कहलाते हैं । कभी-कभी x, y एवं z को समकोणिक घटक भी कहा जाता है। अतः किसी सदिश |\(\vec{r}\)| = xî + yĵ + zk̂ की लम्बाई |\(\vec{r}\)| = |xî + yĵ + zk̂| = \(\sqrt{x^2+y^2+z^2}\) के रूप में प्राप्त होती है।

सदिशों के विशिष्ट गुण
यदि दो सदिश \(\vec{a}\) और \(\vec{b}\) घटक रूप में क्रमशः a₁î + a₂ĵ + a₂k̂ और b₁î + b₂ĵ + b₂k̂ द्वारा दिए गए हैं तो

• सदिश \(\vec{a}\) और \(\vec{b}\) का योग
  \(\vec{a}+\vec{b}\) = (a₁ + b₁)î + (a₂ + b₂)ĵ + (a₃ + b₃)k̂ के रूप में प्राप्त होता है।
• सदिश \(\vec{a}\) और \(\vec{b}\) का अंतर
  \(\vec{a}-\vec{b}\) = (a₁ - b₁)î + (a₂ - b₂)ĵ + (a₃ - b₃)k̂ के रूप में प्राप्त होता है।
• सदिश \(\vec{a}\) और \(\vec{b}\) समान होते हैं यदि और केवल यदि
  a₁ = b₁, a₂ = b₂ और a₃ = b₃
• किसी अदिश 2 से \(\vec{a}\) सदिश का गुणन
  λa = (λa₁)î + (λa₂)ĵ + (λa₃)k̂ द्वारा प्रदत्त है।

सदिशों का योगफल और किसी अदिश से सदिश का गुणन सम्मिलित . रूप में निम्नलिखित वितरण-नियम से मिलता हैमाना कि और 5 कोई दो सदिश हैं और k एवं m दो अदिश राशियाँ हैं तब

• k\(\vec{a}\) + m\(\vec{a}\) = (k + m)\(\vec{a}\)
• k(m\(\vec{a}\)) = (km)\(\vec{a}\)
• k(\(\vec{a}\) + \(\vec{b}\)) = k\(\vec{a}\) + k\(\vec{b}\)

टिप्पणी
1. यदि सदिश \(\vec{a}\) और \(\vec{b}\) घटक रूप में दिए हुए हैं, अर्थात्
\(\vec{a}\) = a₁î + a₂ĵ + a₃k̂ और \(\vec{b}\) = b₁î + b₂ĵ + b₃k̂ , तब दो सदिश संरेख होते हैं यदि और केवल यदि =na
b₁î + b₂ĵ + b₃k̂ = λ(a₁î + a₂ĵ + a₃k̂)
⇔ b₁î + b₂ĵ + b₃k̂ = (λ.a₁)î + (λ.a₂)j + (λ.a₃)k̂
⇔ b₁ = λ.a₁, b₂ = λa₂, b₃ = λa₃
⇔ \(\frac{b_1}{a_1}=\frac{b_2}{a_2}=\frac{b_3}{a_3}\) = λ

2. यदि \(\vec{a}\) = a₁î + a₂ĵ + a₃k̂ तब a₁, a₂, a₃, सदिश \(\vec{a}\) के दिक्-अनुपात कहलाते हैं।

3. यदि l, m, n किसी सदिश के दिक्-कोसाइन हैं तब
lî + mĵ + nk̂ = (cos α)î + (cos β)ĵ + (cos γ)k̂
दिये हुए सदिश की दिशा में मात्रक सदिश है जहाँ α, β एवं γ दिए हुए सदिश द्वारा क्रमशः x, y एवं z-अक्ष के साथ बनाए गए कोण हैं।

दो बिन्दुओं को मिलाने वाला सदिश (Vector Joining Two Points)
माना कि दो बिन्दु P₁,(x₁, y₁, z₁) व P₂(x₂, y₂, z₂) इस प्रकार हैं कि
\(\overline{\mathrm{OP}_1}\) = x₁î + y₁ĵ + z₁k̂ तथा
\(\overline{\mathrm{OP}_2}\) = x₂î + y₂ĵ + z₂k̂
जहाँ पर O मूल बिन्दु है।

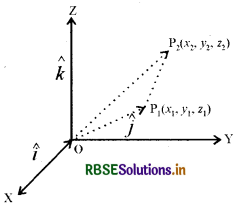
तब \(\overrightarrow{\mathrm{P}_1 \mathrm{P}_2}=\overrightarrow{\mathrm{OP}_2}-\overrightarrow{\mathrm{OP}_1}\)
या \(\overrightarrow{\mathrm{P}_1 \mathrm{P}_2}\) = (x₂î + y₂ĵ + z₂k̂) - (x₁î + y₁ĵ + z₁k̂)
= (x₂ - x₁)î + (y₂ - y₁)ĵ + (z₂ - z₁)k̂
अब \(\left|\overrightarrow{\mathrm{P}_1 \mathrm{P}_2}\right|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}\)

खण्ड सूत्र (Section Formula):
यदि बिन्दुओं P और Q के स्थिति सदिश क्रमशः \(\vec{a}\) और \(\vec{b}\) हैं, रेखा PQ को m :n के अनुपात में विभाजित करने वाले बिन्दु R का स्थिति
सदिश \(\vec{r}\) = \(\frac{m \vec{b}+n \vec{a}}{m+n}\) हैं।

माना कि सदिश P एवं Q के मूल बिन्दु O के सापेक्ष स्थिति सदिश क्रमशः \(\vec{a}\) व \(\vec{b}\) हैं।
अतः \(\overrightarrow{\mathrm{OP}}=\vec{a}\)
और \(\overrightarrow{\mathrm{OQ}}=\vec{b}\)

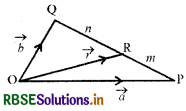
पुनः माना कि रेखा PQ को m :n के अनुपात में विभाजित करने वाला बिन्दु R है, जिसका स्थिति सदिश मूल बिन्दु 0 के सापेक्ष \(\vec{r}\) है।
अर्थात् \(\overrightarrow{\mathrm{OR}}=\vec{r}\)

स्थिति-I
माना कि R, रेखा PQ को अन्तः विभाजित करता है। तब m : n धनात्मक होगा।

स्थिति-II :
यदि बिन्दु R, रेखा PQ को बाह्यतःm : n में विभाजित करता है।
तब m : n ऋणात्मक होगा।
अर्थात् \(\vec{r} = \frac{m \vec{b}-n \vec{a}}{m-n}\)

स्थिति-III :
यदि बिन्दु R, रेखा PQ को मध्य बिन्दु पर विभाजित करता है।
अर्थात्
m: n = 1 : 1, तब \(\vec{r} = \frac{1 \vec{b}+1 \cdot \vec{a}}{1+1}\)
\(\vec{r}=\frac{\vec{b}+\vec{a}}{2}\)

दो सदिशों का गुणनफल (Product of Two Vectors):
साधारण बीजगणित में हम दो अदिश राशियों (Scalar quantities) के गुणनफल के बारे में अध्ययन कर चुके हैं। बीजगणित में अपनाई जाने वाली गुणनफल की साधारण प्रक्रिया को हम दो सदिश राशियों (Vector quantities) के गुणनफल में प्रयोग नहीं कर सकते हैं, क्योंकि सदिश राशि में परिमाण के साथ-साथ दिशा भी होती है अतः दो सदिश राशियों में गुणनफल को दो प्रकार से परिभाषित किया जा सकता है

• अदिश गुणन या बिन्दु गुणन (Scalar or Dot Product)
• संदिश या वज्र गुणन (Vector or Cross Product)।

प्रथम प्रकार के गुणन में दो सदिश राशियों का गुणनफल एक अदिश राशि आती है इसलिये इसकों अदिश गुणन कहते हैं तथा द्वितीय प्रकार के गुणन में दो सदिश राशियों का गुणनफल एक सदिश राशि प्राप्त होती है इसलिए इसको सदिश गुणन कहते हैं।

दो सदिशों का अदिश गुणनफल (Scalar (Or Dot) Product Of Two Vectors)
परिभाषा - यदि \(\vec{a}\) और \(\vec{b}\) दो सदिश राशियाँ हैं और इनके बीच का कोण में है, तो इनका अदिश या बिन्दु गुणन, अदिश राशि ab cos 0 में परिभाषित किया जाता है, जहाँ \(\vec{a}\) व \(\vec{b}\) क्रमशः सदिश \(\vec{a}\)व \(\vec{b}\) के परिमाण (magnitude) हैं तथा 0 ≤ θ ≤ π है।

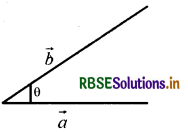
अतः \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\)cos θ
= ab cos θ
अदिश गुणन को \(\vec{a}.\vec{b}\) से व्यक्त किया जाता है, इसी कारण इस गुणन को बिन्दु गुणन भी कहते हैं।

टिप्पणी परिभाषा के अनुसार एक शून्य तथा अशून्य सदिश का बिन्दु गुणन एक अदिश शून्य होता है। x बिन्दु या अदिश गुणन की विशेष स्थितियाँ :
(i) यदि θ = 0° तब (सदिश \(\vec{a}\) तथा \(\vec{b}\) सदिश समान्सर होंगे)
\(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\) cos 0°
या \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\) (∵ cos 0° = 1)

(ii) यदि θ = π हो तब

अदिश गुणनफल के दो महत्त्वपूर्ण गुणधर्म (Two important properties of scalar product):
गुणधर्म 1. :
(अदिश गुणनफल की योगफल पर वितरण नियम) मान लीजिए \(\vec{a}, \vec{b}\) और \(\vec{c}\) तीन सदिश हैं तब \(\vec{a} \cdot(\vec{b}+\vec{c}) = \vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}\).

गुणधर्म 2. : मान लीजिए \(\vec{a}\) और \(\vec{b}\); दो सदिश हैं और λ एक अदिश है, तो
\((\lambda \vec{a}) \cdot \vec{b}=\lambda(\vec{a} \cdot \vec{b})=\vec{a} \cdot(\lambda \vec{b})\)

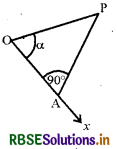
एक सदिश का किसी रेखा पर प्रक्षेप (Projection of A Vector on A Line):
माना कि एक सदिश \(\overrightarrow{\mathrm{AB}}\) किसी दिष्ट रेखा l के साथ वामावर्त दिशा में θ कोण बनाता है जैसा कि आकृति में है। तब \(\overrightarrow{\mathrm{AB}}\) का l पर प्रक्षेप एक सदिश \(\vec{p}\) माना है जिसका परिमाण |\(\overrightarrow{\mathrm{AB}}\)| cos θ है और जिसकी दिशा का l की दिशा के समान अथवा विपरीत होना इस बात पर निर्भर है कि cos θ धनात्मक है अथवा ऋणात्मक। सदिश \(\vec{p}\) को प्रक्षेप सदिश कहते हैं और इसका परिमाण |\(\vec{p}\)|, निर्दिष्ट रेखा l पर सदिश \(\overrightarrow{\mathrm{AB}}\) का प्रक्षेप कहलाता है। उदाहरणतः निम्नलिखित में से प्रत्येक आकृति में सदिश \(\overrightarrow{\mathrm{AB}}\) का रेखा l पर प्रक्षेप सदिश \(\overrightarrow{\mathrm{AC}}\) है। [आकृति (i) से (iv) तक]

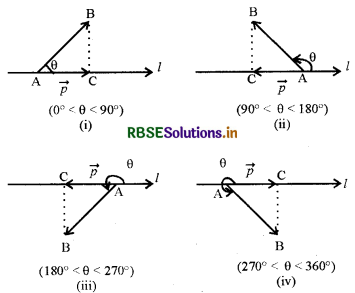
प्रेक्षण :
रेखा l के अनुदिश \(\vec{p}\) में यदि मात्रक सदिश है तो रेखा l पर सदिश \(\vec{a}\) का प्रक्षेप \(\vec{a} \cdot \vec{p}\) से प्राप्त होता है।

2. एक सदिश \(\vec{a}\) का दूसरे सदिश \(\vec{b}\) पर प्रक्षेप \(\vec{a}\).b̂ अथवा \(\vec{a} \cdot\left(\frac{\vec{b}}{|\vec{b}|}\right)\) अथवा \(\frac{1}{|\vec{b}|}(\vec{a} \cdot \vec{b})\) से प्राप्त होता है।

3. यदि θ = 0, तो \(\overrightarrow{\mathrm{AB}}\) का प्रक्षेप सदिश स्वयं \(\overrightarrow{\mathrm{AB}}\) होगा और यदि θ = π तो \(\overrightarrow{\mathrm{AB}}\) का प्रक्षेप सदिश \(\overrightarrow{\mathrm{BA}}\) होगा।

4. यदि θ = \(\frac{\pi}{2}\), अथवा θ = \(\frac{3\pi}{2}\), तो \(\overrightarrow{\mathrm{AB}}\) का प्रक्षेप सदिश शून्य सदिश होगा।

टिप्पणी:
यदि α, β और γ सदिश \(\vec{a}\) = a₁i + a₂j + a₂k के दिक्-कोण हैं तो इसकी दिक्-कोसाइन निम्नलिखित रूप में प्राप्त की जा सकती है
cos α = \(\frac{\vec{a} \cdot \hat{i}}{|\vec{a} \| \hat{i}|}=\frac{a_1}{|\vec{a}|}\) cos β = \(\frac{a_2}{|\vec{a}|}\) and cos γ = \(\frac{a_3}{|\vec{a}|}\)
यह भी ध्यान दीजिए कि |\(\vec{a}\)||cos α, |\(\vec{a}\)||cos β और |\(\vec{a}\)||cos γ क्रमशः OX,OY तथा Oz के अनुदिश त के प्रक्षेप हैं अर्थात् सदिश a के अदिश घटक a₁, a₂ और a₃ क्रमशःx, y एवं z अक्ष के अनुदिश \(\vec{a}\) के प्रक्षेप हैं

दो सदिशों का सदिश गुणनफल (Vector (Or Cross) Product of Two Vectors):
परिभाषा (Definitions): यदि और दो सदिश राशियाँ हैं और θ(0 ≤ θ ≤ r) उनके बीच का कोण है, तो सदिश \(\vec{a}\) तथा \(\vec{b}\) का सदिश गुणन एक ऐसा सदिश है जिसका परिमाण (magnitude)|\(\vec{a}|\vec{b}\)|sinθ है और जिसकी दिशा \(\vec{a}\) और \(\vec{b}\) दोनों सदिशों के तल के लम्बवत् \(\vec{a}\) से \(\vec{b}\) की ओर वामावर्त क्रम (counter clockwise) में है।

\(\vec{a}\) और \(\vec{b}\) के सदिश गुणन को \(\vec{a} \times \vec{b}\) द्वारा व्यक्त किया जाता है, इसलिये इसको वज्र गुणन कहते हैं।

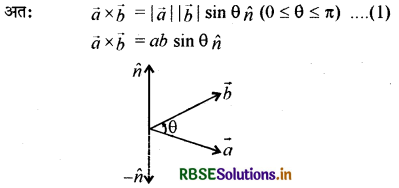
जहाँ n\(\vec{a}\) और \(\vec{b}\) दोनों सदिशों के तल के लम्बवत् \(\vec{a}\) से \(\vec{b}\) की ओर वामावर्त क्रम (counter clockwise) में मात्रक सदिश (unit vector) है। जो सदिश \(\vec{a}\) और \(\vec{b}\) दोनों पर लम्ब है। यहाँ \(\vec{a}\), \(\vec{b}\) एवं n̂ एक दक्षिणावर्ती पद्धति को निर्मित करते हैं । अर्थात् दक्षिणावर्ती पद्धति को \(\vec{a}\) से \(\vec{b}\) की तरफ घुमाने पर यह n̂ है की दिशा में चलती है।

सदिशों के बीच का कोण (Angle between the Vectors):
यदि \(\vec{a}\) और दो सदिश हों \(\vec{a}\) और \(\vec{b}\) उनके बीच का कोण हो, तो परिभाषानुसार
\(\vec{a} \times \vec{b}\) = ab sin θ n̂
|\(\vec{a} \times \vec{b}\)| = |ab sin θ n̂|
= |ab sin θ||n̂|
= ab sin θ[∵ |n̂| = 1]
या sin θ = \(\frac{|\vec{a} \times \vec{b}|}{a b}\)
या sin θ = \(\frac{|\vec{a} \times \vec{b}|}{|\vec{a}||\vec{b}|}\) ....(2)

\(\vec{a}\) और \(\vec{b}\) के तल के लम्बवत् मात्रक सदिश (Unit Vector perpendicular to the plane of \(\vec{a}\) and \(\vec{b}\))
यदि \(\vec{a}\) और \(\vec{b}\) दो सदिश हों तथा n̂ इन दोनों के तल के लम्बवत् \(\vec{a}\) से \(\vec{b}\) की ओर वामावर्त क्रम में मात्रक सदिश हो, तो परिभाषानुसार
\(\vec{a} \times \vec{b}\) = ab sin θ n̂
\(\vec{a} \times \vec{b} = |\vec{a} \times \vec{b}|\) n̂ [समी. (2) से]
n̂ = \(\frac{\vec{a} \times \vec{b}}{|\vec{a} \times \vec{b}|}\) ....(3)

सदिश गुणन की विशेष स्थितियाँ :
(i) यदि सदिश \(\vec{a}\) और \(\vec{b}\) समान्तर (parallel) हों :
इस स्थिति में हैं \(\vec{a}\) और \(\vec{b}\) के बीच का कोण = 0° होगा। :
\(\vec{a} \times \vec{b}\) = ab sin 0° n̂
\(\vec{a} \times \vec{b}\) = 0
अंतः दो समान्तर सदिशों का सदिश गुणन सदैव शून्य सदिश होता है।

विशेषतः (In particular) यदि \(\vec{a} = \vec{b}\) हो, तो
\(\vec{a} \times \vec{a}\) = 0
î × î = ĵ × ĵ = k̂× k̂ = 0
î × ĵ = k̂, ĵ × k̂ = î , k̂ × î = ĵ

(ii) यदि सदिश \(\vec{a}\) और \(\vec{b}\) लम्बवत् (Perpendicular) हों
इस दशा में हैं और 5 के बीच का कोण θ = 90° होगा।
\(\vec{a} \times \vec{b}\) = ab sin 90°n̂
\(\vec{a} \times \vec{b}\) = abn̂
अतः दो लम्बवत् सदिशों का सदिश गुणन, एक सदिश होता है जिसका परिमाण दोनों सदिशों के परिमाणों के गुणनफल के बराबर होता है तथा जिसकी दिशा पहले सदिश से दूसरे सदिश की ओर वामावर्त क्रम में होती है।

विशेषतः (In particular) यदि \(\vec{a}\) और \(\vec{b}\) मात्रक सदिश हों,
\(\vec{a} \times \vec{b}=\hat{n}\)
एक मात्रक सदिश है जो \(\vec{a}\) और \(\vec{b}\) के समतल के लम्बवत् है तथा जिसकी दिशा \(\vec{a}\) से \(\vec{b}\) की ओर वामावर्त क्रम में है।

∵ \(\vec{a} \times \vec{b}=|\vec{a}||\vec{b}|\)sin θ n̂
तथा \(\vec{b} \times \vec{a}=|\vec{b}||\vec{a}|\) sin θ(-n̂) ....(1)
या \(\vec{b} \times \vec{a}=-|\vec{b}||\vec{a}|\)sin θn̂ .....(2)
समीकरण (1) तथा (2) से
\(\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}\)

अर्थात् सदिश गुणन क्रम विनिमेय गुणधर्म का पालन नहीं करता है।
ĵ × î = -k̂, k̂ × î = -î, î × k̂ =-ĵ

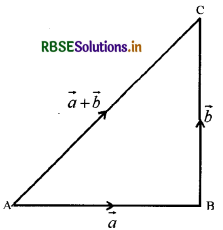
(iv) यदि सदिश और ; किसी त्रिभुज OAB की संलग्न भुजाओं OA व OB को निरूपित करें तो त्रिभुज OAB का क्षेत्रफल \(\frac{1}{2}|\vec{a} \times \vec{b}|\) से निरूपित होता है।
त्रिभुज OAB का क्षेत्रफल = \(\frac{1}{2}\)OA.BC
अब त्रिभुज OBC में

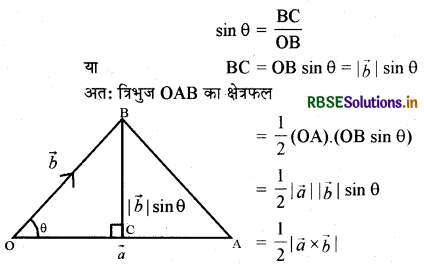
(v) यदि त्रिभुज ABC के शीर्ष के स्थिति सदिश क्रमशः \(\vec{a}, \vec{b}\) व \(\vec{c}\) है तब त्रिभुज ABC का क्षेत्रफल
= \(\frac{1}{2}[\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}]\) फलतः यदि त, \(\vec{a}, \vec{b}\) व \(\vec{c}\) है संरेख हैं तब त्रिभुज का क्षेत्रफल शून्य होगा
\(\frac{1}{2}[\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}]\) =0
\(\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}\) = 0

(vi) सदिश गुणन का ज्यामितीय अर्थ (Geometrical Interpretation of Vector Product):

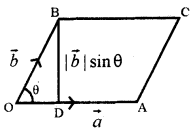
माना OACB एक समान्तर चतुर्भुज है जहाँ पर ।

अतः समान्तर चतुर्भुज OACB का क्षेत्रफल = \(|\vec{a} \times \vec{b}|\)

(vii) गुणधर्म सदिश गुणनफल का योगफल पर वितरण नियम (Distributivity of vector product over addition)
यदि \(\vec{a}, \vec{b}\) और \(\vec{c}\)तीन सदिश हैं और 2 एक अदिश है तो
(1) \(\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}\)
(1) \(\lambda(\vec{a} \times \vec{b})=(\lambda \vec{a}) \times \vec{b}=\vec{a} \times(\lambda \vec{b})\)
मान लीजिए दो सदिश \(\vec{a}\) और \(\vec{b}\) घटक रूप में क्रमशः a₁î + a₂ĵ + a₃k̂ और b₁î + b₂ĵ + b₃k̂

दिये हुए हैं तब उनका सदिश गुणनफल \(\vec{a} \times \vec{b}=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array}\right|\) द्वारा दिया जा सकता है।

व्याख्या :

→ वे राशियाँ जिन्हें पूर्ण रूप से निरूपित करने के लिए परिमाण के साथ-साथ दिशा की भी आवश्यकता होती है, सदिश राशियाँ कहलाती हैं।

→ किसी बिन्दु 0 के सापेक्ष दूसरे बिन्दु A को निरूपित करने वाले सदिश \(\overrightarrow{\mathrm{OA}}\) को बिन्दु A का O के सापेक्ष स्थिति सदिश कहते हैं। यदि निर्देशांक (x, y, z) हैं तो
\(\overrightarrow{\mathrm{OA}}\) = xî + yĵ + zk̂
\(|\overrightarrow{\mathrm{OA}}|=\sqrt{x^2+y^2+z^2}\)

→ किसी सदिश के निर्देशांक अक्षों के साथ बने कोणों के कोज्या को दिक्कोज्या कहते हैं । यदि α, β, γ क्रमशः किसी सदिश के x-अक्ष, y-अक्ष तथा z-अक्ष के साथ बने कोण हों तो cos α, cos β, cos γ को सदिश की दिक्कोज्याएँ कहते हैं। cos α, cos β, cos γ को क्रमशः l, m, n से निरूपित किया जाता है।
cos²α + cos²β + cos²γ = l² + m² + n² = 1

→ संख्याओं a, b तथा c को सदिश \(\vec{r}\) का दिक्अनुपात कहते हैं जहाँ a = lr, b = mr, c = nr .
l = \(\frac{\pm a}{\sqrt{a^2+b^2+c^2}}\)
m = \(\frac{\pm b}{\sqrt{a^2+b^2+c^2}}\)
n = \(\frac{\pm c}{\sqrt{a^2+b^2+c^2}}\)

→ यदि \(\vec{a}, \vec{b}\) तथा \(\vec{c}\) त्रिभुज की तीन भुजाओं को एक क्रम में निरूपित करते हैं तब \(\vec{a}+\vec{b}+\vec{c}=\vec{o}\)

→ सदिशों का योग क्रमविनिमेय तथा साहचर्य होता है अर्थात्
\(\vec{a}+\vec{b}=\vec{b}+\vec{a}\)
\(\vec{a}+(\vec{b}+\vec{c})=(\vec{a}+\vec{b})+\vec{c}\)

→ बिन्दुओं P (x₁, y₁, z₁) तथा Q (x₂, y₂, z₂) को मिलाने वाला
सदिश PQ = (x₂ - x₁) î + (y₂ - y₁) ĵ + (z₂ - z₁) k̂ होता

→ \(\vec{a}\) तथा \(\vec{b}\) के बीच कोण θ है तो इनका सदिश गुणनफल \(\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\)cos θ

→ î.î = ĵ.ĵ = k̂.k̂ = 1
î.ĵ = ĵ.k̂ = k̂.î = 0

→ \(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\)

→ \(\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}\)

→ \(\vec{a}\) का \(\vec{b}\) पर प्रक्षेप \(\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}\) होता है।

→ \(\vec{a}\) व \(\vec{b}\) के बीच सदिश गुणनफल
\(\vec{a} \times \vec{b}=|\vec{a} \| \vec{b}|\) sin θ n̂
जहाँ θ, सदिशों \(\vec{a}\) व \(\vec{b}\) के बीच के मध्य का कोण होता है और । एक इकाई सदिश है जिसकी दिशा में \(\vec{a}\) तथा \(\vec{b}\) की दिशा के लम्बवत है।

→ \(\vec{a} \times \vec{b} \neq \vec{b} \times \vec{a}\) परन्तु \(\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}\)

→ यदि \(\vec{a}\) = a₁î + a₂ĵ + a₃k̂
\(\vec{b}\) = b₁î + b₂ĵ + b₃k̂ हो तो
\(\vec{a} \times \vec{b}=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array}\right|\)

→ \(\vec{a} \times \vec{b}\) = 0 यदि \(\vec{a}\) व \(\vec{b}\) समान्तर हो या (\(\vec{a}\)) = 0 या (\(\vec{b}\)) = 0

→ \(\vec{a} \times \vec{b} = (\vec{a}) (\vec{b})\) sin θ n̂ तो
n̂ = \(\frac{\vec{a} \times \vec{b}}{|\vec{a} \times \vec{b}|}\)

→ समान्तर चतुर्भुज जिसकी आसन्न भुजाएँ \(\vec{a}\) तथा \(\vec{b}\) हैं तो सदिश क्षेत्रफल \(\vec{a} \times \vec{b}\) होता है।

→ समान्तर चतुर्भुज जिसके विकर्ण सदिश \(\vec{d}_1\) तथा \(\vec{d}_2\) हों तो उसका क्षेत्रफल \(\frac{1}{2}\left|\vec{d}_1 \times \vec{d}_2\right|\) होता है।

→ त्रिभुज का ABC क्षेत्रफल \(\frac{1}{2}|\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}| = \frac{1}{2}|\overrightarrow{\mathrm{BA}} \times \overrightarrow{\mathrm{BC}}| = \frac{1}{2}|\overrightarrow{\mathrm{CA}} \times \overrightarrow{\mathrm{CB}}|\) होता है।

→ यदि किसी त्रिभुज की भुजाएँ सदिशों \(\vec{a}, \vec{b}\) तथा \(\vec{c}\) से निरूपित हों तो इसका क्षेत्रफल \(\frac{1}{2}|\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}|\) होता है।
000