RBSE Class 12 Maths Notes Chapter 10 Vector Algebra

These comprehensive RBSE Class 12 Maths Notes Chapter 10 Vector Algebra will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 10 Notes Vector Algebra

Introduction:
In our day to day life, we measure length or height. In these quantities we get only magnitude which is a real number. Such quantities are called scalars. Generally we say a car is going with speed 50 km/h. Here, 50 is also scalar but if we say car is going to north direction with speed 50 km/h. Here, magnitude and direction both are present. Such quantities are called vectors. In mathematics, physics and engineering, we frequently come across with both types of quantities, namely, scalar quantities and vector quantities.

Some Basic Concepts
Scalar Quantities :
The quantities having magnitude only are called scalar quantities. These quantities are not related to any direction in space.
For example, length, density, voltage, resistance etc are scalar quantities.

Vector Quantities :
The quantities which need magnitude as well as direction to represent them are called vector quantities.
For example, Velocity, force, acceleration electric field intensity etc are vector quantities.

Directed Line Segment:
A part of any straight line which is specified by intitial and terminal points is called directed line segment.
Directed line segment is represented in the following figure:

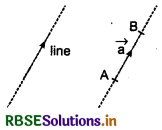
\(\overrightarrow{A B}\) is a directed line segment. Here, A is its initial point and B is its terminal point. Thus, a directed line segment has magnitude as well as direction.

 

Representation of a vector :
Vectors are represented by directed line segment. Directed line segment has magnitude as well as direction. The point O from where the vector \(\overrightarrow{O A}\) starts is called its initial point and the point A where it ends is called its terminal point. The distance between initial and terminal points of a vector is called the magnitude of the vector. The arrow indicates the direction of the vector. Thus, this type of vector is called line vector and it is represented by \(\overrightarrow{O A}\).

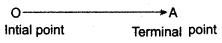
Notation of vectors: Any vector is generally denoted by its initial point and terminal point. If O is initial point and P is terminal point of any vector, then this vector is
represented by \(\overrightarrow{O P}\).

Vectors are represented by small letters of english alphabet and mark an arrow or line upon it.
For example, \(\vec{a}, \vec{b}, \vec{c}\) or a̅, b̅, c̅ etc.

Modulus of a vector:
Modulus of any vector is equal to the positive magnitude of the vector. It is also called absolute value of the vector. Modulus of vector \(\overrightarrow{P Q}\) is represnted by |\(\overrightarrow{P Q}\)| and modulus of vector \(\overrightarrow{a}\) is represented by |\(\overrightarrow{a}\)| or a.

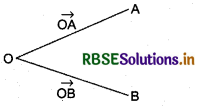
Position vector :
Let O be the origin. Then, the vector \(\overrightarrow{O A}\) having O and A as its initial and terminal points, respectively, is called the position vector of the point A with respect to O and \(\overrightarrow{O B}\) is the position vector of B with respect to O.

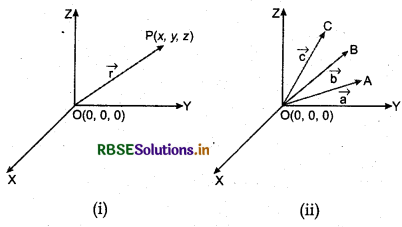
Consider a point P in space, having co-ordinates (x, y, z) with respect to the origin 0(0, 0, 0). Then, \(\overrightarrow{O P}\) is called position vector of P with respect to point O.
Magnitude of \(\overrightarrow{O P}\) (or \(\overrightarrow{r}\)) in Fig (i) is

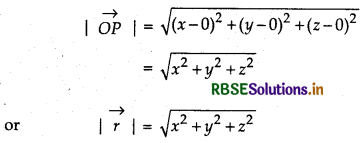
Generally, in space position vectors of A, B, C etc. with respect to origin O are represented by \(\vec{a}, \vec{b}, \vec{c}\) etc respectively as shown in Fig. (ii).

Direction cosines:
Let P be any point in space having co-ordinates (x, y, z). Then, position vector of P with respect to origin O is \(\overrightarrow{O P}\) (\(\overrightarrow{r}\)). The angles α, β, γ made by the vector \(\overrightarrow{O P}\) with the positive directions of x, y and z-axes respectively are called its direction angles. The cosine values of these angles, i.e., cos α, cos β and cos γ are called direction cosines of the vector \(\overrightarrow{O P}\). Direction cosines are usually doneted by l, m and n respectively.

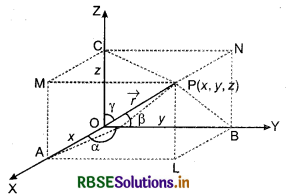
In above figure PA, PB and PC are perpendiculars from point P on the axes X, Y and Z respectively. Then in right angled triangle ΔOAP,

cos α = \(\frac{|\overrightarrow{O A}|}{\mid \overrightarrow{r \mid}}=\frac{x}{r}\) ............(1)
Similarly cos β = \(\frac{y}{r}\) ......(2)
(ΔOBP is right angled triangle)
and cos γ = \(\frac{z}{r}\) ...........(3)
(ΔOCP is right angled triangle)

Squaring and adding equations (1), (2) and (3), we get
cos²α + cos²β + cos²γ = \(\frac{x^{2}}{r^{2}}+\frac{y^{2}}{r^{2}}+\frac{z^{2}}{r^{2}}\)
= \(\frac{x^{2}+y^{2}+z^{2}}{r^{2}}=\frac{r^{2}}{r^{2}}\) = 1 (∵ r² = x² + y² + z²)
or l² + m² + n² = 1 ...(4)

Sum of square of direction cosines is 1.
Again l = cos α = \(\frac{x}{r}\), m = cos β = \(\frac{x}{r}\)
n = cos γ = \(\frac{x}{r}\)
Then x = lr, y = mr, x = nr
Thus, co-ordinate of P (x, y, z) is represented by (lr, mr, nr)
lr, mr and nr are called direction ratios of vector \(\vec{r}\) i.e., if l ∝ a, m ∝ b and n ∝ c,then a, b and c are called direction ratios of vectors \(\vec{r}\)

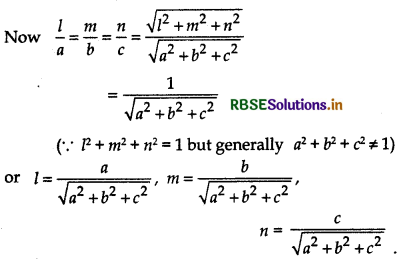
If direction ratios of any vector is given then we can find its direction cosines.

Types of Vectors
Zero Vector or Null Vector : A vector whose initial and terminal points coincide, is called a zero vector (or null vector), and denoted as \(\vec{O}\). Zero vector can not be assigned a definite direction as it has zero magnitude. The vectors \(\overrightarrow{A A}, \overrightarrow{B B}, \overrightarrow{P P}\) etc, represent the zero vector.

Unit Vector:
A vector whose magnitude is unity (i.e., 1 unit) is called a unit vector, i.e.,
if |\(\overrightarrow{O A}\)| = 1 then \(\overrightarrow{O A}\) is a unit vector.
The unit vector in the direction of a given vector is denoted by â, b̂, ...........
If any vector is divided by its modulus then unit vector is obtained in the direction of the vector, i.e.,

Unit vector in the direction of the vector \(\vec{a}\)
â = \(\frac{\vec{a}}{|\vec{a}|}\) or \(\frac{\vec{a}}{a}\)
Similarly, unit vector in the direction of vector \(\overrightarrow{O P}\) is
\(\hat{O P}=\frac{\overrightarrow{O P}}{|\overrightarrow{O P}|}\)

Co-initial vectors:
Two or more vectors which starts at a common point is called co-initial vectors. In other words two or more vectors having the same intial point are called
co-initial vectors.

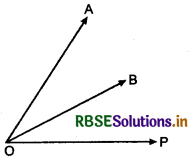
In the given figure, \(\overrightarrow{O A}, \overrightarrow{O B}\) and \(\overrightarrow{O P}\) are co-initial vectors.

Like vectors :
Vectors having the same direction are known as like vectors.

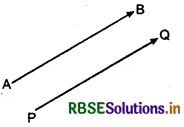
In figure \(\overrightarrow{A B}\) and \(\overrightarrow{P Q}\) are like vectors.

Unlike vectors:
Vectors having opposite direction are known as unlike vectors.

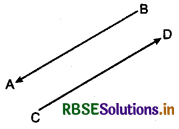
In figure \(\overrightarrow{A B}\) and \(\overrightarrow{C D}\) are unlike vectors.

Parallel vectors :
Vectors which are parallel to each other is called parallel vectors. Like and unlike both types of vectors are parallel vectors.

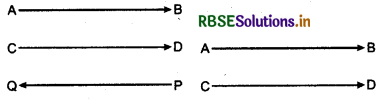
In figure \(\overrightarrow{A B}, \overrightarrow{C D}\) and \(\overrightarrow{P Q}\) are parallel vectors.

Displacement vector:
If a particle is moved from point A to point B then vector \(\overrightarrow{A B}\) is known as displacement regardless of the positions of their initial points, and written vector.

Collinear vectors :
Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions. All like and unlike vectors are collinear vectors.

Coplanar vectors:
Three or more non-zero vectors lying in the same plane or parallel to the same plane are said to be coplanar; otherwise they are said to be non-coplanar.

Equal vectors :
Two vectors \(\vec{a}\) and \(\vec{b}\) are said to be equal, if they have the same magnitude and direction regardless of the positions of their initial points, and written as \(\vec{a}=\vec{b}\)

Negative of a vector :
A vector whose magnitude is same as that of a given vector, but direction is opposite to that of it, is called negative of the given vector.
For example: Vector \(\overrightarrow{Q P}\) is negative of the vector \(\overrightarrow{P Q}\) and written as \(\overrightarrow{Q P}\) = - \(\overrightarrow{P Q}\)

Free vectors :
If the initial point of a vector is not specified, it is said to be free vector.

Localised vectors :
A vector drawn parallel to a given vector through a specified point as the initial point, is known as a localised vector.

Addition of Vectors
Let \(\vec{a}\) and \(\vec{b}\) be any two vectors. Take any point O and draw segments OA and AB such that \(\overrightarrow{O A} = \vec{a}\) and \(\overrightarrow{A B} = \vec{b}\). Join O and B.

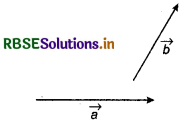
Then, \(\overrightarrow{O B}\) is called the sum or resultant of \(\vec{a}\) and \(\vec{b}\)
Thus, \(\vec{a}+\vec{b}=\overrightarrow{O A}+\overrightarrow{A B}=\overrightarrow{O B}\)

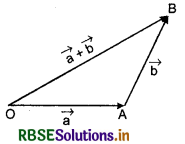
Thus, it is clear from the sum of vectors,
("If two sides of a triangle taken in order represent in magnitude and direction of two vectors then the third side taken in opposite order represent magnitude and direction, the sum or resultant of these vectors.")
This law is known as the triangle law of vector addition of vectors.

Difference of two vectors :
To find difference of two vectors \(\vec{a}\) and \(\vec{b}\), they are positioned so that the initial vectors \(\vec{a}\) point of vector \(\vec{b}\) coincides with the terminal point of vector a and draw AB' equal to magnitude of \(\vec{b}\) but opposite direction, as shown in figure. Now using triangle law of vector addition.

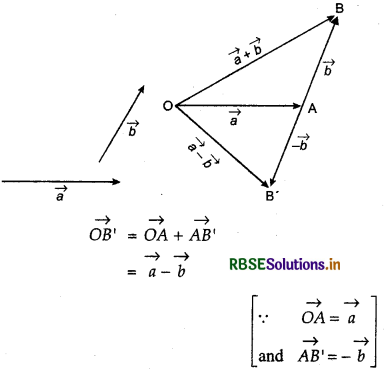
Thus, vector OB' represents the difference of vector \(\vec{a}\) and vector \(\vec{b}\)

Remark :
When the sides of a triangle are taken in order, it leads to Zero resultant. In figure.

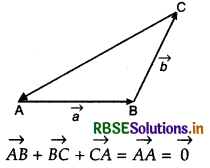
Because initial and terminal points set coincided.
\((\overrightarrow{A C}=-\overrightarrow{C A})\)
We can find sum of two vectors by parallelogram law of vector addition.

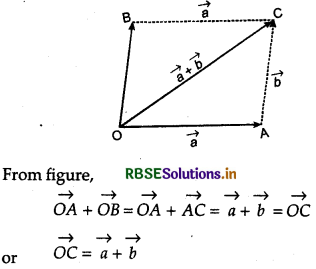
Parallelogram law of vector addition:
"If two vectors are represented in magnitude and direction by the two adjacent sides of a parallelogram drawn from one side of its angular points, then their sum or resultant is represented both in magnitude and direction by the diagonal of the parallelogram whose initial point is the angular point common to the corresponding adjacent sides.

Let two vectors a and b are represented in magnitude and direction by the two adjacent sides OA and OB of a parallelogram then their sum is represented both in magnitude and direction by the diagonal OC of the parallelogram whose initial point is common to the corresponding adjacent sides.

To find the sum of resultant of more than two vectors:
For finding the sum of resultant of more than two vectors we add vectors one by one by law of addition of vectors.

Let we have to find the sum of vectors \(\vec{a}, \vec{b}, \vec{c}, \vec{d}\) etc. We take any point in space. Draw a vector \(\overrightarrow{O A}\) equal to \(\vec{a}\). From point A draw AB equal to \(\vec{b}\) again \(\vec{c}\) from point B draw equal to \(\vec{d}\). Now, join OD which is resultant to vectors \(\vec{a}, \vec{b}, \vec{c}\) and \(\vec{d}\) as shown in figure.

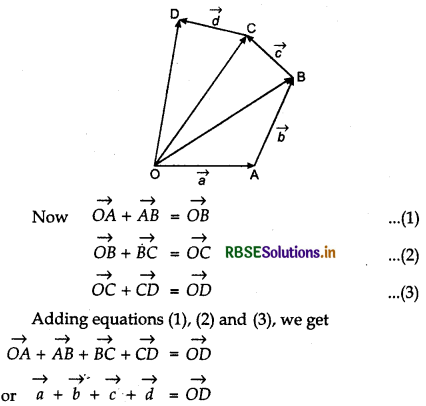
(Resultant vectors of \(\vec{a}, \vec{b}, \vec{c}\) and \(\vec{d}\))

Properties of Vector Addition
Property 1.
Sum of vectors is commutative, i.e., for vectors \(\vec{a}\) and \(\vec{b}\)

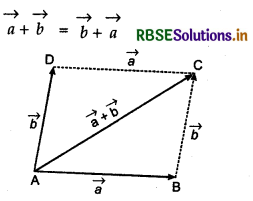
Proof:
Consider a parallelogram ABCD,
Let \(\overrightarrow{A B}=\vec{a}\) and BC = b
Then, in ABC from law of addition of triangle,
\(\overrightarrow{A C}=\vec{a}+\vec{b}\) .........(1)
Since, the opposite sides of a parallelogram ABCD are equal and parallel, i.e.,
AB ∥ DC and AD ∥ BC. 

From figure, \(\overrightarrow{A D}=\overrightarrow{B C}\) and \(\overrightarrow{A B}=\overrightarrow{D C}\)
∴ \(\overrightarrow{A D}=\overrightarrow{B C}=\vec{b} \)and \(\overrightarrow{A B}=\overrightarrow{D C}=\vec{a}\)

Again, using triangle law in ΔADC,
\(\overrightarrow{A C}=\overrightarrow{A D}+\overrightarrow{D C}=\vec{b}+\vec{a}\) ..........(2)
From equations (1) and (2), \(\vec{a}+\vec{b}=\vec{b}+\vec{a}\)

Property 2.
Sum of vectors is associative, i.e., for three vectors \(\vec{a}, \vec{b}\) and \(\vec{c}\)
\((\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\)
Proof:
Let vectors \(\vec{a}, \vec{b}\) and \(\vec{c}\) are represented by \(\overrightarrow{O A}, \overrightarrow{O B}\) and \(\overrightarrow{O C}\) respectively as shown in figure.

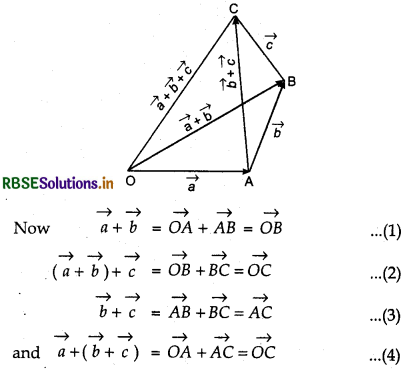
From equations (2) and (4)
\((\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\)
To represent a vector in terms of position vectors of initial and-terminal points : Let \(\overrightarrow{A B}\) is a vector and O is origin. Position vector of \(\overrightarrow{A B}\), end points A and B with respect to O is \(\overrightarrow{O A}\) and \(\overrightarrow{O B}\) respectively, as shown in the given figure. .

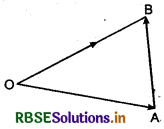
Thus \(\overrightarrow{O A}+\overrightarrow{A B}=\overrightarrow{O B}\)
or \(\overrightarrow{A B}=\overrightarrow{O B}-\overrightarrow{O A}\)
= Position vector of B - Position vector of A

Additive identity:
If \(\vec{a}\) is a vector and \(\vec{0}\) is a zero vector, then
\(\vec{a}+\overrightarrow{0}=\overrightarrow{0}+\vec{a}=\vec{a}\)
Zero vector \(\vec{0}\) is called identity element for addition.

Multiplication of a Vector by a Scalar
Let \(\vec{a}\) is a vector and λ, is a scalar quantity, then λ \(\vec{a}\) is called product of vector a and scalar λ.λ \(\vec{a}\) is a vector whose modulus vector is equal to λ times the modulus of vector \(\vec{a}\) and whose direction is the direction of vector \(\vec{a}\).Vector λ \(\vec{a}\) is a vector collinear to vector \(\vec{a}\). If the value of λ is positive, then the direction of λ \(\vec{a}\) is in the direction of a and if it is negative, then the direction of λ \(\vec{a}\) is in the opposite direction of vector \(\vec{a}\). The magnitude of a is |λ| times the magnitude of vector λ \(\vec{a}\), i.e.',
|λ\(\vec{a}\)| = |λ| |\(\vec{a}\)|
Now, for λ = - 1, λ \(\vec{a}\) = (- 1) \(\vec{a}\) = - \(\vec{a}\), which is a vector whose magnitude is equal to λ \(\vec{a}\) but direction is opposite to the direction of vector λ\(\vec{a}\), as shown in the given figure :

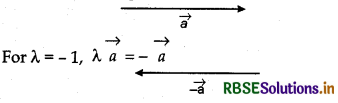
Vector - \(\vec{a}\) is called additive inverse of vector \(\vec{a}\), because
\(\vec{a}+(-\vec{a})=(-\vec{a})+\vec{a}=\overrightarrow{0}\) (Zerovector)
Again, if λ = \(\frac{1}{|\vec{a}|}\) whenever vector X a is not a zero vector, then ‘
\(|\lambda \vec{a}|=|\lambda||\vec{a}|=\frac{1}{|\vec{a}|}|\vec{a}|\) = 1

Thus, λ \(\vec{a}\), represents a unit vector in the direction of vector \(\vec{a}\).
i.e., â = \(\frac{1}{|\vec{a}|}\vec{a}\) is a unit vector in the direction of vector \(\vec{a}\)

If zero vector \(\overrightarrow{0}\) is multiplied by any scalar k then zero vector is obtained i.e., \(\overrightarrow{k 0}=\overrightarrow{0}\)

If m, n are two scalar quantities then for vectors \(\vec{a}\) and \(\vec{b}\)

• m(n \(\vec{a}\)) = (mn) \(\vec{a}\) = n(m \(\vec{a}\)) (Associativeproperty)
• m(\(\vec{a}\) + \(\vec{b}\)) = m\(\vec{a}\) + m\(\vec{b}\) (Distributive property)
• \(\vec{a}\)(m + n)= \(\vec{a}\)m + \(\vec{a}\) n = m \(\vec{a}\) + n \(\vec{a}\) = (m + n) \(\vec{a}\)

Components of o Vector
Let three points A(1, 0,0), B(0,1,0) and C(0,0,1) are on the X-axis, Y-axis and Z-axis respectively, then position vectors of points A, B and C are OA, OB and OC respectively.

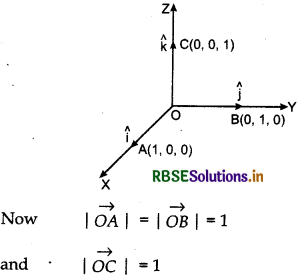
Vectors \(\overrightarrow{O A}, \overrightarrow{O B}\) and \(\overrightarrow{O C}\) each having magnitude 1 are called unit vectors along the axes OX, OY and OZ repsectively and denoted by î, ĵ and k̂ respectively which is shown in figure.
|î| = |ĵ| = |k̂| = 1
Let P(x, y, z) is point in space, whose position vector is \(\overrightarrow{O P}\) as shown in figure. Perpendiculars PL and PM are drawn from point P on the plane XOY and ZOX. Point L is foot of PL. Clearly, PL is parallel to OZ axis.

Unit vectors along x, y and z-axis are î, ĵ and k̂, then

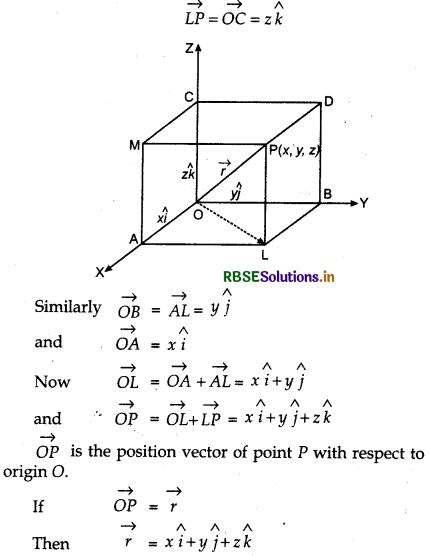
This form of any vector is called its component form.

Here, x, y and z are scalar components of vector, x î, y ĵ and z k̂ are called the vector components of vector r along x-axis, y-axis and z-axis.
Length of vector r = xî + y ĵ + zk̂
In right angled triangle ΔOAL,

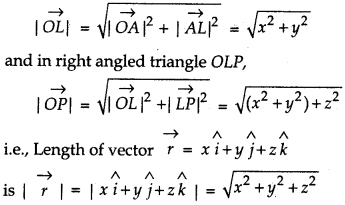
Two vectors a and b are represented by its component form as (a₁ î + a₂ ĵ + a₃ k̂) and (b₁ î + b₂ ĵ + b₃k̂) where a₁ a₂, a₃ and b₁ b₂, b₃ are scalar quantities.
(i) The sum of vectors \(\vec{a}\) and \(\vec{b}\) is represented by its component form :
\(\vec{a}\) + \(\vec{b}\) = (a₁ î + a₂ĵ + a₃k̂) + (b₁î + b₂ ĵ + b₃k̂)
= (a₁ + b₁)î + (a₂ + b₂) ĵ +(a3+b3)k̂

(ii) Difference of these vectors is represented by :
\(\vec{a}\) - \(\vec{b}\) = (a₁ î + a₂ĵ + a₃k̂) - (b₁î + b₂ ĵ + b₃k̂)
= (a₁ - b₁)î + (a₂ - b₂) ĵ + (a₃ - b₃)k̂

(iii) Vectors a and b are equal if and only if a₁ = b₁ a₂ = b₂ and a₃ = b₃.

(iv) Multiplication of vector a by any scalar is given by
λ \(\vec{a}\) = λ(a₁ î + a₂ ĵ + a₃ k̂)
= (λa₁)î + (λa₂)ĵ + (λa₃)k̂

Remark :
(i) Two vectors a and b are given in component form i.e.,
\(\vec{a}\) = a₁ î + a₂ĵ + a₃k̂
and \(\vec{b}\) = b₁î + b₂ ĵ + b₃k̂

These vectors are collinear if and only if
a₁ î + a₂ĵ + a₃k̂ = λ(b₁î + b₂ ĵ + b₃k̂)
or a₁ î + a₂ĵ + a₃k̂ = (λb₁)î + (λb₂) ĵ + (λb₃)k̂
Thus a₁ = λb₁ a₂ = λb₂ and a₁ = λb₃

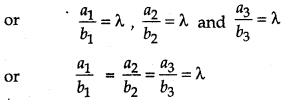
(ii) If \(\vec{a}\) = a₁ î + a₂ĵ + a₃k̂, then a₁ a₂, a₃ are called direction ratios of vector \(\vec{a}\)

(iii) If l,m and n are direction cosines of any vector, then
lî + m ĵ + nk̂ = (cos α)î + (cos β)ĵ + (cos γ)k̂
is unit vector along the direction of given vector, because
\(|l \hat{i}+m \hat{j}+n \hat{k}|=\sqrt{l^{2}+m^{2}+n^{2}}=\sqrt{1}\) = 1,
α, β and γ are the angle from x, y and z-axis respectively.

Vector joining two points
Let P and Q are two points in space, whose co-ordinates are (x₁ y₁ z₁) and (x₂, y₂, z₂). Now PQ is the vector joining P and Q, as shown in the figure. Position vectors of P and Q with respect to origin are \(\overrightarrow{O P}\) and \(\overrightarrow{O Q}\) respectively.

Section Forumla:
Let P and Q are two points in space with respect to origin O.
These points are represented by vectors OP and OQ . The line segment join two points P and Q is divided by two types:

• Internally division
• Externally division.

(i) Internally division : Let R be any point on a line joining P and Q which divides PQ internally. On joining the point R and origin O, vector \(\overrightarrow{O R}\) is obtained.

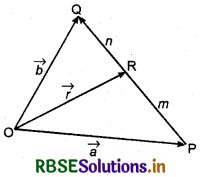
Let \(\overrightarrow{O R}=\vec{r}\)
Because point R, is on the line joining P and Q and divides it in such a way that
m\(\overrightarrow{R Q}\) = n\(\overrightarrow{P R}\), where m and n are positive scalars i.e., point R divides PQ internally in the ratio of m : n. Then in triangles ΔORP and ΔORQ

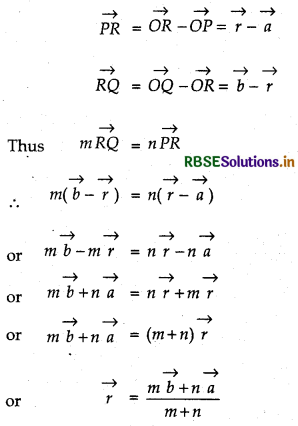
Hence, position vector of point R which divides P and Q internally in the ratio of m:n is given by \(\overrightarrow{O R}=\vec{r}\)
\(\overrightarrow{O R}=\vec{r}=\frac{m \vec{b}+n \vec{a}}{m+n}\)

(ii) Externally division: When point R divides the line joining the points P and Q externally, then in this case R is not a mid point of PQ as shown in the figure. It is on the extended line of PQ.

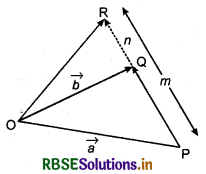
Point R divides the line joining the points P and Q in such a way that

which represents the position vector of R with respect to O.

Remarks: If R is the mid point of PQ (for internally division) then m = n in this case position vector of R
\(\overrightarrow{O R}=\vec{r}=\frac{m \vec{a}+m \vec{b}}{m+n}=\frac{m(\vec{a}+\vec{b})}{2 m}=\frac{\vec{a}+\vec{b}}{2}\)

Product of Two Vectors:
In previous section we have read about addition, subtraction, multiplication with a scalars and components of vectors. Here, in the given section we shall read about multiplication of vectors and their properties. We know that a vector has magnitude as well as direction. Hence, the product of vectors is not same as product of scalar quantities. The multiplication of two vectors is defined in two ways.

• Scalar or Dot product
• Vector or Cross product

Both types of multiplication of vectors has various applications in mechanics and engineering.

Scalar or Dot Product of Two Vectors
Definition : Let \(\vec{a}\) and \(\vec{b}\) are two vectors whose magnitude are a and b respectively. If θ is the angle between \(\vec{a}\) and \(\vec{b}\), then ab cos θ is the scalar product of \(\vec{a}\) and \(\vec{b}\) and it is denoted by \(\vec{a}\) . \(\vec{b}\).

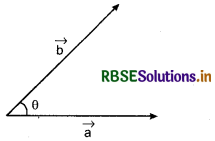
So, scalar product of two vectors \(\vec{a}\) and \(\vec{b}\) is
\(\vec{a}\) . \(\vec{b}\) = |a ||b|cos θ, (0 < θ < π/2)
= ab cos θ
where |\(\vec{a}\)| = a and |\(\vec{b}\)| = b
scalar product of two vectors is equal to the product of their magnitude and cosine between the vectors. It is a real scalar number.
\(\vec{a} \cdot \vec{b}\) is read as \(\vec{a} . \vec{b}\).

If |\(\vec{a}\)| = 0 or |\(\vec{b}\)| = 0, then θ is not defined because zero product has no direction.
In this case
\(\vec{a}\) . \(\vec{b}\) = 0
Let \(\vec{a}\) and \(\vec{b}\) are two non-zero vectors then \(\vec{a}\) . \(\vec{b}\) = 0 if and only if a and b are mutually perpendicular.

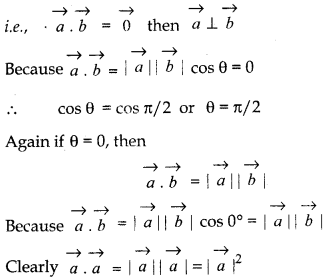
(Because in this case θ = 0°)

We know that unit vectors along axes are i,j and k.

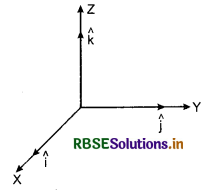
Now î .î = |î| |î| cos0° = (1) (1) (1)= 1
Similarly ĵ.ĵ = 1 and k̂.k̂ = 1
Thus î. î = ĵ.ĵ = k̂. k̂ = 1
Now î .ĵ = |î||ĵ| cos π/2
(Angle between X and Y axes is π/2)
= (1) (1) (0) = 0

Similarly ĵ.k̂ = 0 and k̂.î = 0
î.ĵ = ĵ.k̂ = k̂.î = 0

If angle between two non-zero vector \(\vec{a}\) and \(\vec{b}\) is θ, then

i.e., scalar product of two vectors is commutative.

Two important properties of scalar product
Property 1.
Distribution law of scalar product over addition.
Let \(\vec{a}, \vec{b}\) and \(\vec{c}\) are any three vectors, then
\((\vec{a} \cdot \vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}\)

Property 2.
Let \(\vec{a}\) and \(\vec{b}\) are any two vectors and λ is a scalar, then

Thus \(\vec{a}. \vec{b}\) = a₁b₁ + a₂b₂ + a₃b₃
Then cos θ = \(\frac{a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}}{\sqrt{a_{1}^{2}+a_{2}{ }^{2}+a_{3}{ }^{2}} \sqrt{b_{1}^{2}+b_{2}{ }^{2}+b_{3}{ }^{2}}}\)
Hence, angle θ between two vectors \(\vec{a}\) and \(\vec{b}\) can be find by the following formula:
θ = cos^-1\(\frac{a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}}{\sqrt{a_{1}^{2}+a_{2}{ }^{2}+a_{3}{ }^{2}} \sqrt{b_{1}^{2}+b_{2}{ }^{2}+b_{3}{ }^{2}}}\)
If both the vectors are perpendicular, then
a₁b₁ + a₂b₂ + a₃b₃ = 0

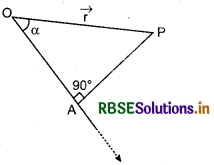
Projection of a Vector on a Line
Let perpendicular PQ is drawn at a line m through point P which meets at point Q from the line. Point Q is called projection of point P at line m. [Fig. (i)]

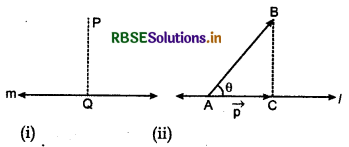
In Fig (ii), \(\overrightarrow{A B}\) is a vector. A perpendicular BC is drawn at line l from interior point B then vector \(\overrightarrow{A C}\) is the projection of the vector \(\overrightarrow{A B}\) on a line l. If the vector \(\overrightarrow{A B}\) makes positive angle θ with the line then the magnitude of projection \(\overrightarrow{A C}\) is |\(\overrightarrow{A B}\)| cos θ and whose direction is in the direction of l.
If \(\overrightarrow{A C}=\vec{p}\)
Then \(|\overrightarrow{A C}|=|\vec{p}|=|\overrightarrow{A B}|\)cos θ

The direction of projection depends upon cos θ which is positive or negative. In the figures given below, the projection \(\overrightarrow{A C}\) of vector \(\overrightarrow{A B}\) is shown.

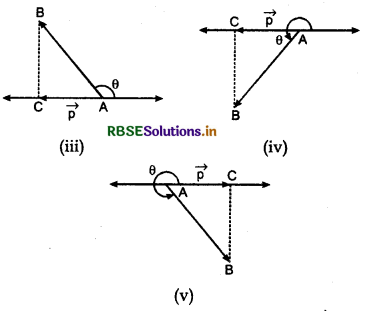
In figure (iii), the direction of projection \(\vec{p}\) is in the opposite direction of line l.
In figure (iv), the direction of projection \(\vec{p}\) is in the opposite direction of line l.
In figure (v), the direction of projection \(\vec{p}\) is in the direction of line l.

In each condition the projection of \(\overrightarrow{A B}\) on line l is \(\overrightarrow{A C}=\vec{p}\)

Again, let unit vector p̂ is along line l, then projection of vector a on line l is find out by a .p̂
If θ = 0 then the projection of \(\overrightarrow{A B}\) is \(\overrightarrow{A B}\) and if θ = π then the projection of \(\overrightarrow{A B}\) is \(\overrightarrow{B A}\).
If θ = \(\frac{\pi}{2}\) or θ = \(\frac{3\pi}{2}\) then the projection of AB is zero vector.

If α, β, and γ are the direction angles of vector
\(\vec{a}\) = a₁ î + a₂ ĵ + a₃k̂ then its direction cosines are:

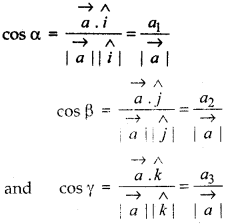
Clearly |\(\vec{a}\)| cos α |\(\vec{a}\)| cos β and |\(\vec{a}\)|cos γ are projections of vector a along OX, O Y and OZ respectively.
i.e., scalar components of \(\vec{a}\) are a₁, a₂ and a₃ along x, y, z-axis is projection of vector \(\vec{a}\). Again, if \(\vec{a}\) is a unit vector then using direction cosine it can be written as
\(\vec{a}\) = cos α î + cos β ĵ + cos γ k̂

Components of a Vector Along and Perpendicular to Another Vector
Let \(\vec{a}\) and \(\vec{b}\) are two vectors which is represented by \(\overrightarrow{O A}\) and \(\overrightarrow{O B}\) respectively and θ is the angle between them.

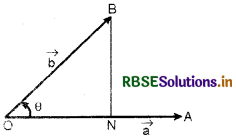
BN is perpendicular to OA from internal point B of vector \(\vec{b}(\overrightarrow{O B})\).

Now in ΔONB,
\(\overrightarrow{O B}=\overrightarrow{O N}+\overrightarrow{N B}=\vec{b}\)
Thus, \(\overrightarrow{O N}\) and \(\overrightarrow{N B}\) are components of the vector \(\vec{b}\) along to vector \(\vec{a}\).

= Components of vector \(\vec{b}\) along to vector \(\vec{a}\).

Vector (or Cross) Product of Two Vectors
The vector product of two vectors \(\vec{a}\) and \(\vec{b}\) is a vector whose modulus (resultant) is equal to product of modulus of two vectors and sine of angle between them and whose direction is perpendicular to two given vectors. Vector product is denoted by \(\vec{a} \times \vec{b}\)

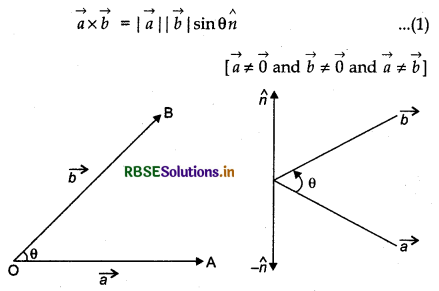
Where angle between \(\vec{a}\) and \(\vec{b}\) is θ, (0 < θ < π) n̂ is a unit vector whose direction is perpendicular to a and b such that directions of \(\vec{a}\) and \(\vec{b}\) and n̂ are in clockwise order. It means when screw rotates from \(\vec{a}\) to \(\vec{b}\), it moves to n̂ direction. (See in figure)

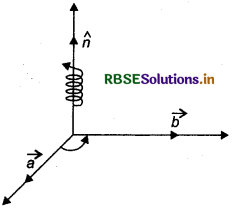
If \(\vec{a}\) = 0 and \(\vec{b}\) = 0, then θ is not defined and in this case take \(\vec{a} \times \vec{b}\) = 0 .
\(\vec{a} \times \vec{b}\) is a vector quantity so it is called vector product and is denoted by × (cross) between two vectors so it is called cross product.

Unit Vector:
Now, by definition, \(|\vec{a} \times \vec{b}|=|\vec{a}||\vec{b}|\) sin θ

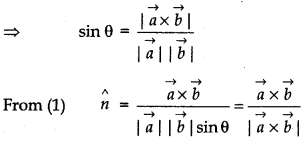
Thus, unit vector perpendicular to \(\vec{a}\) and \(\vec{b}\)
= \(\frac{\vec{a} \times \vec{b}}{|\vec{a} \times \vec{b}|}\)

Geometrical Representation of Vector Product
Since, \(\vec{a} \times \vec{b}=|\vec{a}||\vec{b}|\) sin θn̂

Modulus of cross-product of \(\vec{a}\) and \(\vec{b}\) :
\(|\vec{a} \times \vec{b}|=|\vec{a}||\vec{b}|\) sin θ|n̂|
= \(|\vec{a}||\vec{b}|\) sin θ (∵ |n̂| = 1) .......(2)
This is equal to area of that parallelogram whose two adjacent sides are denoted by \(\vec{a}\) and \(\vec{b} \)(See fig.)

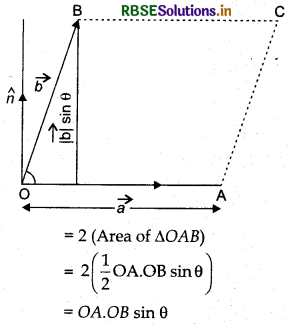
(1) and (2) it is clear that,
Magnitude of vector product \(\vec{a} \times \vec{b}=|\vec{a} \times \vec{b}|\) = area of parallelograms, whose adjacent sides are \(\vec{a}\) and \(\vec{b}\). (Such vector product is called the vector area of the parallelogram.)

Geometrical Interpretation of Vector Product
Let \(\overrightarrow{O A}=\vec{a}, \overrightarrow{O B}=\vec{b}\) be any two non-parallel and non zero vectors and θ be angle between them, n̂ is a unit vector in the direction of rotation of \(\vec{a}\) and \(\vec{b}.\)
\(|\vec{a} \times \vec{b}|=|\vec{a}||\vec{b}|\) sin θ
= (OA)(OB) sin θ
Complete parallelogram OABCB, let OA and OB are adjacent sides.

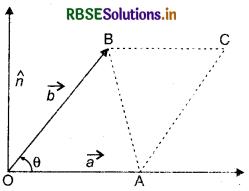
Area of parallelogram OACB
= 2(area of ΔOAB)
= 2 (\(\frac{1}{2}\)OA.OB sin θ)
= OA.OB sin θ ..........(2)
By (1) and (2) it is clear that,

Magnitude of vector proudct \(\vec{a}\) and \(\vec{b}=|\vec{a} \times \vec{b}|\)= area of parallelogram, whose adjacent sides are \(\vec{a}\) and \(\vec{b}\).
(Such vector product is called the vector area of that parallelogram).

Some Important Deduction From Vector Product
(i) Vector Product of Two Parallel Vectors Always be Zero.
Proof:
If \(​​​​​​\vec{a}\) and \(\vec{b}\) are two parallel vectors, then angle
between them will be θ = 0° to θ = 180°. Thus in both cases, sin θ will be zero.
Thus, \(\vec{a} \times \vec{b}\) = ab sin θ n̂
= (0)n̂ = 0

Conversely: If vector product of two non-zero vectors is zero, then those vectors be parallel,
∵ \(\vec{a} \times \vec{b}\) = 0
⇒ absin θn̂ = o
⇒ sin θ = 0 [∵ a = 0, b ≠ 0]
θ = 0 or θ = n
\(\vec{a}\) and \(\vec{b}\) are parallel vectors.

Note:

• \(\vec{a} \times \vec{a}\)= 0
• î × î = ĵ × ĵ = k̂ × k̂

(ii) Magnitude of Vector Product of Two perpendicular Vectors is Equal to the Product of Magnitude of those Vectors.
Proof:
If \(\vec{a}\) and \(\vec{b}\) be two perpendicular vector, then θ = 90°
Thus, \(\vec{a} \times \vec{b}\) = (ab sin90°)n̂ = (ab)n̂
⇒ |\(\vec{a} \times \vec{b}|\) = ab
or, magnitude of vectors \(\vec{a} \times \vec{b}\)
= (Magnitude of \(\vec{a}\))(Magnitude of \(\vec{b}\))

Where n̂ is a unit vector perpendicular to both \(\vec{a}\) and \(\vec{b}\) such that, \(\vec{a}\), \(\vec{b}\) and n̂ form a right handed system.

Special case:
Vector product of unit vectors
î × î = (1)(1)sin 90° k̂ = k̂
Similarly, ĵ × k̂ = î and k̂ × î = ĵ

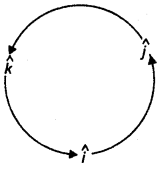
Again, ĵ × î = -k̂
Similarly, k̂ × ĵ = -î and î × k̂= -ĵ
The vector product of î, ĵ and k̂ can be represented by following table.

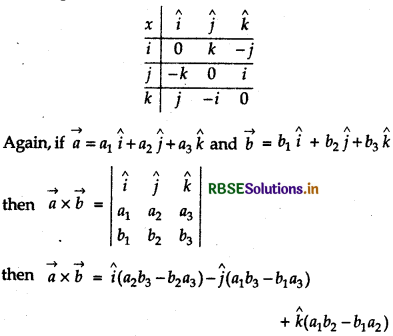
Algebraic Properties of Vector Product
(i) Commutativity: Vector product is not commutative, thus for any two vectors \(\vec{a}\) and \(\vec{b}\)
\(\vec{a} \times \vec{b} \neq \vec{b} \times \vec{a}\)

(ii) Associativity : Vector product is associative, corresponding to any scalar. Thus, if \(\vec{a}\) and \(\vec{b}\) be any two vectors and m be any scalar, then
\(m(\vec{a} \times \vec{b})=(m \vec{a}) \times \vec{b}=\vec{a} \times(m \vec{b})\)

(iii) Distributive property : Vector product follows distributive law over vector addition, thus if \(\vec{a}, \vec{b}\) and \(\vec{c}\) be any three vectors then
\(\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}\)

Angle between two Vectors:
If θ is angle between vectors \(\vec{a}\) and \(\vec{b}\) , then
\(|\vec{a} \times \vec{b}|=|\vec{a}| \times|\vec{b}|\) sin θ|n̂|

Thus, θ is angle between two vectors, then
sin θ = \(\frac{|\vec{a} \times \vec{b}|}{|\vec{a}||\vec{b}|}\) (∵ |n̂| = 1)

Perpendicular unit vector:
If unit vector in direction of \(\vec{a} \times \vec{b}\) is n̂, then perpendicular unit vector from plane of \(\vec{a}\) and \(\vec{b}\)
n̂ = \(\frac{\vec{a} \times \vec{b}}{|\vec{a} \times \vec{b}|}\)

Vector Product of Two vectors in Terms of Components

which is matrix form of \(\vec{a} \times \vec{b}\).

Angle Between Two Vectors
If θ be any angle between \(\vec{a}\) and \(\vec{b}\), then

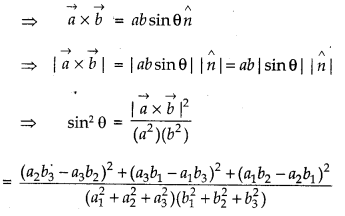
using above formula, θ can be evaluated.

Vector Area of a Triangle
(i) When Two Adjacent Sides of Triangle Denoted by \(\vec{a}\) and \(\vec{b}\) are Given.
Let ABC be a triangle whose sides AB and AC are denoted by vector \(\vec{a}\) and \(\vec{b}\) respectively.

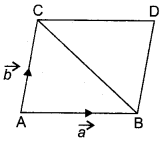
CE ∥AB and BE ∥ AC, then ABEC is a parallelogram, whose adjacent sides are AB and AC which are denoted by vector \(\vec{a}\) and \(\vec{b}\).

Thus, area of parallelogram ABEC = \(|\vec{a} \times \vec{b}|\)
But area of ΔABC
= \(\frac{1}{2}\) × Area parallelogram ABEC
= \(\frac{1}{2}|\vec{a} \times \vec{b}|\)

Thus, sides of any triangle are denoted by vectors \(\vec{a}, \vec{b}\) and \(\vec{c}\) respectively, then

Area of triangle
= \(\frac{1}{2}|\vec{a} \times \vec{b}|=\frac{1}{2}|\vec{b} \times \vec{c}|=\frac{1}{2}|\vec{c} \times \vec{a}|\)

(ii) When Position Vector of Vertices of Triangle A, B, C are \(\vec{a}, \vec{b}\) and \(\vec{c}\) given.
Let \(\vec{a}, \vec{b}\) and \(\vec{c}\) are position vector of vertices A, B and C of triangle ABC with respect to O i.e.,

Condition of Collinearity of Three Points:
Three points will be collinear when area of traingle so formed will be zero.
Thus, \(\frac{1}{2}[\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}]\)= 0
or \(\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a} \)= 0

Thus, three points whose position vector are \(\vec{a}, \vec{b}\) and \(\vec{c}\) will be collinear, if
\(\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}\) = 0.

 → The quantities specified by magnitude and direction both are called vectors.

→ Vector is represented by directed line segment. A directed line segment with initial point O and terminal point A, is a vector represented by \(\overrightarrow{O A}\). Vectors are also represented by \(\vec{a}, \vec{b}\) and \vec{c} etc.

→ The vector \(\overrightarrow{O A}\) having O and A as its inititerminal points, respectively, is called the position vector as the point A with respect to O.

→ A point P in space, having coordinates (x, y, z) with respect to the orgin O (0, 0, 0), then \(\overrightarrow{O P}\) is called the position vector with respect to O and its magnitude is given by
\(|\overrightarrow{O P}|=\sqrt{x^2+y^2+z^2}\)

→ If a vector makes angles α, β, γ with the positive direction of x-axis, y-axis and z-axis respectively. Then cos α, cos β, cos γ are known as its direction cosines and denoted by l, m, n respectively.
cos²α + cos²β + cos²y = l² + m² + n² = 1

→ Three numbers a, b and c are called direction ratios of vector \(\vec{r}\) where
l = \(\frac{\pm a}{\sqrt{a^2+b^2+c^2}}\)
m = \(\frac{\pm b}{\sqrt{a^2+b^2+c^2}}\)
n = \(\frac{\pm c}{\sqrt{a^2+b^2+c^2}}\)

→ Two non-zero vectors a and b are collinear if two non-zero vector x and y are in such a way.
x \(\vec{a}\) + y \(\vec{b}\) = \(\vec{0}\)

→ Vectors \(\vec{a}\) and \(\vec{b}\) are non collinears if
x \(\vec{a}\) + y \(\vec{b}\) = \(\vec{0}\) ⇒ x = y = 0.

→ If vectors \(\vec{a}, \vec{b}\) and \(\vec{c}\) represent three sides of a triangle in order, then
\(\vec{a} + \vec{b} + \vec{c}\) = 0

→ â is denoted as unit vector in the direction of vector â and
â = \(\frac{\vec{a}}{|\vec{a}|}\)

→ Vector addition is commutative and associative. If \(\vec{a}, \vec{b}\) and \(\vec{c}\) are vectors, then.
\(\vec{a}+\vec{b}=\vec{b}+\vec{a}\)
and \(\vec{a}+(\vec{b}+\vec{c})=(\vec{a}+\vec{b})+\vec{c}\)

→ If any point P (x, y, z) is in the space and O is orgin then vector \(\overrightarrow{O P}\).
= x î + y ĵ + zk̂
where î, ĵ and k̂ are unit vectors along coordinate and x, y and z.

→ If \(\overrightarrow{O P}=\vec{r}\) then \vec{r} = x î + y ĵ + zk̂ Scalar components of vector r are x, y and z and xî, yĵ and zk̂ are vector components of vector \vec{r} along axis x, y and z.

→ Vectors joining P(x₁, y₁ z₁) and Q(x₂, y₂, z₂) is
PQ = (x₂ - x₁)î + (y₂ - y₁)ĵ + (z₂ - z₁)k̂

→ Position vector of a point R which divides the points gamming position vector \(\vec{a}\) and \(\vec{b}\) internally in the ratio m : n are
\(\vec{r} = \frac{m \vec{b}+n \vec{a}}{m+n}\)

→ Position vector of a point R which divides the points having position vector \(\vec{a}\) and \(\vec{b}\) externally in the ratio m: n are
\(\vec{r}=\frac{m \vec{b}+n \vec{a}}{m-n}\)

→ Scalar product of \(\vec{a}\) and \(\vec{b}\) is represented by \(\vec{a} \cdot \vec{b}\) and \(\vec{a} \vec{b}=|\vec{a}||\vec{b}|\)cos θ
where θ is the angle between \(\vec{a}\) and \(\vec{b}\)
î. î = ĵ.ĵ = k̂.k̂ = 1
î. ĵ = ĵ .k̂ = k̂. î = 0

(i) Scalar product of vectors is commuatative i.e.; for vectors \(\vec{a}\) and \(\vec{b}\)
\(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\)

(ii) Scalar product of vectors holds distributive law,
i.e. \(\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}\)

→ Projection of vector \(\vec{a}\) on vector \(\vec{b}\) is \(\vec{a} \cdot \frac{\vec{b}}{|\vec{b}|}\)

→ Vector paroduct of vectors \(\vec{a}\) and \(\vec{b}\) is represented by
\(\vec{a} + \vec{b}\) and
\(\vec{a} \times \vec{b}=|\vec{a}||\vec{b}|\) sin θ n̂
where θ is the angle between \(\vec{a}\) and \(\vec{b}\) and n̂ is a unit vector whose direction is perpendicular to vector \(\vec{a}\) and \(\vec{b}\).

→ Vector product of vectors is not commuatative i.e.,
\(\vec{a} \times \vec{b} ≠ \vec{b} \times \vec{a}\)
\(\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}\)

→ If vector is given by its components i.e.,
\(\vec{a}\) = a₁ î + a₂ ĵ + a₃ k̂
and \(\vec{b}\) = b₁ î + b₂ ĵ + b₃k̂
Then \(\vec{a} \times \vec{b}=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array}\right|\)
î × î = 0, ĵ × ĵ = 0, k̂ × k̂ = 0
î × ĵ = k̂, ĵ × k̂ = î, k̂ × î = ĵ

→ If \(\vec{a}+\vec{b}\) = 0 if and only if \(\vec{a}\) and \(\vec{b}\) are parallel.

→ Perpendicular unit vector of \(\vec{a}\) and \(\vec{b}\) = \(\frac{\vec{a} \times \vec{b}}{|\vec{a} \times \vec{b}|}\)

→ If \(\vec{a}\) and \(\vec{b}\) are adjacent sides of a parallogram then its area is \(\vec{a}\) + \(\vec{b}\)

→ If \(\overrightarrow{d_1}\) and \(\overrightarrow{d_2}\) are diagonals of parallelogram then its area is \(\frac{1}{2}\left(\overrightarrow{d_1} \times \overrightarrow{d_2}\right)\)

→ Area of triangle ΔABC = \(\frac{1}{2}|\overrightarrow{B C} \times \overrightarrow{B A}|=\frac{1}{2}|\overrightarrow{A B} \times \overrightarrow{A C}|= \frac{1}{2}|\overrightarrow{C B} \times \overrightarrow{C A}|\)

→ If sides of any triangle represented by \(\vec{a}\), \(\vec{b}\) and \vec{c} then its area
= \(\frac{1}{2}|\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}|\)

→ (i) For any two vectors \(\vec{a}\) and \(\vec{b}\)
\(|\vec{a} \times \vec{b}|^2+|\vec{a} \cdot \vec{b}|^2=|\vec{a}|^2|\vec{b}|^2\)

(ii) For vector \(\vec{a}\)
\(|\vec{a} \times \hat{i}|^2+|\vec{a} \times \hat{j}|^2+|\vec{a} \times \hat{k}|^2=2|\vec{a}|^2\)