RBSE Class 12 Maths Notes Chapter 1 संबंध एवं फलन

These comprehensive RBSE Class 12 Maths Notes Chapter 1 संबंध एवं फलन will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 1 Notes संबंध एवं फलन

भूमिका (Introduction):
हम अपने दैनिक जीवन में अपने विचार व्यक्त करने के लिए अनेक प्रकार के वाक्यों (Sentences) और संकेतों (Symbols) का प्रयोग करते हैं। वाक्यों को दो भागों में विभाजित कर सकते हैं-कथन और खुले वाक्य । परिभाषा : कथन (Statement)-वह वाक्य जो सत्य अथवा असत्य तथ्य को व्यक्त करता हो अर्थात् जो अर्थयुक्त हो, कथन कहलाता है।

उदाहरणार्थ
(i) दिल्ली भारत की राजधानी है।
(ii) 6 - 5 = 5 - 6
(ii) 8 का वर्ग 64 है।
(iv) भारत दुनिया की सर्वाधिक जनसंख्या वाला देश है।
(v) A ∪ B = B ∪ A
(vi) त्रिभुज ABC, त्रिभुज PQR के समरूप है।
(vii) 9 < 8

उपर्युक्त सभी वाक्य अर्थयुक्त हैं जो सत्य अथवा असत्य तथ्य को व्यक्त करते हैं। वाक्य (i), (iii), (v), (vi) सत्य हैं जबकि वाक्य (ii), (iv) और (vii) असत्य हैं। ये सभी वाक्य कथन हैं। कथन (ii), (iii), (v), (vi) एवं (vii) गणितीय कथन हैं।

खुला वाक्य (Open Sentence):
वह वाक्य जो अतिरिक्त जानकारी के बिना न तो सत्य हो और न असत्य, खुला वाक्य कहलाता है। उदाहरणार्थ x + 10 = 6
एक खुला वाक्य है जिसमें 'x' चर राशि है। इस वाक्य में x की जगह कोई संख्या प्रतिस्थापित करने पर यह वाक्य कथन बन जायेगा क्योंकि उस परिस्थिति में इसकी सत्यता अथवा असत्यता निश्चित की जा सकती है। स्पष्ट है, यह वाक्य x = - 4 के लिए सत्य है। जबकि यह x = -3 के लिए असत्य है।
खुले वाक्यों के कुछ अन्य

उदाहरण :

• -6 < x < 3
• x भारत का एक शहर है।
• x श्याम का भाई है।
• x + y = 10
• x + 3y ≤ 9

अन्तिम दो खुले वाक्यों में x तथा y दो चर राशियाँ हैं । ऐसे खुले वाक्यों को जिनमें x और y दो चर राशियाँ हों, प्रायः P(x, y) प्रतीक से व्यक्त करते हैं। ऐसे भी खुले वाक्य हो सकते हैं जिनमें दो से अधिक चर राशियाँ हों, जैसे x + 3y = 6z. में x, y, तीन चर राशियाँ हैं । इस अध्याय में हमारे समक्ष दो चर राशियों के ही खुले वाक्य होंगे। प्रत्येक खुले वाक्य में चर राशि के प्रतिस्थापन में किसी उपयुक्त समुच्चय के अवयवों का प्रयोग किया जाता है, जो प्रतिस्थापन समुच्चय (Replacement Set) कहलाता है।

प्रतिस्थापन समुच्चय का वह उपसमुच्चय जिसके अवयवों से चर राशि को प्रतिस्थापन करने पर खुला वाक्य सत्य कथन बनता है, खुले वाक्य का हल समुच्चय (Solution Set) कहलाता है। जैसे खुले वाक्य (x - 5)² = 49 में प्रतिस्थापन समुच्चय पूर्णांकों का समुच्चय z हो तो इसका हल समुच्चय {- 2, 12} है।

 

क्रमित युग्म (Ordered Pair):
सामान्यतः समुच्चय के अवयवों के क्रम में परिवर्तन करने पर समुच्चय में कोई भी परिवर्तन नहीं होता। जैसे {1, 2} = {2, 1} लेकिन यदि किसी समुच्चय में अवयवों के क्रम का भी महत्व हो तो ऐसे समुच्चय को क्रमित समुच्चय (ordered set) कहते हैं। इसी प्रकार यदि दो अवयवों वाले समुच्चय {a, b} में a का पहला स्थान तथा b का दूसरा स्थान निर्धारित कर दिया जाये तो यह समुच्चय क्रमित युग्म (Ordered Pair) कहलाता है तथा इसे संकेत (a, b) द्वारा व्यक्त किया जाता है। यहाँ (a, b) ≠ (b, a) परिभाषा से स्पष्ट है कि
(a, b) = (c, d) ⇔ a = c तथा b = d

यदि किसी क्रमित समुच्चय में अवयवों की संख्या n हो तो ऐसे समुच्चय को क्रमित n - ट्युपुल (Ordered n-tuple) कहा जाता है तथा इसे (a₁, a₂............a_n) से व्यक्त करते हैं।

दो समुच्चयों का कार्तीय गुणन (Cartesian Product of Two Sets)
दो समुच्चयों A और B का कार्तीय गुणन उन क्रमित युग्मों (a, b) का समुच्चय होता है जिनका पहला अवयव a, समुच्चय A का अवयव हो तथा दूसरा अवयव b, समुच्चय B का अवयव हो। इस गुणन को संकेत Ax B द्वारा व्यक्त किया जाता है अतः
A × B = {(a,b)| a E A, b E B}

परिभाषा से स्पष्ट है कि A × B + B × A जब तक कि A और B बराबर न हों।
उदाहरण-यदि A = {p, q, r} तथा B = {x, y} हो तो
A × B = {(p, x), (p, y), (q, x), (q, y), (r, x), (r, y)}
B × A = {(x, p), (y, p), (x, q), (y, q), (x, r), (y, r)}

टिप्पणियाँ

• यदि A = Φ अथवा B = Φ, तब A × B = Φ यहाँ के रिक्त समुच्चय है।
• यदि A = Φ तथा B = Φ, तब A × B = Φ
• यदि समुच्चय A में अवयवों की संख्या m तथा समुच्चय B में अवयवों की संख्या n हो तो A × B में m × n अवयव होंगे अतः इसके अरिक्त उपसमुच्चयों की संख्या 2^mn - 1 होगी।
• यदि A तथा B अरिक्त समुच्चय हों तथा उनमें से एक अथवा दोनों अपरिमित समुच्चय हों तो A × B में अवयवों . की संख्या अनन्त होगी अर्थात् A × B भी एक अपरिमित समुच्चय होगा।
• A × (B ∩ C) = (A × B) ∩ (A × C)
• A × (B ∪ C) = (A × B) ∪ (A × C)
• A × (B - C) = (A × B) - (A × C)
• A ⊆ B ⇒ A × C ⊆ B × C
• A ⊆ B, C ⊆ D = (A × C) ⊆ (B × D)

सम्बन्ध (Relation):
मान लीजिये कि A और B दो दिये हुए समुच्चय हैं। समुच्चय A से समुच्चय B में कोई सम्बन्ध R की व्याख्या एक खुले वाक्य P(x, y) से की जाती है जिसमें P(a,b) सत्य होगा, यदि A का अवयव a, B के अवयव b से R सम्बन्ध रखता है। इसको प्रायः निम्न प्रकार से निरूपित करते हैं
R = {A, B, P (x, y)}
R = {(x, y) | xRy, Y ∈ A, Y ∈ B}

यदि P(a,b) सत्य कथन है अर्थात् a और b सम्बन्ध R द्वारा सम्बन्धित है तो इस तथ्य को निम्न प्रकार से लिख सकते हैं
a R b या (a,b) ∈ R

इसी प्रकार यदि P(a,b) असत्य कथन है अर्थात् a और b सम्बन्ध R द्वारा सम्बन्धित नहीं है तो तथ्य को निम्न प्रकार से लिख सकते

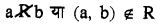
उदाहरण 1.
यदि A = {3, 5, 7, 9,}, B = {4, 6, 8, 10} तथा P(x, y) = x, y से छोटा है, तब
R = {A, B, P (x, y)}

इसे हम इस प्रकार से भी व्यक्त कर सकते हैं
(3,4) ∈ R, (3,6) ∈ R, (3,8) ∈ R, (3,10) ∈ R, (5,6) ∈ R, (5,8) ∈ R, (5,10) ∈ R, (7,8) ∈ R, (7,10) ∈ R, (9,10) ∈ R, परन्तु (5,4) ∉ R, (7,4) ∉ R, (7,6) ∉ R, (9,4) ∉ R, (9,6) ∉ R, (9,8) ∉ R इत्यादि।
sतब R = {(3, 4), (3, 6), (3, 8), (3, 10), (5, 6), (5, 8), (5, 10), (7, 8), (7, 10), (9, 10)}

उदाहरण 2.
यदि A = {2, 3, 4}, B = {3, 6, 8} तथा P(x,y) = xy का भाजक है, तब
R = {A, B, P(x,y)}

A से B में एक सम्बन्ध है। इस सम्बन्ध के अन्तर्गत 2R6, 2R8, 3R3, 3R6, 4R8
लेकिन

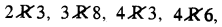
अर्थात् (2,6) ∈ R, (2, 8) ∈ R, (3, 3) ∈ R, (3, 6) ∈ R, (4, 8) ∈ R
परन्तु (2, 3) ∉ R, (3, 8) ∉ R, (4, 3) ∉ R, (4, 6) ∉ R
इत्यादि।

उदाहरण 3.
यदि A = {1, 2, 3, 5, 7}, B = {1, 4, 6, 9} तथा P(x,y) : x का दुगना y है तब R = {A, B, P(x, y)} A से B में एक सम्बन्ध है जिसके अन्तर्गत 2R4, 3R6 लेकिन

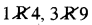
इत्यादि । इसे हम इस प्रकार भी व्यक्त कर सकते हैं (2, 4) ∈ R, (3, 6) ∈ R, परन्तु (1, 4) ∉ R, (3, 9) ∉ R इत्यादि।

टिप्पणी
उपर्युक्त उदाहरणों से स्पष्ट है कि

• यह आवश्यक नहीं है कि A के प्रत्येक अवयव का सम्बन्ध B के किसी न किसी अवयव से हो अर्थात् A में ऐसे अवयव हो सकते हैं जो B के किसी अवयव से सम्बन्धित नहीं हों।
• A के किसी अवयव का सम्बन्ध B के एक या अधिक अवयवों से हो सकता है।
• A के एक से अधिक अवयवों का सम्बन्ध B के एक अवयव से हो सकता है।

क्रमित युग्मों के समूह के रूप में सम्बन्ध (Relation As A Set Of Ordered Pairs):
खुले वाक्य की सहायता से समुच्चय A से समुच्चय B में सम्बन्ध परिभाषित करते समय हमने देखा कि यदि P(a, b) जहाँ aEA, bEB यदि सत्य है तब (a, b)ER अर्थात् सम्बन्ध में जितने भी अवयव होंगे वे सभी A × B के अवयव होंगे। अतः स्पष्ट है कि R ⊆ A × B

विलोमतः A × B का कोई भी उपसमुच्चय (a, b) जैसे क्रमित युग्मों का समुच्चय होगा। अतः A से B में एक सम्बन्ध परिभाषित करेगा। अतः समुच्चय A से समुच्चय B में कोई सम्बन्ध निम्न प्रकार से परिभाषित किया जा सकता हैपरिभाषा-समुच्चय A से समुच्चय B में परिभाषित कोई सम्बन्ध R, A × B का एक उपसमुच्चय है। अर्थात् R ⊆ A × B

नोट
यदि A तथा B में अवयवों की संख्या क्रमशः m तथा n हो तो A × B में अवयवों की संख्या m × n होगी। इसके अरिक्त उपसमुच्चयों की संख्या 2mm -1 होगी। अर्थात् A से B में परिभाषित
होने वाले अरिक्त सम्बन्धों की संख्या भी 2^mn -1 होगी।

सम्बन्ध का प्रान्त तथा परिसर (Domain And Trange of A Relation):
यदि R, समुच्चय A से समुच्चय B में परिभाषित कोई सम्बन्ध हो, तो R के क्रमित युग्मों के प्रथम अवयवों के समुच्चय को सम्बन्ध R का प्रान्त (Domain) तथा द्वितीय अवयवों के समुच्चय को सम्बन्ध R का परिसर (Range) कहते हैं।
अतः R का प्रान्त = {a|(a,b) ∈ R}
R का परिसर = {b|(a,b) ∈ R}
उपर्युक्त से स्पष्ट है कि R का प्रान्त A का उपसमुच्चय तथा R का परिसर B का उपसमुच्चय होगा। ॥

उदाहरण 1.
यदि A = {2, 4, 6, 8}, B={3, 5, 9} तथा A से B में एक सम्बन्ध R इस प्रकार परिभाषित है कि xRy ⇔ x,y से बड़ा है, तब
R = {(4, 3), (6, 3), (6, 5), (8, 3), (8, 5)}

उपर्युक्त सम्बन्ध में
R का प्रान्त = {4, 6, 8}
R का परिसर = {3, 5} ॥

उदाहरण 2.
यदि A = {1, 2, 3, 4, 5} तथा
B = {2, 4, 6, 8, 10} माना R = {(a,b)| a ∈ A, b ∈ B, a,b का भाजक है} A से B में एक सम्बन्ध हो तब R = {(1, 2), (1, 4), (1, 6), (1, 8), (1, 10), (2, 2), (2, 4), (2, 6), (2, 8), (2, 10), (3, 6), (4, 4), (4, 8), (5, 10)}
अतः R का प्रान्त = {1, 2, 3, 4, 5} = A
R का परिसर = {2, 4, 6, 8, 10} = B ॥

उदाहरण 3.
Z में परिभाषित एक सम्बन्ध R = {(x,y)| x,y ∈ Z, x² + y < 4}
तब R का प्रान्त = {-2, -1, 0, 1, 2}
तथा R का परिसर = {-2, -1, 0, 1, 2} ॥

उदाहरण 4.
यदि N पर R = {(x, y) : x + 2y = 8} एक सम्बन्ध है, तो R का परिसर लिखिए।
हल:
यहाँ xRy ⇔ x + 2y = 8
⇔ y = \(\frac{8-x}{2}\), x ∈ N, y ∈ N
जब x = 2, y = \(\frac{8-2}{2}\) = 3 ∈ N
x = 4. y = \(\frac{8-4}{2}\) = 2 ∈ N
x = 6, y = \(\frac{8-6}{2}\) = 1 ∈ N
x = 8, y = \(\frac{8-8}{2}\) = 0 ∉ N
अतः R का परिसर = {0, 1, 2, 3}

प्रतिलोम सम्बन्ध (Inverse Relation):
माना R, समुच्चय A से समुच्चय B में परिभाषित एक सम्बन्ध है। तब R का प्रतिलोम सम्बन्ध R^-1, समुच्चय B से समुच्चय A में निम्न प्रकार परिभाषित किया जाता है
R^-1 = {(b, a) ∈ B × A : (a, b) ∈ R}
अर्थात् (a, b) ∈ R - (b, a) ∈ R^-1
या aRb ⇔ bR^-1a
परिभाषा से स्पष्ट है कि R^-1 का प्रान्त = R का परिसर तथा R^-1 का परिसर = R का प्रान्त ॥

उदाहरण 1.
यदि A = {1; 2, 3}, और B = {0, 4} तथा सम्बन्ध R, समुच्चय A से समुच्चय B में इस प्रकार परिभाषित है कि
R = {(1,0), (2, 0), (3, 0)} तब R का प्रतिलोम सम्बन्ध होगा
R^-1 = {(0, 1), (0, 2), (0, 3)}

उपर्युक्त से स्पष्ट है कि
R^-1 का प्रान्त = {0} = R का परिसर
R^-1 का परिसर = {1, 2, 3} = R का प्रान्त

उदाहरण 2.
यदि N में सम्बन्ध "x, y से छोटा है" द्वारा परिभाषित हो तो R = {(x,y)|x,y ∈ N, x < y} तो इसका प्रतिलोम सम्बन्ध R^-1 = {(x,y)|x,y ∈ N.x > y} जो "xy से बंडा है" द्वारा परिभाषित है।

तत्समक सम्बन्ध (Identity Relation):
किसी समुच्चय A का तत्समक सम्बन्ध वह सम्बन्ध है जिसके अन्तर्गत A का प्रत्येक अवयव स्वयं से और केवल स्वयं से सम्बन्धित है। इसे प्रायः I द्वारा व्यक्त किया जा सकता है अतः
I_A = {(a, a)| ∀ a ∈ A}

यहाँ 1 का चिन्ह 'प्रत्येक' के लिए प्रयोग किया जाता है।
उदाहरण यदि A = {1, 2, 3, 4, 5} हो तो।
I_A = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)}
तत्समक सम्बन्ध की परिभाषा से यह स्वयं सिद्ध होता है कि तत्समक सम्बन्ध का प्रतिलोम सम्बन्ध भी स्वयं तत्समक सम्बन्ध होता है। अर्थात्
I_A^-1 = {(a, a) ∀ a ∈ A} = I_A
I_A का प्रान्त = I_A^-1 का प्रान्त
I_A का परिसर = I_A^-1 का परिसर

सम्बन्धों के प्रकार (Types of Relations)
सम्बन्ध निम्न प्रकार के होते हैं

• स्वतुल्य सम्बन्ध (Reflexive Relation)
• सममित सम्बन्ध (Symmetric Relation)
• प्रतिसममित सम्बन्ध (Anti-Symmetric Relation)
• संक्रामक सम्बन्ध (Transitive Relation)
• तुच्छ सम्बन्ध (Trivial Relation)

स्वतुल्य सम्बन्ध (Reflexive Relation):
यदि सम्बन्ध र किसी समुच्चय A में इस प्रकार परिभाषित हो कि इसके अन्तर्गत A का प्रत्येक अवयव स्वयं से सम्बन्धित हो, तो सम्बन्ध र स्वतुल्य सम्बन्ध कहलाता है। अतः R स्वतुल्य सम्बन्ध है यदि और केवल यदि aRa ∀ a ∈ A
अर्थात् र स्वतुल्य सम्बन्ध है ⇔ (a, a) ∈ R, ∀ a ∈ A

उपर्युक्त परिभाषा से स्पष्ट है कि A में परिभाषित सम्बन्ध R स्वतुल्य सम्बन्ध नहीं होगा यदि A में कम से कम एक अवयव a ऐसा हो, जो स्वयं से सम्बन्धित न हो अर्थात् (a, a) ∉ R
किसी समुच्चय A में परिभाषित स्वतुल्य सम्बन्ध तथा तत्समक

सम्बन्ध I_A की परिभाषाओं से स्पष्ट होता है कि I_A, R का उपसमुच्चय (Subset) होता है, अर्थात् I_A ⊆ R अतः किसी समुच्चय A का तत्समक सम्बन्ध I , आवश्यक रूप से A में एक स्वतुल्य सम्बन्ध होता है, परन्तु A में परिभाषित प्रत्येक स्वतुल्य सम्बन्ध का तत्समक होना आवश्यक नहीं है।

टिप्पणी:
स्वतुल्य सम्बन्ध के लिए (a, a) ∈ R परन्तु इसका अर्थ यह नहीं है कि अवयव a का सम्बन्ध a के अतिरिक्त दूसरे अवयव से न हो। अर्थात् a का सम्बन्ध स्वयं से होने के साथ A के अन्य अवयवों से भी हो सकता है। जबकि तत्समक सम्बन्ध में a का सम्बन्ध a तथा केवल a से होता है। अतः स्पष्ट है कि प्रत्येक तत्समक सम्बन्ध स्वतुल्य सम्बन्ध है परन्तु स्वतुल्य सम्बन्ध तत्समक सम्बन्ध नहीं होता है। स्वतुल्य सम्बन्ध की परिभाषा को स्पष्ट करने के लिए निम्न उदाहरण दिये जा रहे हैं

उदाहरण 1.
यदि N प्राकृत संख्याओं का समुच्चय है और N में एक सम्बन्ध र इस प्रकार परिभाषित है कि xRy x, y का भाजक है ∀ x, y ∈ N तो R एक स्वतुल्य सम्बन्ध होगा, क्योंकि प्रत्येक प्राकृत संख्या स्वयं का भाजक है।

उदाहरण 2.
किसी समतल में स्थित सरल रेखाओं के समुच्चय A में एक सम्बन्ध र यदि इस प्रकार परिभाषित हो कि xRY ⇔ x,y के समान्तर है तो R एक स्वतुल्य सम्बन्ध होगा, क्योंकि प्रत्येक रेखा स्वयं के समान्तर होती है।

उदाहरण 3.
यदि त्रिभुजों के समुच्चय B में एक सम्बन्ध R इस प्रकार से परिभाषित है कि xRy ⇔ xy के सर्वांगसम (congruent) है तो R एक स्वतुल्य सम्बन्ध होगा, क्योंकि प्रत्येक त्रिभुज स्वयं के सर्वांगसम (congruent) होता है।

उदाहरण 4.
समुच्चयों के समुच्चय S में एक सम्बन्ध र निम्न प्रकार परिभाषित है कि ARB ⇔ A, B का उपसमुच्चय है तो R एक स्वतुल्य सम्बन्ध होगा क्योंकि प्रत्येक समुच्चय स्वयं का उपसमुच्चय होता है।

उदाहरण 5. प्राकृत संख्याओं के समुच्चय N में यदि एक सम्बन्ध र इस प्रकार परिभाषित किया जाये कि xRy ⇔ x ≥ y तो R एक स्वतुल्य सम्बन्ध है क्योंकि X ∈ N = x = x परन्तु यदि R इस प्रकार परिभाषित हो कि xRy ∈ x > y तब यह सम्बन्ध स्वतुल्य नहीं होगा क्योंकि N के किसी भी अवयव के लिए.x> x सत्य नहीं है।

उदाहरण 6. माना A = {a, b, c, d} तथा R = {(a, a), (a, d), (b, a), (b, b), (c, d), (c, c), (d, d)} A में परिभषित कोई सम्बन्ध है तो R एक स्वतुल्य सम्बन्ध है क्योंकि (a, a) ∈ R, (b, b) ∈ R, (c, c) ∈ R तथा (d, d) ∈ R परन्तु यदि A में कोई सम्बन्ध R, इस प्रकार से परिभाषित हो कि R₁ = {(a, a), (a, d), (b, c), (b, d), (c, c), (c, d), (d, b)} तब R₁, स्वतुल्य नहीं है क्योंकि b ∈ A परन्तु (b, b)¢R₁, उसी प्रकार d ∈ A परन्तु (d. d) ∉ R₁

सममित सम्बन्ध (Symmetric Relation):
यदि सम्बन्ध र किसी समुच्चय A में इस प्रकार से परिभाषित हो कि जब a का b से सम्बन्ध हो तो b का a से वही सम्बन्ध होगा, तो सम्बन्ध र सममित सम्बन्ध कहलाता है। अतः R सममित सम्बन्ध होगा, यदि और केवल यदि aRb ⇒ bRa, ∀ a, b ∈ A अर्थात् (a, b) ∈ R = (b, a) ∈ R, ∀ a, b ∈ A
उपर्युक्त से स्पष्ट है कि समुच्चय A में परिभाषितं सम्बन्ध R सममित नहीं होगा यदि समुच्चय A में कम से कम दो अवयव a, b ऐसे हों कि a R b परन्तु bKa

नोट:
सममित सम्बन्ध R का प्रतिलोम सम्बन्ध भी स्वयं के बराबर होता है अर्थात् R= R^-1 सममित सम्बन्ध की परिभाषा को स्पष्ट करने के लिए निम्न उदाहरण दिये जा रहे हैं

उदाहरण 1.
एक समतल में स्थित सरल रेखाओं के समुच्चय A में एक सम्बन्ध र इस प्रकार परिभाषित है कि xRy ⇔ x, y के लम्बवत् है तो R एक सममित सम्बन्ध होगा क्योंकि यदि सरल रेखा x, रेखा y के लम्बवत् है तो रेखा y भी रेखा x के लम्बवत् होगी।

उदाहरण 2.
त्रिभुजों के समुच्चय A में "सर्वांगसम (≅)" का सम्बन्ध सममित है क्योंकि Δ₁ ≅ Δ₂ ⇒ Δ₂ ≅ Δ₁

उदाहरण 3. यदि प्राकृत संख्याओं के समुच्चय N में एक सम्बन्ध R इस प्रकार से परिभाषित है कि xRY ⇔ x, y के बराबर (Equal) है, तो R एक सममित सम्बन्ध होगा, क्योंकि किन्हीं दो प्राकृत संख्याओं तथा y के लिए, यदि x. y के बराबर है तो . x के बराबर होता है। उदाहरण 4. यदि किसी समतल में स्थित सरल रेखाओं के समुच्चय A में एक सम्बन्ध र इस प्रकार परिभाषित है कि xRyx, y के समान्तर है तो R एक सममित सम्बन्ध है क्योंकि यदि रेखा l₁, रेखा l₂, के समान्तर है तो रेखा l₂, रेखा l₁, के समान्तर होगी।

उदाहरण 5.
यदि समुच्चय A = {1, 2, 3, 4} पर दो सम्बन्ध R₁ तथा R₂, निम्न प्रकार परिभाषित किये जायें कि ।
R₁ = {(1, 3), (1, 4), (3, 1), (2, 2), (4, 1), (4, 4)}
तथा R₁ = {(1, 1), (2, 2), (3, 3), (1, 3)} तब
R₂ एक सममित सम्बन्ध है, परन्तु R₂, सममित नहीं है क्योंकि (1, 3) ∈ R,
परन्तु (3, 1) ∉ R₂

प्रति-सममित सम्बन्ध (Anti-Symmetric (Relation):
किसी समुच्चय A में परिभाषित सम्बन्ध R के अन्तर्गत अवयव a का अवयव b से सम्बन्ध तथा b का a से सम्बन्ध दोनों एक साथ तभी सत्य हों जब a = b तो R प्रति-सममित सम्बन्ध कहलाता है। अर्थात् R प्रति-सममित होगा यदि और केवल यदि
(a, b) ∈ R तथा (b, a) ∈ R ⇒ a = b, Va, b ∈ A
स्पष्टतः A में परिभाषित कोई सम्बन्ध र प्रति-सममित नहीं होगा यदि A में कम से कम दो अवयव a, b ऐसे विद्यमान हों जिनके लिए (a, b) ∈ R तथा (b, a) ∈ R परन्तु a ≠ b
प्रति-सममित सम्बन्ध की परिभाषा को स्पष्ट करने के लिए निम्न उदाहरण दिये जा रहे हैं

उदाहरण 1.
वास्तविक संख्याओं के समुच्चय A में यदि कोई । सम्बन्ध र इस प्रकार परिभाषित हो कि xRY ⇔ x ≥ y तब R एक प्रति-सममित सम्बन्ध होगा क्योंकि
x ≥ y तथा y ≥ x ⇒ x = y

उदाहरण 2.
यदि प्राकृत संख्याओं के समुच्चय N में एक सम्बन्ध R इस प्रकार से परिभाषित है कि xRy ⇔ x, y का भाजक (divisor) है तो R एक प्रति सममित सम्बन्ध होगा, क्योंकि किन्हीं दो संख्याओं x तथा y के लिए यदि x, y का भाजक है तो y, x का भाजक उसी स्थिति में होगा जबकि x तथा y बराबर हों।

उदाहरण 3.
यदि A = {1, 2, 3} में एक सम्बन्ध र निम्न प्रकार से परिभाषित है R = {(1, 1), (1, 2), (2, 2), (3, 3)} तो R एक प्रतिसममित सम्बन्ध होगा। उदाहरण 4. समुच्चयों के किसी समुच्चय में एक सम्बन्ध र इस प्रकार परिभाषित है कि ARB ⇔ A, B का उपसमुच्चय है तो R एक प्रति-सममित सम्बन्ध होगा क्योंकि किन्हीं दो समुच्चयों A तथा B के लिए A ⊆ B तथा B ⊆ A = AB

संक्रामक सम्बन्ध (Transitive Relation):
यदि सम्बन्ध र किसी समुच्चय A में इस प्रकार से परिभाषित हो कि a का b से सम्बन्ध और b का c से सम्बन्ध होने पर a का सम्बन्ध c से हो, तो सम्बन्ध र संक्रामक सम्बन्ध कहलाता है। अतः R संक्रामक सम्बन्ध होगा, यदि और केवल यदि
aRb और bRc ⇒ aRc ∀ a, b, c ∈ A
अर्थात् (a, b) ∈ R और (b, c) ∈ R ⇒ (a, c) ∈ R उपर्युक्त से स्पष्ट है कि A में परिभाषित कोई सम्बन्ध र संक्रामक सम्बन्ध नहीं होगा, यदि A में कम से कम तीन अवयव a, b, c ऐसे हों कि कोई

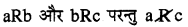
संक्रामक सम्बन्ध की परिभाषा को स्पष्ट करने के लिए निम्न उदाहरण दिये जा रहे हैं

उदाहरण 1.
किसी समतल में स्थित सरल रेखाओं के समुच्चय A में "x, y के समान्तर है" एक संक्रामक सम्बन्ध है क्योंकि l₁, l₂, l₃ ∈ A तथा l₁ ∥ l₂ तथा l₂ ∥ l₃ = l₁ ∥ l₃

उदाहरण 2.
समुच्चय A = {1, 2, 3, 4} में R = {(1, 2), (1, 3), (1, 4), (2, 4), (2, 3)} एक संक्रामक सम्बन्ध है क्योंकि
(1, 2) ∈ R, (2, 4) ∈ R ⇒ (1, 4) ∈ R
(1, 2) ∈ R, (2, 3) ∈ R ⇒ (1, 3) ∈ R

उदाहरण 3.
यदि पूर्णांकों के समुच्चय I में एक सम्बन्ध R इस प्रकार से परिभाषित है कि xRy ⇔ x, y से बड़ा है तो R एक संक्रामक सम्बन्ध होगा, क्योंकि किन्हीं तीन पूर्णांकों x, y तथा के लिए यदि x, y से बड़ा है तथा y, से बड़ा है तो x, y से बड़ा होगा अर्थात् x > y एवं y > z ⇒ x > z

उदाहरण 4.
प्राकृत संख्याओं के समुच्चय N में यदि एक सम्बन्ध R इस प्रकार परिभाषित किया जाये कि xRy ∈ x तथा y दोनों विषम हैं तो R एक संक्रामक सम्बन्ध है क्योंकि x, y, z ∈ N तथा xRy एवं yRz ⇒ x, y तथा y, सभी विषम हैं अर्थात् x, z दोनों विषम हैं अतः xRz.

तुल्यता सम्बन्ध (Equivalence Relation):
किसी समुच्चय A में परिभाषित कोई सम्बन्ध र एक तुल्यता सम्बन्ध कहलाता है यदि

• R स्वतुल्य है अर्थात् (a, a) ∈ R ∀ a ∈ A
• R सममित है अर्थात् (a, b) ∈ R ⇒ (b, a) ∈ R, ∀ a, b, ∈ A.
• R संक्रामक है अर्थात् (a, b) ∈ R तथा (b, c) ∈ R ⇒ (a, c) ∈ R, ∀ a, b, C ∈ A तुल्यता सम्बन्ध की परिभाषा को स्पष्ट करने के लिए निम्न उदाहरण दिये जा रहे हैं

उदाहरण 1.
यदि किसी समतल में स्थित सरल रेखाओं के समुच्चय A में एक सम्बन्ध R इस प्रकार से परिभाषित है कि xRy ∈ x, y के समान्तर है अर्थात् x ∥ y तो R एक तुल्यता सम्बन्ध होगा, क्योंकि समतल में स्थित किन्हीं तीन रेखाओं x, y, z के लिए
(i) प्रत्येक रेखा स्वयं के समान्तर होती है, अर्थात्
x ∥ x, ∀ x ∈ A
∴ (x, x) ∈ R, ∀ x ∈ A
अतः R स्वतुल्य सम्बन्ध है।

(ii) यदि रेखा x, रेखा y के समान्तर है तो रेखा y भी रेखा x
के समान्तर होगी। अर्थात् यदि
x ∥ y = y ∥ x, x, y ∈ A
∴ (x, y) ∈ R = (y, x) ∈ R, ∀ x, y ∈ A
अतः R सममित सम्बन्ध है।

(iii) ∴ x ∥ y तथा y ∥ z = x ∥ z
यदि (x, y) ∈ R एवं (y, z) ∈ R, ⇒ (x, 2) ∈ R, ∀ x, y, Z ∈ A
अतः R संक्रामक सम्बन्ध है।

उदाहरण 2.
एक समतल में स्थित त्रिभुजों के समुच्चय T में एक सम्बन्ध र निम्न प्रकार परिभाषित है कि
xRy ⇔ x, y के सर्वांगसम है। तब R एक तुल्यता सम्बन्ध है, क्योंकि
(i) प्रत्येक त्रिभुज स्वयं के सर्वांगसम होता है अतः
ΔET ⇒ Δ ≅ Δ ⇒ ΔRΔ अर्थात् (Δ, Δ) ∈ R,∀ Δ ∈ Τ
अतः R स्वतुल्य है।

(ii) यदि Δ₁, Δ₂, ∈ T तथा (Δ, Δ) ∈ R
तब (Δ₁, Δ₂) ∈ R = Δ₁ ≅ Δ₂ ⇒ Δ₂ = Δ₁ ⇒ (Δ₂, Δ₁) ∈ R
अतः R सममित है।

(iii) यदि Δ₁, Δ₂, Δ₃ ∈ T तथा (Δ₁, Δ₂) ∈ R तथा (Δ₂, Δ₃) ∈ R
तब (Δ₁, Δ₂) ∈ R तथा (Δ₂, Δ₃) ∈ R ⇒ Δ₁ S Δ₂,
तथा Δ₂ = Δ₃ ⇒ Δ₁ = Δ₃ = (Δ₁, Δ₃) ∈ R
∴ R संक्रामक है।
अतः R एक तुल्यता सम्बन्ध है।

आंशिक क्रम सम्बन्ध (Partial Order Relation):
यदि सम्बन्ध र समुच्चय A में इस प्रकार परिभाषित हो कि

• R स्वतुल्य हो,
• R प्रति-सममित हो,
• R संक्रामक हो,

तो सम्बन्ध र आंशिक क्रम सम्बन्ध कहलाता है।
पुनः यदि समुच्चय A में एक आंशिक क्रम सम्बन्ध र परिभाषित हो समुच्चय A आंशिक क्रमित समुच्चय (Partial Ordered Set) कहलाता है। आंशिक क्रम सम्बन्ध की परिभाषा को स्पष्ट करने के लिए निम्न उदाहरण दिये जा रहे हैं

उदाहरण 1.
समुच्चयों के समूह में "x, y का उपसमुच्चय है" द्वारा परिभाषित एक आंशिक क्रम सम्बन्ध है क्योंकि यह सम्बन्ध स्वतुल्य, प्रति-सममित तथा संक्रामक है।

उदाहरण 2.
प्राकृत संख्याओं के समुच्चय N में "x, y का भाजक है" से परिभाषित सम्बन्ध आंशिक क्रम सम्बन्ध है क्योंकि यह सम्बन्ध स्वतुल्य, प्रति-सममित तथा संक्रामक है।

उदाहरण 3.
प्राकृत संख्याओं के समुच्चय N में "x, y से बड़ा अथवा बराबर है" से परिभाषित सम्बन्ध एक आंशिक क्रम सम्बन्ध है क्योंकि यह सम्बन्ध स्वतुल्य, प्रति-सममित और संक्रामक है।

पूर्ण क्रम सम्बन्ध (Total Order Relation):
यदि सम्बन्ध र समुच्चय A में इस प्रकार परिभाषित हो कि

• R एक आंशिक क्रम सम्बन्ध हो,
• प्रत्येक a, b ∈ A के लिए या तो (a, b) ∈ R या (b, a) ∈ R

या a = b सत्य हो, तो सम्बन्ध र पूर्ण क्रम सम्बन्ध कहलाता है।
एक समुच्चय A जिसमें कोई पूर्ण क्रम सम्बन्ध परिभाषित हो, एक पूर्ण क्रमित समुच्चय कहलाता है। पूर्णक्रम सम्बन्ध की परिभाषा को स्पष्ट करने के लिए निम्न उदाहरण दिये जा रहे हैं

उदाहरण 1.
प्राकृत संख्याओं के समुच्चय N में "xy से बड़ा अथवा बराबर है" से परिभाषित सम्बन्ध एक पूर्ण क्रम सम्बन्ध है क्योंकि

• R एक आंशिक क्रम सम्बन्ध है,
• किन्हीं दो प्राकृत संख्याओं x तथा y के लिए x > y या y>x या x = y में एक सदैव सत्य होगा।

उदाहरण 2.
प्राकृत संख्याओं के समुच्चय N में 'x, y से छोटा अथवा बराबर है' से परिभाषित सम्बन्ध एक पूर्ण क्रम सम्बन्ध है क्योंकि

• R एक आंशिक क्रम सम्बन्ध है,
• किन्हीं दो प्राकृत संख्याओं x तथा y के लिए x < y या y

टिप्पणी
उपर्युक्त के अतिरिक्त दो अतिरिक्त सम्बन्ध भी होते हैं

• रिक्त सम्बन्ध (Empty Relation)-समुच्चय A पर परिभाषित सम्बन्ध र एक रिक्त सम्बन्ध कहलाता है, यदि A का कोई भी अवयव A के किसी भी अवयव से सम्बन्धित नहीं हो, अर्थात् R = Φ ⊂ A × A
• सार्वत्रिक सम्बन्ध (Universal Relation)-समुच्चय A पर परिभाषित सम्बन्ध R, एक सार्वत्रिक सम्बन्ध कहलाता है, यदि A का प्रत्येक अवयव A के सभी अवयवों से सम्बन्धित हो, अर्थात् R = Ax A रिक्त सम्बन्ध एवं सार्वत्रिक सम्बन्ध को कभी-कभी तुच्छ सम्बन्ध (Trivial Relation) भी कहते हैं।

फलनों के प्रकार (Types of Functions):
कक्षा XI में हम फलन की परिभाषा, क्रमित युग्मों के समुच्चय के रूप में फलन, फलन के प्रान्त, सहप्रान्त तथा परिसर, अचर फलन, तत्समक फलन एवं तुल्य फलन का विस्तारपूर्वक अध्ययन कर
चुके हैं।

यहाँ हम फलनों के निम्न प्रकार का अध्ययन करेंगे

• एकैकी फलन (One-One function or Injective function)
• बहु-एकी फलन (Many-One function)
• अन्तर्वैपी फलन (Into function)
• एकैकी अन्तःपी फलन (One-One Into function)
• बहु-एकी अन्त:पी फलन (Many-One Into function)
• आच्छादक फलन (Onto or Surjective function)
• एकैकी आच्छादक फलन (One-One Onto function or Bijection)
• बहु-एकी आच्छादक फलन (Many-One Onto function)
• तत्समक फलन (Identity function)
• अचर फलन (Constant function)

एकैकी फलन (One-One Function)
यदि f : A → B एक फलन हो तो एकैकी फलन कहलाता है यदि के अन्तर्गत A के भिन्न-भिन्न अवयवों के B में भिन्नभिन्न प्रतिबिम्ब हों।
अर्थात् f : A → B एकैकी है यदि a ≠ b ⇒ f(a) ≠ f(b), ∀ a, b, ∈ A
दूसरे शब्दों में f : A → B एकैकी है यदि
f(a) = f(b) ⇒ a = b, ∀ a, b ∈ a

उदाहरण 1.
यदि A = {1, 2, 3, 4}, B = {1, 4, 9, 16} तथा A से B में एक फलन | इस प्रकार परिभाषित हो कि f(x) = x² तो f(1) = 1² = 1, f(2) = 2² = 4, f(3) = 3² = 9, f(4) = 4² = 16
अतः। के अन्तर्गत A के भिन्न-भिन्न अवयवों के B में भिन्न-भिन्न प्रतिबिम्ब हैं। अतः फलन । एकैकी है।

उदाहरण 2.
फलन f : → f(x) = - x एकैकी फलन है क्योंकि किन्हीं a, b ∈ Z के लिए a ≠ b = - a ≠ - b = f(a) ≠ f(b)

उदाहरण 3.
यदि f : A → B तथा g : X → Y निम्न चित्रों से प्रदर्शित होने वाले दो फलन हों :

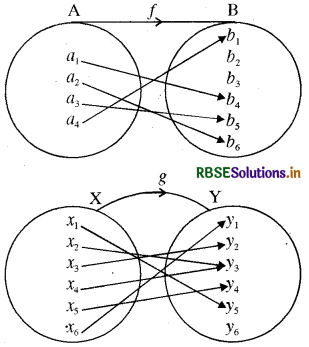
यहाँ पर स्पष्ट है कि f : A → B एकैकी फलन है क्योंकि भिन्न-भिन्न अवयवों के भिन्न-भिन्न प्रतिबिम्ब हैं। जबकि g : X → Y एकैकी फलन नहीं है क्योंकि X के दो अवयवों x₂, तथा x₁, का Y में एक ही प्रतिबिम्ब ), है।

उदाहरण 4.
फलन f : R→ R, f(x) = 2x - 3 एकैकी फलन है क्योंकि f(x) = f(y) = 2x - 3 = 2y - 3 = x = y

परन्तु f : R → R, f(x) = 2x² - 3 एकैकी फलन नहीं है क्योंकि f(x) = f(y) = 2x² - 3 = 2y² - 3
⇒ x² = y²
⇒ x = ± y

टिप्पणी
यदि f : A → B कोई फलन हो तो x = y ⇒ f(x) = f(y), A के सभी अवयवों x, y के लिए सत्य है परन्तु f(x) = f(y) ⇒ x = y केवल तभी सत्य होगा जब f एकैकी फलन हो ।

बहु-एकी फलन (Many-One Function):
समुच्चय A से समुच्चय B में परिभाषित कोई फलन बहु-एकी फलन कहलाता है यदि f के अन्तर्गत A के दो या दो से अधिक अवयवों का B में एक प्रतिबिम्ब है। अतःf : A → B बहु-एकी फलन है, यदि A में कम से कम दो अवयव a तथा b इस तरह से विद्यमान हैं कि a ≠ b परन्तु f (a) = f(b)
इस प्रकार हम देखते हैं कि यदि f : A → B एक एकैकी फलन नहीं है तो यह अवश्य ही बहु-एकी फलन होगा।

उदाहरण 1.
यदि f : A → B तथा g : X → Y निम्न चित्रों से प्रदर्शित होने वाले दो फलन हों

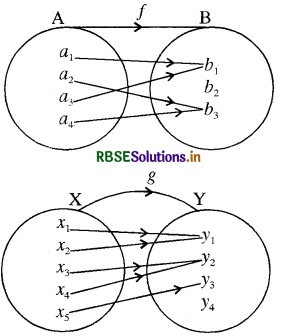
तो तिथा g दोनों ही बहु-एकी फलन हैं।

उदाहरण 2.
फलन f : Z → Z, f(x) = |x| एक बहु-एकी फलन है क्योंकि a ∈ z के लिए a ≠ -a लेकिन f(a) = f(- a) [∵ |a | = | - a]|

उदाहरण 3.
f : R → R, f(x) = sin x एक बह-एकी फलन है। क्योंकि sin x एक आवर्ती फलन है अर्थात् एक से अधिक कोण के लिए sin x का मान समान हो सकता है।

अन्तर्वैपी फलन (Into Function)
समुच्चय A से समुच्चय B में परिभाषित कोई फलन f एक अन्तर्खेपी फलन कहलाता है, यदि समुच्चय B में कम से कम एक ऐसा अवयव विद्यमान हो जो A के किसी भी अवयव का प्रतिबिम्ब नहीं हो अर्थात् जिसका कोई पूर्व प्रतिबिम्ब A में विद्यमान नहीं हो। अतः अन्तःपी है यदि f (A) ≠ (B) (सहप्रान्त)

अन्तःपी फलन दो प्रकार के होते हैं

• एकैकी अन्तर्वैपी फलन
• बहु-एको अन्तर्वैपी फलन।

उदाहरण 1.
f : N → N, f(x) = 2x अन्तर्वैपी फलन है क्योंकि f का परिसर = f(N) = {2, 4, 6,.........} ≠ N ॥

उदाहरण 2.
f: R → R, f(x) = cos.x एक अन्तर्वैपी फलन है क्योंकि f(R) = {x ∈ R | -1 ≤ x ≤ 1} ≠ R

उदाहरण 3.
f: R → R, f(x) = |x| अन्तर्वैपी फलन है। क्योंकि f(R) = R + ∪ {0} ≠ R

एकैकी अन्तःपी फलन (One-One Into Function)
एक फलन , समुच्चय A से समुच्चय B में एकैकी अन्तर्खेपी फलन कहलाता है, यदि एकैकी के साथ-साथ अन्तःपी भी हो, अर्थात् यदि A के भिन्न-भिन्न अवयवों के, B में भिन्न-भिन्न f-प्रतिबिम्ब हो तथा B में कम से कम एक अवयव ऐसा हो जो A के किसी भी अवयव का f-प्रतिबिम्ब नहीं हो। अतः f : A → B एकैकी अन्तःपी है, यदि और केवल यदि (iff) a ≠ b ⇒ f(a) ≠ f(b), a, b, ∈ A तथा f(A) ≠ B ॥

उदाहरण 1.
f : [0, π] → R, f(x) = cos x एकैकी अन्तर्खेपी है

उदाहरण 2.
फलन f : N → N f(x) = 2x + 3 एकैकी अन्तःपी फलन है।

बहु-एकी अन्तःपी फलन ( Many-One Into Function)
एक फलन f, समुच्चय A से समुच्चय B में बहु-एकी अन्तःपी फलन होता है, यदि f बहु-एकी के साथ-साथ अन्तःपी भी हो, अर्थात् यदि A के दो या दो से अधिक अवयवों के B में एक ही f-प्रतिबिम्ब हो तथा B में कम से कम एक अवयव ऐसा हो जो A के किसी भी अवयव का f-प्रतिबिम्ब नहीं हो।
अतःf : A → B बहु-एकी अन्तःपी है, यदि और केवल यदि (iff) ∃ a, b, ∈ A इस प्रकार है कि f(a) = f(b), परन्तु a ≠ b तथा f(A) ≠ B ॥

उदाहरण 1 :
यदि I पूर्णांकों का समुच्चय है और फलन f: I → I f(x) = x² - x द्वारा परिभाषित हो, तो फलन f बहु-एकी अन्त:पी फलन है। क्योंकि वहाँ A के कई दो अवयवों के B में एक ही f-प्रतिबिम्ब है तथा f का परिसर
f(I) = {0, 2, 6, 12 .........} ≠ I (सहप्रान्त)

उदाहरण 2 :
यदि A = {-3, -2, -1, 1, 2, 3} व B = {4, 7, 9, 12} और एक फलन f, A से B में f(x) = x² + 3 से परिभाषित है तो f के अन्तर्गत
f(-1) = (-1)² + 3 = 1 + 3 = 4,
f(1) = 1² + 3 = 4
f(-2) = (-2)² + 3 = 7,
f(2) = 2² + 3 = 7
f(-3) = (-3)² + 3 = 12,
f(3) = 3² + 3 = 12

यहाँ पर देखते हैं कि -1 ≠ 1 लेकिन f(-1) = f(1), इसी प्रकार -2 ≠ 2 लेकिन f(-2) = f(2) है। पुनः f(A) = {4, 7, 12} ≠ B
अतः फलन बिहु-एकी अन्तर्वैपी फलन है।

आच्छादक फलन (Onto Or Surjective (Function)
समुच्चय A से समुच्चय B में परिभाषित कोई फलन f आच्छादक फलन कहलाता है यदि B का प्रत्येक अवयव A के किसी न किसी अवयव का प्रतिबिम्ब हो अर्थात् B के प्रत्येक अवयव का A में कम से कम एक पूर्ण प्रतिबिम्ब विद्यमान हो।।
अत: f : A → B आच्छादक है , यदि और केवल यदि (iff) ∀ b ∈ B ∃ ⇒ a ∈ A इस प्रकार है कि f(a) = b
स्पष्टतः यदि f आच्छादक है तब f(A) = B अर्थात् /का परिसर =f का सहप्रान्त टिप्पणी-यदि किसी फलन f : A → B के लिए के सहप्रान्त तथा परिसर बराबर नहीं हो तो f आच्छादक नहीं होगा।

उदाहरण 1 :
फलन f : Q → Q, f(x) = 2x एक आच्छादक फलन है क्योंकि सहप्रान्त Q के प्रत्येक अवयव x के लिए उसका पूर्व-प्रतिबिम्ब प्रान्त Q में विद्यमान है।

उदाहरण 2 :
यदि A = {-1, -2, 1, 2}, B = {1, 4} तथा f: A → B, f(x) = x² हो तो f के अन्तर्गत A के अवयवों के प्रतिबिम्ब निम्न प्रकार से होंगे
f(-1) = (-1)² = 1, f(1) = 1² = 1
-2) = (-2)² = 4, f(2) = 2² = 4
अतः f(A) = {1, 4} = B, फलतःf एक आच्छादक फलन है।

उदाहरण 3 :
यदि f : A → B तथा g :x → Y निम्न चित्रों से प्रदर्शित हो क्या यहाँ पर तथा g आच्छादक फलन हैं?

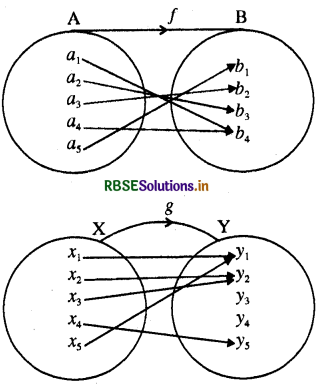
हल:
यहाँ पर f एक आच्छादक फलन है जबकि 8 आच्छादक फलन नहीं है क्योंकि Y के दो अवयवों y₃, y₄, का समुच्चय X में कोई पूर्व प्रतिबिम्ब नहीं है।

एकैकी आच्छादक फलन (One-One Onto Function Or Bijection)
कोई फलन f : A → B एकैकी आच्छादक कहलाता है यदि फलन एकैकी के साथ-साथ आच्छादक भी हो f: A → B एकैकी आच्छादक फलन होगा यदि

• f एकैकी हो अर्थात् f(a) = f(b) ⇒ a = b ∀ a, b ∈ A
• f आच्छादक है अर्थात् ∀ b ∈ B ⇒ ∃ a ∈ A ताकि f(a) = b

उदाहरण 1 :
यदि A = {1, 2, 3, 4} तथा f: A → A, f(x) = 5 - x एक एकैकी आच्छादक फलन है, चूंकि
f(1) = 5 - 1 = 4, f(2) = 5 - 2 = 3, f(3) = 5 - 3 = 2, f(4) = 5 - 4 = 1 अर्थात् f(1, 4), (2, 3), (3, 2), (4, 1)} स्पष्ट है कि प्रान्त A के भिन्न-भिन्न अवयवों के सहप्रान्त A में भिन्न-भिन्न प्रतिबिम्ब है साथ ही.सहप्रान्त A के प्रत्येक अवयव का कोई न कोई पूर्व प्रतिबिम्ब प्रान्त A में विद्यमान है इसलिए, एकैकी आच्छादक फलन है।

उदाहरण 2 :
फलन f : Q → Q. f(x) = 2x + 3 एकैकी आच्छादक है। क्योंकि किन्हीं x₁, x₂, ∈Q के लिए x₁, x₂ ⇒ 2x₁ + 3 ≠ 2x₂ + 3
⇒ f(x₁) ≠ f(x₂) ⇒ f एकैकी है। तथा प्रत्येक x ∈ Q (सह प्रान्त) के लिए \(\frac{x-3}{2}\) ∈ Q (प्रान्त)
x का पूर्व प्रतिबिम्ब है।

बहु-एकी आच्छादक फलन (Many-One Onto Function)
एक फलन , समुच्चय A से समुच्चय B में बहु-एकी आच्छादक फलन कहलाता है यदि बहु-एकी के साथ-साथ आच्छादक भी हो अर्थात् यदि A के दो या दो से अधिक अवयवों के B में एक ही प्रतिबिम्ब हो तथा B का प्रत्येक अवयव, A के किसी न किसी अवयव का f-प्रतिबिम्ब हो। अतःf : A → B बहु-एकी आच्छादक है, यदि और केवल यदि ∃ a,b ∈ A इस प्रकार है कि f(a) = f(b), परन्तु a ≠ b तथा ∀ b ∈ B ∃ a ∈ A इस प्रकार है कि f(a) = b अर्थात् f का परिसर = सहप्रान्त ⇒ f(A) = B

उदाहरण 1 :
फलन f : R → [-1, 1], f(x) = cos x बहु-एकी आच्छादक फलन है।

उदाहरण 2 :
यदि A = {0, 1} तथा f: N → A इस प्रकार से परिभाषित है कि f(2x) = 0, तथा f(2x - 1) = 1
तो फलन हु बहु-एकी आच्छादक होगा, क्योंकि (2) = f (4) परन्तु 2 ≠ 4 इसी प्रकार f(1) = f(3) परन्तु 1 ≠ 3 इत्यादि तथा F(N) = {0, 1} ⇒ f का परिसर = f का सहप्रान्त

टिप्पणी :
फलनों के उपरोक्त विवेचन से यह स्पष्ट होता है कि प्रत्येक फलन आवश्यक रूप से निम्न दो प्रकार का होता है

• एकैकी या बहुएकी तथा
• आच्छादक या अन्तःपी

अतः हम फलनों को निम्न चार भागों में विभक्त कर सकते हैं

• एकैकी आच्छादक
• एकैकी अन्तःपी
• बहु-एकी आच्छादक
• बहु-एकी अन्तःपी

तत्समक फलन (Identity Function):
किसी समुच्चय A का तत्समक फलन I, वह फलन है जिसके अन्तर्गत A का प्रत्येक अवयव स्वयं और केवल स्वयं से सम्बद्ध हो। अतः I(x) = x ∀ x ∈ A उपरोक्त शब्दों से स्पष्ट है कि किसी समुच्चय का तत्समक फलन एकैकी आच्छादक होता है।

उदाहरण 1 :
यदि A = {1, 2, 3, 4, 5} तथा f : A → A, f(x) = x हो तो f तत्समक फलन होगा, क्योंकि f(1) = 1, f(2) = 2, f(3) = 3, f(4) = 4, f(5) = 5

चर फलन (Constant Function):
ऐसा फलन जिसके अन्तर्गत उसके प्रान्त का प्रत्येक अवयव एक ही अवयव से सम्बद्ध हो, अचर फलन कहलाता है। स्पष्ट है, अचर फलन के परिसर में एक ही अवयव होता है, अतः
f: A → B अचर फलन है ⇔ f(x) = C ∀ x ∈ A (जहाँ c, B का एक अवयव है) नोट : यहाँ पर ध्यान रहे कि अचर फलन एकैकी बहु-एकी या आच्छादक कैसा भी हो सकता है।

उदाहरण : फलन f: R → R, f(x) = 6 एक अचर फलन है, क्योंकि f(R) = {6}

फलनों का संयोजन तथा व्युत्क्रमणीय फलन (Composition Of Functions And Invertible Function)
माना A, B.C तीन अरिक्त समुच्चय हैं तथा f : A → B तथा g: B → C दो फलन हैं। चूंकि f, A से B में एक फलन है A के प्रत्येक अवयव x के लिये एक अद्वितीय अवयव f (x), B में विद्यमान होगा। पुनः g, B से C में एक फलन है।
∴ B के इस अवयव f (x) के लिये C में एक अद्वितीय अवयव g {f (x)} विद्यमान होगा।

इस प्रकार से हम देखते हैं कि तथा पर एक साथ विचार करने पर A से C में परिभाषित एक नया फलन प्राप्त होता है। इस फलन को तथा का संयुक्त फलन कहते हैं तथा इसे (gof) से निरूपित करते हैं और इसे निम्न प्रकार से परिभाषित किया जाता है

परिभाषा (Definition):
यदि f: A → B तथा 8 : B →C दो फलन हों तो फलन (gof) : A → C जो निम्न प्रकार परिभाषित हो :
(gof) (x) = g[f(x)], ∀ x ∈ A
g तथा f का संयुक्त फलन कहलाता है।

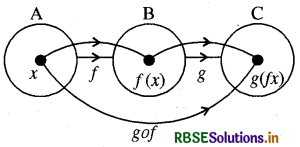
gof gof की परिभाषा से स्पष्ट है कि (gof) तभी परिभाषित होगा जब A के प्रत्येक अवयव x के लिए f(x), g के प्रान्त का अवयव हो ताकि इसका g प्रतिबिम्ब प्राप्त किया जा सके। अतः संयुक्त फलन (gof) के अस्तित्व के लिये f फलन का परिसर (range), g फलन के प्रान्त (domain) का उपसमुच्चय होना आवश्यक है। इसको समझने के लिये निम्न उदाहरण दिये जा रहे हैं

उदाहरण 1.
यदि f : R → R और g : R → R इस प्रकार से परिभाषित हैं कि f (x) = 2x - 1 और g(x) = x2 + 2 हों, तो gof : R → R पर निम्न प्रकार से परिभाषित होगा
(gof) (x) = g [f (x)]
= g [2x - 1] [∵ f (x) = 2x - 1] = (2x - 1) + 2 [∵ g(x) = x² + 2]
= 4x² - 4x + 1 + 2 = 4x² - 4x + 3, ∀ r ∈ R

उदाहरण 2.
यदि f : R → R, f (x) = e^x तथा g : R → R, g(x) = sin x तब (gof) : R →R तथा (fog) : R → R निम्न प्रकार परिभाषित है
(gof) (x) = g [f (x)] = g[e] [∵ f (x) = e]
= sin (e) ∵ g[x] = sin x
यहाँ पर (fog) : R → R भी निम्न प्रकार परिभाषित है :
(fog) (x) = f [g(x)] = f (sin x) = e^{sin x}
यहाँ पर हम देखते हैं कि
(gof) ≠ (fog)

उदाहरण 3.
यदि f : N → I और g : I → Q इस प्रकार से परिभाषित हैं कि f (x) = 3x तथा g(x) = \(\frac{x+2}{3}\) हो, तो gof : N → Q पर निम्न प्रकार से परिभाषित होगा :
(gof ) (x) = g[f (x)]
= g [3x] [∵ f (x) = 3x]
= \(\frac{3 x+2}{2}\), ∀ x ∈ N [∵ g(x) = x+2]

व्युत्क्रमणीय फलन (Invertible Function)
फलन f : X → Y व्युत्क्रमणीयः (Invertible) कहलाता है, यदि एक फलन g : Y →x का अस्तित्व इस प्रकार है कि gof = I, तथा fog = I, है। फलन g को फलन f का प्रतिलोम (Inverse) कहते हैं और इसे प्रतीक f^-1 द्वारा प्रकट करते हैं। अतः यदि व्युत्क्रमणीय है, तो अनिवार्यतः एकैकी तथा आच्छादक होता है और विलोमतः यदि f एकैकी तथा आच्छादक है, तो अनिवार्यतः व्युत्क्रमणीय होता है। यह तथ्य f को एकैकी तथा आच्छादक सिद्ध करके, व्युत्क्रमणीय प्रमाणित करने में महत्त्वपूर्ण रूप से सहायक होता है, विशेष रूप से जब का प्रतिलोम वास्तव में ज्ञात नहीं करना हो।

उदाहरण 1.
मान लीजिये कि f : N → Y, f(x) = 4x + 3, द्वारा परिभाषित एक फलन है, जहाँ Y = {y ∈ N : y = 4x + 3 किसी x ∈ N के लिये}। सिद्ध कीजिये कि f व्युत्क्रमणीय है। प्रतिलोम फलन भी ज्ञात कीजिये।
हल:
f व्युत्क्रमणीय है इसके लिए हम फलन f को एकैकी आच्छादक सिद्ध करेंगे।
एकैकी : माना x₂, x₂ ∈ N इस प्रकार हैं कि f (x₁) = f (x₂)
f (x₁) = f (x₂)
⇒ 4x₁ + 3 = 4x₂ + 3
⇒ 4x₁ = 4x₂
⇒ x₁ = x₂
अतः f (x₁) = f (x₂) = x₁ = x₂, ∀ x₁, x, ∈N एकैकी है।

आच्छादक:
माना y = f(x) = 4x + 3
⇒ y - 3 = 4x
⇒ x = \(\frac{y-3}{4}\) ∈ N, ∀ y ∈ Y

अब y का पूर्व प्रतिबिम्ब प्रान्त N में विद्यमान है। अतः दिया गया फलन आच्छादक है। चूंकि फलन एकैकी आच्छादक है, अतः इसका प्रतिलोम विद्यमान है।
तब f (x) = y ⇔ f^-1(y) = x
f (x) = y
⇒ 4x + 3 = y
⇒ x = \(\frac{y-3}{4}\)
⇒ f^-1(y) = \(\frac{y-3}{4}\)
⇒ f^-1(y) = x = \(\frac{y-3}{4}\)

उदाहरण 2.
यदि f : R → R, f(x) = x² - 3, हो, तो f^-1(13) तथा f^-1(-8) ज्ञात कीजिये।
हल:
माना f^-1(13) = x तब f(x) = 13
f(x) = x² - 3
∴ 13 = x² - 3
⇒ x² = 16 = x = + 4
f^-1(13) = {- 4, 4}
पुनः माना f^-1(-8) = x ∴ f(x) = - 8
⇒ x² - 3 = - 8 ⇒ x² = - 8 + 3 = - 5
x = ± √-5
परन्तु √-5 कोई वास्तविक संख्या नहीं है।
∴ x = ± √-5 ∉ R
∴ f^-1(-8) = Φ

द्वि-आधारी संक्रियाएँ अथवा द्विचर संक्रिया (Binary Operation)
किसी समुच्चय S पर परिभाषित कोई द्वि-आधारी संक्रियाएँ * एक ऐसा नियम है जिसके आधार पर S के किन्हीं दो अवयवों के लिये S का ही एक अद्वितीय अवयव प्राप्त किया जा सके। अर्थात् a ∈ S, b ∈ S, ⇒ a*b ∈ S. अन्य शब्दों में S × S से 5 में परिभाषित किसी फलन को S में एक द्वि-आधारी संक्रिया कहते हैं । सामान्यतः द्वि-आधारी संक्रिया को *, 0 इत्यादि से व्यक्त करते हैं।

उदाहरण 1.
परिमेय संख्याओं के समुच्चय Q में *, जो निम्न प्रकार परिभाषित हो :
a* b = \(\frac{a b}{2}\), ∀ a b ∈ Q

Q में एक द्विचर संक्रिया है क्योंकि
a ∈ Q, b ∈ Q ⇒ \(\frac{a b}{2}\) ∈ Q

उदाहरण 2.
प्राकृत संख्याओं के समुच्चय N में योग तथा गुणन एक द्विचर संक्रिया है, क्योंकि
a ∈ N, b ∈ N ⇒ (a + b) ∈ N, ∀ a, b ∈ N
a ∈ N, b ∈ N ⇒ (a . b) ∈ N, ∀ a, b ∈ N
परन्तु N में व्यवकलन तथा विभाजन द्विचर संक्रिया नहीं है।

उदाहरण 3.
पूर्णांकों का योग (+), व्यवकल (-) और गुणन (x) पूर्णांकों के समुच्चय z में द्विचर संक्रियाएँ हैं। जो Z के किन्हीं दो अवयवों a, b को क्रमशः Z के अद्वितीय अवयव (a + b), (a-b) तथा ab से सम्बद्ध करती हैं।

उदाहरण 4.
किसी समुच्चय S के घात समुच्चय (Power Set) P(S) में समुच्चयों का संघ ∪ तथा सर्वनिष्ठ (∩) द्विचर संक्रियाएँ हैं क्योंकि
A ∈ P(S), B ∈ P(S), = A ∪ B ∈ P(S), तथा A ∩ B ∈ P(S)

उदाहरण 5.
वास्तविक संख्याओं के समुच्चय R में *, जहाँ * निम्न प्रकार परिभाषित हो :
a * b = a + b - ab, ∀ a, b ∈ R
R में एक द्विचर संक्रिया है। क्योंकि
a ∈ R, b ∈ R → (a + b - ab) ∈ R

द्वि-आधारी संक्रियाओं के प्रकार ( Types of Binary Operations):
(i) क्रम विनिमेय संक्रिया (Commutative Operation)
किसी समुच्चय S में एक द्वि-आधारी संक्रिया * क्रम विनिमेय (Commutative) कहलाती है, यदि प्रत्येक a, b ∈ S के लिये a * b = b * a हो। यह आवश्यक नहीं है कि समुच्चय S में द्वि-आधारी संक्रिया * के लिये a * b = b * a सदैव सत्य हो। उदाहरण 1. किसी वास्तविक संख्याओं के समुच्चय R में योग तथा गुणन संक्रियाएँ क्रम विनिमेय संक्रियाएँ हैं परन्तु व्यवकलन नहीं होता है। जैसे
3 + 5 = 5 + 3
3 × 5 = 5 × 3
परन्तु 3 - 5 ≠ 5 - 3

उदाहरण 2.
वास्तविक संख्याओं के समुच्चय R में a × b = ab
द्वारा परिभाषित संक्रिया क्रम विनिमेय नहीं हैं क्योंकि a * b = ai
परन्तु b * a = b^a
⇒ a * b ≠ b * a

उदाहरण 3.
किसी समुच्चय S के घात समुच्चय P(S) में समुच्चयों का संघ (∪) तथा सर्वनिष्ठ (∩) क्रम विनिमेय संक्रियायें हैं। परन्तु समुच्चयों का अन्तर (Difference of Sets) क्रम विनिमेय नहीं है।

(ii) साहचर्य संक्रिया (Associative Operation)
किसी समुच्यय S में परिभाषित संक्रिया (*) साहचर्य संक्रिया कहलाती है। यदि
a* (b * c) = (a * b) * c ∀ a, b ∈ S
यह आवश्यक नहीं कि a* (b * c) = (a * b) * c सदैव सत्य हो।

उदाहरण 1.
किसी समुच्चय S के घात समुच्चय P(S) में समुच्चयों का संघ तथा सर्वनिष्ठ साहचर्य संक्रियाएँ हैं क्योंकि यदि A, B, C, ∈ P(S)
तो (A ∪ B) ∪ C = A ∪ (B ∪ C)
तथा (A ∩ B) ∩ C = A ∩ (B ∩ C)

उदाहरण 2.
पूर्णांकों के समुच्चय z में योग तथा गुणन की संक्रियाएँ साहचर्य हैं परन्तु व्यवकलन की नहीं क्योंकि
a + (b + c) = (a + b) + c, ∀ a, b, C ∈ Z
a . (b . c) = (a . b) . c, ∀ a, b, C ∈ Z
परन्तु a - (b - c) ≠ (a - b) - c

उदाहरण 3.
तीन सदिशों का योग एक साहचर्य संक्रिया है, क्योंकि हम जानते हैं कि किन्हीं तीन सदिशों ā, b̅ , C̅ के लिये
a̅ + (b̅ + c̅ ) = (a̅ + b̅ ) + c̅

उदाहरण 4.
a * b → a + 2b द्वारा प्रदत्त * : R × R → R साहचर्य नहीं है। संक्रिया * साहचर्य नहीं है, क्योंकि
(8 * 5) * 3 = (8 + 10) * 3
= (8 + 10) + 6 = 24
जबकि 8 * (5 * 3) = 8 * (5 + 6)
= 8 * 11 = 8 + 22 = 30

संक्रिया का तत्समक अवयव (Identity Element For An Operation)
माना S कोई अरिक्त समुच्चय है जिसमें * एक द्विचर संक्रिया है।
यदि S में एक ऐसा अवयव विद्यमान है कि a * e = e * a = a, ∀ a ∈ s
तो अवयव e को s में * संक्रिया के लिये तत्समक अवयव कहते हैं।

उदाहरण 1.
प्राकृत संख्याओं के समुच्चय N में योग संक्रिया के लिये तत्समक अवयव विद्यमान नहीं है। परन्तु गुणन संक्रिया के लिये 1 तत्समक अवयव है।

उदाहरण 2.
परिमेय संख्याओं के समुच्चय Q में एक द्विचर संक्रिया * निम्न प्रकार परिभाषित की गई है : .
a * b = \(\frac{a b}{2}\), ∀ a, b ∈ Q
अब यदि e तत्समक अवयव हो, तो a ∈ Q के लिये
a * e = a
⇒ \(\frac{a e}{2}\) = a
⇒ [e = 2]
अतः 2 ∈ Q तत्समक अवयव है।

उदाहरणं 3.
वास्तविक संख्याओं के समुच्चय R में 0 तथा 1 क्रमशः योग एवं गुणन संक्रियाओं के लिये तत्समक अवयव हैं a ∈ R के लिये
0+ a = a + 0 = a तथा 1.a = a.1 = a

प्रमेय-यदि किसी समुच्चय में एक द्विचर संक्रिया का तत्समक अवयव विद्यमान है तो वह अद्वितीय होता है।
हल:
यदि सम्भव हो तो माना कि समुच्चय S में संक्रिया * के लिये e तथा e' दो तत्समक अवयव विद्यमान हैं।
∴ e' * e = e' (∵ e, S में तत्समक है तथा e ∈ S)
पुनः e * e' = e (∵ e, S में तत्समक है तथा e ∈ S)
अतः उपर्युक्त से स्पष्ट है कि ।
e = e'
अतः किसी संक्रिया का तत्समक अवयव, यदि विद्यमान हो, तो अद्वितीय होता है।

प्रतिलोम अवयव (Inverse of An Element)
माना समुच्चय S में * एक द्वि-आधारी संक्रिया है तथा इसका तत्समक अवयव e है। यदि S के किसी अवयव a के लिए 5 में एक ऐसा अवयव b₁ विद्यमान हो कि b₁ * a = e तब b₁ को अवयव a का वाम प्रतिलोम (Left Inverse) कहते हैं। इसी प्रकार यदि a ∈ S के लिए S में एक ऐसा अवयव b₂ विद्यमान हो कि a * b₂ = e तब b₂ को a का दक्षिण प्रतिलोम (Right Inverse) कहते हैं।

यदि समुच्चय S का कोई अवयव b, S के किसी अवयव व का वाम एवं दक्षिण प्रतिलोम दोनों हों तो b को अवयव व का प्रतिलोम अवयव कहते हैं। इसे a^-1 द्वारा निरूपित किया जाता है।
a^-1 = b ⇔ b * a = a * b = e

यदि किसी अवयव a का प्रतिलोम अवयव S में विद्यमान हो तो a, व्युत्क्रमणीय अवयव (Invertible Element) कहलाता है। अतः
a ∈ S व्युत्क्रमणीय है = a^-1 ∈ s
माना समुच्चय S में * संक्रिया के लिये e तत्समक अवयव है
तब e * e = e * e = e अर्थात् e व्युत्क्रमणीय है तथा तत्समक अवयव का प्रतिलोम भी तत्समक ही होता है।

उदाहरण 1.
वास्तविक संख्याओं के समुच्चय R में प्रत्येक a ∈ R के लिये (-a) ∈ R योग संक्रिया के लिये प्रतिलोम अवयव है क्योंकि a + (-a) = (-a) + a = 0 (तत्समक) अतः R का प्रत्येक अवयव योग संक्रिया के लिये व्युत्क्रमणीय

उदाहरण 2.
परिमेय संख्याओं के समुच्चय Q में प्रत्येक अशून्य संख्या गुणन संक्रिया के लिये व्युत्क्रमणीय है तथा
a ∈ Q (a ≠ 0) ⇒ a^-1 = \(\frac{1}{a}\) [∵ a.\(\frac{1}{a}=\frac{1}{a}\) .a = 1]

उदाहरण 3.
प्राकृत संख्याओं के समुच्चय N में योग संक्रिया के लिये कोई भी अवयव व्युत्क्रमणीय नहीं है।

→ सम्बन्ध की परिभाषा-समुच्चय A से समुच्चय B में परिभाषित सम्बन्ध R, A × B का उपसमुच्चय होता है अर्थात् R ⊆ A × B.

→ सम्बन्ध का प्रान्त और परिसर-यदि R समुच्चय A से समुच्चय B में परिभाषित को सम्बन्ध हो, तो R के क्रमित युग्मों के प्रथम अवयवों के समुच्चय को सम्बन्ध R का प्रान्त तथा द्वितीय अवयवों के समुच्चय को सम्बन्ध R का परिसर कहते हैं।

→ किसी समुच्चय A में n अवयव तथा B में n अवयव हों तो A से B सम्बन्धों की कुल संख्या 2^mn होगी।

→ यदि A पर परिभाषित सम्बन्ध R है तो R का प्रतिलोम सम्बन्ध R^-1 = {(b, a) | (a, b) ∈ R}

→ किसी समुच्चय A का तत्समक सम्बन्ध वह सम्बन्ध है जिसके अन्तर्गत A का प्रत्येक अवयव स्वयं से और केवल स्वयं से सम्बन्धित होता है I_A = {(a, a) | ∀ a ∈ A}

→ समुच्चय A पर परिभाषित सम्बन्ध र स्वतुल्य सम्बन्ध है, यदि
(a, a) ∈ R, ∀ a ∈ A

→ समुच्चय A सम्बन्ध र सममित होगा, यदि
(a, b) ∈ R ⇒ (b, a) ∈ R ∀ a, b ∈ A

→ समुच्चय A पर सम्बन्ध र संक्रामक होगा, यदि
(a, b) ∈ R, (b, c) ∈ R ⇒ (a, c) ∈ R, ∀ a, b, C ∈ A

→ A में R = Φ ⊂ A × A द्वारा प्रदत्त सम्बन्ध R, रिक्त सम्बन्ध है।

→ A में R = A × A द्वारा प्रदत्त सम्बन्ध R, सार्वत्रिक सम्बन्ध है।

→ यदि R, स्वतुल्य, सममित तथा संक्रामक सम्बन्ध है तो R तुल्यता सम्बन्ध है।

→ A में, किसी तुल्यता सम्बन्ध R के लिए a ∈ A के संगत तुल्यता वर्ग [a], A का वह उपसमुच्चय है जिसके सभी अवयव a से सम्बन्धित हैं।

→ एक फलन f : A → B एकैकी फलन है, यदि
f(x₁) = f(x₂) ⇒ x₁ = x₂, x₁, x₂, ∈ A
या x₁ ≠ x₂ ⇒ f(x₁) ≠ f (x₂), ∀ x₁, x₂ ∈ A

→ एक फलन f : A → B, आच्छादक (अथवा आच्छादी) फलन है यदि प्रत्येक b ∈ B के लिए, a ∈ A इस प्रकार विद्यमान हो कि f(a) = b

→ यदि फलन एकैकी नहीं है तो वह बहुएकी होगा।

→ यदि फलन आच्छादक नहीं है तो वह अन्तःपी होगा।

→ फलन एकैकी आच्छादक, एकैकी अन्तःपी, बहुएकी आच्छादक या बहुएकी-अन्तःपी होते हैं।

→ फलन f : A → B तथा 8 : B → C का संयोजन फलन gof : A → C है, जो gof (x) = g[f(x)], x ∈ A द्वारा प्राप्त होता है।

→ एक फलन f : A → B व्युत्क्रमणीय है, यदि ∃ g : B → A, इस प्रकार है कि gof = I तथा fog = I

→ एक फलन f : A → B एकैकी आच्छादक है, यदि और केवल यदि व्युत्क्रमणीय है।

→ यदि A तथा B कोई दो अरिक्त समुच्चय परिमित समुच्चय हो, जिसमें क्रमशः m तथा n अवयव हों तो A से B में फलनों की संख्या m" है।

→ A में एक द्विआधारी संक्रिया *, A × A से A तक फलन है।

→ एक अवयव e ∈ A, द्विआधारी संक्रिया * : A × A → A, का तत्समक अवयव है यदि a * e = a = e * a, ∀ a ∈ A

→ कोई अवयव a ∈ A, द्विआधारी संक्रिया * : A × A → A के लिए व्युत्क्रमणीय होता है, यदि एक ऐसे b ∈ A का अस्तित्व है कि
a * b = e = b * a, जहाँ e तत्समक अवयव है। अवयव b, a का प्रतिलोम अवयव है, जिसे ' से निरूपित करते हैं।

→ द्विआधारी संक्रिया * क्रमविनिमेय है यदि a × b = b * a, ∀ a, b ∈ A

→ A में एक द्विआधारी संक्रिया * साहचर्य है यदि a * (b * c) = (a * b) * c, ∀ a, b, C ∈ A

→ यदि किसी परिमित समुच्चय n में n अवयव हों तो A पर द्विआधारी संक्रियाओं की संख्या होती है।