RBSE Class 12 Maths Notes Chapter 1 Relations and Functions

These comprehensive RBSE Class 12 Maths Notes Chapter 1 Relations and Functions will give a brief overview of all the concepts.

RBSE Class 12 Maths Chapter 1 Notes Relations and Functions

Introduction:
The introduced the notation of a relation, its domain, co-domain and range. In our daily life, we colme across many patterns that characterise relations such as brother and sister, father and son, teacher and students. In mathematics also, we come across many relations such as:

• Number 90 is greater than number 69.
• Number 45 is smaller than number 60.
• Line \(\stackrel{\leftrightarrow}{A B}\) is perpendicular to line \(\stackrel{\leftrightarrow}{C D}\).
• Line l is parallel to line m.

In all these, we notice that a relation involves pair of objects in certain order. Let us recall that a relation from a set A to a set B is a subset of A × B. If R is a relation from set A to set B and (a, b) ∈ R, then we say that a is related to b under relation R and we write it as aRb. If (a, b) ∈ R, then we say that a is not related to b under R and we write it as aRb. In this section, we will study different types of relations.

Relation in Any Set:
Definition 1.
Any relation R in set A is subset of A * A. Now, we will discuss relation between two sets.
Let A = {1, 8, 27} and B = {1, 2, 3} then
A × B = {(1, 1), (1, 2), (1, 3), (8, 1), (8, 2), (8, 3), (27, 1), (27, 2), (27, 3)}

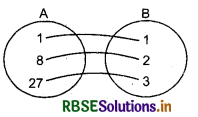
Now, relation from A to,B is such that (x, y) ∈ R, where x = y³ {x ∈ A, y ∈ B}, i.e., in ordered pair (x, y)
(first element) = (second element)³
then R = {(1, 1), (8, 2), (27, 3)}
It is clear that R ⊂ A × B.

Definition 2.
A relation from set A to set B is a subset of A × B, i.e., R ⊆ A × B.

 

Domain and Range of a Relation:
Domain :
Let R be a relation from set A to set B, then the set of all first components or coordinates of the ordered pairs belonging to R is called the domain of R.
Thus, domain of R = {a : a ∈ A {a, b) ∈ R}
Clearly, domain of R ⊂ A

Range:
Let R be a relation from set A to set B, then the set of all second components or coordinates of the ordered pairs belonging to R is called the range of R.
Thus, range of R = {b :b ∈ B (a, b) ∈ R}
Clearly, range of R ⊂ B

Example:
If R = {(1, a), (2, b), (3, c)} is any relation from set A to set B, then
Domain (R) = (1, 2, 3} or domain (R) = A
Range (R) = {a, b, c} or range (R) = B

Inverse Relation
If R be the relation defined from set A to set B, then the inverse of R denoted by R~ 1 is a relation obtained by interchanging the elements of the set of ordered pairs of R.
i.e., R^-1 = {(y, x): y ∈ B, x ∈ A and (x, y) ∈ R]
Clearly, (x, y) ∈ R ⇔ (y, x) ∈ R^-1
Also, domain (R) = range (R^-1)
and range (R) = domain (R^-1)

Example 1.
In A = {a, b, c} and B = {1,2, 3} if R = {(a, 1), (a, 3), (b, 3), (c, 3)} then
R^-1 = {(1, a), (3, a), (3, b), (3, c)}

Example 2.
Relation R is defined on set N × N, such that
R = {(x, y) ∈ N × N: y = x + 1}
then R^-1 = {(y, x) ∈ N × N :x = y -1}

Example 3.

• If xRy means ‘x is square of y then yR^-1x means 'y is square root of x'.
• If xRy means ‘x>y’ then yR^-1x means 'y < x .

Theorem :
Prove that inverse of any inverse relation is initial relation, i.e., (R^-1)^-1 = R.
Proof:
Let R is any relation in A x B.
i.e., R = {(x, y): x ∈ A, y ∈ B}
then R^-1 = {(y, x): y ∈ B, x ∈ A]
Again, inverse of R^-1 is
(R^-1)^-1 = {{x, y): x ∈ A, y ∈ B}
= R

Types Of Relations:
Void or Null or Empty Relation:
A relation R on a set A is said to be void or null or empty relation, if no element of A is related to any other element of A.
Example : Consider the relation R on the set A = {2, 4, 6, 8} defined by
R = {(a, b), a - b = 15}
We observe that a - b ≠ 15 for any two elements of A.
∴ (a, b) ∈ R for any a, b ∈ A.
⇒ R does not contain any element of A × A.
⇒ R is empty set.
⇒ R is the void relation on A.
Note : Null relation is the smallest relation.

Universal Relation:
A relation R defined on a set A is said to be universal relation if each element of A is related to every element of A.
i. e:, R = A × A ⊆ A × A

Example: Consider the relation R on the set A = {1, 2, 3, 4, 5, 6} defined by
R = {(a, b) ∈ R: |a - b| > 0}
We observe that
|a - b| ≥ 0 for all a, b ∈ A ⇒ (a, b) ∈ R for all (a, b) ∈ A × A
⇒ Each element of set A is related to every element of set A.
⇒ R = A × A
⇒ R is universal relation on set A.
Note : It is to be noted that the universal relation on set A is the largest relation on set A. Both the empty (or void) relation and the universal relation are sometimes called trivial relations.

Example : If A = {1, 2, 3}, then R = A × A = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)} is a universal relation.
Again, if relation R is such that R = {(a, b) ∈ R: |a - b| ≥ 0 and a, b ∈ A}, then we see that |a - b| ≥ 0, where a,b ∈ A.
So, from (a, b) ∈ R, (a, b) ∈ A × A
i.e., every element of A is related to itself or other elements,
⇒ R = A × A
i.e., R has a universal relation with set A.

Identity Relation:
Let A be a set, then the relation I_A = {{a, a): a ∈ A} on A is called the identity relation on A.
OR
The relation I_A defined on A is called identity relation if every element of A is related to itself only.
Example : If A = {a, b, c}, then
I_A = {(a, a), (b, b), (c, c)}

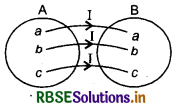
is identity relation in A but relation R = {(a, a), (c, c)} is not identity relation because ordered pair (b, b) does not exist in this relation.
Again, if two relations in A = {p, q, r, s} are as follows :
R₁ = {(p, p)’ (q> (r, r)> (s> s)}
R₂ = {(Pr p), {q, q), (r, r), (s, s), (p, q), (r, s), (p, r)} then relation R₁ is identity relation but R₂ is not identity relation because {p, q), (r, s), (p, r) are included in R₂.

Binary Relation:
Following are the different types of binary relations.
(a) Reflexive Relation: A relation R on a set A is said to be reflexive if every element of A is related to itself. Thus, R is reflexive ⇔ {a, a) ∈ R for all a ∈ A. A relation R on a set A is not reflexive if there exists an element as A such that (a, a) ∈ R.

Example 1.
Let L be the set of all lines in a plane. Then relation R on L defined by (l₁, l₂) ⇔ l₁ is parallel to l₂ is reflexive, since every line is parallel to itself.

Example 2.
Relation 'equal to' is reflexive relation because for each element of any set A, x = x, i.e., xRx x = y, i.e., xRy (in notation form), there is reflexive relation.

Example 3.
The universal relation on a non-void set A is, reflexive.

Example 4.
If A, B, C, ... are subsets, then ARB. If A ⊆ B is reflexive relation since A ⊆ A is true.

Example 5.
If A = {1, 2, 3} and R = {(1, 1), (2, 2), (3, 3)}, then there is reflexive relation.

(b) Symmetric Relation:
A relation R defined on a non-empty set A is said to be symmetric relation if xRy = yRx, i.e., (x, y) ∈ R ⇒ (y,x) ∈ R ∀ x, y ∈ A.
Example 1. The identity and the universal relations on a non-void set are symmetric relations.
Example 2. Relation 'equal to' is symmetric, since x = y ⇒ y = x.
Example 3. In a set of lines in a plane relation 'is perpendicular' is symmetric relation, since x ⊥ y ⇒ y ⊥ x.
Example 4. In a set of positive integers xRy if x + y = 10, (x, y ∈N) is a symmetric relation, since x + y - 10 ⇒ y + x = 10
i.e., (x, y) ∈ R ⇒ (y, x) ∈ R
Note : Any relation R is a symmetric relation if and only if R = R^-1.

(c) Anti-symmetric Relation:
A relation R defined on a non-empty set A is said to be anti-symmetric, if x, y ∈ A; xRy and yRx ⇒ x = y.

Example 1. The relation '⊆' in set of subsets is anti-symmetric relation, since
A ⊆ B, B ⊆ A ⇒ A = B

Example 2. The relation '>' in set of integers is anti-symmetric, since
x ≥ y, y ≥ x ⇒ x = y.

Example 3. The identity relation on a set A is an anti-symmetric relation.

(d) Transitive Relation :
A relation R defined on a non-empty set A is said to be transitive, if x, y ∈ A, then xRy and yRz ⇒ xRz.

Example 1.
xRy if x = y, then R is transitive relation since, if x = y and y = z then x = z.

Example 2.
xRy if x > y, then R is transitive relation since, if x > y and y > z, then x > z.

Example 3.
ARB if A ⊆ B, then R is transitive relation since, if A ⊆ B and B ⊆ C then A ⊆ C.

Example 4.
xRy if x ⊥y, then R is not transitive since, if x,y,z are three lines in a plane and x ⊥ y and y ⊥ z, then x will not be perpendicular to z whereas x ∥ z.

Example 5.
A = {1, 2, 3} and R = {(1, 2), (1, 3), (2, 3)}, then, R is transitive, since (1, 2) ∈ R and (2,3) ∈ R ⇒ (1, 3) ∈ R.

Example 6.
Let L be the set of all straight lines in a plane, then the relation "is parallel to L" is a transitive relation because for any
l₁,l₂,l₃ ∈ L, l₁ ∥ l₂ and l₂ ∥ l₃ l₁ ∥ l₃

Example 7.
The relation 'is congruent to' on the set T of all triangles in a plane is transitive relation.

Theorem: If R is a relation is any set A, then prove that:
(i) R reflexive ⇒ R^-1 reflexive
(ii) R symmetric ⇒ R^-1 symmetric
(iii) R transitive ⇒ R^-1 transitive
Proof:
(i) ∀ a ∈ A, (a, a) ∈ R, R is reflexive.
Now (a, a) ∈ R ⇒ (a, a) ∈ R^-1
∴ ∀ a ∈ A, (a, a) ∈ R^-1
Thus, R^-1 is reflexive.

(ii) (a, b) ∈ R^-1 ⇒ (b, a) ∈ R
But R is symmetric.
∴ (b, a) ∈ R ⇒ (a, b) ∈R
⇒ (b, a) R^-1
(a, b) ∈ R^-1 ⇒ (b, a) ∈ R^-1
Thus, R^-1 is symmetric.

(iii) Let (a, b) and (b, c) ∈ R^-1, then (b, a) ∈ R and (c, b) ∈ R, but R is transitive. Therefore,
(c, b) ∈ R and (b, a) ∈ R ⇒ (c, a) ∈ R
⇒ (a, c) ∈ R^-1
∴ (a, b) ∈ R^-1 and (b, c) ∈ R^-1 ⇒ (a, c) ∈ R^-1
Thus, R^-1 is transitive.

(e) Equivalence Relation: A relation R on set A is said to be an equivalence relation on A iff it is
(i) Reflexive, i.e., (a, a) ∈ R for all a ∈ A
(ii) Symmetric, i.e., (a,b) ∈ R ⇒ (b, a) ∈R for all a, b ∈ A
(iii) Transitive, i.e,, (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R for all a,b,c ∈ A Equivalence relation is generally denoted by

Example 1.
The relation 'parallel' is an equivalence reation in the set of lines in a plane. It can be explained like this also:
If L be the set of lines in a plane and R be the relation in L defined as xRy => x ∥ y; x, y e L, then R is an equivalence relation.
Answer:
(i) x ∥ x, i.e., xRx, V x ∈ L.
(ii) x ∥ y ⇒ y ∥ x, i.e., xRy = yRx, ∀ x, y ∈ L.
(iii) x ∥ y, y ∥ z => x ∥ z
i. e., xRy and yRz ⇒ xRz, ∀ x, y, z ∈ L.

Example 2.
If R and S are equivalence relation in set X, then prove that RuS,RnS are also equivalence relation in set X.
Answer:
According to the question,
R ⊆ X × X, S ⊆ X × X
∴ R ∪ S ⊆ X × X
and R ∩ S ⊆ X × X
According to definition of relation, R ∪ S and R ∩ S, both are relation in set X.
(i) For any a ∈ X, aRa is true,
i. e., (a, a) ∈ R
Similarly (a, a) ∈ S
∴ (a, a) ∈ R ∩ S
And (a, a) ∈ R ∪ S [∵ R and S are reflexive]
i.e., S ∪ S and R ∩ S are reflexive.

(ii) Let a, be X, (a, b) ∈ RnS,
Now (A, b) ∈ R ∩ S
⇒ (a, b) ∈ R and (a, b) ∈ S
⇒ (b, a) ∈ R and (b, A) ∈ S [∵ R and S are symmetric]
⇒ (b, a) ∈ R n S
i.e., R ∩ S is symmetric.

Again (a, b) ∈ R ∪ S
⇒ (a, b) ∈ R or (a, b) ∈ S
⇒ (b, a) ∈ R or (b, a) ∈ S [∵ R and S are symmetric]
⇒ (b, a) ∈ R ∪ S
i.e., R ∪ S is also symmetric.

(iii) Let a, b, c ∈ X,
(a,b) ∈ R ∩ S, (b, c) ∈ R ∩ S
⇒ [(fl, b) ∈ R and (a, b) ∈ S] and [(b, c) ∈ R and (b, c) ∈ S] [(a, b) ∈ R, (b, c) ∈ R] and [(fl, b) ∈ S, (b, c) ∈ S]
⇒ (a, c) ∈ R and (a, c) ∈ S [∵ R and S both are transitive]
⇒ (a, c) ∈ R ∩ S
Thus, R n S is transitive.
Again, let (a, b) ∈ R ∪ S, (b, c) ∈ R ∪ S ⇒ [(a, b) ∈ R and (a, b) ∈ S]
and [(b, c) ∈ R and (b, c) ∈ S] ⇒ [(a, b) ∈ R, (b, C) ∈ R] and [(a, b) ∈ S, (b, c) ∈ S]
⇒ (a, c) ∈ R and (a, c) ∈ S [∵ R and S both are transitive]
⇒ (a, c) ∈ R ∪ S
Thus, R ∪ S is transitive.
RKJ S,RnS also equivalence relation in X.
∴ Hence Proved.

Composition of Two Relations:
Let A, B and C are any three non-zero sets. R is a relation between A and B and S is a relation between B and C. Then composition of two relations So R, is a relation in A to C which is defined as :
So R = {(a, c): b ∈ B is an element such that aRb and bSc; where a ∈ A and c ∈ C]

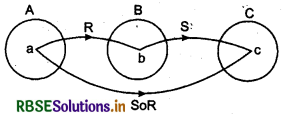
From above it is clear that
aRb, bSc ⇒ aSbRc

Theorem;
In three sets A, B and C, R is a relation in A to B and S is a relation in R to C, i.e., R ⊆ A × B and
S ⊆ B × C, then prove that
(SoR)^-1 = R^-1oS^-1
Proof:
Let (a, c) ∈ SoR, then
(a, c) ∈ SoR ⇔ (c> a) ∈ (SoR)^-1
Now (c, a) ∈ (SoR)^-1
⇔ (a, c) ∈ SoR
⇔ ∃b ∈ B (a, b) e R and (b, c) ∈ S
⇔ ∃ b ∈ B (b, a) e R^-1 and (c, b) ∈ S^-1
⇔ ∃ b ∈ B (c, b) ∈ s^-1 and (b, A) ∈ R^-1
⇔ ∃b ∈ B (c, a) ∈ R^-1oS^-1
Thus (c, a) ∈ (SoR)^-1 ⇔ (c, fl) ∈ R^-1oS^-1
i. e„ (SoR)^-1 = R^-1oS^-1.

Example:
If R = {(4, 5), (1, 4), (4, 6), (7, 6), (3, 7)}, then find (i) RoR, (ii) R^-1oR, (iii) R^-1oR^-1 and (iv) (R^-1xoR)^-1
(Domain) R = {4, 1, 7, 3}
(Range) R = {5, 4, 6, 7}
Answer:
(i) (1,4) ∈ R, (4,5) ∈ R ⇒ (1,5) ∈ ROR
(1,4) ∈ R, (4, 6) ∈ R ⇒ (1,6) ∈ RoR
(3,7) ∈ R, (7,6) ∈ R ⇒ (3,6) ∈ RoR
Thus, RoR = {(1,5), (1,6), (3,6)}

(ii) R -1 = {(5,4), (4,1), (6,4), (6, 7), (7,3)}
Now, (4,5) ∈ R, (5,4) ∈ R^-1 ⇒ (4,4) ∈ R^-1oR
(1.4) ∈R, (4, 1) ∈ R^-1 ⇒ (1,1) ∈ R^-1oR
(4.6) ∈ R, (6, 4) ∈ R^-1 ⇒ (4,4) ∈ R^-1oR
(7.6) ∈ R, (6, 4) ∈ R^-1 ⇒ (7,4) ∈ R^-1oR
(7.6) ∈ R, (6, 7) ∈ R^-1 ⇒ (7, 7) ∈ R^-1oR
(3, 7) ∈ R, (7, 3) ∈ R^-1 ⇒ (3,3) ∈ R^-1oR
(4, 6) ∈ R, (6, 7) ∈ R^-1 ⇒ (4, 7) ∈ R^-1oR
Thus R^-1oR = {(4,4), (1,1), (7,4), (7, 7), (3,3), (4, 7)} or R^-1oR = {(1,1), (3,3), (4,4), (4, 7), (7,4), (7, 7)}

(iii) Again, R^-1 = {(5,4), (4,1), (6,4), (6, 7), (7,3)} then (5,4) ∈ R^-1 and (4,1) ∈ R^-1
⇒ (5,1) ∈ R^-1oR^-1
(6.4) ∈ R^-1 and (4,1) ∈ R^-1
⇒ (6,1) ∈ R^-1oR^-1
(6.7) ∈ R^-1 and (7, 3) ∈ R^-1
⇒ (6,3) ∈ R^-1aoR^-1
Thus, R^-1oR^-1 = {(5,1), (6,1), (6,3)}.

(iv) We know that
(SoR)^-1 = R^-1oS^-1
then (R^-1R)^-1 = R^-1o(R^-1)^-1 = R^-1oR Value of R^-1oR has been obtained in (ii)
Thus, (R^-1oR)^-1 = {(1,1), (3,3), (4,4), (4,7), (7,4), (7,7)} Composition of R and R^-1 i.e. R^-1oR can be represent by the following figure.

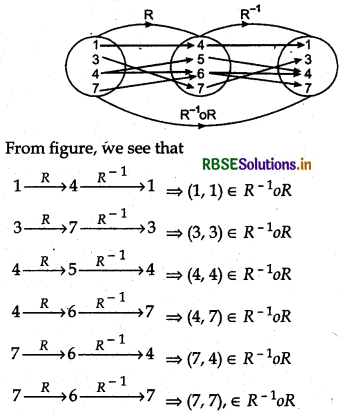
Thus, (R^-1oR)^-1= R^-1oR = {(1, 1), (3, 3), (4, 4), (4, 7), (7, 4), (7, 7)}

Equivalence Class:
Let R be an equivalence relation defined on set A, then the collection of those elements of A, which satisfy the relation xRa, where a ∈ A and x ∈ A is called equivalence class of a. This is represented by [a].

Theorem:
If relation R is equivalence relation in set A and a, b ∈ A, then
1. a ∈ [a], i.e., [a] is non-empty.
2. b ∈ [a] ⇒ [b] = [a]
3. [a] = [b] ⇔ (a, b) ∈ R
4. [a] ∩ [b] = Φ or [a] ≠ [b]
Proof :
1. a ∈ [a]
v R, has equivalence relation in set A. So, R is reflexive, then aRa is true.
But [a] = {x: x ∈ A and xRa]
So, aRa ⇒ a ∈ [a], i.e., [a] in non-empty.

2. Given b G [a], then prove that
[b] = [a]
Now b ∈ [a] ⇒ bRa
Element of equivalence class is arbitrary.
Hence x ∈ [b] ⇒ xRb
But R is trasitive. [R equivalence relation]
So xRb, bRa ⇒ xRa ⇒ x ∈ [a]
Hence x ∈ [b] ⇒ x ∈ [a]
So [b] ⊆ [a] ...(i)
Again, let x be any arbitrary element of equivalent class [a]
re [a] ⇒ xRa
But bRa ⇒ aRb; R is symmetric
[R equivalence relation]
Now xRa, aRb ⇒ xRb
⇒ x ∈ [b]
Hence, x ∈ [a] ⇒ x ∈ [b]
So, [a] ⊆ [b] ...(ii)
From equations (i) and (ii)
[a] = [b]

3. [a] = [b] ⇔ aRb
Let [a] = [b], then prove that aRb.
R is equivalence relation. So, this is reflexive.
then aRa
So, aRa ⇒ a ∈ [a]
⇒ a ∈ [b] [Since [a] = [b]]
⇒ aRb
So [a] = [b] ⇒ aRb

Again, let aRb, then prove that
[a] = [b]
Let x be a any arbitrary element.
When , x ∈ [a] ⇒ xRa But aRb is given.
From equations (i) and (ii),
[a] = [b]

4. [a] ∩ [b] = Φ or [a] ≠ [b]
Let [a] ∩ [b] ≠ Φ, then prove that
[a] = [b]
[a] ∩ [b] ≠ Φ
⇒ There is at least one element x is such that
x ∈ [a] ∩ [b]
Now x ∈ [a] ∩ [b] ⇒ x ∈ [a] and x ∈ [b]
⇒ xRa and xRb
⇒ aRx and xRb [R is symmetric]
⇒ aRb [R transitive]
⇒ M = [b]
So, [a] ∩ [b] ≠ Φ ⇒ [a] = [b]
In other words,
[a] ≠ [b] ⇒ [a] ∩ [b] = Φ

Quotient Set:
The set of all equivalence classes of any set is called quotient set.
Let A be any set and its respectively equivalence classes are [a], [b], [c],....... where a, b,ce A then {[a], [b], [c], ..............} is called quotient set and symbolically written as A/R, i.e., A/R = {[a], [b], [c] ............}

Example 1.
If A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and B = {1, 2, 6}, C = {3, 7, 8}, D = {4, 5}, E = {9, 10}, then prove that {B, C, D, E}, A is quotient set of A.
Answer:
Clearly, B ∪ C ∪ D ∪ E
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} = A

B ∩ C ={1, 2, 6} ∩ {3, 7, 8} = Φ
B ∩ D = (1,2,6} ∩ {4, 5} = Φ, etc.

Example 2.
Find all quotient sets of set A = {a, b, c}.
Answer:
Subsets of set A (except Φ) {a}, {b}, {c}, {a, b}, {b, c}, {c, a}, {a, b, c}.

Quotient set of A
(i ){{a.b,c)}
(ii) {{a}, {b, c}}, {{b}, {a, c}}, {{c}, (a, b}}
(iii) {{a}, {b}, {c}}

Partition of a Set:
If A, B, C,... are non-empty subsets of any non-empty set S, then set of all these subsets is called partition of set S.
i. e., P = {A, B, C,...} is partition of set S.
(i) A ∪ B ∪ C ∪ ........ = S
(ii) For any two subsets A, B ∈ P
A ∩ B = Φ.

Example 1.
If S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {1, 3}, B = {7, 8, 10}, C = {2, 5, 6}, D = {4, 9} then
(i) A ∪ B ∪ C ∪ D = S
(ii) Intersecting of any two sets is empty.
i. e., A ∩ B = Φ, B ∩ C = Φ, A ∩ C = Φ
Thus, set P = {A, B, C, D} is a partition of given set S.

Example 2.1(1= {0, ± 1, ± 2, ± 3, ...............}
or I = {...., - 3, - 2, - 1, 0,1, 2, 3, ................}
then A = {± 1, ± 3, + 5, ...........}
B = {±2, ±4, ±6,................}
C = { 0}
So, P = {A, B, C} is partition of set I.
So, R is symmetric.

Types Of Function:
In earlier class, we have introduced the notion of a function alongwith some special function, modulus function, signum function, etc. alongwith their graphs. Addition, subtraction, multiplication and division of two functions have also been studied in the earlier class. In this chapter, we will study different types of functions.

Definition (1):
A rule or correspondence which associates every element of a set to an unique element of another set is called function or mapping.
If f is a function from A to B and (a, b) ∈ f then f(a) = b, where b is called the image of a under f and a is called the pre-image of b under f The function f from A to B is denoted by f : A → B.

Definition (2):
A function which has either R or one of its subsets as its range is called a real valued function. Further, if its domain is also either R or a subset of R, is called a real function.

Domain, Co-domain and Range:
The set of all first elements of the ordered pairs in a relation R from a set A to a set B is called the domain of the relation R. The set of all second elements in a relation R from set A to set B is called the range of the relation R. The whole set B is called the co-domain of the relation R. Note that range ⊆ co-domain.

Function as a Set of Ordered Pairs:
Let A and B are two non-empty sets. A relation f from A to B, i.e., a subset of A × B is called a function (or a mapping) from A to B. If
(i) ∀ a ∈ A, (a, b) ∈ f whereas be B (i.e., domain of f is complete set A)
(ii) (a, b) ∈ f and (a, c) ∈ f ⇒ b = c (i.e., for each element of A there exist unique element in B)
Note: Each function (mapping) is a relation but each relation is not function (mapping).

Example: If A = {a, b, c} and B = {1, 2, 3, 4} and relation f: A → B such that
f(a) = 2, f(b) = 1 and f(c) = 4, then

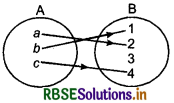
f-image of a is 2
f-image of b is 1
f-image of c is 4
Thus, range of function f, f(A) = {1, 2, 4}
Clearly, f(A) is a proper subset, i,e.,f(A) ⊂ B.
In ordered pair form f= {(a, 2), (b, 1), (c, 4)}

Example:
Which of the following figures are mapping ?

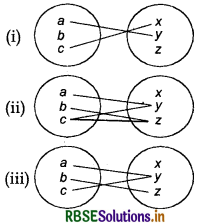
Answer:
(i) Since, b has no image, so figure (i) is not mapping (or function).
(ii) Since, element c has two images y and z, so figure (ii) is not mapping.
(iii) Yes, given figure is mapping or function.

Onto or Surjective Mapping:
f: A → B will be onto mapping, if every element of B is the image of some element of A under f i.e., for every b e B there exists an element a in A such that f(a) = b.

Example:
If A = {a, b, c, d, e), B = {1, 2, 3, 4} and mapping f : A → B is shown as follows :

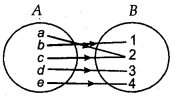
Here, f(a) = 2, f(b) = 1, f(c) = 2, f(d) = 3, f(e) = 4.
We see that each element of co-domain B is image of any element of A. In this case f(A) = B. Thus, f: A → B is onto mapping.

Into Mapping:
If one or more than one element of co-domain are not image of any element of domain, then these mappings are called into mapping.
Symbolically, f: A B will be onto if f(A) ⊂ B.

Example : If A = {1, 2, 3}, B = {a, b, c, d, e} and function f: A → B is shown as follows :
Here, f(1) = a, f(2) = d, f(3) = e
Here, we see that elements b and c are not images of any elements of domain set A. Thus, this is into mapping.

One-One Mapping:
A function f: X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct, i.e., for every x₁, x₂ ∈ X.
f(x₁) = f(x₂) implies x₁ = x₂
Example : If A = {1, 2, 3, 4} and B = {x, y, z, w} and f: A → B is shown in the following figures :

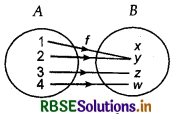
Clearly, 1 and 2 are not equal.
But f(1) = f(2)
i.e., 1 ≠ 2 ⇒ f(1) = f(2) = y
So this is not one-one mapping.
Consider the following figure :

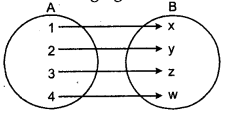
Here f(1) = x,f(2) = y, f(3) = z, f(4) = w
Clearly, images of distinct elements of x under A are distinct so this is one-one mapping.

Many-one Mapping:
A function f: X → Y is defined to be many-one mapping if two or more elements of domain have same images in co-domain. Symbolically, f: X → Y is a many-one mapping if f(x₁) = f(x₂) ⇒ x₁ ≠ x₂ ∀ x₁ x₂ ∈ A
or x₁ ≠ x₂ ⇒ f(x₁) = f(x₂)

Example:

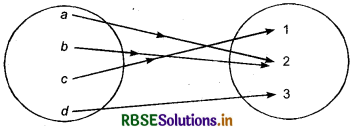
This is many-one mapping.

One-one into Mapping or Injective Mapping:
If a mapping is one-one as well as into, then it is called one-one into mapping.
Symbolically, f: A → B will be one-one into mapping if f(A) ⊂ B then
f(x₁) = f(x₂) ⇒ x₁ = x₂ ∀ x₁ x₂ ∈ A

Example : If A = {a, b, c}, B = {1, 2, 3, 4}

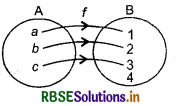
Here, f(a) = 1, f(1>) = 2, f(c) = 3
Since, each element of domain A has one image in B so function is one-one. ... (i)
In co-domain, element 4 which is not the image of any element of domain A so function/is into. ... (ii)
Thus, from (i) and (ii), function/is one-one into.

One-One Onto Mapping or Bijective Mapping:
If a function is onto as well as one-one, then it is called one-one mapping. Symbolically,
f(x₁) = f(x₂) ⇒ x₁ = x₂ ∀ x₁ x₂ ∈ A and f(A) = B.

Example: Consider the following function.

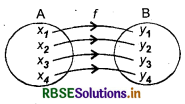
Clearly, f(x₁) = y₁, f(x₂) = y₂, f(x₃) = y₃, f(x₄) = y₄
So, function is one-one onto.

Method of Solving One-one function:

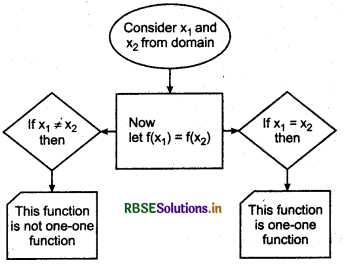
Method of Solving Onto function:
(1) If f: A → B is a function.
(2) Put f(x) = y, where x ∈ A and y ∈ B.
(3) Now, find value of x in terms of y.
(4) If x ∈ A (domain) exist for each value of y ∈ B (co-domain) then this function is onto otherwise not. Here, each element of domain A has distinct image in co-domain B and there is no element in co-domain B which is not the image of any element of domain A.

Example: Prove that function f: N → N defined by f(n) = n - (- 1)ⁿ is one-one onto, where N is a set of natural numbers.
Answer:
Here, two cases arise; n is either even or odd.
Case I: When n is even, then
f(n) = n - 1 [∵ (-1)ⁿ = 1]

One-one : Let n₁ n₂ & N (domain), where n₁ n₂ are even natural numbers.
∴ f(n₁) = f(n₂) ⇒ n₁ - 1 = n₂ - 1
⇒ n₁ = n₂
∴ f is one-one.

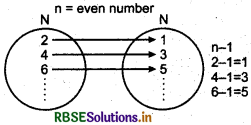
Example: If n = 2 then
f(2) = 2 - (- 1)² = 2 - 1 = 1
If n = 4, then f(4) = 4 - (- 1)⁴ = 4 - 1 = 3
It means for each even number in domain there exist (odd number) in co-domain.
∴ f is one-one.

Onto : Let y be any arbitrary element of co-domain if f(n) = y, then
y = n - 1 ⇒ n = (y + 1) ∈ N (domain)
Thus, f(y + 1) = (y + 1) - 1 = y (f definition of f)
i.e., ∀ y ∈ N (co-domain)
∃ (y + 1) ∈ N (domain) : f(y + 1) = y
∴ f[N] = N
i.e. f is onto.
Thus, function f is one-one onto.

Case II: When n is odd, then
f(n) = n - (- 1) = n + 1 [∵ (- 1)ⁿ = -1]

One-one : Let n₁, n₂ = N (domain), where n₁, n₂ are odd numbers.
f(n₁) = f(n₂) ⇒ n₁ + 1 = n₂ + 1
⇒ n₁ = n₂
∴ f is one-one.

Example : If n = 1, then
f(l) = 1 - (-1)¹ = 1 + 1 = 2

If n - 3, then
f(3) = 3 - (- 1)³ = 3 + 1 = 4

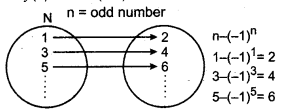
i.e., For each odd number in domain there exist an element (even number) in co-domain. Thus, f is one-one.

Onto : Let y be any arbitrary element of co-domain.
If f(n) = y, then
y = n + 1
⇒ n = (y - 1) ∈ N (domain)
∴ f(y - 1) = (y - 1) + 1 = y (f by definition off)
i.e., ∀ y ∈ N (co-domain)
∃ (y - 1) ∈ N (domain) : f(y -1) = y
∴ f(N) = N.
f is onto.
Thus, function f is one-one onto.

Many-one Into Mapping:
If a function is many-one and into also, then it is called many-one into mapping.
Symbolically, f: A → B is many-one into mapping if f(x₁) = f(x₂) ⇒ x₁ x₂; ∀ x₁, x₂ ∈ A and f(A) ⊂ B.
Example : Let A = {- 1, 1, 2, - 2}, B = {1, 2, 3, 4} then function f: A → B where f(x) = x² is many-one into mapping.
f(x) = x²

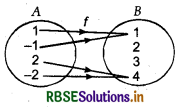
In general form,
f(Z) → Z
f(x) = x², ∀ x ∈ Z is a many-one into mapping.

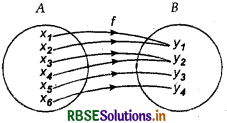
Many-One Onto Mapping:
If a function is many-one and onto also, then it is called many-one onto mapping.
Symbolically, f: A → B is a many-one onto function, if
f(x₁) = f(x₂) ⇒ x₁ x₂;
∀ x₁, x₂ ∈ A and f(A) = B.

Following figure shows the many-one onto function.

Example :
If R is a set of real numbers and A = {0, 1} and if f: R → A is defined as :

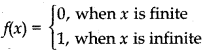
Now, f(0) = 0, f(1) = 0, f(2) = 0, f(3) = 0, ... etc. and f(π) = 1, f(e) = 1, f(√2) =1, f(√5) = 1,... etc.
So, f[R] = A
Thus, function/is many-one onto mapping.

Some Specific Functions:
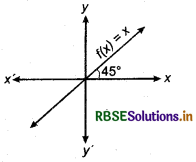
1. Identity Function :
A function that associates each real number to itself is called an identity function and is usually denoted by I.
Clearly, the function I: R → R defined by I(x) = x for all x ∈ R is called the identity function.
Clearly, the domain and range of the identity function are both equal to R. The graph of the identity function is a straight line passing through the origin and inclined at an angle of 45° with x-axis. ‘

Example: If A = {1, 4, 7} then f: A → A, where f(1) = 1, f(4) = 4, f(7) = 7 is identity function.

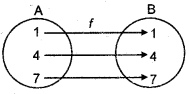
In ordered pair form, f = {(1, 1), (4, 4), (7, 7)} is identity function.

2. Inclusion Function: If set A is proper subset of B, i.e., A c B and any function f: A → B is such that f(x) = x, ∀ x ∈ A, then this function is called inclusion function. Clearly, inclusion function is one-one into.
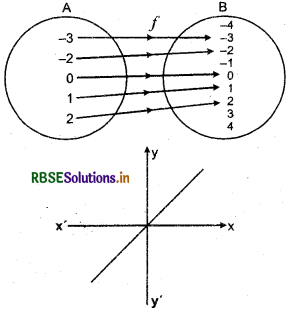
Example : If A = {- 3, - 2, 0,1, 2} and B = {- 4, - 3, - 2, - 1, 0,1, 2, 3, 4}, also A ⊂ B then function f: A → B where f(0) = 0, f(1) = 1, f(2) = 2, f(- 2) = - 2, f(- 3) = - 3, is inclusion function. Graph of inclusion function will be a straight line which will pass through origin.

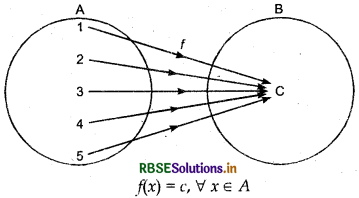
3. Constant Function: If function f: R → R is such that image of all the elements of domain is a single element of co-domain then this function is called constant function. Clearly, in such function, range f(R) is a singleton set. Symbolically, f: R → R is a constant function if ∀ x ∈ R, f(x) = c, c ∈ R is a constant.

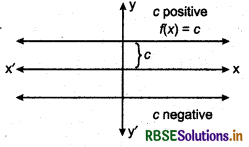
The graph of a constant function f(x) = c is a straight line parallel to x-axis which is above or below x-axis according as c is positive or negative. If c = 0, then the straight line is co-incident to x-axis.

4. Modulus Function: If a function/is defined such that

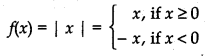
then function f is called modulus function.
Clearly, domain of modulus function is a set of real numbers and its range is a set of non-negative real numbers.
The graph of modulus function is shown in the following figure:

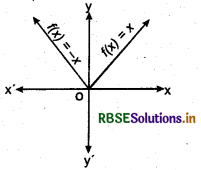
Modulus Function

Properties of modulus function for real numbers :
|x| ⇔ \(\sqrt{x^{2}}\) (for any real number x)
(i) If a and b are positive real numbers, then
x² ≥ a² ⇔ |x| ≥ a ⇔ x ≤ -a
or x ≥ a ⇒ x ∈ (- ∞, - a] u [a, ∞]
x² ≤ a² ⇔ |x| ≤ a ⇔ -a ≤ x ≤ a =>x ∈ [-a,a]
a² ≤ x² ≤ b² ⇔ a ≤ |x| ≤ b ⇔ x ∈ [- b,-a] ∪ [a, b]

Similarly
a² ≤ x² < b² ⇔ a ≤ |x| < b
⇔ x ∈ (- b, - a) ∪ (a, b).

(ii) For any two real numbers x and y
|x + y| = |x| + |y| ⇔ (x ≥ 0 and y ≥ 0) or (x < 0 and y < 0)
But |x - y| = |x| - |y| if and only if (x ≥ 0)and |x| ≥ |y|)
or (x ≤ 0, y ≤ 0and |x| ≥ |y|)

Note: |x ± y| ≤ |x| + |y|
or |x ± y| ≥ |x| - |y|

5. Greatest Integer Function (Floor Function):
For any real number x, we use the symbol [x] or [x] to denote the greatest integer less than or equal to x.
Example : [2.5] = 2, [1.73] = 1, [0.34] = 0, [- 6.8] = - 7, etc.

The function f: R → R defined by f(x) = [x] for all x ∈ R is called the greatest integer function or the floor function. It is also called a step function.
Clearly, domain of the greatest integer function is the set R of all real numbers and the range is the set Z of all integers as it attains only integer values.
The graph of the greatest integer function is shown in the following figure.

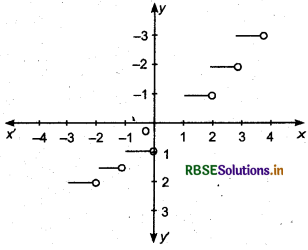
Greatest Integer Function

Properties of Greatest Integer function for any real number: If n is an integer and x is a real number between n and n +1 (n < x < n + 1), then
(i) [- n] = - [n] when n ∈ Z
(ii) [- x] = - [x] - 1 where x ∈ R
(iii) [x + k] = [x] + k, for any integer k

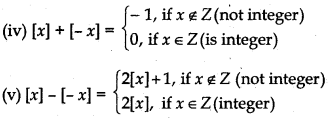
(vi) [x] ≥ k ⇒ x ≥ k if k is integer
(vii) [x] ≥ k ⇒ x ≥ k + 1 where k ∈ S (integer)
(viii) [x] < k ⇒ x < k +1 where k ∈ Z (integer)
(ix) [x] < k ⇒ x < k where k ∈ Z
(x) [x + y] = [x] + [y + x- [x]] where x, y ∈ R
(xi) [x] + \(\left[x+\frac{1}{n}\right]+\left[x+\frac{2}{n}\right]+\ldots+\left[x+\frac{n-1}{n}\right]\)
= [nx], n ∈ N (Natural number)

6. Smallest Integer Function or Ceiling Function: For any real number x, we use the symbol [x] to denote the smallest integer greater than or equal to x. For example:
[3.7] =4, [-7.2] =-7, [0.46] = 1, [8] = 8, [8.4] = 9,etc.
The function f: R → R defined by f(x) = [x] for all x ∈ R is called the smallest integer function or the ceiling function.

It is also a step function. We observe that the domain of the smallest integer function is the set R of the real numbers and the range is the set Z of all integers. The graph of the smallest integer function is shown in the following figure:

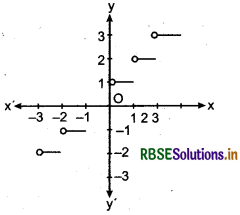
Smallest Integer Function

Properties of Smallest Integer Function :
Following are some properties of smallest integer function :
(i) [-n] = [n], where n ∈ Z
(ii) [- x] = - [x] + 1, where x ∈ R
(iii) [x + n] = [x] + n, where x ∈ R and n ∈ Z

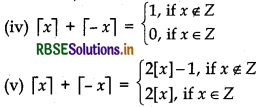
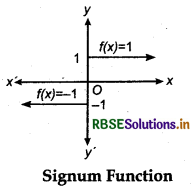
7. Signum Function: If for any real number x function f is defined such that

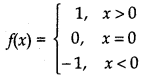
Then function f is called signum function. Clearly, domain of signum function is a set of real numbers R and its range is {- 1,0,1}.
The graph of the signum functions is shown in the following figure:

8. Logarithmic Function : If for any positive real number x a function/is defined such that f(x) = log_a x, where a > 0 and a ≠ 1 then this function is called logarithmic function. Clearly, domain of logarithmic function is a set of all non-negative numbers, i.e., (0, ∞) and its range is a set of all real numbers iR.

Graph of logarithmic function is shown in the following figure:
Case I: When a > 1
In this case, we have

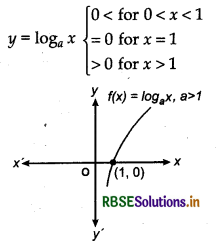
Case II: When 0 < a < 1
In this case, we have

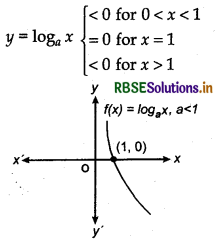
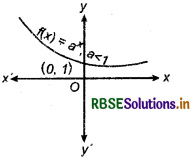
9. Exponential Function : If for any real number x a function/is defined such that f(x) = a^x, where a is any positive real number and a ≠ 1, then function f is called exponential function.
Clearly, domain of exponential function is a set of real numbers R and its range is a subset (0, ∞) of real numbers R as it attains only positive values.

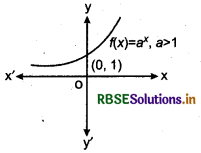
Case I: When a > 1

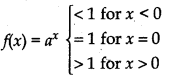
Thus, the graph of f(x) = a^x for a> 1 is as shown in the following figure:

Case II: When 0 < a < 1

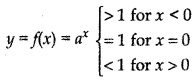
Thus the graph of f(x) = a^x for 0 < x < 1 is as shown in 10.

10. Reciprocal Function : If for any real number x(x ≠ 0) function f is defined such that f(x) = \(\frac{1}{x}\) then function f is called reciprocal function. In other words, function
f: R - [0] → R defined by f(x) = \(\frac{1}{x}\) is called the reciprocal function. Clearly, domain of the reciprocal function is R - [0] and its range is also R - |0}.
Graph of reciprocal function is shown in the following figure:

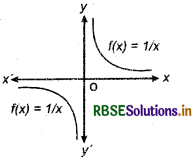
Composition Of Functions And Invertible Function:
In this section, we will study composition of functions and the inverse of a bijective function. Consider the set A of all students, who appeared in Class X of a board examination in 2020. Each student appearing in the board examination is assigned a roll number by the board which is written by the students in the answer script at the time of examination. In order to have confidentiality, the board arranges to deface the roll numbers of students in the answer scripts and assigns a fake code number to each roll number.

Let B ⊂ N be the set of all roll numbers and C ⊂ N be the set of all .code numbers. This gives rise to two functions f: A → B and g : B → C given by f(a) = the roll number assigned to the student a and g(b) = the code number assigned to the roll number b. In this process each student Is assigned a roll number through the function land each roll number is assigned a code number through the function g. Thus, by the combination of these two functions, each student ¡s eventually attached’ a code number.

Definition of Composition of Function:
Let f: A → B and g : B → C be two functions. Then the composition of/andg, denoted by gof is defined as the function gof: A → C given by
gof(x) = g(f{x)), ∀ x ∈ A.

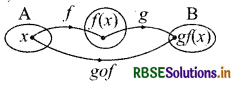
Note : For the composition of f and g it is essential that:
(1) Range of f ⊆ Domain of g.
(2) Generally, gof ≠ fog, i.e., composition of functions do not follow commutative law.
(3) If range of f n domain of g = Φ, then gof is not obtained, i,e., we can obtained gof only when range of n domain of g = Φ Similarly, fog can be obtained if:
range of g n domain of f = Φ
(4) If f and g both are one-one onto or bijective, then fog and gof both will be one-one onto.
(5) The composition of function follow the associative law. e.g.,
f:A → B, g:B → C and h: C → D are three functions. then [ho(gof)] (x) = [(hog) of] (x)
i.e., ho (gof) = (hog) of

Inverse Image:
Let f: A → B is any mapping :
where f(a) = x then a is the pre-image or inverse of x under/and we write as f^-1(x) = a
f(b) = y then f^-1(y) = b
f(e) = z then f^-1(z) = c
f(d) = z then f^-1(z) = d
It should be noted that the inverse of an element under a function may consist of a single element, two or more elements or no element depending upon whether function is injective or many-one, onto. If f: A → B is a many-one and into function, then the inverse of same elements of B may or may not exist or the inverse of same element of B may consists of more than one element. If f is a bijection, then for each x ∈ B,f^-1(x) exists and it consists of a single element only.

Inverse of a Function:
Let A and B be two sets and let f: A → B be a one- one onto function then inverse of f, i.e., f^-1 is the set of those ordered pairs whose elements when interchanged became ordered pair of function f.
Clearly, f^-1 = {(b, a) : (a, b) ∈ f}

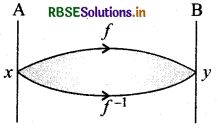
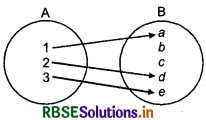
Example: Let set A = {a, b, c, d, e) and function f: A → A, g: A → A and h: A → A are defined by following figures.


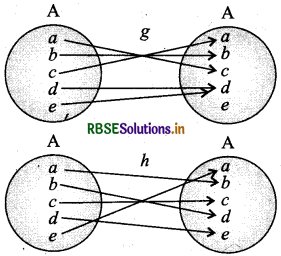
Here, we will have to see that the inverse of which function can be obtained. We can get inverse of any function, when function is one-one onto.
From given figures, it is clear that only h is such function which is .one-dne and onto. Thus, we confind inverse of function h. Functions/and g are not bijective so we cannot find their inverse.

Definition: Let f: A → B be a bijection. Then a function g:B → A which associates each element y ∈ B to a unique element x ∈ A such f(x) = y ⇔ g(y) = x
The inverse of f is generally denoted by f^-1.
Thus, if f: A → B is a bijection, then f^-1: B → A is such that f(x) = y ⇔ f^-1 (y) = x.
In Ordered pair form,
If f= {(x, y): x ∈ A, y ∈ B], then f^-1 = {(y, x): x ∈ A, y ∈ B},

In order to find the inverse of a bijection, we may follow the following algorithm.
Algorithm : Let f : A → B be a bijection. To find the inverse of/we follow the following steps.
Step 1. Put f(x) = y when ye B and x ∈ A
Step 2. Solve f(x) = y to obtain x in terms of y
Step 3. In the relation obtained in step 2 replace x by f(y) to obtain the required inverse of f

Invertible function:
A function f: X → Y is defined to be invertible, if there exists a function g : Y → X such that gof= I_x and fog = I_y. The function is called the inverse of f and is denoted by f^-1.
Thus, if f is invertible, then f must be one-one and onto and conversely, if f is one-one and onto, then f must be invertible. This fact significantly helps for proving a function f to be invertible by showing that f is one-one and onto, specially when the actual inverse of f is not to be determined.

Binary Operations:
In earlier classes, we have studied about various operations like addition, subtraction, multiplication, division of numbers, union and intersection of sets, composition of functions, etc. Actually, all these operations are operated on two elements of the given set to get a unique element. In this chapter, we will study such operations as functions from the cartisian product of a set with the set itself.

We know that, in the set of natural numbers, addition and multiplication operation follow closure law, i.e., if a and b are any two natural numbers, then
a +b ∈ N and ab ∈ N, where N is set of natural numbers.

Symbolically, we can write it as follows :
(+):N × N → M such that + (a, b) = a + b
and (.): N × N → N such that. (a, b) = a.b

Definition:
Let S be a non-empty set. A function f: S × S → S is called a binary operation on set S.

Example 1.
Addition and multiplication of natural numbers are binary operations, because the sum and product of two natural numbers are natural numbers. i.e., if a, b ∈ N
⇒ a + b ∈ N (Sum of natural numbers)
and if a,b ∈ N
⇒ a.b ∈ N (Product of natural numbers)

Example 2.
Addition and multiplication are also binary operations on Z (the set of integers) Q (the set of rational numbers), R (the set of real numbers) and C (the set of complex numbers).

Example 3.
Subtraction (-) is not a binary operation on N, because subtraction of two natural numbers is not always a natural number. Example : 3 - 5 = - 2 g N. However, subtraction is a binary operation on Z, Q, R and C.

Remark : ∨ (4, 7) i.e. 4 ∨ 7 (maximum (4, 7) and ∧ (4, - 7) i.e. 4 ∧ (- 7) = - 7 (minimum (4, - 7))

When number of elements in a set A is small, we can express a binary operation * on the set A through a table called the operation table for the operation *. For example, consider A = {1,2, 3}. Then, the operation ∨ on A can be expressed by the following operation table 1. Here, ∨ (1,3) = 3, ∨ (2, 3) = 3, ∨ (1, 2) = 2.

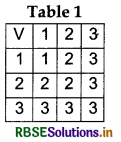
Here, we are having 3 rows and 3 columns in the operation table with (i, j) the entry of the table being maximum of zth and jth elements of the set A. This can be generalised for general operation *:A × A → A.IfA = [a₁, a₂, ..., a_n}. Then the operations table will be having n rows and n columns with (i, j)th entry being a_i * a_j. Conversely, given any operation table having n rows and n columns with each entry being an element of A = {a₁, a₂, ......... a_n], we can define a binary operation * : A × A → A given by a_i * a_j = the entry in the ith row and jth column of the operation table.

Number of Binary Operations:
Let S be a finite set consisting of n elements. Then S × S has n² elements. We know that the total number of functions from a finite set A to a finite set B is [n(B)]n(A). Therefore, the total number of binary operations on S is n.
For example: If there are two elements in S = {a, b}, then number of binary operations on S = 2⁴ = 16.

Types of Binary Operations:
(1) Commutativity : A binary operation * on the set X is called commutative, if a * b = b * a, for every, a,b ∈ X.
(2) Associativity: A binary operation * : A × A → A is said to be associative if (a * b) * c = a* (b* c), ∀ a,b, c, ∈ A

Remark:
Associative property of a binary operation is very important in the sense that with this property of a binary operation, we can write a₁* a₂* ... * a_n which is not ambiguous. But in absence of this property, the expression a₁* a₂* ... * a_n is ambiguous unless brackets are used. Recall that in the earlier classes brackets were used whenever substraction or division operations or more than one operation occurred.

(3) Distributivity : Let S be a non-empty set and * and '.' be two binary operations on S. Then '*' is said to be distributive over (.) if for all a,b,c ∈ S.
a* (b. c) = (a* b). (a* c) [Left distributivity of * over (.)]
and (b . c) * a = (b * a) . (c * a) [Right distributivity of * over (.)]

(4) Identity Element: For the binary operation'+' on R, the interesting feature of the number zero is that a + 0 = a = 0 + a, i.e., any number remains unaltered by adding zero. But in case of multiplication, the number 1 plays this role, as a × 1 = a = 1 × a, ∈ a in R.

Definition: Given a binary operation *: A × A → A, an element ee A, if it exists, is called identity for the operation *, ii a* e = a = e* a, ∀ a ∈A.

Remark: Zero is identity for the addition operation on R but it is not identity for the addition operation on N, as 0 g N. In fact the addition on N does not have any identity.
One further notices that for the addition operation + :R × R → R, given any at R, there exists - a in R such that a + (- a) = 0 (identity for'+') = (- a) + a.

Inverse of an Element:
For the multiplication operation on R, given any a ≠ 0 in R, we can choose - in R such that a × \(\frac{1}{a}\) = 1 (identity a a for 'x')= \(\frac{1}{a}\) × a.
This leads to the following definition :

Definition:
Given a binary operation *: A * A → A with the identity element e in A, an element a ∈ A is said to be invertible with respect to the operation *, if there exists an element bin A such that a* b = e = b* a and b is called the inverse of a and is denoted by a^-1.

Thereom 1:
Let * be an associative binary operation on a set S with the identity element e in S. Then, the inverse of an invertible element is unique.
Proof :
Let a be an invertible element in S. If possible let b and a*b = b*a = e and a*c = c*a = e.
Now, (b*a)*c = e*c = c [∵ b* a = e]
and b*(a*c) = b*e = b [∵ e is the identity element]
= b [∵ a* c = e] [∵ e is the identity element]
Since is an associative binary operation on S. Therefore
(b* a)* c = b* (a* c)
⇒ c = b
Hence, a has unique inverse.
Hence Proved.

Note : Generally inverse of a is denoted by a^-1

Theorem 2.
Let * be an associative binary operation on a set S and a be an invertible element of S. Then (a^-1)^-1 = a
Proof:
Let e be the identity element in S for the binary operation * on S. Then
a* a^-1 = e = a^-1 * a
⇒ a^-1 * a = e = a* a^-1
⇒ a is inverse of a^-1.
⇒ a = (a^-1)^-1
Hence Proved.

Composition Table:
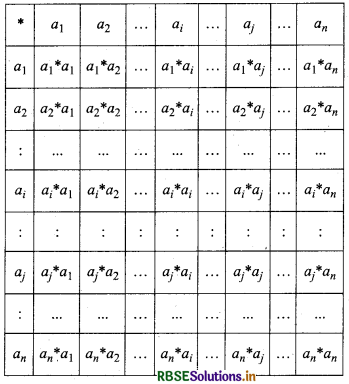
A binary operation on finite set can be completely described by means of a table known as a composition table.
Or
The composition table is the tabular form in which a binary composition in a finite set can be exhibited. Let S = {a₁, a₂,... a_n] be a finite set and * be a binary operation on S. Then the composition table for * is constructed in the manner indicated below.

From the composition table following results are obtained:

• If all the entries of the table are elements of set S and each element of S appears once and, only once in row and in each column, then the operation is a binary operation.
• If the entries in the table are symmetred with respect to the diagonal which starts at the upper left comer of the table and terminals at the lower right comer we say that the binary operation is commutative on S, otherwise non commutative.
• If the row headed by an element say a_j coincides with the row at the top and the column headed by coincides with the column on extreme left, then a_j is the identity element in S for the binary operation * on S.
• If each row except the top most row or each column except the left most column contains the identity elements then each element of S is invertible with respect to *.
• To find inverse of any element say we consider row (or column) headed by a_j. Then we determine the position of identity element in this raw (or column). If it (identity) appears in the column (or row) headed by a_j then a_j and a_j are inverse of each other.

We shall now introduce two binary operations on the set Z_n of integers modulo n. These two binary operations are called addition modulo n and multiplication modulo n and are expressed by (a + n^b) and a × n^b respectively, where a,b ∈ Z_n

Table for Additive modulo n:
Let n be a positive integer greater than 1 and a, b ∈ Z_n , where Z_n = {0 ,1, 2, ........... (n - 1)}. Then, we define addition modulo n i.e. + n as follows :
a + n^b = least non-negative remainder when a + b is divided by n

Example:
(i) 8 + 5⁹ = (Least non-negative remainder, when 8 + 5 = 13 is divided by 5) = 2
(ii) 11 + 7⁹ = (Least non-negative remainder, when 11 + 9 = 20, is divided by 7) = 6
The composition table for + 5 on Z₅ = { 0, 1, 2, 3, 4} is as given below :

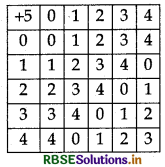
We observe the following points from the composition table:

• All entries of the table are elements of set Z₅.
• The table is symmetic with respect to the principal diagonal therefore + 5 is a commutative binary operation on Z₅.
• The row headed by O consists of the top most row and the column headed by O coincides with the left-most column. So, O is the identity elements for + 5 on Z₅.
• Each row and column consists of the identity element O. So, every element of Z₅ is invertible.
• Again 0 + ₅0 = 0 is inverse of itself
  • 1 + ₅4 = 0 => 1 is inverse of 4
  • 2 + ₅3 = 0 => 2 is inverse of 4
  • 3 + ₅2 = 0 => 3 is inverse of 3
  • 4 + ₅1 = 0 => 4 is inverse of 4
• (2 + ₅3) + ₅4 = 5 + ₅4 = 4
  and 2 + ₅(3 + ₅4) = 2 + ₅7 = 4
  (2 + ₅3) + ₅4 = 2 + ₅(3 + ₅4)
  (1 + ₅2) + ₅3 = 3 + ₅3 = 1
  and 1 + ₅(2 + ₅3) = 1 + ₅5 = 1

Thus (1 + ₅2) + ₅3 = 1 + ₅(2 + ₅3)
Similarly, it can be verified for other elements of Z₅ that + 5 is associative on Z₅.

Multiplication Modulo n:
Let n be a positive integer greater than 1 and a, b ∈ Z_n where
Z_n = (0,1, 2, ........... (n - 1)} then multiplication modulo n is divided as:
a χnb = least non-negative remainder when ab is divided by n

Example:
(i) 3 × 5⁷ = least non-negative remote when 3 × 7 = 21 is divisible by 5) = 1
(ii) 4 × 7⁶ = (Least non-negative remainder when 4 × 6 = 24, is divisible by 7) = 3
(iii) 7 × n⁹ = (Least non negative remainder when 7 × 9 = 63, is divisible by 11) = 8
(iv) 8 × 13¹⁰ = (Least non-negative remainder when 8
1. AH entries of the table are elements of S. So ×₅ is a binary operation on S.
2. The table is symmetric with respect to the principal diagonal ×₅ is commutative on S.
3. The row headed by 1 coincides with the top most row and the column headed by 1 coincides with the left most column. Their intersection is 1. So 1, is the identity element for ×₅ on S.
4. Since, each row and each column consists of the identity elements so each element of S is invertible.
⇒ 2 × ₅3 = 1 ⇒ 2^-1 = 3 (inverse of 2 is 3)
1 × ₅1 = 1, 1 = i
i.e. 1 is inverse of itself
4 × ₅4 = 1 ⇒ 4^-1 = 4
i.e. 4 is inverse of itself
(1 × ₅3) × ₅2 = 3 × ₅2 = 1
and 1 × ₅(3 × ₅2) = 1 × ₅1 = 1
Thus, (1 × ₅3) × ₅2 = 1 × ₅(3 × ₅2)
Note: Multiplication modulo n is associative because the remainders when the integers (a × b) × c and a × (b × c) are divided by n are same.

→ Empty relation is the relation R in X given by
R = Φ ⊂ X × X.

→ Universal relation is the relation R in X given by
R = X × X.

→ Reflexive relation R in X is a relation with (a, a) ∈ R ∀ a ∈ X.

→ Symmetric relation R in X is a relation satisfying (a, b) ∈ R implies (b, a) ∈ R.

→ Transitive relation R in X is a relation satisfying (a, b) ∈ R and (b, a) ∈ R implies that (a, c) ∈ R.

→ Equivalence relation R in X is a relation which is reflexive, symmetric and transitive.

→ Equivalence class [a] containing a ∈ X for an equivalence relation R in X is the subset of X containing all elements b related to a.

→ A function f: X → Y is one-one (or injective) if f(x₁) = f(x₂) ⇒ x₁ = x₂ ∀ x₁, x₂ ∈ X.

→ A function f: X → Y is onto (or surjective) if given any y ∈ Y, ∃ x ∈ X such that f(x) = y.

→ A function f: X → Y is one-one and onto (or bijective), if f is both one-one and onto.

→ The composition of functions f: A → B and g : B → C is the function gof: A → C given by gof(x) = g(f(x)) ∀ x ∈ A.

→ A function f: X → Y is invertible if ∃ g: Y → X such that gof = I_X and fog = I_Y.

→ A function f: X → Y is invertible if and only if f is one- one and onto.

→ Given a finite set X, a function f : X → X is one-one (respectively onto) if and only if f is onto (respectively one-one). This is the characteristic property of a finite set. This is not true for infinite set.

→ A binary operation * on a set A is a function * from A × A to A.

→ An element e ∈ X is the identity element for binary operation *: X × X → X, if a * e = a = e * a ∀ a ∈ X.

→ An element a ∈ X is invertible for binary operation * : X × X → X, if there exists b ∈ X such that a*b = e = b* a where, e is the identity for the binary operation *. The element b is called inverse of a and is denoted by a^-1

→ An operation * on X is commutative if a*b = b* a ∀ a, b in X.

→ An operation * on X is associative if (a * b) * c = a * (b * c) ∀ a, b, c in X.

→ Empty relation is the relation R in X given by
R = Φ ⊂ X × X.

→ Universal relation is the relation R in X given by
R = X × X.

→ Reflexive relation R in X is a relation with (a, a) ∈ R ∀ a ∈ X.

→Symmetric relation R in X is a relation satisfying
(a, b) ∈ R implies (b, a) ∈ R.

→ Transitive relation R in X is a relation satisfying (a, b) ∈ R and (b, a) ∈ R implies that (a, c) ∈ R.

→ Equivalence relation R in X is a relation which is reflexive, symmetric and transitive.

→ Equivalence class [a] containing a ∈ X for an equivalence relation R in X is the subset of X containing all elements b related to a.

→ A function f: X → Y is one-one (or injective) if f(x₁) = f(x₂) ⇒ x₁ = x₂ V x₁ x₂ ∈ X.

→ A function f: X → Y is onto (or surjective) if given any y ∈ Y, ∃ x ∈ X such that f(x) = y.

→ A function f: X → Y is one-one and onto (or bijective), if f is both one-one and onto.

→ The composition of functions f: A → B and g : B → C is the function gof: A → C given by gof(x) = g(f(x)) ∀ x ∈ A.

→ A function f: X → Y is invertible if ∃ g: Y → X such that gof = IX and fog = IY.

→ A function f: X → Y is invertible if and only if f is one- one and onto.

→ Given a finite set X, a function f: X → X is one-one (respectively onto) if and only if f is onto (respectively one-one). This is the characteristic property of a finite set. This is not true for infinite set.

→ A binary operation * on a set A is a function * from A × A to A.

→ An element e ∈ X is the identity element for binary operation *:X × X → X, if a* e = a = e * a ∀ a ∈ X.

→ An element a ∈ X is invertible for binary operation * : X × X → X, if there exists b ∈ X such that a * b = e = b * a where, e is the identity for the binary operation *. The element b is called inverse of a and is denoted by cf

→ An operation * on X is associative if (a * b) * c = a * (b * c) ∀ a, b, c in X.