RBSE Class 12 Maths Important Questions Chapter 9 Differential Equations

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 9 Differential Equations Important Questions and Answers.

RBSE Class 12 Maths Chapter 9 Important Questions Differential Equations

Question 1.
Write the order and degree of the differential equation
x³\(\left(\frac{d^2 y}{d x^2}\right)^2\) + x\(\left(\frac{d y}{d x}\right)^4\) = 0
Answer:
Since, the highest order derivative present in the differential equation is \(\frac{d^2 y}{d x^2}\), so its order is 2. As the given equation is a polynomial in \(\frac{d^2 y}{d x^2}\) and \(\frac{d y}{d x}\) and the highest power raised to \(\frac{d^2 y}{d x^2}\) is 2, so its degree is 2.

Question 2.
Write the sum of the order and degree of the differential equation
\(\left(\frac{d^2 y}{d x^2}\right)^2\) + \(\left(\frac{d y}{d x}\right)^3\) + x⁴ = 0
Answer:
Given, differential equation is
\(\left(\frac{d^2 y}{d x^2}\right)^2\) + \(\left(\frac{d y}{d x}\right)^3\) + x⁴ = 0
Here, we see that the highest order derivative is \(\frac{d^2 y}{d x^2}\), whose degree is 2.
Here, order = 2 and degree = 2
Thus, sum of the order and degree = 2 + 2 = 4

Question 3.
Write the degree of the differential equation
x\(\left(\frac{d^2 y}{d x^2}\right)^3\) + y\(\left(\frac{d y}{d x}\right)^4\) + x³ = 0
Answer:
Here, the highest order derivative is \(\frac{d^2 y}{d x^2}\), whose degree is 1. So, the degree of differential equation is 1.

Question 4.
Show that the function y = e^-x + 2 is a solution of the differential equation \(\frac{d y}{d x}\) + y = 2.
Answer:
The given function is
y = e^-x + 2
Differentiating equation (1) w.r.t 'x', we get
\(\frac{d y}{d x}\) = - e^-x
From equations (1) and (2), we get

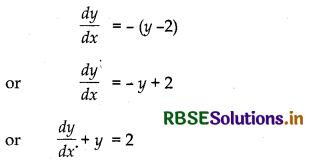
Thus, the function y = e^-x + 2 is the solution of the differential equation \(\frac{d y}{d x}\) + y = 2.
Hence Proved.

Question 5.
Prove that the function y = sin x is a solution of the differential equation(1 - x²)y₂ - xy₁ = 0, i.e.,
(1 - x²)\(\frac{d^2 y}{d x^2}\) - x\(\frac{d y}{d x}\) = 0
Answer:
The given function is:
y = sin^-1 x
Differentiating equation (1) w.r.t ‘x, we get

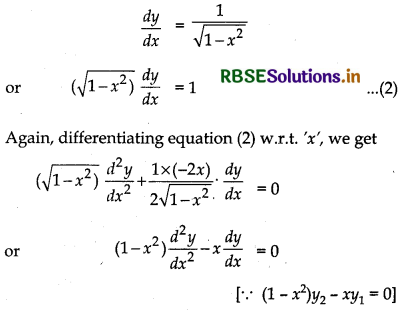
Thus, function y = sin^-1 x is the solution of the differential equation
(1 - x²)\(\frac{d^2 y}{d x^2}\) - x\(\frac{d y}{d x}\) = 0

Question 6.
Show that the function y = ax + 2a² is a solution of the differential equation
2\(\left(\frac{d y}{d x}\right)^2\) + x\(\left(\frac{d y}{d x}\right)\) - y = 0
Answer:
The given function is
y = ax + 2a²
Differentiating equation (1) w.r.t. ‘x’, we get
\(\frac{d y}{d x}\) = a
Substituting the value 'a' in equation, we get

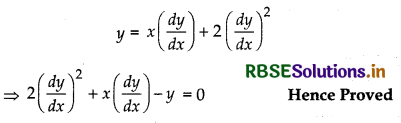
Hence proved.

Question 7.
Find the differential equation representing the family of curves y = ae^{bx + 5} where a and b are arbitrary constants.
Answer:
We have, y = ae^{bx + 5}
On differentiating both sides w.r.t. x, we get

which is the required differential equation.

Question 8.
Form the differential equation of the family of circles in the second quadrant and touching the coordinate axes.
Answer:
Let a be the radius of family of circles in the second quadrant, which touch the coordinate axes.
Then, coordinates of centre of circle = (- a, a).

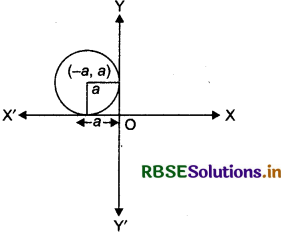
We know that, equation of circle whose centre (h, k) and radius r is given by
(x - h)² + (y - k)² = r²
Here, (h, k) = (- a, a) and r = a
∴ Equation of family of such circles is
(x + a)² + (y - a)² = a² ................... (i)
On differentiating both sides w.r.t. x, we get
2(x + a) + 2(y - a)\(\frac{d y}{d x}\) = 0
⇒ x + a + (y - a).y' = 0 (∵ \(\frac{d y}{d x}\) = y')
⇒ x + yy' = - a + ay'
⇒ a = \(\frac{x+y y^{\prime}}{-1+y^{\prime}}\)
On putting above value of a in Eq.(i), we get

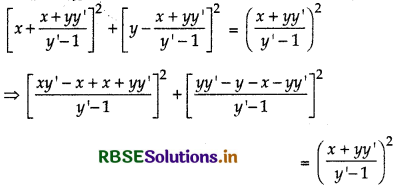
On multiplying both sides by (y - 1)², we get
(xy' + yy’)² + (y + x)² = (x + yy')²
(x + y)² (y')² + (x + y)² = (x + yy’)²
∴ (x + y)² [(y’)² + 1] = (x + yy’)²
which is the required differential equation.

Question 9.
If y(x) is a solution of the differential equation \(\left(\frac{2+\sin x}{1+y}\right) \frac{d y}{d x}\) = - cos x and y(0) = 1, then find the value of y \(\left(\frac{\pi}{2}\right)\).
Answer:
Given, differential equation is

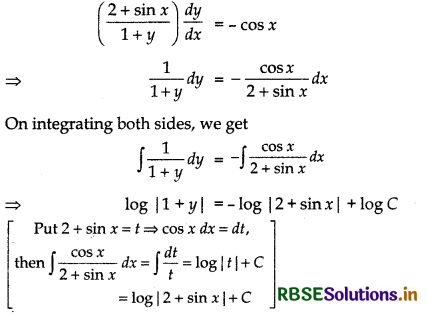
⇒ log |1 + y| + log|2 + sin x| = log C
⇒ log (|1 + y| |2 + sin x|) = log C [∵ log m + log n = log mn]
⇒ (1 + y) (2 + sin x) = C .............. (i)
Also, given that at x = 0, y = 1.
On putting x = 0 and y = 1 in Eq. (i), we get
(1 + 1) (2 + sin 0) = C ⇒ C = 4
On putting C = 4 in Eq. (i), we get
(1 + y) (2 + sin x) = 4

Question 10.
Find the particular solution of the differential equation
\(\frac{d y}{d x}=\frac{x(2 \log |x|+1)}{\sin y+y \cos y}\)
given that y = \(\frac{\pi}{2}\), when x = 1.
Answer:
Given, differential equation is
\(\frac{d y}{d x}=\frac{x(2 \log |x|+1)}{\sin y+y \cos y}\)
On separating the variables, we get
(sin y + y cos y)dy = x(2 log |x| + 1) dx
⇒ sin y dy + y cos y dy = 2x log |x| dx + x dx
On integrating both sides, we get

On substituting the value of C in Eq. (i), we get
y sin y = x² log |x| + \(\frac{\pi}{2}\)
which is the required particular solution.

Question 11.
Find the particular solution of the differential equation
e^x \(\sqrt{1-y^2}\) dx + \(\frac{y}{x}\) dy = 0,
given that y = 1, when x = 0.
Answer:
Given, differential equation is

Also, given that y = 1, when x = 0
On putting y = 1 and x = 0 in Eq, (i), we get
\(\sqrt{1-1}\) = 0 - e⁰ + C
⇒ c = 1 [∵ e⁰ = 1]
On substituting the value of C in Eq. (i), we get
\(\sqrt{1-y^2}\) = xe^X - e^x + 1
which is the required particular solution of given differential equation.

Question 12.
Find the solution of differential equation
\(\frac{d y}{d x}=\frac{x+y+1}{2 x+2 y+3}\)
Answer:
Given differential equation is
\(\frac{d y}{d x}=\frac{x+y+1}{2 x+2 y+3}\)

where C is an integrating constant,
6v + log (3v + 4) = 9x + 4 (where C₁ = 9C)
or 6(x + y) + log(3x + 3y + 4) = 9x + 4
(Putting the value of v)
or 6y - 3x + log (3x + 3y + 4) = C₁
which is the required solution.

Question 13.
Solve the following differential equation:
xy log\(\left|\frac{y}{x}\right|\) dx + [y² - x² log\(\left|\frac{y}{x}\right|\)] dy = 0
Answer:
Given differential equation is


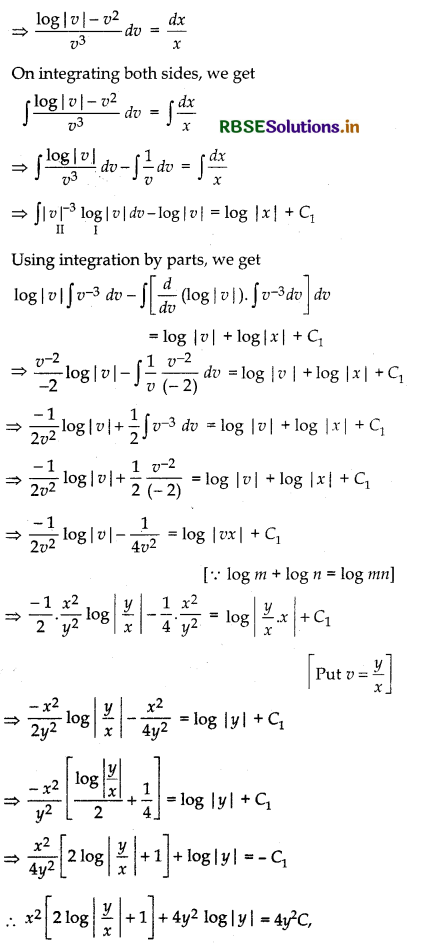
where C = - C₁
which is the required solution.

Question 14.
Find the particular solution of the differential equation \(\frac{d y}{d x}=\frac{x y}{x^2+y^2}\) given that y = 1, when x = 0.
Answer:
Given differential equation is

Question 15.
Solve the differential equation x\(\frac{d y}{d x}\) + y = x. cos x + sin x, given that y = 1 when x = \(\frac{\pi}{2}\).
Answer:
Given differential equation is:

⇒ xy = x sin x - ∫1.sin x dx - cos x + C
⇒ xy = x sin x + cos x - cos x + C
⇒ xy = x sin x + C
⇒ y = sin x + C.\(\frac{1}{x}\) .......... (i)
Also, given that at x = \(\frac{\pi}{2}\); y = 1
On putting x = \(\frac{\pi}{2}\). and y = 1 in Eq.(i), we get
1 = 1 + C. \(\frac{2}{\pi}\) ⇒ C = 0
On putting the value of C in Eq. (1), we get
y = sin x
which is the required solution of the given differential equation.

Question 16.
Solve the differential equation \(\frac{d y}{d x}\) + y cot x = 2 cos x, given that y = 0, when x = \(\frac{\pi}{2}\).
Answer:
Given differential equation is
\(\frac{d y}{d x}\) + y cot x = 2 cos x
which is a linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q
Here, P = cot x and Q = 2 cos x
∴ IF = e^{∫p dx} = e^{∫cot x dx} = e^{log |sin x|}
⇒ IF = sin x
The general solution is given by
y × IF = ∫(IF × Q) dx × C
⇒ y sin x = ∫2 sin x cos x dx + C
⇒ y sin x = ∫sin 2x dx + C
⇒ y sin x = - \(\frac{\cos 2 x}{2}\) + C
Also, given that y = 0, when x = \(\frac{\pi}{2}\)
On putting x = \(\frac{\pi}{2}\) and y = 0 in Eq. (i), we get

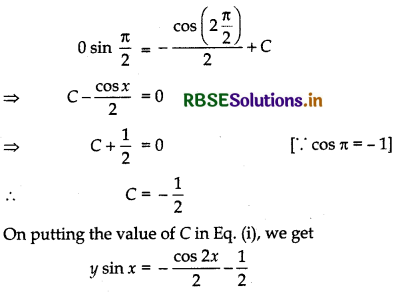
∴ 2y sin x + cos 2x + 1 = 0
which is the required solution.

Question 17.
Solve the following differential equation:
(x² + 1) \(\frac{d y}{d x}\) + 2 xy = \(\sqrt{x^2+4}\)
Answer:
Given differential equation is:

Multiple Choice Questions

Question 1.
The solution of the differential equation
\(\frac{d y}{d x}\) = (x² + xy + y²)/x² is:
(a) tan^-1\(\frac{x}{y}\) = log y + C
(b) tan^-1 \(\frac{y}{x}\) = log x + C
(c) tan^-1\(\frac{x}{y}\) = log x + C
(d) tan^-1 \(\frac{y}{x}\) = log y + C
Answer:
(b) tan^-1 \(\frac{y}{x}\) = log x + C

Question 2.
The differential equation \(\frac{d y}{d x}\) + Py = Qyⁿ, n > 2 can be reduced to linear form by substituting:
(a) z = y^{n - 1}
(b) z = yⁿ
(c) z = y^{n + 1}
(d) z = y^{1 - n}
Answer:
(d) z = y^{1 - n}

Question 3.
If a and b are the order and degree of the differential equation y \(\frac{d y}{d x}+x^3\left(\frac{d^2 y}{d x^2}\right)\) + xy = cos x, then:
(a) a < b
(b) a = b
(c) a > b
(d) none of these
Answer:
(c) a > b

Question 4.
The differential equation
\(\left(\frac{d^2 y}{d x^2}\right)^{2 / 3}=\left(y+\frac{d y}{d x}\right)^{1 / 2}\) is of:
(a) first order, fourth degree
(b) second order, fourth degree
(c) second order, third degree
(d) second order, second degree
Answer:
(b) second order, fourth degree

Question 5.
The order of the differential equation
\(\frac{d^2 y}{d x^2}=\sqrt{1+\left(\frac{d y}{d x}\right)^2}\) is:
(a) 1
(b) 2
(c) 3
(d) none of these
Answer:
(b) 2

Question 6.
The solution of the differential equation
(1 + x²)\(\frac{d y}{d x}\) + 1 + y² = 0 is:
(a) tan¹ x - tan¹ y = tan¹ C
(b) tan¹ x - tan¹ x = tan¹ C
(c) tan¹ y + tan¹ x = sin C
(d) tan¹ y + tan¹ x = tan¹ C
Answer:
(d) tan¹ y + tan¹ x = tan¹ C

Question 7.
The differential equation (x + y)dx + x dy = 0, is:
(a) homogeneous but not linear
(b) linear but not homogeneous
(c) both homogeneous and linear
(d) none of these
Answer:
(c) both homogeneous and linear

Question 8.
What is integrating factor of \(\frac{d y}{d x}\) + y sec x = tan x?
(a) sec x + tan x
(b) log (sec x + tan x)
(c) e^sec
(d) sec x
Answer:
(a) sec x + tan x

Question 9.
The order and degree of the differential equation
\(\left(\frac{d^3 y}{d x^3}\right)^2-3 \frac{d^2 y}{d x^2}+2\left(\frac{d y}{d x}\right)^4\) = y⁴ are
(a) 1, 4
(b) 3, 2
(c) 2, 4
(d) 3, 4
Answer:
(b) 3, 2

Question 10.
Integrating factor of the differential equation \(\frac{d y}{d x}\) + y = \(\frac{1+y}{x}\) is:
(a) e^x
(d) xe^x
(c) \(\frac{e^x}{x}\)
(d) \(\frac{x}{e^x}\)
Answer:
(c) \(\frac{e^x}{x}\)

Question 11.
The differential equation of the family of curves y² = 4a (x + a) is:
(a) 2y\(\frac{d y}{d x}\) = 4a
(b) y²\(\left(\frac{d y}{d x}\right)\) + 4y = 0
(c) y² = 4 \(\frac{d y}{d x}\left(x+\frac{d y}{d x}\right)\)
(d) \(y^2\left(\frac{d y}{d x}\right)^2+2 x y \frac{d y}{d x}-y^2\) = 0
Answer:
(d) \(y^2\left(\frac{d y}{d x}\right)^2+2 x y \frac{d y}{d x}-y^2\) = 0

Question 12.
Which of the following functions is a solution of the differential equation \(\left(\frac{d y}{d x}\right)^2-x \frac{d y}{d x}\) + y = 0?
(a) y = 2
(b) y = 2x
(c) y = 2x - 4
(d) y = 2x² - 4
Answer:
(c) y = 2x - 4

Question 13.
The solution of the differential equation
sin x cos y dy + cos x sin y dx = 0 is:
(a) sin x + sin y = c
(b) cos x + cos y = c
(c) sin x.sin y = c
(d) \(\frac{\sin x}{\sin y}\) = c
Answer:
(c) sin x.sin y = c

Question 14.
Which of the following is the integrating factor of x log\(\frac{d y}{d x}\) + y = 2 log x?
(a) x
(b) e^x
(c) log x
(d) log (log x)
Answer:
(c) log x

Question 15.
The solution of \(\frac{d y}{d x}+\sqrt{\frac{1-y^2}{1-x^2}}\) = 0 is:
(a) tan^-1 x + cot^-1 x = C
(b) sin^-1 x + sin^-1 y = C
(c) sec^-1 x + cosec^-1 x = C
(d) none of these
Answer:
(b) sin^-1 x + sin^-1 y = C

Fill in The Blanks

Question 1.
The degree of the differential equation 1 + \(\left(\frac{d y}{d x}\right)^2\) = x is ..........................
Answer:
2

Question 2.
The integrating factor of the differential equation x\(\frac{d y}{d x}\) + 2y = x² is ..................... .
Answer:
x²

Question 3.
The solution of the differential equation \(\frac{d y}{d x}\) = 2^-y is .........................
Answer:
2^y = x log 2 + C

Question 4.
The solution of the differential equation \(\frac{d y}{d x}\) = x³ e^-2y is .......................
Answer:
2e^2y = x⁴ + C

Question 5.
An equation involving derivative of the dependent variable with respect to the independent variable is called a ......................... equation.
Answer:
differential

True/False

Question 1.
A differential equation involving derivatives of the dependent variable with respect to only one independent variable is called an ordinary differential equation
Answer:
True

Question 2.
Order of a differential equation is the highest order derivative of the dependent variable
Answer:
True

Question 3.
Order and degree of a differential equation are always negative integers
Answer:
False

Question 4.
The solution which contains arbitrary constants is called the general solution of the differential equation
Answer:
True

Question 5.
The solution obtained from the general solution by giving particular values to the arbitrary constants is called a particular solution of the differential equation
Answer:
True