RBSE Class 12 Maths Important Questions Chapter 8 Application of Integrals

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 8 Application of Integrals Important Questions and Answers.

RBSE Class 12 Maths Chapter 8 Important Questions Application of Integrals

Question 1.
Using integration, find the area bounded by the curve x² = 4y and the line x = 4y - 2.
Answer:
Given curves are
x² = 4y ............. (i)
and x = 4y - 2 ................ (ii)
Eq. (i) represents a parabola with vertex at origin and axis along positive direction of Y-axis. Eq. (ii) represents a straight line which meets the coordinate axes at (- 2,0) and \(\left(0, \frac{1}{2}\right)\) respectively.
To find the points of intersection of the given parabola and the line, we solve Eq. (i) and (ii), simultaneously.
On substituting x = 4y - 2 in Eq. (i), we get
(4y - 2)² = 4y
⇒ 16y² + 4 - 16y = 4y
⇒ 16y² - 20y + 4 = 0
⇒ 4y² - 5y + 1 = 0
⇒ (4y - 1) (y - 1) = 0
⇒ y = 1, \(\frac{1}{4}\)
On putting the values of y in Eq. (ii), we get
x = 2,- 1
So, the points of intersection of the given parabola and the line are (2, 1) and (- 1, 1/4).

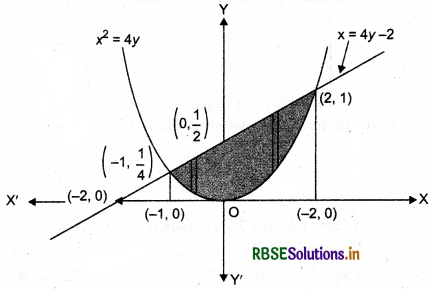
The region whose area is to be found out is shaded in the figure.
∴ Required area, A is:

Question 2.
Using integration, find the area of the region:
{(x, y):0 ≤ 2y ≤ x², 0 ≤ y ≤ x, 0 ≤ x ≤ 3}.
Answer:
Given region is:
{(x, y):0 ≤ 2y ≤ x², 0 ≤ y ≤ x, 0 ≤ x ≤ 3}.
which can be represented graphically as shown below.

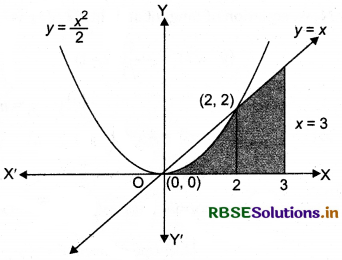
Now, let us find the point of intersection of y = x and y = \(\frac{x^2}{2}\)
For this consider,
x = \(\frac{x^2}{2}\)
⇒ x² - 2x = 0
⇒ x(x -2) = 0
⇒ x = 0 or 2
Clearly, when x = 0, then y = 0
and when x = 2, then y = 2
Thus, the points of intersection are (0, 0) and (2, 2).

Question 3.
Using integration, find the area of the triangle formed by positive X-axis and tangent and normal to the circle x² + y² = 4 at (1, √3).
Answer:
Given equation of circle is
x² + y² = 4
On differentiating both sides of equation (i), w.r.t. x, we get

Now, the Eqs. (ii) and (iii) can be represented in graph as shown below:

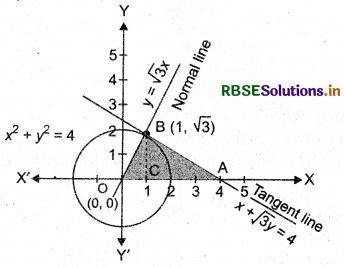
On putting y = 0 in Eq. (ii), we get
x + 0 = 4 ⇒ x = 4
∴ The tangent line x + √3y = 4 cuts the X-axis at A(4, 0).
∴ Required area = Area of shaded region OAB

Question 4.
Using integration, find the area of the region bounded by the lines 2x + y = 4, 3x - 2y = 6 and x - 3y + 5 = 0.
Answer:
Given lines are
2x + y = 4 ........... (i)
3x - 2y = 6 ............ (ii)
and x - 3y = - 5 .......... (iii)
Clearly, the line 2x + y = 4 passes through the points (2, 0) and (0, 4), the line 3x - 2y = 6 passes through the points (2, 0) and (0, - 3) and the line x - 3y = - 5 passes through the points (- 5, 0) and \(\left(0, \frac{5}{3}\right)\).
Now, the region bounded by these lines is shown below:

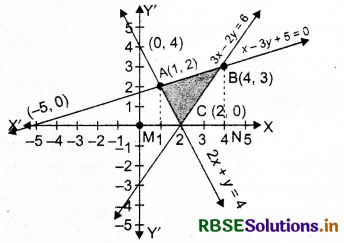
On solving Eqs. (i) and (ii), we get
x = 2 and y = 0
So, lines 2x + y = 4 and 3x - 2y = 6 meet at the point C(2, 0).
Again, solving Eqs. (ii) and (iii), we get
x = 4 and y = 3
So, lines 3x - 2y = 6 and x - 3y = - 5 meet at the point B(4, 3).
On solving Eqs. (iii) and (i), we get x = 1 and y = 2
So, lines 2x + y = 4 and x - 3y = - 5 meet at the point A(1, 2).
Now, required area of ∆ABC
= Area of region ABNMA - (Area of ∆AMC + Area of ∆BCN)

Question 5.
Find the area of the region bounded by the two parabolas x² = 4y and y² = 4x.
Answer:
Equations of given parabolas are
y² = 4x ........ (i)
x² = 4y ....... (ii)
Solving these equations, we get (0, 0) and (4, 4) their intersecting points as

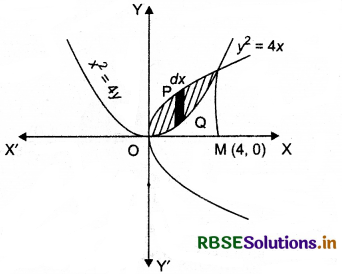
Required area = Area of OQAPO
= Area of OMAPO - Area of OMAQO

Question 6.
Find the area bounded by ellipse \(\frac{x^2}{25}+\frac{y^2}{16}\) = 1.
Answer:
Given equation are

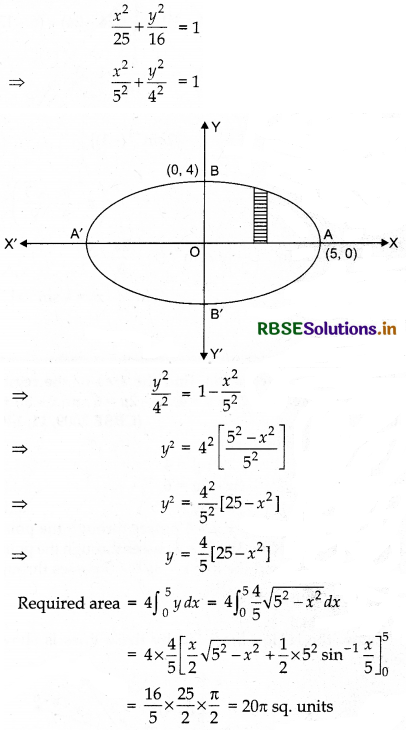
Multiple Choice Questions

Question 1.
The area enclosed between the curve y² = 4x and the line y = x is:
(a) 1/2 sq. unit
(b) 2/3 sq. unit
(c) 4/3 sq. unit
(d) 8/3 sq. unit
Answer:
(d) 8/3 sq. unit

Question 2.
The area of the region bounded by the parabola y = x² + 1 and the straight line x + y = 3 is given by:
(a) 45/7 sq. unit
(b) 25/4 sq. unit
(c) 9/4 sq. unit
(d) none of these
Answer:
(c) 9/4 sq. unit

Question 3.
The area of the region bounded by the lines x = 0, x = π/2 and f(x) = sin x, Φ(x) = cos x is:
(a) √3 - 1 sq. unit
(b) 2(√2 + 1) sq. unit
(c) 2(√3 - 1) sq. unit
(d) 2(√2 - 1) sq. unit
Answer:
(d) 2(√2 - 1) sq. unit

Question 4.
The area bounded by the curve x = at², y = 2at and the x-axis (1 ≤ t ≤ 3) is:
(a) 26 a² sq. unit
(b) 26 a²/3 sq. unit
(c) 104 a²/3 sq. unit
(d) 8 a² sq. unit
Answer:
(c) 104 a²/3 sq. unit

Question 5.
The area of the region bounded by the curve y = 2x - x² and the line y = x is:
(a) 1/6 sq. units
(b) 1/4 sq. units
(c) 1/3 sq. units
(d) 1/2 sq. units
Answer:
(a) 1/6 sq. units

Question 6.
The area between \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 and the straight line \(\frac{x}{a}+\frac{y}{b}\) = 1. is:
(a) \(\frac{1}{2}\) πab sq. units
(b) \(\frac{1}{4}\) ab sq. units
(c) \(\frac{1}{2}\) ab sq. units
(d) \(\frac{\pi a b}{4}-\frac{a b}{2}\) sq. units
Answer:
(d) \(\frac{\pi a b}{4}-\frac{a b}{2}\) sq. units

Question 7.
The area bounded by the curve y = sec x, the x-axis and the lines x = 0 and x = π/4 is:
(a) √2 sq.units
(b) \(\frac{1}{2}\) sq.units
(c) log (√2 + 1) sq. units
(d) log (√2 - 1) sq. units
Answer:
(c) log (√2 + 1) sq. units

Question 8.
The area bounded by the curve y = x² + 2, y = x, x = o and x = 3 is
(a) \(\frac{21}{3}\) sq. units
(b) \(\frac{21}{4}\) sq. units
(c) \(\frac{21}{2}\) sq. units
(d) none of these
Answer:
(c) \(\frac{21}{2}\) sq. units

Question 9.
The area of the figure bounded by the curves: y = sin x and x = 0, x = π, y = 0 is:
(a) 4 sq. units
(b) 3 sq. units
(c) 2 sq. units
(d) none of these
Answer:
(c) 2 sq. units

Question 10.
The area bounded by the curve y = sin x , x-axis and ordinates x = π and x = 10π is equal to:
(a) 8 sq. units
(b) 10 sq. units
(c) 18 sq. units
(d) 20 sq. units
Answer:
(c) 18 sq. units

Fill in the Blanks

Question 1.
The formulae of elementary ..................... allow us to calculate areas of many simple figures.
Answer:
geometry

Question 2.
If the position of the curve under consideration is below the x-axis, then the areas come out to be ........................
Answer:
negative

Question 3.
If the area is negative, we take its ............................. value.
Answer:
absolute

Question 4.
We can consider either .......................... strips or ..................... strips for calculating the area of the region.
Answer:
horizontal, vertical

Question 5.
The area of the region bounded by the y-axis, y = cos x and y = sin x, 0 ≤ x ≤ \(\frac{\pi}{2}\) is .......................
Answer:
(√2 - 1) sq.units

True/False

Question 1.
The formulae of elementary geometry allow us to calculate areas enclosed by curves.
Answer:
False

Question 2.
For calculating the areas enclosed by curves, we need the concepts of Integral Calculus.
Answer:
True

Question 3.
If the area is negative, we take its absolute value.
Answer:
True

Question 4.
The area bounded by the curve y = f(x), the X-axis and the ordinates x = a and x = b is calculated as
Area = \(\int_a^b x\) dy = \(\int_a^b\) f(y)dx.
Answer:
False

Question 5.
The area bounded by the curve x f(y), the Y-axis and the lines y = c and y = d is calculated as
Area = \(\int_a^b\) x dy = \(\int_a^b\) f(y) dy
Answer:
True