RBSE Class 12 Maths Important Questions Chapter 7 समाकलन

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 7 समाकलन Important Questions and Answers.

RBSE Class 12 Maths Chapter 7 Important Questions समाकलन

अन्य महत्त्वपूर्ण प्रश्

प्रश्न 1.
∫(sin^-1 x + cos^-1 x) dx बराबर है:
(A) \(\frac{\pi}{2}\)
(B) 0
(C) \(\frac{\pi}{2}\) x + C
(D) 1
उत्तर:
(C) \(\frac{\pi}{2}\) x + C

हल:
∫(sin^-1 x + cos^-1 x) dx = ∫\(\frac{\pi}{2}\) . dx = \(\frac{\pi}{2}\)∫dx = \(\frac{\pi}{2}\).x + C
अतः सही विकल्प (C) है।

प्रश्न 2.
∫\(\frac{d x}{x \log _e x}\) का मान होगा
(A) |log x| + C
(B) \(\frac{1}{x}\) + C
(C) log |log x| + C
(D) - \(\frac{1}{x^2}\) + C
उत्तर:
(C) log |log x| + C

हल:
∫\(\frac{d x}{x \log _e x}\) मान log_ex = t
\(\frac{1}{x}\) dx = dt
∴ ∫\(\frac{d t}{t}\) = log|t| C
= log |log x| + C
अतः सही विकल्प (C) है।

प्रश्न 3.
∫\(\frac{d x}{1-e^x}\) का मान बराबर होगा
(A) - log (1 - e^-x) + C
(B) log (1 + e^x) + C
(C) log (1 + e^-x) + C
(D) log \(\left(\frac{1+e^x}{e^{-x}}\right)\) + C
उत्तर:
(A) - log (1 - e^-x) + C

हल:

अतः सही विकल्प (A) है।

प्रश्न 4.
∫\(\frac{d x}{x^2-9}\) बराबर है-
(A) \(\frac{1}{6} \log \left(\frac{x-3}{x+3}\right)\) + C
(B) \(\frac{1}{6} \log \left(\frac{x+3}{x-3}\right)\) + C
(C) \(\frac{1}{3} \log \left(\frac{x-3}{x+3}\right)\) + C
(D) \(\frac{1}{3} \log \left(\frac{x+3}{x-3}\right)\) + C
उत्तर:
(A) \(\frac{1}{6} \log \left(\frac{x-3}{x+3}\right)\) + C

हल:

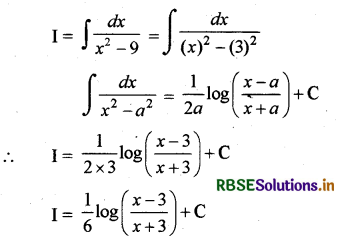
अतः सही विकल्प (A) है।

प्रश्न 5.
∫sin² x dx का मान होगा
(A) \(\frac{x}{2}+\frac{\sin 2 x}{4}\) + C
(B) \(\frac{x}{2}-\frac{\sin 2 x}{4}\) - C
(C) \(\frac{x}{2}+\frac{\cos 2 x}{4}\) + C
(D) \(\frac{x}{2}-\frac{\cos 2 x}{4}\) + C
उत्तर:
(B) \(\frac{x}{2}-\frac{\sin 2 x}{4}\) - C

हल:

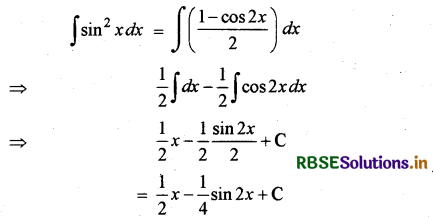
अतः सही विकल्प (B) है।

प्रश्न 6.
\(\int_0^{\pi / 4}\) tan² x dx का मान है-
(A) 1 - \(\frac{\pi}{4}\)
(B) 1 + \(\frac{\pi}{4}\)
(C) - 1 + \(\frac{\pi}{4}\)
(D) - 1 - \(\frac{\pi}{4}\)
उत्तर:
(A) 1 - \(\frac{\pi}{4}\)

हल:

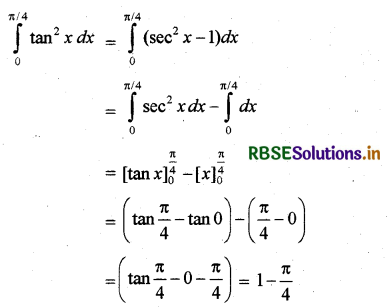
अतः सही विकल्प (A) है।

प्रश्न 7.
\(\int_0^1 \log \left(\frac{1}{x}-1\right)\) dx का मान है-
(A) 0
(B) 1
(C) log 2
(D) log \(\frac{3}{2}\)
उत्तर:
(A) 0

हल:

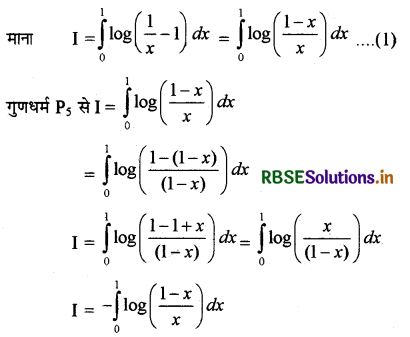
अतः सही विकल्प (A) है।

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
\(\int \frac{\sin ^3 x+\cos ^3 x}{\sin ^2 x \cos ^2 x}\) dx का मान ज्ञात कीजिये।
हल:

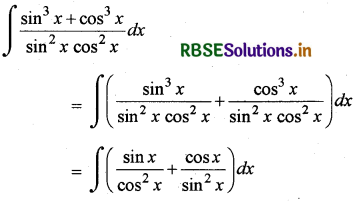
= ∫(tan x sec x + cot x cosec x) dx
= ∫tan x sec x dx + ∫cot x cosec x dx
= sec x - cosec x + C

प्रश्न 2.
∫2^x dx का मान ज्ञात कीजिए।
हल:
∫2^x dx = \(\frac{2^x}{\log 2}\) + C
चूँकि हम जानते हैं
∫a^x dx = \(\frac{a^x}{\log _e a}\) + C होता है।

प्रश्न 3.
∫\(\frac{1}{x}\) dx का मान ज्ञात कीजिए।
हल:
∫\(\frac{1}{x}\) dx = log x + C

प्रश्न 4.
∫b^2x db का मान ज्ञात कीजिए।
हल:
∫b^2x db
यहाँ पर हमें समाकलन 6 के सापेक्ष करना है

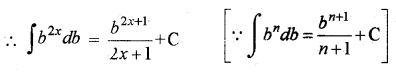
प्रश्न 5.
∫\(\sqrt{1-\sin 2 x}\) dx का मान ज्ञात कीजिए।
हल:

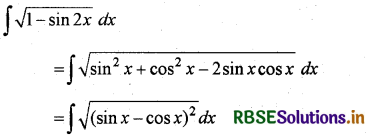
= ∫(sin x - cos x) dx = ∫sin x dx - ∫cos x dx
= - cos x – sin x + C

प्रश्न 6.
∫(1 + x) (1 + x²) (1 - x) dx का मान ज्ञात कीजिए।
हल:
∫(1 + x) (1 + x²) (1 - x) dx
⇒ ∫(1 + x) (1 - x) (1 + x²) dx
⇒ ∫(1 - x²) (1 + x²) dx
⇒ ∫(1 - x⁴) dx = ∫dx - ∫x⁴ dx
⇒ x - \(\frac{x^5}{5}\) + C

प्रश्न 7.
∫e^{3 log_e x} dx का मान लिखिए।
हल:
माना I = ∫e^{3 log_e x} dx
= ∫e^{log_e x3} dx = ∫x³ dx = \(\frac{1}{4}\) x⁴ + C

प्रश्न 8.
निम्न फलन का x के सापेक्ष समाकलन कीजिए-
\(\frac{1-x^2}{1+x^2}\)
हल:
माना I = ∫\(\frac{1-x^2}{1+x^2}\) dx
यहाँ पर बीजीय फलन में अंश के बहुपद की घात, हर के बहुपद की घात के बराबर है। इसलिये अंश में हर का भाग देकर समाकलन किया जा सकता है।

प्रश्न 9.
निम्न फलन का समाकलन कीजिए-
cos³ x. e^log_e sin x
हल:
मानाI = ∫cos³ x. e^log_e sin x dx
हम जानते हैं e_{loge x} होता है
∴ I = ∫cos³ x . sin x dx
माना (put) cos x = t
- sin x dx = dt
⇒ sin x dx = - dt

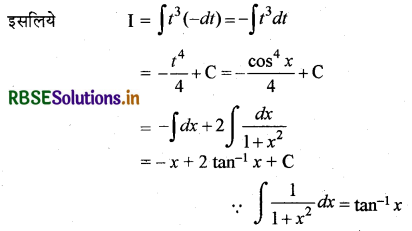
प्रश्न 10.
∫cosec² x sec² x dx ज्ञात लिखिए|
हल:
∫cosec² x sec² x dx

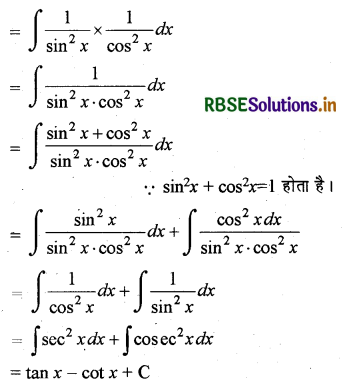
प्रश्न 11.
\(\int \frac{\sin x^{1 / 3}}{x^{2 / 3}}\) dx का मान लिखिए
हल:

⇒ 3∫sin t dt ⇒ 3(- cos t) + C
⇒ - 3 cos t + C ⇒ - 3 cos x^{\(\frac{1}{3}\)} + C

प्रश्न 12.
∫sin² x dx का मान ज्ञात कीजिए।
हल:
माना I = ∫sin² x dx

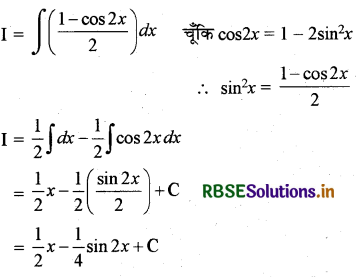
प्रश्न 13.
\(\int \frac{e^x d x}{\sqrt{1-e^{2 x}}}\) का मान लिखिए।
हल:

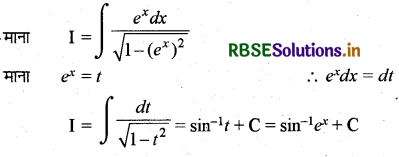
प्रश्न 14.
\(\int \frac{x d x}{\left(1-x^2\right)^{3 / 2}}\) का मान लिखिए।
हल:

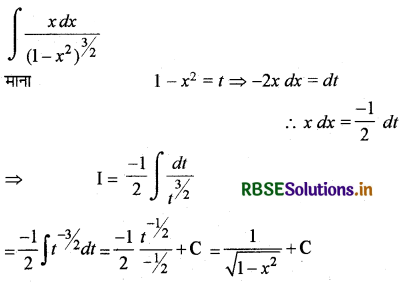
प्रश्न 15.
∫log_a x dx का मान ज्ञात कीजिए।
हल:
माना I = ∫log_a x dx
आधार परिवर्तन करने पर
I = ∫log_ex . log_a e dx

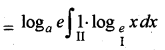
इकाई को द्वितीय फलन लेकर खण्डशः समाकलन करने पर
I = log_a e[log_e x . x - ∫\(\frac{1}{x}\) . x dx]
= log_a e[x log_ex - x] + C
= x log_a e[log_ex - 1] + C

प्रश्न 16.
∫x cosec² x dx का मान लिखिए।
हल:

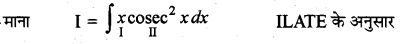
I = x(- cot x) - ∫1.(- cot x) dx
= - x cot x + ∫cot x dx
= - x cot x + log sin x + C

प्रश्न 17.
\(\int_0^{\frac{\pi}{2}} \sqrt{1+\sin x}\) dx का मान लिखिए।
हल:

प्रश्न 18.
\(\int_{-4}^4\) |x| dx का मान लिखिए।
हल:

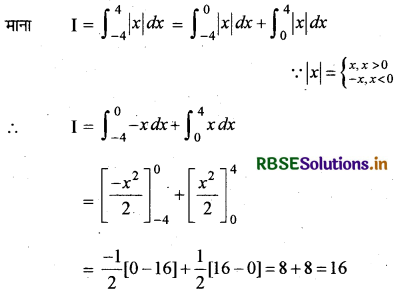
प्रश्न 19.
\(\int_0^\pi\) sin² x dx का मान लिखिए।
हल:

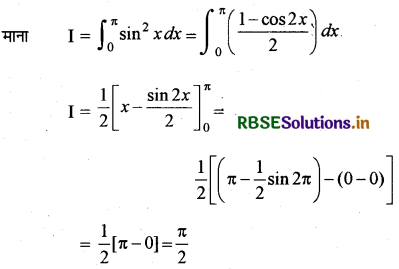
प्रश्न 20.
\(\int_0^1 \frac{\left(x^2-x\right)}{\sqrt{x}}\) dx का मान लिखिए।
हाल:

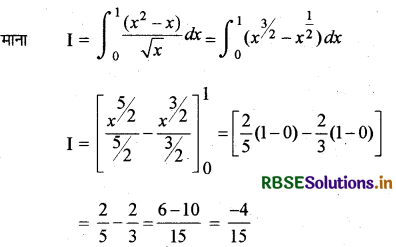
प्रश्न 21.
\(\int_0^a \frac{d x}{\sqrt{a^2-x^2}}\) का मान लिखिए।
हाल:

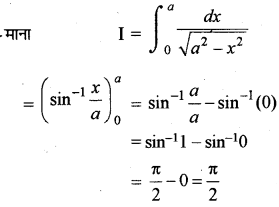
प्रश्न 22.
\(\int_0^1 \frac{d x}{x^2+2 x+2}\) का मान ज्ञात कीजिए।
हाल:

प्रश्न 23.
मान ज्ञात कीजिए
\(\int_0^2 \sqrt{4-x^2}\) dx
हल:

प्रश्न 24.
मान ज्ञात कीजिए: ∫a^{3 log_a x} dx
हल:
माना = ∫a^{3 log_a x} dx
या I = ∫a^{log_a x 3} ∵ log_a mⁿ = n log_am
हम जानते हैं e^log_ex = x होता है।
∴ I = ∫x³ dx = \(\frac{x^4}{4}\) + C

प्रश्न 25.
मान ज्ञात कीजिए: \(\int_1^2 \frac{x e^x}{(1+x)^2}\) dx
हल:

प्रश्न 26.
हल कीजिए : ∫cos^-1 (sin x) dx
हल:
I = ∫cos^-1 (sin x) dx
= ∫cos^-1 [cos\(\left(\frac{\pi}{2}-x\right)\)] dx
= ∫\(\left(\frac{\pi}{2}-x\right)\) dx = \(\frac{\pi}{2}\)∫dx - ∫x dx
= \(\frac{\pi}{2}\)x - \(\frac{x^2}{2}\) + C

लघूत्तरात्मक प्रश्न

प्रश्न 1.
\(\int \frac{\sin 2 x}{a \sin ^2 x+b \cos ^2 x}\) dx का मान ज्ञात कीजिये।
हल:
माना I = ∫\(\frac{\sin 2 x}{a \sin ^2 x+b \cos ^2 x}\) dx
माना (put) a sin²x + b cos² x = t^
{2a sin x cos x + 2 b cos x (- sin x)} dx = dt
⇒ (a - b) sin 2x dx = dt

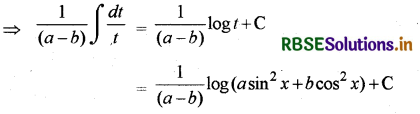
प्रश्न 2.
\(\int \frac{\sin 2 x d x}{(a-b \cos x)^2}\) का मान ज्ञात कीजिये।
हल:

प्रश्न 3.
\(\int \frac{\sec ^2 x d x}{\tan x \sqrt{\tan ^2 x-1}}\) का मान ज्ञात कीजिये।
हल:
माना I = \(\int \frac{\sec ^2 x d x}{\tan x \sqrt{\tan ^2 x-1}}\) dx
माना (Put) tan x = t
⇒ sec² x dx = dt
अतः \(\int \frac{d t}{t \sqrt{t^2-1}}\) = sec^-1 (t) + C
= sec^-1 (tan x) + C

प्रश्न 4.
∫\(\frac{\sin x}{\sqrt{1+\sin x}}\) dx का मान ज्ञात कीजिये।
हल:

प्रश्न 5.
फलन \(\frac{x}{1+\sin x}\) का x के सापेक्ष समाकलन कीजिये।
हल:

I = x ∙ tan x - ∫1 ∙ tan x dx - [x ∙ sec x - ∫1 ∙ sec x dx]
= x tan x - ∫tan x dx - x sec x + ∫sec x dx
= x tan x - log sec x - x sec x + log (sec x + tan x) + C
= x (tan x - sec x) + log \(\left(\frac{\sec x+\tan x}{\sec x}\right)\) + C

प्रश्न 6.
फलन \(\frac{\sin ^{-1} x}{\left(1-x^2\right)^{3 / 2}}\) का x के सापेक्ष समाकलन कीजिये।
हल:

प्रश्न 7.
फलन \(\frac{e^{a \tan ^{-1} x}}{\left(1+x^2\right)^{3 / 2}}\) का x के सापेक्ष समाकलन कीजिये।
हल:

प्रश्न 8.
फलन \(\frac{\log x}{(1+\log x)^2}\) का x के सापेक्ष समाकलन कीजिये।
हल:

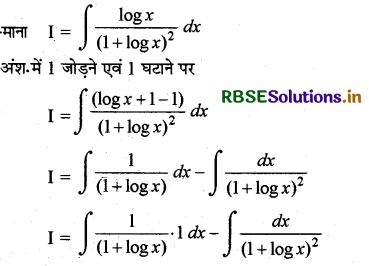
प्रथम समाकलन में '1' इकाई को द्वितीय फलन लेकर खण्डशः
समाकलन करने पर

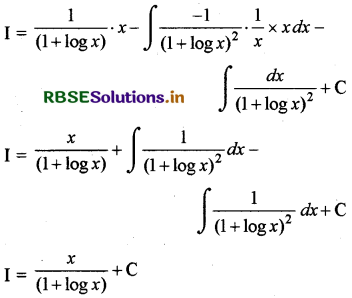
प्रश्न 9.
मान ज्ञात कीजिए: ∫\(\sqrt{5-4 x-x^2}\) dx.
हल:

प्रश्न 10.
सिद्ध कीजिये कि-
\(\int_a^b \frac{f(x) d x}{f(x)+f(a+b-x)}=\frac{b-a}{2}\)
हल:

प्रश्न 11.
\(\int_0^\pi \frac{e^{\cos x}}{e^{\cos x}+e^{-\cos x}}\) dx का मान ज्ञात कीजिये।
हल:

प्रश्न 12.
मान ज्ञात कीजिये
\(\int \frac{x^3}{(x-1)\left(x^2+1\right)}\) dx
हल:

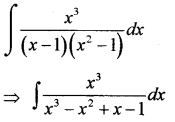
यहाँ पर अंश तथा हर की घातें बराबर हैं। इसलिए अंश में हर का भाग देने पर हमें प्राप्त होता है।

प्रश्न 13.
मान ज्ञात कीजिये
\(\int \frac{\sin x-x \cos x}{x(x+\sin x)}\) dx
हल:
माना

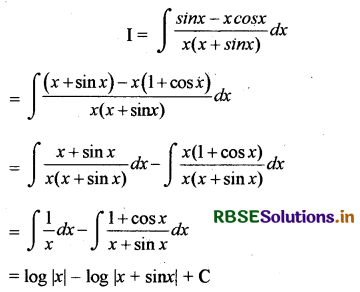
प्रश्न 14.
ज्ञात कीजिए \(\int \frac{d x}{\sqrt{9+8 x-x^2}}\)
हल:
माना

निबन्धात्मक प्रश्न

प्रश्न 1.
मान ज्ञात कीजिये
\(\int \frac{x^2 d x}{(x \sin x+\cos x)^2} \)
हल:

प्रश्न 2.
∫e^x\(\left(\frac{1-x}{1+x}\right)^2\) का मान ज्ञात कीजिये।
हल:

अत: इसका रूप ∫[f(x) + f"(x)]e^x dx का है।
अतः इसका मान e^x f(x) + C होता है।
इसलिये इसका मान होगा

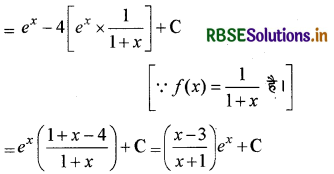
प्रश्न 3.
मान ज्ञात कीजिये
\(\int_{-\pi}^\pi \frac{2 x(1+\sin x)}{1+\cos ^2 x}\) dx
हल:

प्रश्न 4.
मान ज्ञात कीजिये
\(\int_0^{\frac{\pi}{2}} \frac{x \sin x \cos x}{\sin ^4 x+\cos ^4 x}\) dx
हल:

प्रश्न 5.
मान ज्ञात कीजिये-
\(\int_0^{\frac{\pi}{2}} \frac{\cos ^2 x}{1+3 \sin ^2 x}\) dx
हल:
माना कि

प्रश्न 6.
मान ज्ञात कीजिये-
\(\int_0^{\frac{\pi}{4}}\left(\frac{\sin x+\cos x}{3+\sin 2 x}\right)\) dx
हल:
माना कि
I = \(\int_0^{\frac{\pi}{4}}\left(\frac{\sin x+\cos x}{3+\sin 2 x}\right)\) dx
यहाँ पर sinx - cosx = t रखने पर
(cos x + sin x) dx = dt
अतः यदि x = \(\frac{\pi}{4}\) तो t = 0 तथा यदि
x = 0 तो t = - 1
(sin x - cos x)² = 1 - 2 sin x cosx = 1 - sin 2x
∴ sin 2x = 1 - (sin x - cos x)
= 1 - t²