RBSE Class 12 Maths Important Questions Chapter 6 Application of Derivatives

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 6 Application of Derivatives Important Questions and Answers.

RBSE Class 12 Maths Chapter 6 Important Questions Application of Derivatives

Question 1.
The surface area of a spherical bubble is increasing at the rate of 2 cm²/s. When the radius of the bubble is 6 cm. at that rate is the volume of the bubble increasing?
Answer:
Let r, V and S be respectively the radius, volume and surface area of the spherical bubble at time t.
∴ V = \(\frac{4}{3}\) πr³
and S = 4πr²
Given, the rate of change of surface area with respect to ‘t’ is

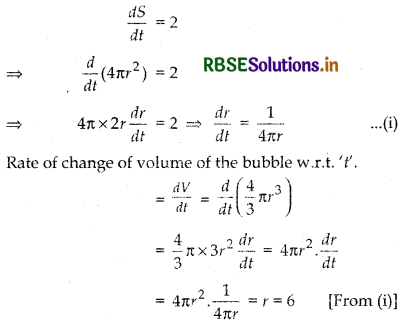
Thus, the volume of the spherical bubble is increasing at the rate of 6 cm³/sec.

 

Question 2.
Find the point on the curve y² = 8x for which the abscissa and ordinate change at the same rate.
Answer:
Let the required point be (x, y).
Given, \(\frac{d y}{d x}\) = \(\frac{d x}{d t}\) ........... (i)
And y² = 8x ......... (ii)
On differentiating both sides of equLition (ii) a’.r.t.’t’,
we get
2y\(\frac{d y}{d x}\) = 8. \(\frac{d x}{d t}\) ⇒ 2y = 8 [From (i)i
⇒ y = 4
On putting y = 4 in equation (ii), we get
8x = 16 ⇒ x = 2
Thus, the required point is (2, 4).

Question 3.
The volume of a spherical.balloon is increasing at a rate of 25 cm³/sec. Find the rate of change of its surface area at the instant when radius is 5 cm.
Answer:
Let r be the radius, V he the volume and S be the surface area of a sphere at any instant ‘t’.

Question 4.
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.
Answer:
Given that length x of a rectangle is decreasing at the rate of 5 cm/mm.
∴ \(\frac{d x}{d t}\) = - 5 cm/min ............ (i)
Also, the breadth y of rectangle is increasing at the rate of 4 cm/min.
∴ \(\frac{d y}{d t}\) = 4 cm/min ............ (ii)

(i) Here, we have to find rate of change of perimeter, i.e. dP/dt and we know that, perimeter P = 2(x + y)
On differentiating both sides w.r.t. t, we get
\(\frac{d P}{d t}=2\left(\frac{d x}{d t}+\frac{d y}{d t}\right)\)
⇒ \(\frac{d P}{d t}\) = 2 (- 5 + 4) = 2(- 1) = - 2 cm/min
[From Eqs. (i) and (ii)]
Hence, perimeter of rectangle is decreasing at the rate of 2 cm/min.

(ii) Here, we have to find rate of change of area \(\frac{d A}{d t}\).
We know that, area of rectangle A = xy
On differentiating both sides w.r.t. t, we get

Thus, the area of rectangle is increasing at the rate of 2 cm/mm.

Question 5.
The radius of a cylinder is increasing at the rate of 2 cm/sec and its altitude is decreasing at the rate of 3 cm/sec. Find the rate of change of volume when radius is 3 cm and altitude is 5 cm.
Answer:
Let the radius and height of cylinder be r and h respectively.
Given, \(\frac{d r}{d t}\) = 2 cm/s
and \(\frac{d h}{d t}\) = - 3 cm/s
Also, V = πr²h
On differentiating w.r.t 't', we get
\(\frac{d V}{d t}=\pi\left[r^2 \frac{d h}{d t}+h .2 r \frac{d r}{d t}\right]\)
At r = 4 cm and h = 5 cm
\(\frac{d V}{d t}\) = π[(4)² × (- 3) + 2(5) (4) × 2]
= π[- 48 + 80] = 32 π cm³/s
Thus, the rate of change of volume is 32 π cm³/s.

Question 6.
The money to be spend for the welfare of the employees of a firm is proportional to the rate of change of its total revenue (Marginal revenue). If the total revenue (in rupees) received from the sale of x units of a product is given by
R(x) = 3x² + 36x + 5
Find the marginal revenue, when x = 5 and write which value does the question indicate.
Answer:
Marginal Revenue (MR)
= \(\frac{d R}{d x}\) = \(\frac{d}{d x}\) (3x² + 36x + 5) = 6x + 36
∴ When x = 5, then
Marginal Revenue (MR) = 6 × 5 + 36 = 66

Question 7.
Find the intervals on which the following functions are increasing and decreasing:
(i) f(x) = 2x³ - 15x² + 36x + 1
Answer:
Given, f(x) = 2x³ - 15x² + 36x + 1
On differentiating both sides w.r.t.’x’, we get
f’(x) = 6x² - 30x + 36
⇒ f’(x) = 6(x² - 5x + 6)
= 6[x² - 3x - 2x + 6]
= 6[x(x - 3) - 2(x - 3)]
= 6 [(x - 3) (x - 2)]
Now, put f’(x) = 0
⇒ 6(x - 3) (x - 2) = 2
⇒ x = 3, 2
The points x = 2 and x = 3 divide the real line into three disjoint intervals (- ∞, 2), (2, 3) and (3, ∞)

Note that,
x ∈ (- ∞, 2), f’(x) > 0
x ∈ (2, 3), f’(x) < 0 X ∈ (3, ∞), f’(x) > 0
Thus, f (x) is increasing in the interval (- ∞, 2) and (3, ∞) and f (x) is decreasing in the interval (2, 3).

(ii) f(x) = 2x³ + 9x² + 12x + 20
Answer:
Given, f(x) = 2x³ + 9x² + 12x + 20
On differentiating both sides w.r.t. x, we get
f’(x) = 6x² + 18x + 12
Put f ‘(x) =0, we get
6x² + 18x + 12 = 0
⇒ 6(x² + 3x + 2) = 0
⇒ 6(x + 1) (x + 2) = 0
= (x + 1) (x + 2) = 0
Either x + 1 = 0 or x + 2 = 0
∴ x = - 2, - 1
Now, we find intervals and check in which interval
f(x) is strictly increasing and strictly decreasing.

We know that, a function f (x) is said to be strictly increasing function, if f ‘(x) > 0 and strictly decreasing, if f ‘(x) < 0. So, given function is increasing on intervals (- ∞, - 2) and (- 1, ∞)) and decreasing on interval (- 2, -1).
Since, f(x) is a polynomial function, so it is continuous at x = - 1, - 2.
Thus, given function is
(a) increasing on intervals (- ∞, - 2] and [- 1, ∞).
(b) decreasing on interval [-2, - 1].

(iii) f(x) = x³ - 12x² + 36x + 17
Answer:
Given f(x) = x³ - 12x² + 36x + 17
On differentiating both sides w.r.t.’x’, we get
f’(x) = 3x² - 24x + 36
⇒ f'(x) = 3(x² - 8x + 12)
= 3[x² - 6x - 2x + 12]
= 3[x(x - 6) - 2 (x - 6)]
= 3(x - 2) (x - 6)
Now, put f’(x) = 0
⇒ 3(x - 2) (x - 6) = 0
⇒ x = 2, 6
The points x = 2 and x = 6 divide the real line into three intervals (- ∞, 2), (2, 6) and (6, ∞)

Note that
for x ∈ (- ∞, 2),f’(x) > 0
for x ∈ (2, 6), f‘(x) < 0 for x ∈ (6, ∞), f ‘(x) > 0
Thus, the given function is increasing on intervals (-∞, 2) and (6, ∞) and decreasing on interval (2, 6).

(iv) f(x) = x³ - 6x² + 9 x + 15
Answer:
Given f(x) = x³ - 6x² + 9x + 15
On differentiating both sides w.r.t.’x’, we get
⇒ f’(x) = 3x² - 12x + 9
⇒ f’(x) = 3(x² - 4x + 3)
= 3[x² - 3x - x + 3]
= 3[x(x - 3) - 1 (x - 3)]
= 3(x - 1) (x - 3)
Now, put f’(x) = 0
⇒ 3(x - 1) (x - 3) = 0
x = 1, 3
The points x = 1 and x = 3 divide the real line into three intervals (- ∞, 1), (1, 3) and (3, ∞)

Note that
for x ∈ (- ∞, 1), f’(x) > 0
for x ∈ (1, 3), f’(x) < 0 for x ∈ (3, ∞), f ‘(x) > 0
Thus, the given function is increasing on intervals (- ∞, 1) and (3, ∞) and decreasing on interval (1, 3).

(v) f(x) = 3x⁴ - 4x³ - 12x² + 15
Answer:
Given f(x) = 3x⁴ - 4x³ - 12x² + 15
On differentiating both sides w.r.t.x’, we get
f’(x) = 12x³ - 12x² - 24x
= 12x(x² - x - 2)
= 12x[x² - 2x + x - 2]
= 12x[x(x - 2) + 1(x - 2)]
= 12x(x + 1) (x - 2)
Now, put f’(x) = 0
⇒ 12x(x + 1) (x - 2) = 0
⇒ x = 0, - 1, 2
The points x = 0 and x = - 1 and x = 2 divide the real line into four intervals (- ∞, - 1), (- 1, 0), (0, 2) and (2, ∞)

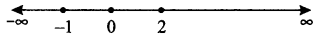
Note that
for x ∈ (- ∞, - 1), f ‘(x) < 0 for x ∈ (- 1, 0),f ‘(x) > 0
for x ∈ (0, 2), f ‘(x) < 0 for X ∈ (2, ∞), f‘(x) > 0
Thus, the given function is increasing on intervals (- 1, 0) and (2, ∞) and decreasing on interval (- ∞, - 1) and (0, 2).

(vi) f(x) = \(\frac{3}{2}\)x⁴ - 4x³ - 45x² + 51
Answer:
Given f(x) = \(\frac{3}{2}\)x⁴ - 4x³ - 45x² + 51
On differentiating both is sides w.r.t 'x', we get
f’(x) = \(\frac{3}{2}\) × 4x³ - 4 × 3x² - 45 × 2x + 0
= 6x³ - 12x² + 90x
= 6x (x² - 2x - 15]
= 6x[x² - 5x + 3x - 15]
= 6x[x(x - 5) + 3(x - 5)]
= 6x(x + 3) (x - 5)
Now, put f’(x) = 0
⇒ 6x(x + 3) (x - 5) = 0
⇒ x = 0, -3, 5
The points x = 0, x = - 3 and x = 5 divide the real line into four disjoints intervals namely (- ∞, - 3), (- 3, 0), (0, 5) and (5, ∞).

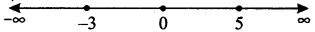
Note that
for x ∈ (- ∞, - 3), f’(x) <0 for x ∈ (- 3, 0), f’(x) > 0
for x ∈ (0, 5), f’(x) < 0 for x ∈ (5, ∞), f’(x) > 0
Thus, the given function is increasing on intervals (- 3, 0) and (5, ∞); and it is decreasing on intervals (- ∞, - 3) and (0, 5).

(vii) f(x) = log (2 + x) - \(\frac{2 x}{2+x}\) X ∈ R
Answer:
Given f(x) = log (2 + x) - \(\frac{2 x}{2+x}\)
On differentiating both sides w.r.t. 'x', we get

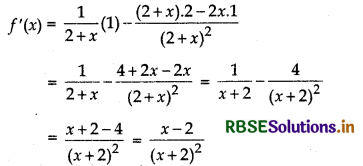
Now, (x + 2)² is always positive.
Also, x - 2 > 0 for x > 2.
And, x - 2 < 0 for x < 2. So, f ‘(x) > 0 for x > 2.
And, f (x) < 0 for x < 2.
Thus, the given function increases on intervals (2, ∞) and decreases on interval (- ∞, 2).

Question 8.
Show that f (x) = e^2x is increasing on R.
Answer:
Let x₁ and x₂ be real numbers such that
x₁ < x₂
Multiplying both sides by 2, we have
2x₁ < 2x₂
Taking exponential on both sides, we have
e^2x₁ < e^2x₂
⇒ f(x₁) < f(x₂)
Thus, f(x) is strictly increasing on R.
Hence proved

Question 9.
Prove that the function f(x) = x³ - 6x² + 12x - 18 is increasing on R.
Answer:
Given, f(x) = x³ - 6x + 12x - 18
On differentiating both sides w.r.t.’x, we get
f’(x) = 3x² - 12x + 12
= 3(x² - 4x + 4)
∴ f’(x) > 0
This shows that the given function is increasing on R.
Hence proved.

Question 10.
Find the intervals in which fix) = (x + 2)e^-x is increasing or decreasing.
Answer:
Given, f(x) = (x + 2)e^-x
On differentiating both sides w.r.t.’x’, we get
f’(x) = (x + 2)e^-x (- 1) + e^-x (1 + 0)
= - (x + 2)e^-x + e^-x
= e^-x (- x - 2 + 1)
= e^-x (- x - 1)
= - e^-x (x + 1)
Now, put f’(x) = 0 ⇒ - e^-x(x + 1) = 0 ⇒ x = - 1
Note that
for x ∈ (- ∞, - 1),f’(x) > 0
for x ∈ (- 1, ∞),f’(x) < 0
Thus, the given function increases for (- 1, ∞) and decreases for (- ∞, - 1).

Question 11.
Find the intervals in which fix) = log (1 + x) - \(\frac{x}{1+x}\) is increasing or decreasing.
Answer:
Given, f(x) = log (1 + x) - \(\frac{x}{1+x}\)
On differentiating both sides w.r,t.’x’, we get

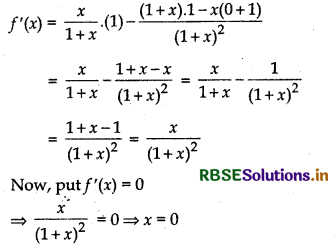
Note that
for x ∈ (- ∞, 0), f’(x) < 0 for x ∈ (0, ∞), f'(x) > 0
Thus, the given function increases for (0, ∞) and decreases for (- ∞, 0).

Question 12.
Prove that the function f (x) = 4x³ - 18x² + 27x - 27 is increasing on R.
Answer:
We have, f (x) = 4x³ - 18x² + 27x - 27
On differentiating both sides w.r.t. x, we get
f’(x) = 12x² - 36x + 27
⇒ f’(x) = 3(4x² - 12x + 9)
⇒ f’(x) = 3(2x - 3)²
⇒ f’(x) ≥ 0
⇒ For any x ∈ R, (2x - 3)² ≥ 0
Since, a perfect square number cannot be negative, so, the given function f(x) is an increasing function on R.
Hence proved

Question 13.
Find the equation of the tangent and the normal to 16x² + 9y² = 145 at (x₁, y₁) where x₁ = 2 and y₁ > 0.
Answer:
Given equation of curve is
16x² + 9y² = 145
Clearly, when x = 2, then
16(2)² + 9y² = 145
⇒ 9y² = 145 - 64
⇒ 9y² = 81
⇒ y² = 9
y = ±3
[taking square root on both sides]
But it is given that y₁ > 0
∴ y = 3
Thus, the point of contact (x₁, y₁) = (2, 3)
Now, on differentiating both sides of Eq. (i) w.r.t. x, we get

Now, equation of tangent at point (2, 3) is
(y - 3) = \(\frac{-32}{27}\)(x - 2)
⇒ 32x + 27y = 145
and equation of normal at point (2, 3) is
(y - 3) = \(\frac{27}{32}\)(x - 2)
Thus, 27x - 32y = - 42

Question 14.
Find all the tangents to the curve y = cos (x + y), - 2π ≤ x ≤ 2π. that are parallel to the line x + 2y = 0.
Answer:
Given equation of curve is
y = cos(x + y), - 2π ≤ x ≤ 2π ........ (i)
and equation of line is x + 2y = 0 ...... (ii)
⇒ y = - \(\frac{1}{2}\) x
Clearly, slope of tangents to the curve is - \(\frac{1}{2}\).
Let (x₁, y₁) be the point of contact, then we have
y₁ = cos(x₁ + y₁) [from Eq. (i)] ......... (iii)
and slope of tangent = \(\left(\frac{d y}{d x}\right)_{\left(x_1, y_1\right)}\)
= \(\frac{-\sin \left(x_1+y_1\right)}{1+\sin \left(x_1+y_1\right)}\)

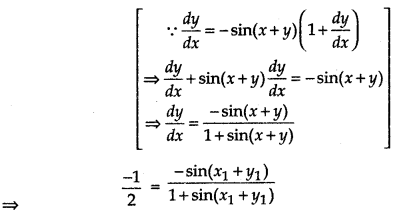
⇒ 1 + sin(x₁ + y₁) = 2 sin(x₁ + y₁)
⇒ sin(x₁ + y₁) = 1 ....... (iv)
On squaring and adding Eqs. (iii) and (iv), we get
cos²(x₁ + y₁) + sin²(x₁ + y₁) = 1 + y₁²
⇒ 1 + y₁² = 1
⇒ y₁² = 0
⇒ y₁ = 0
On putting y₁ = 0 in Eq. (iii), we get cos x₁ = 0

Question 15.
Find the equations of tangent and normal to the following curves at the indicated points:
(i) y² = 4ax at (x₁, y₁)
Answer:
Given equation of curve is y² = 4ax
Differentiating both sides w.r.t. ’x’, we get

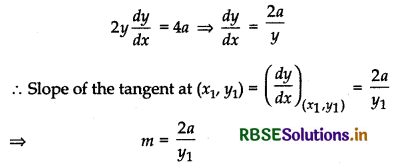
Equation of tangent at point(x₁, y₁) is
y - y₁ = m(x - x₁)
⇒ y - y₁ = \(\frac{2 a}{y_1}\)(x - x₁)
⇒ yy₁ - y₁² = 2ax - 2ax₁
⇒ y₁² = 2ax₁ + yy₁ - 2ax
And slope of normal at point (x₁, y₁)
⇒ m’ = \(\frac{-1}{m}=\frac{-1}{\frac{2 a}{y}}\) ⇒ m’ = \(\frac{-y}{2 a}\)
Equation of normal at point (x₁, y₁) is:
y - y₁ = m’ (x - x₁)
⇒ y - y₁ = \(\frac{-y}{2 a}\)(x - x₁)
⇒ 2ay - 2ay₁ = - xy + x₁y

(ii) \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 at (√2a, b)
Answer:
Given equation of curve is:

Question 16.
The equation of the tangent at (2, 3) on the curve y² = ax³ + b is y = 4x - 5. Find the values of a and b.
Answer:
Given, equation of the curve is
y² = ax³ + 1 .......... (i)
and equation of tangent is
y = 4x - 5 ......... (ii)
On differentiating both sides of Eq. (i) w.r.t. x, we get
2y\(\frac{d y}{d x}\) = 3ax² ⇒ \(\frac{d y}{d x}\) = \(\frac{3 a x^2}{2 y}\)
Now, slope of tangent at (2, 3) = \(\left(\frac{d y}{d x}\right)_{(2,3)}\)
= \(\frac{3 a(2)^2}{2(3)}\) = 2a
But, from Eq. (ii), we have slope of tangent 4
∴ 2a ⇒ 4 a = 2
Since, (2, 3) lies on the curve, therefore from Eq. (i),
we get
9 = 8a + b ⇒ 9 = 16 + b [∵ a = 2]
⇒ b = - 7
Thus, a = 2 and b = - 7

Question 17.
Find an equation of normal line to the curve y = x³ + 2x + 6 which is parallel to the line x + 14y + 4 = 0
Answer:
Given equation of curve is
y = x³ + 2x + 6 .............. (i)
and the given equation of line is
x + 14y + 4 = 0
On differentiating both sides of Eq. (i) w.r.t. x, we get
\(\frac{d y}{d x}\) = 3x² + 2
∴ Slope of normal = \(\frac{-1}{\left(\frac{d y}{d x}\right)}=\frac{-1}{3 x^2+2}\)
Also, slope of the line x + 14y + 4 = 0 is - \(\frac{1}{14}\)
[∵ slope of the line Ax + By + C = 0 is - \(\frac{A}{B}\)]
We know that, if two lines are parallel, then their slopes are equal.
\(-\frac{1}{3 x^2+2}=-\frac{1}{14}\)
⇒ 3x² = 12 ⇒ x² = 4
⇒ x = ±2
When x = 2, then from Eq. (i),
y = (2)³ + 2(2) + 6 = 8 + 4 + 6 = 18
and when x = - 2, then from Eq. (1),
y = (- 2)³ + 2(- 2) + 6 = - 6
∴ Normal passes through (2, 18) and (- 2, - 6).
Also, slope of normal = \(\frac{-1}{14}\)
Hence, equation of normal at point (2, 18) is
⇒ y - 18 = \(\frac{-1}{14}\) (x - 2) ⇒ 14y - 252 = - x + 2
⇒ x + 14y = 254
and equation of normal at point (- 2, - 6) is
y + 6 = - \(\frac{1}{14}\) (x + 2).
⇒ 14y + 84 = - x - 2
⇒ x + 14y = - 86
Hence, the two equations of normal are x + 14y = 254 and x + 14y = - 86.

Question 18.
Find the angle between the parabolas y² = 4ax and x² = 4 by at their point of intersection other than the origin.
Answer:
Given equations of curves are
y² = 4ax ............ (i)
and x² = 4by ............. (ii)
Clearly, the angle of intersection of curves (i) and (ii) is the angle between the tangents to the curves at the point of intersection.
So, let us first find the intersection point of given curves.
On substituting the value of y from Eq. (ii) in Eq. (i), we get
\(\left(\frac{x^2}{4 b}\right)^2\) = 4ax ⇒ \(\frac{x^4}{16 b^2}\) = 4ax
⇒ x⁴ = 64ab²x ⇒ x⁴ - 64ab²x = 0
⇒ x(x³ - 64ab²) = 0
⇒ x = 0 or x = 4a^1/3b^2/3
Clearly, when x = 0, then from Eq. (i), y = 0 and when x = 4a^1/3b^2/3, then from Eq. (i),
y² = 16a^4/3b^2/3 ⇒ y = 4a^2/3b^1/3
Thus, the points of intersection are (0, 0) and (4a^1/3b^2/3, 4a^2/3b^1/3).
Now, let us find the angle of intersection at (0, 0) and (4a^1/3b^2/3, 4a^2/3b^1/3).
Let m₁ be the slope of tangent to the curve (i) and m₂ be the slope of tangent to the curve (ii).

Angle of intersection at (0, 0)

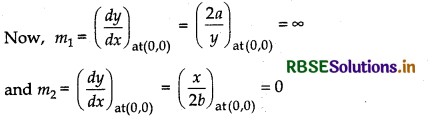
⇒ Tangent to the curve (j) is parallel to Y-axis and tangent to the curve (ii) is parallel to X-axis.
∴ Angle between these two curves is \(\frac{\pi}{2}\).
⇒ The angle of intersection of the curves is \(\frac{\pi}{2}\).

Angle of intersection (4a^1/3b^2/3, 4a^2/3b^1/3)

Question 19.
If the radius. of a sphere is measured as 9 cm with an error of 0.03 cm, then find the approximate error in calculating its volume.
Answer:
Let r be the radius of the sphere and ∆r be the error in measuring the radius.
Here, r = 9 cm and ∆r = 0.03 cm
Now, volume of the sphere, V = \(\frac{4}{3}\) ≠ r³
⇒ \(\frac{d V}{d r}=\frac{4}{3} \pi \times 3 r^2 \Rightarrow \frac{d V}{d r}=4 \pi r^2\)
Therefore, dV = \(\left(\frac{d V}{d r}\right)\) ∆r = (4πr²) ∆r
= 4π(9)² (0.03) = 9.72π cm³
Thus, the approximate error in calculating the volume is 9.72π cm³

Question 20.
Using differentials, find the approximate value of the following:
(i) √26
Answer:
Let y = √x, x = 25, ∆x = 26 - 25 = 1

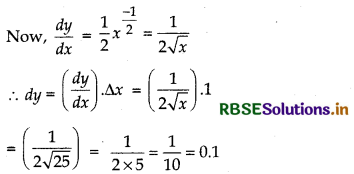
Thus, √26 = y + ∆y = 5 + 0.1 = 5.1

(ii) √37
Answer:
Let y = √x, x = 36 ⇒ y = √36 = 6
And ∆x = 37 - 36 = 1

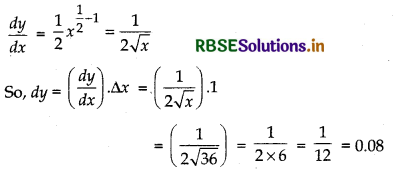
Thus, √37 = y + ∆y = 6 + 0.08
= 6.08

(iii) √0.48
Answer:

(iv) (82)^{\(\frac{1}{4}\)}
Answer:

(v) √49.5
Answer:
Let y = √x, and x = 49 ⇒ y = √49 = 7
∆x = 49.5 - 49 = 0.5

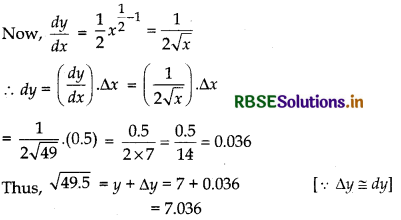
(vi) (3.968)^{\(\frac{3}{2}\)}
Answer:

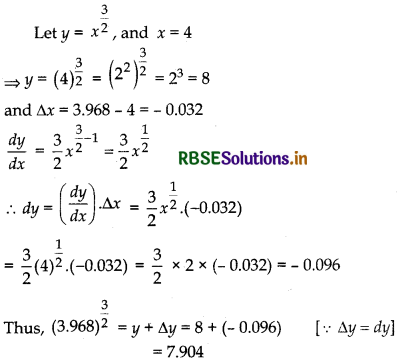
Question 21.
Find maximum and minimum values of the following:
(a) 2x³ - 15x² + 36x + 10
(b) - |x + 1| + 3
(c) |sin 4x + 3|
Answer:
(a) Let y = 2x³ - 15x² + 36x + 10
⇒\( \frac{d y}{d x}\) = 6x² - 30x + 36
For maxima or minima, \(\frac{d y}{d x}\) = 0
⇒ 6x² - 30x + 36 = O
⇒ 6(x² - 5x + 6) = 0
⇒ (x - 3) (x - 2) = 0
⇒ x = 2, 3
Now, \(\frac{d^2 y}{d x^2}\) = 12x - 30

(i) \(\left(\frac{d^2 y}{d x^2}\right)_{x=2}\) = 12 × 2 - 30 = 24 - 30 = - 6 (- ve)
At x = 2, maximum value of function
= 2(2)³ - 15(2)² + 36 × 2 + 10
= 16 - 60 + 72 + 10 = 38

(ii) \(\left(\frac{d^2 y}{d x^2}\right)_{x=3}\) = 12 × 3 - 30 = 36 - 30 = 6 (+ ve)
At x = 3, minimum value of function
= 2(3)² - 15(3)² + 36(3) + 10
= 54 - 135 + 108 + 10 = 37

(b) Let g(x) = - |x + 1| + 3
- x + 11 < 0, so function has no minimum value.
Again,minimum value of - |x + 1| is 0.
∴ - |x + 1| = 0 ⇒ x = - 1, then maximum value of g(x) is 3.
[∵ g(- 1) = - |- 1 + 1| + 3 = 3]

(c) Let f(x) = |sin 4x + 3|
sin 4x has maximum value as 1.
∴ Maximum value of f(x)is |1 + 3| = 4
Again, minimum value of sin 4x = |- 1 + 3| - |2| = 2

Question 22.
Find maximum and minimum of the following in the given interval:
(a) x + sin 2x, x ∈ [0, 2π]
(b) x³ - 18x² + 96x, x ∈ [0, 9]
Answer:
Let y = x + sin 2x ⇒ \(\frac{d y}{d x}\) = 1 + 2 cos 2x
For maxima or minima f’(x) = 0
⇒ 1 + 2 cos 2x = 0 ⇒ 2 cos 2x = - 1

Hence, maximum value of function is 2π at x = 2π and minimum value of function is 0 at x = 0.

(b) x³ - 18x² + 96x, x ∈ [0, 9]
Answer:
Let y = x³ - 18x² + 96x, x ∈ [0, 9]

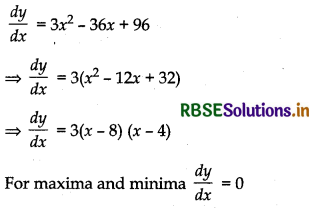
⇒ 3(x - 8) (x - 4) = 0 ⇒ x = 4,8
Now, y_o = (0)³ - 18(0)² + 96(0) = 0
y₄ = (4)³ - 18(4)² + 96 × 4
= 64 - 288 + 384 = 160
y₈ = (8)³ - 18(8)² + 96 × 8
= 512 - 1152 + 768 = 128
y₉ = (9)³ - 18(9)² + 96(9)
= 729 - 1458 + 864 = 135
So, at x = 0 minimum value = 0
and at x = 4 maximum value 160

Question 23.
Find the extreme value of the following functions:
(a) sin x.cos 2x
Answer:
Let y = sin x.cos 2x
\(\frac{d y}{d x}\) = sin x.(- sin 2x) + cos 2x.cos x
= - 4 sin² x.cos x + (1 - 2 sin² x).cos x
= - 4 sin² x.cos x + cos x - 2 sin² x cos x
= cos x(1 - 6 sin² x) ......... (ii)
\(\frac{d^2 y}{d x^2}\) = cos x[0 - 12 sin x cos x] + (1 - 6 sin² x).(- sin x)
= - 12 sin x cos 2x - sin x + 6 sin³x .......... (iii)
For maxima and minima \(\frac{d y}{d x}\) = 0
For Eq. (ii), cos x[1 - 6 sin² x] = 0
When cos x = 0, then
cos x = cos \(\frac{\pi}{2}\) = cos \(\frac{3 \pi}{2}\)
⇒ x = \(\frac{\pi}{2}\), \(\frac{3 \pi}{2}\)
When 1 - 6 sin² x = 0, then

(b) \(\frac{1}{x}\).log x, x ∈ (0, ∞)
Answer:

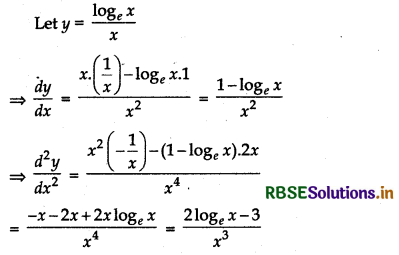
For maxima or minima
\(\frac{d y}{d x}\) = 0 ⇒ \(\frac{1-\log _e x}{x^2}\) = 0
⇒1 - log x = 0
⇒ log_e x = 1 = log_e e
Now, put x = e
\(\frac{d^2 y}{d x^2}=\frac{2 \log _e e-3}{e^3}=\frac{2-3}{e^3}=-\frac{1}{e^3}\)
At x = e function is maximum, and maximum value = \(\frac{\log _e e}{e}=\frac{1}{e}\)

Question 24.
Prove that the value of \(\frac{x}{1+x \tan x}\) is minimum at x = cos x.
Answer:

Question 25.
Prove that y = sin^p θ.cos^q θ is maximum at tan θ = \(\sqrt{\frac{p}{q}}\).
Answer:
Let y = sin^p θ cos^q θ
\(\frac{d y}{d \theta}\) = sin^p θ[q cos^{q - 1}θ(- sin θ)} + cos^q θ{p sin^{p - 1} θ cos θ}
= - q sin^{(p + 1)} θ cos ^{(q - 1)} θ + p sin^{p - 1} θ cos^{(q + 1)} θ

= - y{(q + p) + (p + q)} + 0 = - 2y(p + q)
= 2(sin^P θ cos^q θ) (p + q) = - ve
So, y will be maximum.
Hence, y will be of maximum if
θ = tan^-1 \(\sqrt{\frac{p}{q}}\) or tan θ = \(\sqrt{\frac{p}{q}}\)

Question 26.
If the sum of the lengths of the hypotenuse and a side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between them is \(\frac{\pi}{3}\).
Answer:
Let us consider a right-angled triangle with base = x and hypotenuse = y. Let x + y = k, where k is a constant. Let θ be the angle between the base and the hypotenuse. Let A be the area of the triangle, then


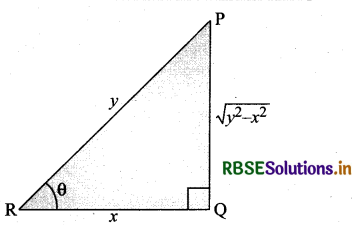
Thus, the area of triangle is maximum, when θ = \(\frac{\pi}{3}\).
Hence Proved.

Question 27.
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of the material will be least when depth of the tank is half of its width.
Answer:
Let x be the length of a side of square base and y be the length of vertical side. Also, let V be the given quantity of water.

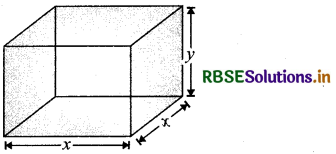
Then, V = x²y[∵ Volume of cuboid = L × B × H] ....... (i)
Clearly, surface area, S = 4xy + x²

Thus, the cost of material will be least when depth of the tank is half of its width.

Question 28.
Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.
Answer:
Let VAB be the cone of base radius r, height h and radius of base of the inscribed cylinder be x.

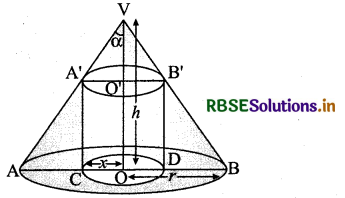
Question 29.
A wire of length 20 m is to be cut into two pieces. One of the pieces will be bent into shape of a square and the other shape of an equilateral triangle. Where the wire should be cut so that the sum of the areas of the square and triangle is minimum?
Answer:
Let the two pieces be x and y.
Given, x + y = 20
Perimeter of square = x

Question 30.
Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is 6√3r.
Answer:
Let ABC be the given isosceles triangle, with AB = AC.

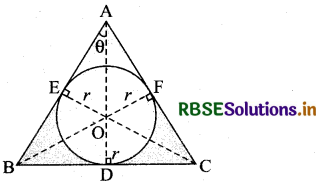
Clearly, OD ⊥ BC, OF ⊥ AC, OE ⊥ AB
[∵ radius is perpendicular to the tangent at the point of contact]
and BD = BE, CD = CF, AE = AF
[∵ tangents from an external point to a circle are equal in length]
Since, AD is an altitude of isosceles MBC,
Therefore, BD = CD
[∵ in an isosceles triangle, altitude from common vertex of equal sides bisect the third side]
⇒ BD = BE = CF = CD [∵ BE = BD and CD = CF]
Now, perimeter (P) of ∆ABC = AB + BC + AC
= AE + BE + BD + DC + AF + FC
= (AE + AF) + (BE + BD + DC + FC)
= 2AE + 4BD
Consider ∆OEA, in this we have ............ (i)

Now, put P’(θ) = 0
- 2 cos² θ + 4 sin³ θ + 4 sin² θ = 0
- 2(1 - sin²θ) + 4 sin³θ + 4 sin²θ = 0
- 2 + 2 sin²θ + 4 sin³θ + 4 sin²θ = 0
2 sin³θ + 3 sin²θ - 1 = 0
(sin θ + 1) (2 sin²θ + sin θ - 1) = 0
Either sin θ - 1
[∵ sin θ ≠ - 1, as θ can't be more than 900]
or 2 sin² θ + sin θ - 1 = 0
∴ (2 sin θ - 1) (sin θ + 1) = 0
⇒ sin θ = \(\frac{1}{2}\) [∵ sin θ ≠ - 1]
∵ θ = \(\frac{\pi}{6}\)
On differentiating both sides of Eq. (iii) w.r.t. θ, we get
P''(θ) = r(4 cosec²θcot θ + sec³ θ + 4 sec θ tan²θ + sec²θ tan θ)

Multiple Choice Questions

Question 1.
The equation of tangent to curve y = e^-|x| at the points where the curve cuts the line x = 1 is:
(a) x + y = e
(b) e(x + y) = 1
(c) y + cx = 1
(d) None of these
Answer:
(d) None of these

Question 2.
The least natural number a for which x + ax² > 2 for all x ∈ R⁺ is:
(a) 1
(b) 2
(c) 5
(d) 9
Answer:
(b) 2

Question 3.
The number of solutions of equations 3x² + x sin x + cos x = 0 is:
(a) 3
(b) 2
(c) 1
(d) 0
Answer:
(d) 0

 

Question 4.
The equation of the tangent to the curve y = 4 + sin²x at x = 0 is:
(a) y = 2
(b) y = 3
(c) y = 4
(d) y = 6
Answer:
(c) y = 4

Question 5.

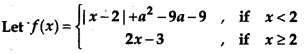
If f(x) has local minimum at x = 2, then:
(a) a ≤ -2
(b) 1 ≤ a ≤ 10
(c) 0 ≤ a ≤ 9
(d) None of these
Answer:
(d) None of these

Question 6.
A particle moves along a straight line according to the laws = \(\frac{1^3}{3}\) - 3t² + 9t +17, where distance is in the metres and t in seconds. Velocity decreases when:
(a) 0 < t < 5
(b) 0 < t < 3 (c) t > 5
(d) t > 3
Answer:
(b) 0 < t < 3

Question 7.
The maximum and minimum value of ab sin x + \(\sqrt{1-a^2}\). cos x + c lie in the interval where |a| < 1, b > 0:
(a) [b - c, b + c]
(b) (b - c, b + c)
(c) [c - b, b + c]
(d) None
Answer:
(c) [c - b, b + c]

Question 8.
The function \(\frac{\sin (x+\alpha)}{\sin (x+\beta)}\) has no maximum or minimum if (where k ∈ I):
(a) β - α = kπ
(b) β - α = kπ
(c) β - α = 2kπ
(d) None of these
Answer:
(b) β - α = kπ

Question 9.
The angle of intersection of the curves y = x², 6y = 7 - x³ at (1, 1) is:
(a) \(\frac{\pi}{4}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{\pi}{2}\)
(d) None of these
Answer:
(b) \(\frac{\pi}{3}\)

Question 10.
Let f(x) = ax³ - 6ax² + 9ax + 18, then f(x) is strictly decreasing in:
(a) (-∞, 1]
(b)[3, ∞)
(c) [- ∞, 1] u [3, ∞)
(d) (1, 3)
Answer:
(d) (1, 3)

Question 11.
On the interval (0, \(\frac{\pi}{2}\)) the function log sin x is:
(a) increasing
(b) decreasing
(c) neither increasing nor decreasing
(d) none of these
Answer:
(a) increasing

Question 12.
If f(x) = 1 + 2x² + 2²x⁴ +.... + 2¹⁰x²⁰, then f(x) has:
(a) more than one minima
(b) exactly one minima
(c) atleast one maxima
(d) none of these
Answer:
(b) exactly one minima

Question 13.
The function f(x) = \(\frac{\log (\pi+x)}{\log (e+x)}\) (x ≥ 0) is:
(a) increasing in [0, ∞)
(b) decreasing in [0, ∞)
(c) increasing in [0, \(\frac{\pi}{e}\)) and decreasing [\(\frac{\pi}{e}\), ∞)
(d) decreasing in [0, \(\frac{\pi}{e}\)) and increasing [\(\frac{\pi}{e}\), ∞)
Answer:
(b) decreasing in [0, ∞)

Question 14.
If h(x) = f(x) - [f(x)]² + [f(x)]² for every real number x, then:
(a) h is increasing whenever/is increasing
(b) h is increasing whenever/is decreasing
(c) is decreasing whenever/is increasing
(d) Nothing can be said in general
Answer:
(a) h is increasing whenever/is increasing

Question 15.
The parabolas x² = 5 - 4y and y = x² cut at the point (1,1) at an angle:
(a) \(\frac{\pi}{2}\)
(b) \(\frac{\pi}{4}\)
(c) \(\frac{\pi}{3}\)
(d) None of these
Answer:
(a) \(\frac{\pi}{2}\)

Fill in the Blanks

Question 1.
The tangent line is parallel to x-axis if θ = _______________.
Answer:
0°

Question 2.
The tangent line is parallel to y-axis if θ = _______________.
Answer:
\(\frac{\pi}{2}\)

Question 3.
The least value of the function
f(x) = ax + \(\frac{b}{a}\)(a > 0, b > 0, x > 0) is _______________
Answer:
2\(\sqrt{a b}\)

Question 4.
The slope of the tangent to the curve y = x³ - x at the point (2,6) is _______________
Answer:
11

Question 5.
The rate of change of the area of a circle with respect to its radius r, when r = 3 cm, is _______________
Answer:
6π cm²/m

True/False

Question 1.
f is strictly increasing in (a, b), if f '(x) > 0 for each x ∈ (a, b).
Answer:
True

Question 2.
f is strictly decreasing in (a, b), if f '(x) < 0 for each x ∈ (a, b).
Answer:
True

Question 3.
If θ = 0°, then the tangent line is parallel to y-axis.
Answer:
False

Question 4.
If θ = \(\frac{\pi}{2}\), then the tangent line is perpendicular to x-axis.
Answer:
True

Question 5.
The condition for two curve to be perpendicular is m₁m₂ = -1.
Answer:
True