RBSE Class 12 Maths Important Questions Chapter 6 अवकलज के अनुप्रयोग

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 6 अवकलज के अनुप्रयोग Important Questions and Answers.

RBSE Class 12 Maths Chapter 6 Important Questions अवकलज के अनुप्रयोग

अन्य महत्त्वपूर्ण प्रश्न

प्रश्न 1.
एक कण का गत समीकरण S = t² - 4t + 5 है, इसकी चाल के शन्य होने का समय है
(A) 1 से०
(B) 2 से०
(C) 3 से०
(D) 4 से०
उत्तर:
(B) 2 से०

हल:
S = t² - 4t + 5
\(\frac{d \mathrm{~S}}{d t}\) = 2t - 4
प्रश्नानुसार ⇒ 2t - 4 = 0 = 1 = 2 से०
अतः उत्तर का सही विकल्प (B) है।

प्रश्न 2.
एक पत्थर ऊपर की ओर फेंका गया, जिसकी गति का समीकरण S = 9.8 t - 4.9t² है, जहाँ 5 मीटर में वो सेकण्ड में है। अधिकतम ऊँचाई प्राप्त करने का समय होगा
(A) 2 से
(B) 1½ से०
(C) 1 से०
(D) ½ से०
उत्तर:
(C) 1 से०

हल
S = 9.8t - 4.9t²
\(\frac{d \mathrm{~S}}{d t}\) = 9.8 - 9.8t
अधिकतम ऊँचाई पर पहुँचने पर अन्तिम वेग शून्य होगा
0 = 9.8 - 9.81
t = \(\frac{9.8}{9.8}\) = 1 से.
अतः उत्तर का सही विकल्प (C) है।

प्रश्न 3.
यदि सरल रेखा में गतिमान एक कण की । समय में चली गई दूरी x समीकरण x = 2t² - 5t + 1 में दी जाती है, तो कण का 5 सेकण्ड बाद वेग है
(A) 15
(B) 20
(C) 25
(D) 26
उत्तर:
(A) 15

हल:
x = 2t² - 5t + 1
V = \(\frac{d x}{d t}\) = 4t - 5
∴ \(\left(\frac{d x}{d t}\right)_{\text {at } t=5}\) = 4 × 5 - 5 = 15
अतः उत्तर का सही विकल्प (A) है।

प्रश्न 4.
वक्र y = f(x) के किसी बिन्दु पर खींचा गया अभिलम्ब x-अक्ष से 135° का कोण बनाता हो तो उस बिन्दु पर का मान होगा
(A) 1
(B) - 1
(C) 0
(D) ∞
उत्तर:
(B) - 1

हल:
चूँकि खींचा गया अभिलम्ब x-अक्ष से 135° का कोण बनाता है
∴ \(\frac{d y}{d x}\) = tan 135°
\(\frac{d y}{d x}\) = - 1
अतः उत्तर का सही विकल्प (B) है।

प्रश्न 5.
वक्र y² = 4x के बिन्दु (1, 2) पर स्पर्श रेखा का ढाल है
(A) 2
(B) - 2
(C) 1
(D) - 1
उत्तर:
(C) 1

हल:
y² = 4x
∴ 2y\(\frac{d y}{d x}\) = 4
या \(\left(\frac{d y}{d x}\right)=\frac{4}{2 y}\)
या \(\left(\frac{d y}{d x}\right)_{\text {at }(1,2)}=\frac{4}{2 \times 2}\) = 1
अतः उत्तर का सही विकल्प (C) है।

प्रश्न 6.
वक्र y = x + sin x cos x के बिन्दु x = \(\frac{\pi}{2}\) पर अभिलम्ब का समीकरण है
(A) x = 2
(B) x = π
(C) x = - π
(D) x = \(\frac{\pi}{2}\)
उत्तर:
(D) x = \(\frac{\pi}{2}\)

हल:
y = x + sin x cos x = x + 2 sin 2x

अतः उत्तर का सही विकल्प (D) है।

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि वक्र y² = ax³ + b के बिन्दु (2, 3) पर खींची गई स्पर्श रेखा का झुकाव 4 हो, तो 'a' का मान लिखिये।
हल:
y² = ax³ + b
x के सापेक्ष अवकलन करने पर

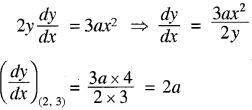
प्रश्नानुसार 2a = 4
∴ a = 2

प्रश्न 2.
वक्र y = 2x² - x + 1 पर वह बिन्दु लिखिये जिस पर स्पर्श रेखा उस रेखा के समान्तर है, जिसका ढाल 3 है।
हल:
वक्र y = 2x² - x + 1
\(\frac{d y}{d x}\) = 4x - 1
माना वह बिन्दु (x₁, y₁) है। ∴ y₁ = 2x₁² - x₁ + 1
\(\left(\frac{d y}{d x}\right)_{\left(x_1, y_1\right)}\) = 4x₁ - 1.
प्रश्नानुसार, 4x₁ - 1 = 3
∴ x₁ = 1
और y₁ = 2(1)² - 1 + 1 = 2
अतः बिन्दु (1, 2) है।

प्रश्न 3.
अवकल गुणांक \(\frac{d y}{d x}\) से क्या तात्पर्य है?
उत्तर:
अवकल गुणांक \(\frac{d y}{d x}\) उस कोण की स्पर्शज्या है जो वक्र y = f(x) के किसी बिन्दु P(x, y) पर खींची गई स्पर्श रेखा x-अक्ष के साथ बनाती है। सामान्यतः इसे बिन्दु P पर वक्र की प्रवणता कहते हैं।

प्रश्न 4.
स्पर्श रेखा y अक्ष पर लम्बवत् हो तो का मान कितना होता है?
हल:
स्पर्श रेखा y अक्ष पर लम्बवत् है अर्थात् x-अक्ष के समान्तर है।
∴ \(\frac{d y}{d x}\) = tan 0 = 0

प्रश्न 5.
फलन y = f(x) के लिए यदि \(\frac{d y}{d x}\) = 6 (x - 2) (x - 3) है, तो y के अधिकतम मान के लिए x का मान ज्ञात कीजिए।
हल:
उच्चिष्ठ एवं निम्निष्ठ के लिए \(\frac{d y}{d x}\) = 0
⇒ 0 = 6(x - 2) (x - 3)
या x = 2, 3
\(\frac{d y}{d x}\) = 6 (x - 2) (x - 3) = 6 (x² - 5x + 6)
\(\frac{d^2 y}{d x^2}\) = 6 (2x - 5) = 12x - 30
\(\left(\frac{d^2 y}{d x^2}\right)_{\text {at } x=2}\) = 12 × 2 - 30 = - 6 < 0
अतः x = 2 पर y अधिकतम है।

प्रश्न 6.
यदि किसी फलन (x) के लिए f(c) < 0 तथा f"(c) > 0 तो x = c पर f(x) क्या होगा?
उत्तर:
उच्चिष्ठ एवं निम्निष्ठ में से कोई नहीं।

प्रश्न 7.
वक्र y = x - x³ + 1 के बिन्दु (0, 1) पर अभिलम्ब का ढाल लिखिये।
हल:
\(\frac{d y}{d x}\) = 1 - 3x²
\(\left(\frac{d y}{d x}\right)_{(0,1)}\) = 1 - 3 × 0 = 1
स्पर्श रेखा का ढाल = 1
इसलिए अभिलम्ब का ढाल = - 1 (∵ m₁ = - \(\frac{1}{m_2}\))

प्रश्न 8.
a sin x + b cos x का अधिकतम मान कितना होता है?
हल:
माना y = a sin x + b sin x

प्रश्न 9.
वक्र y = (x² - 1) (x - 2) जिस बिन्दु पर y-अक्ष को काटती है, उस बिन्दु पर वक्र की स्पर्श रेखा का समीकरण लिखिये।
हल:
y = (x² - 1) (x - 2)
जब वक्र y-अक्ष को काटती है तो y-अक्ष पर x = 0 ⇒ y = 2
अतः बिन्दु (0,2)
\(\frac{d y}{d x}\) = 2x . (x - 2) + (x² - 1)× 1
= 2x² - 4x + x² - 1
= 3x² - 4x - 1 [∴ \(\left(\frac{d y}{d x}\right)_{(0,2)}\) = - 1]
बिन्दु (0,2) पर स्पर्श रेखा का समीकरण
y - 2 = - (x - 0) ⇒ x + y = 2

प्रश्न 10.
वक्रों xy = a² तथा x² - y² = 2a² का प्रतिच्छेद कोण लिखिये।
हल:

अतः वक्र एक-दूसरे को समकोण पर काटेंगे, अर्थात् वक्रों का प्रतिच्छेदन कोण \(\frac{\pi}{2}\) है।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
एक गोलीय बुलबुले का पृष्ठीय क्षेत्रफल 2 सेमी/सेकण्ड की दर से बढ़ रहा है। बुलबुले का आयतन किस दर से बढ़ रहा है, जबकि बुलबुले की त्रिज्या 6 सेमी. है।
हल:
माना कि गोलीय बुलबुले की त्रिज्या r और उसका पृष्ठीय क्षेत्रफल S व आयतन V है।

प्रश्न 2.
एक कण एक सरल रेखा में इस प्रकार गतिमान है कि t समय पर इसकी एक स्थिर बिन्दु से दूरी S, समय की n घात के समानुपाती है। यदि । समय पर इसका वेग (V) तथा a त्वरण हो तो सिद्ध कीजिए
V² = \(\frac{n a \mathbf{S}}{(n-1)}\)
हल:
दिया गया है-
दूरी (S) ∝ (समय)ⁿ
∴ S ∝ tⁿ
⇒ S = k tⁿ

प्रश्न 3.
अन्तराल ज्ञात कीजिये जिसके लिये f(x) = x⁴ - 2x² वर्धमान या ह्रासमान है।
हल:
दिया है
f(x) = x⁴ - 2x²
इसलिये f'(x) = 4x³ - 4x
f'(x) = 4x (x² - 1)
f(x) = 4x (x + 1) (x - 1)
f(x) वर्धमान हो, इसके लिये f' (x) > 0 होना चाहिये
इसलिये 4x(x + 1) (x - 1) > 0
⇒ x(x + 1) (x - 1) > 0
⇒ - 1 < x < 0 या x > 1
⇒ x ∈ (-1, 0) ∪ (1, ∞) - -0+0 -0 + -

इसलिये f(x), अन्तराल (-1, 0) ∪ (1, ∞) में वर्धमान है।
f(x) ह्रासमान हो, इसके लिये f'(x) < 0
⇒ 4x (x + 1) (x - 1) < 0
⇒ x (x + 1) (x - 1) < 0 ∴ 4 > 0
⇒ x < - 1 या 0 < x < 1
⇒ x ∈ (- ∞, - 1) ∪ (0, 1)

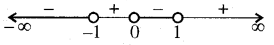
इसलिये f(x) अन्तराल (- ∞, -1) ∪ (0, 1) में ह्रासमान है।

प्रश्न 4.
a का न्यूनतम मान ज्ञात कीजिये कि फलन f(x) = x² + ax + 10 अन्तराल [3, 6] में वर्धमान है।
हल:
दिया है
f(x) = x² + ax + 10
इसलिये f'(x) = 2x + a
चूंकि x ∈ [3, 6] ⇒ 3 ≤ x ≤ 6
⇒ 6 ≤ 2x ≤ 12
⇒ 6 + a ≤ 2x + a ≤ 12 + a
⇒ 6 + a ≤ f'(x) ≤ 12 + a
यदि f(x) a वर्धमान है तो f"(x) > 0
6 + a > 0 ⇒ a > - 6
इसलिये a का न्यूनतम मान - 6 है।

प्रश्न 5.
वह अन्तराल ज्ञात कीजिये जिसमें फलन
f(x) = 2 log (x - 2) - x² + 4x + 1 वृद्धिमान है।
हल:
यहाँ f(x) = 2 log (x - 2) - x² + 4x + 1
⇒ y = 2 log (x - 2) - x² + 4x + 1

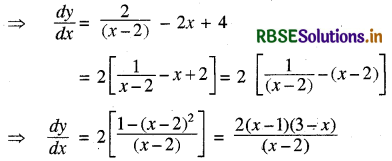
चूँकि दिया गया फलन f(x) वर्धमान है।
इसलिये \(\frac{d y}{d x}\)
⇒ \(\frac{2(x-1)(3-x)}{(x-2)}\) > 0
⇒ 2(x - 1) (3 - x) > 0
⇒ (x - 1) (3 - x) > 0 [∵ 2 > 0]
⇒ 1 < x < 3
अतः अभीष्ट अन्तराल 1 < x < 3 है।

प्रश्न 6.
वह अन्तराल ज्ञात कीजिये जिसमें फलन f(x) = x³ - 3x² - 24x + 5 वर्धमान है।
हल:
दिया है- '.
f(x) = x³ - 3x² - 24x + 5
या y = x³ - 3x² - 24x + 5

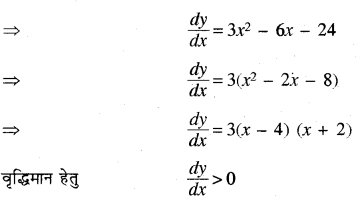
इसलिये 3(x - 4) (x + 2) >0
⇒ (x - 4) (x + 2) >0 [∵ 3 > 0]
स्थिति I x - 4 > 0, (x + 2) > 0 ⇒ x > 4, x > - 2
स्थिति II x - 4 < 0, (x + 2) < 0 ⇒ x < 4, x < - 2
x ∈ (- ∞, - 2) ∪ (4, ∞)

प्रश्न 7.
वक्र x² + y² - 2x - 3 = 0 पर उन बिन्दुओं को ज्ञात कीजिये जहाँ स्पर्श रेखा दोनों अक्षों से समान कोण बनाती है।
हल:
दिया गया वक्र x² + y² - 2x - 3 = 0 ....... (1)
x के सापेक्ष अवकलन करने पर,

⇒ y = 1 - x
y = 1 - x समीकरण (1) में रखने पर
x² + 1 (1 - x)² - 2x - 3 = 0
⇒ x² + 1 - 2x + x² - 2x - 3 = 0
⇒ 2x² - 4x - 2 = 0
⇒ x² - 2x - 1 = 0
⇒ x = \(\frac{2 \pm \sqrt{4+4}}{2 \times 1}\) = \(\frac{2 \pm 2 \sqrt{2}}{2}\)
⇒ x = 1 ± √2
जब x = 1 + √2 तब y = 1 - (1 + √2) = -√2
जब x = 1 - √2 तब y = 1 - (1 - √2) = √2
अतः अभीष्ट बिन्दु (1 + √2, - √2), (1 - √2, √2)

प्रश्न 8.
सिद्ध कीजिए कि निम्न वक्र समकोण पर काटते हैं
x² = 7 + 6y और y = x³
हल:
दिये गये वक्रों के समीकरण से
x² = 7 + 6y ....... (1)
y = x³ ......... 92)
समीकरण (1) तथा (2) को हल करने पर
x² = 7 + 6x³
⇒ 6x³ - x² + 7 = 0
x = - 1 इसका एक मूल है।
y का मान निकालने पर।
y = x³ = (- 1)³
अतः प्रतिच्छेद बिन्दु (- 1, - 1)
पहले वक्र से
x² = 7 + 6y
x के सापेक्ष अवकलन करने पर

यहाँ पर m₁ × m₂ = - 1 प्राप्त हो रहा है।
अतः दिये गये वक्र समकोण पर काटते हैं।

प्रश्न 9.
निम्नलिखित फलन का उच्चिष्ठ एवं निम्निष्ठ मान ज्ञात कीजिये
2x³ - 15x² + 36x + 10
हल:
माना
y = 2x³ - 15x² + 36x + 10
इसलिये \(\frac{d y}{d x}\) = 6x² - 30x + 36
तथा \(\frac{d^2 y}{d x^2}\) = 12x - 30
उच्चिष्ठ एवं निम्निष्ठ के लिये \(\frac{d y}{d x}\) = 0
इसलिये 6x² - 30x + 36 = 0
⇒ 6(x² - 5x + 6) = 0
⇒ x² - 5x + 6 =0
या (x - 3) (x - 2) = 0
⇒ x = 2, 3
अब x = 2 पर, \(\frac{d^2 y}{d x^2}\) = 12 × 2 - 30 = - 6 < 0
x = 2 पर फलन का मान उच्चिष्ठ होगा तथा फलन का उच्चिष्ठ
मान
= 2(2)³ - 15(2)² + 36(2) + 10
= 16 - 60 + 72 + 10
= 38
पुनः x = 3 पर \(\frac{d^2 y}{d x^2}\) = 12 × 3 - 30 = 6 > 0
x = 3 पर फलन का मान निम्निष्ठ होगा तथा फलन का निम्निष्ठ मान
= 2(3)³ - 15(3)² + 36 (3) + 10
= 2 × 27 - 15 × 9 + 108 + 10
= 54 - 135 + 108 + 10 = 37

प्रश्न 10.
सिद्ध कीजिये कि फलन sin²x(1 + cos x), cos x = \(\frac{1}{3}\) पर उच्चिष्ठ है।
हल:
माना y = sin²x(1 + cos x)
इसलिये \(\frac{d y}{d x}\) = sin²x(- sin x) + (1 + cos x) × 2 sin x cos x
या \(\frac{d y}{d x}\) = - sin³x + 2 sin x cos x + 2 sin x cos²x
\(\frac{d y}{d x}\) = sin x (- sin²x + 2 cos x + 2 cos²x)
= sin x (- 1 + cos²x + 2 cos x + 2 cos²x)
= sin x (3 cos²x + 2 cos x - 1)
उच्चिष्ठ एवं निम्निष्ठ के लिये \(\frac{d y}{d x}\) = 0
0 = sin x (3 cos²x + 2 cos x - 1) = 0
⇒ sin x = 0, 3 cos²x + 2 cos x - 1 = 0

अतः cos x = \(\frac{1}{3}\) पर फलन का मान उच्चिष्ठ होगा।

प्रश्न 11.
वक्र y = x³ - x + 1 की स्पर्श रेखा की प्रवणता उस बिन्द पर ज्ञात कीजिए x-निर्देशांक 1 है। इस बिन्दु पर अभिलम्ब का समीकरण भी ज्ञात कीजिए।
हल:
प्रश्नानुसार y = x³ - x + 1
∴ \(\frac{d y}{d x}\) = 3x² - 1
x = 1 रखने पर
\(\left(\frac{d y}{d x}\right)_{\text {at } x=1}\) = 3 × (1)² - 1 = 3 - 1 = 2
दिये गये वक्र में x = 1 रखने पर
y = (1)³ - 1 + 1 = 1 - 1 + 1 = 1
यहाँ पर स्पर्श रेखा की प्रवणता = 2 है
इसलिये अभिलम्ब रेखा की प्रवणता = -\(\frac{1}{2}\) होगी।
अतः अभिलम्ब रेखा का समीकरण होगा
(y - 1) = -\(\frac{1}{2}\)(x - 1)
⇒ 2y - 2 = - x + 1
⇒ x + 2y - 3 = 0

प्रश्न 12.
एक गोले की त्रिज्या 9 cm मापी जाती है जिसमें 0.02 cm की त्रुटि है। इसके आयतन के परिकलन में सन्निकट त्रुटि ज्ञात कीजिए।
हल:
मान लीजिये कि गोले की त्रिज्या r है और इसके मापन में त्रुटि ∆r होती है।
यहाँ पर दिया है
r = 9 cm और ∆r = 0.02 cm
गोले का आयतन v = \(\frac{4}{3}\)πr³ से दिया जाता है।

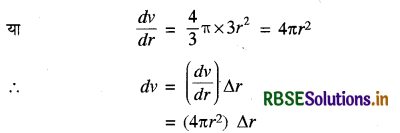
मान रखने पर
= (4π (9)²) × 0.02
= 4 × 81 × 0.02 π
= 6.48 π cm³
अतः आयतन के परिकलन में सन्निकट त्रुटि = 6.48 π cm³

प्रश्न 13.
अन्तराल [1, 5] में f (x) = x² - 4x + 8 द्वारा प्रदत्त फलन के निरपेक्ष उच्चतम और निम्नतम मानों को ज्ञात कीजिए।
हल:
हमें ज्ञात है
f(x) = x² - 4x + 8
या f'(x) = 2x - 4 = 2 (x - 2)
ध्यान दीजिये f'(x) = 0 से x = 2 प्राप्त होता है।
अब हम इस बिन्दु और अन्तराल [1, 5] के अंत्य बिन्दुओं अर्थात् x = 1, x = 2 और x = 5 पर के मान का परिकलन करेंगे।
अब ∴ f (x) = x² - 4x + 8
∴ f (1) = (1)² - 4 × 1 + 8 = 5.
f(2) = (2)² - 4 × 2 + 8 = 4
f (5) = (5)² - 4 × 5 + 8 = 13
इस प्रकार हम इस निष्कर्ष पर पहुँचते हैं कि अन्तराल [1,5] पर फलन f के लिये x = 5 पर निरपेक्ष उच्चतम मान 13 और x = 2 पर निरपेक्ष निम्नतम मान 4 है।

निबन्धात्मक प्रश्न

प्रश्न 1.
वक्र 2x² - y² = 14 पर सरल रेखा x + 3y = 6 के समान्तर अभिलम्ब के समीकरण ज्ञात कीजिये।
हल:
माना कि वक्र 2x² - y² = 14 पर बिन्दु (x₁ y₁) है जहाँ पर अभिलम्ब सरल रेखा x + 3y = 6 के समान्तर है।
तब 2x₁² - y₁² = 14 ....... (1)
वक्र 2x² - y² = 14 का x के सापेक्ष अवकलन करने पर

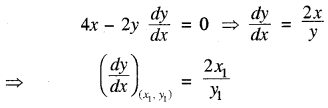
∵ बिन्दु (x₁, y₁) पर अभिलम्ब, रेखा x + 3y = 6 के समान्तर है।
इसलिये (x₁, y₁) पर अभिलम्ब का ढाल = दी गयी रेखा x + 3y = 6 का ढाल

⇒ 18x₁² - 4x₁² = 126
⇒ 14x₁² = 126 ⇒ x₁² = 9
⇒ x₁ = ± 3.
जब x₁ = 3, y₁ = \(\frac{2}{3}\) × 3 = 2
जब x₁ = - 3, y₁ = 3 (-3) = - 2
इसलिये बिन्दुओं (3, 2) तथा (-3, -2) पर अभिलम्ब रेखा x+ 3y = 6 के समान्तर है।
बिन्दु (3, 2) पर अभिलम्ब का समीकरण है।

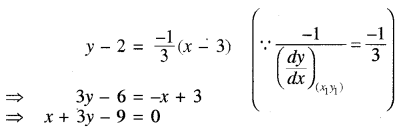
तथा बिन्दु (-3, -2) पर अभिलम्ब का समीकरण है।
(y + 2) = \(\frac{-1}{3}\)(x + 3)
या 3y + 6 = -x - 3
या x + 3y + 9 = 0

प्रश्न 2.
सिद्ध कीजिये कि n के प्रत्येक मान के लिये वक्र \(\left(\frac{x}{a}\right)^n+\left(\frac{y}{b}\right)^n\) = 2 सरल रेखा \(\frac{x}{a}+\frac{y}{b}\) = 2 को बिन्दु (a, b) पर स्पर्श करता है।
हल:
n के प्रत्येक मान के लिये वक्र का दिया हुआ समीकरण

जो कि दी हुई सरल रेखा है, चाहे n का मान कुछ भी हो।

प्रश्न 3.
यदि वक्र √x - √y = √a के किसी बिन्दु पर स्पर्श रेखा Ox तथा OY अक्षों को क्रमशः P और बिन्दुओं पर काटे तो सिद्ध कीजिये कि OP + OQ = a जहाँ 0 मूल बिन्दु है।
हल:
माना कि वक्र के किसी बिन्दु (x₁, y₁) पर स्पर्श रेखा खींची जाती है।
अतः √x₁ - √y₁ = √a .............. (1)
वक्र का समीकरण
√x - √y = √a
x के सापेक्ष अवकलन करने पर

प्रश्न 4.
यदि वक्र \(x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}\) का अभिलम्ब x-अक्ष से Φ कोण बनाता है तो सिद्ध कीजिये कि उसका समीकरण y cos Φ - x sin Φ = a cos 2 Φ
हल:
माना कि वक्र पर कोई बिन्दु (x₁, y₁) पर अभिलम्ब x-अक्ष से Φ कोण बनाता है।

⇒ x₁ = a sin³Φ, y₁ = a cos³Φ
अतः बिन्दु (a sin³Φ, a cos³Φ) पर अभिलम्ब का समीकरण है।
(y - a cos³Φ) = tan Φ (x - a sin³Φ)
या y - a cos³Φ = \(\frac{\sin \phi}{\cos \phi}\) (x - a sin³Φ)
या y cos Φ - a cos⁴Φ = x sin Φ - a sin⁴Φ
या y cos Φ - x sin Φ = a(cos⁴Φ - sin⁴Φ)
या y cos Φ - x sin Φ = a(cos²Φ - sin²Φ) (cos²Φ + sin²Φ)
या y cos Φ - x sin Φ = a . cos 2Φ . 1
या y cos Φ - x sin Φ = a cos 2Φ

प्रश्न 5.
वक्र x = a sec Φ, y = b tan Φ + के बिन्दु + पर स्पर्श रेखा एवं अभिलम्ब के समीकरण ज्ञात कीजिए।
हल:
दिया गया है
x = a sec Φ, y = b tan Φ

प्रश्न 6.
प्रदर्शित कीजिए कि वक्र ax² + by² = 1 तथा वक्र a¹x² + b¹y² = 1 एक-दूसरे को समकोणीय प्रतिच्छेद करेंगे, यदि \(\frac{1}{a}\) - \(\frac{1}{b}\) = \(\frac{1}{a^1}-\frac{1}{b^1}\)
हल:
माना दोनों वक्रों के प्रतिच्छेदन बिन्दु (h, k) हैं।
तो ah² + bk² = 1 तथा a¹h² + b¹k² = 1
अब वक्र ax² + by² = 1 के लिए
दोनों पक्षों का x के सापेक्ष अवकलन करने पर

प्रश्न 7.
वृत्त x + y = 4 के पहले चतुर्थांश के भाग के किसी बिन्दु पर बनी स्पर्श रेखा x-अक्ष को बिन्दु A वY-अक्ष को बिन्दु B पर काटती है। यदि 0, वृत्त का केन्द्र हो, तो (OA + OB) का न्यूनतम मान ज्ञात कीजिए।
हल:
माना वृत्त x² + y² = 4 के पहले चतुर्थांश के भाग के किसी
बिन्दु पर AB स्पर्श रेखा है जो कि x-अक्ष तथा y-अक्ष पर OA तथा OB अन्त:खण्ड काटती है। माना
S = OA + OB
S = OA + OB .......... (1)
OP के द्वारा बना हुआ कोण θ है जो x-अक्ष की धनात्मक दिशा से बनाती है।
बिन्दु P के निर्देशांक = (2 cos θ, 2 sin θ)
बिन्दु A के निर्देशांक = (2 sec θ, 0)
बिन्दु B के निर्देशांक = (0, 2 cosec θ)
समीकरण (1) में मान रखने पर
S = 2 sec θ + 2 cosec θ
⇒ \(\frac{d \mathrm{~S}}{d \theta}\) = 2[sec θ tan θ - cosec θ cot θ]
उच्चिष्ठ एवं निम्निष्ठ के लिये 
⇒ \(\frac{d \mathrm{~S}}{d \theta}\) = 0 ⇒2{sec θ tan θ - cosec θ cot θ} = 0