RBSE Class 12 Maths Important Questions Chapter 5 सांतत्य तथा अवकलनीयता

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 5 सांतत्य तथा अवकलनीयता Important Questions and Answers.

RBSE Class 12 Maths Chapter 5 Important Questions सांतत्य तथा अवकलनीयता

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
k का मान जो फलन

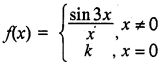
संतत बना देता है, होगा
(A) 3
(B) \(\frac{1}{3}\)
(C) 1
(D) 0
हल:
(A) 3

x= 0 पर f(o) = k

प्रश्न 2.
यदि f(x) = \(\frac{1-\cos x}{x^2}\), x = 0 पर संतत है, तो f(0) बराबर होगा
(A) \(\frac{1}{2}\)
(B) 2
(C) \(\frac{1}{4}\)
(D) 4
हल:
(A)

दिया गया फलन x = 0 पर संतत है. इसलिए

 

प्रश्न 3.
यदि फलन

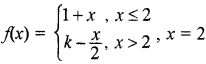
पर संतत हो, तो k का मान होगा
(A) 1
(B) 2
(C) 3
(D) 4.
हल:
(D) 4

x = 2 पर फलन का मान होगा
f(2) = 1 + 2 = 3
f(2 + h) = k - \(\left(\frac{2+h}{2}\right)\)
f(2 - h) = 1 + (2 - h) = (3 - h)
R.H.L. का मान होगा

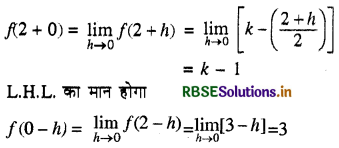
फलन x = 2 पर संतत है इसलिए
f(2) = R.H.L. = L.H.L.
3 = k - 1 = 3 ∴ k = 4
अतः सही विकल्प (D) है।

प्रश्न 4.
k के किस मान के लिए निम्न फलन x = 1 पर संतत है

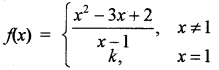
(A) 1
(B) - 1
(C) 0
(D) 3
हल:
(B) - 1

x= 1 पर फलन का मान
f(1) = k

R.H.L. का मान निकालने पर

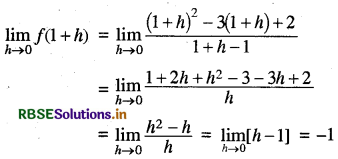
चूँकि फलन x = 1 पर संतत है इसलिए
f(1) = R.H.L.
∴ k = -1
अतः सही विकल्प (B) है।

प्रश्न 5.
यदि फलन

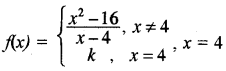
पर संतत है, तो k का मान है.
(A) 4
(B) -4
(C) 8
(D) - 8
हल:
(C) 8

x= 4 पर फलन का मान
f(4) = k

x = 4 पर दायीं सीमा (R.H.L) का मान निकालने पर

⇒ k = 8
अतः सही विकल्प (C) है।

प्रश्न 6.
फलन

पर संतत हो, तो λ का मान है
(A) 1
(B) 2
(C) 3
(D) 4
हल:
(A) 1

x = 3 पर फलन का मान
f(3) = 4
बायीं सीमा का मान निकालने पर

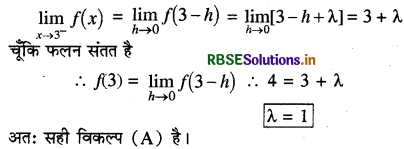
प्रश्न 7.
cos^-1(4x³ - 3x) का अवकलज है

हल:
(B) \(\frac{-3}{\sqrt{1-x^2}}\)
x = cos θ लेने पर
cos^-1(4x3 - 3x) = cos^-1(4 coss θ - 3 cos θ)
= cos^-1(cos 3θ) = 3θ = 3 cos^-1x [∵ x = cos θ]
\(\frac{d}{dx}\)(3cos^-1x) = 3\(\frac{d}{dx}\)(cos^-1 x) = 3\(\left\{\frac{-1}{\sqrt{1-x^2}}\right\}\)
= \(\frac{-3}{\sqrt{1-x^2}}\)
अतः सही विकल्प (B) है।

प्रश्न 8.
tan^-1\(\left(\frac{1+x}{1-x}\right)\) का अवकलज है
(A) \(\frac{1}{1+x^2}\)
(B) -\(\frac{1}{1+x^2}\)
(C) \(\frac{2}{1+x^2}\)
(D) - \(\frac{2}{1+x^2}\)
हल:
tan^-1\(\left(\frac{1+x}{1-x}\right)\) = tan^-11 + tan^-1x
\(\frac{d}{dx}\)(tan^-11 + tan^-1x) = 0 + \(\frac{1}{1+x^2} = \frac{1}{1+x^2}\)
अतः सही विकल्प (A) है।

प्रश्न 9.
यदि y = x log_e x तो \(\frac{d^2 y}{d x^2}\) का मान होगा
(A) \(\frac{1}{1+x}\)
(B) 1 + log_e x.
(C) log_e (1 + x)
(D) \(\frac{1}{x}\)
हल:
(D) \(\frac{1}{x}\)

दिया गया है y = x logx
\(\frac{dy}{dx}\) = 1. logx + x. \(\frac{1}{x}\) = 1 + log_e x.

पुनः अवकलन करने पर
\(\frac{d}{d x}\left(\frac{d y}{d x}\right)=\frac{d}{d x}\)(1 + log_ex) = 0 + \(\frac{1}{x}=\frac{1}{x}\)
⇒ \(\frac{d^2 y}{d x^2}=\frac{1}{x}\)
अतः सही विकल्प (D) है।

प्रश्न 10.
यदि फलन f(x) = x² - 5x + 6; x ∈ [2, 3] के लिए रोल प्रमेय सत्य है तो c का मान होगा
(A) \(\frac{5}{2}\)
(B) \(\frac{5}{3}\)
(C) \(\frac{12}{5}\)
(D) \(\frac{7}{3}\)
हल:
(A) \(\frac{5}{2}\)

दिये गये फलन के लिए रोल प्रमेय सत्य है।
f(x) = x² - 5x + 6 ∴ f'(x) = 2x - 5
⇒ f'(c) = 2c - 5
f'(c) = 0 रखने पर
0 = 2c - 5 ∴ c = \(\frac{5}{2}\)
अतः सही विकल्प (A) है।

प्रश्न 11.
यदि फलन f(x) = x (x - 1); x ∈ [1, 2] के लिए लाग्रांज माध्यमान प्रमेय सत्य है तो c का मान होगा-
(A) \(\frac{5}{4}\)
(B) \(\frac{4}{3}\)
(C) \(\frac{3}{2}\)
(D) \(\frac{5}{2}\)
हल:
(C) \(\frac{3}{2}\)

दिये गये फलन के लिए लाग्रांज माध्यमान प्रमेय सत्य है।
इसलिए f'(c) = \(\frac{f(b)-f(a)}{b-a}\)
f(x) = x(x – 1) = x² – x
f'(x) = 2x - 1 इसलिए f'(c) = 2c - 1 .
f(x) = x² –x

यहाँ पर a = 1, b = 2
f(1) = 1² - 1 = 0, f(2) = (2)² – 2 = 4 - 2 = 2
2c - 1 = \(\frac{2-0}{2-1}\) = 2
⇒ 2c = 2 + 1 = 3 इसलिए c = \(\frac{3}{2}\)
अतः सही विकल्प (C) है।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि निम्न फलन x = 2 पर संतत हो तो k का मान ज्ञात कीजिये

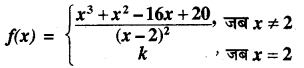
हल:
दिया गया फलन

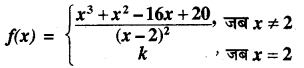
x= 2 पर फलन का मान
f(2) = k

R.H.L. का मान निकालने पर

प्रश्न 2.
फलन

पर संतत हो तब m का मान लिखिये।
हल:
दिया गया फलन

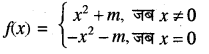
x = 0 पर फलन का मान
f(x) = –x² - m
f(0) = - 0 - m = - m ....(1)

R.H.L. का मान निकालने पर

प्रश्न 3.

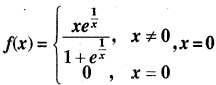
परसातत्य का परीक्षण कीजिये।
हल:
दिया गया फलन

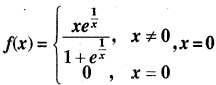
पर सातत्य है।

∴ दायीं सीमा (R.H.L.) का मान निकालने पर

प्रश्न 4.
यदि फलन f(x) = \(\frac{1-\cos (c x)}{x \sin x}\), x ≠ 0 और f(0) = \(\frac{1}{2}\) तथा f(x), x = 0 पर संतत है तो c का मान ज्ञात करो।
हल:
दिया गया फलन

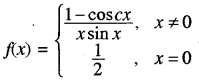
x = 0 पर संतत है।
x = 0 पर फलन का मान निकालने पर
f(x) = \(\frac{1}{2}\). f(0) = \(\frac{1}{2}\)

फलन की दायीं सीमा (R.H.L.) का मान निकालने पर

प्रश्न 5.
यदि फलन

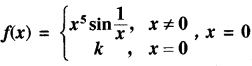
पर संतत हो, तो k का मान लिखिये।
हल:
x= 0 पर फलन का चयन
f(x) = k, जब x = 0
f(0) = k

दायीं सीमा (R.H.L.) का मान निकालने पर

प्रश्न 6.

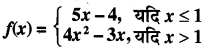
पर सातत्य का परीक्षण कीजिये।
हल:
x = 1 पर फलन की बायीं सीमा (L.H.L.) का मान निकालने पर

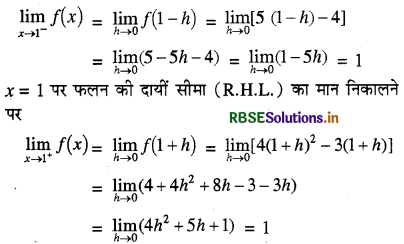
x = 1 पर फलन का मान निकालने पर
फलन का चयन
f(x) = 5x - 4
f(1) = 5 × 1 - 4 = 5 - 4 = 1
f(1) = \(\lim _{h \rightarrow 0}\) f(1 - h) = \(\lim _{h \rightarrow 0}\) f(1 + h)
अतः फलन x = 1 पर संतत है तथा x = 1 के अतिरिक्त भी फलन बहुपदीय फलन होने के कारण सर्वत्र संतत है।

प्रश्न 7.
सिद्ध कीजिये कि f(x) = x - |x|, x ∈ R से परिभाषित फलन x = 0 पर संतत है।
हल:
फलन को मापांक से मुक्त करने पर निम्न प्रकार से लिखा जा सकता है

प्रश्न 8.
यदि निम्न फलन x = 0 पर संतत है तो k का मान लिखो

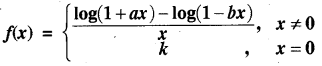
हल:
x = 0 पर फलन की दायीं सीमा का मान निकालने पर

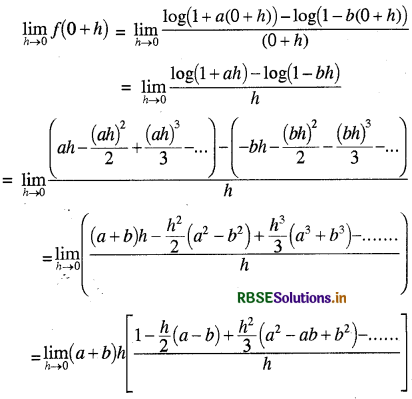
= a + b
तथा f(o) = k
∵ फलन x = 0 पर संतत है।
∴ f(0) = \(\lim _{h \rightarrow 0}\) f(0+h)
∴ k = a + b

प्रश्न 9.
यदि फलन f(x) = \(\frac{\sqrt{x}-\sqrt{a}}{x-a}\), x = a पर संतत है, तो f(a) का मान ज्ञात कीजिये।
हल:
फलन की दायीं सीमा (R.H.L.) का मान निकालने पर

प्रश्न 10.
यदि फलन

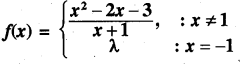
बिन्दु x = -1 पर संतत है तो λ का मान ज्ञात कीजिये।
हल:
x = -1 के लिए फलन का चयन
f(x) = λ ∴ f(-1) = λ

x = -1 पर फलन की दायीं सीमा (R.H.L.) का मान निकालने पर

प्रश्न 11.
निम्न फलन का x के सापेक्ष अवकलन ज्ञात कीजिये
log(\(\sqrt{x-1}+\sqrt{x+1}\))
हल:
मान लीजिए कि
y = log(\(\sqrt{x-1}+\sqrt{x+1}\))

अब x के सापेक्ष अवकलन करने पर

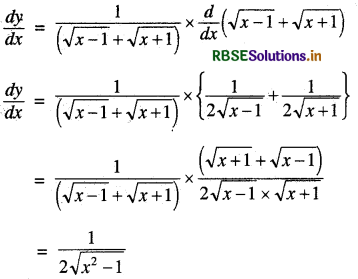
प्रश्न 12.
tan^-1\(\left[\frac{\sin x+\cos x}{\cos x-\sin x}\right]\) फलन का के सापेक्ष अवकलन कीजिये।
हल:
मान लीजिये कि y = tan^-1\(\left[\frac{\sin x+\cos x}{\cos x-\sin x}\right]\)

प्रश्न 13.
यदि y = sin[2tan^-1\(\left(\sqrt{\frac{1-x}{1+x}}\right)\)] है, तब \(\frac{dy}{dx}\) का मान ज्ञात कीजिये।
हल:
माना x = cos θ या θ = cos^-1x

प्रश्न 14.
y = x + \(\frac{1}{x+\frac{1}{x+\frac{1}{x+\ldots \ldots \ldots . \infty}}}\) का x के सापेक्ष अवकलन करें।
हल:
y = x + \(\frac{1}{y}\) लिखने पर
⇒ y² = xy + 1
⇒ y² - xy = 1

अब x के सापेक्ष अवकलन करने पर

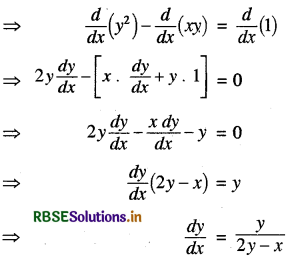
प्रश्न 15.
फलन f(x) = sin 2x के लिए रोल प्रमेय अन्तराल \(\left[0, \frac{\pi}{2}\right]\) में सत्य है, तो c का मान लिखिये।
हल:
दिया गया फलन f(x) = sin 2x
⇒ (x) = d(sin2x) = 2 cos 2x
f(c) = 2 cos 2c = 0
cos 2c = \(\frac{0}{2}\) = 0 = cos \(\frac{\pi}{2}\)
⇒ 2c = \(\frac{\pi}{2}\): c = \(\frac{\pi}{2}\) ∈ (0, \(\frac{\pi}{2}\))
इसलिए c = \(\frac{\pi}{4}\)

प्रश्न 16.
फलन f(x) = \(\frac{x^2-4 x}{x+2}\) के लिए अन्तराल [0, 4] में रोल प्रमेय का सत्यापन कीजिये तथा वह बिन्दु ज्ञात कीजिये जहाँ अवकलंज शून्य है।
हल:
दिया गया फलन f(x) = \(\frac{x^2-4 x}{x+2}\), दो संतत फलनों का भागफल है। चूँकि (x² - 4x) व (x + 2) दोनों ही x का बहुपद हैं इसलिए x के प्रत्येक मान के लिए संतत है। अतः f(x) भी x के प्रत्येक मान के लिए संतत है फलतः f(x), विशेष रूप से x ∈ [0, 4] के लिए संतत है।

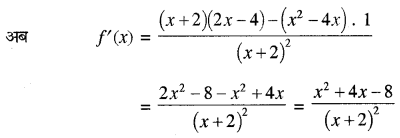
जो कि अन्तराल (0, 4) के प्रत्येक बिन्दु पर विद्यमान है अर्थात् परिभाषित है, अतः f(x), अन्तराल [0, 4] में अवकलनीय है।

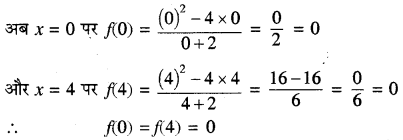
इस प्रकार f(x) रोल प्रमेय के तीनों प्रतिबन्धों को संतुष्ट करता है, अतः f'(c) = 0

अतः कम से कम एक c ∈ (0, 4) इस प्रकार है कि
f'(c) = 0 जहाँ पर c = -2 + 2√3
फलतः रोल प्रमेय का सत्यापन हुआ।

प्रश्न 17.
फलन f(x) = x(x + 3)e^-x/2 के लिए अन्तराल [-3, 0] में रोल प्रमेय का सत्यापन कीजिये।
हल:
यहाँ पर फलन f(x) फलनों x(x + 3) और e^-x/2 का गुणनफल है। x(x + 3), x का बहुपद फलन है जो कि x के प्रत्येक मान के लिए संतत है और e^-x/2 भी x के प्रत्येक मान के लिए संतत है, चूँकि यह चरघातांकी फलन है।

अत: f(x) भी x के प्रत्येक मान के लिए संतत है।
अतः विशेष रूप से f(x), x ∈ [-3, 0] के लिए संतत है।
अब f(x) = x(x +3)e^-x/2 = (x +3x). e^-x/2
f'(x) = (2x +3). e^-x/2 + (x² + 3x){-\(\frac{1}{2}\)e^-x/2}
f'(x) = e^-x/2((2x + 3) - 1(x + 3x)
= \(\frac{1}{2}\)e^-x/2(4x + 6 - x² - 3x)
= \(\frac{1}{2}\)e^-x/2(x + 6 - x.)

जो कि अन्तराल (-3, 0) के प्रत्येक बिन्दु पर,परिभाषित है। अतः f(x), अन्तराल (-3, 0) में अवकलनीय है।
f(a) = f(-3) = -3(-3 + 3)e^-3/2 = 0
f(b) = f(0) = 0

इस प्रकार से f(x) रोल प्रमेय के तीनों प्रतिबन्धों को संतुष्ट करता है। अतः
f"(x) = 0 ⇒ \(\frac{1}{2}\)e^-x/22(6+x-x.) = 0
⇒ e^-x/2 = 0 या 6 + x - x² = 0
⇒ e^-x/2 = 0 या (2 + x)(3 - x) = 0
⇒ x अनन्त या x = -2, 3 जिनमें से x = -2 ∈ (-3, 0) में है।
अतः कम से कम एक c ∈ (-3,0) इस प्रकार से है कि f"(c) = 0 जहाँ पर c = -2
अतः रोल प्रमेय का सत्यापन हुआ।

प्रश्न 18.
निम्न फलन के लिए लाग्रांज माध्यमान प्रमेय के c का मान ज्ञात कीजिये
f(x) = x + \(\frac{1}{x}\), x ∈ [\(\frac{1}{2}\), 3]
हल:
यहाँ पर f(x) = x + \(\frac{1}{x}\), x ∈ [\(\frac{1}{2}\), 3]
इसलिए f'(x) = 1 -
यहाँ पर f"(x) का मान अन्तराल [\(\frac{1}{2}\) 3] में एक परिमित राशि के रूप में प्राप्त होता है।
अत: f(x) अन्तराल (\(\frac{1}{2}\), 3) में अवकलनीय है।
अब f(x) = x + \(\frac{1}{x}=\frac{x^2+1}{x}\) संतत है।
चूँकि यह दो संतत फलनों का भागफल है,

अतः f(x) = x + \(\frac{1}{x}\) अन्तराल [2.3] में संतत है।

अतः लाग्रांज माध्यमान प्रमेय के दोनों प्रतिबन्ध संतुष्ट होते हैं।

प्रश्न 19.
फलन (x - \(\frac{1}{x}\)) के लिए अन्तराल [\(\frac{1}{2}\), 2] में लाग्रांज माध्यमान प्रमेय सत्यापित कीजिये एवं c का मान ज्ञात कीजिये।
हल:
माना f(x) = x - \(\frac{1}{x}\). x ∈ [\(\frac{1}{2}\), 2]
⇒ f'(x) = 1 + \(\frac{1}{x^2}\) अन्तराल [\(\frac{1}{2}\), 2] में एक परिमित राशि है
अत: f(x), अन्तराल (\(\frac{1}{2}\), 2) में अवकलनीय है।
अब f(x) = x - \(\frac{1}{x}=\frac{x^2-1}{x}\) संतत है।

चूँकि यह दो संतत फलनों का भागफल है।
अतः लाग्रांज माध्यमान प्रमेय के दोनों प्रतिबन्धों को संतुष्ट करता है।

अतः लाग्रांज माध्यमान प्रमेय सत्यापित होती है।

प्रश्न 20.
फलन f(x) = x² + 3x - 5 के लिए अन्तराल [1, 2] में लाग्रांज माध्यमान प्रमेय का सत्यापन कीजिये व c का मान ज्ञात कीजिये।
हल:
दिया गया फलन f(x) = x² + 3x - 5 एक बहुपद फलन है।
अतः यह अन्तराल [1, 2] में संतत तथा (1, 2) में अवकलनीय है। चूँकि अवकलनीय के लिए f' (x) = 2x + 3 अन्तराल (1, 2) में परिभाषित है।
f(a) = f(1) = (1)² + 3 × 1 -5 = 1 + 3 - 5 = -1
f(b) = f(2) = (2)² + 3 × 2 - 5 = 4 + 6 - 5 = 5
f'(c) = 2c + 3 [∵ f(x) = 2x + 3]

अतः [1, 2] के मध्य वक्र पर एक बिन्दु c अवश्य इस प्रकार है कि

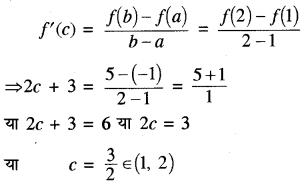
इसलिए लाग्रांज माध्यमान प्रमेय सत्यापित होती है।

प्रश्न 21.
निम्न फलन की सातत्यता का परीक्षण कीजिए

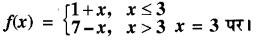
हल:
प्रश्नानुसार

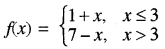
x = 3 पर f(3) = 1 + 3 = 4 ....(1)

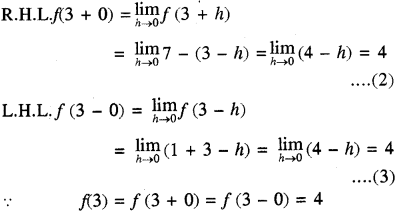
∴ x = 3 पर फलन संतत होगा। उत्तर

प्रश्न 22.
यदि y = \(\frac{\sin ^{-1} x}{x}\) तो सिद्ध कीजिए कि x(1 - x²)y₂ + (2 - 3x²) y₁ - xy = 0
हल:
y = \(\frac{\sin ^{-1} x}{x}\) या xy = sin^-1x
x के सापेक्ष अवकलन करने पर
xy₁ + y . 1 = \(\frac{\sin ^{-1} x}{x}\)
या \(\sqrt{1-x^2}\)[xy₁ + y] = 1

दोनों पक्षों का वर्ग करने पर
या (1 - x²) (xy₁ + y)² = 1

पुनः x के सापेक्ष अवकलन करने पर
(1 - x²) 2 (xy₁ + y) x {xy₂ + y₁ . 1 + y1} + (xy₁ + y)² (-2x) = 0
या 2 (xy₁ + y) [(1 - x²) (xy₂ + 2y₁) + (xy₁ + y) (-x)] = 0
या (1 - x²) (xy₂ + 2y) - x²y1 - xy = 0
(1 - x²) xy₂ + 2 (1 - x) y₁ - xy₁ - xy = 0
या x(1 - x²) y₂ + (2 - 3x²) y₁ - xy = 0

प्रश्न 23.
\(\frac{dy}{dx}\) का मान θ = \(\frac{\pi}{4}\) पर ज्ञात कीजिए जबकि
x = ae^θ (sin θ - cos θ) और
y = ae^θ (sin θ + cos θ)
हल:
x = ae^θ (sin θ - cos θ)

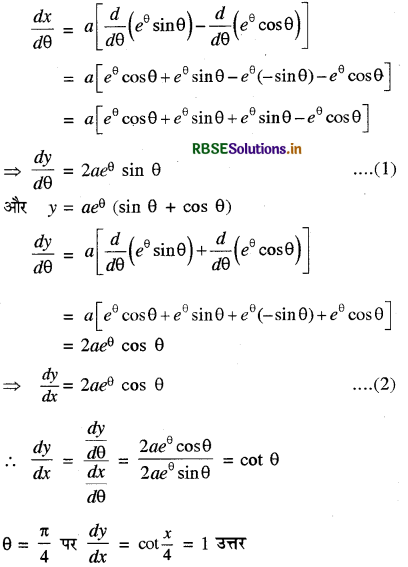
प्रश्न 24.
यदि y = Pe^ax + Qe^bx तब प्रदर्शित कीजिए
\(\frac{d^2 y}{d x^2}\) - (a + b)\(\frac{dy}{dx}\) + aby = 0
हल:
y = Pe^ax + Qe^bx ......(1)
x के सापेक्ष अवकलन करने पर
⇒ \(\frac{dy}{dx}\) = Pae^ax + Qbe^bx ...........(2)

पुनः x के सापेक्ष अवकलन करने पर
\(\frac{d^2 y}{d x^2}\) = Pa²e^ax + Qb^ee^bx .............(3)

L.H.S. = \(\frac{d^2 y}{d x^2}\) - (a+b) \(\frac{d y}{d x}\) + aby
= Pa²e^ax + Qb²e^bx - (a + b) (Pae^an + Qbe^bx) + ab (Pe^ax + Q₁)
= a²P e^qx + b²Qe^bx - a²Pe^qx – ab Qe^bx - ab Pe^ax – b²Qe^bx + ab Pe^ax + ab Qe^ax
0 = R.H.S

प्रश्न 25.
फलन f(x) = |x| + |x - 1| की अंतराल (-1, 2) में सातत्यता तथा अवकलनीयता की विवेचना कीजिये।
हल:
दिया गया फलन
f(x) = |x| + |x - 1|

दिये गये फलन को निम्न प्रकार से लिखा जा सकता है

प्रश्न 26.
दर्शाइये कि फलन

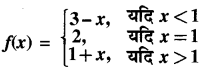
x = 1 पर संतत है।
हल:
फलन का मान x = 1 पर
f(1) = 2
बायीं सीमा (LHL) का मान निकालने पर
\(\lim _{h \rightarrow 0}\) f(1 - h) = \(\lim _{h \rightarrow 0}\) 3 - (1 - h)
अतः बायीं सीमा का मान = 2

इसी तरह से दायीं सीमा का मान निकालने पर
\(\lim _{h \rightarrow 0}\) f(1 + h) = \(\lim _{h \rightarrow 0}\) 1 + (1 + h)
अतः दायीं सीमा का मान = 2
अतः फलन का मान = बायीं सीमा का मान = दायीं सीमा क़ा मान
अतः x = 1 पर फलन संतत है।

निबन्धात्मक प्रश्न

प्रश्न 1.
यदि निम्नलिखित फलन x = 1 पर संतत है तो a तथा b के मान ज्ञात कीजिये

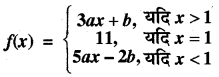
हल:
दिया गया फलन

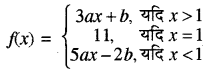
बायीं सीमा (L.H.L.) का मान निकालने पर

⇒ 11 = 3a + b = 5a - 2b
⇒ 5a - 2b = 11 ....(1)
तथा 3a + b = 11 ....(2)
समीकरण (1) तथा (2) को हल करने पर a = 3 तथा b = 2
अतः a = 3, b = 2

प्रश्न 2.
निम्नलिखित फलन का x = 2 तथा x = 3 पर संततता का परीक्षण कीजिये
f(x) = |x - 2| + |x - 3|
हल:
दिया गया फलन f(x) = |x - 2| + |x - 3|,
जिसे निम्न प्रकार लिखा जा सकता है

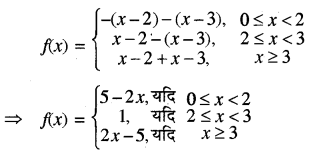
(i) x = 2 पर फलन की संततता का परीक्षण करने पर

(ii) x = 3 पर फलन की संततता का परीक्षण करने पर

प्रश्न 3.
\(\frac{dy}{dx}\) का मान ज्ञात कीजिये
(a) y = \(\sin x^{\sin x^{\sin x} \ldots}\)
(b) y = \(\sqrt{\log _e x+\sqrt{\log _e x+\sqrt{\log _e x+\ldots \ldots \ldots \infty}}}\)
(c) y = \(e^{x+e^{x+e^{x+\ldots} \ldots \ldots}}\)
हल:
(a) y = \(\sin x^{\sin x^{\sin x} \ldots}\)
y = (sin x)^y
दोनों पक्षों का लघुगणक लेने पर
log_ey = log_e(sin x)^y
log_e y = y log_e(sin x)

दोनों पक्षों का x के सापेक्ष अवकलन करने पर

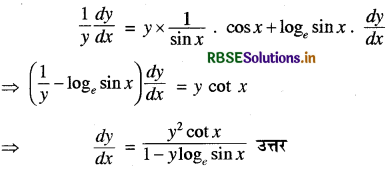
(b) y = \(\sqrt{\log _e x+\sqrt{\log _e x+\sqrt{\log _e x+\ldots \ldots \ldots \infty}}}\)
या y = \(\sqrt{\log _e x+y}\)
या y² = log_ex + y

अब x के सापेक्ष अवकलन करने पर

(c) y = \(e^{x+e^{x+e^{x+\ldots} \ldots \ldots}}\)
या y = e^x+y

दोनों पक्षों का लघुगणक लेने पर
log y = log_ee^x+y
log_ey = (x + y) log_ee
या log_ey = x + y (∵ log_ee = 1)

x के सापेक्ष अवकलन करने पर

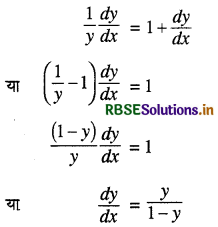
प्रश्न 4.
\(\frac{dy}{dx}\) का मान ज्ञात कीजिये
(a) \(\sqrt{x^2+y^2}\) = log_e(x² - y²)
(b) y = \(x^{x^{x^x \ldots \ldots \ldots \ldots \ldots+\infty}}\)
(c) xy log (x + y) = 1
हल:
(a) \(\sqrt{x^2+y^2}\) = log_e(x² - y²)
x के सापेक्ष अवकलन करने पर

(b) y = \(x^{x^{x^x \ldots \ldots \ldots \ldots \ldots+\infty}}\)
⇒ y = x^y
⇒ logy = log_ex^y = y log_ex

अब x के सापेक्ष अवकलन करने पर

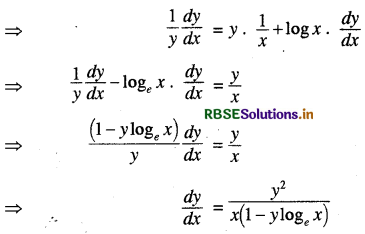
(c) xy log_e(x + y) = 1
x के सापेक्ष अवकलन करने पर

प्रश्न 5.
यदि x = sin^-1\(\left(\frac{2 t}{1+t^2}\right)\), y = cos^-1\(\left(\frac{1-t^2}{1+t^2}\right)\) है, तो \(\frac{dy}{dx}\) ज्ञात कीजिये।
हल:
दिया गया है
x = sin^-1\(\left(\frac{2 t}{1+t^2}\right)\), y = cos^-1\(\left(\frac{1-t^2}{1+t^2}\right)\)
x = tan θ रखने पर
इसलिए x = sin^-1\(\left(\frac{2 \tan \theta}{1+\tan ^2 \theta}\right)\) y = cos^-1\(\left(\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\right)\)
x = sin^-1(sin 2θ), y = cos^-1(cos 2θ)
x = 2θ, y = 2θ
∴ x = 2 tan^-1t, y = 2 tan^-1t

अब t के सापेक्ष अवकलन करने पर

प्रश्न 6.
यदि x² + y² = t - \(\frac{1}{t}\) तथा x⁴ + y⁴ = t² + \(\frac{1}{t^2}\) तो सिद्ध कीजिये कि x\(\frac{dy}{dx}\) + y = 0
हल:
दिया गया है कि x² + y² = t - \(\frac{1}{t}\) तथा x⁴ + y⁴ = t² + \(\frac{1}{t^2}\)

इसलिए वर्ग करने पर (x² + y²)² = (t - \(\frac{1}{t}\))²

= x⁴ + y⁴ + 2x²y² = t² + \(\frac{1}{t^2}\) - 2
लेकिन दिया गया है कि
x⁴ + y⁴ = t² + \(\frac{1}{t^2}\)
इसलिए 2x²y² =-2
x²y² = -1

अब x के सापेक्ष अवकलन करने पर
x².2y\(\frac{dy}{dx}\) + 2x.y² = 0
= - 2x²y\(\frac{dy}{dx}\) + 2xy² = 0

दोनों पक्षों में 2xy का भाग देने पर
x\(\frac{dy}{dx}\) + y = 0

प्रश्न 7.
यदि x³ + y³ = t - \(\frac{1}{t}\) तथा x⁶ + y⁶ = t² + \(\frac{1}{t^2}\) तो सिद्ध कीजिये : x⁴y²\(\frac{dy}{dx}\) = 1
हल:
दिया गया है
x³ + y³ = t - \(\frac{1}{t}\) ....(1)
x⁶ + y⁶ = t² + \(\frac{1}{t^2}\) ....(2)

समीकरण (1) का दोनों पक्षों का वर्ग करने पर
(x³ + y³)² = (t - \(\frac{1}{t}\))²
⇒ x⁶ + 2x³y³ + y⁶ = t² - 2 + \(\frac{1}{t^2}\)

लेकिन समीकरण (2) से x⁶ + y⁶ = t² + \(\frac{1}{t^2}\)
इसलिए 2x³y³ = -2
x³y³ = -1 ......(3)

अब x के सापेक्ष अवकलन करने पर

प्रश्न 8.
यदि x = a cos θ + b sin θ और y = a sin θ - b cos θ तो सिद्ध कीजिए : y²y₂ - xy₁ + y = 0
हल:
दिया गया है कि x = a cos θ + b sin θ
और y = a sin θ - b cos θ
= x² + y² = (a cos θ + b sin θ)2 + (a sin θ - b cos θ)2
= a²cos² θ + 2ab sin θ cos θ + b² sin²θ + a²sin²θ - 2ab sin θ cos θ + b² cos²θ
= x² + y² = a(cos² θ + sin² θ) + b²(cos²θ + sin² θ)
= x² + y² = a² + b²

अब x के सापेक्ष अवकलन करने पर
⇒ 2x + 2y y₁ = 0.
⇒ y₁ = \(\frac{-x}{y}\)....(1)

पुनः x के सापेक्ष अवकलन करने पर

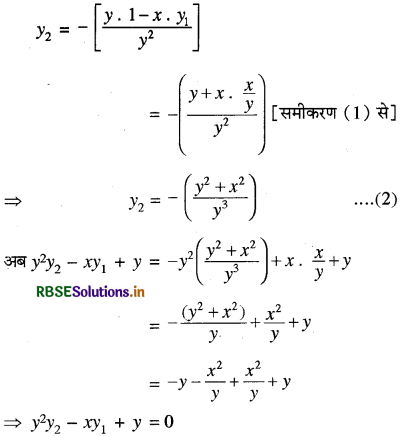
प्रश्न 9.
यदि x = a cos³θ, y = a sin³θ तो \(\left(\frac{d^2 y}{d x^2}\right)_{\theta=\frac{\pi}{4}}\) का मान ज्ञात कीजिये।
हल:
दिया गया है x = a cos θ, y = a sin θ

प्रश्न 10.
सिद्ध कीजिए कि \(\frac{d}{d x}\left[\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}\right] = \sqrt{a^2-x^2}\)
हल:

प्रश्न 11.
यदि y = x cos (log x) तो सिद्ध कीजिए
x²y₂ - xy₁ + 2y = 0
हल:
दिया गया है
y= x cos (log x) ......(1)

दोनों पक्षों का x के सापेक्ष अवकलन करने पर
y₁ = 1 . cos (log x) + x[-sin(log x).\(\frac{1}{x}\)]
या y₁ = cos (log x) – sin (log x) .... (2)

दोनों पक्षों का x के सापेक्ष पुनः अवकलन करने पर
या y₂ = \(\frac{-\sin (\log x)}{x}-\frac{\cos (\log x)}{x}\)
या xy₂ = - sin (log x) - cos (log x)

दोनों पक्षों में x का गुणा करने पर
या x²y₂ = - x sin (log x) - x cos (log x)

समीकरण (1) तथा (2) से
या x²y₂ = - y + x[y₁ - cos (log x)]
या x²y₂ = - y + xy₁ - y [समीकरण (1) से]
या x²y₂ - xy₁ + 2y = 0

प्रश्न 12.
यदि y³ + 3ax² + x³ = 0 तो सिद्ध कीजिए कि
\(\frac{d^2 y}{d x^2}+\frac{2 a^2 x^2}{y^5}\) = 0
हल:
यहाँ पर दिया गया है कि
y³ + 3ax² + x³ = 0

दोनों पक्षों का x के सापेक्ष अवकलन करने पर
3y²\(\frac{dy}{dx}\) + 6ax + 3x² = 0
या y²\(\frac{dy}{dx}\) + x² + 2ax = 0 ..........(2)
या \(\frac{d y}{d x}=-\left(\frac{x^2+2 a x}{y^2}\right)\) ......(3)

पुनः (2) के दोनों पक्षों का x के सापेक्ष अवकलन करने पर

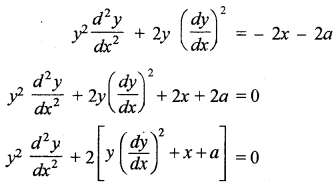
समीकरण (1) से \(\frac{dy}{dx}\) का मान रखने पर

प्रश्न 13.
यदि x^y + y^x = b^a + a^b तो ज्ञात कीजिए।
हल:
प्रश्नानुसार x^y + y^x = b^a + a^b
या u + y = b^a + a^b जबकि u = x^y, v = y^x मानने पर

लघुगुणक लेने पर
log u = log x^y = y log x [∵ log mⁿ = n log m]

अब x के सापेक्ष अवकलन करने पर

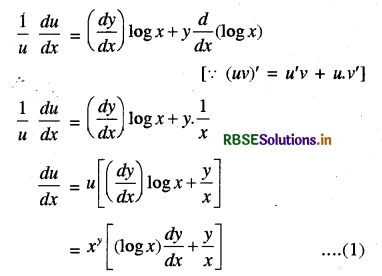
पुनः v = y^x

लघुगणक लेने पर
log v = log y = x log y[∵ log mⁿ = n log m]
log v = x log y

अब x के सापेक्ष अवकलन करने पर

प्रश्न 14.
यदि x = a (cos 2t + 2t sin 2t) तथा y = a (sin 2t - 2t cos 24) हैं, तो \(\frac{d^2 y}{d x^2}\) ज्ञात कीजिए।
हल:
x = a (cos 2t + 2t sin 2t) तथा
y = a (sin 2t - 2t cos 2t)
\(\frac{dx}{dt}\) = a (-2 sin 2t + 2 (1. sin 2t + 2t cos 2t))
= a (- 2 sin 2t + 2 sin 2t + 4t cos 2t)
\(\frac{dx}{dt}\) = 4at cos 2t

इसी प्रकार से
\(\frac{dy}{dt}\) = a ((2cos 2t - 2 (1.cos 2t – 2t sin 2t))
= a (2 cos 2t – 2 cos 2t + 4t sin 2t)
\(\frac{dy}{dt}\) = 4at sin 2t

प्रश्न 15.
यदि (ax + b) e^y/x = x है, तो दिखाइये कि
x³\(\frac{d^2 y}{d x^2}\) = (x\(\frac{dy}{dx}\) - y)²
हल:
दिया है
(ax + b) e^y/x = x

दोनों तरफ लघुगणक लेने पर
⇒ log_e (ax + b) e^y/x = log_ex
⇒ log_e (ax + b) + log_e e^y/x = log_ex
⇒ log_e (ax + b) + \(\frac{y}{x}\) log_ee = log_ex
⇒ loge (ax + b) + \(\frac{y}{x}\) = log_ex [∵ log_ee = 1]
⇒ \(\frac{y}{x}\) = log_ex - log_e (ax + b)

x के सापेक्ष अवकलन करने पर

प्रश्न 16.
यदि y = x^x + x^a + a^x + a^a हो, तो \(\frac{dy}{dx}\) ज्ञात कीजिए।
हल:
माना कि
y = x^x + x^a + a^x + a^a
x के सापेक्ष अवकलन करने पर
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\)(x^x)+ ax^a-1 + a log_ea + 0
⇒ \(\frac{dy}{dx}\) = \(\frac{d}{dx}\)(x^x) + ax^a-1 + a^x log_ea ........(1)

माना कि u = x^x
:. log u = log. x^x = x log_ex
\(\frac{1}{u} \frac{d u}{d x}\) = 1.log_ex + x \(\frac{1}{x}\) = 1 + log_ex
\(\frac{d}{dx}\)(x^x) = \(\frac{du}{dx}\) = u(1 +log_ex) = x^x(1 + log_ex)

समीकरण (1) में \(\frac{d}{dx}\)(x^x) का मान रखने पर
\(\frac{dy}{dx}\) = x^x (1 + log_ex) + ax^a-1 + a^x log_ea