RBSE Class 12 Maths Important Questions Chapter 5 Continuity and Differentiability

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 5 Continuity and Differentiability Important Questions and Answers.

RBSE Class 12 Maths Chapter 5 Important Questions Continuity and Differentiability

Question 1.
Show that the function f(x) = 2x - |x| is continuous at X = 0.
Answer:
Given, f(x) = 2x - |x|
This function can be written as:

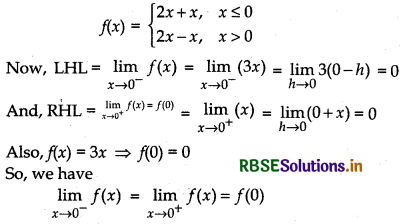
Question 2.
If the function f(x) given by

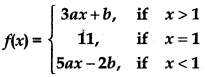
is continuous at x = 1, then find the value of a and b.
Answer:

Also, given that f(1) = 11
On substituting these values in Eq. (i), we get
5a - 2b 3a + b = 11
⇒ 3a + b = 11 .............. (ii)
and 5a - 2b = 11 .............. (iii)
On subtracting 3 × Eq. (iii) from 5 × Eq. (ii), we get
15a + 5b - 15a + 6b = 55 - 33
⇒ 11b - 22 ⇒ b = 2
On putting the value of b in Eq. (ii), we get
3a + 2 = 11
⇒ 3a = 9
⇒ a = 3
Thus, a = 3 and b = 2.

Question 3.

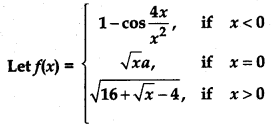
Determine the value of a so that f(x) is continuous at x = 0.
Answer:

Question 4.
Find the value of ‘a’ for which the function f defined by

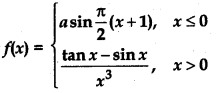
is continuous at x = 0.
Answer:

Question 5.
Find the value of k for which

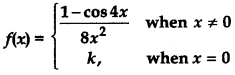
Answer:

On substituting this value in Eq. (i), we get
1 = f(0) ⇒ 1 = k [∵ f(0) = k, (given)]
Thus, for k = 1, the given function f(x) is continuous at x = 0.

Question 6.
In each of the following, find the value of the constant k so that the given function is continuous at the indicated point:
(i)

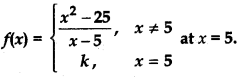
Answer:

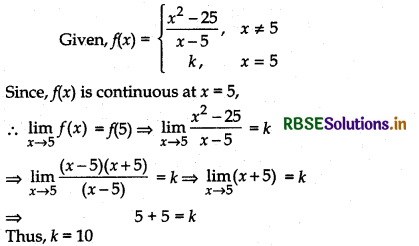
(ii)

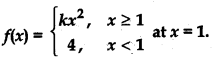
Answer:

(iii)

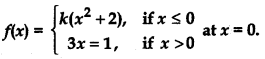
Answer:

Question 7.
Determine the value of constant 'k' so that the function

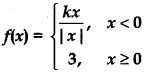
is continuous at x = 0.
Answer:

Question 8.
Show that the function f(x) = |x + 1| |x - 1| for all x ∈ R, is not differentiable at x = - 1 and x = 1.
Answer:
Given, f(x) = |x + 1| + |x - 1| ∀ X ∈ R
It can be rewritten as

∵ Lf(1) ≠ Rf(1)
∴ f is not differentiable at x =1.
Thus,f is not differentiable at x = 1 and - 1.

Question 9.
Show that f(x) = |x - 3| is continuous but not differentiable at x = 3.
Answer:
First, we check the continuity of f(x) at x = 3

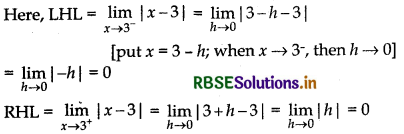
and f(3) = |3 - 3| = 0
Thus, LHL = RHL = f(3)
Hence,f is continuous at x =3.
Now, let us check the differentiability of f(x) at x = 3.

Since, LHD ≠ RHD at x = 3
Thus, f is not differentiable.

Question 10.
Discuss the continuity and differentiability of the function f(x) = |x| + |x - 1| in the interval (- 1, 2).
Answer:
Given, f(x) = |x| + |x + 1|
It can be written as:

(LHL)_{x = 0} = (LHL0_{x = 0}
Thus, f is continuous at x = 0.
Now, let us check the differentiability at x = 0

Here (LHD)_{x = 0} ≠ (RHD)_{x = 0}
Thus, f is continuous but not differentiable at x = 0.
Now, we check at x = 1

Here, (LHD)_{x = 1} ≠ (RHD)_{x = 1}
So,f is continuous but not differentiable at x = 1.
Thus, f is continuous everywhere in (- 1, 2) but not differentiable at x = 0, 1 in (- 1, 2).

Question 11.
Find the values of a and b if the function f(x) defined by

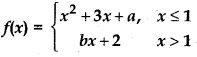
is differentiable at x = 1.
Answer:

Clearly, for Rf’(1) to be exist b - a - 2 should be equal to 0, i.e.,
b - a - 2 = 0 ...... (ii)

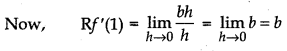
From Eq. (i), we have
Lf’(1) = Rf’(1)
⇒ 5 = b ⇒ b = 5
Now, on substituting b = 5 in Eq. (ii), we get
5 - a - 2 = 0 ⇒ a = 3
Thus, a = 3 and b = 5

Question 12.
If f(x) = \(\sqrt{x^2+1}\), g(x) = \(\frac{x+1}{x^2+1}\) and h(x) = 2x - 3 then find f'(h'(g'(x)).
Answer:

Question 13.
Differentiate the following functions with respect to x:
tan^-1\(\left[\frac{\sqrt{1+x^2}-1}{x}\right]\), x ≠ 0
Answer:

Question 12.
Differentiate (x² + y²)² = xy with respect to x.
Answer:
Given, (x² + y²)² = xy
⇒ x⁴ + y⁴ + 2x²y⁴ = xy
Differentiating both sides w.r.t.’x’, we get

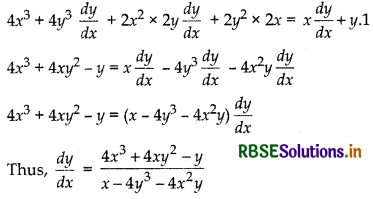
Question 14.
If y = tan^-1\(\left[\frac{\sqrt{1+x^2}+\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\right]\), x² ≤ 1, then find \(\frac{d y}{d x}\).
Answer:

Question 15.
Differentiate the following with respect to x: tan^-1\(\left(\frac{1+\cos x}{\sin x}\right)\)
Answer:

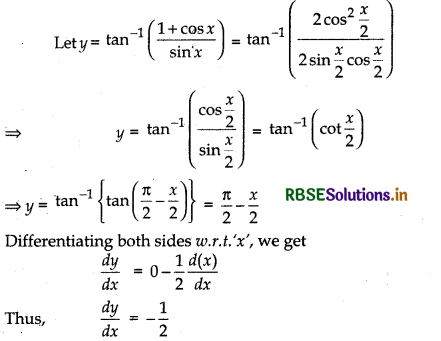
Question 16.
Differentiate the following w.r.t. x:
sin^-1\(\left\{\sqrt{\frac{1+\cos x}{2}}\right\}\)
Answer:

Question 17.
If y = cos^-1\(\left[\frac{2 x-3 \sqrt{1-x^2}}{\sqrt{13}}\right]\), then find \(\frac{d y}{d x}\).
Answer:

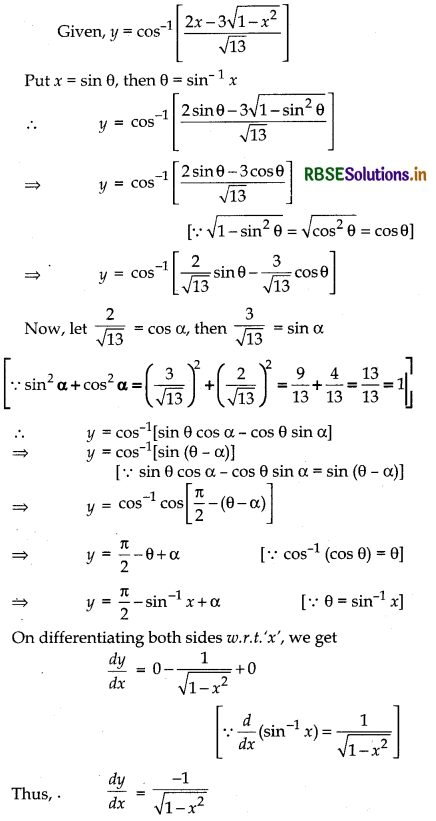
Question 18.
If y = sin^-1(6x\(\sqrt{1-9 x^2}\)), - \(\frac{1}{3 \sqrt{2}}\) < x < \(\frac{1}{3 \sqrt{2}}\), then find \(\frac{d y}{d x}\).
Answer:
Given, y = sin^-1 (6x\(\sqrt{1-9 x^2}\))
⇒ y = sin^-1(2.3x\(\sqrt{1-(3 x)^2}\))
Put 3x = sin θ, then
y = sin^-1 (2 sin θ\(\sqrt{1-\sin ^2 \theta}\))
⇒ y = sin^-1 (2 sin θ. cos θ)
⇒ y = sin^-1(sin 2θ) = 2θ
⇒ y = 2 sin^-1(3x) [∵ θ = sin^-1(3x)J]
⇒ \(\frac{d y}{d x}=\frac{2}{\sqrt{1-9 x^2}}(3)\)
⇒ \(\frac{d y}{d x}=\frac{6}{\sqrt{1-9 x^2}}\)

Question 19.
If sin y = x sin(a + y), then prove that
\(\frac{d y}{d x}=\frac{\sin ^2(a+y)}{\sin a}\)
Answer:
Given, sin y = x sin(a + y) ................ (1)
Differentiating both sides w.r.t.’x’, we get

Question 20.
If x\(\sqrt{1+y}\) + y\(\sqrt{1+x}\) = 0, prove that:
(1 + x)²\(\frac{d y}{d x}\) + 1 = 0
Answer:
Given, x\(\sqrt{1+y}\) + y\(\sqrt{1+x}\) = 0
⇒ x\(\sqrt{1+y}\) = - y\(\sqrt{1+x}\)
Squaring both sides, we get
x²(1 + y) = y²(1 + x)
⇒ x² + x²y = y² + xy² ⇒ x² - y² = xy² - x²y
⇒ (x - y) (x + y) = xy(y - x)
⇒ (x - y) (x + y) = - xy(x - y)
⇒ x + y = - xy ⇒ x = - xy - y
= x = - y(x + 1) = y = \(\frac{-x}{1+x}\)
Differentiating both sides w.r.t.x, we get

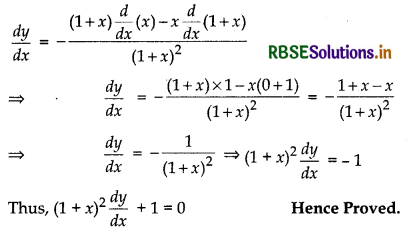
Question 21.
If y = sin^-1\(\left(\frac{\sqrt{1+x}+\sqrt{1-x}}{2}\right)\), then show that \(\frac{d y}{d x}=\frac{-1}{2 \sqrt{1-x^2}}\).
Answer:

Question 22.
Differentiate y = e^{x sin x} with respect to x.
Answer:
Given y = e^{x sin x}
Differentiate both sides w.r.t. x, we get
\(\frac{d y}{d x}=\frac{d}{d x}\) (e^{x sin x})
= e^{x sin x}. \(\frac{d^{(x \sin x)}}{d x}\)
= e^{x sin x} [x \(\frac{d}{d x}\) (sin x) + sin x \(\frac{d}{d x} (x)\)]
= e^{x sin x} [x cos x + sin x]

Question 23.
If e^x + e^y = e^{x + y}, then prove that \(\frac{d y}{d x}\) + e^{y - x} = 0.
Answer:
Given, e^x + e^y = e^{x + y} ............. (i)
Dividing Eq.(i) be e^{x + y}, we get
e^-y + e^-x = 1 .............. (ii)
Differentiating both sides of Eq.(ii) w.r.t. 'x', we get

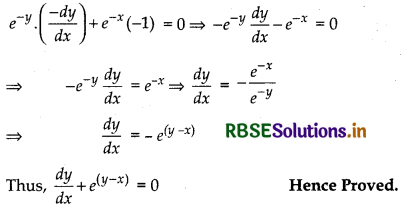
Question 24.
If y = tan^-1 \(\left(\frac{a}{x}\right)\) + log\(\sqrt{\frac{x-a}{x+a}}\), prove that \(\frac{d y}{d x}=\frac{2 a^3}{x^4-a^4}\).
Answer:

Question 25.
Find the derivative of the function sin^-11(e^-x) with respect to x.
Answer:
Let y = sin^-1(e^-x)
Differentiating both sides w.r.t.’x’, we get

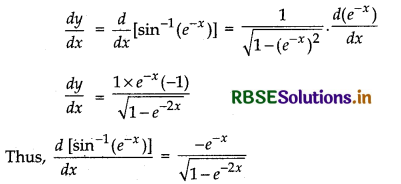
Question 26.
If y = \(\frac{e^x+e^{-x}}{e^x-e^{-x}}\), then find \(\frac{d y}{d x}\).
Answer:

Question 27.
Differentiate the function x^{cot x} + \(\frac{2 x^2-3}{x^2+x-3}\) with respect to x.
Answer:
Given y = x^{cot x} + \(\frac{2 x^2-3}{x^2+x-3}\)
Let u = x^{cot x} and v = \(\frac{2 x^2-3}{x^2+x-3}\)
Then, given equation becomes
y = u + v
Differentiating both sides w.r.t x, we get
⇒ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)
Consider u = x^{cot x}
Taking log of both sides, we get
log u = cot x log x
Differentiating both sides w.r.t.’x’, we get

Question 28.
If x^y = e^{x - y}, then prove that \(\frac{d y}{d x}=\frac{\log x}{(1+\log x)}\)
Answer:
Given, x^y = e^{x - y},
Taking log of both sides, we get
y log_e x = (x - y)log_e e
⇒ y log_e x = x - y [∵ log_e e = 1]
⇒ y(1 + log x) = x

Question 29.
If e^{sin x} + (tan x)^x, then find \(\frac{d y}{d x}\).
Answer:
Let y = e^{sin x} + (tan x)^x
Let u = e^{sin x} and v = (tan x)^x
Then y = u + v

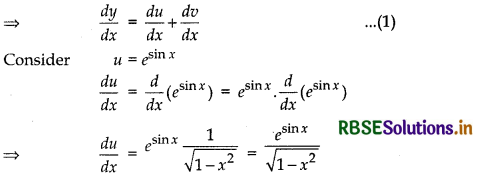
and v = (tan x)^x
Taking log of both sides, we get
log v = log(tan x)^x
⇒ log v = x log(tan x)

Question 30.
Differentiate the following functions with x.
(cos x)^x + (sin x)^{\(\frac{1}{x}\)}
Answer:
Given, y = (cos x)^x + (sin x)^{\(\frac{1}{x}\)}
Let u = (cos x)^x and v = (sin x)^{\(\frac{1}{x}\)}
Then, given equation becomes
y = u + v
Differentiating both sides w.r.t. 'x', we get
⇒ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ........... (i)
Consider u = (cos x)^x
Taking log of both sides, we get
⇒ log u = log (cos x)^x
log u = x log (cos x) [∵log mⁿ = n log m]
Differentiating both sides w.r.t. 'x', we get

Question 31.
If y = 2^{cos(x2 + 5)}
Prove that \(\frac{d y}{d x}\) = 2 log 2.2^{cos(x2 + 5)}.
Answer:
Given, f(x) = 2^{cos(x2 + 5)}
Differentiating both sides with respect to 'x', we get
\(\frac{d}{d x} [f(x)] =\frac{d}{d x}\)[2^{cos(x2 + 5)}]
= 2^{cos(x2 + 5)}.log 2.\(\frac{d}{d x}\)[cos(x² + 5)]
= log 2.2^{cos(x2 + 5)}[- sin (x² + 5)]\( \frac{d}{d x}\) (x² + 5)
= - log 2 sin (x² + 5) 2^{cos(x2 + 5)} (2x + 0)
f'(x) = - 2x log 2 sin(x² + 5) 2^{cos (x2 + 5)}

Question 32.
If y = a(tan^-1 x)², then prove that
\(\frac{d y}{d x}=\frac{2 \tan ^{-1} x}{1+x^2}\) log a.(tan^-1 x)²
Answer:
Given y = a(tan^-1 x)²
Differentiating both sides w.r.t 'x', we get
\(\frac{d y}{d x}\) = (tan^-1 x)².log a.\(\frac{d}{d x}\) (tan^-1 x)²
= log a(tan^-1 x)² 2 tan^-1 x\(\frac{d}{d x}\)(tan^-1 x)
= \(\frac{2 \tan ^{-1} x \log a\left(\tan ^{-1} x\right)^2}{1+x^2}\)

Question 33.
If x^y - y^x = a^b, find \(\frac{d y}{d x}\).
Answer:
Given x^y - y^x = a^b
Let x^y = u and y^x = v
⇒ \(\frac{d u}{d x}-\frac{d v}{d x}\) = 0
Now, u = x^y
⇒ log u = y log x

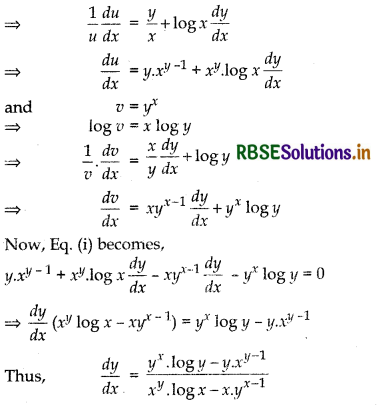
Question 34.
If x = b sin² θ and y = a cos² θ, then find \(\frac{d y}{d x}\).
Answer:
Given, x = b sin² θ
Differentiating both sides w.r.t θ, we get
\(\frac{d x}{d \theta}\) = 2b sin θ. cos θ
and y = a cos² θ
Differentiating both sides w.r.t. θ, we get
\(\frac{d y}{d \theta}\) = - 2a cos θ. sin θ
Now, \(\frac{d y}{d x}=\frac{\frac{d y}{d \theta}}{\frac{d x}{d \theta}}=\frac{-2 a \cos \theta \cdot \sin \theta}{2 b \sin \theta \cdot \cos \theta}=-\frac{a}{b}\)

Question 35.
If x = 2 cos θ - cos 2θ and y = 2 sin θ - sin 2θ, then prove that \(\frac{d y}{d x}\) = tan \(\left(\frac{3 \theta}{2}\right)\).
Answer:
Given, x = 2 cos θ - cos 2θ
\(\frac{d x}{d \theta}\) = - 2 sin θ + 2 sin 2θ
and y = 2 sin θ - sin 2θ
⇒ \(\frac{d y}{d \theta}\) = 2 cos θ - 2 cos 2θ

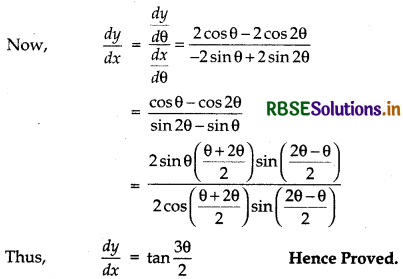
Question 36.
If x = a\(\left[\frac{1+t^2}{1-t^2}\right]\) and y = \(\frac{2 t}{1-t^2}\), then find \(\frac{d y}{d x}\).
Answer:

Question 37.
If x = a(θ - sin θ) and y = a(1 + cos θ), then find\( \frac{d y}{d x}\) at θ = \(\frac{\pi}{3}\).
Answer:
Given, x = a(θ - sin θ)
Differentiating both sides w.r.t. 'θ', we get
\(\frac{d x}{d \theta}\) = a(1 - cos θ)
and y = a(1 + cos θ)
⇒ \(\frac{d x}{d \theta}\) = a(0 - sin θ) = - a sin θ

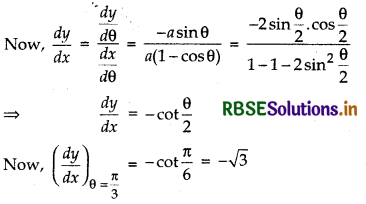
Question 38.
If x = a sin 2t(1 + cos 2t) and y = b cos 2t(1 - cos 2t), then show at t = \(\frac{\pi}{4}, \frac{d y}{d x}=\frac{b}{a}\)
Answer:
Given, x = a sin 2t(1 + cos 2t)
and y = b cos 2t (1 - cos 2t)
Differentiating x and y separately w.r.t.’f’, we get
\(\frac{d y}{d t}\) = a[sin 2t\(\frac{d}{d t}\)(1 + cos 2t) + (1 + cos 2t)\(\frac{d}{d t}\)(sin 2t)]
[by using product rule of derivative]
= a[sin 2t × (0 - 2 sin 2t) + (1 + cos 2t) (2 cos 2t)]
= a(- 2 sin² 2t + 2 cos 2t + 2 cos² 2t)
= a[2(2 cos² 2t - sin² 2t) + 2 cos 2t]
= a(2 cos 4t + 2cos 2t) = 2a(cos 4t + cos 2t)
[∵ cos² 2θ - sin² 2θ = cos 4θ]

= b[cos 2t × (0 + 2 sin 2t) + (1 - cos 2t) (- 2 sin 2t)]
= b(2 sin 2t cos 2t - 2 sin 2t + 2 sin 2t cos 2t)
= 2b(2 sin 2t cos 2t - sin 2t)
= 2b(sin 4t - sin 2t) [∵ 2 sin 2θ cos 2θ = sin 4θ]

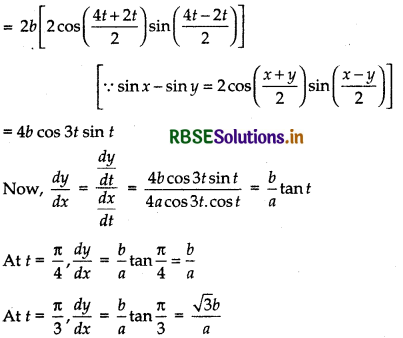
Question 39.
If x = cos t (3 - 2 cos²t) and y = sin t (3 - 2 sin²t), then find the value of \(\frac{d y}{d x}\) at t = \(\frac{\pi}{4}\).
Answer:
Given, x = cos t (3 - 2 cos²t)
⇒ x = 3 cos t - 2 cos³ t
Differentiating both sides w.r.t.’x’, we get
\(\frac{d x}{d t}\) = 3(- sin t) - 2(3) cos²t (- sin t)
⇒ \(\frac{d x}{d t}\) = - 3 sin t + 6 cos²t sin t
Also, y = sin t (3 - 2 sin² t)
⇒ y = 3 sin t- 2 sin³ t
Differentiating both sides w.r.t.’t’, we get
\(\frac{d y}{d t}\) = 3 cos t - 2 × 3 × sin²t cos t
⇒ \(\frac{d y}{d t}\) = 3 cos t - 6 sin²t cos t

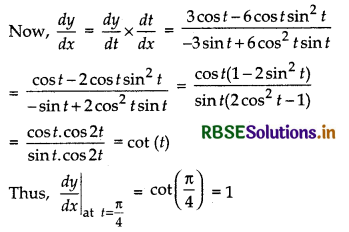
Question 40.
If x = a (2θ - sin 2θ) and y = a(1 - cos 2θ), then find \(\frac{d y}{d x}\) when θ = \(\frac{\pi}{3}\).
Answer:
We have, x = a(2θ - sin 2θ)
and y = a(1 - cos 2θ)

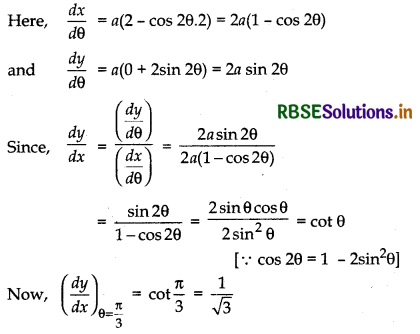
Multiple Choice Questions

Question 1.

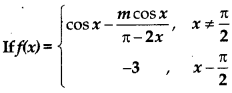
is continuous a x = \(\frac{\pi}{3}\) then value of m is:
(a) 3
(b) 6
(c) -3
(d) -6
Answer:
(a) 3

Question 2.

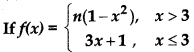
is continuous at x = 3, then value of n is :
(a) 2.25
(b) 1.25
(c) - 2.25
(d) -1.25
Answer:
(b) 1.25

Question 3.

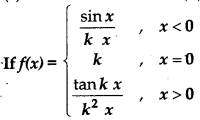
is continuous at x = 0, then value of k is :
(a) k = 1
(b) k = 0
(c) k = ± 1
(d) k = ± 2
Answer:
(d) k = ± 2

 

Question 4.

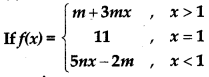
is continuous at x = 1 then m = .... and n ....?
(a) m = 2, n = 3
(b) m = 2,n = 3
(c) m = 2, n = 3
(d) m = 3, n = 3
Answer:
(a) m = 2, n = 3

Question 5.
If f(x) = \(\frac{2-(256+5 x)^{\frac{1}{8}}}{(5 x+32)^{\frac{1}{5}}-2}\) (x ≠ 0), then for f to be continuous every where f(0) is equal to:
(a) \(\frac{2}{7}\)
(b) -\(\frac{7}{32}\)
(c) \(\frac{7}{64}\)
(d) -\(\frac{7}{64}\)
Answer:
(b) -\(\frac{7}{32}\)

Question 6.
If f(x) = \(\frac{\tan \left(\frac{\pi}{4}-x\right)}{\cot 2 x}\) x ≠ \(\frac{\pi}{4}\) the value of \(\left(\frac{\pi}{4}\right)\) so that
(a) 0.50
(b) 0.25
(c) 0.75
(d) 1.25
Answer:
(a) 0.50

Question 7.

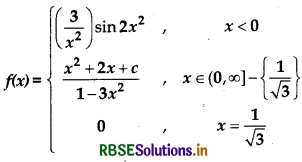
that f to be continuous at x = 0, value of c is :
(a) 2
(b) 4
(c) 6
(d) 8
Answer:
(d) 8

Question 8.
Let a function f be defined by f(x) = \(\frac{x-|x|}{x}\), x ≠ 0 and f(0) = 2, then f is :
(a) Continuous no where
(b) Continuous everywhere
(c) Continuous for all x except x = 1
(d) Continuous for all x except x = 0
Answer:
(d) Continuous for all x except x = 0

Question 9.
The value of f(k > 0) for which the function
f(x) = \(\frac{\left(e^x-1\right)^4}{\sin \left(\frac{x^2}{k^2}\right) \log \left(1+\frac{x^2}{2}\right)}\), x ≠ 0, f(0) = 8 may be continuous at x = 0 is:
(a) 1
(b) 2
(c) 4
(d) 3
Answer:
(d) 3

Question 10.

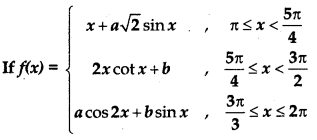
is continuous on [2, 2π], then a = ......... and b = ....
(a) a = \(\frac{5 \pi}{2}\), b = \(\frac{5 \pi}{4}\)
(b) a = -\(\frac{5 \pi}{2}\), b = -\(\frac{5 \pi}{4}\)
(c) a = -\(\frac{5 \pi}{2}\), b = \(\frac{5 \pi}{4}\)
(d) a = -\(\frac{5 \pi}{2}\), b = \(\frac{5 \pi}{2}\)
Answer:
(a) a = \(\frac{5 \pi}{2}\), b =\(\frac{5 \pi}{4}\)

Question 11.
If f(x) = \(\frac{5^{\frac{1}{x}}-5^{1 \frac{1}{x}}}{5^{\frac{1}{x}}+5^{-\frac{1}{x}}}\); x ≠ 0, and \(\lim _{x \rightarrow 0}\) f(x) = a, \(\lim _{x \rightarrow 0}\)f(x) = 0
then the value of a and b are:
(a) a = 1, b = -1
(b) a = 0, b = 1
(c) a = -1, b = 1
(d) a = 1, b = 0
Answer:
(a) a = 1, b = -1

Question 12.

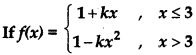
continuous at x = 3 then
the value of k is:
(a) k = 0, k = 1
(b) k = 0
(c) k = 1, k = - 1
(d) k ∈ R- {0, ± 1]
Answer:
(b) k = 0

Question 13.
The value p for which the function
f(x) = \(\frac{\left(4^x-1\right)^3}{\sin \left(\frac{x}{p}\right) \log \left(1+\left(\frac{x^2}{3}\right)\right)}\), x ≠ 0 f(x) = 12 (log 4)³, x = 0 may be continuous at x = 0 is :
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(a) 1

Question 14.
The value of m and n for which the function

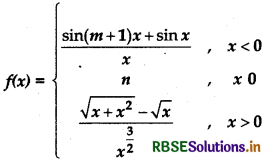
is continuous for ∀ x ∈ R?
(a) m = -\(\frac{3}{2}\), n = -\(\frac{1}{2}\)
(b) m = \(\frac{1}{2}\), n = \(\frac{3}{2}\)
(c) m = \(\frac{1}{2}\), n = -\(\frac{3}{2}\)
(d) m = \(\frac{5}{2}\), n = \(\frac{1}{2}\)
Answer:
(b) m = \(\frac{1}{2}\), n = \(\frac{3}{2}\)

Question 15.
If f(x) = \(\frac{\sqrt{a^2-a x+x^2}-\sqrt{a^2+a x+x^2}}{\sqrt{a+x}-\sqrt{a-x}}\); x ≠ 0 is continuous at x = 0 then f(0) = ........
(a) a√a
(b) √a
(c) -√a
(d) -a√a
Answer:
(a) a√a

Fill in the Blanks

Question 1.
If f is discontinuous at c, then c is called a point of ___________ of f
Answer:
discontinuity

Question 2.
A function is said to be differentiable in an interval (a, b) if it is ___________ at every point of (a, b).
Answer:
differentiable

Question 3.
The number of points of discontinuity of f defined by f(x) = |x| - |x + 1| is ___________
Answer:
zero

Question 4.
If f(x) = 2|x| + 3|sin x| + 6, then the right hand derivative of f(x) at x = 0 is ___________
Answer:
5

Question 5.
If f(x) = x |x|, then f (x) = ___________
Answer:
2|x|

True/False

Question 1.
A function is continuous at x = c if the value of the function at x = c equals the limit of the function at x = c.
Answer:
True

Question 2.
A real function f is said to be continuous if it is continuous at every point in the domain off.
Answer:
True

Question 3.
If f and g are two real functions, then (fog)(x) =g(f(x))
Answer:
False

Question 4.
Leibnitz or product rule is (uv)' = u' ± v'
Answer:
False

Question 5.
If y = x¹⁵, then \(\frac{d^2 y}{d x^2}\) = 210x¹³.
Answer:
True