RBSE Class 12 Maths Important Questions Chapter 4 Determinants

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 4 Determinants Important Questions and Answers.

RBSE Class 12 Maths Chapter 4 Important Questions Determinants

Question 1.
Evaluate the following determinant:
\(\left|\begin{array}{cc} a+i b & c+i d \\ -c+i d & a-i b \end{array}\right|\)
Answer:
Let A = \(\left|\begin{array}{cc} a+i b & c+i d \\ -c+i d & a-i b \end{array}\right|\)
= (a + ib) (a - ib) - (-c + id)(c + id)
= (a² - i²b²) - (-c² + i²d²)
= [a² - (-1)b²] - [-c² + (-1)d²] [∵ i² = (-1)]
= (a² + b²) - (-c² - a²)
= a² + b² + c² + d²

Question 2.
Find the value of x if \(\left|\begin{array}{cc} x+1 & x-1 \\ x-3 & x+2 \end{array}\right|=\left|\begin{array}{cc} 4 & -1 \\ 1 & 3 \end{array}\right|\)
Answer:
Given \(\left|\begin{array}{cc} x+1 & x-1 \\ x-3 & x+2 \end{array}\right|=\left|\begin{array}{cc} 4 & -1 \\ 1 & 3 \end{array}\right|\)
On expanding, we get
⇒ (x + 1)(x + 2) - (x - 1)(x - 3) = 4 × 3 - (-1) × 1
⇒ (x² + x + 2x + 2) - (x² - x - 3x + 3) = 12 + 1
⇒ (x² + x + 2x + 2) - (x² - 4x + 3) = 13
⇒ x² + 3x + 2 - x² + 4x - 3 = 13
⇒ 7x - 1 = 13 ⇒ 7x = 1 + 13 ⇒ 7x = 14
Thus, x = 2

Question 3.
If A = \(\left|\begin{array}{ll} p & 2 \\ 2 & p \end{array}\right| \)and |A³| = 125, then find the value of p.
Answer:
Given, A = \(\left|\begin{array}{ll} p & 2 \\ 2 & p \end{array}\right|\)
∴ |A| = \(\left|\begin{array}{ll} p & 2 \\ 2 & p \end{array}\right|\) = p² - 4
⇒ |A|³ = 125 [∵ |A|³ = |A³|]
⇒ (p² - 4)³ = 125
⇒ p² - 4 = 5 ⇒ p² = 9
Thus, p = ±3

Question 4.
Prove the following:
(i) \(\left|\begin{array}{ccc} a & b & c \\ a-b & b-c & c-a \\ b+c & c+a & a+b \end{array}\right|\) = a³ + b³ + c³ - 3abc
Answer:

On expanding along C₁, we get
= (a + b + c) [(b - c) (a + b - 2c) - (c - a) (c + a - 2b)]
= (a + b + c) [(ab + b² - 2bc - ca - bc + 2c²) - (c² + ca - 2bc - ac - a² + 2ab)]
= (a + b + c)[ab + b² - 3bc -ca + 2 c² - c² + 2bc + a² - 2ab]
= (a + b + c) (a² + b² + c² - ab - bc - ca)
= a³ + b³ + c³ - 3abc
= RHS

(ii) \(\left|\begin{array}{lll} a+b & b+c & c+a \\ b+c & c+a & a+b \\ c+a & a+b & b+c \end{array}\right|=2\left|\begin{array}{lll} a & b & c \\ b & c & a \\ c & a & b \end{array}\right|\)
Answer:

On interchanging R₁ and R₂ and after that interchanging R₂ and R₃, we get
Δ = 2\(\left|\begin{array}{lll} a & b & c \\ b & c & a \\ c & a & b \end{array}\right|\) = RHS
Hence Proved.

(iii) \(\left|\begin{array}{ccc} a-b-c & 2 a & 2 a \\ 2 b & b-c-a & 2 b \\ 2 c & 2 c & c-a-b \end{array}\right|\) = (a + b + c)³
Answer:

On expanding along Ry we get
= (a + b + c)[1.(a + b + c)(a + b + c) - 0] - 0 + 0
= (a + b + c) (a + b + c) (a + b + c)
= (a + b + c)³ = RHS
Hence Proved.

(iv) \(\left|\begin{array}{ccc} a & a+b & a+2 b \\ a+2 b & a & a+b \\ a+b & a+2 b & a \end{array}\right|\) = 9(a + b)b²
Answer:

On expanding along R₁, we get
= 3b²(a + b)[0 - 1(- 4 + 1) + 0]
= 3b²(a + b)(-1) (-3) = 3(a + b)b² (3)
= 9b²(a + b) = R.H.S.
Hence proved

(v) \(\left|\begin{array}{ccc} a+b+c & -c & -b \\ -c & a+b+c & -a \\ -b & -a & a+b+c \end{array}\right|\) = 2(a + b)(b + c)(c + a)
Answer:
L.H.S = \(\left|\begin{array}{ccc} a+b+c & -c & -b \\ -c & a+b+c & -a \\ -b & -a & a+b+c \end{array}\right|\)
On applying R₂ → R₂ + R₁ and R₃ → R₃ + R₁, we get
= \(\left|\begin{array}{ccc} a+b+c & -c & -b \\ a+b & a+b & -(a+b) \\ a+c & -(a+c) & a+c \end{array}\right|\)
Taking (a + b) and (a + c) common from R₂ and R₃ respectively, we get

Expanding along R₃ we get
= (a + b)(a + c) [1. {0 + 2 (b + c)}]
= (a + b)(a + c)[2 (b + c)]
= 2 (a + b)(a + c)(b + c)
= R.H.S.

(vi) \(\left|\begin{array}{ccc} a^2+2 a & 2 a+1 & 1 \\ 2 a+1 & a+2 & 1 \\ 3 & 3 & 1 \end{array}\right|\) = (a - 1)³
Answer:

Expanding along C₃, we get
= (a - 1)²[1.(a + 3) - 4]
= (a - 1)² (a - 1)
= (a - 1)³ = R.H.S.
Hence Proved.

(vii) \(\left|\begin{array}{ccc} a^3 & 2 & a \\ b^3 & 2 & b \\ c^3 & 2 & c \end{array}\right|\) = 2(a - b)(b - c)(c - a)(a + b + c)
Answer:
L.H.S = \(\left|\begin{array}{ccc} a^3 & 2 & a \\ b^3 & 2 & b \\ c^3 & 2 & c \end{array}\right|\)

On Applying R₁ → R₁ - R₂ and R₂ → R₂ - R₃

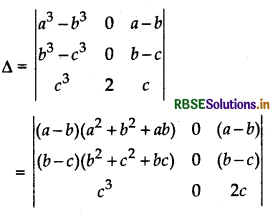
Taking common (a - b) and (b - c) from R₁ and R₂ respectively, we get

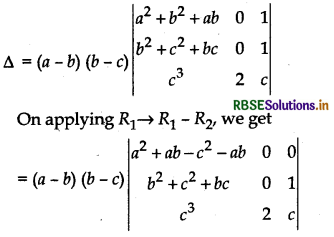
On expanding along Rt, we get
= (a - b) (b - c) (a² + ab - c² - bc) [0 - 2 * 1]
= - 2(a - b) (b - c) (a² - c² + ab - bc)
= - 2 (a - b) (b - c) [(a - c) (a + c) + b(a - c)]
= -2 (a - b)(b - c)(a - c)(a + b + c)
= 2 (a - b) (b - c) (c - a) (a + b + c)
= R.H.S.
Hence Proved.

Question 5.
Solve the following:
(i) \(\left|\begin{array}{ccc} x+a & b & c \\ a & x+b & c \\ a & b & x+c \end{array}\right|\) = 0
Answer:

On expanding along R₁ we get
(x + a + b + c)[ 0 - 0 - x {1.b - 1. (x + b)}] = 0
⇒ (x + a + b + c) [-x(b - x - b)] = 0
⇒ (x + a + b + c) (- x) (- x)= 0
⇒ (x + a + b + c) (x²) = 0
Either x² = 0, then x = 0 (Impossible)
or x + a + b + c = 0
Thus, x = -(a + b + c)

(ii) \(\left|\begin{array}{ccc} 4-x & 4+x & 4+x \\ 4+x & 4-x & 4+x \\ 4+x & 4+x & 4-x \end{array}\right|\) = 0
Answer:

On expanding along Ry we get
(12 + x)[1{(- 2x) (- 2x) - 0} - 0 + 0] = 0
⇒ 4(12 + x)x² = 0
Either 12 + x = 0
x = -12
or x² = 0 ⇒ x = 0
Thus, x = 0, -12

Question 6.
If a, b and c are all non-zero and \(\left|\begin{array}{ccc} 1+a & 1 & 1 \\ 1 & 1+b & 1 \\ 1 & 1 & 1+c \end{array}\right|\) = 0 then prove that \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\) + 1 = 0.
Answer:

Expanding along Ry we get
a[b( 1 + c) + c] - 0 + 1 [be - 0] = 0
⇒ a(b + be + c) +1 (be) = 0
⇒ ab + abc + ca + be = 0
⇒ ab + bc + ca + abc = 0

Dividing both sides by abc, we get
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\) + 1 = 0
Hence Proved.

Question 7.
If \(\left|\begin{array}{ccc} a & b-y & c-z \\ a-x & b & c-y \\ a-x & b-y & c \end{array}\right|\) determinant find the value of \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\), where x, y, z ≠ 0
Answer:
Given, \(\left|\begin{array}{ccc} a & b-y & c-z \\ a-x & b & c-y \\ a-x & b-y & c \end{array}\right|\) = 0

Taking common x from C₁, y from C₂ and z from C₃, we get

Taking (\(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\) - 2) common from C₁, we get

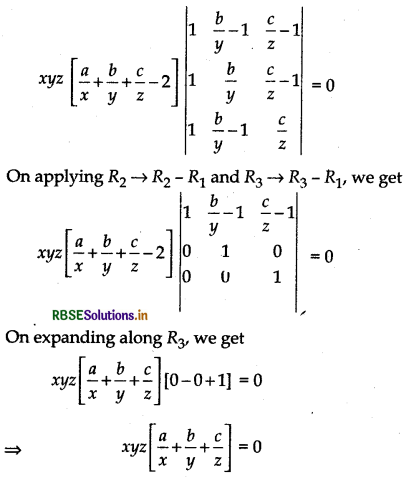
Since, xyz ≠ 0
Thus, \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\) = 2

Question 8.
Using Properties of determinants, prove that \(\left|\begin{array}{ccc} 1 & 1 & 1+3 x \\ 1+3 y & 1 & 1 \\ 1 & 1+3 z & 1 \end{array}\right|\) = 9(3xyz + xy + yz + zx)
Answer:
Let Δ = \(\left|\begin{array}{ccc} 1 & 1 & 1+3 x \\ 1+3 y & 1 & 1 \\ 1 & 1+3 z & 1 \end{array}\right|\)

On applying R₂ → R₂ - R₃ and R₃ → R₃ - R₁
Δ = \(\left|\begin{array}{ccc} 1 & 1 & 1+3 x \\ 3 y & -3 z & 0 \\ 0 & 3 z & -3 x \end{array}\right|\)

On applying along R₁, we get
Δ = 9xy - 0] + (1 + 3x) (9yz - 0)
= 9zx + 9xy + 9yz + 27xyz = 9(3xyz + yz + zx + xy)
= 9(3xyz + yz + zx + xy)
= 9(3xyz + xy + yz + zx)
Hence proved

Question 9.
Using properties of determinants, prove that
\(\left|\begin{array}{lll} (b+c)^2 & a^2 & b c \\ (c+a)^2 & b^2 & c a \\ (a+b)^2 & c^2 & a b \end{array}\right|\)
= (a - b) (b - c) (c - a) (a + b + c) (a² + b² + c²)
Answer:

Expanding along C₁ we get
= (b - a) (c - a) (a² + b² + c²) [- b(b + a) + c(c + a)]
= (b - a) (c - a) (a² + b² + c²) [- b² - ab + c² + ac]
= (b - a) (c - a) (a² + b² + c²) [(c² - b²) + (ca - ab)]
= (b - a) (c - a) (a² + b² + c²) [(c - b) (c + b) + a(c - b)]
= (b - a) (c - a) (a² + b² + c²) (c - b) (a + b + c)
= (a - b) (b - c) (c - a) (a + b + c) (a² + b² + c²) = RHS.
Hence proved

Question 10.
If x, y, z are different and \(\left|\begin{array}{lll} x & x^2 & 1+x^3 \\ y & y^2 & 1+y^3 \\ z & z^2 & 1+z^3 \end{array}\right|\) = 0, then using properties of determinants show that 1 + xyz = 0.
Answer:

On expanding along R₁, we get
(1 + xyz).1[(y - x) (z + x) (z - x) - (y + x) (y - x) (z - x)] = 0
⇒ (1 + xyz) (y - x) (z - x) (z + x - y - x) = 0
⇒ (1 + xyz) (x - y) (y - z) (z - x) = 0
As, x, y, z are different, so x - y ≠ 0, y - z ≠ 0, z - x ≠ 0
Thus, 1 + xyz = 0

Question 11.
Using properties of determinants prove that \(\left|\begin{array}{lll} a-b & b+c & a \\ b-c & c+a & b \\ c-a & a+b & c \end{array}\right|\) = a³ + b³ + c³ - 3abc.
Answer:

Expanding along C₃, we get
= (a + b + c) [(b - c) (a + b - 2c)] - (c - a) (c + a - 2b)
= (a + b + c) [ab + b² - 2bc - ac - bc + 2c² - c² - ac + 2bc + ac + a² - 2ab]
= (a + b + c) (a² + b² + c² - ab - bc - ca)
= a³ + b³ + c³ - 3abc
Hence proved

Question 12.
If a, b, c are p^th, q^th and r^th terms respectively of G.P, then prove that
\(\left|\begin{array}{lll} \log a & p & 1 \\ \log b & q & 1 \\ \log c & r & 1 \end{array}\right|\) = 0
Answer:
Let A be the first term and R be the common ratio of the G.P. Then, we have
a = AR^{p - 1}
⇒ log a = log A + (p - 1) log R
b = AR^{q - 1}
⇒ log b = log A + (q - 1) log R
c = AR^{r - 1}
⇒ log c = log A + (r - 1) log R

Question 13.
Find the value of λ, so that the points (1, -5), (4, -5) and (λ, 7) are collinear.
Answer:
Given, the points (1, - 5), (4, 5) and (λ, 7) are collinear, then
\(\left|\begin{array}{ccc} 1 & -5 & 1 \\ -4 & 5 & 1 \\ \lambda & 7 & 1 \end{array}\right|\) = 0
On applying R₂ → R₂ - R₁, and R₃ → R₃ - R₁, we get
⇒ \(\left|\begin{array}{ccc} 1 & -5 & 1 \\ -5 & 10 & 0 \\ \lambda-1 & 12 & 0 \end{array}\right|\) = 0
Expanding along C₃, we get
1[- 60 - 10(λ - 1)] = 0
⇒ - 60 - 10λ + 10 = 0
⇒ - 10λ = 50
Thus, λ = - 5

Question 14.
Using determinants, find the area of the triangle with vertices A (5, 4), B (-2, 4) and C (2, -6).
Answer:
The area of triangle is given by:
∆ = \(\frac{1}{2}\left|\begin{array}{ccc} 5 & 4 & 1 \\ -2 & 4 & 1 \\ 2 & -6 & 1 \end{array}\right|\)
Expanding along R₁, we get
= \(\frac{1}{2}\) [5 (4 + 6) - 4 (2 - 2) + 1(12 - 8)]
= \(\frac{1}{2}\) [5 × 10 - 4(- 4) + 1 × 4]
= \(\frac{1}{2}\) [50 + 16 + 4]
= \(\frac{1}{2}\) × 70 = 35 sq. units

Question 15.
Find the value of x if the area of ∆ is 35 square cm with vertices (x, 4), (2 - 6) and (5, 4).
Answer:
If vertices of a traingle are (x₁, y₁), (x₂, y₂) and (x₃, y₃), then the area of the triangle is given by,

Expanding along R1, we get
⇒ x(- 6 - 4) - 4(2 - 5) + 1(8 + 30) = ± 70
⇒ [- 10x + 12 + 38] = ± 70
⇒ - 10x + 50 = ± 70
Taking positive sign, we get
⇒ - 10x + 50 = 70
⇒ - 10x = 20 ⇒ x = - 2
Taking negative sign, we get
⇒ - 10x + 50 = - 70
⇒ - 10x = - 120 ⇒ x = 12
Thus, x = - 2, 12

Question 16.
Find the equation of the line joining A (1, 3) and B (0, 0) using determinants and find k if D (k, 0) is a point such that area of ∆ABD is 3 sq.units.
Answer:
Let P(x, y) be any point on line AB. Then,
Area of ∆ABP = 0
⇒ \(\frac{1}{2}\left|\begin{array}{lll} 1 & 3 & 1 \\ 0 & 0 & 1 \\ x & y & 1 \end{array}\right|\) = 0
⇒ \(\frac{1}{2}\)[1 (0 - y) - 3(0 - x) + 1(0 - 0)] = 0
⇒ 3x - y = 0
which is the required equation of AB.
Now, area ∆ABD = 3 sq. units

⇒ 1(0 - 0) - 3(0 - k) + 1(0 - 0) = ± 6
⇒ 3k = ± 6
Thus, k = ± 2

Question 17.
If ∆ = \(\left|\begin{array}{lll} 1 & 2 & 3 \\ 2 & 0 & 1 \\ 5 & 3 & 8 \end{array}\right|\), write the minor of element a₂₂.
Answer:
Minor of element a₂₂ = \(\left|\begin{array}{ll} 1 & 3 \\ 5 & 8 \end{array}\right|\) = 8 - 15 = - 7

Question 18.
Find the minor of the element of second row and third column (a₂₃) in the following determinant
\(\left|\begin{array}{ccc} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{array}\right|\)
Answer:
Minor of a₂₃ = \(\left|\begin{array}{cc} 2 & -3 \\ 1 & 5 \end{array}\right|\)
= 10 - (- 3) = 10 + 3 = 13

Question 3.
Find minors and cofactors of each element of determinant \(\left|\begin{array}{ccc} 3 & -3 & -4 \\ 1 & 2 & -2 \\ -1 & 2 & 1 \end{array}\right|\).
Answer:

⇒ a₁₁ = 3, a₁₂ = - 3, a₁₃ = - 4
a₂₁ = 1, a₂₂ = 2, a₂₃ = - 2
a₃₁ = - 1, a₃₂ = 2, a₃₃ = 1

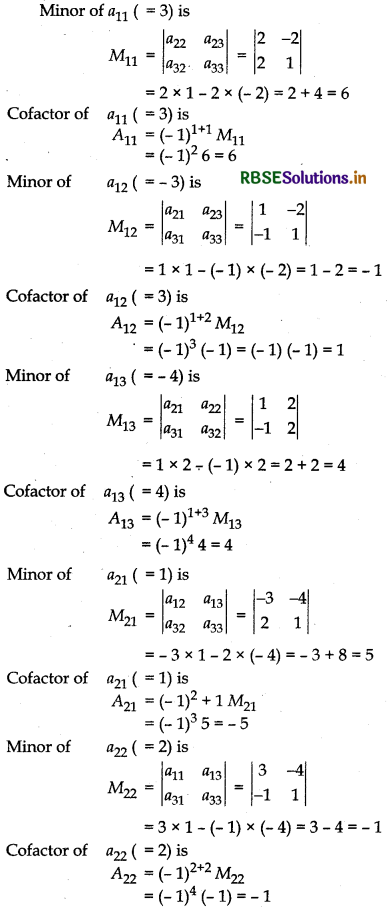
Question 19.
If A = \(\left|\begin{array}{ccc} 2 & 4 & 1 \\ 8 & 5 & 2 \\ -1 & 3 & 7 \end{array}\right|\), then find minors and co-factors of all elements of second row, also find det A.
Answer:

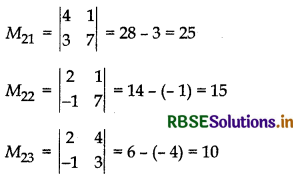
∴ A₂₁ = - M₂₁ = - 25, A₂₂ = M₂₂ = 15,
A₂₃ = - M₂₃ = - 10
Now, det A = 8.A₂₁ + 5.A₂₂ + 2.M₂₃
= 8(- 25) + 5(15) + 2(- 10)
= - 200 + 75 - 20 = - 145

Question 20.
Write minors and co-factors of following determinants corresponding to first column, also find the value of determinants:
(i) \(\left|\begin{array}{ccc} 1 & -3 & 2 \\ 4 & -1 & 2 \\ 3 & 5 & 2 \end{array}\right|\)
Answer:

= - 6 - (- 2) = - 6 + 2 = - 4
Cofactor of a₃₁ is A₃₁ = (- 1)³⁴ M₃₁
= 1 × (- 4) = - 4
So, determinant |A| = a₁₁ A₁₁ + a₂₁A₂₁ + a₃₁A₃₁
= 1. (- 12) + 4. (16) + 3. (- 4)
= 12 + 64 - 12 = 40

(ii)
\(\left|\begin{array}{lll} a & h & g \\ h & b & f \\ g & f & c \end{array}\right|\)
Answer:

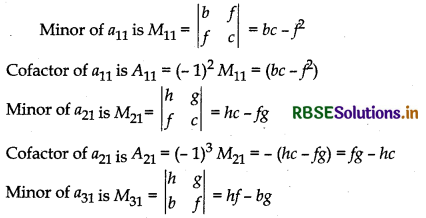
Cofactor of a₃₁ is A₃₁ = (- 1)⁴ M₃₁ = (hf - bg) = hf - bg
So, determinant
|A| = a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁
= a. (bc - f²) + h. (fg - hc) + g. (hc - bg)
= abc - af² + fgh - h²c + fgh - bg²
= abc + 2fgh - af² - bg² - ch²

Question 21.
If ∆ = \(\left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|\) and F₁₁, F₁₂, F₁₃, ......... are the corresponding cofactors of a₁₁, a₁₂, a₁₃ ...., then which of the following is true:
(a) a₁₂F₁₂ + a₂₂F₂₂ + a₃₂F₃₂ = 0
(b) a₁₂F₁₂ + a₂₂F₂₂ + a₃₂F₃₂ ≠ ∆
(c) a₁₂F₁₂ + a₂₂F₂₂ + a₃₂F₃₂ = ∆
(d) a₁₂F₁₂ + a₂₂F₂₂ + a₃₂F₃₂ = ∆
Answer:
(c) a₁₂F₁₂ + a₂₂F₂₂ + a₃₂F₃₂ = ∆
So, option (c) is correct.

Question 22.
Show that A = \(\left[\begin{array}{cc} 2 & -3 \\ 3 & 4 \end{array}\right]\) satisfies the equation x² - 6x + 17 = 0. Hence, find A^-1.
Answer:

Hence, the matrix A satisfies the equation x² - 6x + 17
Now, A² - 6A + 17I₂ = 0
⇒ A² - 6A = - 17I
⇒ A^-1(A² - 6A) = A^-1(- 17I)
[Pre-multiplying both side by A^-1]
A^-1A² - 6A^-1A = - 17(A^-1) = A - 6I = - 17A^-1
A^-1 = - \(\frac{1}{17}\)(A - 6I) = \(\frac{1}{17}\)(6I - A)
= \(\frac{1}{17}\left\{\left[\begin{array}{ll} 6 & 0 \\ 0 & 6 \end{array}\right]-\left[\begin{array}{cc} 2 & -3 \\ 3 & 4 \end{array}\right]\right\}=\frac{1}{17}\left[\begin{array}{cc} 4 & 3 \\ -3 & 2 \end{array}\right]\)

Question 23.
Given, A = \(\left[\begin{array}{cc} 2 & -3 \\ -4 & 7 \end{array}\right]\), compute A^-1 and show that 2A^-1 = 9I - A.
Answer:

Question 24.
If A = \(\left[\begin{array}{cc} 3 & 2 \\ 4 & -2 \end{array}\right]\) find the value of λ, so that A² = λA - 2I. Hence, find A^-1.
Answer:

Equating the corresponding elements, we have
⇒ 2λ = 2 ⇒ λ = 1 .
Now, A² = λA - 2I
A²A^-1 = λA × A^-1 - 2IA^-1
A = λI - 2A^-1
2A^-1 = I - A
A^-1 = \(\frac{1}{2}\)(I - A)
A^-1 = \(\frac{1}{2}\left\{\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]-\left[\begin{array}{cc} 3 & 2 \\ 4 & -2 \end{array}\right]\right\}\)
Thus A^-1 = \(\frac{1}{2}\left[\begin{array}{cc} -2 & -2 \\ -4 & 3 \end{array}\right]\)

Question 25.
If A^-1 = \(\left[\begin{array}{ccc} 3 & 1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2 \end{array}\right]\) and B = \(\left[\begin{array}{ccc} 1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1 \end{array}\right]\) find (AB)^-1.
Answer:
Given, B = \(\left[\begin{array}{ccc} 1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1 \end{array}\right]\)
|B| = 1(3 - 0) - 2(- 1 - 0) - 2(2 - 0)
= 3 + 2 - 4 = 5 - 4 = 1 ≠ 0
So, B^-1 exists.
Cofactors of |B| are:
b₁₁ = (- 1)^{1 + 1} (3 - 0) = 3
b₁₂ = (- 1)^{1 + 2}(- 1 - 0) = 1
b₁₃ = (- 1)^{1 + 3} (2 - 0) = 2
b₂₁ = (- 1)^{2 + 1} (2 - 4) = 2
b₂₂ = ( 1)^{2 + 2} (1 - 0) = 1
b₂₃ = (- 1)^{2 + 3}(- 2 - 0) = 2
b₃₁ = (- 1)^{3 + 1} (0 + 6) = 6
b₃₂ = (- 1)^{3 + 2} (0 - 2) = 2
b₃₃ = (- 1)^{3 + 3}(3 + 2) = 5
Matrix formed by the cofactors of B is

Question 26.
If A = \(\left[\begin{array}{ccc} 1 & -2 & 3 \\ 0 & -1 & 4 \\ -2 & 2 & 1 \end{array}\right]\), find (A^T)^-1.
Answer:

= 1 (- 1 - 8) - 0(- 2 - 6) - 2( - 8 + 3)
= - 9 + 10 = 1 ≠ 0
So, (A^T)^-1 exists.
Cofactors of |A^T| are:
a₁₁ = (- 1)^{1 + 1} (- 1 - 8) = - 9
a₁₂ = (- 1)^{1 + 2}(- 2 - 6) = 8
a₁₃ = (- 1)^{1 + 3} (- 8 + 3) = - 5
a₂₁ = (- 1)^{2 + 1} (0 + 8) = - 8
a₂₂ = ( 1)^{2 + 2} (1 + 6) = 7
a₂₃ = (- 1)^{2 + 3}(4 - 0) = - 4
a₃₁ = (- 1)^{3 + 1} (0 - 2) = - 2
a₃₂ = (- 1)^{3 + 2} (2 - 4) = 2
a₃₃ = (- 1)^{3 + 3}(- 1 - 0) = - 1
Matrix formed by the cofactors of |A^T| is:

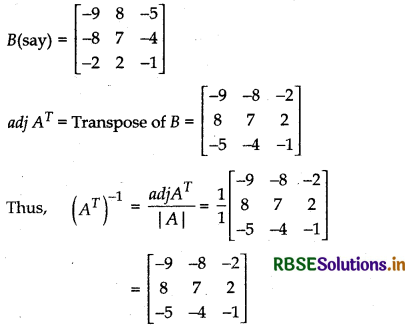
Question 27.
Find A^-1, where A = \(\left[\begin{array}{ccc} 1 & 2 & -3 \\ 2 & 3 & 2 \\ 3 & -3 & -4 \end{array}\right]\). Hence, solve the system of equations, x + 2y - 3z = - 4, 2x + 3y + 2z = 2, and 3x - 3y - 4z = 11.
Answer:

The given system of equation is
x + 2y - 3z = - 4.
2x + 3y + 2z = - 2
3x - 3y - 4z = 11
We know that AX = B

Thus, x = 3, y = - 2 and z = 1 is the required solution.

Question 28.
The sum of three numbers is 6. If we multiply the third number by 2 and add the first number to the result, we get 7. By adding second and third numbers to three times the first number, we get 12. Using matrices find the number.
Answer:
Let the three numbers be x, y and z respectively.
Then,
x + y + z = 6
x + 2z = 7
3x + y + z = 12
We obtain the following system of simultaneous linear equations:
x + y + z = 6
x + 0y + 2z = 7
3x + y + z = 12
The above system of equation can be written in matrix form as:

= 1 (0 - 2) - (1 - 6) + 1 (1 - 0)
= - 2 + 5 + 1 = 4 ≠ 0
So, the above system of equations has a unique solutions given by X = A^-1B
Cofactors of |A| are:
a₁₁ = - 2, a₁₂ = 5, a₁₃ = 1, a₂₁ = 0, a₂₂ = - 2, a₂₃ = 2, a₃₁ = 2, a₃₂ = - 1 and a₃₃ = - 1.
Matrix formed by the cofactors of |A| is:

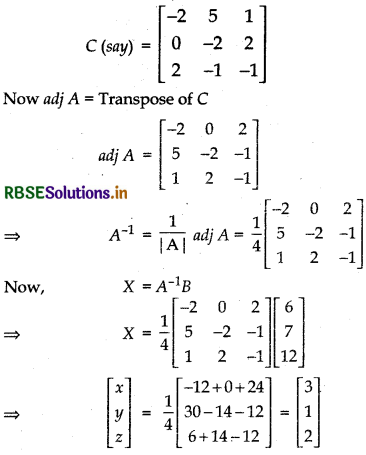
x = 3, y = 1, z = 2
Hence, the numbers are 3, 1 and 2 respectively.

Question 29.
If A = \(\left[\begin{array}{ccc} 1 & -1 & 0 \\ 2 & 3 & 4 \\ 0 & 1 & 2 \end{array}\right]\) and B = \(\left[\begin{array}{ccc} 2 & 2 & -4 \\ -4 & 2 & -4 \\ 2 & -1 & 5 \end{array}\right]\) are square matrices. Find AB and hence solve the system of linear equations:
x - y = 3, 2x + 3y + 4z = 17, y + 2z = 17.
Answer:

⇒ AB = 6I
Multiplying both sides by A^-1, we get
⇒ A BA^-1 = 6IA^-1
⇒ BI = 6IA^-1 [∵ AA^-1 = I]
⇒ B = 6A^-1

Question 30.
A total amount of ₹ 7000 is deposited in three different saving bank accounts with annual interest rate 5%, 8% and 8\(\frac{1}{2}\) % respectively. The total annual interest from these three accounts is ₹ 550. Equal amounts have been deposited in the 5% and 8% savings accounts. Find the amount deposited in each of the three accounts, with the help of matrices.
Answer:
Let the amount deposited in each three accounts be x, y, z respectively.
As per given data x + y + z = 7000 .................... (i)
Total annual interest is ₹ 550.
⇒ \(\frac{5}{100}\) x + \(\frac{8}{100}\) y +\( \frac{8.5}{100}\) z = 550
⇒ 5x + 8y + 8.5z = 55000 .................... (ii)
It is given that two amounts are equal.
Let x = y
∴ x - y = 0 .............. (iii)
From equations (i), (u) and (iii), we get
⇒ |A| = 1(0 + 8.5) - 1(0 - 8.5) + 1(- 5 - 8)
= 1 (8.5) - 1 (-8.5) + 1 (- 13)
= 8.5 + 8.5 - 13 = 4
Cofactors of |A| are:
C₁₁ = (- 1)^{1 + 1} (0 + 8.5) = 8.5
C₁₂ = (- 1)^{1 + 2}(0 - 8.5) = 8.5
C₁₃ = (- 1)^{1 + 3} (- 5 - 8) = - 13
C₂₁ = (- 1)^{2 + 1} (0 + 1) = - 1
C₂₂ = ( 1)^{2 + 2} (0 - 1) = - 1
C₂₃ = (- 1)^{2 + 3}(- 1 - 1) = 2
C₃₁ = (- 1)^{3 + 1} (8.5 - 8) = 0.5
C₃₂ = (- 1)^{3 + 2} (8.5 - 5) = - 3.5
C₃₃ = (- 1)^{3 + 3}(8 - 5) = 3
Matrix formed by the cofactors of |A| is:

Equating the coefficients of both sides,
Thus, X = ₹ 1125, y = ₹ 1125, z = ₹ 4750

Question 31.
A shopkeeper has 3 varieties of pens A, B and C. Meenu purchased 1 pen of each variety for a total of ₹ 21. Jeen purchased 4 pens of A variety, 3 pens of B variety and 2 pens of C variety for ₹ 60. While Shikha purchased 6 pens of A variety, 2 pens of B variety and 3 pens of C variety for ₹ 70. Using matrix method find the cost of each pen.
Answer:
From the given information we can form a matrix as follows:

From above we get three equations,
⇒ A + B + C = 21 .............. (i)
⇒ - B - 2C = - 24 ....... (ii)
⇒ 5C = 40
⇒ C = 8 ............. (iii)
Substituting C = 8 in Eq. (ii), we get
⇒ - B = - 2 × 8 = - 24
⇒ -B = - 24 + 16 ⇒ B = 8
Substituting values of B and C in Eq. (i), we get,
⇒ A + 8 + 8 = 21
⇒ A + 16 = 21
∴ A = 5
Thus, the cost of pen of variety A is ₹ 5, the cost of pen of variety B is ₹ 8 and the cost of pen of variety C is ₹ 8.

Question 32.
Solve the following system of equation by matrix methods:
x - y + 2z = 7
2x - y + 3z =12
3x + 2y - z = 5
Answer:
Writing given equation in matrix form

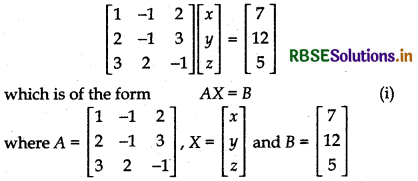
Here |A| = 1(1 - 6) + 1(- 2 - 9) + 2(4 + 3)
= - 5 - 11 + 14 = - 2 ≠ O
Now, the cofactors of |A| are:
a₁₁ = (- 1)^{1 + 1} (1 - 6) = - 5
a₁₂ = (- 1)^{1 + 2}(- 2 - 9) = 11
a₁₃ = (- 1)^{1 + 3} (4 + 3) = 7
a₂₁ = (- 1)^{2 + 1} (1 - 4) = 3
a₂₂ = ( 1)^{2 + 2} (- 1 - 6) = - 7
a₂₃ = (- 1)^{2 + 3}(2 + 3) = - 5
a₃₁ = (- 1)^{3 + 1} (- 3 + 2) = - 1
a₃₂ = (- 1)^{3 + 2} (3 - 4) = 1
a₃₃ = (- 1)^{3 + 3}(- 1 + 2) = 1
Matrix formed by the cofactors of |A| is

Multiple Choice Questions

Question 1.
If A is a square matrix of order 3, such that A(adj A) = 101, then |adj A| is equal to :
(a) 1
(b) 10
(c) 100
(d) 101
Answer:
(c) 100

Question 2.
If A is a 3 × 3 matrix such that |A| = 8, then |3A| equals:
(a) 8
(b) 24
(c) 72
(d) 216
Answer:
(d) 216

Question 3.
If \(\left|\begin{array}{lll} 2 & 3 & 2 \\ x & x & x \\ 4 & 9 & 1 \end{array}\right|\) + 3 = 0, then the value of x is:
(a) 3
(b) 0
(c) -1
(d) 1
Answer:
(c) -1

 

Question 4.
Let A = \(\left[\begin{array}{cc} 200 & 50 \\ 10 & 2 \end{array}\right]\) and B = \(\left[\begin{array}{cc} 50 & 40 \\ 2 & 3 \end{array}\right]\), then |AB| is equal to:
(a) 460
(b) 2000
(c) 3000
(d) -7000
Answer:
(d) -7000

Question 5.
If A = \(\left[\begin{array}{lll} a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & a \end{array}\right]\), then det(adj A) equals:
(a) a²⁷
(b) a⁹
(c) a⁶
(d) a²
Answer:
(c) a⁶

Question 6.
If \(\left|\begin{array}{ccc} 3 x-8 & 3 & 3 \\ 3 & 3 x-8 & 3 \\ 3 & 3 & 3 x-8 \end{array}\right|\) = 0, then x = .........
(a) \(\frac{3}{2}, \frac{3}{11}\)
(b) \(\frac{3}{2}, \frac{11}{3}\)
(c) \(\frac{2}{3}, \frac{11}{3}\)
(d) \(\frac{2}{3}, \frac{3}{11}\)
Answer:
(c) \(\frac{2}{3}, \frac{11}{3}\)

Question 7.
If \(\left|\begin{array}{ccc} (b+c)^2 & a^2 & a^2 \\ b^2 & (c+a)^2 & b^2 \\ c^2 & c^2 & (a+b)^2 \end{array}\right|\) = k (abc)(a + b + c)³, then k = ............
(a) 1
(b) -1
(c) -2
(d) 2
Answer:
(d) 2

Question 8.
\(\left|\begin{array}{ccc} \sqrt{11}+\sqrt{3} & \sqrt{20} & \sqrt{5} \\ \sqrt{15}+\sqrt{22} & \sqrt{25} & \sqrt{10} \\ 3+\sqrt{55} & \sqrt{15} & \sqrt{25} \end{array}\right|\) = ..............
(a) 5(5√3 - 3√2)
(b) 5(5√2 + 5√3)
(c) -5(5√3 + 3√2)
(d) 5(5√2 - 5√3)
Answer:
(d) 5(5√2 - 5√3)

Question 9.
If 2s = a + b + c and A = \(\left[\begin{array}{ccc} a^2 & (s-a)^2 & (s-a)^2 \\ (s-b)^2 & b^2 & (s-b)^2 \\ (s-c)^2 & (s-c)^2 & \left(c^2\right) \end{array}\right]\) then det A = .................
(a) 2s²(s - a)(s - b)(s - c)
(b) 2s³(s - a)(s - b)(s - c)
(c) 2s(s - a)²(s - b)²(s - c)²
(d) 2s²(s - a)²(s - b)²(s - c)²
Answer:
(b) 2s³(s - a)(s - b)(s - c)

Question 10.
Let A = \(\left[\begin{array}{ccc} 4 & 4 k & k \\ 0 & k & 4 k \\ 0 & 0 & 4 \end{array}\right]\). If det(A²) = 16 then |k| is .........
(a) 1
(b) \(\frac{1}{4}\)
(c) 4
(d) 4²
Answer:
(b) \(\frac{1}{4}\)

Question 11.
If \(\left|\begin{array}{ccc} x^2+x & x+1 & x-2 \\ 2 x^2+3 x-1 & 3 x & 2 x-3 \\ x^2+2 x+3 & 2 x-1 & 2 x-1 \end{array}\right|\) = 24x + B then B = ...........
(a) -12
(b) 12
(c) 24
(d) -8
Answer:
(a) -12

Question 12.
\(\left|\begin{array}{ccc} \tan ^2 x & -\sec ^2 x & 1 \\ -\sec ^2 x & \tan ^2 x & 1 \\ -10 & 12 & 2 \end{array}\right|\) = ..........
(a) 12 tan²x - 10 sec²x
(b) 12 sec²x - 10 tan²x + 2
(c) 0
(d) tan²x . sec²x
Answer:
(c) 0

Question 13.
\(\left|\begin{array}{ccc} 1 & a & a^2-b c \\ a & b & b^2-c a \\ 1 & c & c^2-a b \end{array}\right|\) = .............
(a) (a² - bc)(b² - ac)(c² - ab)
(b) 5
(c) (a - b)(b - c)(c - a)
(d) -1
Answer:
(a) (a² - bc)(b² - ac)(c² - ab)

Question 14.
If the system of equations x + ay = 0, ax + y = 0, ax + z = 0 has infinite number of solutions then a =
(a) 0
(b) 1
(c) -1
(d) - 2
Answer:
(c) -1

Question 15.
The equations x + 2y + 3z = 1,2x + y + 3z = 2, 5x + 5y + 9z = 4 have
(a) no solution
(b) unique solution
(c) infinite solutions
(d) can not say anything
Answer:
(b) unique solution

Fill in the Blanks:

Question 1.
If A = \(\left[\begin{array}{cc} 0 & -1 \\ 0 & 2 \end{array}\right]\) and B = \(\left[\begin{array}{ll} 3 & 5 \\ 0 & 0 \end{array}\right]\), then |AB| = .................
Answer:
0

Question 2.
If \(\left|\begin{array}{cc} 3 x & 7 \\ -2 & 4 \end{array}\right|=\left|\begin{array}{ll} 8 & 7 \\ 6 & 4 \end{array}\right|\), then the value of x is ________________
Answer:
-2

Question 3,
The value of the determinant \(\left|\begin{array}{cc} p & p+1 \\ p-1 & p \end{array}\right|\) is ________________
Answer:
1

Question 4.
If Δ = \(\left|\begin{array}{lll} 1 & 2 & 3 \\ 2 & 0 & 1 \\ 5 & 3 & 8 \end{array}\right|\), then the minor of element a₂₂ is ________________
Answer:
-7

Question 5.
For x = ________________, the matrix \(\left[\begin{array}{ll} 6-x & 4 \\ 3-x & 1 \end{array}\right]\) is a singular matrix.
Answer:
2

True/False

Question 1.
For matrix A, |A| is read as modulus of A.
Answer:
False

Question 2.
We must expand the determinant along that row or column which contains maximum number of zeros.
Answer:
True

Question 3.
The value of the determinant changed, if its rows and columns are interchanged.
Answer:
True

Question 4.
If any two rows (or columns) of a determinant are interchanged, then sign of determinant does not change.
Answer:
False

Question 5.
If some or all elements of a row or column of a determinants are expressed as sum of two (or more) terms, then the determinant can be expressed as sum of two (or more) determinants.
Answer:
True