RBSE Class 12 Maths Important Questions Chapter 3 आव्यूह

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 3 आव्यूह Important Questions and Answers.

RBSE Class 12 Maths Chapter 3 Important Questions आव्यूह

अन्य महत्त्वपूर्ण प्रश्न

प्रश्न 1.
यदि A = \(\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\) हो, तो A है
(A) अदिश आव्यूह
(B) इकाई आव्यूह
(C) विकर्ण आव्यूह
(D) शून्य आव्यूह
उत्तर:
(B) इकाई आव्यूह

हल:
चूँकि विकर्ण के प्रत्येक अवयव का मान 1 है और शेष सभी अवयव शून्य हैं।

प्रश्न 2.
यदि A = \(\left[\begin{array}{lll} 3 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{array}\right]\) तो A होगा
(A) विकर्ण आव्यूह
(B) अदिश आव्यूह
(C) इकाई आव्यूह
(D) उपर्युक्त में से कोई नहीं
उत्तर:
(A) विकर्ण आव्यूह

हल:
चूँकि एक वर्ग आव्यूह विकर्ण आव्यूह कहलाता है, यदि विकर्ण के अतिरिक्त इसके अन्य सभी अवयव शून्य होते हैं।

प्रश्न 3.
यदि एक आव्यूह सममित एवं विषम-सममित हो, तो वह आव्यूह होगा
(A) शून्य आव्यूह
(B) त्रिभुजाकार आव्यूह
(C) विकर्ण आव्यूह
(D) उपर्युक्त में से कोई नहीं
उत्तर:
(A) शून्य आव्यूह

हल: चूँकि शून्य आव्यूह ही एक ऐसी आव्यूह है जो कि सममित तथा विषम सममित भी होती है।

प्रश्न 4.
यदि A = \(\left[\begin{array}{lll} 1 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 1 \end{array}\right]\) तो A² होगा
(A) 2A
(B) - 2A
(C) A
(D) - A
उत्तर:
(A) 2A

हल:

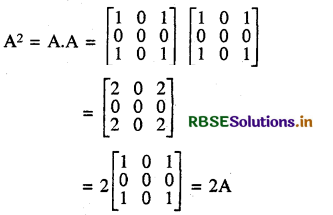
अतः सही विकल्प (A) है।

प्रश्न 5.
किसी वर्ग आव्यूह A के लिए A + A' होगा-
(A) इकाई आव्यूह
(B) सममित आव्यूह
(C) विषम सममित आव्यूह
(D) शून्य आव्यूह
उत्तर:
(B) सममित आव्यूह

प्रश्न 6.
यदि A = \(\left[\begin{array}{cc} \sin ^2 \theta & \sec ^2 \theta \\ {cosec}^2 \theta & \frac{1}{2} \end{array}\right]\) तथा B = \(\left[\begin{array}{cc} \cos ^2 \theta & -\tan ^2 \theta \\ -\cot ^2 \theta & \frac{1}{2} \end{array}\right]\) हो, तो A + B का मान होगा-
(A) \(\left[\begin{array}{cc} 1 & -1 \\ 1 & 1 \end{array}\right]\)
(B) \(\left[\begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array}\right]\)
(C) \(\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]\)
(D) \(\left[\begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array}\right]\)
उत्तर:
(D) \(\left[\begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array}\right]\)
हल:

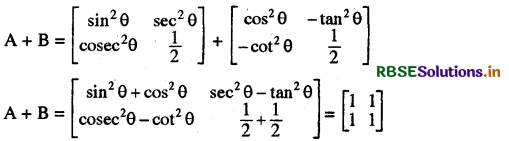
अतः सही विकल्प D है।

प्रश्न 7.
यदि आव्यूह B = [b_ij]_{2 × 4} हो, तो B में अवयवों की संख्या होगी-
(A) 2
(B) 4
(C) 6
(D) 8
उत्तर:
(D) 8
आव्यूह B में दो पंक्ति और चार स्तम्भ हैं।
∴ अवयवों की संख्या = 2 × 4 = 8
सही विकल्प (D) है।

प्रश्न 8.
यदि A = \(\left[\begin{array}{ll} 1 & a \\ 0 & 1 \end{array}\right]\) हो, तो A⁴ बराबर है
(A) \(\left[\begin{array}{ll} 1 & a^4 \\ 0 & 1 \end{array}\right]\)
(B) \(\left[\begin{array}{cc} 4 & 4 a \\ 0 & 4 \end{array}\right]\)
(C) \(\left[\begin{array}{cc} 4 & a^4 \\ 0 & 4 \end{array}\right]\)
(D) \(\left[\begin{array}{cc} 1 & 4 a \\ 0 & 1 \end{array}\right]\)
उत्तर:
(D) \(\left[\begin{array}{cc} 1 & 4 a \\ 0 & 1 \end{array}\right]\)
हल:

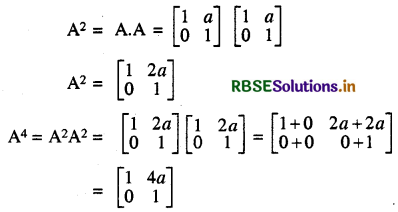
अतः सही विकल्प (D) है।

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
4 × 4 क्रम का इकाई आव्यूह लिखिए।
हल:
\(\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]_{4 \times 4}\)

प्रश्न 2.
यदि \(\left[\begin{array}{cc} k+4 & -2 \\ 3 & k-6 \end{array}\right]\) = \(\left[\begin{array}{ll} a & -2 \\ 3 & -1 \end{array}\right]\) तो a का मान लिखिए।
हल:
चूंकि दोनों आव्यूह आपस में बराबर हैं अतः इसके संगत अवयव भी बराबर होंगे।
∴ k - 6 = - 1
k = - 1 + 6 = 5
तथा k + 4 = a
∴ 5 + 4 = a या a = 9

प्रश्न 3.
6 अवयवों वाले आव्यूह के सम्भावित क्रम क्या होंगे?
हल:
1 × 6, 6 × 1, 2 × 3, 3 × 2

प्रश्न 4.
आव्यूह A = \(\left[\begin{array}{cccc} 4 & -2 & 3 & 8 \\ 1 & 0 & -5 & 7 \\ 2 & 3 & 8 & 4 \end{array}\right]\) में
(A) कितनी पंक्तियाँ हैं?
(B) कितने स्तम्भ हैं?
(C) इसका क्रम क्या है?
(D) इसमें कुल कितने तत्व हैं?
हल:
(A) पंक्तियों की संख्या = 3
(B) स्तम्भों की संख्या = 4
(C) आव्यूह में 3 पंक्ति तथा 4 स्तम्भ हैं। अतः इसका क्रम 3 × 4 है।
(D) तत्वों/अवयवों की कुल संख्या = 12 उत्तर

प्रश्न 5.
आव्यूह \(\left[\begin{array}{cccc} 1 & 1 & 0 & 2 \\ -3 & 2 & 4 & -5 \\ 5 & -6 & -4 & 6 \end{array}\right]\) के अवयवों a₁₁, a₂₂, a₃₂ तथा a₂₁ को ज्ञात कीजिए।
हल:
उपर्युक्त आव्यूह में a₁₁ = 1, a₂₂ = 2
a₃₂ = - 6 तथा a₂₁ = - 3 हैं।

प्रश्न 6.
एक विकर्ण आव्यूह लिखिए जो अदिश आव्यूह न हो।
हल:
अभीष्ट आव्यूह एक ऐसा आव्यूह होगा जिसके विकर्ण के अवयव असमान तथा अशून्य हों तथा शेष सभी अवयव शून्य हों। अत: A = \(\left[\begin{array}{lll} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 1 \end{array}\right]\) अभीष्ट आव्यूह होगा।

प्रश्न 7.
यदि A = \(\left[\begin{array}{lll} 1 & 2 & 3 \\ 2 & 1 & 4 \end{array}\right]\) हो, तो - 3A का मान ज्ञात कीजिए।
हल:
∵ A = \(\left[\begin{array}{lll} 1 & 2 & 3 \\ 2 & 1 & 4 \end{array}\right]\)
∴ - 3A = - 3\(\left[\begin{array}{lll} 1 & 2 & 3 \\ 2 & 1 & 4 \end{array}\right]\) = \(\left[\begin{array}{ccc} -3 & -6 & -9 \\ -6 & -3 & -12 \end{array}\right]\)

प्रश्न 8.
यदि A = [2 3 4 5], B = [0 0 0 1], C = [1 0 10] हो, तो A + 2B + 3C का मान लिखिए।
हल:
A+ 2B + 3C= [2 3 4 5] + 2 [0 0 0 1] + 3 [1 0 1 0]
= [2 3 4 5] + [0 0 0 2] + [3 0 3 0]
= [5 3 7 7]

प्रश्न 9.
1, 2, 0, 4 अंकों द्वारा निम्न आव्यूह को लिखिए
(i) भिन्न-भिन्न चार 1 × 4 क्रम के आव्यूह
हल:
भिन्न-भिन्न चार 1 × 4 क्रम के आव्यूह निम्नलिखित हैं
[1 2 0 4], [1 2 4 0], [4 2 0 1], [0 4 1 2]
इनके अतिरिक्त भी अन्य आव्यूह बनाए जा सकते हैं।

(ii) भिन्न-भिन्न चार 4 × 1 क्रम के आव्यूह।
हल:
भिन्न-भिन्न चार 4 × 1 क्रम के आव्यूह निम्नलिखित हैं
\(\left[\begin{array}{l} 1 \\ 2 \\ 0 \\ 4 \end{array}\right],\left[\begin{array}{l} 4 \\ 0 \\ 2 \\ 1 \end{array}\right],\left[\begin{array}{l} 1 \\ 4 \\ 0 \\ 2 \end{array}\right],\left[\begin{array}{l} 2 \\ 1 \\ 0 \\ 4 \end{array}\right]\)
इनके अतिरिक्त अन्य आव्यूह भी बनाए जा सकते हैं।

प्रश्न 10.
यदि A = \(\left[\begin{array}{cc} \cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{array}\right]\) तब A² ज्ञात कीजिए।
हल:
हम जानते हैं कि A² = A.A

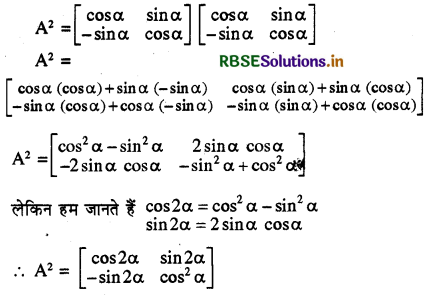
प्रश्न 11.
यदि A = \(\left[\begin{array}{ll} 1 & 5 \\ 6 & 7 \end{array}\right]\), A + A' ज्ञात कीजिए।
हल:

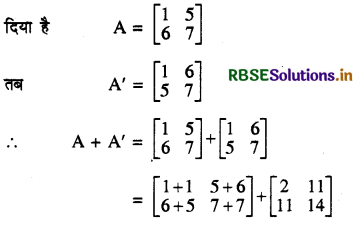
प्रश्न 12.
A ज्ञात कीजिए, यदि A + B = \(\left[\begin{array}{ll} 5 & 2 \\ 0 & 9 \end{array}\right]\) तथा A - B = \(\left[\begin{array}{cc} -3 & -6 \\ 4 & -1 \end{array}\right]\)
हल:

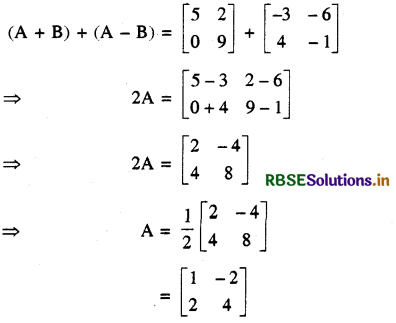
प्रश्न 13.
यदि A = \(\left[\begin{array}{c} -2 \\ 4 \\ 5 \end{array}\right]\) तथा B = [1 4 -6] तो AB ज्ञात करें।
हल:

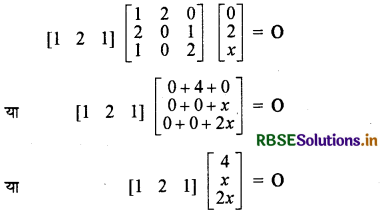
प्रश्न 14.
यदि A = \(\left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\) के लिए, Det (Aⁿ) का मान ज्ञात कीजिए।
हल:
दिया है

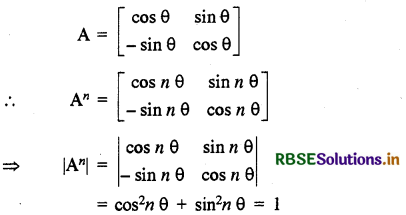
प्रश्न 15.
यदि 2A + B = \(\left[\begin{array}{cc} 3 & -1 \\ 2 & 4 \end{array}\right]\) तथा B = \(\left[\begin{array}{cc} -1 & -5 \\ 0 & 2 \end{array}\right]\) तो A ज्ञात कीजिए।
हल:
दिया गया है
2A + B = \(\left[\begin{array}{cc} 3 & -1 \\ 2 & 4 \end{array}\right]\)
B का मान रखने पर

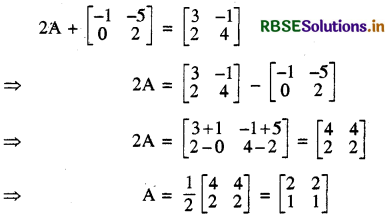
प्रश्न 16.
यदि A = [1 2 3] तथा B = \(\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]\), तो (AB)' ज्ञात कीजिए।
हल:
AB = [1 2 3]_{1 × 3} \(\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]_{3 \times 1}\)
⇒ AB = [1 × 1 + 2 × 2 + 3 × 3]_{1 × 1} = [14]_{1 × 1}
∴ (AB)' = [14]_{1 × 1}

उत्तर लघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि A, B कोई दो सममित आव्यूह हैं। तब सिद्ध कीजिए कि AB + BA एक सममित आव्यूह होगा।
हल:
प्रश्नानुसार A तथा B कोई दो सममित आव्यूह हैं। .
∴ A' = A तथा B' = B
अब (AB + BA)' = (AB)' + (BA)'
= B'A' + A'B'
= BA + AB [∵ B' = B और A' = A]
= AB + BA
⇒ AB + BA एक सममित आव्यूह है।

प्रश्न 2.
यदि A = \(\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]\),
तब A² - 3A + 2I का मान ज्ञात कीजिए।
हल:

प्रश्न 3.
प्रारम्भिक पंक्ति संक्रियाओं (रूपान्तरणों) के प्रयोग से निम्न आव्यूह का प्रतिलोम ज्ञात कीजिये-
\(\left[\begin{array}{lll} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 0 \end{array}\right]\)
हल:
हम जानते हैं कि A = IA

प्रश्न 4.
यदि A = \(\left[\begin{array}{lll} 1 & 2 & 2 \\ 2 & 1 & 2 \\ 2 & 2 & 1 \end{array}\right]\) और A² - 4A = kI₃ हो, तो k का
मान ज्ञात कीजिये। (यहाँ I₃ एक 3 क्रम का तत्समक आव्यूह हैं)
हल:
यदि A = \(\left[\begin{array}{lll} 1 & 2 & 2 \\ 2 & 1 & 2 \\ 2 & 2 & 1 \end{array}\right]\)
और A² - 4A = KI₃
यहाँ पर I₃ एक 3 क्रम का तत्समक आव्यूह है।
A² का मान निकालने पर

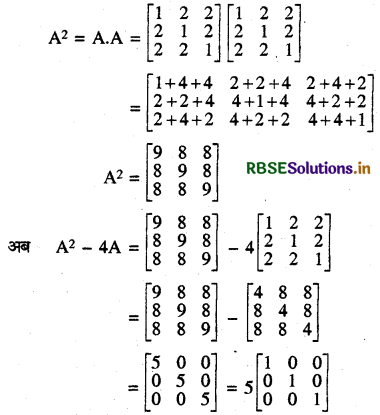
A² - 4A = 5 I
इससे सिद्ध होता है कि k = 5 होगा।

आव्यूह निबन्धात्मक प्रश्न

प्रश्न 1.
आव्यूह B = \(\left[\begin{array}{ccc} 2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3 \end{array}\right]\) को एक सममित आव्यूह तथा एक विषम सममित आव्यूह के योगफल के रूप में व्यक्त कीजिए।
हल:

अतः आव्यूह B एक सममित आव्यूह तथा एक विषम सममित आव्यूह के योगफल के रूप में व्यक्त किया गया।

प्रश्न 2.
A और B दो परिवार हैं। परिवार A में, 4 पुरुष, 6 महिलाएँ तथा 2 बच्चे हैं और परिवार B में, 2 पुरुष, 2 महिलाएँ तथा 4 बच्चे हैं। प्रति पुरुष, महिला व बच्चे को क्रमशः 2400, 1900 तथा 1800 कैलोरी की दैनिक मात्रा देने का सुझाव है, और क्रमशः 45, 55 तथा 33 ग्राम प्रोटीन देने का सुझाव दिया जाता है। उपर्युक्त सूचना व तथ्य को आव्यूह द्वारा निरूपित कीजिए। आव्यूह गुणनफल का प्रयोग करके, प्रत्येक परिवार के लिए कैलोरी तथा प्रोटीन की दी जाने वाली कुल मात्रा ज्ञात कीजिए। इस प्रश्न से आप लोगों के बीच सन्तुलित आहार के लिए किस प्रकार की जागरूकता उत्पन्न कर सकते हैं?
हल:
परिवार A तथा B में पुरुष, महिलायें तथा बच्चों को हम 2 × 3 मैट्रिक्स के रूप में प्रदर्शित कर सकते हैं।

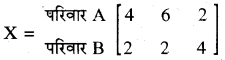
और सुझाव के आधार पर पुरुष, महिलाओं और बच्चों को दी जाने वाली कैलोरी और प्रोटीन की मात्रा को 3 × 2 मैट्रिक्स के रूप में प्रदर्शित करने पर

प्रत्येक परिवार के लिये कैलोरी तथा प्रोटीन की दी जाने वाली कुल मात्रा का मान हम दोनों मैट्रिक्स के गुणनफल से ज्ञात कर सकते हैं। अतः

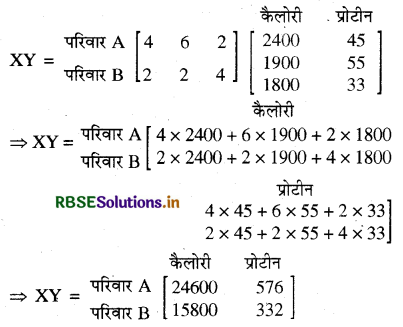
अतः परिवार A के लिये 24,600 कैलोरी तथा 576 प्रोटीन की मात्रा दी गयी है और परिवार B के लिये 15,800 कैलोरी तथा 332 प्रोटीन की मात्रा दी गयी है।
मूल्य-इस प्रश्न से हम लोगों के बीच सन्तुलित आहार के प्रति जागरूक कर सकते हैं क्योंकि सन्तुलित आहार से ही व्यक्ति शारीरिक व मानसिक रूप से स्वस्थ रह सकता है।