RBSE Class 12 Maths Important Questions Chapter 3 Matrices

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 3 Matrices Important Questions and Answers.

RBSE Class 12 Maths Chapter 3 Important Questions Matrices

Question 1.
If \(\left[\begin{array}{cc} x-y & 2 x+z \\ 2 x-y & 3 z+\omega \end{array}\right]\)= \(\left[\begin{array}{rr} -1 & 5 \\ 0 & 13 \end{array}\right]\) = \(\left[\begin{array}{rr} -1 & 5 \\ 0 & 13 \end{array}\right]\), find x, y, z and w
Answer:
Given, matrix equation is:
\(\left[\begin{array}{cc} x-y & 2 x+z \\ 2 x-y & 3 z+w \end{array}\right]\)= \(\left[\begin{array}{cc} -1 & 5 \\ 0 & 13 \end{array}\right]\)
On equating the corresponding elements, we get
x - y = - 1 ...... (i)
2x - y = 0 ....... (ii)
2x + z = 5 ...... (iii)
3z + w = 13 .......... (iv)
Subtracting eq. (ii), from (i), we get

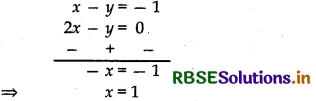
Substituting x = 1 in eq. (i), we get
1 - y = - 1
⇒ - y = - 2
⇒ y = 2
Substituting the value of x in Eq. (iii), we get
2 × 1 + z = 5
⇒ z = 5 - 2 = 3
Substituting the value of z in Eq. (iv), we get
3 × 3 + w = 13
⇒ w = 13 - 9
w = 4
Thus, x = 1, y = 2, z = 3, w = 4

Question 2.
Construct a 2 × 2 matrix A = [a_ij] whose elements are given by:
(i) a_ij = \(\frac{(i-2 j)^2}{2}\)
Answer:
Matrix of order 2 × 2 will be as follows:

(ii) a_ij = \(\frac{(2 i+j)^2}{2}\)
Answer:
Since, it is a 2 × 2 matrix, it has 2 rows and 2 columns.
Let the matrix be A,

Question 3.
If \(\left[\begin{array}{cc} x-y & z \\ 2 x-y & w \end{array}\right]\) = \(\left[\begin{array}{rr} -1 & 4 \\ 0 & 5 \end{array}\right]\), find x, y, z and w.
Answer:
Given, matrix equation is:
\(\left[\begin{array}{cc} x-y & z \\ 2 x-y & w \end{array}\right]\) = \(\left[\begin{array}{cc} -1 & 4 \\ 0 & 5 \end{array}\right]\)
On equating the corresponding elements, we get
x - y = - 1 ...... (i)
2x - y = 0 ....... (ii)
z = 4 ........ (iii)
w = 5 ........ (iv)
Subtracting equation (ii), from (j), we get

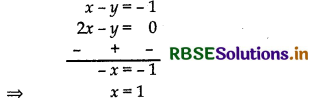
Substituting the value of x in Eq. (ii), we get
y = 2
Thus, x = 1, y = 2, z = 4 and w = 5

Question 4.
If \(\left[\begin{array}{cc} 2 x+1 & 5 x \\ 0 & y^2+1 \end{array}\right]\) = \(\left[\begin{array}{cc} x+3 & 10 \\ 0 & 26 \end{array}\right]\), find the value of (x + y).
Answer:
Given, matrix equation is:
\(\left[\begin{array}{cc} 2 x+1 & 5 x \\ 0 & y^2+1 \end{array}\right]\) = \(\left[\begin{array}{cc} x+3 & 10 \\ 0 & 26 \end{array}\right]\)
On equating the corresponding elements, we get
2x + 1 = x + 3
⇒ x = 2
And y² + 1 = 26
⇒ y² = 26 - 1 = 25
⇒ y = ±5
If y = + 5, then x + y = 2 + 5 = 7
and if y= - 5, then x + y = 2 - 5 = - 3

Question 5.
Construct a 2 × 2 matrix A = [a_ij] whose elements are given by a_ij = |(i)² - j|.
Answer:
Matrix of order 2 × 2 will be as follows:
A = \(\left[\begin{array}{ll} a_{11} & a_{12} \\ a_{22} & a_{23} \end{array}\right]\)
Now, a_ij = [(i)² - j]
a₁₁ = (1)² - 1 = 1 - 1 = 0
a₁₂ = (1)² - 2 = 1 - 2 = - 1
a₂₁ = (2)² - 1 = 4 - 1 = 3
a₂₂ = (2)² - 1 = 4 - 2 = 2
Thus, the matrix of order 2 × 2 is:
A = \(\left[\begin{array}{cc} 0 & -1 \\ 3 & 2 \end{array}\right]\)
then 3A = 3\(\left[\begin{array}{rr} 1 & -3 \\ 0 & 3 \end{array}\right]\) = \(\left[\begin{array}{rr} 3 \times 1 & 3 \times(-3) \\ 3 \times 0 & 3 \times 3 \end{array}\right]\)
= \(\left[\begin{array}{rr} 3 & -9 \\ 0 & 9 \end{array}\right]\)

Question 6.
Find a matrix X such that 2A + B + X = 0, where A = \(\left[\begin{array}{rr} -1 & 2 \\ 3 & 4 \end{array}\right]\) and B = \(\left[\begin{array}{rr} 3 & -2 \\ 1 & 5 \end{array}\right]\).
Answer:
We have
2A + B + X = 0
x = - 2A - B

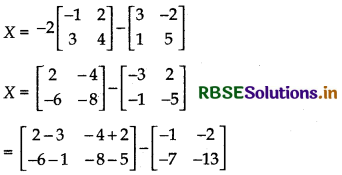
Question 7.
Find a matrix A such that 2A - 3B + 5C = 0, where B = \(\left[\begin{array}{rrr} -2 & 2 & 0 \\ 3 & 1 & 4 \end{array}\right]\) and C = \(\left[\begin{array}{rrr} 2 & 0 & -2 \\ 7 & 1 & 6 \end{array}\right]\).
Answer:
We have,
2A - 3B + 5C = 0
2A = 3B - 5C
A = \(\frac{3 B-5 C}{2}\) = \(\frac{3}{2}\)B - \(\frac{5}{2}\)C

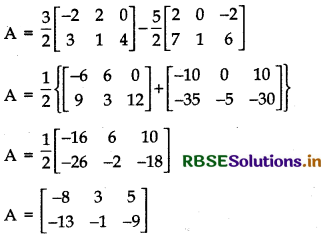
Question 8.
The monthly incomes of Aryan and Baban are in the ratio 3 :4 and their monthly expenditures are In the ratio 5 : 7. If each saves ₹ 1500 per month, find their monthly incomes using matrix method. This problem reflects which values.
Answer:
Let the incomes of Aryan and Baban be 3x and 4x respectively. Similarly, their expenditures would be 5y and 7y respectively.
Since, each saves ₹ 1500, we get
3x - 5y = 1500
4x - 7y = 1500
This can be written form as:

∴ x = 3000
Thus, their incomes was 3 × 3000 = ₹ 9,000 and 4 × 3000 = ₹ 12000 respectively.

Question 9.
If A = \(\left[\begin{array}{ll} 1 & -1 \\ 2 & -1 \end{array}\right]\), B = \(\left[\begin{array}{rr} a & 1 \\ b & -1 \end{array}\right]\) and (A + B)² = A² + B², find a and b.
Answer:
We have
(A + B)² = A² + B²
⇒ (A + B) (A + B) = A² + B²
⇒ A² + BA + AB + B² + A² + B²
⇒ BA + AB = 0

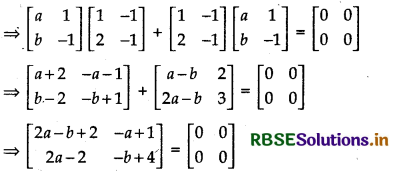
On equating the corresponding elements, we get
⇒ 2a - b + 2 = 0 ......... (i)
- a + 1 = 0 ....... (ii)
2a - 2 = 0 ........ (iii)
- b + 4 = 0 ....... (iv)
On solving these equations, we get
a = 1, b = 4

Question 10.
Find the value of x, for the following:
\(\left[\begin{array}{lll} 1 & x & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & 3 & 2 \\ 2 & 5 & 1 \\ 15 & 3 & 2 \end{array}\right]\left[\begin{array}{l} 1 \\ 2 \\ x \end{array}\right]\) = 0
Answer:
We have
⇒ \(\left[\begin{array}{lll} 1 & x & 1 \end{array}\right]\left[\begin{array}{c} 7+2 x \\ 12+x \\ 21+2 x \end{array}\right]\) = 0
⇒ 7 + 2x + 12x + x² + 21 + 2x = 0
⇒ x² + 16x + 28 = 0
⇒ (x + 14) (x + 2) = 0
Either x+ 14 = 0 ⇒ x = - 14
or x + 2 = 0 ⇒ x = - 2

Question 11.
If A is a square matrix such that A² = 1, then find the simplified value of (A - I)³ + (A + I)³ - 7A.
Answer:
We have, A² = I
∴ A³ = A².A = IA = A
We know that
(A + B)³ = A³ + 3A²B + 3AB² + B²
(A - B)³ = A³ - 3A²B + 3AB² - B³
Provided that AB = BA
Since AI = IA = A
∴ (A + I)³ = A³ + 3A²I + 3AI² + I
⇒ (A - I)³ = A³ - 3A²I + 3AI² - I
∴ (A + I)³ + (A - I)³ = 2(A³ + 3A)
⇒ (A + I)³ × (A - I)³ = 2(A + 3A) [By (i)]
⇒ (A + I)³ + (A - I)³ = 8A
Thus, (A - I)³ + (A + I)³ - 7A
= 8A - 7A = A

Question 12.
Find the matrix A such that
(i) \(\left[\begin{array}{rr} 2 & -1 \\ 1 & 0 \\ -3 & 4 \end{array}\right]\) A = \(\left[\begin{array}{rr} -1 & -8 \\ 1 & -2 \\ 9 & 22 \end{array}\right]\)
Answer:

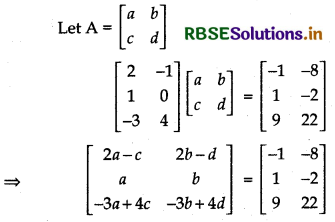
On equating the corresponding elements, we get
⇒ 2a - c = - 1 ........... (i)
2b - d = - 8 .......... (ii)
a = 1 ......... (iii)
b = - 2 ......... (iv)
- 3a + 4c = 9 .......... (v)
- 3b + 4d = 22 .......... (vi)
On solving these equations, we get
a = 1, b = - 2, c = 3, d = 4
Thus, A = \(\left[\begin{array}{cc} 1 & -2 \\ 3 & 4 \end{array}\right]\)

(ii) A\(\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array}\right]=\left[\begin{array}{rrr} -7 & -8 & -9 \\ 2 & 4 & 6 \end{array}\right]\)
Answer:
It is given that:
\(\mathrm{A}\left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array}\right]=\left[\begin{array}{ccc} -7 & -8 & -9 \\ 2 & 4 & 6 \end{array}\right]\)
The matrix given on the R.H.S. of the equation is a 2 × 3 matrix and the one given on the L.H.S. of the equation is a 2 × 3 matrix.
Therefore, A is a 2 × 2 matrix.

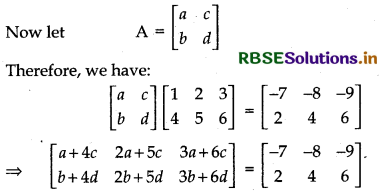
Equating the corresponding elements of the two
matrices, we get
a + 4c = - 7
2a + 5c = 8 ........ (ii)
3a + 6c = - 9 ......... (iii)
b + 4d = 2 ....... (iv)
2b + 5d = 4 ........ (v)
3b + 6d = 6 ........ (vi)
Now, from (i), we have
a + 4c = - 7
⇒ a - 7 - 4c .......... (vii)
From (ii), we have
∴ 2a + 5c = - 8 ⇒ - 14 - 8c + 5c = - 8
⇒ - 3c = 6 ⇒ c = - 2
Substituting c = - 2 in Eq. (vii), we get
∴ a = - 7 - 4(- 2)
= - 7 + 8 = 1
Now, from (iv), we get
b + 4d = 2
⇒ b = 2 - 4d ...... (viii)
From eqs. (y) and (viii), we get
⇒ 4 - 8d + 5d = 4
⇒ - 3d = 0
⇒ d = 0
Substituting d = 0 in Eq. (viii), we get
∴ b = 2 - 4(0) = 2
Thus, a = 1, b = 2, c = - 2, d = 0
Hence, the required matrix A is \(\left[\begin{array}{cc} 1 & -2 \\ 2 & 0 \end{array}\right]\).

Question 13.
If A = \(\left[\begin{array}{rr} -3 & 2 \\ 1 & -1 \end{array}\right]\) and I = \(\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\), find scalar K so that A² + I = KA.
Answer:

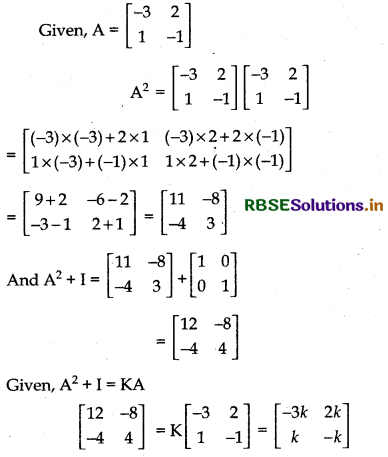
On equating the corresponding elements, we get
- 3k = 12 ⇒ k = - 4

Question 14.
If A = \(\left[\begin{array}{c} -1 \\ 2 \\ 3 \end{array}\right] \)and B = [- 2 - 1 - 4], verify that (AB)^T = B^TA^T.
Answer:

From (i) and (ii), we get
(AB)^T = B^TA^T
Hence, proved

Question 15.
Show that the elements on the main diagonal of a skew symmetric matrix are all zero.
Answer:
Let A = [a_ij] be a skew-symmetric matrix.
Then a_ij = - a_ij for all i, j
Put i = j, we get
a_ii = - a_ii for all values of i
2a_ii = 0
= a_ii = 0 for all values of i
a₁₁ = a₂₂ = a₃₃ = ........................ = a_m = 0
Thus, all the diagonals of a skew-symmetric matrix are zero.
Hence proved

Question 16.
If A = \(\left[\begin{array}{ll} 2 & 3 \\ 4 & 5 \end{array}\right]\), prove that A - A^T, is a skew-symmetric matrix.
Answer:
Given, A = \(\left[\begin{array}{ll} 2 & 3 \\ 4 & 5 \end{array}\right]\)
Let B = A - A^T
B is a skew -symmetric matrix if B^T = - B
Now, B = A - A^T

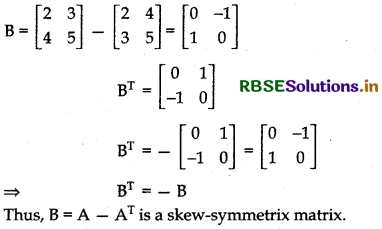
Question 17.
Express the matrix A = \(\left[\begin{array}{ccc} 4 & 2 & -1 \\ 3 & 5 & 7 \\ 1 & -2 & 1 \end{array}\right]\) as the sum of a symmetric and skew-symmetric matrix.
Answer:
Any square matrix A can be expressed as the sum of a symmetric and skew-symmetric, i.e., A = \(\frac{\mathrm{A}+\mathrm{A}^{\prime}}{2}\) + \(\frac{\mathrm{A}-\mathrm{A}^{\prime}}{2}\), where \(\frac{\mathrm{A}+\mathrm{A}^{\prime}}{2}\) and \(\frac{\mathrm{A}-\mathrm{A}^{\prime}}{2}\) are symmetric and skew-symmetric matrices respectively.


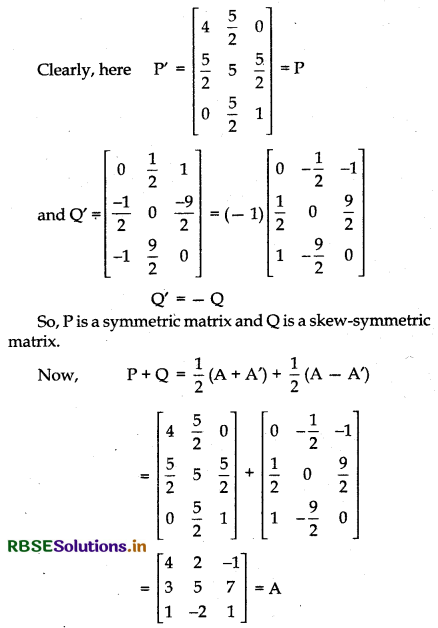
Thus, matrix A is expressed as the sum of symmetric matrix and skew-symmetric matrix.

Question 18.
Express the matrix \(\left[\begin{array}{ccc} 3 & -2 & -4 \\ 3 & -2 & -5 \\ -1 & 1 & 2 \end{array}\right]\) as the sum of a symmetric and skew-symmetric matrix and verify your result.
Answer:

Thus, matrix A is expressed as the sum of symmetric matrix and skew-symmetric matrix.

Question 19.
Find the matrix A = \(\left[\begin{array}{ll} 2 & 3 \\ 5 & 7 \end{array}\right]\), find A + A^T and verify then it is a symmetric matrix.
Answer:

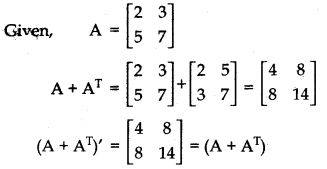
Thus, (A + A)^T is a symmetric matrix.
Hence proved.

Question 20.
Given a skew-symmetric matrix A = \(\left[\begin{array}{ccc} 0 & a & 1 \\ -1 & b & 1 \\ -1 & c & 0 \end{array}\right]\) the value of (a + b + c)² is ................. .
Answer:
A = \(\left[\begin{array}{ccc} 0 & a & 1 \\ -1 & b & 1 \\ -1 & c & 0 \end{array}\right]\) is a skew-symmetric matrix, then the value of (a + b + c)² is 0.

Question 21.
Express A = \(\left[\begin{array}{ll} 4 & -3 \\ 2 & -1 \end{array}\right]\) as a sum of a symmetric and a skew-symmetric matrix.
Answer:

Thus, matrix A is expressed as the sum of symmetric matrix and skew-symmetric matrix.

Question 22.
Show that the matrix A = \(\left[\begin{array}{lll} 1 & 2 & 2 \\ 2 & 1 & 2 \\ 2 & 2 & 1 \end{array}\right]\) satisfies the equation A² - 4A - 5I₃ = 0 and hence find A^-1.
Answer:

Now, A² - 4A - 5I = 0
A² - 4A = 5I
A²A^{- 1} - 4A.A^-1 = 5IA^-1
A - 4I = 5A^-1

Question 23.
Find A^-1, by using elementary row transformation for matrix A = \(\left[\begin{array}{ll} 3 & 2 \\ 7 & 5 \end{array}\right]\).
Answer:

Question 24.
Find the inverse of matrix A = \(\left[\begin{array}{ccc} 1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1 \end{array}\right]\) by using elementary row transformations.
Answer:
We know that
AA^-1 = I

Question 25.
Find the inverse of each of the following matrices by using elementary row transformation.
(i) \(\left[\begin{array}{rr} 1 & 2 \\ 2 & -1 \end{array}\right]\)
Answer:

(ii)
\(\left[\begin{array}{ll} 2 & 5 \\ 1 & 3 \end{array}\right]\)
Answer:

(iii)
\(\left[\begin{array}{ccc} 2 & -1 & 4 \\ 4 & 0 & 2 \\ 3 & -2 & 7 \end{array}\right]\)
Answer:

(iv) \(\left[\begin{array}{ccc} 3 & 0 & -1 \\ 2 & 3 & 0 \\ 0 & 4 & 1 \end{array}\right]\)
Answer:

Question 26.
Obtain the inverse of the following matrix using elementary operations:
A = \(\left[\begin{array}{ccc} 2 & 1 & -3 \\ -1 & -1 & 4 \\ 3 & 0 & 2 \end{array}\right]\)
Answer:

Question 27.
If A = \(\left[\begin{array}{rrr} 1 & 3 & 2 \\ 2 & 0 & -1 \\ 1 & 2 & 3 \end{array}\right]\), then show that A³ - 4A² - 3A +111 = 0. Hence, find A^-1.
Answer:

Now, A³ - 4A² - 3A + 111 = 0
Pre-multiplied by A^-1, we get
A^-1A³ - 4A^-1A² - 3A^-1A + 11A^-1
⇒ A² - 4A - 3I + 11A^-1 = 0 [∵ A^-1A = I]
⇒ 11A^-1 = 3I + 4A - A²

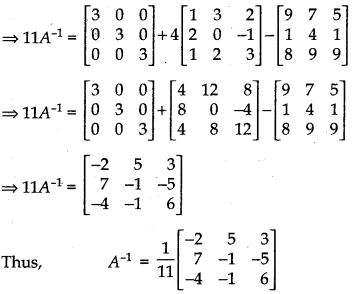
Multiple Choice Questions

Question 1.
If A = [2, -3, 4], B = \(\left[\begin{array}{l} 3 \\ 2 \\ 2 \end{array}\right]\), X = [1, 2, 3] and Y = \(\left[\begin{array}{l} 2 \\ 3 \\ 4 \end{array}\right]\), then AB + XY equals:
(a) [28]
(b) [24]
(c) 28
(d) 24
Answer:
(a) [28]

Question 2.
If A = \(\left[\begin{array}{lll} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & a & 1 \end{array}\right]\), A^-1 = \(\left[\begin{array}{rrr} \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ -4 & 3 & c \\ \frac{5}{2} & -\frac{3}{2} & \frac{1}{2} \end{array}\right]\), then:
(a) a = 2, c = -\(\frac{1}{2}\)
(b) a = 1, c = -1
(c) a = -1, c = 1
(d) a = \(\frac{1}{2}\), c = \(\frac{1}{2}\)
Answer:
(b) a = 1, c = -1

 

Question 3.
If A = \(\left[\begin{array}{rrr} 1 & 2 & 1 \\ 5 & 2 & 6 \\ -2 & -1 & -3 \end{array}\right]\), then A³ = ________________
(a) I
(b) A^T
(c) O
(d) A^-1
Answer:
(c) O

Question 4.
If A = \(\left[\begin{array}{rr} 3 & -4 \\ 1 & -1 \end{array}\right]\), then Aⁿ = ________________
(a) \(\left[\begin{array}{cc} 3 n & -4 n \\ n & -n \end{array}\right]\)
(b) \(\left[\begin{array}{rr} 2+n & 5-n \\ n & -n \end{array}\right]\)
(c) \(\left[\begin{array}{ll} 3^n & (-4)^n \\ 1^n & (-1)^n \end{array}\right]\)
(d) \(\left[\begin{array}{rc} 2 n+1 & -4^n \\ n & -1-2 n \end{array}\right]\)
Answer:
(d) \(\left[\begin{array}{rc} 2 n+1 & -4^n \\ n & -1-2 n \end{array}\right]\)

Question 5.
Suppose a matrix A satisfies A² - 5A + 7I = O. If A⁵ = aA + bI then the value of 2a - 3b must be ....
(a) 4135
(b) 1435
(c) 1453
(d) 3145
Answer:
(c) 1453

Question 6.
If A = \(\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right]\), then A²⁰¹³ = ............
(a) 3²⁰¹³A
(b) -3²⁰¹²I
(c) 3²⁰¹¹A
(d) 3¹⁰⁰⁶A
Answer:
(c) 3²⁰¹¹A

Question 7.

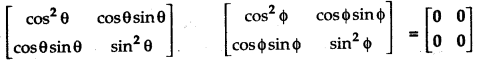
Provided θ - Φ = ......, n ∈ Z
(a) nπ
(b) \(\frac{(2 n+1) \pi}{2}\)
(c) \(\frac{n \pi}{2}\)
(d) 2nπ
Answer:
(b) \(\frac{(2 n+1) \pi}{2}\)

Question 8.
If A = \(\left[\begin{array}{ll} \alpha & 0 \\ 1 & 1 \end{array}\right]\) and B = \(\left[\begin{array}{ll} 1 & 0 \\ 5 & 1 \end{array}\right]\), then A² = B for
(a) α = 4
(b) α = 1
(c) α = -1
(d) no α
Answer:
(d) no α

Question 9.
If A = \(\left[\begin{array}{ll} \alpha & 0 \\ 2 & 3 \end{array}\right]\) and I = \(\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\), then A² = 9I for
(a) α = 4
(b) α = 3
(c) α = -3
(d) no α =
Answer:
(c) α = -3

Question 10.
If A = \(\left[\begin{array}{rr} 3 & 1 \\ -9 & -3 \end{array}\right]\), then I + 2A + 3A² + ........ + ∞ = ...........

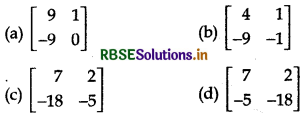
Answer:

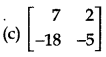
Question 11.
If A = \(\left[\begin{array}{rr} 1 & 0 \\ -1 & 7 \end{array}\right]\) and A² = 8A + kI², then k = ...........
(a) 1
(b) -1
(c) 7
(d) -7
Answer:
(d) -7

Question 12.
The identity element in the group M = {\(\left[\begin{array}{lll} x & x & x \\ x & x & x \\ x & x & x \end{array}\right]\)/ x ∈ R, x ≠ 0} with respect to matrix multiplication is ............

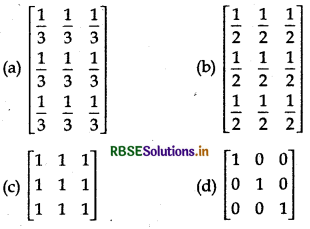
Answer:

Fill in the blanks:

Question 1.
If A + B = \(\left[\begin{array}{ll} 1 & 0 \\ 1 & 1 \end{array}\right]\) and A - 2B =\(\left[\begin{array}{cc} -1 & 0 \\ 1 & -1 \end{array}\right]\), then A = ________________
Answer:
\(\left[\begin{array}{ll} \frac{1}{3} & \frac{1}{3} \\ \frac{2}{3} & \frac{1}{3} \end{array}\right]\)

Question 2.
If \(\left[\begin{array}{cc} x+y & 7 \\ 9 & x-y \end{array}\right]=\left[\begin{array}{cc} 2 & 7 \\ 9 & 4 \end{array}\right]\), then x,y ________________
Answer:
-3

Question 3.
If [2 1 3] \(\left[\begin{array}{ccc} -1 & 0 & -1 \\ -1 & 1 & 0 \\ 0 & 1 & 1 \end{array}\right]\left[\begin{array}{c} 1 \\ 0 \\ -1 \end{array}\right]\) = A, then the order of matrix A is ________________
Answer:
1 × 1

Question 4.
If matrix A = \(\left[\begin{array}{cc} 1 & -1 \\ -1 & 1 \end{array}\right]\) and A² = KA, then the value of k is ________________
Answer:
2

Question 5.
If \(\left[\begin{array}{ll} 1 & 3 \\ 4 & 5 \end{array}\right]\left[\begin{array}{l} x \\ 2 \end{array}\right]=\left[\begin{array}{l} 5 \\ 6 \end{array}\right]\), then x = ________________
Answer:
-1

True/False

Question 1.
In the matrix, the number or function is called the data of the matrix.
Answer:
False

Question 2.
A matrix having m rows and n columns is called a matrix of order n*m.
Answer:
False

Question 3.
A matrix is said to be a column matrix if it has only one column.
Answer:
True

Question 4.
A matrix is said to be diagonal matrix if all its elements are zero.
Answer:
False

Question 5.
Two matrices are said to be equal if they are of the same order.
Answer:
True