RBSE Class 12 Maths Important Questions Chapter 2 Inverse Trigonometric Functions

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 2 Inverse Trigonometric Functions Important Questions and Answers.

RBSE Class 12 Maths Chapter 2 Important Questions Inverse Trigonometric Functions

Question 1.
Find the principal value of each of the following:
(i) tan^-1 √3 - sec^-1 (- 2)
Answer:

(ii) cot^-1 (- √3)
Answer:
Let cot^-1 (- √3) = x ⇒ cot x = - √3
⇒ cot x = - cot \(\frac{\pi}{3}\) ⇒ cot x = cot (π - \(\frac{\pi}{3}\))
⇒ cot x = cot \(\frac{2 \pi}{3}\)
We know that the range of the principal value of cot^-1 x is (0, π) and cot \(\left(\frac{2 \pi}{3}\right)\) = - √3
Thus, the principal value of cot^-1 (- √3) is \(\frac{2 \pi}{3}\).

(iii) cosec^-1 (- 2)
Answer:
Let cosec^-1 (- 2) = x ⇒ cosec x = - 2
⇒ cosec x = - cosec \(\frac{\pi}{6}\)
⇒ cosec x = cosec \(\left(-\frac{\pi}{6}\right)\)
[∵ cosec (- θ) = - cosec θ]
We know that the range of the principal value of
cosec^-1 x is \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\) - [0] and cosec \(\left(-\frac{\pi}{6}\right)\) = - 2.
Thus, the principal value of cosec^-1 (- 2) is \(\frac{-\pi}{6}\).

(iv) cot [sin^-1 {cos (tan^-1 1)}]
Answer:
Given, cot [sin^-1 {cos (tan^-1 1)}]
= cot \(\left[\sin ^{-1}\left\{\cos \frac{\pi}{4}\right\}\right]\)
= cot \(\left[\sin ^{-1}\left(\frac{1}{\sqrt{2}}\right)\right]\)
= cot \(\frac{\pi}{4}\) = 1

(v) sec^-1 \(\left(\frac{-2}{\sqrt{3}}\right)\).
Answer:
sec^-1 = - \(\left(\frac{-2}{\sqrt{3}}\right)\) = an angle θ ∈ \(\left[0, \frac{\pi}{2}\right) \cup\left(\frac{\pi}{2}, \pi\right]\) such sec \(\left[0, \frac{\pi}{2}\right) \cup\left(\frac{\pi}{2}, \pi\right]\) = - \(\frac{2}{\sqrt{3}}\) ⇒ θ = \(\frac{5 \pi}{6}\)

Question 2.
Find the domain of sec^-1 (3x - 1).
Answer:
We know that the range of sec x is (- ∞, - 1) ∪(1, ∞)
∴ 3x - 1 < - 1 and 3x - 1 ≥ 1
⇒ 3x < - 1 + 1 and 3x ≥ 1 + 1
⇒ 3x < 0 and x ≥ \(\frac{2}{3}\)

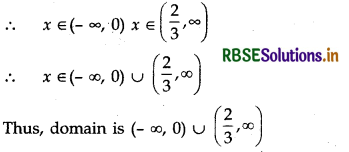
Question 3.
Prove the following results:
(i) tan^-1 \(\frac{1}{4}\) + tan^-1 \(\frac{2}{9}\) = \(\frac{1}{2}\) cos^-1\(\frac{3}{5}\) = \(\frac{1}{2}\) sin^-1 \(\frac{4}{5}\)
Answer:

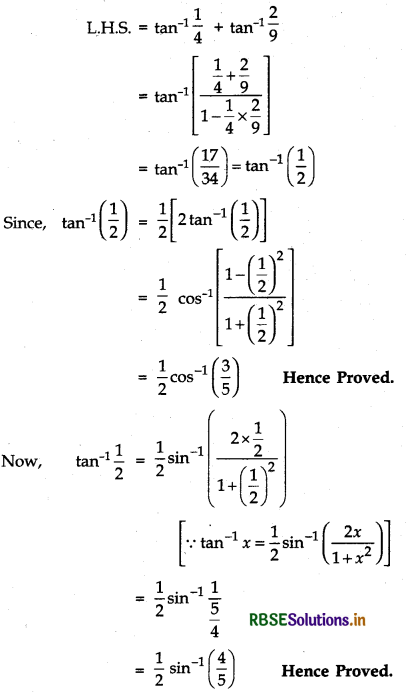
(ii) tan^-1\(\left(\frac{1}{7}\right)\) + 2 tan^-1\(\left(\frac{1}{3}\right)\) = \(\frac{\pi}{4}\)
Answer:

(iii) 2 tan^-1\(\frac{3}{4}\) - tan^-1 \(\frac{17}{31}\) = \(\frac{\pi}{4}\)
Answer:

(iv) 2 tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{7}\) = tan^-1 \(\frac{31}{17}\)
Answer:

Question 4.
Solve the following equations for x:
(i) tan^-1 \(\left(\frac{2 x}{1-x^2}\right)\) + cot\(\left(\frac{1-x^2}{2 x}\right)\) = \(\frac{\pi}{3}\). x > 0
Answer:

(ii) 2 tan^-1 (sin x) = tan^-1 (2 sec x), x ≠ \(\frac{\pi}{2}\).
Answer:
Given, 2 tan^-1 (sin x) = tan^-1 (2 sec x)

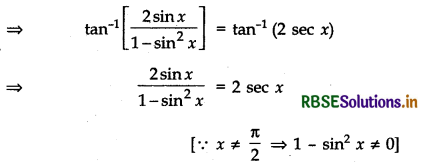
⇒ \(\frac{2 \sin x}{\cos ^2 x}\) = 2 sec x
⇒ \(\frac{2 \sin x}{\cos ^2 x}\) = 2 sec x
⇒ sin x = sec x. cos² x
⇒ sin x = \(\frac{1}{\cos x}\) . cos² x
⇒ sin x = cos x
⇒ tan x = 1 x = tan \(\frac{\pi}{4}\)
⇒ x = \(\frac{\pi}{4}\)
Thus, the required solution is x = \(\frac{\pi}{4}\).

(iii) tan^-1\(\left(\frac{x-2}{x-1}\right)\) + tan^-1\(\left(\frac{x+2}{x+1}\right)\) = \(\frac{\pi}{4}\).
Answer:

⇒ 2x² - 4 = 3
⇒ 2x² - 4 - 3 = 0
⇒ 2x² - 7 = 0
⇒ 2x² = 7
⇒ x² = \(\frac{7}{2}\)
⇒ x = ± \(\sqrt{\frac{7}{2}}\)
Thus, the required solution is x = ± \(\sqrt{\frac{7}{2}}\)

Question 5.
Prove that:
sin^-1 (2x\(\sqrt{1-x^2}\)) = 2 cos^-1 x, \(\frac{1}{\sqrt{2}}\) ≤ x ≤ 1.
Answer:
Let x = cos θ
θ = cos^-1 x
L.H.S. = sin^-1 (2x\(\sqrt{1-x^2}\))
= sin^-1(2 cos θ\(\sqrt{1-\cos ^2 \theta}\))
= sin^-1 (2 cos θ sin θ)
= sin^-1 (sin 2θ)
= 2θ = 2 cos^-1 x = R.H.S.
Hence Proved.

Question 6.
Prove that: tan^-1\(\frac{1}{4}\) + tan^-1\(\frac{2}{9}\) = \(\frac{1}{2}\)sin^-1\(\left(\frac{4}{5}\right)\)
Answer:

Question 7.
If (tan^-1 x)² + (cot^-1 x)² = \(\frac{5 \pi^2}{8}\), then find x,
Answer:
(tan^-1 x)² + (cot^-1 x)² = \(\frac{5 \pi^2}{8}\)
⇒ (tan^-1 x + cot^-1 x)² - 2 tan^-1 x cot^-1 x = \(\frac{5 \pi^2}{8}\)
⇒ 16(tan^-1 x)² - 8π(tan^-1 x) - 3π² = 0
(On solving by tan^-1 x + cot^-1 x = \(\frac{\pi}{2}\))
⇒ 16\(\left(\tan ^{-1} x-\frac{3 \pi}{4}\right) \left(\tan ^{-1} x+\frac{\pi}{4}\right)\) = 0
⇒ tan^-1 x = - \(\frac{\pi}{4}\) ⇒ x = - 1 [∵ - \(\frac{\pi}{2}\) < tan^-1 x < \(\frac{\pi}{2}\)]

Question 8.
Prove that:
\(\frac{9 \pi}{8}-\frac{9}{4} \sin ^{-1}=\left(\frac{1}{3}\right)=\frac{9}{4} \sin ^{-1}\left(\frac{2 \sqrt{2}}{3}\right)\)
Answer:

Question 9.
Find the value of sin^-1 \(\left[\sin \left(-\frac{17 \pi}{8}\right)\right]\).
Answer:
We have,

Multiple Choice Questions

Question 1.
The value of sin^-1(cos\(\frac{3 \pi}{5}\)) is:
(a) \(\frac{\pi}{10}\)
(b) \(\frac{3 \pi}{5}\)
(c) -\(\frac{\pi}{10}\)
(d) -\(\frac{3 \pi}{5}\)
Answer:
(c) -\(\frac{\pi}{10}\)

Question 2.
The value of tan[\(\frac{1}{2}\)cos^-1\(\left(\frac{\sqrt{5}}{3}\right)\)] is:
(a) \(\frac{3+\sqrt{5}}{2}\)
(b) \(\frac{3-\sqrt{5}}{2}\)
(c) \(\frac{-3+\sqrt{5}}{2}\)
(d) \(\frac{-3-\sqrt{5}}{2}\)
Answer:
(b) \(\frac{3-\sqrt{5}}{2}\)

Question 3.
sin[2 cos^-1\(\frac{3}{5}\)] =
(a) \(\frac{24}{25}\)
(b) \(\frac{2 \sqrt{6}}{5}\)
(c) \(\frac{4}{5}\)
(d) \(\frac{3}{10}\)
Answer:
(a) \(\frac{24}{25}\)

Question 4.
Cos^-1(cos x) = x is satisfied by:
(a) x ∈ R
(b) x ∈ [0, π]
(c) x ∈ [-1, 1]
(d) x ∈ (0, π)
Answer:
(b) x ∈ [0, π]

Question 5.
If sin^-1\(\frac{5}{x}\) + sin^-1\(\frac{12}{x}=\frac{\pi}{x}\), then x =
(a) 10
(b) 12
(c) 13
(d) 14
Answer:
(c) 13

 

Question 6.
If sin^-1x + sin^-1b + sin^-1c = π, then the value of a\(\sqrt{1-a^2}\) + b\(\sqrt{1-b^2}\) + c\(\sqrt{1-c^2}\) will be:
(a) 2abc
(b) a² + b² + c²
(c) ab + bc + ca
(d) 0
Answer:
(a) 2abc

Question 7.
If sin^-1x + sin^-1y + sin^-1z = \(\frac{\pi}{2}\), then x² + y² + z² + 2xyz is equal to:
(a) 0
(b) 1
(c) -1
(d) 2
Answer:
(b) 1

Question 8.
cos^-1\(\frac{a b+1}{a-b}\) + cos^-1\(\frac{b c+1}{b-c}\) + cot^-1\(\frac{c a+1}{c-a}\) =
(a) 0
(b) 2
(c) π/4
(d) -1
Answer:
(a) 0

Question 9.
If a, b, c are positive real numbers and
θ = tan^-1\(\sqrt{\frac{a(a+b+c)}{b c}}\) + tan^-1\(\sqrt{\frac{b(a+b+c)}{c a}}\) + tan^-1\(\sqrt{\frac{c(a+b+c)}{a b}}\), then tan θ =
(a) 0
(b) π/2
(c) π
(d) π/4
Answer:
(a) 0

Question 10.
The solution of sin^-1\(\frac{2 a}{1+a^2}\) - cos^-1\(\frac{1-b^2}{1+b^2}\) = tan^-1\(\frac{2 x}{1-x^2}\) IS:
(a) \(\frac{a-b}{1-a b}\)
(b) \(\frac{1+a b}{a-b}\)
(c) \(\frac{a b-1}{a+b}\)
(d) \(\frac{a-b}{1+a b}\)
Answer:
(d) \(\frac{a-b}{1+a b}\)

Question 11.
If tan^-1x + tan^-1y + tan^-1z = π, then x + y + z =
(a) xyz
(b) 0
(c) 3
(d) 2xyz
Answer:
(a) xyz

Question 12.
The value of cot^-1\(\left(\frac{\sqrt{1-\sin x}+\sqrt{1+\sin x}}{\sqrt{1-\sin x}-\sqrt{1+\sin x}}\right)\) is:
(a) π - x
(b) 2π - x
(c) \(\frac{x}{2}\)
(d) π - \(\frac{x}{2}\)
Answer:
(d) π - \(\frac{x}{2}\)

Question 13.
sec²(tan^-12) + cosec²(cot^-13) =
(a) 5
(b) 10
(c) 15
(d) 20
Answer:
(c) 15

Question 14.
sin{cot^-1(tan cos^-1x)} =
(a) x
(b) \(\sqrt{1-x^2}\)
(c) 1/x
(d) -x
Answer:
(a) x

Question 15.
If sin^-1 x + sin^-1y = \(\frac{2 \pi}{3}\), then cos^-1 x + cos^-1y =
(a) 2π/3
(b) π/3
(c) π/6
(d) π
Answer:
(b) π/3

Fill in the Blanks

Question 1.
Sin^-1 is a function whose domain is ____________
Answer:
[-1, 1]

Question 2.
The branch with range [0, π] is called the principal value branch of the function ____________
Answer:
cos^-1

Question 3.
cosec^-1 can be defined as a function whose domain is ____________
Answer:
R - (-1, 1)

Question 4.
The branch with range [0, π] - \(\left\{\frac{\pi}{2}\right\}\) is called the principal value branch of the function ____________
Answer:
sec^-1

Question 5.
If sin(sin^-1\(\frac{1}{5}\) + cos^-1x) = 1, then the value of x is ____________
Answer:\(\frac{1}{5}\)

True/False

Question 1.
If tan^-1x + tan^-1y = \(\frac{\pi}{4}\); xy < 1, then the value of x + y + xy is 1.
Answer:
True

Question 2.
The value of tan (2tan^-1\(\frac{1}{5}\)) is \(\frac{12}{5}\).
Answer:
False

Question 3.
The value of tan^-1[2sin(2cos^-1\(\frac{\sqrt{3}}{2}\))] is \(\frac{\pi}{3}\).
Answer:
True

Question 4.
Write the value of cos^-1(\(\frac{1}{2}\)) - 2sin^-1(-\(\frac{1}{2}\)) is \(\frac{2 \pi}{3}\).
Answer:
True

Question 5.
The value of tan^-1(tan \(\frac{3 \pi}{3}\)) is\( \frac{\pi}{3}\).
Answer:
False