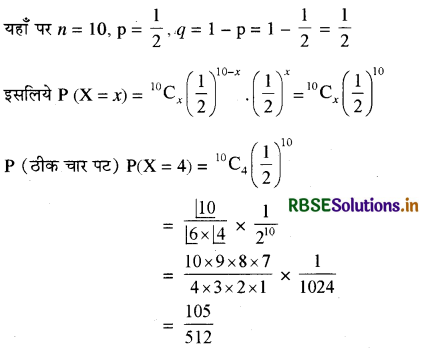RBSE Class 12 Maths Important Questions Chapter 13 प्रायिकता

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 13 प्रायिकता Important Questions and Answers.

RBSE Class 12 Maths Chapter 13 Important Questions प्रायिकता

अन्य महत्त्वपूर्ण प्रश्न

प्रश्न 1.
एक थैले में 4 सफेद व 3 काली गेंदें हैं। दूसरे थैले में 3 सफेद व 4 काली गेंदें हैं। यदि एक गेंद उठाई जाये और वह काली निकले तो इस काली गेंद के दूसरे थैले से निकलने की प्रायिकता है
(A) \(\frac{1}{7}\)
(B) \(\frac{2}{7}\)
(C) \(\frac{3}{7}\)
(D) \(\frac{4}{7}\)
उत्तर:
(D) \(\frac{4}{7}\)

हल:
माना E₁ = पहले थैले से गेंद निकालने की घटना
E₂ = दूसरे थैले से गेंद निकालने की घटना
∴ P(E₁) = \(\frac{1}{2}\) तथा P(E₂) = \(\frac{1}{2}\)
पहले थैले में कुल गेंदे
= 4 + 3 = 7
और काली गेंदों की संख्या
= 3
इसलिए पहले थैले से एक काली गेंद निकालने की प्रायिकता
P\(\left(\frac{A}{E_1}\right)=\frac{{ }^3 C_1}{{ }^7 C_1}=\frac{3}{7}\)
दूसरे थैले से एक काली गेंद निकालने की प्रायिकता

= \(\frac{4}{7}\)
अतः सही विकल्प (D) है।

प्रश्न 2.
यदि दो निष्पक्ष पासों की एक जोड़ी को एक बार फेंका जाता है तो दोनों पासों पर अंकों का योग 5 होने की प्रायिकता है
(A) \(\frac{5}{36}\)
(B) \(\frac{1}{12}\)
(C) \(\frac{1}{18}\)
(D) \(\frac{1}{9}\)
उत्तर:
(D) \(\frac{1}{9}\)

हल:
दोनों पासों को एक साथ फेंकने पर कुल तरीके = 6 × 6
अंकों का योग 5 निम्न प्रकार से प्राप्त हो सकता है = 36
{(1,4), (4,1), (2,3), (3,2)} = 4

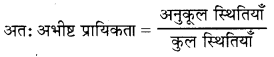
= \(\frac{4}{36}\) = \(\frac{1}{9}\)
अतः सही विकल्प (D) है।

प्रश्न 3.
अंकों 1, 2, 3, 4, 5, 6, 7 में से 4 अंक लिये गये हैं। इन चारों अंकों का योग 12 से कम होने की प्रायिकता है-
(A) \(\frac{3}{35}\)
(B) \(\frac{4}{35}\)
(C) \(\frac{2}{35}\)
(D) \(\frac{1}{35}\)
उत्तर:
(C) \(\frac{2}{35}\)

हल:
दिये गये अंकों में से 4 अंक लेने के कुल तरीके
= 7 × 6 × 5 × 4
चारों अंकों को जिनका योग 12 से कम है उनके लेने के कुल तरीके
{1,2,3,4} व {1,2,3,5}

अतः सही विकल्प (C) है।

प्रश्न 4.
एक ताश की गड्डी में 4 इक्के, 4 बादशाह, 4 बेगम तथा 4 गुलाम हैं। दो पत्ते यादृच्छया खींचे जाते हैं। उनमें कम से कम एक इक्का आने की प्रायिकता है
(A) \(\frac{1}{5}\)
(B) \(\frac{3}{16}\)
(C) \(\frac{9}{20}\)
(D) \(\frac{1}{9}\)
उत्तर:
(C) \(\frac{9}{20}\)

हल:
ताश की गड्डी में कुल पत्ते = 4 + 4 + 4 + 4 = 16
दो पत्ते यादृच्छया खींचने की विधियाँ = ¹⁶C₂
कम से कम एक इक्का आने की प्रायिकता

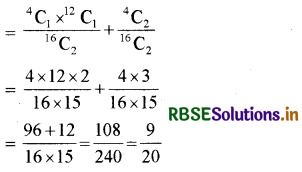
अतः सही विकल्प (C) है।

प्रश्न 5.
दो घटनायें A व B इस प्रकार हैं कि P(A) = \(\frac{1}{4}\), P(A/B) = \(\frac{1}{2}\) तथा P(B/A) = \(\frac{2}{3}\), तब P(B) का मान है-
(A) \(\frac{1}{6}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{1}{2}\)
उत्तर:
(B) \(\frac{1}{3}\)

हल:
हम जानते हैं कि

अतः सही विकल्प (B) है।

प्रश्न 6.
एक पासा फेंका जाता है। माना A, 3 से अधिक संख्या प्राप्त करने की घटना है तथा B, 5 से कम संख्या प्राप्त करने की घटना है तब P(A ∪ B) का मान है-
(A) \(\frac{3}{5}\)
(B) 10
(C) 1
(D) \(\frac{2}{5}\)
उत्तर:
(C) 1

हल:
प्रश्नानुसार, A = {4, 5, 6}
तथा B = {1, 2, 3, 4}, A ∩ B = {4}
इसलिए n(A) = 3, n(B) = 4, n(A ∩ B) = 1
इसलिए n(S) = 6
इसलिए P(A) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
P(B) = \(\frac{4}{6}\) = \(\frac{2}{3}\)
P(A ∩ B) = \(\frac{1}{6}\)
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)

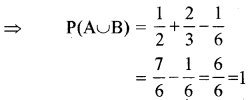
इसलिए P(A ∪ B) = 1
अतः सही विकल्प (C) है।

प्रश्न 7.
A के सच बोलने की प्रायिकता \(\frac{4}{5}\) है जबकि B के लिये \(\frac{3}{4}\) है जब वे एक तथ्य पर बोलते हैं तो विरोधाभास होने की प्रायिकता है
(A) \(\frac{7}{20}\)
(B) \(\frac{1}{5}\)
(C) \(\frac{3}{20}\)
(D) \(\frac{4}{5}\)
उत्तर:
(A) \(\frac{7}{20}\)

हल:

अतः सही विकल्प (A) है।

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि P(A) = \(\frac{5}{7}\), तथा P(B) = 0, तो क्या हम P\(\left(\frac{A}{B}\right)\) निकाल सकते हैं? यदि हाँ तो इसका मान निकालिए।
हल:

प्रश्न 2.
बताएँ कि एक प्रतिदर्श समष्टि का विभाजन एक है या एक से अधिक?
हल:
प्रतिदर्श समष्टि का विभाजन एक से अधिक हो सकता है।

प्रश्न 3.
बेज़ प्रमेय का दूसरा नाम क्या है?
हल:
बेज़ प्रमेय को कारणों की प्रायिकता का सूत्र भी कहते हैं या प्रतिलोम प्रायिकता-प्रमेय भी कहते हैं।

प्रश्न 4.
निम्नलिखित क्या X का प्रायिकता बंटन है?

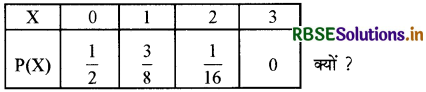
हल:
क्योंकि ΣP(X) = \(\frac{1}{2}\) + \(\frac{3}{8}\) + \(\frac{1}{16}\) + 0 = \(\frac{8+6+1}{16}\) = \(\frac{15}{16}\) ≠ 1
अतः X प्रायिकता बंटन नहीं है। चूंकि सभी प्रायिकताओं का योग एक होना चाहिए।

प्रश्न 5.
यदि A और B दो स्वतंत्र घटनाएँ हैं, जहाँ P(A) = \(\frac{1}{2}\), P (A ∪ B) = \(\frac{3}{5}\) तथा P(B) = x तब x का मान ज्ञात कीजिए।
हल:
क्योंकि A और B दो स्वतंत्र घटनाएँ हैं।
अतः P (A ∪ B) = P(A) + P(B) - P(A ∩ B)
या P(A ∪ B) = P(A) + P(B) - P(A). P(B)

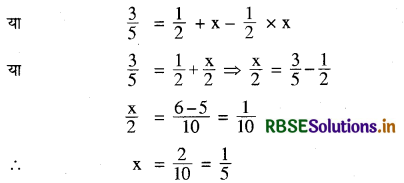
प्रश्न 6.
52 पत्तों की एक गड्डी में से यादृच्छया एक के बाद एक बिना प्रतिस्थापित किए दो पत्ते निकाले गए। दोनों पत्तों के लाल रंग का होने की प्रायिकता ज्ञात कीजिए।
हल:
प्रश्नानुसार ताश की गड्डी में कुल पत्ते = 52
लाल रंग के पत्तों की संख्या = 26
लाल रंग का एक पत्ता निकालने की प्रायिकता :
P(A) = \(\frac{26}{52}\) = \(\frac{1}{2}\)
एक पत्ता निकालने के बाद गड्डी में 51 पत्ते हैं जिनमें 25 लाल पत्ते हैं।
∴ दूसरा लाल पत्ता निकालने की प्रायिकता = \(\frac{25}{51}\)
अर्थात् बिना प्रतिस्थापन किये दो लाल पत्ते निकालने की प्रायिकता
= \(\frac{1}{2} \times \frac{25}{51}\)
= \(\frac{25}{102}\)

निबन्धात्मक प्रश्न

प्रश्न 1.
तीन थैलों में रंगीन गेंदें निम्न सारणी में दर्शाये गये तरह से आबंटित की गई हैं

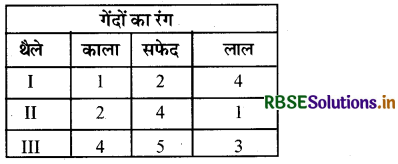
एक थैले को यादृच्छया चुना गया और फिर उसमें से दो गेंदें निकाली गईं। यदि गेंद का रंग काला और लाल है तो इसकी क्या प्रायिकता है कि गेंद को थैला I से निकाला गया है?
हल:
माना E₁, E₂ और E₃ थैला I, II और III चुनने की घटना है।
∴ P(E₁) = P(E₂) = P(E₃) = \(\frac{1}{3}\)
माना E घटना लाल और काली गेंद खींचने की है

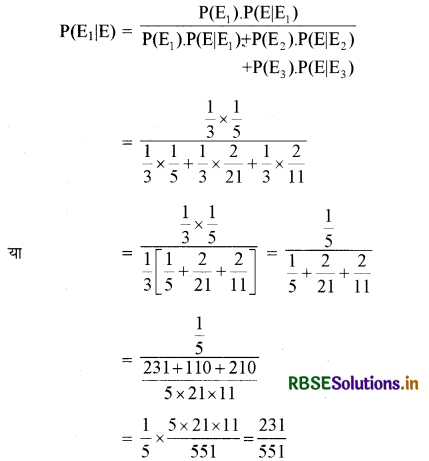
बेज़-प्रमेय द्वारा (By Bayes' Theorem)
अभीष्ट प्रायिकता

प्रश्न 2.
यदि एक निष्पक्ष सिक्के को 20 बार उछाला जाता है और मान लीजिये कि n बार शीर्ष दिखाई देता है, तो n के विषम होने की प्रायिकता का मान ज्ञात कीजिए।
हल:
सिक्के के एक उछाल में शीर्ष आने की प्रायिकता
P = \(\frac{1}{2}\)
सिक्के के एक उछाल में शीर्ष न आने की प्रायिकता
q = 1 - \(\frac{1}{2}\) = \(\frac{1}{2}\)
विषम बार शीर्ष आने की प्रायिकता

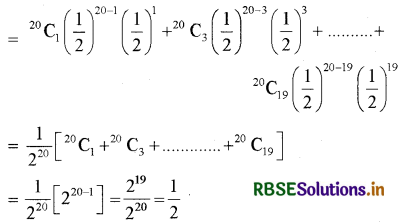
प्रश्न 3.
एक थैले में 4 लाल और 6 काली गेंदें हैं और एक अन्य थैले में 3 लाल और 5 काली गेंदें हैं।दोनों थैलों में से एक को यादृच्छया चुना जाता है और उसमें से एक गेंद निकाली जाती है जो कि लाल है। इस बात की क्या प्रायिकता है कि गेंद दूसरे थैले से निकाली गई है?
हल:
थैले I का चयन होना को E₁ से और थैले II के चयन को E₂ मानने पर माना कि लाल रंग की गेंद निकालने की घटना को A से निरूपित करते हैं।
तब P(E₁) = P(E₂) = \(\frac{1}{2}\)
साथ ही निकालना) P(A | E₁) = P (थैले I में से लाल रंग की गेंद और निकालना)
= \(\frac{4}{10}\) = \(\frac{2}{5}\)
और P(A | E₂) = P (थैले II में से लाल रंग की गेंद निकालना)
= \(\frac{3}{8}\)
अब थैले II में से गेंद निकालने की प्रायिकता जबकि यह ज्ञात है कि वह लाल रंग की है = P(E₂ | A), बेज प्रमेय द्वारा

प्रश्न 4.
15 बल्बों में से 5 बल्ब टियुक्त हैं। 4 बल्बों को निकाला जाता है। एक के बाद एक निकालकर पुनः डाला जाता है। त्रुटियुक्त बल्बों के प्रायिकता वितरण को ज्ञात कीजिए। विघटन का माध्य भी ज्ञात कीजिए।
हल:
15 में से 5 बल्ब त्रुटियुक्त हैं और 10 सही बल्ब हैं।
p (त्रुटियुक्त बल्ब) = \(\frac{5}{15}\) = \(\frac{1}{3}\)
q (सही बल्ब) = \(\frac{2}{3}\)
x = त्रुटियुक्त बल्ब का यादृच्छिक चर जिसके मान
0, 1, 2, 3 या 4 होगा।
तब p (x = r) = ⁿC_r (p)^r (q)^{n - r}

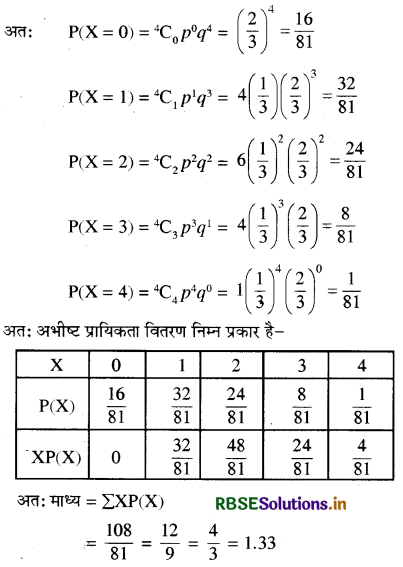
प्रश्न 5.
मान लीजिये कि कोई लड़की एक पासा उछालती है। यदि उसे 1 या 2 की संख्या प्राप्त होती है, तो वह एक सिक्के को तीन बार उछालती है और 'पट' की संख्या नोट करती है। यदि उसे 3,4, 5 या 6 की संख्या प्राप्त होती है, तो वह एक सिक्के को एक बार उछालती है और यह नोट करती है कि उस पर चित' या पट' प्राप्त हआ।यदि उसे ठीक एक पट' प्राप्त होता है, तो उसके द्वारा उछाले गये पासे पर 3,4,5 या 6 प्राप्त होने की प्रायिकता क्या है?
हल:
एक पासे को उछालने से 6 (1, 2, 3, 4, 5, 6) परिणाम प्राप्त होते
माना कि घटना E₁ : 1 या 2 प्राप्त होना तथा
E₂ : 3, 4, 5, 6 का प्राप्त होना
E : सिक्का/सिक्के उछालने पर पट प्राप्त होना।
P (E₁) : P (पासा उछालने पर 1, 2 का प्राप्त होना)
= \(\frac{2}{6}\) = \(\frac{1}{3}\)
P(E₂) : P (पासा उछालने पर 3, 4, 5, 6 का प्राप्त होना)
= \(\frac{4}{6}\) = \(\frac{2}{3}\)
तीन सिक्के उछालने पर कुल परिणाम
{TTT, TTH, THT, HTT, HHT, HTH, THH, HHH} = 8 है।
एक पट प्राप्त होने के तरीके THH, HTH, HHT यानी 3 तरीके अर्थात् P(E/E₁) = P (पासा फेंकने पर 1, 2 प्राप्त होने तथा तीन सिक्के उछालने पर 1 पट का प्राप्त होना)
= \(\frac{3}{8}\)
जब एक सिक्का फेंका जाये तो पट आने की प्रायिकता = \(\frac{1}{2}\)
अर्थात् P(E/E₂) = P (पासा फेंकने पर 3, 4, 5, 6 आना तथा 1 सिक्के के फेंकने से पट आना)
= \(\frac{1}{2}\)
अतः बेज प्रमेय से

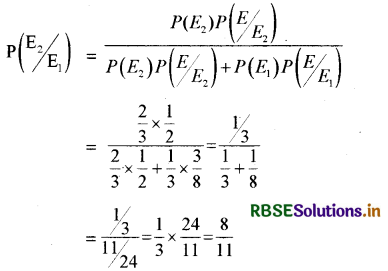
प्रश्न 6.
एक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। प्रायिकता ज्ञात कीजिए कि 5 कदम चलने के पश्चात्, यह व्यक्ति प्रारम्भिक बिन्दु से एक कदम दूर है।
हल:
माना आगे बढ़ने के कदमों की संख्या को x से प्रदर्शित किया गया है।
∴ X = 0, 1, 2, 3, 4 या 5 हो सकते हैं।
P = एक कदम आगे बढ़ने की प्रायिकता = \(\frac{4}{10}\) = \(\frac{2}{5}\)
q = एक कदम पीछे बढ़ने की प्रायिकता = \(\frac{6}{10}\) = \(\frac{3}{5}\)
यहाँ पर, P (X = r) = ⁿC_r p^r q^{n - r}
r= 0, 2, 3, ................ n
अभीष्ट प्रायिकता का मान
= P (तीन कदम आगे बढ़ना और 2 कदम पीछे हटना या 2 कदम आगे बढ़ना और तीन कदम पीछे हटना)
= P (X = 3) + P (X = 2)

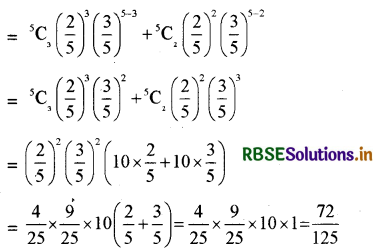
प्रश्न 7.
एक कलश में 5 लाल व 2 काली गेंदें हैं।दो गेंदें बिना प्रतिस्थापना के यादृच्छया निकाली गई। मान लीजिए कि x निकाली गई काली गेंदों की संख्या को व्यक्त करता है। X के सम्भावित मान क्या हैं? क्या X एक यादृच्छिक चर है? यदि हाँ, तो X का माध्य व प्रसरण ज्ञात कीजिए।
हल:
काली गेंदों की संख्या 2 है।
X के मान 0, 1 और 2 हो सकते हैं। इनके संगत प्रायिकता P(x) ज्ञात की जा सकती है इसलिये X एक यादृच्छिक चर है।

प्रश्न 8.
एक पासे को दो बार उछाला गया और प्रकट हुई संख्याओं का योग 7 पाया गया।संख्या 3 के न्यूनतम एक बार प्रकट होने की सप्रतिबंध प्रायिकता ज्ञात कीजिए।
हल:
मान लीजिये E घटना 'संख्या 3 का न्यूनतम एक बार प्रकट होना' और F घटना दोनों पासों पर प्रकट संख्याओं का योग 7 होने' को दर्शाते है।
तब E = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1, 3), (2, 3), (4, 3), (5, 3), (6, 3)}
और F = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
हम जानते हैं कि P(E) = \(\frac{11}{36}\), P(F) = \(\frac{6}{36}\)
तथा E ∩ F = {(3, 4), (4, 3)}
अब P(E ∩ F) = \(\frac{2}{36}\)
अत: वांछित प्रायिकता

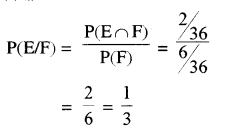
प्रश्न 9.
यदि एक न्याय्य सिक्के को 10 बार उछाला जाता है, ठीक चार पट आने की प्रायिकता ज्ञात कीजिए।
हल:
एक सिक्के को बार-बार उछालना बरनौली परीक्षण होते हैं। 10 परीक्षणों में पट आने की संख्या को X मान लीजिये । स्पष्टतया X बंटन n = 10 और p = \(\frac{1}{2}\) वाला द्विपद बंटन है।
इसलिये P(X = x) = ⁿC_x q^{n - x} p^x