RBSE Class 12 Maths Important Questions Chapter 13 Probability

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 13 Probability Important Questions and Answers.

RBSE Class 12 Maths Chapter 13 Important Questions Probability

Question 1.
If P(Ā) = 0.7, P(B) = 0.7 and P\(\left(\frac{B}{A}\right)\) = 0.5 then find P(A/B) and P(A ∪ B).
Answer:
P(Ā) = 0.7
then P(A) = 1 - P(Ā) = 1 - 0.7 = 0.3
P(B) = 0.7
∴ P(B/A) = \(\frac{P(B \cap A)}{P(A)}\)
∴ P(B ∩ A) = P\(\left(\frac{B}{A}\right)\)
= 0.5 × 0.3 = 0.15
Now P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
= 0.3 + 0.7 - 0.15
= 1 - 0.15 = 0.85
Thus P(A/B) = \(\frac{P(A \cap B)}{P(B)}\)
= \(\frac{0 \cdot 15}{0 \cdot 7}=\frac{15}{70}=\frac{3}{14}\)

Question 2.
In a college 25% student failed in maths, 15% in chemistry and 10% in maths and chemistry both. A student is randomly chosen:
(i) If he failed in chemistry what will be the probability that he will failed in mathematics.
(ii) If he failed in maths, then what will be probability that he will failed in chemistry?
(iii) What will be probability that he will failed in maths or chemistry?
Answer:
Let failing in mathematics is event E₁ and failing in chemistry is event E₂, then

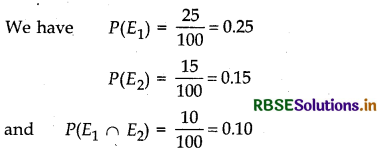
If one student is randomly selected, then
(i) Probability of failing in mathematics when failed in chemistry

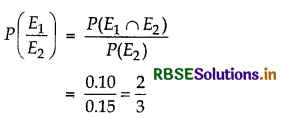
(ii) Probability of failing in chemistry, when he failed in mathematics

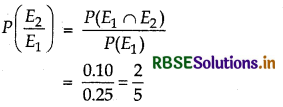
(iii) Probability that student failed in mathematics or chemistry
P(E₁ ∪ E₂) = P(E₁) + P(E₂) - P(E₁ ∩ E₂)
= 0.25 + 0.15 - 01.0
= 0.30

Question 3.
There are two black and two white balls in a box. One ball is drawn from the box without replacement. Answer the following:
(i) Find the probability of drawing second black ball when first withdrawn ball is white.
(ii) Find the probability of drawing second black ball when first withdrawn ball is black.
Answer:
Let E₁ = Event of withdrawing first white ball
E₂ = Event of withdrawing first black ball
E₃ = Event of withdrawing second black ball.
Black and white balls are B₁, B₂, W₁ and W₂ respectively, then
E₁ = {(W₁, W₂), (W₁, B₁), (W₁, B₂), (W₂, B₁), (W₂, B₂)}
∴ n(E₁) = 5
E₂ = {(B₁, B₂), (B₁, W₁), (B₂, W₂), (B₂, W₁), (B₂, W₂)}
∴ n(E₂) = 5
E₃ = (W₁, B₁), (W₁, B₂), (W₂, B₁), (W₂, B₂)
∴ n(E₃) = 4
Again E₂ ∩ E₃ = {(W₁, B₁), (W₁, B₂) (W₂, B₁), (W₂, B₂)
∴ n(E₁ ∩ E₂)=4
Again E₂ ∩ E₃ = {(B₁, B₂)}
∴ n(E₁ ∩ E₃) = 1

(i) Probability of drawing second black ball, when first ball is white,

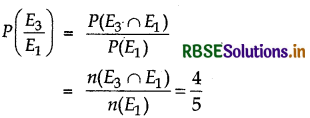
(ii) Probability of drawing second black ball, when first ball is black,

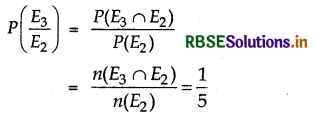
Question 4.
If A and B are two independent events such that P(Ā ∩ B) = \(\frac{2}{15}\) and P(A ∩ B̄) = \(\frac{1}{6}\) then find P(A) and P(B).
Answer:
Given, A and B are two independent events with P(Ā ∩ B) = \(\frac{2}{15}\) and P(A ∩ B̄) = \(\frac{1}{6}\).
We. know that, if A and B are independent, then Ā, B and A, B̄ are independent events.

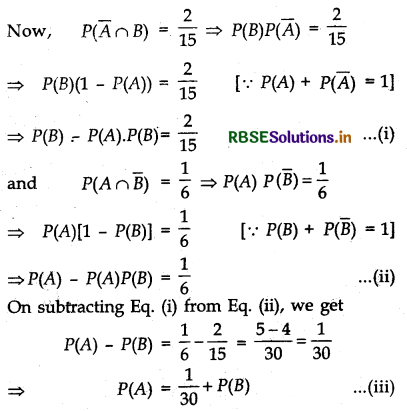
Now, on substituting this value in Eq. (i), we get
P(B) - (\(\frac{1}{30}\) + P(B)) P(B) = \(\frac{2}{15}\)
Let P(B) = x, then
⇒ x - (\(\frac{1}{30}\) + x).x = \(\frac{2}{15}\)
⇒ 30x - (1 + 30x)x = 4
⇒ 30x - x - 30x² = 4
⇒ 30x² - 29x + 4 = 0
⇒ (6x - 1) (5x - 4) = 0 ⇒ x = \(\frac{1}{6}\) or x = \(\frac{4}{5}\)
⇒ P(B) = \(\frac{1}{6}\) or P(B) = \(\frac{4}{5}\) [put x = P(B)]

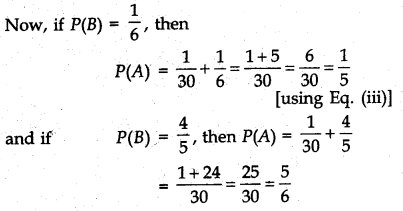
Question 5.
P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree in stating the same fact? Do you think, when they agree, means both are speaking truth?
Answer:
Let P_T: Event that P speaks truth
and Q_T: Event that Q speaks truth.

∴ Percentage of P(A and B are agree to each other)
= \(\frac{62}{100}\) × 100 = 62%
No, agree does not mean that they are speaking truth.

Question 6.
A and B throw a pair of dice alternately. A wins the game, if he gets a total of 7 and B wins the game, if he gets a total of 10. if A starts the game, then find the probability that B wins.
Answer:
Here, n(S) 6 × 6 = 36
Let A = Event of getting a sum of 7 in pair of dice
{(1, 6), (2, 5), (3, 4), (6, 1), (5, 2), (4, 3)}
⇒ n(A) = 6
and B = Event of getting a sum of 10 in pair of dice
= {(4, 6), (5, 5), (6, 4)) ⇒ n(B) = 3

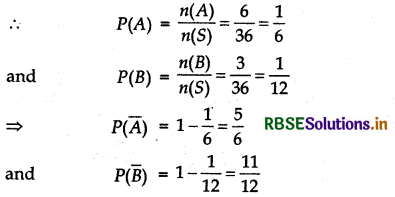
Now, the probability that if A start the game, then B wins
P(B wins) = P(A̅ ∩ B) + P(A̅ ∩ B̅ ∩ A̅ ∩ B̅) + P(A̅ ∩ B̅ ∩ A̅ ∩ B̅ ∩ A̅ ∩ B) + .......
= P(A̅) P(B) + P(A̅) P(B̅) P(A̅) P(B) + P(A̅) P(B̅) P(A̅) P(B̅) P(A̅) P(B) + .............
[∵ events are independent]

Question 7.
In a class, 5% of boys and 10% of girls have an IQ of more than 150. In the class, 60% are boys and rest are girls. If a student is selected at random and found to have an IQ of more than 150,then find the probability that the student is a boy.
Answer:
Let us define the events as
E₁ : Boy is selected
E₂ : Girl is selected
A : The student has an IQ of more than 150 students.
Now, P(E₁) = 60% = \(\frac{60}{100}\)
Now, P(E₂) = 40% = \(\frac{40}{100}\)
[∵ in the class 60% students are boys, so 40% are girls, given]
Now, P(A/E₁) = Probability that boys has an IQ of more than 150
= 5% = \(\frac{5}{100}\)
and P(A/E₂) = Probability that girls has an IQ of more than 150 = 10% = \(\frac{10}{100}\)
The probability that the selected boy having IQ more than 150 is

Hence, the required probability is 3/7.

Question 8.
A man is known to speak the truth 3 out of 5 times. He throws a die and reports that it is ‘1’. Find the probability that it is actually 1.
Answer:
Let E₁ = Event that 1 occurs in a die
E₂ = Event that 1 does not occur in a die
A = Event that the man reports that 1 occur in a die
Then, P(E₁) = \(\frac{1}{6}\) and P(E₂) = \(\frac{5}{6}\)
∴ P(man reports that I occurs when 1 occur)
= P\(\left(\frac{A}{E_1}\right)=\frac{3}{5}\)
and P (man reports that 1 occur but 1 does not occur)
= P\(\left(\frac{A}{E_2}\right)=\frac{2}{5}\)
Thus, by Bayes theorem, we get
P(get actually 1 when he reports that 1 occur)

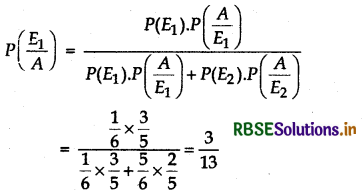
Question 9.
A card from a pack of 52 playing cards is lost. From the remaining cards of the pack three cards are drawn at random (without replacement) and are found to be all spades. Find the probability of the lost card being a spade.
Answer:
Let us define the following events:
E₁ = lost card is a spade card
E₂ = lost card is not a spade card
A = drawn cards are spade cards
Then,

Question 10.
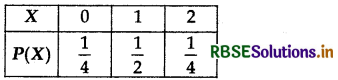
Find the probability distribution of X, the number of heads in a simultaneous toss of two coins.
Answer:
When two corns are tossed, there may be 1 head, 2 heads or no head at all. Thus, the possible values of X are 0, 1, 2.
Now, P(X = 0) = P (Getting no head) = P(TT) = \(\frac{1}{4}\)
P(X = 1) = P (Getting one head) = P(HT or TH) = \(\frac{2}{4}\) = \(\frac{1}{2}\)
P(X = 2) = P (Getting two heads) = P(HH) = \(\frac{1}{4}\)
Thus, the required probability distribution of X is

Question 11.
Two numbers are selected at random (with out replacement) from the first five positive integers. Let X denotes the larger of the two numbers obtained. Find the mean and variance of X.
Answer:
Total number of possibles outcomes
= ⁵P₂ = \(\frac{5 !}{3 !}\) = 5 × 4 = 20
Here, X denotes the larger of two numbers obtained.
∴ X can take values 2, 3, 4 and 5.
Now, P(X = 2) = P (getting (1, 2) or (2, 1))
= \(\frac{2}{20}=\frac{1}{10}\)
P(X = 3) = P (getting (1, 3) or (3, 1) or (2, 3) or (3, 2))
= \(\frac{4}{20}=\frac{2}{10}\)
P(X = 4) = P(getting (1, 4) or (4, 1) or (2, 4) or (4, 2) or (3, 4) or (4, 3))
= \(\frac{6}{20}=\frac{3}{10}\)
and P(X = 5) = P (getting (1, 5) or (5, 1) or (2, 5) or (5, 2) or (3, 5) or (5, 3) or (4, 5) or (5, 4))
= \(\frac{8}{20}=\frac{4}{10}\)
Thus, the probability distribution of X is

Question 12.
There are 4 cards numbered 1, 3, 5 and 7, one number on one card. Two cards are drawn at random without replacement. Let X denotes the sum of the numbers on the two drawn cards. Find the mean and variance of X.
Answer:
Here, S = {(1, 3), (1, 5), (1, 7), (3, 1) (3, 5), (3, 7), (5, 1), (5, 3), (5, 7), (7, 1), (7, 3), (7, 5))
⇒ n(S) = 12
Let random variance X denotes the sum of the numbers on two cards drawn. So, the random variables X may have values 4, 6, 8, 10 and 12.

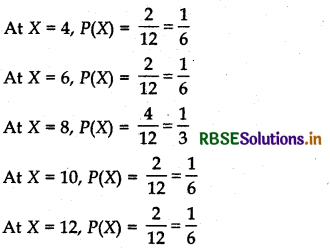
Therefore, the required probability distribution is as follows:

Question 13.
A pair of dice is thrown 4 times. What will be the probability to get maximum two 7?
Answer:
In throwing a pair of dice, number of sample points in space:
n(S) = 6 × 6 = 36
E event to get 7
= ((6, 1), (1, 6), (5, 2), (2, 5) (4, 3), (3, 4)
n(E) = 6
∴ Probability to get 7
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)
P = \(\frac{1}{6}\) ⇒ q = 1 - \(\frac{1}{6}\) = \(\frac{5}{6}\)
In throwing four times, corresponding probability distribution
= (q + p)ⁿ = \(\left(\frac{5}{6}+\frac{1}{6}\right)^4\)
Thus, probability to get maximum two 7 = Probability to not get single 7+ Probability to get one 7+ Probability to get two 7

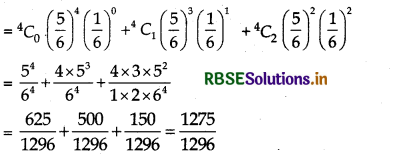
Question 14.
From well shuffled pack of 52 cards, 4 cards are drawn one by one and drawn cards are replaced. Find the probability that:
(i) all cards are of heart
(ii) 3 cards are of heart
(iii) no one card of heart
Answer:
Probability to get card of heart
P = \(\frac{13}{52}=\frac{1}{4}\)
∴ Probability not to get card of heart
q = 1 - p = 1 - \(\frac{1}{4}=\frac{3}{4}\)
If random variable X denotes number of cards of heart, then by formula P(X = r) = ⁿC_r p^r q^{n - r} where n = 4
(i) P(X = 4) = ⁴C₄ p⁴ q^{4 - 4}
= 1 × \(\left(\frac{1}{4}\right)^4 \times\left(\frac{3}{4}\right)^0=\left(\frac{1}{4}\right)^4\)

(ii) P(X = 3) = ⁴C₃ p⁴ q^{4 - 3}
= 4 × \(\left(\frac{1}{4}\right)^3 \times\left(\frac{3}{4}\right)^1 = 12\left(\frac{1}{4}\right)^4\)

(iii) P(X = 0) = ⁴C₀ p⁰ q^{4 - 0}
= 1 × \(\left(\frac{1}{4}\right)^0 \times\left(\frac{3}{4}\right)^4=\left(\frac{3}{4}\right)^4\)

Question 15.
How many times a coin is tossed so that probability to get at least one tail is 87.5%?
Answer:
Probability to get tail in one throw = \(\frac{1}{2}\)
and probability to get head = \(\frac{1}{2}\)
∴ Probability distribution is \(\left(\frac{1}{2}+\frac{1}{2}\right)^n\)
Probability to get at least one tail
= P(1) + P(2) + P(3) + ........ + P(n)

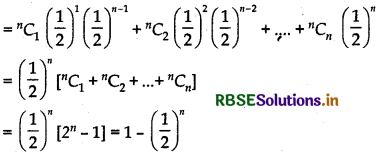
According to question,
1 - \(\left(\frac{1}{2}\right)^n\) = 0.875 = 1 - 0.125
⇒ \(\left(\frac{1}{2}\right)^n\) = 0.125 = (0.5)³ = \(\left(\frac{1}{2}\right)^3\)
∴ n = 3 ⇒ will be tossed 3 times.
Thus, coin should be tossed three times.

Multiple Choice Questions

Question 1.
A card is picked at random from a pack of 52 playing cards. Given that the picked card is a queen. the probability of this card to be a card of spade is:
(a) \(\frac{1}{3}\)
(b) \(\frac{4}{13}\)
(c) \(\frac{1}{4}\)
(d) \(\frac{1}{2}\)
Answer:
(c) \(\frac{1}{4}\)

Question 2.
A die is thrown once. Let A be the event that the number obtained is greater than 3. Let B be the event that the number obtained is less than 5. Then P(A ∪ B) is:
(a) \(\frac{2}{5}\)
(b) \(\frac{3}{5}\)
(c) 0
(d) 1
Answer:
(d) 1

Question 3.
From the set {1, 2, 3, 4, 5}, two numbers a and b (a ≠ b) are chosen at random. The probability that \(\frac{a}{b}\) is an integer, is:
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{3}{5}\)
Answer:
(c) \(\frac{1}{2}\)

Question 4.
A bag contains 3 white, 4 black and 2 red balls, if 2 balls are drawn at random (without replacement), then the probability that both the balls are white, is:
(a) \(\frac{1}{18}\)
(b) \(\frac{1}{36}\)
(c) \(\frac{1}{12}\)
(d) \(\frac{1}{24}\)
Answer:
(c) \(\frac{1}{12}\)

Question 5.
Three dice are thrown simultaneously. The probability of obtaining a total score of 5 is:
(a) \(\frac{5}{216}\)
(b) \(\frac{1}{6}\)
(c) \(\frac{1}{36}\)
(d) \(\frac{1}{49}\)
Answer:
(c) \(\frac{1}{36}\)

Question 6.
A box contains 24 identical balls of which 12 are white and 12 are black. The balls are drawn at random from the box one at a time with replacement. The probability that a white ball is drawn for the 4th time on the 7th draw is:
(a) \(\frac{5}{64}\)
(b) \(\frac{27}{32}\)
(c) \(\frac{5}{32}\)
(d) \(\frac{1}{2}\)
Answer:
(c) \(\frac{5}{32}\)

Question 7.
A fair coin is tossed a fixed number of times. If the probability of getting seven heads is equal to that of getting nine heads, the probability of getting two heads is:
(a) 15/2⁸
(b) \(\frac{2}{15}\)
(c) 15/2¹³
(d) none of these
Answer:
(c) 15/2¹³

Question 8.
A fair die is tossed 180 times, the S.D. of the number of sixes, is:
(a) √30
(b) 5
(c) 25
(d) 30
Answer:
(b) 5

Question 9.
If the mean and variance of a binomial variate X are 2 and 1 respectively, then the probability that X takes a value greater than 1 is:
(a) \(\frac{11}{16}\)
(b) \(\frac{4}{5}\)
(c) \(\frac{7}{8}\)
(d) \(\frac{15}{16}\)
Answer:
(a) \(\frac{11}{16}\)

Question 10.
The parameters n and p of BD. are 16 and \(\frac{1}{2}\) respectively, then its S.D. is equal to:
(a) 2
(b) √2
(c) 2√2
(d) 4
Answer:
(c) 2√2

Fill in the Blanks

Question 1.
Two or more events are said to be ................ exclusive, if they cannot both occur at the same time.
Answer:
mutually

Question 2.
Probability of an impossible event is ......................
Answer:
zero

Question 3.
If two events are independent, then their complements are also ............... events.
Answer:
independent

Question 4.
The mean of the number obtained on throwing a die having written 1 on three faces, 2 on two faces and 5 on one face is .......................
Answer:
2

Question 5.
Two cards are drawn at random and without replacement from a pack of 52 playing cards. The probability that both the cards are black, is .....................
Answer:
\(\frac{25}{102}\)

True / False

Question 1.
If E and F be events of a sample space S of an experiment, then P(S/F) = P(F/F) = 1.
Answer:
True

Question 2.
The set (E ∪ F) denote the event that both E and F have occurred.
Answer:
True

Question 3.
If E and F are two events such that the probability of occurrence of one of them is not affected by occurrence of the other, then such events are called independent events.
Answer:
True

Question 4.
Terms ‘independent’ and ‘mutually exclusive’ have the same meaning.
Answer:
False