RBSE Class 12 Maths Important Questions Chapter 12 Linear Programming

Rajasthan Board RBSE Class 12 Maths Important Questions Chapter 12 Linear Programming Important Questions and Answers.

RBSE Class 12 Maths Chapter 12 Important Questions Linear Programming

Question 1.
By graphical method, solve the following linear programming problem for minimization.
Objective function
Z = 5x + 7y
Constraints 2x + y ≥ 8
x + 2y ≥ 10
x ≥ 0, y ≥ 0
Answer:
Graph under the given constraints is:

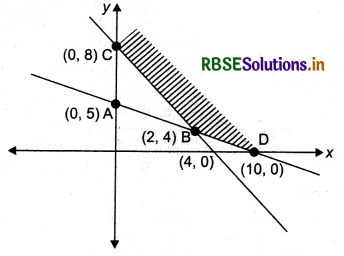
Shaded region is the required region.
Now, Z = 5x + 7y

Corner Point	Z = 5x + 7y
D(10, 0)	ZD = 50
C(0, 8)	ZC = 56
B(2, 4)	ZB = 38

∵ Z_min = 38, when x = 2 and y = 4

Question 2.
Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below:
2x + 4y ≤ 8; 3x + y ≤ 6
x + y ≤ 4; x ≥ 0, y ≥ 0.
Answer:
We have the following LPP:
Maximise, Z = 2x + 5y
Subject to the constraints
2x + 4y ≤ 8 or x + 2y ≤ 4
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0
Now, considering the inequations as equations, we get
x + 2y = 4 ........... (i)
3x + y = 6 ........... (ii)
and x + y = 4 ............. (iii)
Table for line x + 2y = 4 is

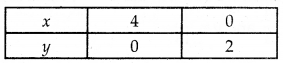
So, the line passes through (4, 0) and (0, 2).
On putting (0,0) in the inequality x + 2y ≤ 4 we get
0 + 0 ≤ 4 [which is true]
So, the half plane is towards the origin.
Table for line 3x + y = 6 is

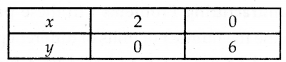
So, the line passes through (2, 0) and (0, 6).
On putting (0, 0) in the inequality 3x + y ≤ 6, we get
0 + 0 ≤ 6 [which is true]
So, the half plane is towards the origin
Table for line x + y = 4 is

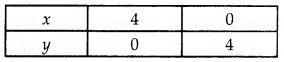
On putting (0, 0) in the inequality x + y ≤ 4, we get
0 + 0 ≤ 4 [which is true]
So, the half plane is towards the origin.
Also, x ≥ 0, y ≥ 0, so the region lies in the 1st quadrant.
The graphical representation of the above system of inequations is given below:

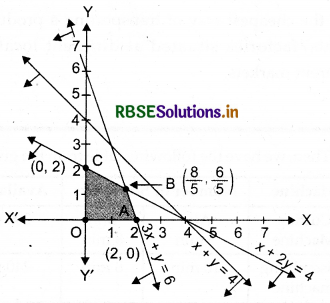
Clearly, the feasible region is QABCO.
The intersection point of lines (1) and (ii) is B\(\left(\frac{8}{5}, \frac{6}{5}\right)\).
Thus, the corner points are
O(0, 0), A(2, 0), B\(\left(\frac{8}{5}, \frac{6}{5}\right)\), C(0, 2).
The values of Z at corner points are as follows

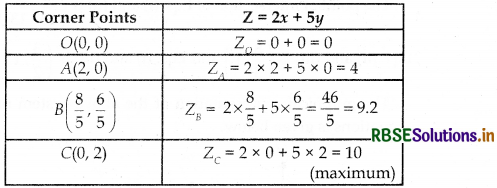
Hence, the maximum value of Z is 10.

Question 3.
Maximise Z = 8x + 9y subject to the constraints given below
2x + 3y ≤ 6
3x - 2y ≤ 6
y ≤ 1
x, y ≥ 0
Answer:
We have the following LPP, Maximise Z = 8x + 9y
Subject to the constraints
2x + 3y ≤ 6
3x - 2y ≤ 6
y ≤ 1 and x, y ≥ 0
Now, considering the inequations as equations, we get
2x + 3y = 6 ....... (i)
3x - 2y = 6 ....... (ii)
and y = 1 ......... (iii)
Table for line 2x + 3y = 6 is

So, it passes through the points (3, 0) and (0, 2).
On putting (0, 0) in the inequality 2x + 3y ≤ 6, we get
0 ≤ 6 [which is truel
So, the half plane is towards the origin.
Table for line 3x - 2y = 6 is

So, it passes through the points (2, 0) and (0, - 3).
On putting (0, 0) in the inequality 3x - 2y ≤ 6, we get
0 ≤ 6 [which is true]
So, the half plane is towards the origin.
The line y = 1 is perpendicular to Y-axis.
On putting (0, 0) in the inequality y ≤ 1, we get
0 ≤ 1 [which is true]
So, the half plane is towards the origin.
Also, x ≥ 0, y ≥ 0, so the feasible region lies in the first quadrant.
The point of intersection of Eqs. (i) and (ii) is \(\left(\frac{30}{13}, \frac{6}{13}\right)\), Eqs. (ii) and (iii) is \(\left(\frac{8}{3}, 1\right)\) and Eqs. (i)and (iii) is \(\left(\frac{3}{2}, 1\right)\)
The graphical representation of the above system of inequations is given below.

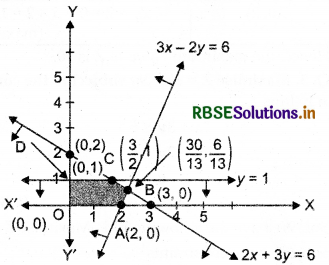
Clearly, feasible region is OABCDO. whose corner
points are O(0, 0), A(2, 0), B\(\left(\frac{30}{13}, \frac{6}{13}\right)\), C\(\left(\frac{3}{2}, 1\right)\) and D(0, 1).
The values of Z at corner points are as follows:

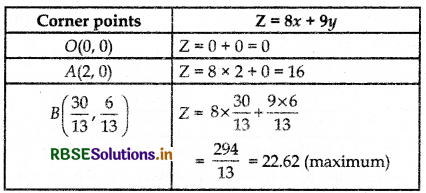
Question 4.
A company manufactures three kinds of calculators : A, B and C in its two factories I and II. The company has got an order for manufacturing at least 6400 calculators of kind A, 4000 of kind B and 4800 of kind C. The daily output of factory I is of 50 calculators of kind A, 50 calculators of kind B and 30 calculators of kind C. The daily output of factory II is of 40 calculators of kind A, 20 of kind B and 40 of kind C. The cost per day to run factory I is ₹ 12000 and of factory II is ₹ 15000. How many days do the two factories have to be in operation to produce the order with the minimum cost? Formulate this problem as an LPP and solve it graphically.
Answer:
Let factory (1) run for x days and factory (II) run for y days. Then,
Total cost (in ₹) = 12000x + 15000y
and our problem is to
Minimise Z = 12000x + 15000y
Subject to the constraints
50x + 40y ≥ 6400 or 5x + 4y ≥ 640
50x + 20y ≥ 4000 0r 5x + 2y ≥ 400
30x + 40y ≥ 4800 or 3x + 4y ≥ 480
Now, considering the inequations as equations, we get
5x + 4y = 640 ......... (i)
5x + 2y = 400 ......... (ii)
3x + 4y = 480 ........ (iii)
Table for line 5x + 4y = 640 is

So, the line passes through the points (128, 0) and (0, 160).
On putting (0, 0) in the inequality 5x + 4y ≥ 640, we get
0 + 0 ≥ 640 [which is false]
So, the half plane is away from the origin.
Table for line 5x + 2y = 400 is

So, the line passes through the points (80, 0) and (0, 200).
On putting (0, 0) in the inequality 5x + 2y ≥ 400, we get
0 + 0 ≥ 400 [which is false]
So, the half plane is away from the origin.
The graphical representations of the above system of inequations is given below:

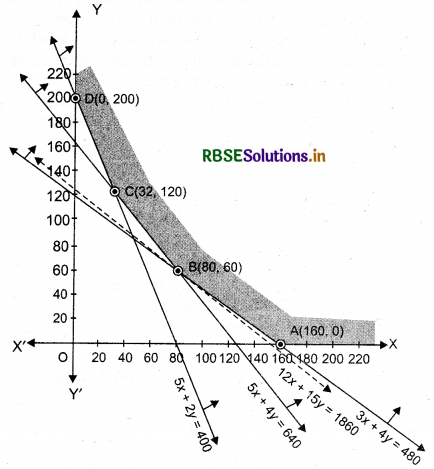
Clearly, feasible region is ABCD (shaded region), whose corner points are A(160, 0), B(80, 60), C(32, 120), and D(0, 200).
The values of Z at corner points are as follows

Corner Point	Z = 12000x + 15000y
A(10, 0)	ZA = 12000 × 160 + 0 = 1920000
B(0, 8)	ZB = 12000 × 80 + 15000 × 60 = 186000 (minium)
C(2, 4)	ZC = 12000 × 32 + 15000 × 120 = 2184000
D(0, 200)	ZD = 0 + 15000 × 200 = 3000000

In the table, we find that minimum value of Z is 1860000, occur at the point B(80, 60). But we can’t say that it is a minimum value of Z as region is unbounded.

Therefore, we have to draw the graph of the inequality 12000z + 15000 < 1860000
or 12x + 15y < 1860
From the figure, we see that the open half plane represented by 12x + 15y < 1860 has no point in common with feasible region. Thus, the minimum value of Z is ₹ 1860000 attained at the point (80, 60). Hence, factory (I) should run for 80 days and factory (II) should run for 60 days to get a minimum cost.

Question 5.
A manufacturer has employed 5 skilled men and 10 semi-skilled men and makes two models A and B of an article. The making of one item of model A requires 2 h work by a skilled man and 2 h work by a semi-skilled man. One item of model B requires 1 h by a skilled man and 3 h by a semi-killed man. No man is expected to work more than 8 h per day. The manufacturer profit on an item of model A is ₹ 15 and on an item of models B is ₹ 10. How many of items of each models should be made per day in order to maximize daily profit? Formulate the above LPP and solve it graphically and find the maximum profit.
Answer:
Let the company produce x items of A model and y items of B model.
Maximize profit is P = 15x + 10y
Now, total time spent by 5 skilled men = 2x + y and it should be less than 40.
∴ 2x + y ≤ 40 ...... (i)
Also, the total time spent by 10 semi-skilled men = 2x + 3y and it should be less than 80.
∴ 2x+3y ≤ 80 ...(ii)
Also, x ≥ 0 and y ≥ 0
Now, our problem is to maximise Z = 15x + 10y
Subject to the constraints
Zr + y ≤ 40
Zr + 3y ≤ 80
and x, y ≥ 0
Let us draw all the 4 lines on the graph and find the common area.

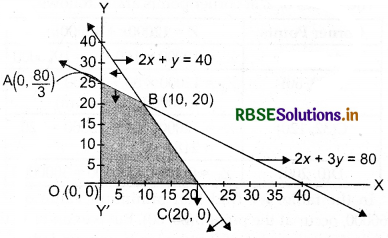
From above we get the region OABC is the feasible region with A(0, \(\frac{80}{3}\)), B(10, 20), C(20, 0), O(0, 0).
Since, the feasible is a bounded region, we can check the profit function at all the vertices to find the maxima.
At point A : Z = 15(0) + 10\(\left(\frac{80}{3}\right)\) = \(\frac{800}{3}\)
At point B : Z = 15(10) + 10(20) = 350
At point C: Z = 15(20) + 10(0) = 300
At point O: Z = 15(0) + 10(0) = 0
Thus, the maxima lies at point B having coordinates x = 10 and y =20 and the maximum profit = ₹ 350.
Hence, the manufacturer should makes 10 items of A model and 20 items of B model for maximum profit of ₹ 350.

Question 6.
A dealer in rural area wishes to purchase a number of sewing machines. He has only ₹ 5760 to invest and has space for atmost 20 items for storage. An electronic sewing machine cost ₹ 360 and a manually operated sewing machine ₹ 240. He can sell an electronic sewing machine at a profit of ₹ 22 and a manually operated sewing machine at a profit of ₹ 18. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximise his profit? Make it as an LPP and solve it graphically.
Answer:
Let the dealer purchased x electronic sewing machines and y manually operated sewing machines.
Now, we can construct the following table

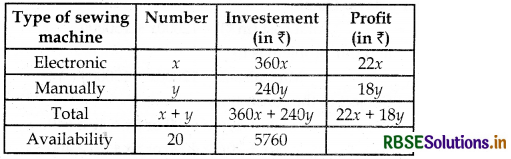
Then, given LPP is
maximise, Z = 22x + 18y ............. (i)
Subject to constraints, x + y ≤ 20
360x + 240y ≤ 5760 or 3x + 2y ≤ 48
x ≥ 0, y ≥ 0
Let us consider the inequalities as equations, we get
x + y = 20 .............. (ii)
3x + 2y = 48 ............ (iii)
and x = 0, y = 0 ........... (iv)
Table for line x + y = 20 is

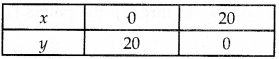
So, it passes through the point (0, 20) and (20, 0).
On putting (0, 0) in the inequality x + y ≤ 20, we get
0 + 0 ≤ 20 ⇒ 0 ≤ 20 [which is true]
So, the half plane is towards the origin.
Table for line 3x + 2y =48 is

So, it passes through the points (0, 24) and (16, 0).
On putting (0, 0) in the inequality 3x + 2y ≤ 48, we get
0 ≤ 48 [which is true]
So, the half plane is towards the origin.
On solving Eqs. (ii) and (iii), we get
x = 8 and y = 12
So, the point of intersection of the lines (ii) and (iii) is (8, 12). Also x ≥ 0 and y ≥ 0, so the feasible region lies in the first quadrant.

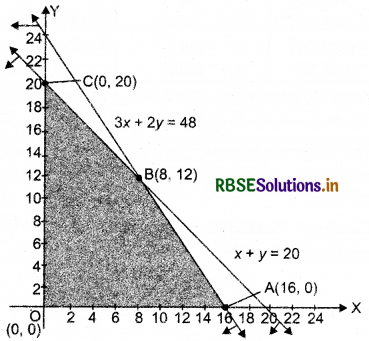
Now, on drawing all the inequalities on a graph paper
and we get the feasible region OABCO, which is hounded.
The comer points of the feasible region are O(0, 0), A(16, 0), B(8, 12) and C(O, 20).
The values of Z at corner points are as follows

Corner Points	Z = 22x + 18y
O(0, 0)	Z = 22(0) + 18(0) = 0
A(16, 0)	Z = 22 × 16 + 0 = 352
B(8, 12)	Z = 22 × 8 + 18 × 12 = 392 (Maximum)
C(0, 20)	Z = 22 × 0 + 18 × 20 = 360

From the table, maximum value of Z = ₹ 392 at point B(8, 12).
Hence, dealer should purchased 8 electronic and 12 manually operated sewing machines to get maximum profit.

Multiple Choice Questions

Question 1.
By graphical method, the solution of the linear programming problem. Maximum z = 3x₁ + 5x₂,
subject to 3x₁ + 2x₂ ≤ 18, x₁ ≤ 4, x₂ ≤ 6, x₁, x₂ ≥ 0 is:
(a) x₁ = 2, x₂ = 0, z = 6
(b) x₁ = 2, x₂ = 6, z = 36
(c) x₁ = 4, x₂ = 3, z = 27
(d) x₁ = 4, x₂ = 6, z = 42
Answer:
(d) x₁ = 4, x₂ = 6, z = 42

Question 2.
Minimize z = \(\sum_{j=1}^n \sum_{i=1}^m\) c_ij x_ij, subject to \(\sum_{j=1}^n\) x_ij ≤ a_i, i = 1, 2, .......... m \(\sum_{i=1}^m\) x_ij = b_j, j = 1, 2, ...... n is a (LPP) with number of constraints
(a) m + n
(b) m - n
(c) mn
(d) \(\frac{m}{n}\)
Answer:
(a) m + n

Question 3.
Shaded region is represented by:

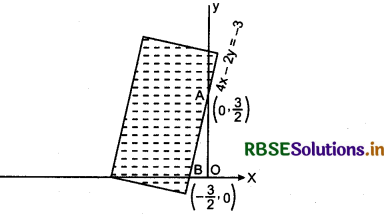
(a) 4x - 2y ≤ 3
(b) 4x - 2y ≤ - 3
(c) 4x - 2y ≥ 3
(d) 4x - 2y ≥ - 3
Answer:
(b) 4x - 2y ≤ - 3

Question 4.
The maximum value of P = x + 3y such that 2x + y ≤ 20, x + 2y ≤ 20, x ≥ 0, y ≥ 1 is:
(a) 10
(b) 60
(c) 30
(d) none of these
Answer:
(c) 30

Question 5.
The constraints - x₁ + x₂ ≤ 1, - x₁ + 3x₂ ≤ 9, x₁, x₂ ≥ 0 defines on:

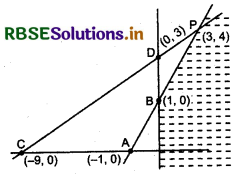
(a) bounded feasible space
(b) unbounded feasible space
(c) both bounded and unbounded feasible space
(d) none of these
Answer:
(b) unbounded feasible space

Question 6.
The maximum value of P = 6x + 8y subject to constraints 2x + y ≤ 30, x + 2y ≤ 24, x ≥ 0, y ≥ 0 is:
(a) 90
(b) 120
(c) 96
(d) 240
Answer:
(b) 120

Fill in the Blanks

Question 1.
The minimum and maximum value of an objective function is called the ........................... value of LPP.
Answer:
optimal

Question 2.
The points that are within and are on the boundary of the feasible region, represent .......................... solution of the constraints.
Answer:
feasible

Question 3.
The linear inequalities or equations on the variables of a linear programming problem are called .........................
Answer:
constraints

Question 4.
The maximum or minimum value of any objective function is always lies on ............................ points of the feasible region.
Answer:
corner

Question 5.
If maximum or minimum exist in two corner points of the feasible region, then it exist on the ............................ joining these two points.
Answer:
line segment

True / False

Question 1.
An optimisation problem may involve finding maximum profits, minimum cost, or minimum use of resources etc.
Answer:
True

Question 2.
Linear programming is a special but a very important class of optimisation problem.
Answer:
True

Question 3.
A linear function Z = ax + by, where a, b are constants, which has to be maximised or minimized is called a linear constraints.
Answer:
False

Question 4.
The region other than feasible region is called an infeasible region.
Answer:
True

Question 5.
Any point outside the feasible region is called feasible solution.
Answer:
False